文/Sobereva@北京科音  2025-Jun-26

原子、分子間的相互作用在化學體系中無處不在。化學體系中的相互作用可以按強度大體分為化學鍵相互作用和弱相互作用，也可以按作用特征大體分為共價和非共價相互作用。這些相互作用普遍在數值層面上進行研究，如研究相互作用能及其物理成份（能量分解）、幾何參數、鍵級、AIM拓撲分析考察鍵臨界點屬性，等等。而如今，這些相互作用的可視化分析（visual analysis）日趨流行，在計算化學研究文章中被應用得越來越普遍、在文獻中越來越常見。這些方法可以令化學家們十分直觀生動地認識相互作用出現的位置、強度、本質，不僅應用十分便利，也對傳統的基于數值的研究相互作用的方式提供了關鍵性的互補。這些方法在近年來還得到了快速發展，涌現了許多新的分析手段。顯然，對這些可視化分析方法進行全面、系統的綜述是極為重要且迫切的。

近期，北京科音自然科學研究中心（http://www.keinsci.com）的盧天應知名的Angew. Chem. Int. Ed.期刊的邀請，發表了名為Visualization Analysis of Covalent and Noncovalent Interactions in Real Space的綜述，可在此訪問：https://onlinelibrary.wiley.com/doi/10.1002/anie.202504895。若未訂閱，也可以免費閱讀此文在ChemRxiv上的預印版https://doi.org/10.26434/chemrxiv-2025-9t442（內容和正式版基本一樣，寫文章時請引用正式版）。

推薦使用Multiwfn程序做文中介紹的各種可視化分析時引用此綜述！

此綜述是到目前為止最完整和系統介紹各種化學體系中相互作用可視化分析方法的文章，面向廣大化學家，特別是計算化學家。文章的寫作注重令內容清晰易懂、深入淺出，且引發廣泛讀者們的興趣。通過此文，化學研究者們可以快速且充分了解各種可視化分析方法的基本思想、適用范疇，并且結合文中提供的豐富的例子，讀者能夠充分體會到它們的重要實用價值。在看過本文有了基本的知識框架后，若想進一步深究物理、算法細節等方面的知識以及了解更多實際應用，推薦再閱讀此綜述中引用的各種方法的原文和相關文章。

此綜述介紹的可視化分析方法十分全面，并且囊括了最新進展。主要介紹了NCI（亦稱RDG）、IRI、IRI-pi、IGM、IGMH、mIGM、aNCI、amIGM、Hirshfeld表面分析、靜電勢分析、范德華勢分析、ELF、LOL、LOL-pi、電子密度拉普拉斯函數、變形密度、價層電子密度。值得一提的是，其中IRI、IRI-pi、IGMH、mIGM、amIGM、范德華勢分析、價層電子密度分析都是此文的作者所提出的。

綜述中還簡要提及了文章作者開發的十分流行的波函數分析程序Multiwfn（主頁：http://www.shanxitv.org/multiwfn），這是唯一可以實現此文介紹的所有方法的程序，有很多方法還是此程序獨家支持的。Multiwfn對于大量相互作用可視化分析方法在計算學領域的普及和推廣起到了關鍵性的作用，此綜述里幾乎所有圖都是基于Multiwfn計算的數據繪制的。Multiwfn的相關信息見《Multiwfn FAQ》（http://www.shanxitv.org/452）和介紹文章J. Chem. Phys., 161, 082503 (2024) DOI: 10.1063/5.0216272。

此外，http://www.shanxitv.org/667介紹的盧天在2024年發表的Visualization Analysis of Weak Interactions in Chemical Systems（Comprehensive Computational Chemistry Vol.2中的一章）和前述的綜述有極為密切的聯系，此文介紹的方法專注于弱相互作用，涉及的方法更少，而由于有明顯更多的篇幅，因而對它們的介紹明顯更深入細致，故和上面的綜述有極大的互補性，強烈建議閱讀！

還十分推薦閱讀以下文章及其中引用的文章獲取更多相關知識以及計算操作細節：
使用Multiwfn做IGMH分析非常清晰直觀地展現化學體系中的相互作用
http://www.shanxitv.org/621（http://bbs.keinsci.com/thread-28147-1-1.html）
使用IRI方法圖形化考察化學體系中的化學鍵和弱相互作用
http://www.shanxitv.org/598（http://bbs.keinsci.com/thread-23457-1-1.html）
使用Multiwfn做Hirshfeld surface分析直觀展現分子晶體和復合物中的相互作用
http://www.shanxitv.org/701（http://bbs.keinsci.com/thread-43178-1-1.html）
談談范德華勢以及在Multiwfn中的計算、分析和繪制
http://www.shanxitv.org/551（http://bbs.keinsci.com/thread-17271-1-1.html）
在Multiwfn中單獨考察pi電子結構特征
http://www.shanxitv.org/432（http://bbs.keinsci.com/thread-10610-1-1.html）
ELF綜述和重要文獻小合集
http://bbs.keinsci.com/thread-2100-1-1.html
靜電勢與平均局部離子化能相關資料合集
http://bbs.keinsci.com/thread-219-1-1.html
使用Multiwfn研究分子動力學中的弱相互作用
http://www.shanxitv.org/186
使用Multiwfn做aNCI分析圖形化考察動態過程中的蛋白-配體間的相互作用
http://www.shanxitv.org/591（http://bbs.keinsci.com/thread-21826-1-1.html）
通過電子定域化函數(ELF)、價層電子密度分析討論親核進攻的方向
http://www.shanxitv.org/606（http://bbs.keinsci.com/thread-23982-1-1.html）
通過價層電子密度分析展現分子電子結構
http://www.whxb.pku.edu.cn/EN/10.3866/PKU.WHXB201709252

此外，筆者的18碳環及相關體系的研究文章中充分利用了文中介紹的許多方法，是很好的應用實例，研究匯總見http://www.shanxitv.org/carbon_ring.html。

量子化學波函數分析與Multiwfn程序培訓班（http://www.keinsci.com/WFN）對前述的綜述中幾乎所有方法都有十分全面、透徹、系統的介紹，并對各種分析方法在Multiwfn中的實際操作做了細致的演示并傳授大量技巧，信息量遠比綜述里的大得多得多，因而很推薦對這些分析方法感興趣者關注和參加。

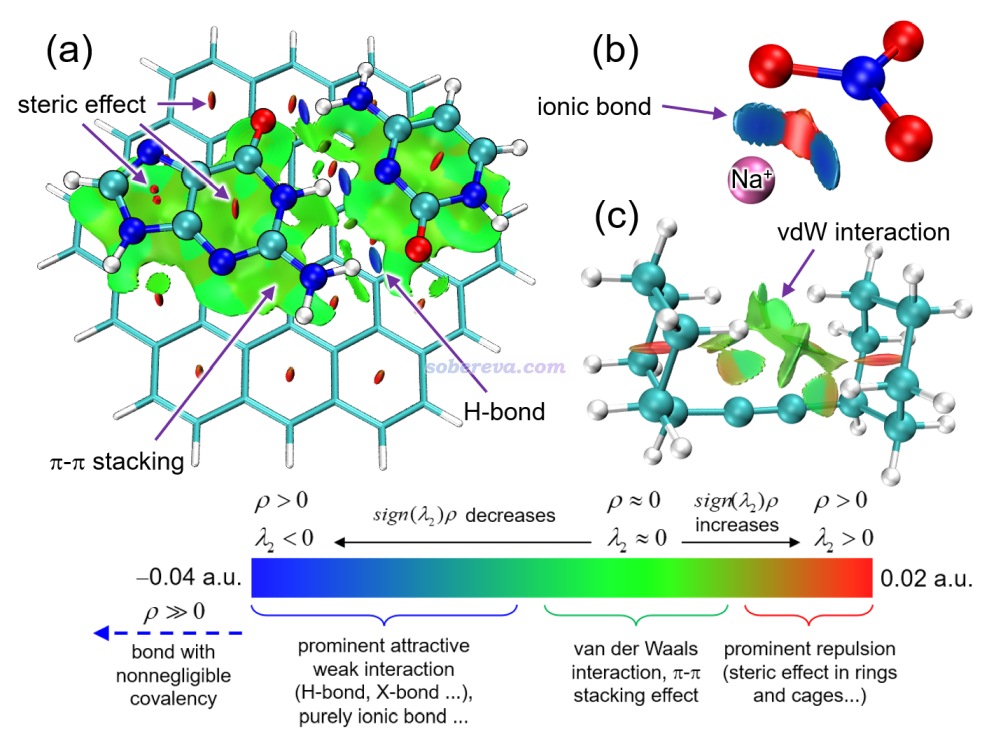
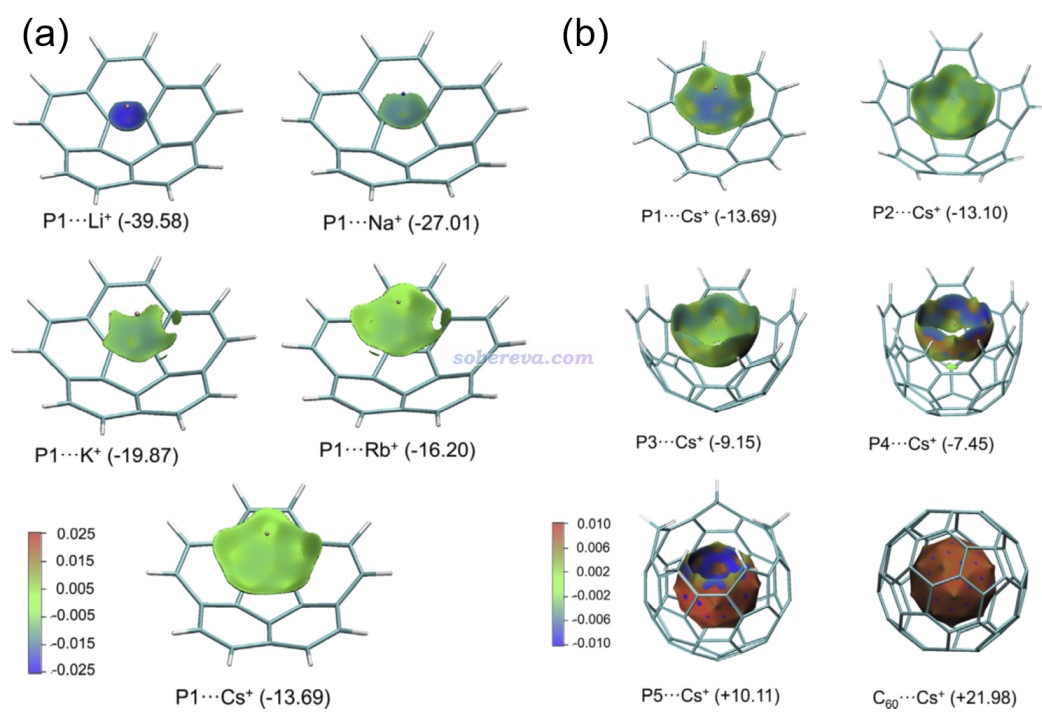
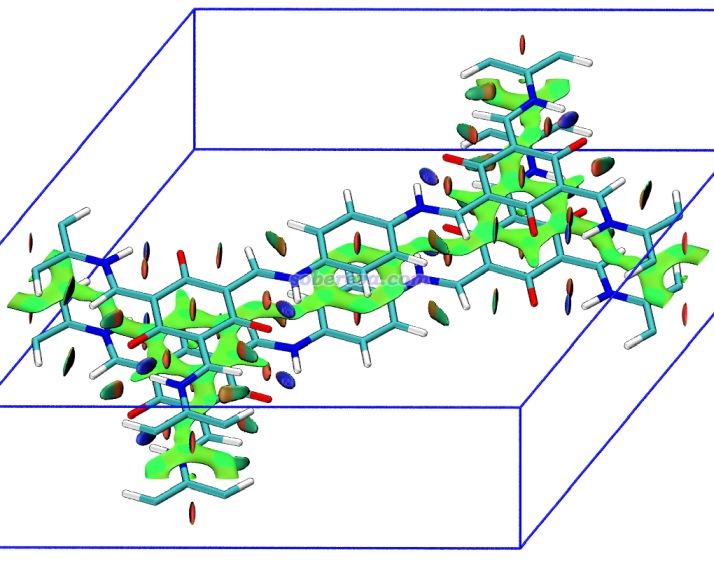
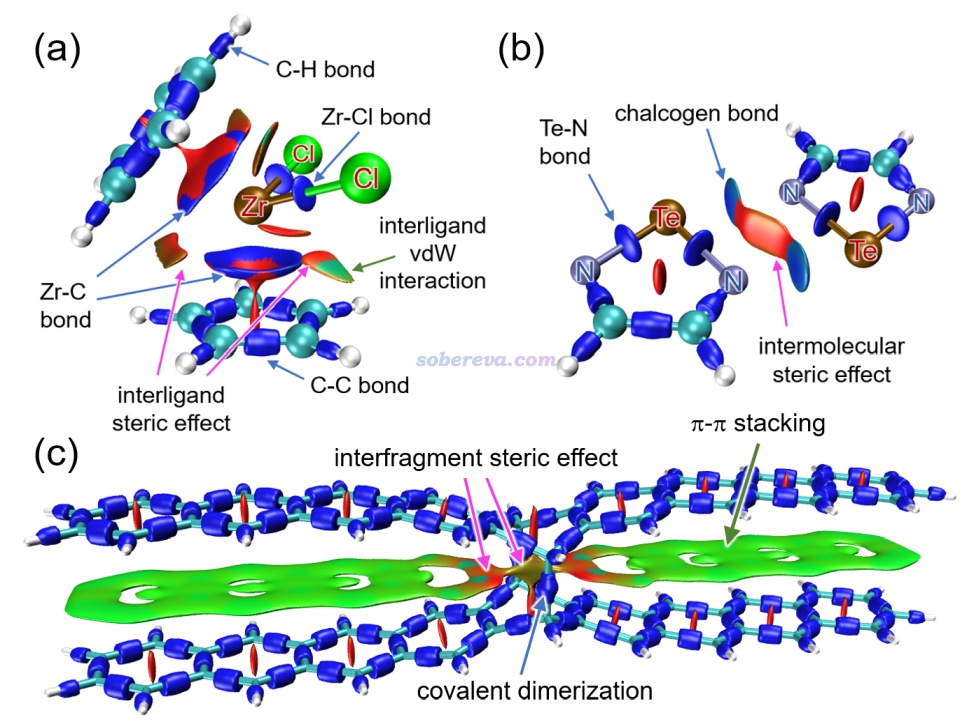
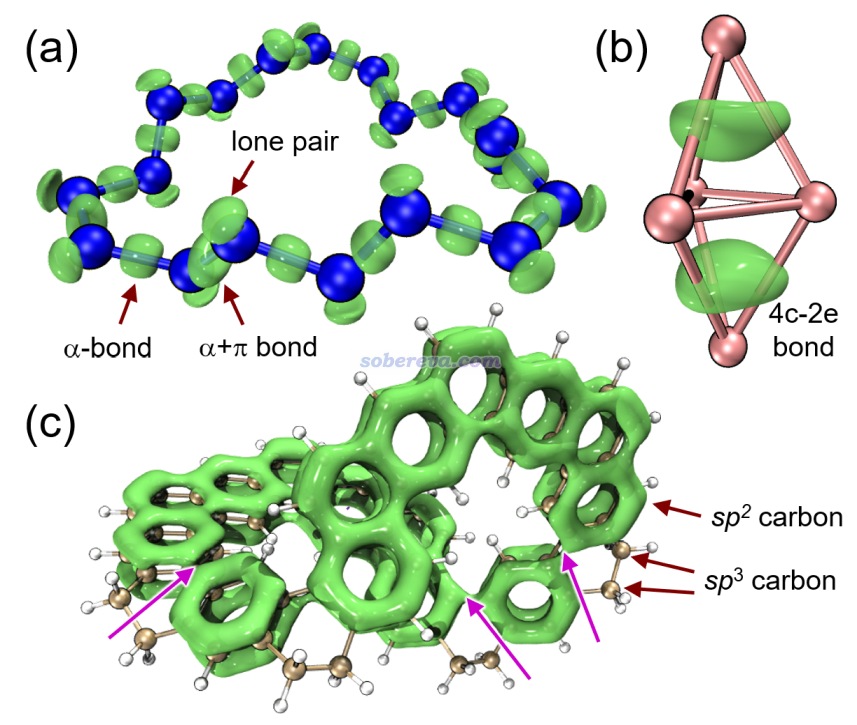
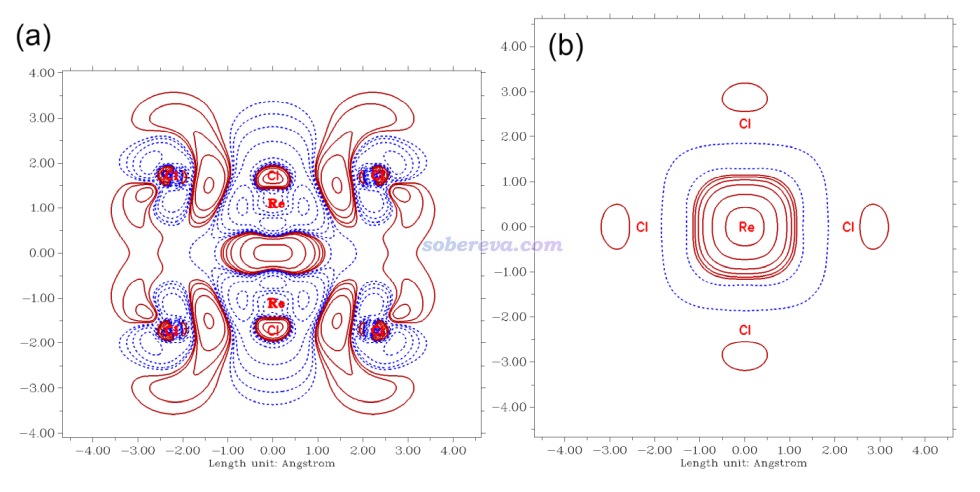
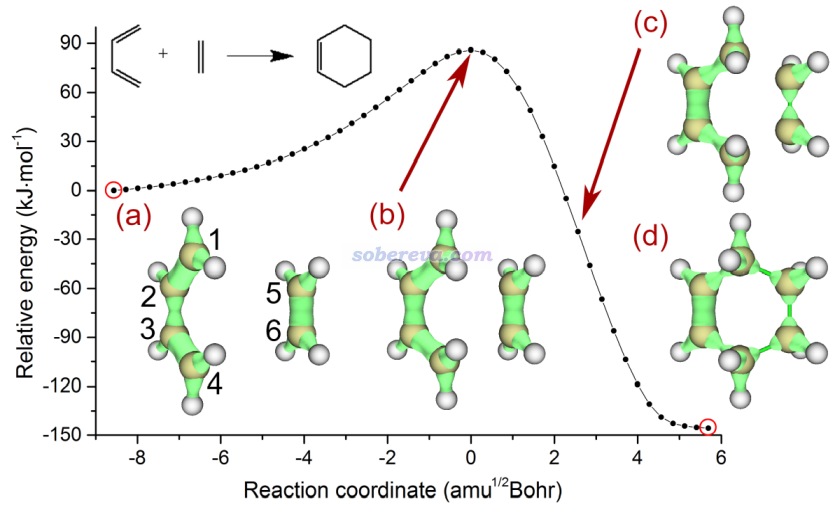
下面是Visualization Analysis of Covalent and Noncovalent Interactions in Real Space綜述中的圖，供預覽。

文/Sobereva@北京科音   2025-Jun-11

0 前言

NICS和磁感生電流是非常常用的磁響應性質一類的考察芳香性的方法，在《衡量芳香性的方法以及在Multiwfn中的計算》（http://www.shanxitv.org/176）里有簡要介紹并里面附了大量我寫過的相關博文，而在“量子化學波函數分析與Multiwfn程序培訓班”（http://www.keinsci.com/WFN）的“芳香性與離域性分析”一節里有極為全面深入的介紹。很多人對這兩個方法在衡量芳香性方面的認識局限在：
(1)NICS(1)ZZ約為0說明環是非芳香性，明顯為負說明環是芳香性且越負芳香性越強，明顯為正說明環是反芳香性且越正反芳香性越強。注意NICS的形式很多，這里僅以最常用的NICS(1)ZZ舉例
(2)感生電流的方向如果滿足左手定則（diatropic電流），電流越大芳香性越強；如果與左手定則方向相反（paratropic電流），電流越大反芳香性越強。電流大小一般通過對鍵截面上的電流密度做積分來衡量，稱為bond current strength (BCS)
但實際上，僅光憑以上知識討論芳香性或反芳香性，在一些情況下會得到不正確甚至嚴重錯誤的結論。在本文筆者介紹一些大多數人都普遍沒有注意到的用NICS和感生電流討論芳香性方面的重要問題。把這些問題都徹底搞清楚了，基于磁屬性研究芳香性時就不懼審稿人comment了。

本文中的計算用的幾何結構，若無專門提及，皆是B3LYP/6-31G*下優化的無虛頻結構。

1 NICS、感生電流與HOMO-LUMO gap的關系

感生電流和NICS計算公式都涉及到對占據軌道和空軌道的循環，并且空軌道與占據軌道能量之差出現在分母項中，這一點看《深入理解分子軌道對磁感生電流的貢獻》（http://www.shanxitv.org/703）里的公式1、2、3便知。總的來說，HOMO-LUMO gap越大，空軌道與占據軌道整體能量差越大，導致NICS和感生電流越接近0。因此，如果兩個體系的gap相差較大，不應直接憑NICS或BCS判斷二者的芳香性強弱，還應該把gap差異對結果的影響考慮進去。在《深度揭示互為等電子體的苯、無機苯和carborazine的芳香性的顯著差異》（http://www.shanxitv.org/731）里介紹的筆者的Chem. Eur. J., 30, e202403369 (2024)一文中就注意到了這一點，文中研究的carborazine的HOMO-LUMO gap（7.30 eV）明顯小于苯（11.20 eV）和無機苯（12.18 eV），因此文中提到：It is noteworthy that the aromaticity of carborazine compared to benzene and borazine is more or less quantitatively overestimated by the value of BCS and NICS。

4n電子的Huckel反芳香性體系的HOMO-LUMO gap比4n+2的Huckel芳香性體系的整體更小，Chem. Soc. Rev., 44, 6597 (2015)認為這是前者的BCS比后者更大的原因。例如反芳香性的環丁二烯和芳香性的苯在B3LYP/6-31G*級別算的HOMO-LUMO gap分別為3.692和6.800 eV，使用《使用SYSMOIC程序繪制磁感生電流圖和計算鍵電流強度》（http://www.shanxitv.org/702）介紹的SYSMOIC算出來的環丁二烯的BCS為-0.7941（長C-C鍵）和-0.7499 a.u.（短C-C鍵），而苯的C-C鍵的BCS大小則小得多，只有0.4216 a.u.。

如《正確地認識分子的能隙(gap)、HOMO和LUMO》（http://www.shanxitv.org/543）所說，HF成份越低的泛函算出來的HOMO-LUMO gap越低，因此若發現HF成份低的泛函算出來的NICS和BCS的絕對值較大，大概率也是上述原因（但并非HF成份越低的泛函算出來的總是越大，因為泛函的差異還影響到其它方面）。

2 NICS的環尺寸的依賴性

原理上，感生電流比NICS判斷芳香性更合理，因為NICS對環尺寸有依賴性。雖然有的文章說NICS的環尺寸依賴性弱，但那往往只是對較小的環之間對比做的結論，再加上本身不同體系的芳香性就有所不同，令那種說法更不確切。

電流對特定位置產生的磁場可以用Biot–Savart方程得到。如果是環形電流，則在環中心產生的磁場為μ0*I/(2*R)，其中μ0是真空磁導率，I是電流大小，R是環的半徑，更多信息見https://en.wikipedia.org/wiki/Biot%E2%80%93Savart_law。因此，對芳香性的情況，當感生電流相同時，對應芳香性的環形路徑整體半徑越大、原子距離環中心整體越遠，在環中心產生的磁屏蔽效果就越弱、NICS的絕對值越小。如果認為感生電流I的大小是芳香性強弱的準確體現，那么顯然用NICS對比環尺寸明顯不同的體系的芳香性的大小就是不甚嚴格的，因為對越大的環會越低估芳香性。所以，如果要基于磁屬性對比明顯不同大小的環的芳香性，建議用感生電流而非NICS說事。對于反芳香性，也有和上面完全類似的情況。

3 感生電流對積分截面的依賴性

對應芳香性的環上，如果只考慮對芳香性有貢獻的電子的感生電流，原理上來說在垂直于鍵（更確切來說是垂直于電流方向）的各個截面上積分電流密度得到的BCS都應該是相同的。但實際得到的BCS沒有這么理想化，環上的各個鍵的BCS往往不完全相同，在于：
(1)積分的數值誤差、有限的積分截面尺寸
(2)積分截面可能并不嚴格垂直于電流方向
(3)在一些鍵上存在方向彼此相反的感生電流的抵消作用，此效應對于多環芳烴等并環的情況尤為明顯
(4)環周圍的原子的感生電流產生的干擾，以及環上原子的定域化的電子（內核電子、sigma電子、孤對電子等）產生的局部感生電流添亂，這導致計算的BCS對鍵上的積分截面位置的選取可能存在不可忽視的依賴性
(5)基組不夠完備，導致感生電流計算不夠準確。對D2h點群的環丁二烯（反芳香性）極小點結構，用SYSMOIC在B3LYP/6-31G*下計算的短和長C-C鍵的BCS分別為0.7499和0.7941 a.u.，而基組用完備得多的def2-QZVP計算結果分別為0.7116和0.7111 a.u.，可見后者明顯更等價

若發現要考察芳香性的環上的各個鍵的BCS不等價性不可忽視，可以取感生電流較明確、被上述的(4)干擾小的鍵的BCS作為環電流值衡量芳香性，或者對環上的鍵的BCS取平均作為環電流值（適合碳環、環丁二烯等情況）。此外，也可以嘗試計算BCS時只考慮對芳香性有貢獻的電子所占據的分子軌道，例如用感生電流研究pi芳香性時就只考慮pi軌道。

4 感生電流判斷芳香性和反芳香性方面相對于NICS的優勢

NICS很有可能給出關于芳香性錯誤的結論，不如觀看和積分感生電流，以及觀看《通過Multiwfn繪制等化學屏蔽表面(ICSS)研究芳香性》（http://www.shanxitv.org/216）里介紹的ICSS圖來得靠譜，這一節給出幾個例子。

JCTC, 6, 1131 (2010)發現NICS用于考察氟化氫三聚體(HF)3的芳香性有問題。在wB97XD/def-TZVP下優化出的此體系的結構如下所示。憑基本常識就知道這個體系是非芳香性的，但是B3LYP/def2-TZVP算出來的NICS(0)ZZ為13.52 ppm，仿佛有顯著反芳香性似的。不過NICS(1)ZZ為-0.04 ppm，這倒是正確體現出此體系并沒有反芳香性。

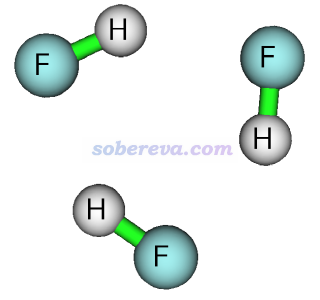
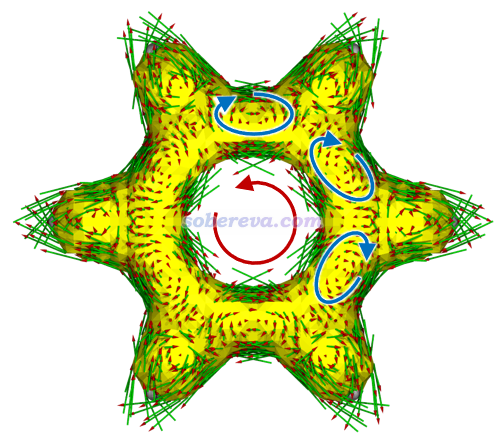
為什么(HF)3的NICS(0)ZZ那么正？這可以從此體系所在平面上的感生電流圖上理解，如下圖所示（磁場垂直于屏幕向外）。可見此體系并沒有形成環繞整體的感生電流，但由于存在環繞各個HF的sigma鍵的dia電流，導致在環中央區域呈現出等效的para電流的特征（紅色箭頭所示），使得環中央是去屏蔽的，因而NICS(0)ZZ為正。而由于這種效應在垂直于體系平面方向上衰減很快，因此NICS(1)ZZ幾乎為0。這也體現出，對于小環體系，由于sigma鍵的感生電流產生的磁場離環中心太近，NICS(0)ZZ用來衡量芳香性是極差的做法。但對于18碳環及其等電子體B6N6C6這樣的大環倒不是什么問題，因為局域的電子對應的局部的感生電流造成的磁場在環中心處都基本衰減沒了，這也是為什么《18碳環等電子體B6N6C6獨特的芳香性：揭示碳原子橋聯硼-氮對電子離域的關鍵影響》（http://www.shanxitv.org/696）介紹的文章中用了NICS(0)ZZ討論。

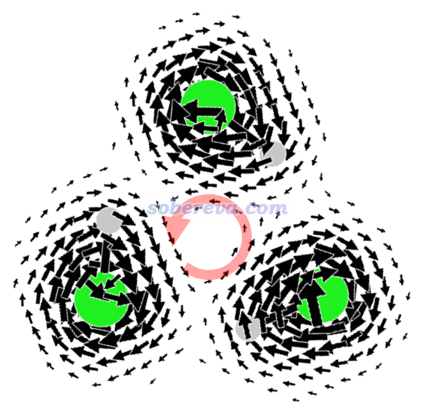
實際上對于苯分子也有類似情況。下圖是苯分子的pi以外的電子產生的感生電流圖，可見由于局域的sigma電子產生的局部dia電流的存在，在環中心也有等效的para電流（紅色箭頭所示）并使得環中心產生磁去屏蔽效應。不過由于苯的pi電子造成的全局的dia電流在環中心產生的磁屏蔽效應遠強于para電流的磁去屏蔽效應，因此苯的NICS(0)ZZ還是負值。

我極其推薦閱讀《使用Multiwfn繪制一維NICS曲線并通過積分衡量芳香性》（http://www.shanxitv.org/681）中的討論，了解sigma和pi電子對NICS_ZZ的貢獻在垂直于環方向上的變化特征。

《18個氮原子組成的環狀分子長什么樣？一篇文章全面揭示18氮環的特征！》（http://www.shanxitv.org/725）里介紹的我的ChemPhysChem, 25, e202400377 (2024)文章中，對18氮環的最穩定構型計算了NICS(0)ZZ，為3.42 ppm，也是表面上體現出了輕微的反芳香性。然而通過ICSS等值面圖和AICD感生電流圖，都充分確認了此體系沒有芳香性或反芳香性特征，詳見博文里的圖。這也是個很好地體現NICS(0)ZZ展現（反）芳香性不靠譜的例子。

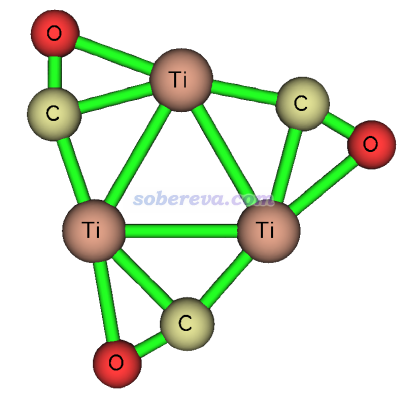
NICS亦有可能把非芳香性體系誤判成芳香性的。Theor. Chem. Acc., 134, 8 (2015)指出NICS衡量很多過渡金屬團簇的芳香性也是不合理的。其中一個例子是如下所示的Ti3(CO)3。基于PCCP, 13, 4576 (2011)的SI里給出的BP86/6-311+G(d)級別下優化的結構，我用PBE0/def2-TZVP算出的NICS(0)ZZ和NICS(1)ZZ分別是-141.1和-11.7 ppm，乍看起來明顯芳香性。

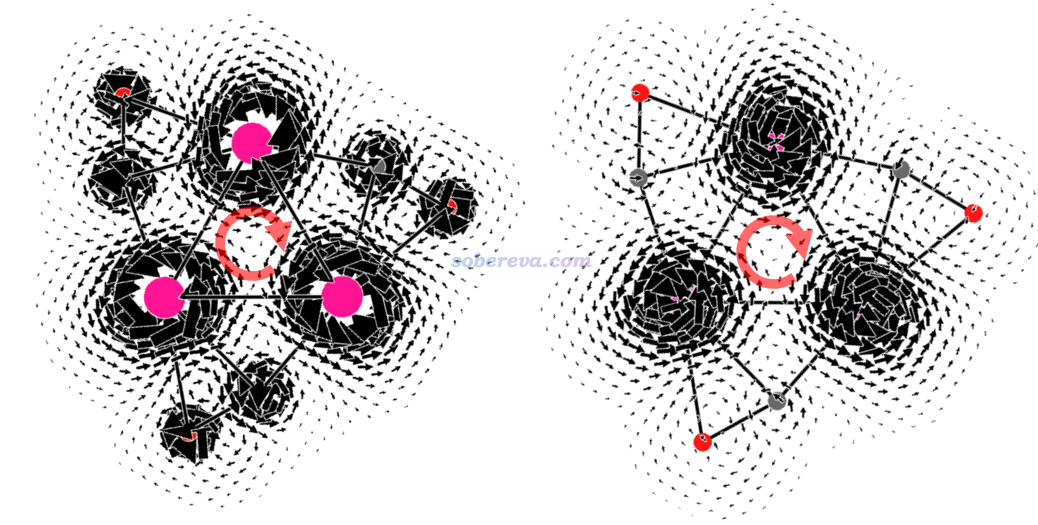
下圖左側和右側分別是Ti3(CO)3的分子平面上和分子平面上方1埃處的感生電流，數值過大的部分截掉了，粉色大圓球是Ti，磁場垂直屏幕向外。由圖可見，無論是在分子平面上還是在其上方1埃處，都有顯著的環繞Ti原子的para電流，很大程度等效帶來了在環中心及其上方的dia電流的效果（紅色箭頭所示），即令環中心及其上方一定區域都是磁屏蔽的，這是NICS(0)ZZ和NICS(1)ZZ都為負值的原因。然而從圖上并沒有看到環繞整體的連貫的感生電流，因此Ti3(CO)3就是非芳香性的。可見此例不僅NICS(0)ZZ，連NICS(1)ZZ都誤判了芳香性。

5 顯著且連貫的dia感生電流未必能證明有明顯的芳香性

從上一節看到，感生電流判斷芳香性比個別位置的NICS更為嚴格且直觀，但即便是感生電流，也未必總能正確衡量芳香性，這里以[N6H6]2+體系為例進行說明，更多討論見ChemistrySelect, 2, 863 (2017)。下圖展示了此體系的平面構型

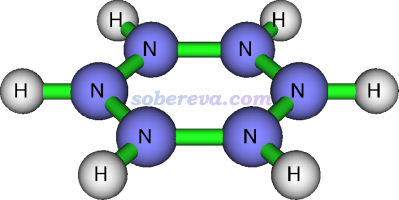
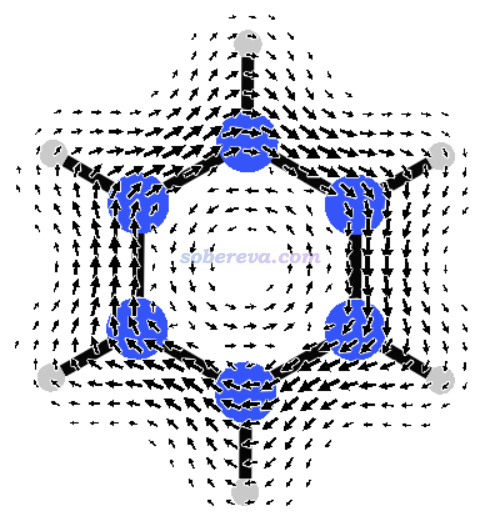
此構型并不是極小點，而是有很多破壞平面的虛頻，并且其能量甚至比其開環后的線型結構的還要高，因此明顯沒有芳香穩定化作用。用Multiwfn計算出它的多中心鍵級幾乎為0（0.00035），也進一步體現出沒有pi共軛。如果用《在Multiwfn中單獨考察pi電子結構特征》（http://www.shanxitv.org/432）的做法繪制它的LOL-pi圖，也會看到各個氮都有定域的孤對電子，根本沒有像苯的pi電子一樣在環上充分離域。然而，下圖所示的[N6H6]2+平面構型的分子上方1埃處的感生電流（磁場垂直于屏幕向外）則是完全順時針的dia電流，和具有顯著芳香性的苯的情況看起來完全一樣！

為什么[N6H6]2+的平面構型不是極小點？這是因為如下圖的軌道占據情況所示，盡管此體系表面上有10個pi電子，看似滿足Huckel的4n+2芳香性規則因而芳香性會使此構型被穩定化，但e2u對稱性的軌道的反pi特征顯著（對于苯來說是沒有占據的），因此pi共軛作用很弱，再加上如此眾多的孤對電子間的強烈互斥作用，顯然令其極不穩定。

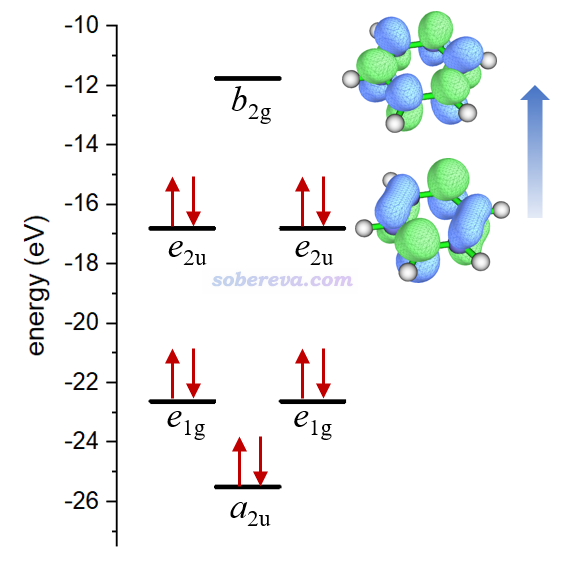
為什么[N6H6]2+的平面構型像普通芳香性體系一樣有顯著的貫穿整個環的dia電流？這需要利用《深入理解分子軌道對磁感生電流的貢獻》（http://www.shanxitv.org/703）里介紹的知識，沒看過者強烈建議認真閱讀。此文說了，感生電流可視為由各種占據軌道向各種空軌道躍遷所貢獻，上圖藍色箭頭標注的躍遷是此結構下對感生電流貢獻最大的躍遷（因為這種躍遷能最小），其中非占據的b2g軌道比占據的e2u軌道軌道多一個節面，這種躍遷是平動允許的，因此對dia電流有貢獻。這和造成苯分子的dia電流的機制是完全相同的，只不過苯分子的dia電流主要是e1g到e2u躍遷所貢獻的。

由此例可見，光靠是否存在全局的dia感生電流判斷芳香性并不總是可靠！因為這種電流是否存在，和體系是否真的有芳香性特征并沒有內在的必然聯系，而與它關系真正最直接、最緊密的是軌道的對稱性特征！

可能大多數人覺得，有芳香性的體系有滿足左手定則的dia電流的原因在于：某個環有芳香性意味著環上有明顯離域的電子，因此在外磁場的作用下會像經典電磁學描述的導體一樣在環上產生dia電流。但實際上真正本質并非如此，不能忽視關鍵性的量子力學效應！一般的芳香性體系有dia電流實際上是一個表象，在于它們的軌道對稱特征和躍遷正好能滿足產生顯著dia電流的條件，而能產生顯著dia電流的并非只有芳香性體系。因此，要這樣認為：有顯著的貫穿整個環的dia電流是這個環具有芳香性的必要非充分條件。

由于磁屏蔽特征是感生電流的進一步衍生屬性，[N6H6]2+的平面構型既然都和苯一樣具有相同感生電流特征了，其自然NICS(0)ZZ和NICS(1)ZZ也都為負，分別為-178.1和-24.6 ppm。

此例彰顯出判斷芳香性最好不要光基于磁屬性，即便這種判斷芳香性的做法極為流行。同時結合多中心鍵級等基于電子結構的方法，以及結合芳香穩定化能或離域化能這種能量層面的方法，結論會更可靠、更有說服力。本節的[N6H6]2+的例子也體現出，形式上滿足4n+2規則的體系未必真的有芳香性，若電子都沒法在環上充分離域、不構成共軛體系，滿足4n+2也仍是非芳香性的。

6 顯著且連貫的para感生電流未必能證明有明顯的反芳香性

J. Org. Chem., 88, 14831 (2023)通過一系列分子指出，即便環上存在顯著且連貫的para電流，也未必能可靠地證明這個環就有明顯的反芳香性。這一節就用其中最簡單的體系，苯+1電荷的陽離子自由基（具有5個pi電子）和-1電荷的陰離子自由基（具有7個pi電子）來說明這一點，這種體系的（反）芳香性沒法基于經典的Huckel規則判斷。

如下所示，JOC文中給出了苯陽離子、中性苯、苯陰離子的分子平面上方1 Bohr處的感生電流，磁場垂直于屏幕向外，計算用的是對各自狀態優化的幾何結構，電場強度越大箭頭越藍、越小越紅。可見，苯陽離子和苯陰離子在碳環上方的電流都是逆時針的para電流，與中性苯的情況相反，乍看起來苯的陰、陽離子都是顯著反芳香性的。

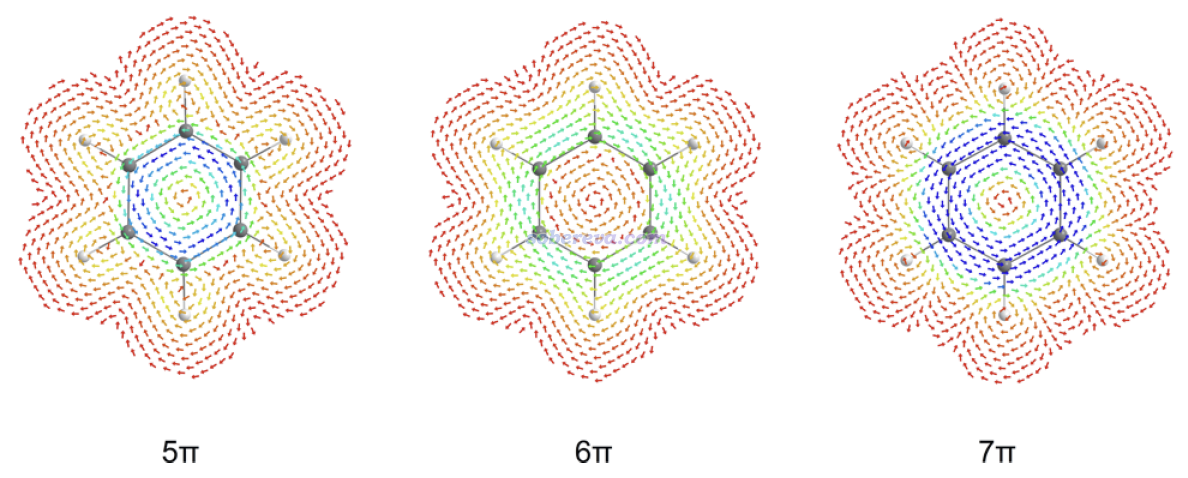
然而，JOC這篇文章計算了苯的陰、陽離子的芳香穩定化能（用到的反應見文章的SI），發現這兩個體系是有芳香穩定化作用的，因此從能量角度來說是有芳香性的。我還通過Multiwfn在文中給的苯離子的極小點結構下在B3LYP/6-31G*級別計算了六中心鍵級，苯的陽離子和陰離子的結果分別為0.044和0.045，只有中性苯的0.086的約一半。具體來說，苯陽離子和陰離子的六中心鍵級分別幾乎來自于alpha和beta電子的貢獻（且和中性苯的相應自旋電子的貢獻差不多），而另一個自旋幾乎沒貢獻。也就是說，相對于苯，離子狀態下電子數改變1的那個自旋的電子對芳香性沒明顯貢獻，而電子數未變的自旋的電子對芳香性的貢獻基本保持不變。

由于從能量和電子結構角度都確認了苯的陰、陽離子是芳香性的，那么為什么它們的感生電流是para的，顯得像普通反芳香性體系一樣？JOC文中給了下面的圖對感生電流進行了解釋。由于Jahn-Teller效應，陽離子（5π）和陰離子（7π）體系的對應于苯的二重簡并的pi軌道發生了輕微分裂。圖中藍色大箭頭標注了對感生電流產生主導的躍遷。對苯離子體系的情況，由于能級分裂造成的能量差較小，明顯小于1→2的躍遷，因此對陽離子和陰離子分別是1→1和2→2躍遷對感生電流產生了主導性的貢獻。由于這種躍遷涉及的兩個軌道的節面數相同，是轉動允許的，因此如《深入理解分子軌道對磁感生電流的貢獻》所述，貢獻的是para電流。

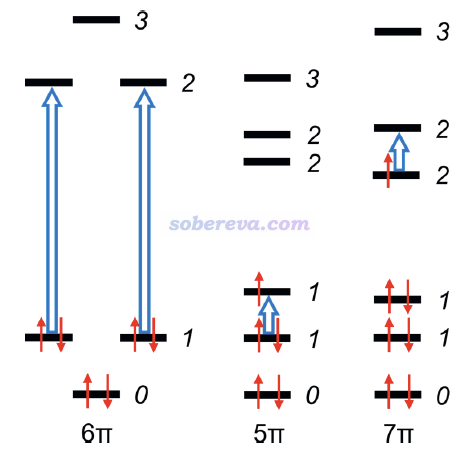
由本節和上一節的例子可見，雖然感生電流對大多數體系判斷芳香性是合理的，而且比起只看個別位置的NICS_ZZ可靠不少，但在極個別體系上還是能暴露出其局限性。因此若有可能，除了基于磁屬性分析外，還是建議再結合一兩種靠譜的手段，特別是可靠又容易計算的多中心鍵級，來衡量芳香性，減少誤判芳香性、被審稿人懟的可能（本來芳香性這方面的“說法”和“觀點”就相當多）。

但也沒必要盲目用過多的方法衡量芳香性，否則一方面太冗余，另一方面本身有的芳香性指標就不那么靠譜、普適，納入討論反倒無益于揭示芳香性的真相。有文章認為鍵的均衡化、出現dia和para的感生電流，屬于芳香性的二階（次級）特征，而能量的穩定化和電子的離域，才算是芳香性的一階（即最關乎本質的）特征，這個觀點我是認可的。

文/Sobereva@北京科音  2025-Apr-5

1 前言

Dalton這個量子化學程序雖然用起來復雜，但有很多獨特的亮點，例如可以在SOPPA(CCSD)和CASSCF級別下計算各種磁屬性（筆者最近在Chem. Eur. J., e202404138 (2025)文中就用Dalton在CASSCF下算了NICS），可以用響應方式較準確地計算磷光壽命，可以算雙光子吸收（北京科音高級量子化學培訓班http://www.keinsci.com/KAQC里專門有一節講了)，可以用高級別耦合簇方法算激發態（見《使用Dalton通過CC3方法極高精度計算激發態》http://www.shanxitv.org/463），等等。可惜Dalton的SCF收斂方面做得一般，比不上Gaussian，而且單靠Dalton無法產生一些重要的軌道，比如UHF計算產生的UNO軌道經常被用于CASSCF的初猜，但Dalton甚至連UHF都做不了，因為Dalton里開殼層只支持RO形式。

為解決以上問題，從2025-Apr-5更新的Multiwfn開始，Multiwfn產生Dalton輸入文件的功能支持了將Multiwfn中當前的軌道波函數寫入到Dalton的輸入文件.dal里作為初猜波函數。因此借助Multiwfn，Dalton用戶可以用Gaussian、ORCA、GAMESS-US等諸多主流的量子化學程序產生的波函數當初猜，從而解決Dalton遇到SCF不收斂的問題。而且，Dalton用戶還可以直接用Multiwfn產生的UNO、定域化分子軌道（LMO，見http://www.shanxitv.org/380）等當CASSCF初猜。

下面就通過例子簡單演示一下具體實現方法，本文中涉及的文件都可以在http://www.shanxitv.org/attach/740/file.zip下載。Multiwfn可以在http://www.shanxitv.org/multiwfn免費下載，相關常識看《Multiwfn FAQ》（http://www.shanxitv.org/452）。如果讀者還不知道Dalton怎么安裝、運行、產生輸入文件的話，看《量子化學程序Dalton的編譯方法和運行方式簡介》（http://www.shanxitv.org/463）。本文用的Multiwfn是2025-Apr-5更新的版本，Gaussian是G16 B.01，Dalton是2022版。

如果本文介紹的Multiwfn的功能給你的研究帶來了幫助，請在論文中引用Multiwfn剛啟動時提示的Multiwfn程序的原文，這是對Multiwfn開發和維護最好的支持！

2 把Gaussian收斂的HF波函數當Dalton做CCSD(T)的初猜

這一節以CH3NH2為例演示把Gaussian收斂的HF/cc-pVTZ波函數當Dalton做CCSD(T)/cc-pVTZ的初猜。首先用Gaussian做一個普通的單點計算，輸入文件是本文文件包里的CH3NH2.gjf，內容如下所示。算完后把得到的CH3NH2.chk用formchk轉成CH3NH2.fch。

%chk=D:\CH3NH2.chk
# HF/cc-pVTZ int=NoBasisTransform
[空行]
test
[空行]
0 1
 C                  0.05159500    0.70381800    0.00000000
 H                  0.59439800    1.06209400    0.88166000
 H                  0.59439800    1.06209400   -0.88166000
 H                 -0.94293100    1.18451300    0.00000000
 N                  0.05159500   -0.76078400    0.00000000
 H                 -0.45830300   -1.10306000    0.81258800
 H                 -0.45830300   -1.10306000   -0.81258800
[空行]
[空行]

之后啟動Multiwfn，載入CH3NH2.fch，依次輸入
100  //其它功能（Part 1）
2  //產生輸入文件
19  //產生Dalton輸入文件
CCSDpT.dal  //要產生的輸入文件名
[回車]  //要產生的.mol文件名用默認的CH3NH2.mol
y  //由于當前內存里有基函數信息，Multiwfn問你是否把軌道展開系數寫入到.dal文件里
1  //使用Dalton標準格式（4F18.14）方式寫入。即四個值換一行，每個值占18列、小數位數14個

此時當前目錄下就有了CCSDpT.dal和CH3NH2.mol。把CH3NH2.mol里的基組名都替換為cc-pVTZ_emsl。目前CCSDpT.dal里的計算設置對應B3LYP算單點，自行把關鍵詞改為CCSD(T)計算用的，此時CCSDpT.dal的內容如下
**DALTON INPUT
.RUN WAVE FUNCTIONS
**WAVE FUNCTIONS
.CC
*CC INPUT
.CC(T)
*ORBITAL
.MOSTART     //代表從**MOLORB部分讀取軌道展開系數作為初猜
 FORM18
**MOLORB (Punched by Multiwfn)
 -0.00001750284370  0.00060444251600  0.00013849165900 -0.00001024308040
  0.00002442752580 -0.00001726827680 -0.00014237439200  0.00004058047020
...略
**END OF INPUT

用Dalton進行計算，可以看到SCF一輪就收斂了，達到了我們的目的：
@ *** DIIS converged in   1 iterations !
@     Converged SCF energy, gradient:    -95.252488149534    1.44D-07
    - total time used in SIRFCK :              0.00 seconds
之后CCSD(T)計算也順利跑完了。

一些注意事項和相關信息：
? 對于廣義或部分廣義收縮基組，都應當用int=NoBasisTransform關鍵詞，拿不準就始終帶上。詳見《將Gaussian等程序收斂的波函數作為ORCA的初猜波函數的方法》（http://www.shanxitv.org/517）里對此關鍵詞的解釋。
? 把Gaussian的cc-pVDZ、cc-pVTZ的波函數當Dalton的初猜時，Dalton要用cc-pVDZ_emsl、cc-pVTZ_emsl基組，而不要用不帶_emsl后綴的，否則還是需要迭代很多次才能收斂（甚至可能不收斂），但帶不帶_emsl的版本收斂后的結果是相同的。而如果是def、def2系列基組，沒什么特別要注意的，比如Gaussian里def-TZVP和def2-TZVP做的計算，在Dalton里基組名分別寫成Turbomole-TZVP、def2_tzvp即可，注意對大小寫有要求，必須對應Dalton目錄下的basis子目錄里的基組文件名。
? Dalton默認是基于球諧型基函數做的計算，因此如果在Gaussian里使用的是比如6-31G*等D殼層默認是笛卡爾型基函數的基組，應當寫上5d關鍵詞強行要求用球諧型，詳見《談談5d、6d型d殼層基函數與它們在Gaussian中的標識》（http://www.shanxitv.org/51）。雖然Dalton也可以用笛卡爾型基函數，但Multiwfn往Dalton輸入文件里寫入初猜軌道系數的功能不支持此情況。
? 只要一個量子化學程序能輸出Multiwfn可以識別的帶有基函數信息的波函數文件，并且用的是球諧型基函數，則波函數都可以通過以上方式作為Dalton的初猜。支持的文件詳見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379）。例如ORCA做計算產生的molden文件也可以載入Multiwfn后像上面那樣產生帶初猜波函數的Dalton輸入文件。

3 把Gaussian收斂的DFT波函數當Dalton做DFT的初猜

此例以順鉑體系為例，把Gaussian收斂的PBE0波函數當Dalton做PBE0計算的初猜，對Pt用Stuttgart小核贗勢，對配體用6-311G*。Gaussian輸入文件如下（本文文件包里的Ptcoord.gjf）：

%chk=D:\Ptcoord.chk
#P PBE1PBE/genecp int=NoBasisTransform
[空行]
b3lyp/def2TZVP opted    //眾所周知這是純給自己看的標題行，別問為什么寫成這個
[空行]
0 1
[坐標略...]
[空行]
N H Cl
6-311G*
****
Pt
SDD
****
[空行]
Pt
SDD
[空行]
[空行]

按照和上一節例子相同的過程，把chk轉成fch，再用Multiwfn產生.dal和.mol文件。.dal里的泛函名改成PBE0，然后設置.mol里的基組和贗勢成為下面這樣，當前對Pt用的贗勢和贗勢基組和Gaussian里的情況一樣（若不確定的話，可以Gaussian里用gfinput關鍵詞輸出定義，并和Dalton的基組、贗勢目錄下的相應文件對照）。

ATOMBASIS
test molecule
Generated by Multiwfn
Atomtypes=4 Angstrom Nosymmetry charge=0
Charge=1.0 Atoms=6 Basis=6-311G*
H1   -0.82596600    1.64390200    2.14978600
H2    0.00000000    2.40772900    0.93575300
H3    0.82596600    1.64390200    2.14978600
H4   -0.82596600   -1.64390200    2.14978600
H5   -0.00000000   -2.40772900    0.93575300
H6    0.82596600   -1.64390200    2.14978600
Charge=7.0 Atoms=2 Basis=6-311G*
N1    0.00000000    1.59755500    1.56108400
N2   -0.00000000   -1.59755500    1.56108400
Charge=17.0 Atoms=2 Basis=6-311G*
Cl1    0.00000000    1.70827400   -1.36819100
Cl2   -0.00000000   -1.70827400   -1.36819100
Charge=78.0 Atoms=1 Basis=stuttgart_rsc_1997_ecp ECP=stuttgart_rsc_1997_ecp
Pt1   -0.00000000   -0.00000000    0.18195700

用Dalton計算后，經過4輪SCF就輕易收斂了，結果為-1152.597056，和Gaussian給出的-1152.596983非常接近。而如果此例Gaussian和Dalton都用HF的話，會和上例一樣，結果精確相同且SCF一輪可收斂。

4 把UNO軌道當Dalton做CASSCF的初猜

之前在《CASSCF計算雙自由基以及雙自由基特征的計算》（http://www.shanxitv.org/264）里示例過用Gaussian基于UNO初猜軌道做CASSCF(2,2)計算的方法，不了解這種計算和UNO概念的話建議先看看。這一節演示使用Gaussian產生UHF波函數，讀入Multiwfn并產生UNO軌道，然后寫入.dal文件用于Dalton做CASSCF(2,2)計算的初猜軌道的流程。示例體系還是264號博文里的C4H8雙自由基，基組還是此文里的6-31G*。

首先用以下Gaussian輸入文件（本文文件包里的C4H8.gjf）對C4H8做UHF計算得到對稱破缺波函數。不了解為什么用guess=mix的話看《談談片段組合波函數與自旋極化單重態》（http://www.shanxitv.org/82）。

%chk=D:\C4H8.chk
# UHF/6-31G* guess=mix 5d
[空行]
ub3lyp/6-31g(d) opted
[空行]
0 1
C     -0.74742092    1.77656753    0.00000000
H     -0.62438907    2.32965189    0.92333358
H     -0.62438907    2.32965189   -0.92333358
C     -0.74742092    0.30933780    0.00000000
H     -1.24978876   -0.09122321    0.88294562
H     -1.24978876   -0.09122321   -0.88294562
C      0.74742092   -0.30933780    0.00000000
H      1.24978876    0.09122321   -0.88294562
H      1.24978876    0.09122321    0.88294562
C      0.74742092   -1.77656753    0.00000000
H      0.62438907   -2.32965189   -0.92333358
H      0.62438907   -2.32965189    0.92333358
[空行]
[空行]

計算完畢后把C4H8.chk轉成C4H8.fch，載入Multiwfn，然后依次輸入
200  //其它功能（Part 2）
16  //基于fch文件里的密度矩陣產生自然軌道。這個功能在《在Multiwfn中基于fch產生自然軌道的方法與激發態波函數、自旋自然軌道分析實例》（http://www.shanxitv.org/403）里有專門的介紹
SCF  //讀取fch里的SCF類型的密度矩陣
1  //產生空間自然軌道
此時從屏幕上看到如下信息，這便是UNO軌道的占據數。其中最高占據自然軌道（HONO）和最低非占據自然軌道（LUNO）的占據數分別是1.123225和0.876775，都偏離整數顯著，很滿足期望。

 Occupation numbers:
    2.000000    2.000000    1.999999    1.999999    1.999904    1.999898
    1.999881    1.999835    1.999309    1.999120    1.999004    1.998977
    1.996829    1.996536    1.996053    1.123225    0.876775    0.003947
    0.003464    0.003171    0.001023    0.000996    0.000880    0.000691
...略

接著輸入
n  //不把自然軌道導出成new.mwfn文件并重新載入，因為當前不需要如此（如果你想看一下當前的UNO軌道圖像的話，應選y，之后用Multiwfn主功能0觀看軌道）
0  //返回主菜單
100  //其它功能（Part 1）
2  //產生輸入文件
19  //產生Dalton輸入文件
CASSCF.dal  //要產生的輸入文件名
[回車]  //要產生的.mol文件名用默認的C4H8.mol
y  //把當前內存里的軌道（即UNO）的展開系數寫入到.dal文件里
1  //使用Dalton標準格式（4F18.14）方式寫入

當前C4H8.mol里的基組默認就是6-31G*，不用改。修改CASSCF.dal，把以下兩行
.DFT
 B3LYPg
替換為CASSCF(2,2)計算的設置：
.MCSCF
*CONFIGURATION INPUT
.CAS SPACE
2
.ELECTRONS
2
.INACTIVE
15

Dalton計算完畢后，活性空間內自然軌道占據數為1.2679和0.7320，能量為-156.024938 Hartree，和Gaussian在同級別做CASSCF精確一致。你若想看Dalton做CASSCF產生的自然軌道，把計算產生的.tar.gz文件里的molden.inp解壓出來載入Multiwfn，并效仿《使用Multiwfn觀看分子軌道》（http://www.shanxitv.org/269）的方式觀看即可。

5 關于線性依賴基函數的問題

較大基組（尤其是帶彌散函數的），計算原子分布較致密的體系很容易出現線性依賴問題，Gaussian和Dalton此時都會自動去除線性依賴基函數，導致最終求解出來的軌道數會少于基函數數目。這種情況下，Gaussian輸出信息中的NBsUse（實際用的基函數數目，等同于實際求解出來的軌道數）小于NBasis，Dalton輸出文件中的Total number of orbitals小于Number of basis functions。這給上文的傳軌道帶來了麻煩。有兩個解決方法：
(1)不去除線性依賴基函數：Gaussian計算時帶著IOp(3/32=2)關鍵詞、Dalton計算時在**WAVE FUNCTIONS里面加上以下內容，從而讓兩個程序都不去除線性依賴基函數
*ORBITAL
.AO DELETE
1E-100
這種做法的缺點是可能導致數值不穩定性。
(2)自動去除線性依賴基函數，但讓Dalton少讀取軌道：比如Gaussian計算顯示NBsUse=50、NBasis=54，因此自動去除了4個線性依賴基函數。因此當Multiwfn載入fch文件后，最后4個軌道的展開系數都會為0，導出到.dal文件里也是如此。此時Dalton若照常讀取全部軌道，計算一開始會報錯*** ORTHO-FATAL ERROR ***。解決方法是在*ORBITAL里寫上
.DELETE
4
這樣Dalton就不會讀取最后4個軌道了，計算可以正常進行。

6 .dal里的軌道展開系數存在星號而無法讀取的問題

有時候Multiwfn寫入到.dal里的軌道展開系數會存在一堆星號，導致Dalton讀取軌道時提示input conversion error錯誤。這不是Multiwfn的問題，而是Dalton自身設計不周。Dalton定義的**MOLORB字段中記錄展開系數的格式在前面說了，每個數值都是F18.14格式，因此當有的軌道展開系數特別大，超過了其整數位記錄上限，就會被記錄成一堆星號。這種問題在基組較彌散而又不讓自動去除線性依賴基函數的情況下出現概率大。這是為什么Multiwfn導出Dalton輸入文件的時候特意讓你選擇記錄的格式，前面的例子都是選1用4F18.14格式，還可以選2用4E20.12格式，這是使用科學計數法輸出，因此就不會出現數值過大記錄成星號的問題了。相應地，必須自己修改Dalton的讀取軌道展開系數的源代碼。對于Dalton 2022版，需要修改Dalton源代碼目錄下的DALTON/sirius/sirgp.F文件，把PFMT = '(4F18.14)'替換為PFMT = '(4E20.12)'，之后重新編譯即可。

7 其它

Multiwfn就相當一個大熔爐，能讀取諸多量子化學程序產生的波函數，又能導出波函數作為諸多量子化學程序的初猜，這在《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379）里專門說了。對于傳軌道到ORCA的情況我之前還專門寫過《將Gaussian等程序收斂的波函數作為ORCA的初猜波函數的方法》（http://www.shanxitv.org/517）。

MOKIT也是很好的可以實現不同程序間傳軌道的工具，fch到.dal和.mol的轉換可以用里面的fch2dal子程序。相對于MOKIT，本文介紹的用Multiwfn傳軌道有幾個額外的好處：
(1)Multiwfn不需要安裝MOKIT所需的Python環境。尤其是對于Windows用戶，Multiwfn解壓即用明顯更為方便
(2)Multiwfn特意考慮了.dal里記錄軌道展開系數的格式的問題并給了解決辦法，上一節說了
(3)Multiwfn自身可以產生諸多類型的軌道（定域化分子軌道、空間/自旋自然軌道、NAdO、AdNDP、NTO、雙正交化軌道等等）并輸出作為Dalton的初猜
而fch2dal也有額外的優點，它會把fch里的基組、贗勢的具體定義直接寫到輸出的.mol里，因此如果Gaussian計算時用的基組、贗勢在Dalton里沒有自帶也能直接計算而不需要自定義。并且fch2dal支持用笛卡爾型基函數的情況。

文/Sobereva@北京科音   2025-Mar-31

0 前言

使用計算化學程序過程中普遍離不開可視化問題，對如今已經非常流行、十分強大、巨快、開源免費的第一性原理程序CP2K自然也不例外。最近有人在思想家公社QQ群里問“cp2k可視化一般搭配哪個程序呢？”，針對這個問題，筆者簡要羅列一下我推薦的在CP2K使用過程中的可視化程序，主要面向初學者。本文只是粗略概述，這些程序在筆者講授的北京科音CP2K第一性原理計算培訓班（http://www.keinsci.com/KFP）中都會反復利用和詳細演示具體操作。除本文說的外，還有大量其它可視化程序，比如Avogadro、gabedit、Chemcraft等，我認為對于CP2K用戶來說，用好本文提到的這些就已經完全足夠了。文中提到的Multiwfn可以在官網http://www.shanxitv.org/multiwfn下載，相關信息見《Multiwfn FAQ》（http://www.shanxitv.org/452）。

1 建模階段的可視化

能夠構建用于做第一性原理計算的周期性體系的程序很多，其中我十分推薦GaussView，這是絕大多數內行做量子化學計算的人都會用的可視化程序，其圖形界面設計得很好，所見即所得，大多數情況用這一個程序就可以很好完成CP2K計算前的建模。GaussView可以直接讀取記錄周期性體系原子坐標和晶胞信息的最常見的cif文件。在GaussView里構建好結構后，可以保存成Gaussian程序的輸入文件（gjf），里面有原子坐標信息和晶胞的平移矢量信息（Tv開頭的行），然后用Multiwfn載入這樣的gjf文件后，就可以按照《使用Multiwfn非常便利地創建CP2K程序的輸入文件》（http://www.shanxitv.org/587）文中說的創建CP2K輸入文件了，整個過程相當方便。

許多人誤以為GaussView只是結合Gaussian使用的，或者至多是用于量子化學程序算孤立體系建模的，這是大錯特錯！由于Gaussian本來就有計算周期性的功能（但由于功能性和效率的原因，極少有人用Gaussian算周期性體系），所以Gaussian的御用圖形界面GaussView也支持周期性體系，可以直接對周期性體系添加/刪除/替換原子、調整鍵長/鍵角/二面角、平移/旋轉片段、把其它體系粘貼到當前體系里、測量幾何參數，等等，對周期性體系和對分子體系操作一樣非常靈活和順手。并且GaussView專門有個PBC editor界面，在里面可以定義晶胞參數、重新定義晶胞、修改周期性、晶軸變換、擴胞、切晶面、判斷空間群、居中體系、刪除晶胞外的原子、把晶胞外的原子卷入晶胞，等等，常用的操作幾乎都提供了。GaussView對于周期性體系建模相當好用，然而其這方面的價值卻被很多人低估，甚至有人明明不了解還胡亂貶損。

點擊下圖紅色箭頭處的按鈕就可以進入前述的PBC editor界面。紅、綠、藍邊框分別是晶胞的a、b、c軸。

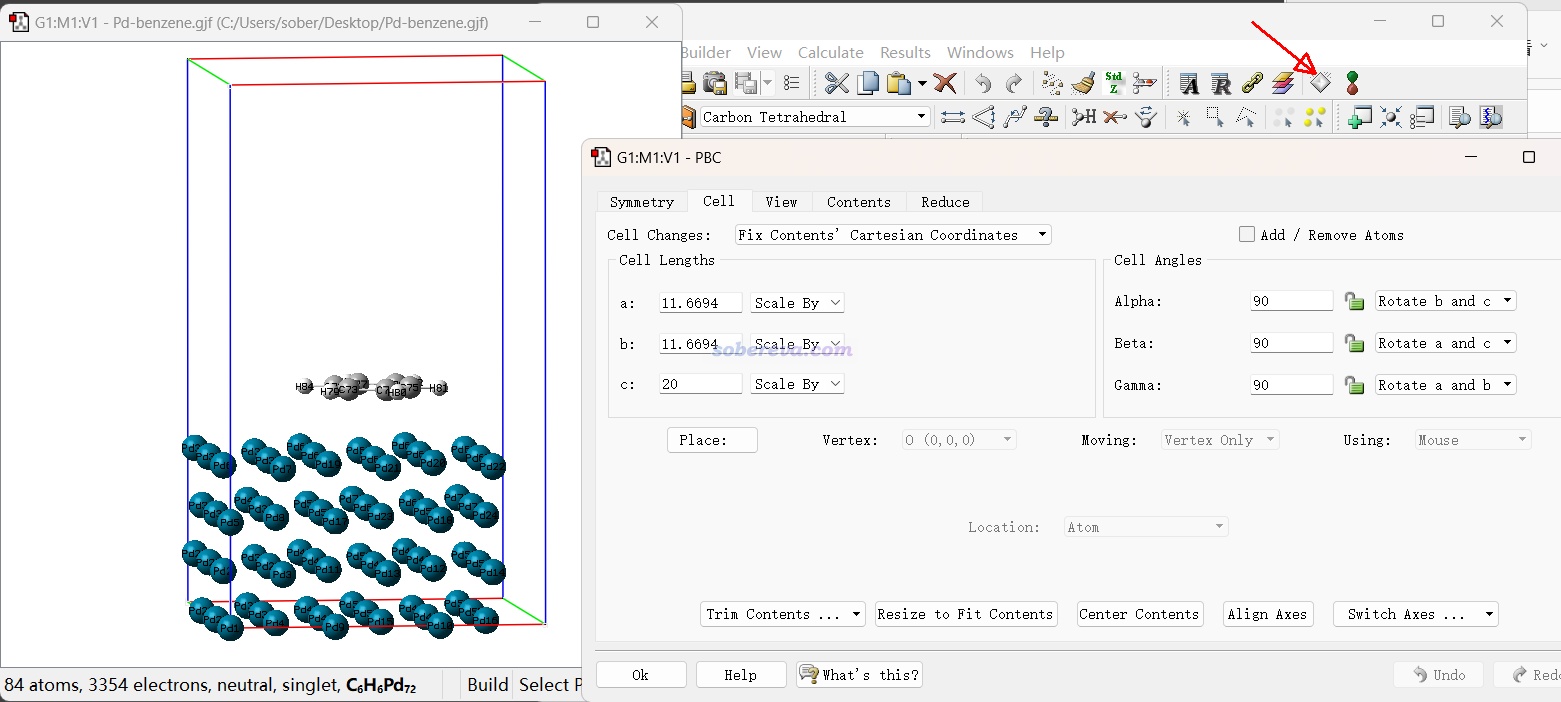
還值得一提的是，GaussView的菜單欄的Tools中的Atom selection界面很有用。用滑框選擇工具選擇一批原子成為黃色后，Atom selection界面里就可以看到選中的原子序號，格式和Multiwfn程序里要求的完全一致。例如在Multiwfn里創建幾何優化任務的輸入文件時，若你選擇要凍結某些原子，就可以把序號從這里復制出來并直接粘貼到Multiwfn的窗口中，這樣實現諸如slab邊緣原子的凍結設置巨方便。

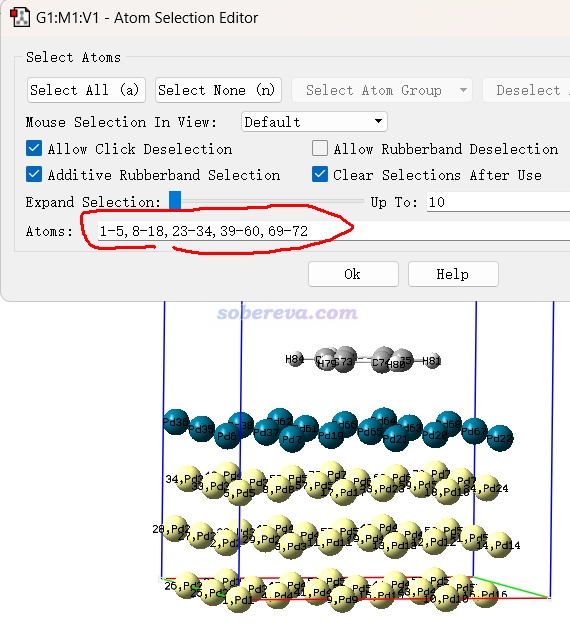
Multiwfn還可以載入CP2K的輸入文件、Quantum ESPRESSO的輸入文件、VASP的POSCAR等格式，主功能100的子功能2里選擇保存為gjf或者cif文件后，也可以用GaussView載入并觀看和編輯。順帶一提，在建模方面Multiwfn也提供了很多實用功能，很多還是GaussView沒有的，見《Multiwfn中非常實用的幾何操作和坐標變換功能介紹》（http://www.shanxitv.org/610）。

2 幾何優化結果的可視化

如果要看CP2K做幾何優化得到的最終結構，最簡單的方法是用Multiwfn載入此任務產生的restart文件，之后進入主功能0直接就看到了，例如下面的聚噻吩體系。界面上方的菜單以及圖形界面右側有一大堆選項可以調整效果，諸如視圖的旋轉和縮放、鍵的粗細、成鍵判斷閾值、原子序號是否顯示/字號/顏色、原子球大小、高亮特定原子。菜單欄的Tools列表里還有一些輔助工具，比如測量幾何參數、導出所有內坐標、輸出笛卡爾或分數坐標，等等。

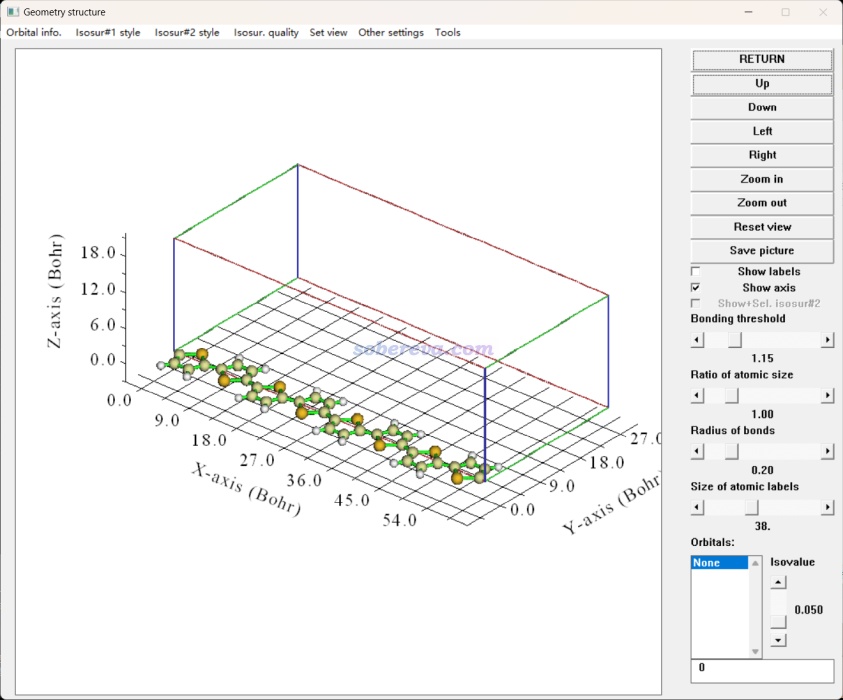
很多時候我們還關心優化的過程，尤其是當體系結構復雜時，不觀看優化軌跡的話，往往都不好判斷優化過程中哪里發生了何種變化，心里沒數。觀看優化軌跡最好的程序是VMD，在http://www.ks.uiuc.edu/Research/vmd/可免費下載，強烈建議用VMD 1.9.3（撰此文時1.9.4還沒發布正式版，其測試版的bug巨多，強烈不建議用）。CP2K的幾何優化任務默認會輸出.xyz文件，這是多幀的軌跡文件，里面記錄了優化過程的每一幀的坐標，不熟悉xyz格式的話看《談談記錄化學體系結構的xyz文件》（http://www.shanxitv.org/477）。把xyz文件載入VMD就可以觀看優化軌跡了。即便任務沒跑完，也可以載入此文件看看最新一步的結構。

xyz文件里不記錄晶胞信息，因此在VMD里沒法顯示出晶胞邊框，給觀看周期性體系造成不便。對于不變胞的優化，可以用Multiwfn載入restart文件，此時屏幕上不僅顯示晶胞信息，還會顯示在VMD里定義晶胞的命令，如下圖所示。

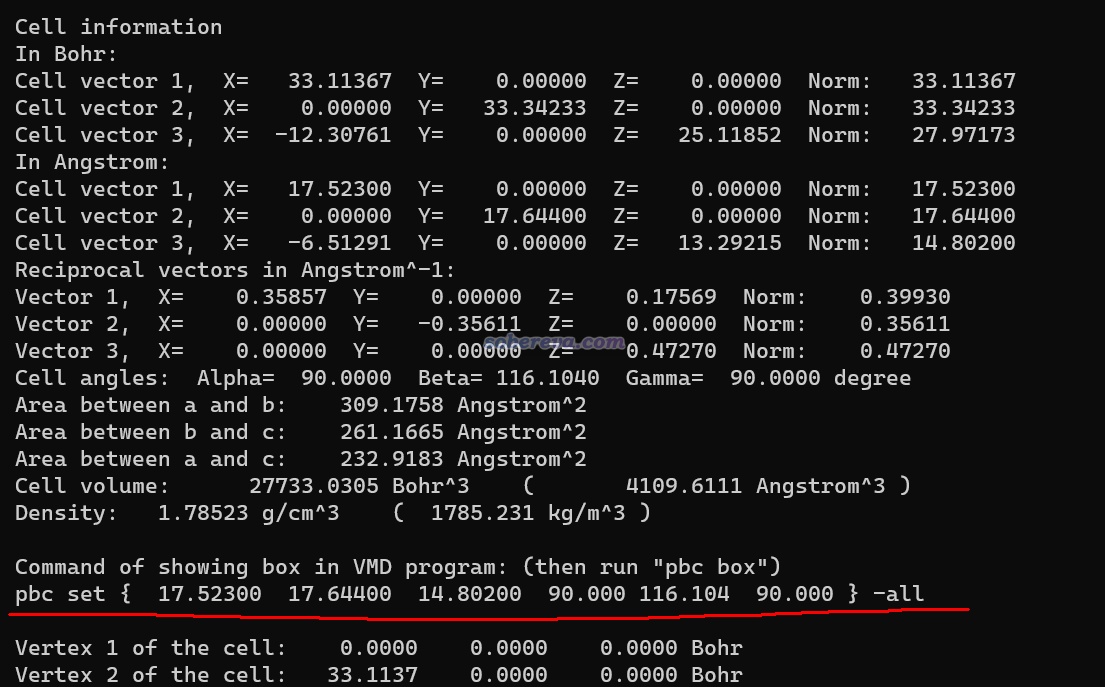
 把這命令復制到VMD的命令行窗口運行，之后再輸入pbc box命令，晶胞在VMD里就顯示出來了，如下所示。

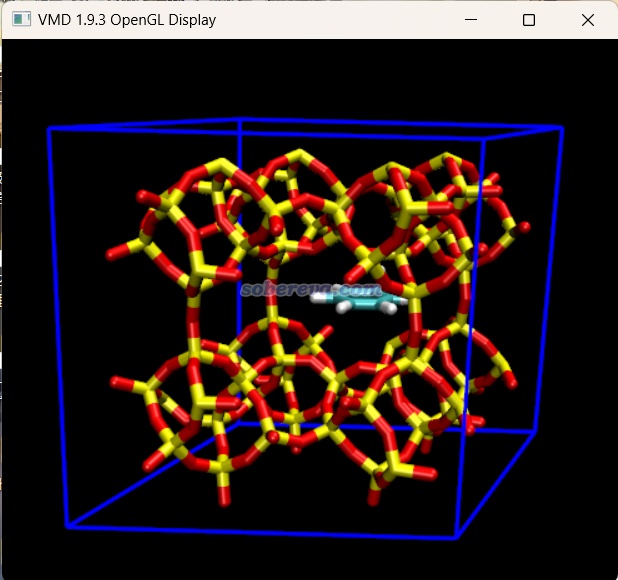
如果做的是變胞優化任務，晶胞在優化過程中不是固定不變的，此時建議讓CP2K輸出pdb格式的優化軌跡，里面記錄了每一幀的晶胞信息。此文件載入VMD并顯示盒子后，會看到隨著軌跡的播放，盒子也實時變化。

上述說明不僅適用于優化極小點，對于dimer方法優化過渡態也是一樣的。

VESTA（http://jp-minerals.org/vesta/en/）也是一個很好且免費的主要面向周期性體系的可視化工具，默認情況下的顯示效果往往比VMD甚至還更好些。若想用VESTA看CP2K優化的結果，可以把restart文件載入Multiwfn，主功能100的子功能2里選擇導出cif或VASP的輸入文件（POSCAR），然后就能載入VESTA了。

3 反應路徑的可視化

CP2K做NEB類任務需要對給定的初始結構之間插點。CP2K雖然能夠自動插點（點=image），但沒法在計算前進行預覽。利用《sobNEB：產生CP2K的NEB的插點的方便的工具》（http://www.shanxitv.org/660）里介紹的筆者的sobNEB程序插點的話，可以直接產生traj.xyz軌跡文件，放到VMD里通過播放動畫或者多幀疊加顯示，就可以直觀判斷初始的NEB的image是否合理了。

NEB類任務計算過程中是好多副本一起算的，每個副本都會在計算過程中輸出它所負責的那個image優化過程的xyz軌跡文件。要想觀看最終收斂的NEB軌跡，需要自己把這些副本輸出的軌跡的最后一幀合并在一起作為新的xyz軌跡，放到VMD里就可以觀看最終的反應路徑動畫了。手動做比較麻煩，建議用腳本實現。北京科音CP2K第一性原理計算培訓班（http://www.keinsci.com/KFP）里專門給了個shell腳本自動做這件事情，運行后就會在當前目錄下產生[項目名]_traj.xyz文件，里面記錄了NEB最新一步的軌跡（即便任務還沒跑完，也可以看最新的NEB軌跡是什么樣），同時還會產生[項目名]_ene.txt，里面記錄了最新一步的各個點的能量。下面是培訓里的一個實例，對載入的[項目名]_traj.xyz文件做多幀疊加顯示，直觀顯示了Na的遷移軌跡

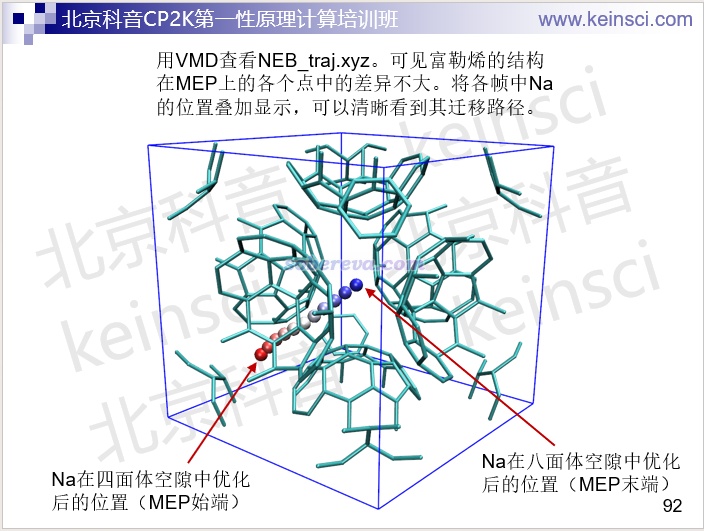
4 振動分析的可視化

CP2K做完振動分析后往往需要觀看振動矢量了解振動的特征。推薦做法是用《使CP2K計算的振動模式可以被GaussView觀看的程序：MfakeG》（http://www.shanxitv.org/656）里介紹的筆者開發的MfakeG工具，把記錄振動模式信息的.mol后綴的molden文件轉化成仿Gaussian輸出文件，之后載入GaussView就可以用Results - Vibrations選項觀看振動模式了，例如下圖的草酸晶體的例子

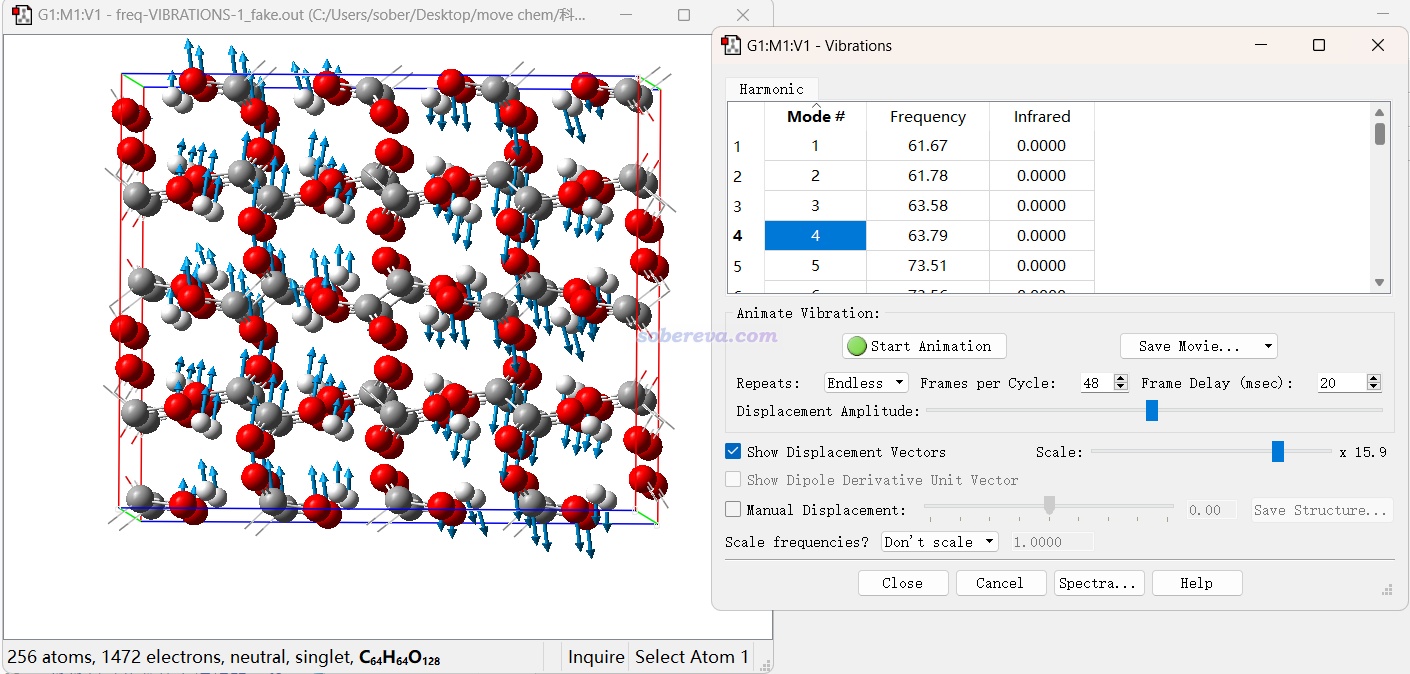
還有一種做法是使用免費的可視化程序Jmol（https://jmol.sourceforge.net），也可以載入CP2K產生的molden文件觀看振動模式。不過我還是覺得GaussView用起來舒服。

如果要基于CP2K的振動分析觀看振動光譜，推薦用Multiwfn。Multiwfn具有非常強大的繪制各種光譜的功能，見《使用Multiwfn繪制紅外、拉曼、UV-Vis、ECD、VCD和ROA光譜圖》（http://www.shanxitv.org/224）和《使用Multiwfn繪制NMR譜》（http://www.shanxitv.org/565）。Multiwfn可以載入CP2K做振動分析產生的輸出文件按博文所述繪制紅外光譜，如果要求計算了拉曼還可以繪制拉曼光譜。此外，Multiwfn還可以載入常規TDDFT和XAS-TDDFT任務的輸出文件分別繪制UV-Vis光譜和X光吸收光譜，還可以考慮旋軌耦合效應，例如下圖是CP2K+Multiwfn繪制的NaAlO2晶體的Al的K-edge XAS。Multiwfn還可以載入CP2K的NMR任務的輸出文件繪制NMR譜。這些在北京科音CP2K第一性原理計算培訓班（http://www.keinsci.com/KFP）里有非常系統的講解和豐富的例子。

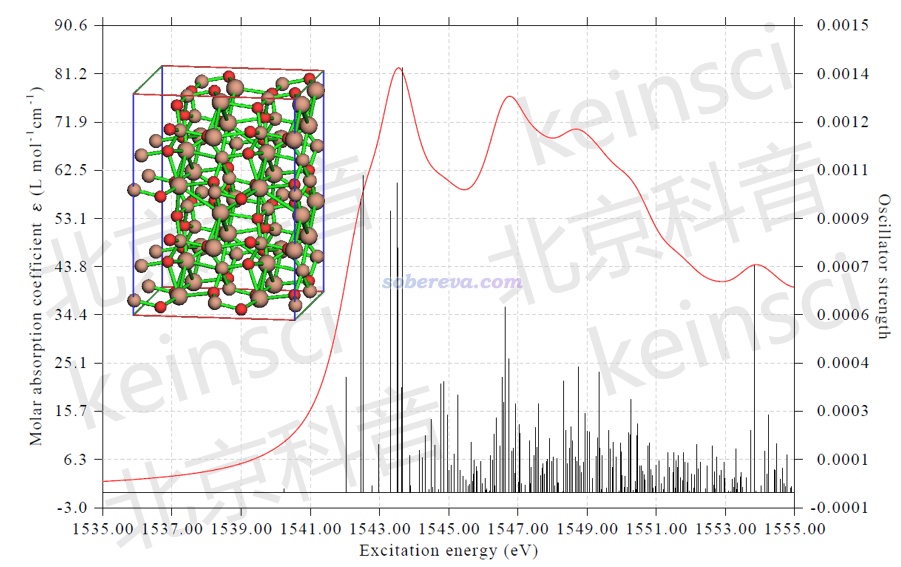
5 動力學軌跡可視化

CP2K的第一性原理動力學（叫從頭算動力學也行）是CP2K的杰出強項之一。和GROMACS、AMBER、NAMD等經典力場動力學程序的情況一樣，VMD也是觀看其動力學軌跡的不二的選擇。例如培訓里有個模擬質子轟擊石墨烯層的例子，VMD載入軌跡后并多幀疊加顯示、根據幀號著色，直觀展現了模擬過程中質子的運動軌跡：

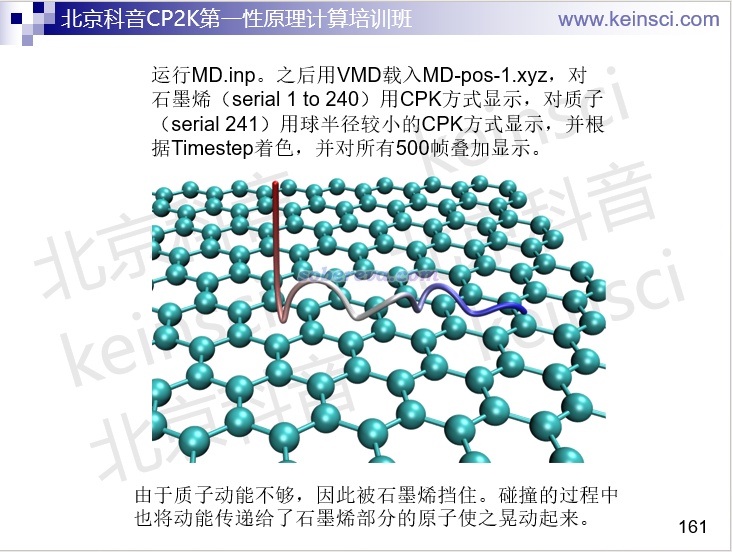
還可以自己寫VMD腳本從CP2K產生的記錄原子速度的xyz文件中把速度信息讀入VMD，并根據速度著色，展現出質子的動能是如何傳遞到石墨烯板上并擴散開來的。下圖黃色是打入的質子，越藍的石墨烯原子的速度越大。

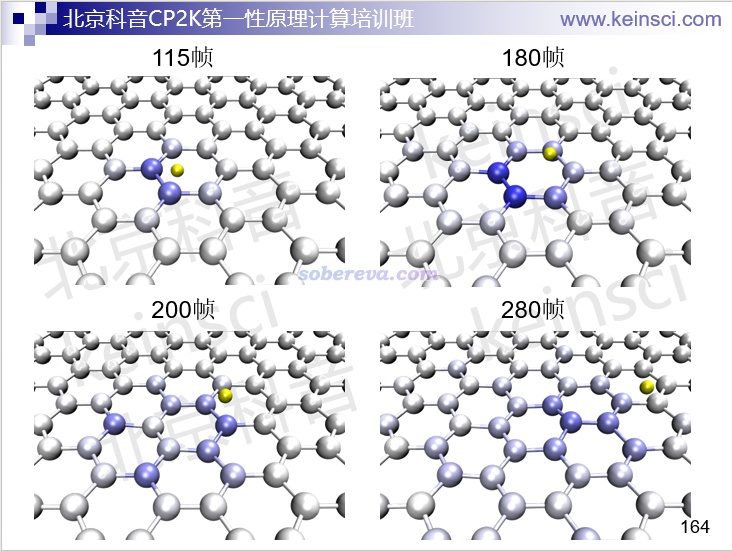
VMD不僅可以觀看動力學過程中結構的變化，還可以繪制等值面圖觀看電子結構的變化，例如下圖這個例子，直觀展現了水合電子是怎么在模擬過程中出現的。

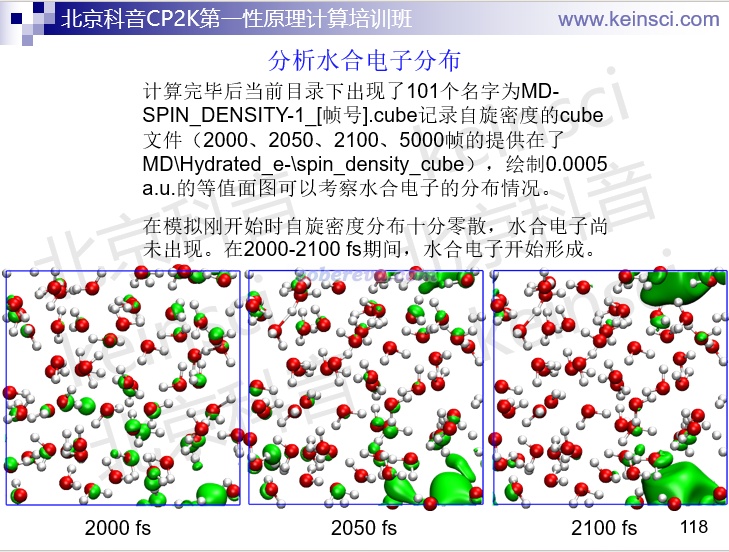
通過寫VMD tcl腳本，還可以實現很復雜的分析，如下面幻燈片里講的高溫下正癸烷的裂解產物分析。PS：做動力學的，不會寫分析腳本的話，稍微做深一點就會寸步難行。

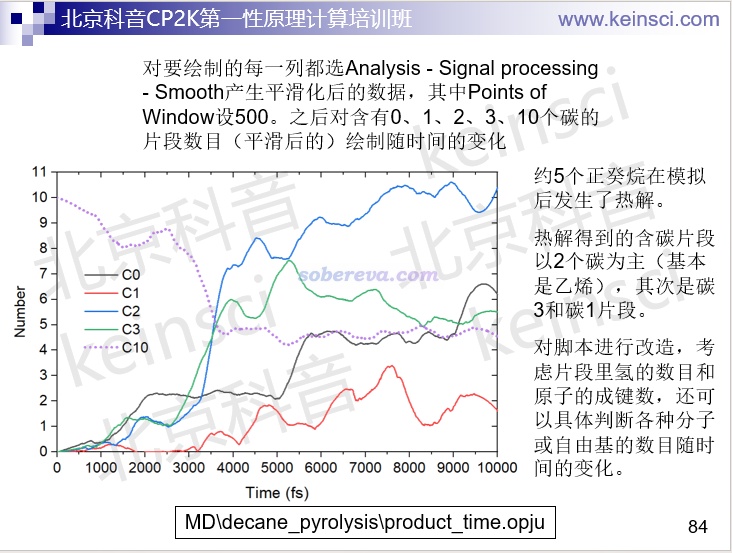
北京科音分子動力學與GROMACS培訓班（http://www.keinsci.com/KGMX）專門用約100頁幻燈片特別完整、詳細講VMD的使用，并且還額外用近100頁幻燈片深入講VMD腳本的編寫，如果想系統學習VMD的話這是極佳的途徑。

筆者偶爾看到有人用OVITO程序可視化CP2K產生的軌跡，我沒用過那個程序，也完全不理解為什么有人不用VMD而用OVITO，明明VMD已經可以完美地滿足一切需求。筆者在答疑時看到有一些CP2K用戶還被OVITO坑了：OVITO根據邊緣原子位置自動確定了盒子邊框，有人以為那就是實際的晶胞邊界，導致對結果產生了嚴重誤解。

6 電子結構的可視化和分析

Multiwfn可以基于CP2K的輸出文件繪制效果非常理想的能帶結構圖，如CrO2體系：

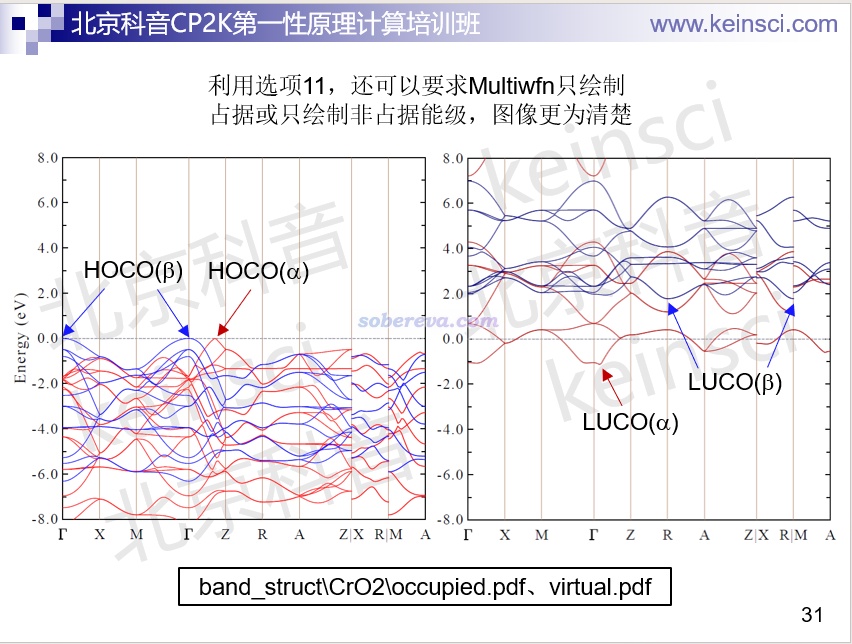
《詳談使用CP2K產生給Multiwfn用的molden格式的波函數文件》（http://www.shanxitv.org/651）中介紹了怎么用CP2K產生molden文件。Multiwfn將之載入后，就可以在《使用Multiwfn繪制態密度(DOS)圖考察電子結構》（http://www.shanxitv.org/482）講的基礎上舉一反三繪制效果很好的DOS、PDOS、OPDOS、LDOS圖，下圖是WO3體系：

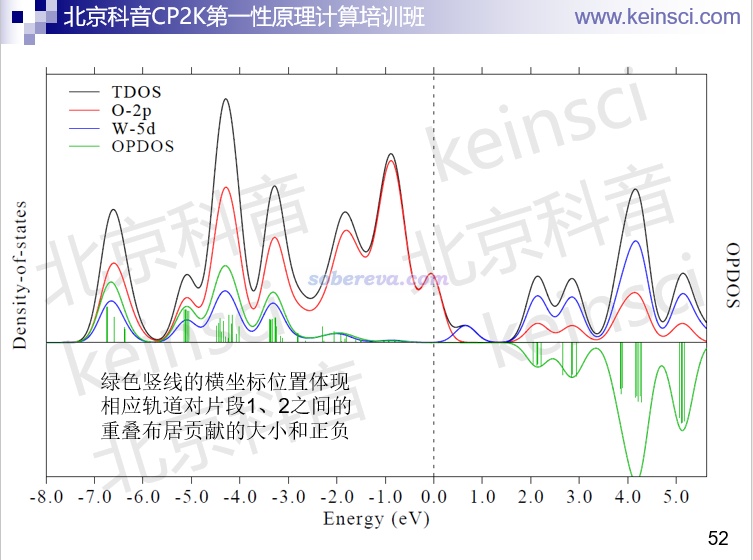
Multiwfn還能基于CP2K的molden文件觀看軌道，做法可參考《使用Multiwfn觀看分子軌道》（http://www.shanxitv.org/269）。還支持對特定k點看軌道：

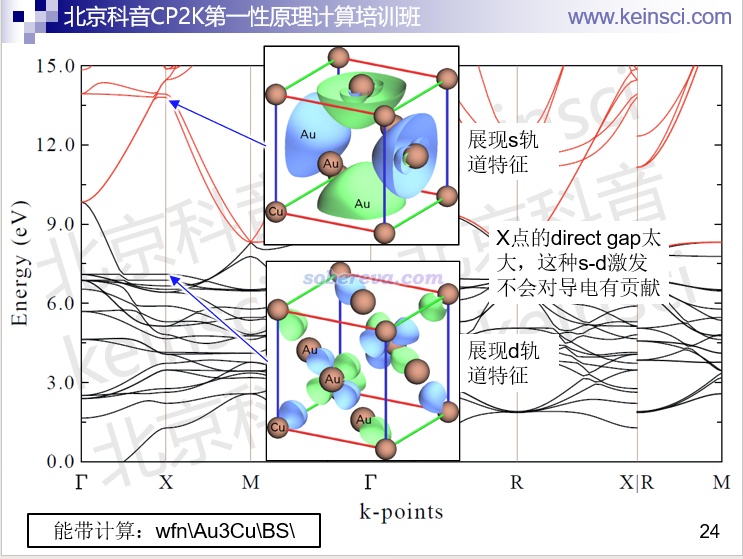
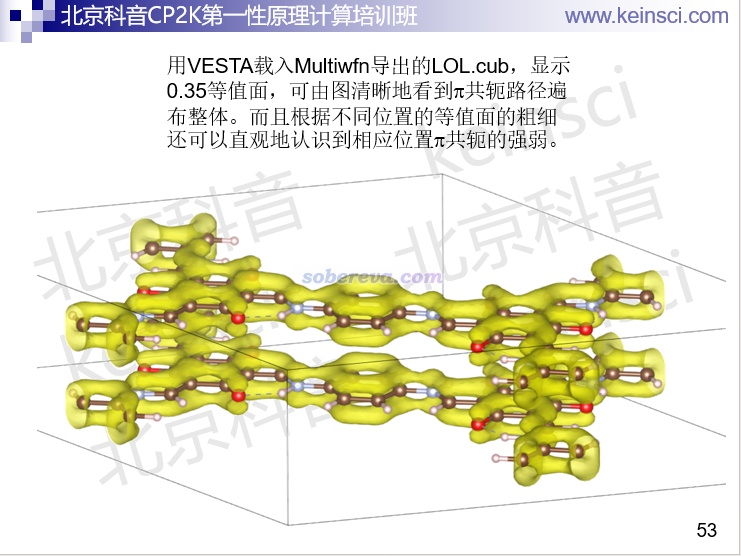
Multiwfn還能對周期性體系做超級豐富的波函數分析，其中很多都是以圖形方式展現的，比如可以基于《在Multiwfn中單獨考察pi電子結構特征》（http://www.shanxitv.org/432）和《使用Multiwfn考察周期性體系的芳香性》（http://www.shanxitv.org/722）講的做法計算LOL-pi格點數據，之后可以在Multiwfn里直接觀看等值面；也可以導出成cube文件后，載入VMD或VESTA程序繪制，如下所示，極為生動直觀地展現了一個COF體系的pi電子共軛路徑

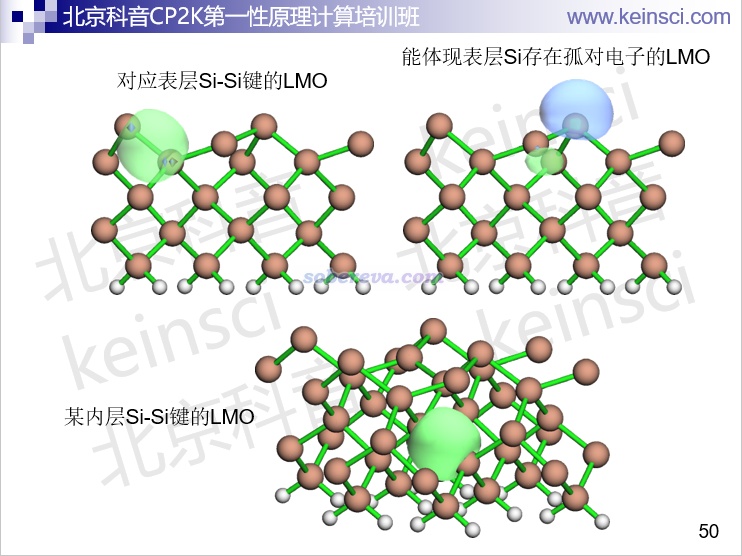
再比如下圖是Multiwfn載入CP2K對硅表面計算產生的molden文件，做軌道定域化后直接顯示出軌道等值面圖，直觀展現了體系不同位置的電子結構特征。相關信息見《Multiwfn的軌道定域化功能的使用以及與NBO、AdNDP分析的對比》（http://www.shanxitv.org/380）。

為避免此章太長，Multiwfn可以針對周期性體系做的巨量的可視化分析這里就不一一提及，很多分析我都寫過博文，感興趣的讀者請閱讀：
使用Multiwfn結合CP2K的波函數模擬周期性體系的隧道掃描顯微鏡（STM）圖像
http://www.shanxitv.org/671（http://bbs.keinsci.com/thread-37740-1-1.html）
使用Multiwfn對周期性體系做鍵級分析和NAdO分析考察成鍵特征
http://www.shanxitv.org/719（http://bbs.keinsci.com/thread-47176-1-1.html）
使用Multiwfn結合CP2K做周期性體系的atom-in-molecules (AIM)拓撲分析
http://www.shanxitv.org/717（http://bbs.keinsci.com/thread-46927-1-1.html）
使用Multiwfn結合CP2K對周期性體系做電荷分解分析（CDA）
http://www.shanxitv.org/716（http://bbs.keinsci.com/thread-46878-1-1.html）
使用Multiwfn做IGMH分析非常清晰直觀地展現化學體系中的相互作用
http://www.shanxitv.org/621（http://bbs.keinsci.com/thread-28147-1-1.html）
使用IRI方法圖形化考察化學體系中的化學鍵和弱相互作用
http://www.shanxitv.org/598（http://bbs.keinsci.com/thread-23457-1-1.html）
使用Multiwfn結合CP2K通過NCI和IGM方法圖形化考察固體和表面的弱相互作用
http://www.shanxitv.org/588（http://bbs.keinsci.com/thread-21742-1-1.html）
使用Multiwfn繪制分子和固體表面的距離投影圖
http://www.shanxitv.org/589（http://bbs.keinsci.com/thread-21754-1-1.html）
使用Multiwfn圖形化展現原子對色散能的貢獻以及色散密度
http://www.shanxitv.org/705（http://bbs.keinsci.com/thread-44723-1-1.html）
使用Multiwfn做Hirshfeld surface分析直觀展現分子晶體和復合物中的相互作用
http://www.shanxitv.org/701（http://bbs.keinsci.com/thread-43178-1-1.html）
使用CP2K結合Multiwfn對周期性體系模擬UV-Vis光譜和考察電子激發態
http://www.shanxitv.org/634（http://bbs.keinsci.com/thread-28006-1-1.html）
使用Multiwfn計算分子和晶體中孔洞的直徑
http://www.shanxitv.org/643（http://bbs.keinsci.com/thread-30696-1-1.html）
使用Multiwfn計算晶體結構中自由區域的體積、圖形化展現自由區域
http://www.shanxitv.org/617（http://bbs.keinsci.com/thread-25241-1-1.html）
使用CP2K結合Multiwfn繪制密度差圖、平面平均密度差曲線和電荷位移曲線
http://www.shanxitv.org/638（http://bbs.keinsci.com/thread-28225-1-1.html）

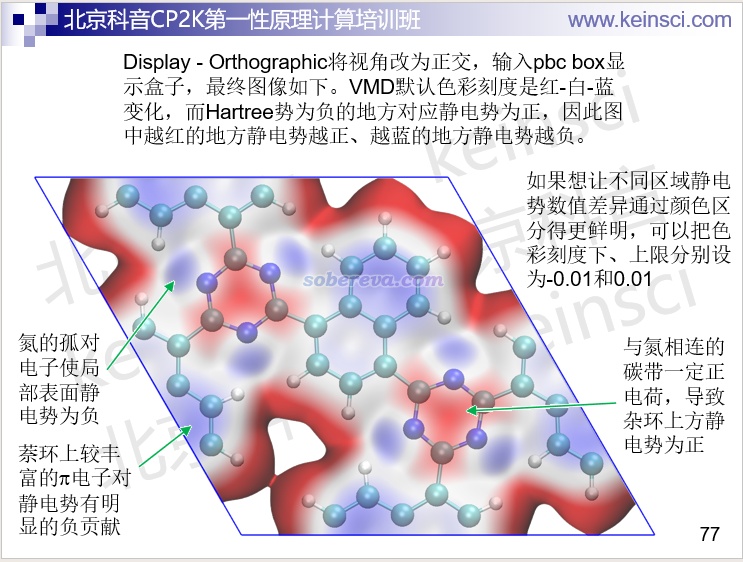
此外，用VMD載入CP2K產生的Hartree勢（靜電勢的負值），還可以實現對晶體表面靜電勢的可視化，一個COF體系的例子如下所示。靜電勢在研究靜電主導的相互作用方面有重要意義，參見《靜電勢與平均局部離子化能相關資料合集》（http://bbs.keinsci.com/thread-219-1-1.html）里面的資料。

和靜電勢同等重要的是筆者提出的范德華勢，適用于考察范德華作用主導的相互作用，可以由Multiwfn計算，見《談談范德華勢以及在Multiwfn中的計算、分析和繪制》（http://www.shanxitv.org/551）。

文/Sobereva@北京科音   2025-Feb-21

1 前言

《使用Multiwfn做IGMH分析非常清晰直觀地展現化學體系中的相互作用》（http://www.shanxitv.org/621）里介紹的筆者提出的圖形化展現相互作用的方法IGMH已被廣為使用，之前我寫的《全面揭示各種碳環與富勒烯之間獨特的pi-pi相互作用！》（http://www.shanxitv.org/727）和《談談pi-pi相互作用》（http://www.shanxitv.org/737）里涉及到了IGMH的等值面面積，至少對pi-pi作用來說它和相互作用強度有密切的正相關性。有不少讀者都問我怎么得到面積，本文就專門說一下。計算面積的同時還會順帶得到等值面內包圍的體積。此文說的IGMH等值面具體是指IGMH方法里定義的δg_inter函數的等值面。如果讀者不熟悉IGMH，應先把http://www.shanxitv.org/621看了。讀者應使用Multiwfn官網http://www.shanxitv.org/multiwfn上的最新版本以免和本文的情況不符。不了解Multiwfn者參看《Multiwfn FAQ》（http://www.shanxitv.org/452）和《Multiwfn入門tips》（http://www.shanxitv.org/167）。

下面介紹兩種做法，第一種方法是使用Multiwfn的定量分子表面分析（主功能12）計算IGMH等值面面積和體積，這種情況只適合存在一個等值面，且這個等值面就是你要研究的等值面的情況。另一種方法更為普適，需要借助免費的ChimeraX程序載入Multiwfn產生的cub文件顯示IGMH等值面，可以測量圖中任意一個等值面的面積和體積，對于《使用IRI方法圖形化考察化學體系中的化學鍵和弱相互作用》（http://www.shanxitv.org/598）介紹的IRI函數、《談談范德華勢以及在Multiwfn中的計算、分析和繪制》（http://www.shanxitv.org/551）介紹的范德華勢等各種函數也都可以這么測量。

2 使用Multiwfn的定量分子表面分析功能計算IGMH等值面的面積和體積

這一節以18碳環與C60富勒烯的復合物為例演示怎么直接用Multiwfn得到IGMH等值面的面積和體積。前述的《全面揭示各種碳環與富勒烯之間獨特的pi-pi相互作用！》介紹的筆者的Chem. Eur. J., 30, e202402227 (2024)研究中得到的此體系的波函數文件C60-C18.wfn在http://www.shanxitv.org/attach/738/file.rar里提供了。此體系的IGMH圖如下所示（δg_inter函數等值面為0.002 a.u.）

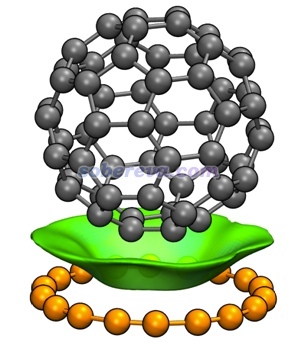
首先將Multiwfn目錄下的settings.ini里的iuserfunc設為91，這代表把用戶自定義函數（user-defined function）設為IGMH方法的δg_inter函數。在Multiwfn手冊2.7節里有可用的用戶自定義函數的完整列表。之后啟動Multiwfn，載入C60-C18.wfn，之后依次輸入
1000   //隱藏功能
16  //定義片段
2  //定義兩個片段
1-18  //18碳環里的原子序號范圍
19-78   //富勒烯里的原子序號范圍
12  //定量分子表面分析功能
1  //設置用于定義表面的函數
2  //某個實空間函數
100  //用戶自定義函數
0.002  //定義表面用的等值面數值
6  //開始分析，不考慮被映射的函數
接下來程序開始計算δg_inter的格點數據，過一會兒，在屏幕上看到以下信息
 Volume:    69.13431 Bohr^3  (  10.24465 Angstrom^3)
 Estimated density according to mass and volume (M/V):  151.8505 g/cm^3
 Overall surface area:         323.36643 Bohr^2  (  90.55182 Angstrom^2)

在后處理菜單選-3可以觀看當前考察的δg_inter函數的0.002 a.u.等值面，如下所示，確實就是前面給出的筆者的論文Chem. Eur. J., 30, e202402227 (2024)里的那個等值面。其體積是上面顯示的10.24 ?^3，面積是90.55 ?^2，和文中報道的一致。

順帶一提，在后處理菜單中還可以選-2將當前算出來的δg_inter的格點數據導出為surf.cub，之后可以被第三方程序可視化和分析。

還值得一提的是進入主功能12的時候可以看到選項3 Spacing of grid points for generating molecular surface用來設置格點間距，默認是0.25 Bohr，數值設得越小計算耗時越高而統計精度越高。

Multiwfn對各種實空間函數（包括從外部的.cub等格點數據文件讀入的）都可以利用定量分子表面分析功能計算其等值面的面積和體積，另一個使用例子見《使用Multiwfn計算軌道的體積》（http://www.shanxitv.org/734）。

3 使用Multiwfn結合ChimeraX獲得IGMH等值面的面積和體積

這一節以2-pyridoxine和2-aminopyridine的二聚體為例演示利用ChimeraX程序得到特定的IGMH等值面的面積和體積。examples\2-pyridoxine_2-aminopyridine.wfn是Multiwfn程序包里自帶的這個體系的波函數文件，在0.01 a.u.的δg_inter等值面數值下分子間的IGMH等值面圖如下所示，可見有兩個等值面，此例分別獲得它們的面積和體積

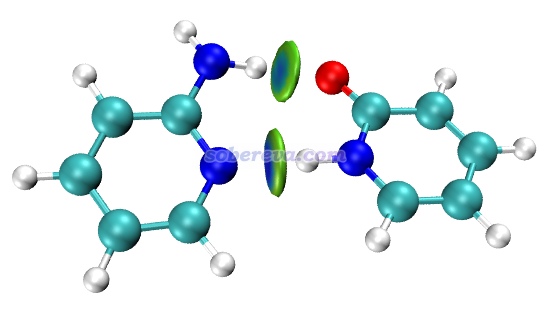
首先照常對這個二聚體做IGMH分析。啟動Multiwfn，然后依次輸入
examples\2-pyridoxine_2-aminopyridine.wfn
20  //弱相互作用可視化分析
11  //IGMH分析
2  //兩個片段
1-12  //第1個片段
c  //其它原子作為第2個片段
4  //設置格點間距（格點分布覆蓋整個體系）
0.2  //格點間距為0.2 Bohr
3  //導出格點數據
當前目錄下有了dg_inter.cub，是δg_inter的cub文件。

之后退回到Multiwfn主菜單，輸入xyz后按回車，再輸入2-pyridoxine_2-aminopyridine.xyz，當前目錄下就得到了記錄當前結構的2-pyridoxine_2-aminopyridine.xyz文件。

去https://www.rbvi.ucsf.edu/chimerax/download.html下載ChimeraX并安裝。本文用的是ChimeraX 1.9。

啟動ChimeraX，將2-pyridoxine_2-aminopyridine.xyz和dg_inter.cub依次拖入程序界面載入，然后左右隨便拖動一下下圖紅箭頭所示的豎杠，激活這個等值面的設置，然后再在下圖藍箭頭所示的文本框里輸入要用的等值面數值0.01，之后看到的等值面就是下圖這樣

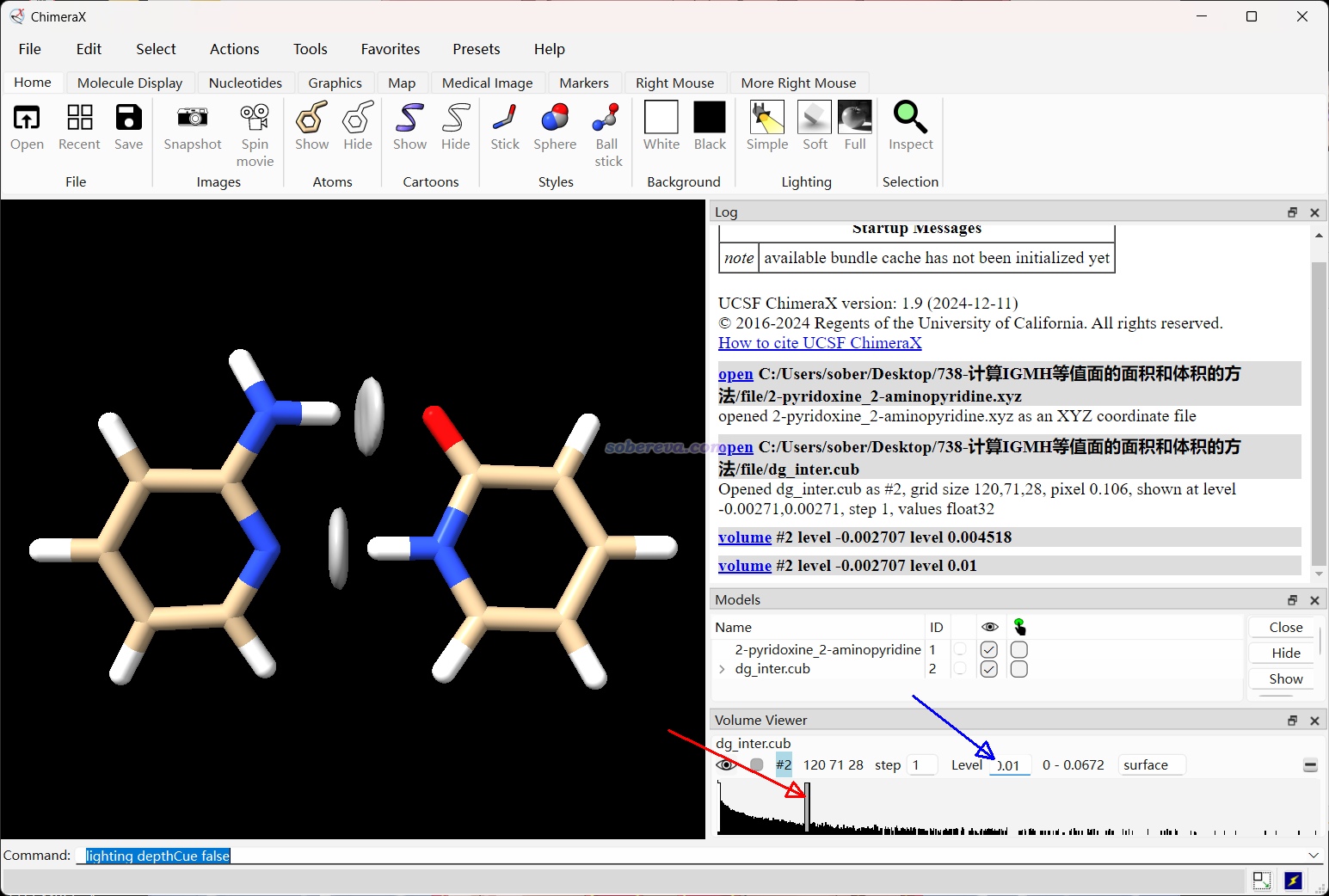
之后選擇窗口上方的Tools - Volume Data - Measure and Color Blobs，之后按住Alt鍵并點擊你要考察面積和體積的那個等值面，那個等值面就被自動著色了，并且在界面右下角顯示了其體積和面積，如下所示，分別為0.31 ?^3和3.28 ?^2。

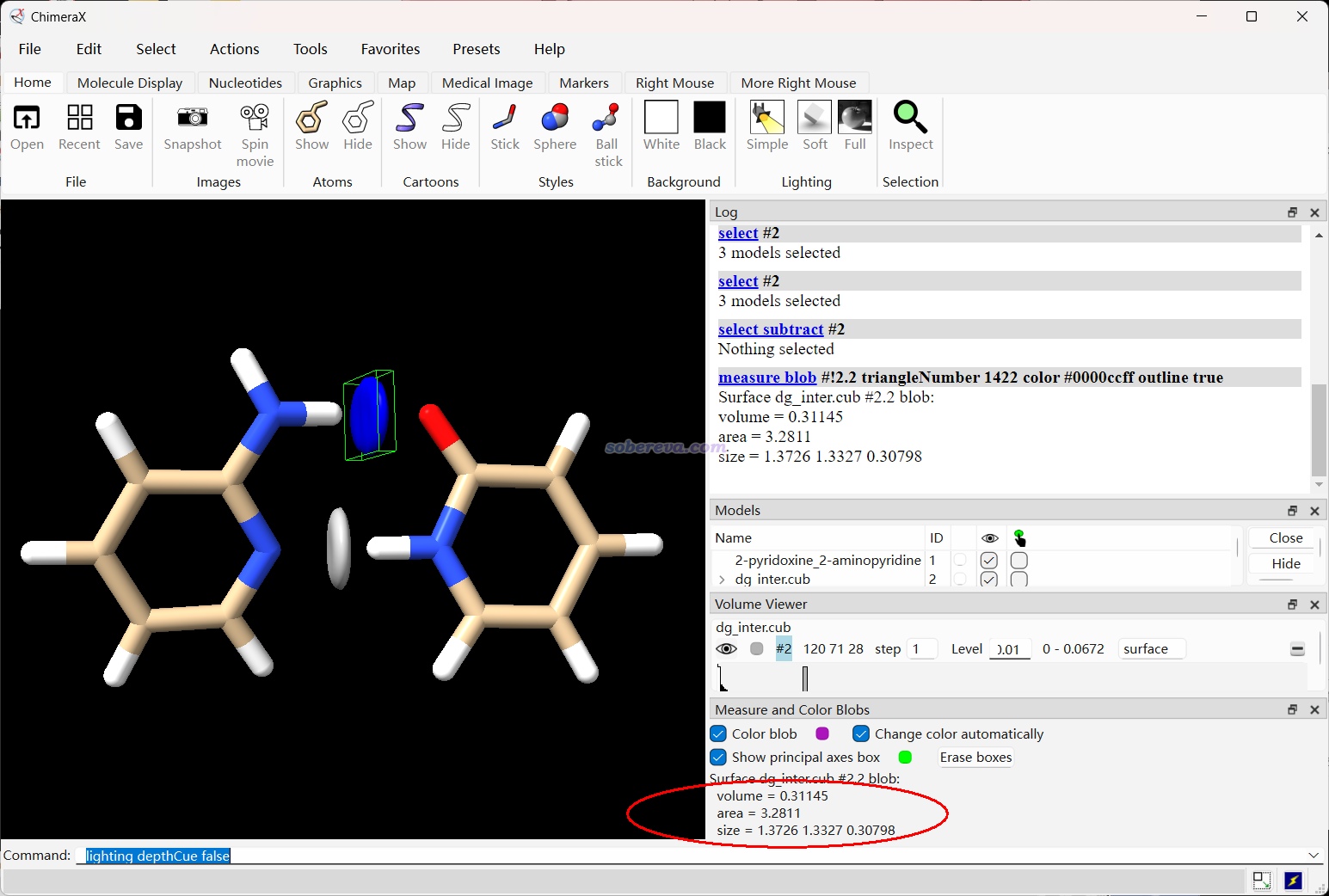
值得一提的是，由于ChimeraX和Multiwfn的定量分子表面分析功能產生等值面的算法不同，因此得到的等值面的面積和體積會有輕微差異。例如用ChimeraX對上一節的18碳環和富勒烯之間的δg_inter=0.002 a.u.的等值面進行測量，得到的面積是89.90 ?^2，體積是10.65 ?^3，面積和Multiwfn給出的90.55 ?^2相差0.7%。

筆者之前還錄過一個視頻《使用Multiwfn和ChimeraX繪制自定義著色的電子定域化函數(ELF)等值面圖》（https://youtu.be/vC48iEB8PwI、https://www.bilibili.com/video/av85684420）演示ChimeraX里的和等值面顯示、測量相關的操作，感興趣的讀者可以看看。

文/Sobereva@北京科音

First release: 2025-Feb-18   Last update: 2025-Feb-19

0 前言

pi-pi相互作用（pi-pi interaction）是化學體系中很常見而且很重要的一種弱相互作用，本文全面談談這種相互作用的各方面特征，以令讀者對其有充分的認識、能在自己的研究中正確分析討論。我在互聯網上廣泛答疑時也時不時看到有關于pi-pi作用的非常錯誤的理解，比如有人被一些文章誤導，竟以為pi-pi作用來自于軌道相互作用或靜電相互作用，而且這種說法還廣泛以訛傳訛，筆者希望通過此文以正視聽。此外，氫鍵、范德華作用等概念在結構化學書里普遍都有，但pi-pi作用鮮有提及，我也推薦相關書籍作者和結構化學教師參考此文的內容將pi-pi作用納入書籍和教學。本文中大量涉及非常流行的波函數分析程序Multiwfn，相關信息見《Multiwfn FAQ》（http://www.shanxitv.org/452）。

我有不少研究文章都和pi-pi作用有密切聯系，是pi-pi作用研究的典型范例，非常推薦讀者閱讀并歡迎引用：
? Theoretical Insight into Complexation Between Cyclocarbons and C60 Fullerene, Chem. Eur. J., 30, e202402227 (2024)。在《全面揭示各種碳環與富勒烯之間獨特的pi-pi相互作用！》（http://www.shanxitv.org/727）中有詳細介紹，專門研究了不同尺寸的碳環和富勒烯之間的pi-pi作用
? Intermolecular interaction characteristics of the all-carboatomic ring, cyclo[18]carbon: Focusing on molecular adsorption and stacking, Carbon, 171, 514-523 (2021)。在《全面探究18碳環獨特的分子間相互作用與pi-pi堆積特征》（http://www.shanxitv.org/572）中有詳細介紹，其中涉及兩個18碳環之間的pi-pi作用
? Molecular assembly with a figure-of-eight nanohoop as a strategy for the collection and stabilization of cyclo[18]carbon, Phys. Chem. Chem. Phys., 25, 16707 (2023)。在《8字形雙環分子對18碳環的獨特吸附行為的量子化學、波函數分析與分子動力學研究》（http://www.shanxitv.org/674）中有詳細介紹，其中涉及18碳環與OPP雙環分子的pi-pi作用
? Comment on “18 and 12 – Member carbon rings (cyclo[n]carbons) – A density functional study”, Mat. Sci. Eng.: B, 273, 115425 (2021)。在《18碳環（cyclo[18]carbon）與石墨烯的相互作用：基于簇模型的研究一例》（http://www.shanxitv.org/615）中有詳細介紹，其中涉及18碳環與石墨烯的pi-pi作用

1 pi-pi作用的基本特征

pi-pi作用的定義和說法比較亂，這里給出我認為最嚴格準確的定義：“pi-pi作用是相距較近的兩個片段上彼此朝向相對的pi電子之間的獨特的色散吸引作用”。這里做幾個注釋，結合后文的實例讀者會了解得更充分：

(1)pi-pi作用可以是分子間的也可以是分子內的，滿足以上定義即可
(2)諸如苯分子里面的pi電子之間的作用不叫pi-pi作用，那屬于共享電子作用
(3)兩套pi電子的分布必須近乎彼此相對才可能算pi-pi作用。而諸如兩套pi電子近乎肩并肩挨著就不能算pi-pi作用，像是不能說環丁二烯里面兩套近乎定域的pi電子之間是分子內pi-pi作用
(4)“相距較近”一般是在4.0-4.5埃以內。也不是說更遠距離就完全沒有pi-pi作用了，只不過由于色散作用隨作用距離r呈-1/r^6快速衰減行為，因此距離稍微一遠pi-pi作用就非常弱了，就不太值得一提了。但相互作用的片段間距離也不能太近，若顯著小于相接觸的原子的范德華半徑之和，則顯著的位阻互斥作用會遠大于pi-pi吸引作用，使得pi-pi作用也相對不值得一提
(5)pi-pi作用最常出現在碳原子間，因為碳最容易帶顯著的pi電子。碳的Bondi和CSD范德華半徑分別為1.70和1.77埃。如果沒有特殊的因素影響相互作用距離的話，在平衡結構（勢能面極小點結構）下，C-C間的pi-pi作用出現在3.4-3.6埃左右是最常見的
(6)pi-pi作用屬于弱相互作用和非共價相互作用范疇。雖然名義上算作弱相互作用，但實際強度可大可小，直接取決于作用面積，詳見后文
(7)有一個詞叫pi-pi堆積（pi-pi stacking），這個詞往往和pi-pi作用混用。但在我來看，這個詞更適合用來形容由于pi-pi作用的吸引效果使得相互作用的兩個部分發生緊密結合從而產生的彼此堆積的結構特征

下圖就是一個再典型不過的存在顯著pi-pi作用的體系，是暈苯的二聚體。高精度理論計算的極小點結構下平面間距大約在3.45埃

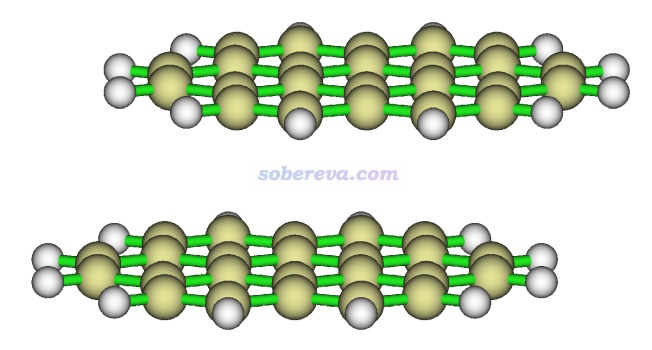
苯二聚體有不同構型，彼此垂直的T型二聚體是能量最低構型，還有一種能量與之非常接近的局部極小點構型是平行位錯構型，屬于pi-pi堆積結構。按照《在Multiwfn中單獨考察pi電子結構特征》（http://www.shanxitv.org/432）的做法繪制出的幾何結構結合pi電子等值面圖如下所示，兩個分子的pi電子的分布非常清楚直觀，可以看到彼此相對。注意并非必須兩個分子的所有pi電子都彼此對著才算pi-pi作用，像下圖這樣哪怕只要一部分對著也同樣算pi-pi作用。而如果完全沒有對著、完全錯開了，那就不算pi-pi作用了。更多的展現pi電子分布的圖見筆者的Theor. Chem. Acc., 139, 25 (2020)一文。

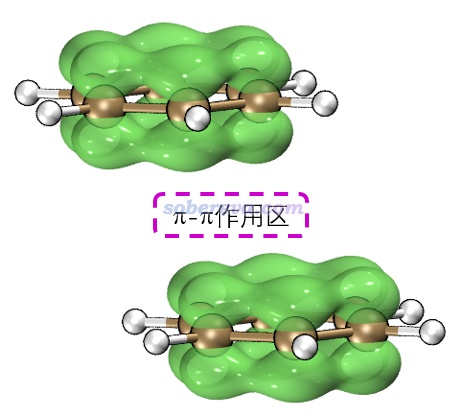
2 pi-pi作用的物理本質

我在《談談“計算時是否需要加DFT-D3色散校正？” 》（http://www.shanxitv.org/413）提到過，原子間相互作用從物理本質上可以基本分為靜電、色散、交換、Pauli互斥、軌道相互作用；我在《談談“計算時是否需要加DFT-D3色散校正？”》（http://www.shanxitv.org/413）里也說過物理本質和相互作用表象之間的關系。pi-pi作用類似于氫鍵、鹵鍵等，是屬于表象層面的，用來描述一種具有特定特征的相互作用，其內在本質就是前面說的來自于相距較近的pi電子之間的色散作用，這一點在Grimme的一篇經典的討論pi-pi作用本質的文章Angew. Chem. Int. Ed., 47, 3430 (2008)中通過嚴格的理論計算和分析對比已經論證得十分嚴格充分，而且也早已是量子化學領域內行人的共識。

有的文章試圖從軌道相互作用解釋pi-pi堆積出現的本質，這是極其有誤導性的，卻還廣泛以訛傳訛。2007年的時候wiki上的詞條說pi-pi作用來自于pi共軛體系間p軌道的重疊，前述Angew文章的腳注中專門對此進行了批判，指出沒有任何量子化學計算能支持這種說法。這也不難理解，本來兩個分子的pi軌道之間重疊程度極低（可以用《分子間軌道重疊的圖形顯示和計算》http://www.shanxitv.org/163介紹的方法考察），遠低于形成共價鍵時原子軌道間的重疊程度，因此有效重疊不足。而且兩個分子的pi占據軌道之間混合會產生全占據的成鍵和反鍵軌道，二者效果充分抵消了，對成鍵沒貢獻；而若一個分子的pi占據軌道和另一個分子的pi非占據軌道混合，意味著要出現分子間pi->pi*電子轉移，這通常又沒有明顯能使體系能量變得更低的內在驅動力（不像常見的較近距離的n->pi*超共軛往往可以明顯降低體系能量）。此外，按照《Multiwfn支持的分析化學鍵的方法一覽》（http://www.shanxitv.org/471）說的，用Multiwfn對pi-pi堆積的兩個分子間去計算衡量兩個部分之間有效共享電子對數的Mayer鍵級、模糊鍵級或離域化指數（DI），會發現數值很接近0，比如《全面揭示各種碳環與富勒烯之間獨特的pi-pi相互作用！》（http://www.shanxitv.org/727）介紹的文章里對18碳環與富勒烯之間算的Mayer鍵級僅為可忽略不計的0.04，也充分體現出pi-pi作用中的軌道相互作用成份基本可忽略不計。所以無論從哪個角度，pi-pi堆積的出現都不是軌道相互作用驅動的，頂多是在色散作用驅動下，pi-pi堆積結構出現后順帶出現了點可忽略的軌道相互作用而已。所以pi-pi作用在主流學術界被歸為非共價相互作用范疇，這是完全正確的。然而有一些論文試圖從軌道相互作用分析pi-pi作用的特征，還擺出一堆軌道圖，比如Phys. Chem. Chem. Phys., 15, 9397 (2013)就是典型文章，切勿把這類文章太當回事，很多都是瞎討論、尬討論。

pi-pi堆積的體系有一個普遍特點是在極小點結構下，pi-pi作用區域的原子間通常不是正好對著，而是相互錯位。下圖是暈苯二聚體的俯視圖，其中一個暈苯用紅色顯示，可以很清楚看到錯位特征，即一層的碳對著另一層的六元環中心。一層層堆疊的石墨中每一層之間也同樣是這樣錯位的。出現自發錯位有不同的解釋并且存在一定爭議，有人認為是因為錯位的結構下比嚴格面對面的結構下的原子間的Pauli互斥更低，例如Chem. Sci., 11, 6758 (2020)持這種觀點。也有人認為是因為錯位的結構下的靜電相互作用能更負（靜電吸引作用更強），在Phys. Chem. Chem. Phys., 24, 8979 (2022)中作者通過能量分解論證了這一點并反駁了Chem. Sci.那篇文章。靜電作用引起位錯的原因從邏輯上容易理解：形成pi-pi堆積的兩部分都有豐富的pi電子，面對面構型下pi電子間靜電互斥會較大，錯開后互斥自然就沒那么強了。雖然筆者更同意靜電效應是位錯出現的主導，但我也不否認降低Pauli互斥也可能是產生位錯的另一個驅動力，盡管相對次要。

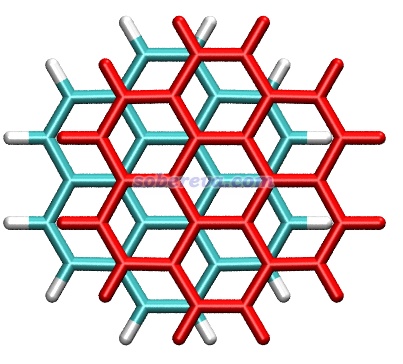
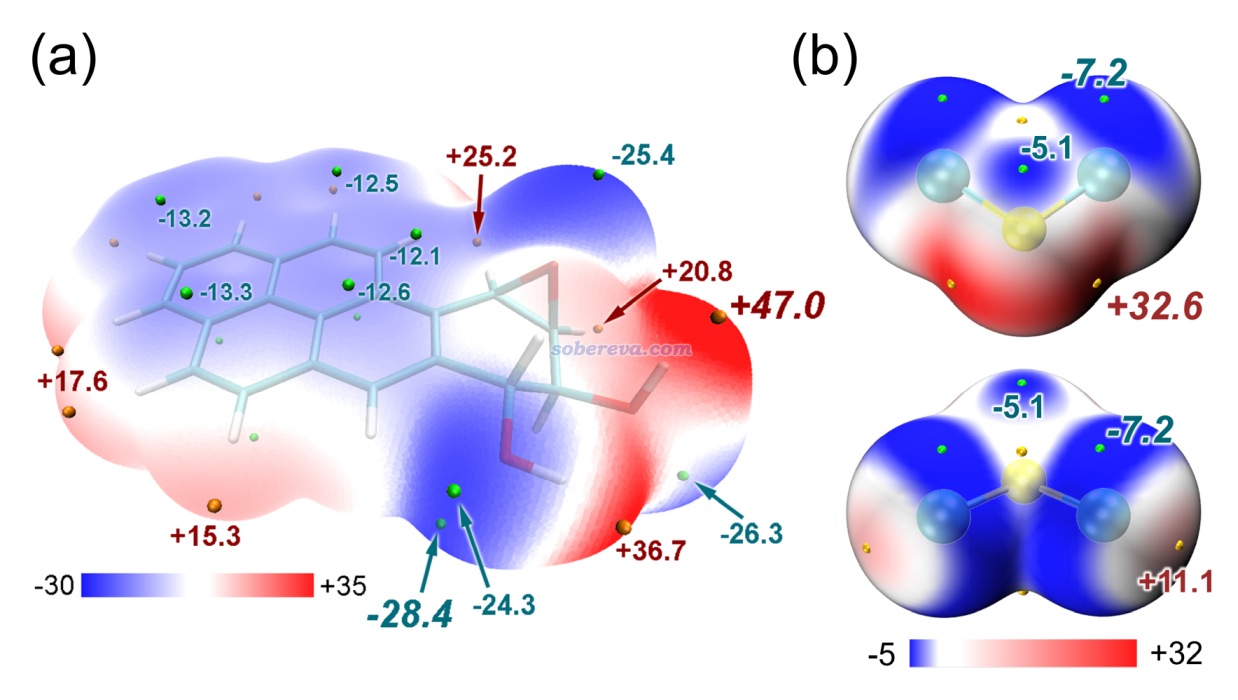
順帶一提，不止是pi-pi堆積二聚體，還有很多其它體系都是色散吸引作用驅動分子間結合，而靜電作用進一步影響幾何結構。《靜電效應主導了氫氣、氮氣二聚體的構型》（http://www.shanxitv.org/209）介紹的筆者的研究就是很好的例子，H2、N2的各種二聚體的相互作用能通過能量分解分析可以發現都是色散作用為主，但不同構型下的靜電作用的差異則直接影響不同構型的穩定性乃至存在與否，并且筆者發現通過靜電勢互補原理可以給出很直觀的解釋。這種靜電勢互補的分析方法也在《全面探究18碳環獨特的分子間相互作用與pi-pi堆積特征》（http://www.shanxitv.org/572）介紹的筆者的論文中也用來解釋為什么18碳環的pi-pi堆積二聚體是錯位的。平面環狀結構的18碳環具有獨特的平面內和平面外兩套pi電子，此文中確認了18碳環能夠形成分子間彼此平行的pi-pi堆積二聚體，下圖是按照《使用Multiwfn+VMD快速地繪制靜電勢著色的分子范德華表面圖和分子間穿透圖》（http://www.shanxitv.org/443）繪制的二聚體極小點結構下的單體的靜電勢著色的分子范德華表面的疊加圖，可以看到兩個碳環表面靜電勢為正和為負的區域在錯位的結構下是以互補的方式重疊的，很清晰地解釋了錯位的產生原因，即這種構型下的靜電吸引作用比一個個碳原子彼此精確對著的時候更強。

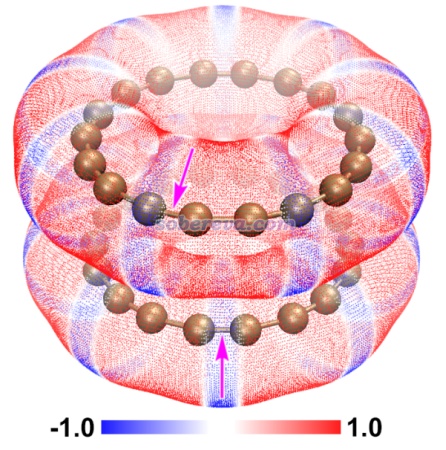
要注意的是，有些文章作者極度夸大了靜電作用對于pi-pi堆積形成的作用，不僅認為平行位錯構型的出現是因為此時靜電吸引作用最有利，還鼓吹pi-pi堆積結構的形成的本質就是靜電吸引作用，這是大錯特錯！最典型的這種文章就是Chem. Sci.,3 , 2191 (2012)，這篇文章的發表嚴重誤導了很多讀者。此文雖然是在前述的Grimme的pi-pi作用的研究之后寫的，而且文中還引了那篇文章，但給我的感覺是此文的作者完全沒好好看那篇文章，似乎也完全不懂什么叫電子相關作用，而依然基于古老且過于簡單（忽略了pi電子結構和穿透效應）的Hunter和Sanders的四極矩觀點盲目、主觀、武斷、信誓旦旦地解釋pi-pi堆積的位錯結構形成的本質，而完全沒有可信、嚴格的理論和計算數據作為依據，各種自說自話，并且還錯誤地解釋一些文獻里的理論計算數據，甚至還不承認pi-pi作用的概念。作者還執拗地認為非得是存在精確面對面堆積才能說明pi-pi作用的存在，并因為實際pi-pi堆積體系的極小點結構不是面對面堆積就被他用來否認存在pi-pi作用。此文文中給出了下圖，令一些初學者不明覺厲，誤以為不僅清晰解釋了為什么平行位錯結構比精確面對面結構更有利，還誤以為這種二聚體的形成主要靠的就是靜電吸引作用，完全沒分清楚pi-pi堆積二聚體的形成中色散作用和靜電作用的主次關系。還有不少其它文章如J. Chem. Soc., Dalton Trans., 2000, 3885也是類似地對pi-pi作用存在嚴重誤解、給出誤導性的示意圖，讀者看到這種文章時切勿當回事！

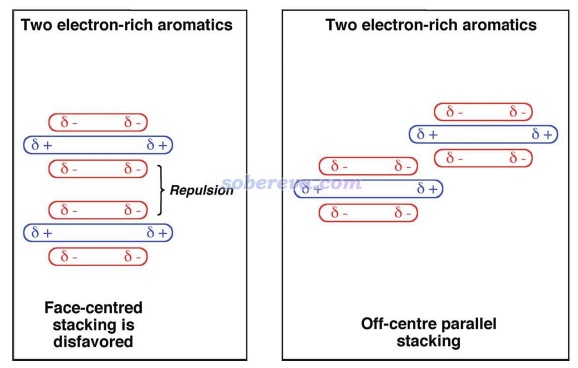
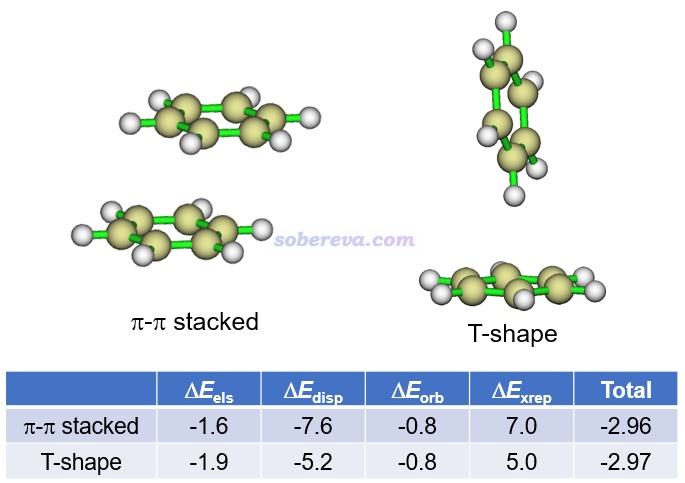
能量分解分析在pi-pi作用的研究中應用得非常普遍，對于認識其本質非常有幫助。這類方法將總的相互作用能分解成不同物理成份。例如將《使用sobEDA和sobEDAw方法做非常準確、快速、方便、普適的能量分解分析》（http://www.shanxitv.org/685）介紹的筆者提出的流行的sobEDAw能量分解方法用于苯的兩種二聚體構型可得到如下結果（計算級別：B3LYP-D3(BJ)/6-311+G(2d,p)并考慮counterpoise，單位為kcal/mol），可見色散項ΔE_disp遠比靜電作用項ΔE_els更負，軌道相互作用項ΔE_orb更是微乎其微，故色散作用對苯的分子間結合起到主導作用。特別是在平行位錯的結構下的ΔE_disp比T構型下的明顯負得多（同時ΔE_els的大小還變小），充分體現出平行位錯結構下才有的pi-pi作用的本質是色散作用，這和上文對pi-pi作用本質的討論相一致。平行位錯結構下，色散作用對總吸引作用項的貢獻百分比是：-7.6/(-7.6-0.8-1.6)*100=76%。

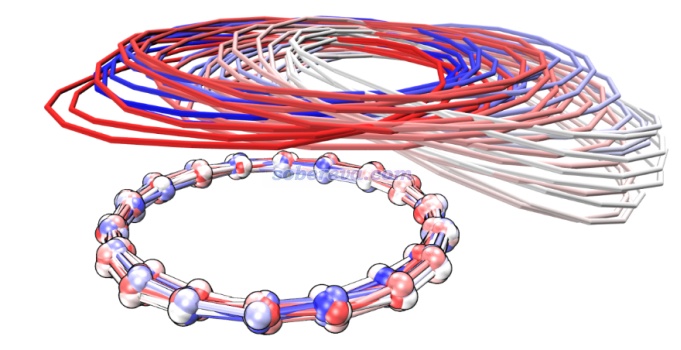
順帶一提，pi-pi堆積的結構在現實環境中一般很容易發生分子間相對滑移（除非有額外的位阻效應等阻礙），這是由于滑移導致能量變化很小。Carbon, 171, 514-523 (2021)文中做18碳環二聚體的勢能面掃描、Phys. Chem. Chem. Phys., 24, 8979 (2022)中做的苯分子平行二聚體的勢能面掃描都體現了這一點。并且由于滑移方向的勢能面很緩，哪怕室溫下也非常容易出現滑移。在Carbon, 171, 514-523 (2021)文中我給出了18碳環二聚體在100K下的4 ps的從頭算動力學的軌跡疊加圖（消除了下方的18碳環的整體運動以著重表現相對運動），如下所示，分子位置根據模擬時間按照藍-白-紅變化，可見在模擬過程中的確出現了顯著的滑移

3 pi-pi作用的強度

pi-pi堆積的極小點結構下的每一對近距離接觸的原子的pi-pi作用都是非常弱的，就是普通范德華作用的程度，但是當涉及pi-pi作用的原子很多時，就可以達到很高的強度，甚至能達到近乎化學鍵的程度。最強的pi-pi作用就是從微觀來看無限延展的石墨中的層間pi-pi作用了。下面看一些實例，以令讀者更好地理解pi-pi作用的強度特征。

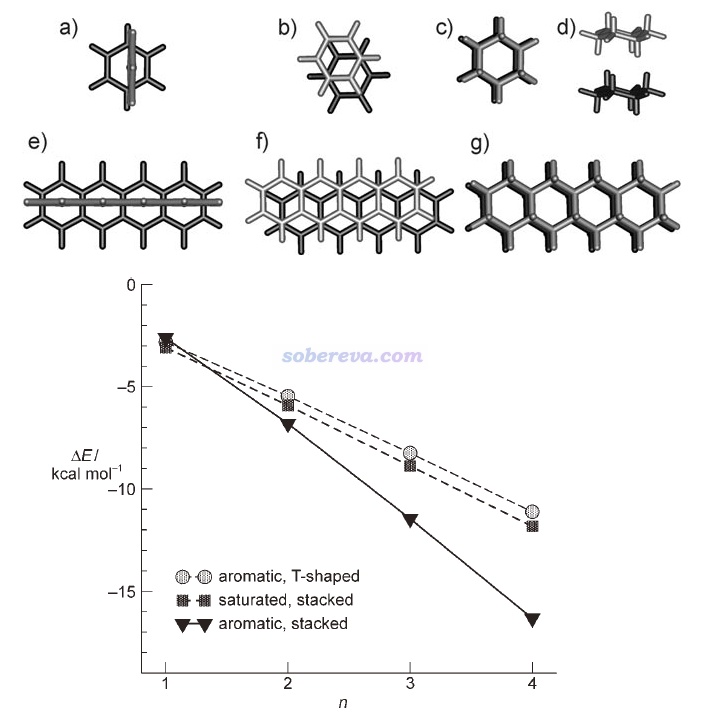
Angew. Chem. Int. Ed., 47, 3430 (2008)文中計算了T型苯二聚體（下圖a）、平行位錯苯二聚體（下圖b）、環己烷二聚體（下圖c和d是兩個視角）的相互作用能，并且還將它們的環數n從1逐漸加到4（分別對應下圖e、f、g的結構），以考察了三種作用類型的相互作用能隨環數的變化，分別對應下圖的aromatic T-shaped、aromatic stacked和saturated stacked三條曲線。由圖可見，當pi-pi作用涉及的原子很少時，即苯二聚體，由于pi-pi作用還不夠強，因此平行位錯二聚體的能量比靜電吸引作用更強的苯T型二聚體略微更高，相互作用強度比起無pi-pi作用特征的環己烷二聚體沒優勢。但隨著環數增加，pi-pi作用強度不斷增大，使得具有pi-pi堆積結構的二聚體的相互作用變得顯著強于不具備這種特征的二聚體。四并苯的二聚體的相互作用能已達到-16 kcal/mol（67 kJ/mol），這已經是水二聚體這種普通強度氫鍵作用能的3倍左右了。

可見，前面提到的Chem. Sci.,3 , 2191 (2012)那篇文章拿兩個苯及其衍生物在液體和晶體中普遍缺少平行位錯構型的出現，以及平行位錯的苯二聚體不是能量最低構型，以此鼓吹pi-pi作用不是一種客觀存在的作用，這明顯是極其狹隘的。

對本文第1節的兩個暈苯的二聚體，在DLPNO-CCSD(T)級別下算出來的相互作用能達到-20 kcal/mol，也是相當強了。

前面給出的18碳環二聚體的相互作用能，在Carbon, 171, 514-523 (2021)中我用ωB97X-V/def2-QZVPP結合counterpoise校正的計算結果為-9.2 kcal/mol（-38.5 kJ/mol），達到平行位錯的苯二聚體的相互作用能的大約三倍，無疑也是非常顯著的pi-pi作用了。

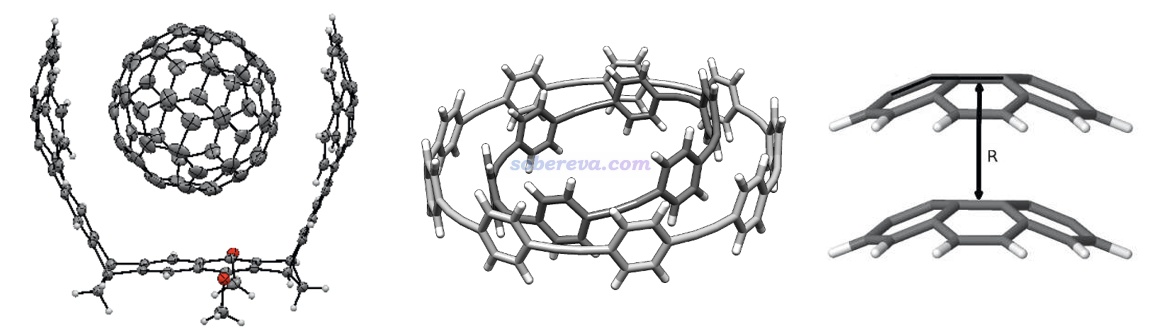
不是只有平面區域之間才可能有pi-pi作用，例如下面三個體系的pi-pi作用區域都是有顯著曲率的。下圖左邊的結構是Org. Lett., 17, 5292 (2015)中合成出的主-客體復合物晶體的一部分，由于客體分子與富勒烯之間的pi-pi作用面積頗大，B97D/QZVP級別計算的相互作用能達到了-50 kcal/mol，已經是弱化學鍵的強度了。下圖右側是碗烯的pi-pi堆積二聚體，相互作用的研究見J. Phys. Chem. A, 116, 11920 (2012)。

4 圖形化展現pi-pi作用區域

《使用Multiwfn做IGMH分析非常清晰直觀地展現化學體系中的相互作用》（http://www.shanxitv.org/621）以及《一篇最全面介紹各種弱相互作用可視化分析方法的文章已發表！》（http://www.shanxitv.org/667）中的綜述詳細介紹的筆者提出的IGMH方法用于圖形化展現片段間相互作用效果極佳，已被廣為使用。IGMH用于展現自定義片段間的pi-pi作用、判斷pi-pi作用是否存在尤為好用，因此在此給出一些簡單例子予以體現。其方法的原理、細節、計算操作見上面的文章。如果你不知道pi-pi作用可能出現在哪，不方便定義片段，則應當用《使用IRI方法圖形化考察化學體系中的化學鍵和弱相互作用》（http://www.shanxitv.org/598）介紹的筆者的IRI方法，可以把體系中所有相互作用區域全都展現出來，也包括化學鍵作用區域。

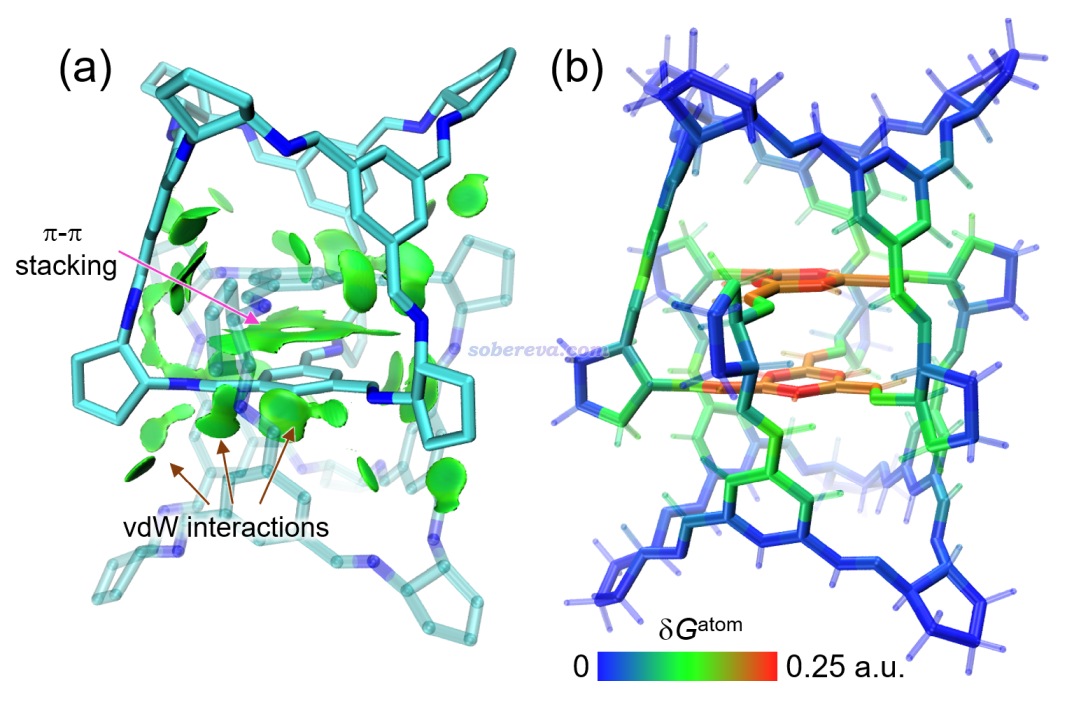
不是只有純碳的pi區域之間才可能有pi-pi作用，pi-pi作用也可以涉及到其它原子。眾所周知，DNA結構中相鄰層的堿基與堿基之間是平行堆疊的，再加上堿基區域有大量pi電子，所以這也屬于典型的pi-pi作用。下圖是從DNA中截取的堆疊的GCGC堿基對，兩層分子各定義為一個做IGMH分析的片段，兩層之間的綠色的IGMH方法定義的delta_g_inter函數的0.004 a.u.等值面非常清晰、優雅地展現出了pi-pi作用的主體區域。圖中還有個面積較小的等值面出現在O...O之間，雖然C=O鍵的O有pi電子，但這倆O的pi電子不是彼此對著的，所以這就只能算是普通的范德華作用區域了。

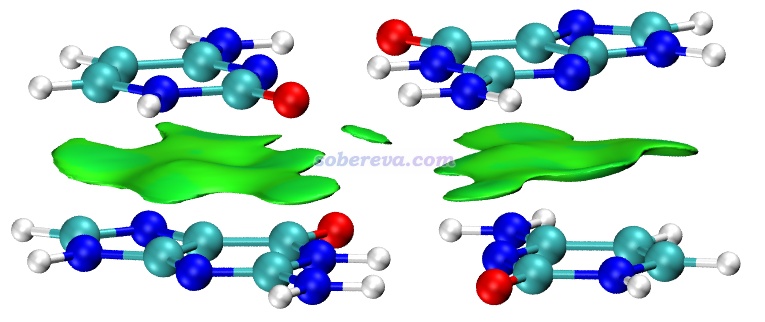
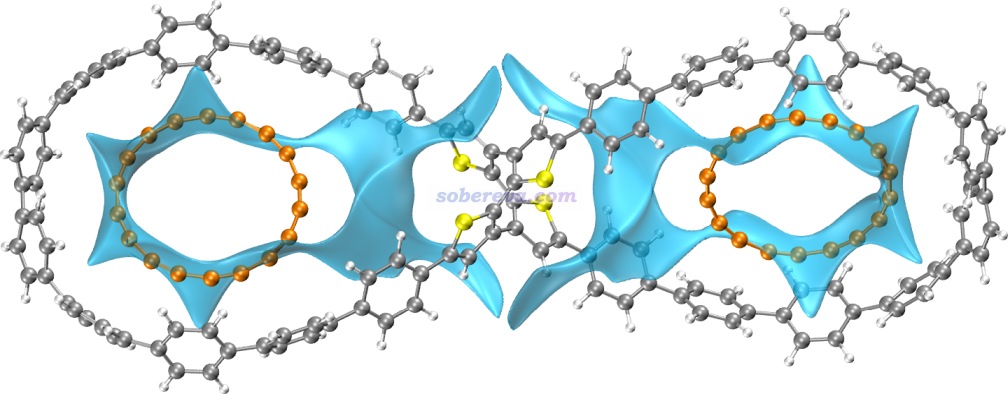
下圖是《8字形雙環分子對18碳環的獨特吸附行為的量子化學、波函數分析與分子動力學研究》（http://www.shanxitv.org/674）介紹的筆者的論文中的一張圖，研究的是OPP雙環分子結合兩個18碳環后的復合物。圖中綠色等值面直觀地展現出在什么區域18碳環與OPP主體分子間有顯著的pi-pi作用。可見pi-pi作用主要出現在OPP和18碳環近距離接觸的體系的兩端，而OPP靠中間區域離18碳環較遠因此缺乏pi-pi作用。順帶一提，18碳環是極少有的同時具有平面內（in-plane）和平面外（out-of-plane）兩套全局離域的pi電子的體系，當前體系中18碳環主要憑借的是平行于環方向分布的pi電子與OPP大環上的垂直于苯環的pi電子產生pi-pi作用，這是極為新穎、獨特的pi-pi作用形式。如果讀者對碳環類體系感興趣，非常建議進入http://www.shanxitv.org/carbon_ring.html觀看筆者發表的所有碳環相關的理論研究和對應的深入淺出的評述文章。

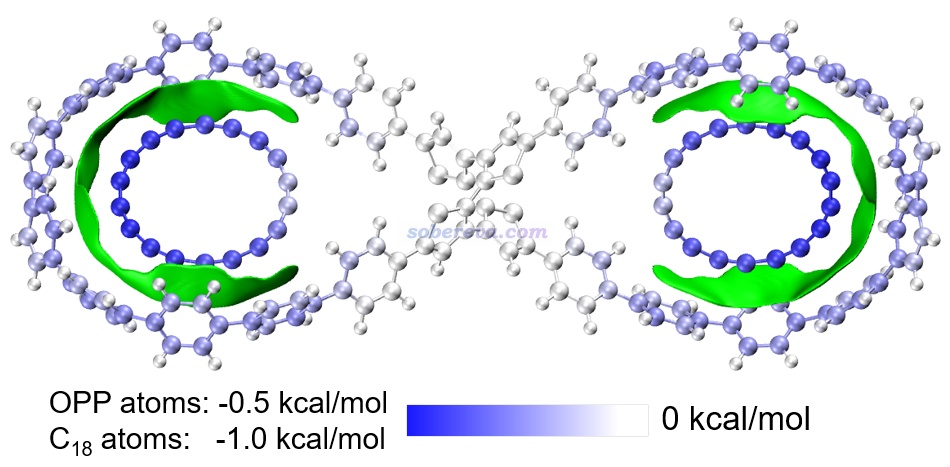
上圖中還對利用Multiwfn的基于力場的能量分解（EDA-FF）功能計算了各個原子對分子間相互作用的貢獻并對原子進行了著色，展現出了更豐富的信息。這種分析見《使用Multiwfn做基于分子力場的能量分解分析》（http://www.shanxitv.org/442）。

在《全面揭示各種碳環與富勒烯之間獨特的pi-pi相互作用！》（http://www.shanxitv.org/727）介紹的文章中，筆者全面研究了碳環與富勒烯的相互作用，其中給出了下圖，展示了不同尺寸的兩個碳環與富勒烯形成的三聚體。并且為了直觀區分富勒烯-碳環和碳環-碳環兩種pi-pi作用，分別將對應的等值面用綠色和青色著色。可見此圖極好地將體系中兩種pi-pi作用出現的主要位置展現了出來，比起在文中只是給出個幾何結構圖信息豐富得多。

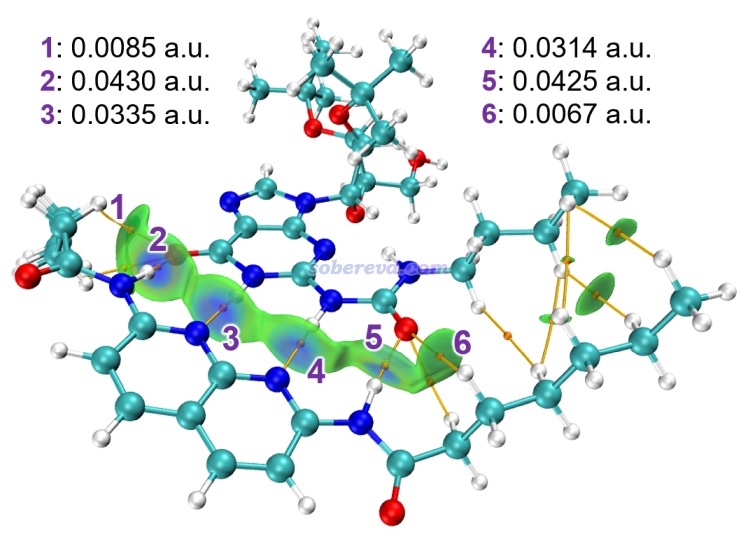
標準的IGMH圖是通過sign(λ2)ρ函數對等值面著色的，ρ是電子密度。按照IGMH方法的標準的色彩刻度著色的話，ρ接近0的區域的等值面都是綠色。由于pi-pi作用區域、普通范德華作用、極弱的氫鍵（如C-H作為氫鍵給體時）等情況的作用區域的電子密度都很低（0.01 a.u.以內），因此相應的標準方式著色的IGMH等值面都會是綠色或很接近綠色。因此解釋IGMH圖的等值面時必須結合不同特征的弱相互作用的基本定義，不能單純根據顏色去亂解釋。比如網上有人問我“下面這個圖里紅圈部分是pi-pi作用嗎？”，這實在是匪夷所思的問題。跨越那個等值面和右下方苯環的pi電子區域直接作用的是一個氫原子，氫原子又沒pi電子，怎么可能是pi-pi作用！？而且右下方的苯環也明顯不可能和左上方的苯環有pi-pi作用，一方面二者離得老遠，另一方面二者的pi電子區域也根本不相互對著，顯然無論如何也不可能算是pi-pi作用。

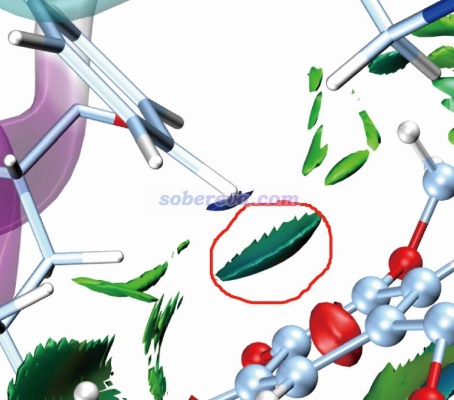
那么上圖中紅圈里的等值面算什么作用？明顯這是pi-氫鍵，C-H作為氫鍵給體，其中氫帶一定正電荷（這一點用H的原子電荷就能體現，原子電荷的相關知識見《一篇深入淺出、完整全面介紹原子電荷的綜述文章已發表！》http://www.shanxitv.org/714這篇綜述），右下角的苯環上的pi電子令苯環上方顯負電性而作為氫鍵受體（用靜電勢可直接體現，參見http://bbs.keinsci.com/thread-219-1-1.html里匯總的靜電勢相關資料和我的相關博文）。

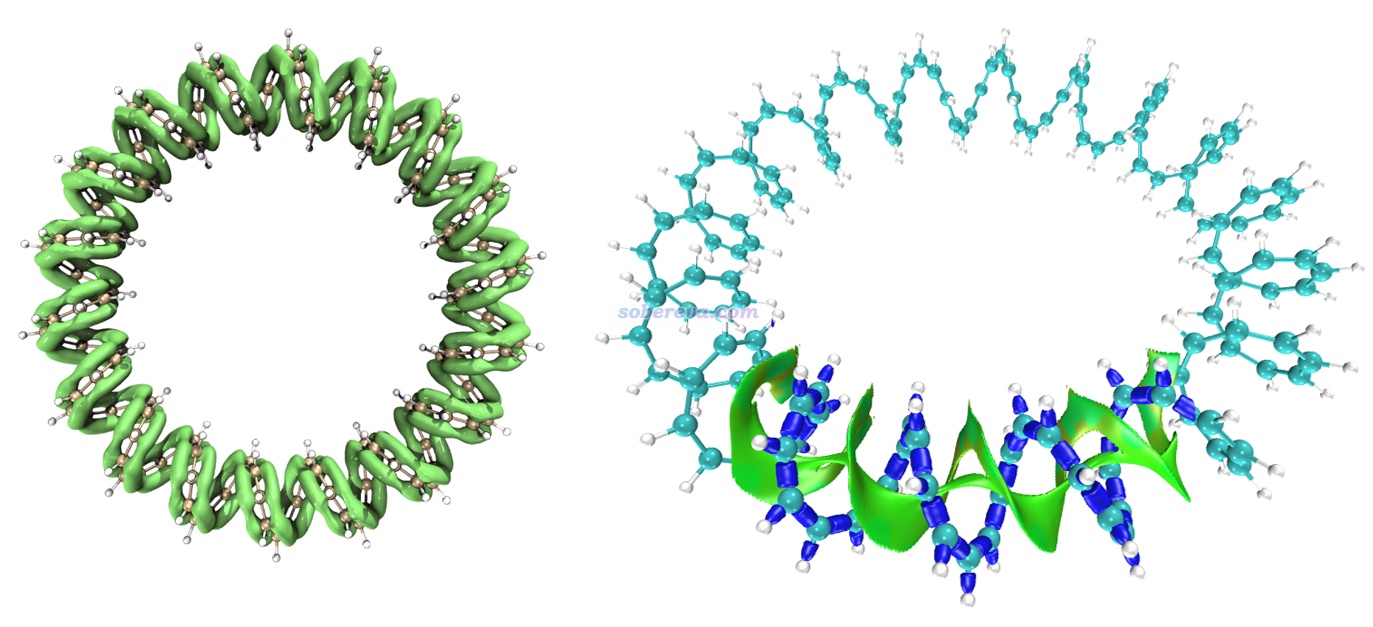
下面再舉一個IRI圖展現pi-pi作用區域的例子。Multiwfn的原文之一J. Chem. Phys., 161, 082503 (2024)里給出了144-輪烯的LOL-pi函數的等值面圖，如下圖左側所示，此圖清晰直觀地展現出了這個全局大共軛體系的pi電子的主要離域路徑。根據此圖展現的pi電子的分布情況，憑直覺就知道這個體系里肯定存在pi-pi作用。下圖右側是對這個體系的其中一個局部區域繪制的IRI等值面圖，藍色的等值面展現出了化學鍵作用區域，綠色的等值面清楚直觀地展現出了pi-pi作用區域。可見這個體系非常有趣，pi-pi作用區域綿延不斷貫通整個體系！也正是有分子內pi-pi作用的存在，此體系才能形成螺旋狀結構，要不然就散了（如同用不能描述色散作用的理論方法優化DNA結構時結構會散掉）。

5 衡量pi-pi作用強度的方法

這一節說一下如何衡量pi-pi作用強度。最簡單的方法就是計算pi-pi堆積二聚體的相互作用能，作用能越負說明作用越強。但如果要討論二聚體的熱力學穩定性，則需要計算結合自由能，溶劑環境中還得考慮溶劑模型。相關知識參見《談談分子間結合能的構成以及分解分析思想》（http://www.shanxitv.org/733）。復合物AB在特定結構下，A和B的相互作用能的最常規的計算方法就是用E(AB)-E(A)-E(B)方式手動計算，做sobEDAw能量分解（http://www.shanxitv.org/685）時也會順帶給你相互作用能。

以上述方法算相互作用能的一個問題是，如果兩個分子之間不僅僅有pi-pi作用，還有其它作用（如氫鍵），那么得到的只是總相互作用能。如果想只得到pi-pi作用能，有幾個辦法可以用：
(1)用《使用Multiwfn做基于分子力場的能量分解分析》（http://www.shanxitv.org/442）介紹的EDA-FF能量分解方法，將兩個分子的pi作用區域定義為兩個片段，讓Multiwfn給出基于分子力場的這兩個部分的相互作用能，取其中的范德華作用能（即色散作用和交換-互斥作用之和）。如果你只需要色散部分，還有另一種做法，見《使用Multiwfn圖形化展現原子對色散能的貢獻以及色散密度》（http://www.shanxitv.org/705）。這兩種做法還都可以給出具體原子產生的貢獻，并可以對原子進行著色以便通過圖像直觀展現和考察
(2)如果分子間同時有pi-pi作用和氫鍵，且其它作用可忽略不計，可以按《透徹認識氫鍵本質、簡單可靠地估計氫鍵強度：一篇2019年JCC上的重要研究文章介紹》（http://www.shanxitv.org/513）介紹的方法使用Multiwfn做拓撲分析估計出氫鍵作用能，從總相互作用能中扣掉之作為pi-pi作用能
(3)對體系進行恰當改造，基本保留每個分子參與pi-pi作用的部分，然后將總相互作用能近似當成pi-pi作用能。

如果是分子內的pi-pi作用能的估計，還可以參考《計算分子內氫鍵鍵能的幾種方法》（http://www.shanxitv.org/522）里的說明舉一反三處理。

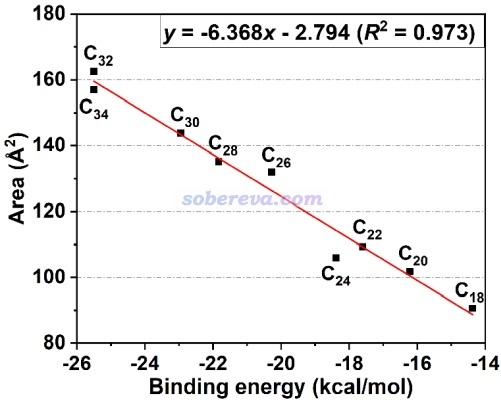
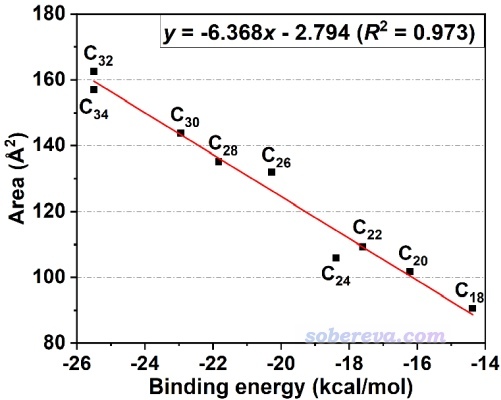
在特定條件下，pi-pi作用強度和IGMH的等值面面積有密切的正相關性。《全面揭示各種碳環與富勒烯之間獨特的pi-pi相互作用！》（http://www.shanxitv.org/727）介紹的文章中給出了下圖，是不同原子數的碳環與富勒烯之間的相互作用能和描述pi-pi作用的IGMH等值面面積的關系，可見有挺理想的線性關系。通過這種關系，可以直接根據pi-pi作用區域的等值面面積估計對應的pi-pi相互作用能。這種面積的計算方法見《計算IGMH等值面的面積和體積的方法》（http://www.shanxitv.org/738）。

Chem. Commun., 48, 9239 (2012)提出的LOLIPOP方法值得一提。基于單個分子的波函數文件，就可以用Multiwfn非常容易地計算體系中的各個六元環的LOLIPOP指數，此值越小說明這個環發生pi-pi堆積的能力越強，原文對不同體系以苯分子作為探針分子進行了測試證實了這一點。Multiwfn手冊3.100.14節有LOLIPOP的詳細介紹，4.100.14節有計算實例。

6 不同理論方法描述pi-pi作用的能力

色散作用的更深層本質是電子的庫侖相關作用，因此做量子化學或第一性原理計算時，若想描述好pi-pi作用，用的方法必須能描述好庫侖相關，顯然高精度后HF方法都沒問題，比如CCSD(T)在計算pi-pi作用上可以算是金標準。至于低級別的后HF方法MP2則傾向于明顯高估pi-pi作用，絕對不要用。

對于特別常用的DFT，描述pi-pi作用的能力基本等同于描述普通色散作用的能力，如果泛函原本描述色散作用爛（如PBE、PBE0）或者完全不能描述（如B3LYP），就必須帶色散校正，參考《談談“計算時是否需要加DFT-D3色散校正？” 》（http://www.shanxitv.org/413）、《DFT-D色散校正的使用》（http://www.shanxitv.org/210）、《談談量子化學研究中什么時候用B3LYP泛函優化幾何結構是適當的》（http://www.shanxitv.org/557）。本來就帶色散校正的wB97M-V、wB97X-D3等直接就能很好描述pi-pi作用。M06-2X描述pi-pi作用雖然定性正確但不算太好，加了零阻尼DFT-D3色散校正后對pi-pi作用的描述有明顯改進，但還是不如B3LYP-D3(BJ)，對比測試見考慮了很多pi-pi作用體系的L7測試集的原文（J. Chem. Theory Comput., 9, 3364 (2013)）。雙雜化泛函由于帶有MP2項，所以都有描述pi-pi作用的能力，但一般在考慮了色散校正后才會變得足夠好，如revDSD-PBEP86-D3(BJ)。

實際上DFT-D那種形式的色散校正在原理上對于描述pi-pi作用并非很理想，因為pi電子不是繞著原子核球對稱分布的，而DFT-D校正能的公式依賴的只是原子間距離（這里不考慮三體校正項），沒體現出pi電子在原子核周圍的具體分布特征。不過這倒也不是明顯問題，常用的DFT-D3、DFT-D4色散校正對于描述pi-pi作用從實際效果上來看并沒有什么問題。

在半經驗方法層面，專門考慮了對色散作用描述的GFN2-xTB、PM6-D3H4X'、PM6-ML在表現pi-pi作用方面優秀，見J. Chem. Theory Comput., 21, 678 (2025)里3圖基于L7測試集的測試，PM6-D3和PM7只能算是定性正確。至于沒專門考慮對色散作用描述的諸如PM6、AM1等方法則完全失敗。

主流的分子力場，如GAFF、AMBER、CHARMM、OPLS-AA、MMFF94等，對pi-pi作用的描述雖然跟像樣的量子化學方法比算不上出色，但至少也算定性正確，因為它們都有描述色散作用的能力。J. Chem. Inf. Model., 49, 944 (2009)的測試專門體現了這點（不過這篇文章也有不少漏洞和槽點）。

7 疏水作用與pi-pi作用的關系

眾所周知，疏水效應使得水環境下非極性物質傾向于發生聚集，本質是溶劑的熵效應。兩個石墨烯片段在水中會自發堆積在一起，這算疏水作用還是pi-pi作用？實際上二者都有，對于堆積結構的形成起到協同作用。疏水效應更為普遍，無論兩個溶質的接觸區域是否有pi電子，只要溶質是基本無極性的，在水中都有疏水作用促使它們發生結合。而對于pi電子區域暴露的兩個溶質，疏水效應則在pi-pi作用的基礎上進一步促進了它們的pi-pi堆積結構的出現。如《全面揭示各種碳環與富勒烯之間獨特的pi-pi相互作用！》（http://www.shanxitv.org/727）介紹的文章的理論計算所示，在水環境下碳環與富勒烯之間的結合自由能的大小顯著大于在真空下，充分體現了這一點。

順帶一提，前述的Chem. Sci.,3 , 2191 (2012)一文居然誤以為溶劑環境下pi共軛體系間出現堆積結構僅僅是因為溶劑效應，并似乎試圖靠這個否認真空環境下也存在pi-pi相互作用，甚至說the terms "pi-stacking" or "pi–pi interactions" do not describe any physically meaningful interaction，實在是難以理喻！！！PS：這樣的文章能通過Chem. Sci.的審稿真是離譜。

8 總結&判斷pi-pi作用的標準

本文系統地對pi-pi作用的各個方面進行了介紹，包括其基本特征、物理本質、強度范圍、圖形化展現方法、考察強度的方法、理論計算方法的精度、疏水作用與它的關系。通過本文，讀者應該已經對pi-pi作用有了較全面的了解，能夠進行正確的分析討論，并且能認識到哪些文章或書籍里的說法是有誤導性的。我也推薦讀者接下來閱讀本文一開始提到的筆者的一系列和pi-pi作用有關的研究文章和對應的介紹博文。

最后再總結一下pi-pi作用的常規判斷標準，便于讀者能確切判斷哪些作用算是pi-pi作用。通過下面第1、2條就可以進行粗略判斷，3、4、5可以作為進一步檢驗。一般意義的pi-pi作用應當能同時滿足所有條件
(1)相互作用的兩部分都有pi電子且其分布彼此相互對著。如果拿不準有沒有pi電子分布、分布朝向如何，可以按照《在Multiwfn中單獨考察pi電子結構特征》（http://www.shanxitv.org/432）介紹的方法直接把pi電子密度等值面圖畫出來，一目了然
(2)相互作用的pi電子之間離得不太遠。比如明顯超過5埃的直接就可以忽略了
(3)用Multiwfn做IGMH分析（如果得不到波函數文件或體系太大難以算得動的話，可以改用極便宜且只依賴于原子坐標的mIGM），在等值面數值調到諸如0.003 a.u.這樣較小的值時，在預期出現pi-pi作用的區域能明顯看到等值面
(4)兩部分之間的Mayer鍵級或模糊鍵級或離域化指數非常小（遠小于0.1），故而軌道相互作用可基本忽略。注：如《Multiwfn支持的分析化學鍵的方法一覽》（http://www.shanxitv.org/471）所述，Multiwfn在主功能9里計算鍵級之前可以用選項-1定義兩個片段，之后做鍵級計算時會給出兩個部分之間的總鍵級，即片段間每一對原子的鍵級的總和
(5)使用sobEDAw等能量分解方法分析，色散項應當占所有吸引項總和的大部分，軌道相互作用項應當占比微小

文/Sobereva@北京科音  2025-Jan-1

1 前言

有人在思想家公社QQ群（http://www.shanxitv.org/QQrule.html）里問怎么計算分子軌道的體積，并且貼了一張軌道等值面圖。只要計算出這個等值面里包圍的體積就可以達到這個目的（雖然也可以有其它方式的定義，但沒這么簡單直觀）。這里我介紹一下怎么利用Multiwfn程序的定量分子表面分析功能來實現這個目的。定量分子表面分析功能之前在《使用Multiwfn的定量分子表面分析功能預測反應位點、分析分子間相互作用》（http://www.shanxitv.org/159）有簡要介紹，結合Multiwfn的極度靈活的設計，這個功能還能做很多其它的分析，正如本文所展示的。

如果讀者不熟悉Multiwfn，應當閱讀《Multiwfn FAQ》（http://www.shanxitv.org/452）、《Multiwfn入門tips》（http://www.shanxitv.org/167）、《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379）。Multiwfn可以在http://www.shanxitv.org/multiwfn免費下載，不要用上古版本。

2 實例

這里以Multiwfn計算下面這個D-pi-A體系的HOMO軌道的體積為例，圖中的軌道等值面數值為0.05，此體系的波函數文件是Multiwfn目錄下的examples\excit\D-pi-A.fchk。注意等值面包圍的體積直接依賴于等值面數值的選取，橫向對比時必須統一。

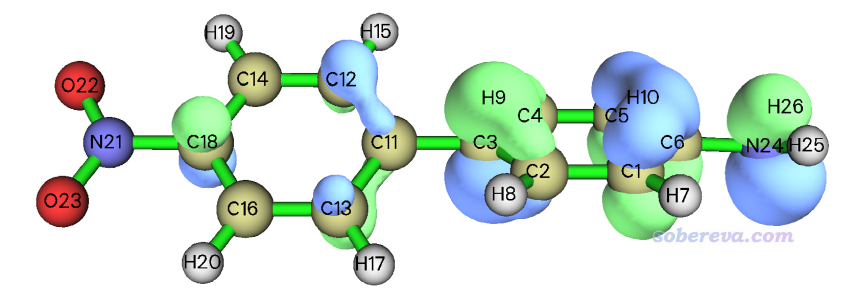
啟動Multiwfn，然后輸入
examples\excit\D-pi-A.fchk
5  //計算格點數據
4  //軌道波函數
h  //HOMO
4  //設置格點間距
0.25  //0.25 Bohr是精度和耗時的較好權衡。體系大的話也可以用大一些的格點間距來節約耗時但會損失一些精度
0  //返回主菜單
13  //處理格點數據
11  //格點數據運算
13  //取絕對值。軌道波函數有正有負，這一步使之都變成正值
-1  //返回主菜單
12  //定量分子表面分析
1  //選擇定義表面的方式
11  //用內存中的格點數據定義等值面
0.05  //等值面數值
6  //開始表面分析且不考慮被映射的函數

從屏幕上可以看到以下結果，即體積為14.2 Angstrom^3，順帶著軌道等值面的面積69.0 Angstrom^2也顯示出來了。

 Volume:    95.86111 Bohr^3  (  14.20515 Angstrom^3)
 Estimated density according to mass and volume (M/V):   25.0417 g/cm^3
 Overall surface area:         246.50998 Bohr^2  (  69.02983 Angstrom^2)

感興趣的話，還可以選擇選項-3 Visualize the surface看一下當前等值面對應的圖像，體積就是這個等值面里面包圍的部分

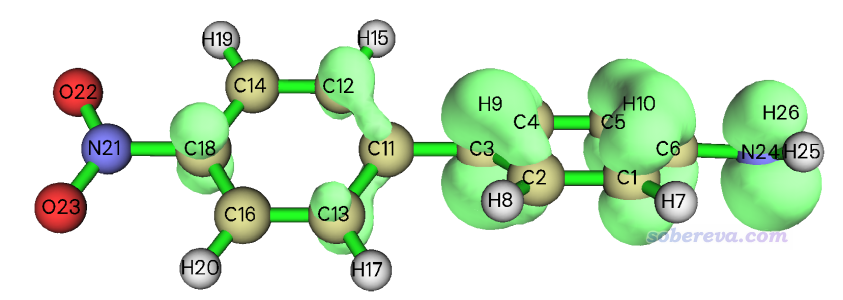
對比一下，看看下面這個第18號分子軌道的體積如何

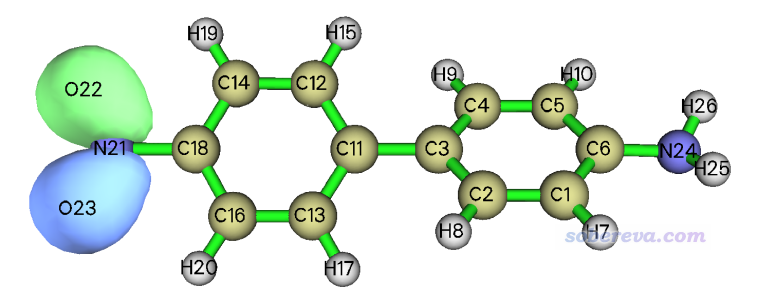
退回到主菜單，把下面這一串命令復制到Multiwfn窗口里即可，結果是7.3 Angstrom^3，可見只有HOMO的一半，和肉眼看上去的軌道體積差異相一致。
5
4
18
4
0.25
0
13
11
13
-1
12
1
11
0.05
6

3 批量計算

在《詳談Multiwfn的命令行方式運行和批量運行的方法》（http://www.shanxitv.org/612）里專門講了怎么用Multiwfn批處理計算。這里提供一個腳本，可以便捷地用前文的方法批量計算特定序號范圍的軌道的體積。http://www.shanxitv.org/attach/734/orbvol.sh是個Bash shell腳本，用來計算examples\excit\D-pi-A.fchk這個體系所有占據軌道（1到56號）的體積，內容如下所示。其中istart和iend是起始和終止的軌道序號，這倆值和被處理的波函數文件路徑都可以根據實際需要修改。運行之前，Multiwfn可執行文件所在目錄需要添加到PATH環境變量下使得能夠通過Multiwfn命令啟動之。

#!/bin/bash
istart=1
iend=56
for ((i=$istart;i<=$iend;i=i+1))
do
cat << EOF >> orbvol.txt
5
4
$i
4
0.25
0
13
11
13
-1
12
1
11
0.05
6
-1
-1
EOF
done
echo "q" >> orbvol.txt
echo "Running Multiwfn..."
Multiwfn examples/excit/D-pi-A.fchk < orbvol.txt >> result.txt
grep "Volume:" result.txt | nl -v$istart
rm ./orbvol.txt result.txt

運行后，屏幕上看到各個軌道的體積：
     1   Volume:     2.88332 Bohr^3  (   0.42726 Angstrom^3)
     2   Volume:     2.89404 Bohr^3  (   0.42885 Angstrom^3)
     3   Volume:     2.42980 Bohr^3  (   0.36006 Angstrom^3)
     4   Volume:     2.40622 Bohr^3  (   0.35656 Angstrom^3)
...略
    54   Volume:    95.10824 Bohr^3  (  14.09359 Angstrom^3)
    55   Volume:    95.86240 Bohr^3  (  14.20534 Angstrom^3)
    56   Volume:    95.86111 Bohr^3  (  14.20515 Angstrom^3)

將軌道體積相對于軌道序號作柱形圖，如下所示。可見前16號軌道的體積非常小，這是因為它們都是內核軌道。

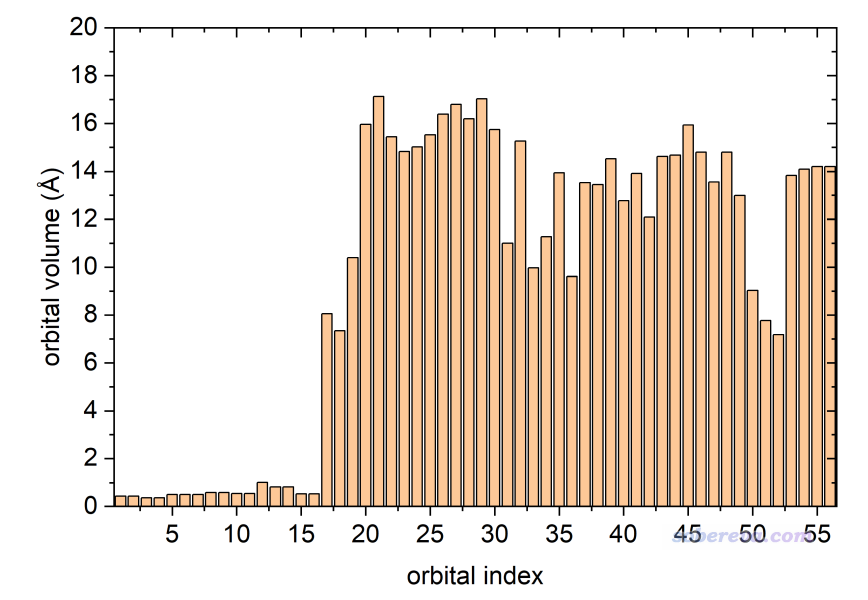
筆者之前寫過《通過軌道離域指數(ODI)衡量軌道的空間離域程度》（http://www.shanxitv.org/525），里面用我提出的ODI指數考察了與本文相同的D-pi-A體系的各個軌道的離域程度，并且繪制了ODI與軌道序號之間的柱形圖。將上圖與ODI的柱形圖相對比，可以看到兩個圖有明顯的互補性，即ODI越低（體現軌道越離域、越能同時覆蓋很多原子），軌道體積傾向于越大。如果你的目的就是想衡量軌道的離域程度，ODI相對更嚴格，畢竟不依賴于軌道等值面數值的選取（軌道等值面數值設得很大的話，軌道等值面就完全看不到了，體積為0）。而用軌道體積來說事的好處是可以直接與等值面圖相對應，結合圖像討論非常清楚直觀。

4 其它

本文的做法不限于計算考察分子軌道的體積，對任意軌道都可以考察，如定域化軌道、NTO軌道、雙正交化軌道、NAdO軌道、AdNDP軌道等等，載入含有相應軌道的波函數文件即可，產生方法在下文說了。
Multiwfn的軌道定域化功能的使用以及與NBO、AdNDP分析的對比
http://www.shanxitv.org/380
用于非限制性開殼層波函數的雙正交化方法的原理與應用
http://www.shanxitv.org/448
使用鍵級密度(BOD)和自然適應性軌道(NAdO)圖形化研究化學鍵
http://www.shanxitv.org/535
使用AdNDP方法以及ELF/LOL、多中心鍵級研究多中心鍵
http://www.shanxitv.org/138

文/Sobereva@北京科音  2024-Dec-12

1 前言

眾所周知，苯具有極其顯著的芳香性特征。它的重要的等電子體borazine（硼吖嗪）也被稱為無機苯，具有B3N3H6的化學組成，是把苯的六元碳環上的碳替換為交替相連的氮和硼。無機苯的芳香性雖然早就被很多文章研究過，都指出其芳香性明顯不及苯，但不同文章里關于它的芳香性強度說法不一，甚至出入很大，還有的文章使用不嚴謹的方法對其芳香性進行表征得到了誤導性的結論。New J. Chem., 39, 2483 (2015)提出了carborazine（我將它譯為碳硼吖嗪）分子，是苯的另一種等電子體，它的結構介于苯與無機苯之間，如下所示，雖然此文指出了它具有芳香性，但對芳香性研究得并不深入和嚴格。

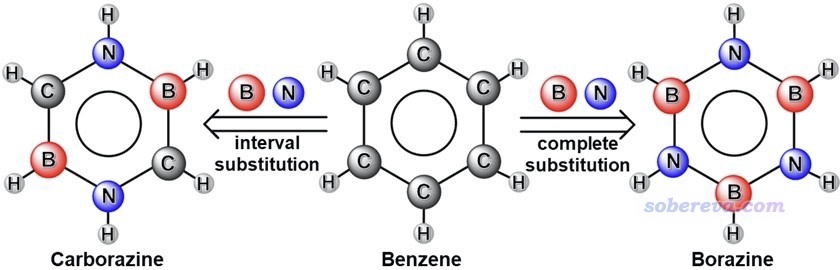
為了真正全面、透徹闡釋苯及其上述兩種等電子體的芳香性特征、揭示芳香性差異的內在本質，以及了解carborazine的特點，北京科音自然科學研究中心的盧天和江蘇科技大學的劉澤玉等人近期在知名的Chem. Eur. J.（歐洲化學）期刊上發表了專門的研究文章充分研究了上述體系的電子結構和芳香性，非常歡迎大家閱讀和引用：

Yang Wu, Xiufen Yan, Zeyu Liu,* Tian Lu,* Mengdi Zhao, Jingbo Xu,
Jiaojiao Wang, Aromaticity in Isoelectronic Analogues of Benzene, Carborazine and Borazine, from Electronic Structure and Magnetic Property, Chem. Eur. J., 30, e202403369 (2024) DOI: 10.1002/chem.202403369

此文可通過以下鏈接免費在線閱讀：
https://onlinelibrary.wiley.com/share/author/PYSFYG86FNTHBBWXITBI?target=10.1002/chem.202403369

這篇文章還被選為了Chem. Eur. J.的封面文章（DOI: 10.1002/chem.202486603）：

下文將對這篇文章的主要內容做深入淺出的介紹，便于讀者快速順利地了解文章的研究結論，并且同時附加一些額外信息，使得讀者可以更充分了解研究思想和計算細節，從而能夠參考本文的內容更好地做自己的研究。

本文充分利用了強大的Multiwfn程序（http://www.shanxitv.org/multiwfn）做波函數分析討論芳香性，是波函數分析方法和Multiwfn程序的很好且十分典型的應用范例。Multiwfn能做的芳香性分析在《衡量芳香性的方法以及在Multiwfn中的計算》（http://www.shanxitv.org/176）里有簡略介紹，在北京科音量子化學波函數分析與Multiwfn程序培訓班（http://www.keinsci.com/WFN）里有多達160頁以上的幻燈片極為完整、全面、系統地講授芳香性的各種概念和全部分析手段，非常推薦參加！

與本文的研究有密切相關的是《18碳環等電子體B6N6C6獨特的芳香性：揭示碳原子橋聯硼-氮對電子離域的關鍵影響》（http://www.shanxitv.org/696）介紹的Inorg. Chem., 62, 19986 (2023)一文，十分建議看完下文后認真閱讀。

2 苯、無機苯和carborazine的結構和穩定性

文中首先用ωB97XD/def2-TZVP對上述三個體系做了幾何優化，這是相當穩的級別，也被用于http://www.shanxitv.org/carbon_ring.html列舉的18碳環及其各種衍生物的研究中，后文的各種分析也都是在這個級別下做的。得到的苯的C-C鍵長1.387埃和電子衍射實驗測定的1.399埃相符極好，得到的無機苯的B-N鍵長1.426埃也完全在X光衍射測定的1.422-1.429埃范圍內。所有三個結構都是純平面的，苯、無機苯和carborazine分別屬于D6h、D3h和C2h點群。

尚未合成的carborazine的穩定性并不得而知，跑從頭算動力學（AIMD）是一種有效的檢驗手段，例如在《18個氮原子組成的環狀分子長什么樣？一篇文章全面揭示18氮環的特征！》（http://www.shanxitv.org/725）介紹的文章里通過AIMD直接證明了18氮環非常不穩定。本文對carborazine和borazine用ORCA程序在ωB97XD/6-311G*級別下做了50 ps AIMD，由于AIMD的昂貴耗時使得模擬時間很有限，文中故意用了1000 K的較高溫度令勢能面的采樣盡量充分。文中還確認了當前溫度下的AIMD過程的平均總能量是高于極小點結構下的ZPE的，因此當前的模擬不會低估實際的振動基態能量。這種模擬在北京科音高級量子化學培訓班（http://www.keinsci.com/KAQC）里有超詳細的講解，在《使用ORCA做從頭算動力學(AIMD)的簡單例子》（http://www.shanxitv.org/576）里講了一些粗略的信息。模擬軌跡多幀疊加圖如下所示，每1 ps繪制一次，按照模擬時間顏色按藍-白-紅變化。可見模擬過程中carborazine和無機苯一樣始終保持結構穩定，并未解離或異構化，而且結構波動范圍相仿佛，這很大程度體現了carborazine像無機苯一樣是穩定的物質，在未來很有可能被成功合成出來。

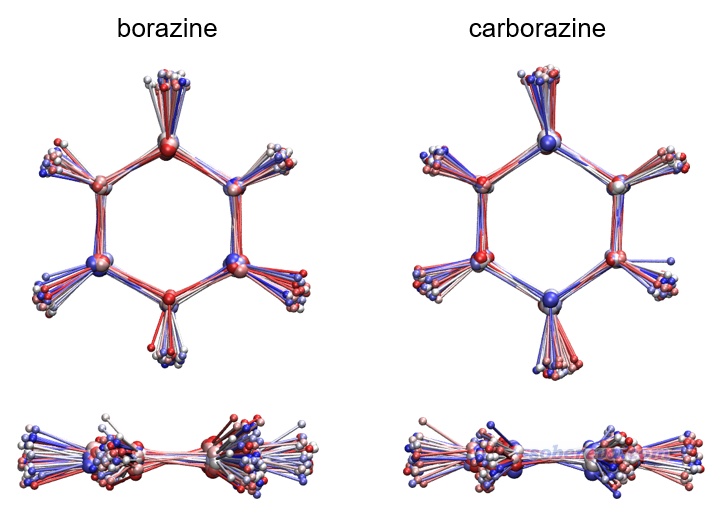
文中還在ωB97XD/def2-TZVP下計算了原子化能，carborazine的原子化能-1200.9 kcal/mol和無機苯的-1225.6 kcal/mol非常接近，進一步體現出carborazine具有顯著的穩定性。

值得一提的是carborazine的結構并非是其B2C2N2H6的化學組成的所有的可能異構體中能量最低的，這從文中在SI里給出的各種可能的異構體相對于carborazine的能量可以看出，如下所示，可見讓兩個碳挨在一起的能量更低。但由于原子的遷移要破壞原先的C-N和C-B鍵，決速步的能壘必定巨高，因此這樣的自發異構化并不會在現實中發生。

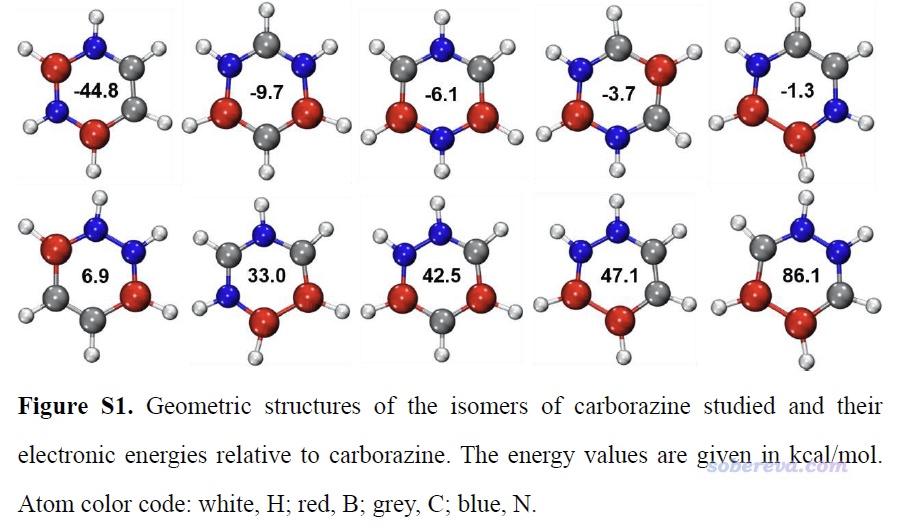
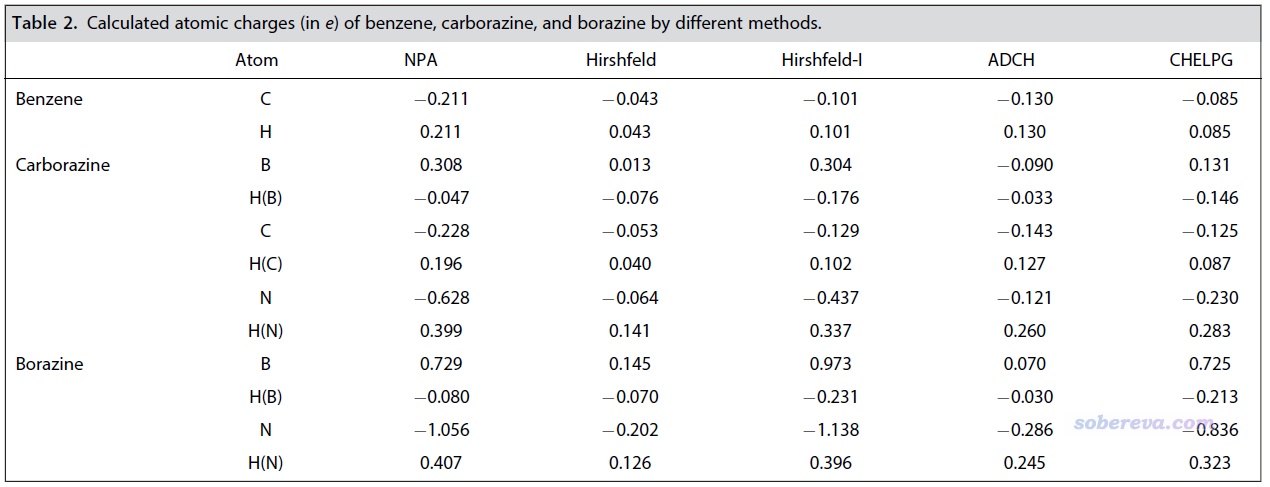
3 苯、無機苯和carborazine的電荷分布

原子電荷的概念在《一篇深入淺出、完整全面介紹原子電荷的綜述文章已發表！》（http://www.shanxitv.org/714）介紹的筆者的文章里有充分介紹，這是定量衡量體系電荷分布最常用的指標。本文通過流行的ADCH方法以及NPA、Hirshfeld和Hirshfeld-I、CHELPG方法都對前述三個體系計算了原子電荷，結果如下所示。可見雖然不同方法計算的原子電荷存在定量差異，但結論都是共通的，即硼和氮由于電負性一個很小一個極大，導致分別帶顯著的正電荷和負電荷，而在carborazine中它們的差異遠小于在無機苯中，這體現出在硼和氮之間插入的碳可以極大地均衡體系中的電荷分布。另外，carborazine中的碳的原子電荷的大小很小，體現出旁邊的氮和硼并沒有對碳的凈電荷帶來明顯影響。

《在Multiwfn中單獨考察pi電子結構特征》（http://www.shanxitv.org/432）介紹了Multiwfn對pi電子的分析功能。本文使用Multiwfn通過Mulliken方法計算了前述體系的非氫原子的pi布居數以考察它們pi電子的分布情況。結果是苯(C=0.995)、無機苯(B=0.429, N=1.558)、carborazine (B=0.586, C=0.985, N=1.411)。此結果清楚地體現了相對于無機苯，carborazine中在硼和氮之間引入的碳原子可以平衡它們的pi電子數的差異。而carborazine中的碳的pi布居數和它在苯中幾乎沒區別。

為什么要討論環上的pi電子分布？因為它的分布量和分布均衡性與芳香性有關鍵的聯系。較強的pi芳香性必須同時滿足環上的pi電子豐富、pi電子分布較均衡，以及pi電子在環上的離域性較強這三個條件。雖然無機苯的pi電子數和苯一樣，都是6個電子，但環上的原子的pi布居數的最小值，即硼的pi布居數，僅有0.429，因此姑且不論其電子的離域性與苯的差距有多大，光憑這點，其芳香性至多也只有苯的約40%。反之，carborazine六元環上硼的pi布居數達到0.586，因此可以認為其芳香性的上限約有苯的60%。

4 苯、無機苯和carborazine的pi軌道

pi分子軌道的特征與pi電子的芳香性有密切聯系，所以此文也考察了pi軌道的特征。前述三個體系的HOMO、LUMO軌道都是pi軌道，它們的能級和等值面圖如下所示，其它兩個占據的pi軌道也一起顯示了。可見carborazine的HOMO-LUMO gap比苯和無機苯明顯更小，一定程度暗示可能其穩定性相對更弱一些。

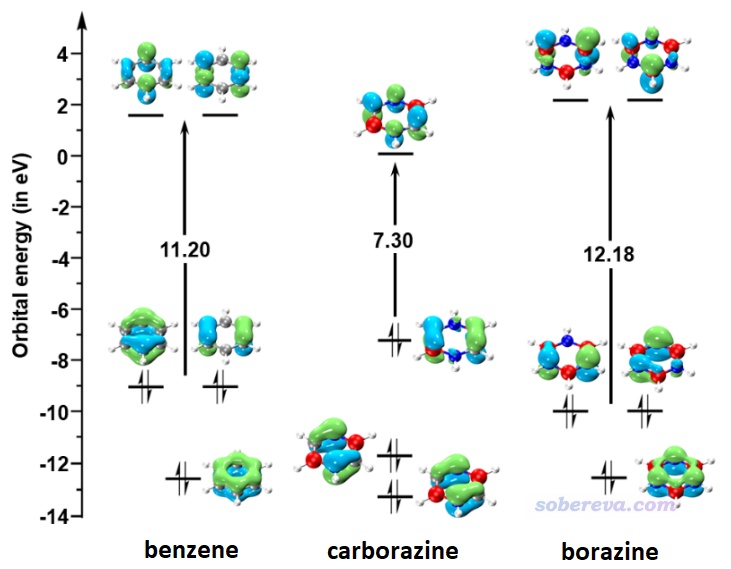
Multiwfn可以非常便利地計算軌道成份，見《談談軌道成份的計算方法》（http://www.shanxitv.org/131）。使用Mulliken方法計算的上面圖中展示的占據的pi軌道的成份如下所示。可見無機苯的所有pi軌道全都是由氮原子貢獻所主導的，這也必定導致無機苯的pi電子幾乎都集中且定域在氮原子上，因此在這點上它就不可能有顯著的芳香性。而雖然carborazine的HOMO-3和HOMO-5也是以氮原子的貢獻為主（因為氮的pz原子軌道的能量比碳和硼的都要低，故偏向于對能量較低的分子軌道貢獻較多），但還不至于起到絕對的主導性，而其HOMO的主要貢獻則來自硼和碳。由于carborazine的硼、碳、氮都同時明顯參與了pi占據軌道，它勢必有比無機苯強得多的六中心pi電子離域。

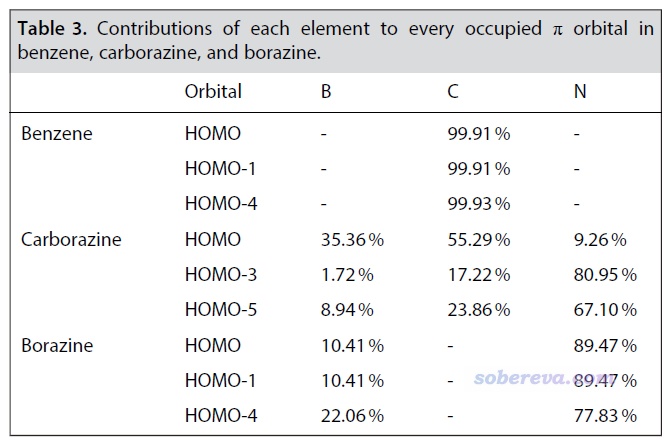
5 苯、無機苯和carborazine的成鍵特征

鍵級的概念在《Multiwfn支持的分析化學鍵的方法一覽》（http://www.shanxitv.org/471）中做了簡要介紹。文中用Multiwfn對上述三個體系計算了Mayer鍵級，它體現兩個原子間等效共享的電子對兒數，結果如下表左側所示，并且還按照《在Multiwfn中單獨考察pi電子結構特征》（http://www.shanxitv.org/432）所述的方法將sigma和pi電子的貢獻分別給出了。可見雖然B-N、C-N、C-B的pi鍵級都比C-C鍵的更小，但數值也都不低，所以它們的pi作用都是不容忽視的，也因此切勿以為B-N鍵只能算作純sigma鍵。carborazine六元環上的各個鍵的pi鍵級都大于無機苯的B-N鍵，這點已在一定程度上能體現出carborazine的整體pi共軛是強于無機苯的。

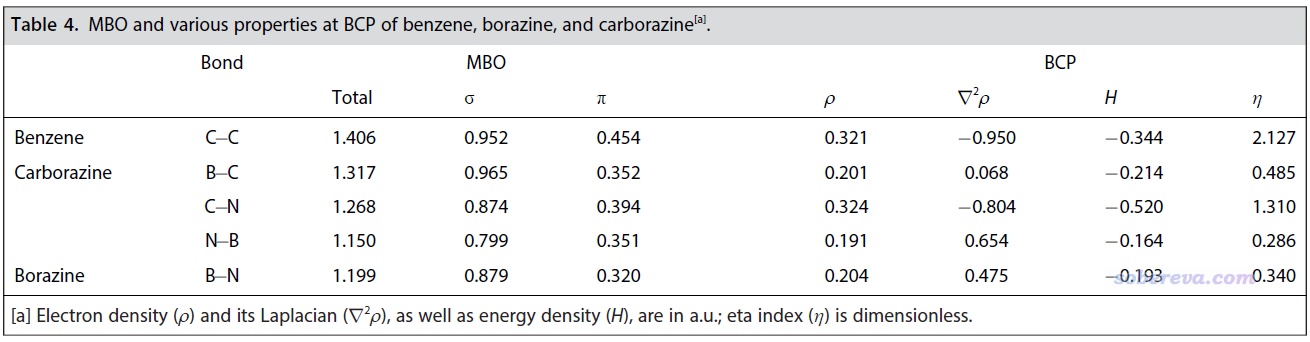
文中還對前述體系用Multiwfn做了流行的atom-in-molecules (AIM)拓撲分析，以從鍵臨界點（BCP）處的實空間函數角度考察體系的成鍵特征，結果如上表右側所示。AIM的相關知識和Multiwfn里的操作見AIM學習資料和重要文獻合集（http://bbs.keinsci.com/thread-362-1-1.html）里提到的內容。共價鍵在BCP處的能量密度（H）應當為負，并且eta指數（η）大于1是最典型共價鍵的特征。當前的結果體現出苯的C-C鍵和carborazine的C-N鍵都具有最典型的共價鍵特征，而carborazine和無機苯的N-B的共價性相對最低、離子性相對最強，因此H沒那么負且η顯著小于1，這無疑是硼和氮的巨大電負性差異所帶來的。

要注意切勿把B-N當做離子鍵。有些文章盲目使用BCP位置的電子密度拉普拉斯函數（▽2ρ）的正負作為共價鍵的判據，如Inorg. Chim. Acta., 360, 619 (2007)以這個為理由說B-N是離子鍵，這是很誤導的。之前我在《AIM鍵臨界點處電子密度拉普拉斯值符號判斷相互作用類型失敗原因的圖形分析》（http://www.shanxitv.org/161）中專門說過類似情況。對B-N鍵，如前所示Mayer鍵級顯著大于1，而且BCP處的能量密度明顯為負，就已經充分體現出這屬于共價鍵了。文中更進一步在補充材料里還用Multiwfn繪制了電子定域化函數（ELF）和變形密度圖，分別如下圖左側和右側所示，可見B-N之間有顯著的電子高定域性區域，并且從孤立狀態變成分子過程中在B-N鍵上有顯著的電子密度增加（圖中紅色實線為正值部分），這都進一步證明B-N鍵本質上是共價鍵，只不過極性很強而已。關于變形密度的知識見《使用Multiwfn作電子密度差圖》（http://www.shanxitv.org/113）和《通過價層電子密度分析展現分子電子結構》（http://www.whxb.pku.edu.cn/EN/10.3866/PKU.WHXB201709252），關于ELF的知識見《ELF綜述和重要文獻小合集》（http://bbs.keinsci.com/thread-2100-1-1.html）和《電子定域化函數的含義與函數形式》（http://www.whxb.pku.edu.cn/EN/10.3866/PKU.WHXB20112786），繪制方法參考Multiwfn手冊4.4節，在量子化學波函數分析與Multiwfn程序培訓班（http://www.keinsci.com/WFN）里有更豐富的例子、更細致的講解和各種技巧的傳授。

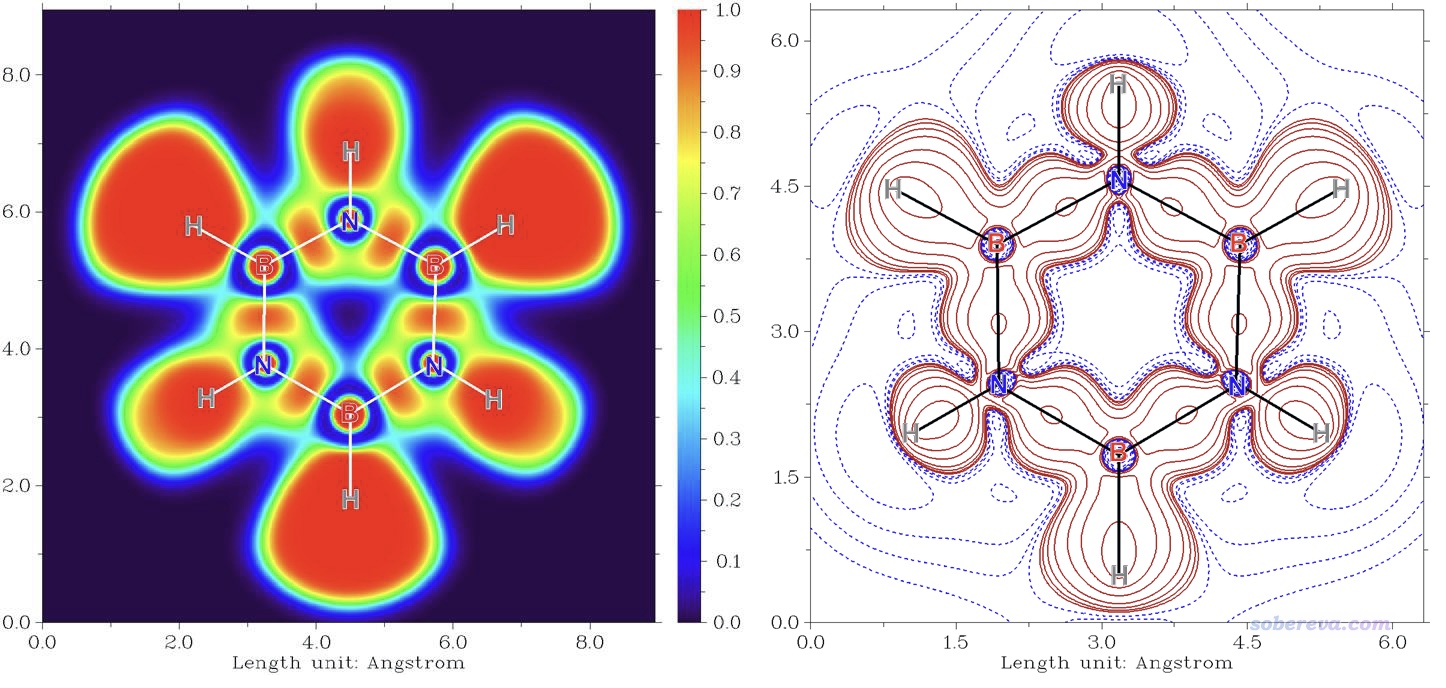
6 苯、無機苯和carborazine的電子離域特征

如《在Multiwfn中單獨考察pi電子結構特征》（http://www.shanxitv.org/432）和筆者的Theor. Chem. Acc., 139, 25 (2020)所提到的，pi電子的局域軌道指示函數（LOL），即LOL-pi，對于展現pi電子的離域性極為直觀。對前述三個體系用Multiwfn計算并用VMD繪制的LOL-pi等值面圖如下所示，可見苯的六中心共軛作用最強，等值面均勻、理想地貫穿六元環。雖然carborazine和無機苯的LOL-pi等值面都沒有分布得很均勻，特別是在B-N鍵處受到了阻礙，算是電子共軛的“瓶頸”，但是carborazine的每個B-C-N單元上的等值面較為均勻、連貫，這是無機苯不具有的，因此從LOL-pi展現的電子離域性圖上可以期望carborazine有明顯更強的芳香性。

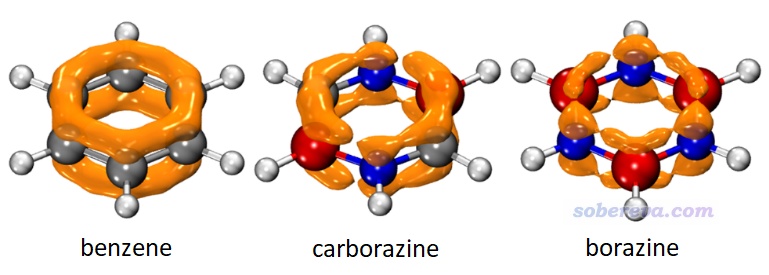
文中還繪制了EDDB_P-π等值面圖，詳見原文。LOL-pi展現的是不同區域電子的離域程度，而EDDB_P-π展現的是不同區域離域的pi電子量，二者體現的信息存在互補性。EDDB_P-π等值面圖及其布居分析展現出無論是carborazine還是無機苯，硼上的離域的pi電子都比環上的其它原子更少，原因之一是硼上的pi電子數本來就非常少，這在前面的pi布居分析中已經體現了。相比之下，carborazine的硼的離域的pi電子為0.360，明顯多于無機苯的0.184，這進一步體現出carborazine具有更強的pi芳香性。并且0.360這個值是苯的碳原子的離域pi電子數0.885的41%，這說明carborazine至少有苯41%的芳香性。

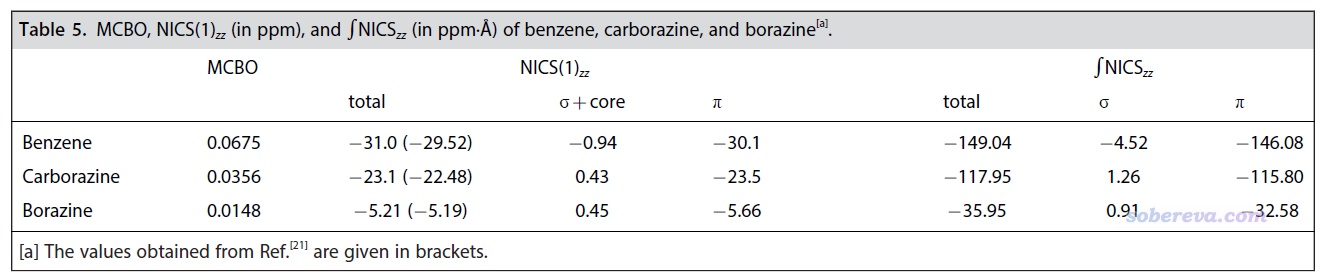
進一步，文章還使用Multiwfn計算了多中心鍵級（MCBO），以及sigma+core和pi電子各自的貢獻量，相關知識參看《使用AdNDP方法以及ELF/LOL、多中心鍵級研究多中心鍵》（http://www.shanxitv.org/138）和《衡量芳香性的方法以及在Multiwfn中的計算》（http://www.shanxitv.org/176）。結果如下所示，可見六中心電子離域性是苯 > carborazine > 無機苯，差異非常鮮明，這和上述其它分析給出的結論非常一致。從MCBO的數值大小來說，carborazine具有苯的大約一半的芳香性，而無機苯則連carborazine芳香性的一半都不到。

7 苯、無機苯和carborazine的磁屏蔽特征

有大量的方法從體系對外磁場的屏蔽角度衡量芳香性，參考筆者寫過的《衡量芳香性的方法以及在Multiwfn中的計算》（http://www.shanxitv.org/176）、《使用Multiwfn繪制一維NICS曲線并通過積分衡量芳香性》（http://www.shanxitv.org/681）、《使用Multiwfn計算FiPC-NICS芳香性指數》（http://www.shanxitv.org/724）、《通過Multiwfn繪制等化學屏蔽表面(ICSS)研究芳香性》（http://www.shanxitv.org/216）、《使用Multiwfn巨方便地繪制二維NICS平面圖考察芳香性》（http://www.shanxitv.org/682），在《量子化學波函數分析與Multiwfn程序培訓班》（http://www.keinsci.com/WFN）里有更全面系統的講授。本文從磁屏蔽角度對苯、無機苯和carborazine的芳香性特征進行了定量的考察以及直觀的展現。

NICS及其變體在定量衡量芳香性強弱方面極為常用，文中對苯、無機苯和carborazine計算了NICS最理想的形式之一NICS(1)ZZ，并通過《基于Gaussian的NMR=CSGT任務得到各個軌道對NICS貢獻的方法》（http://www.shanxitv.org/670）介紹的做法分解成了sigma+core和pi電子各自的貢獻，數值越負說明芳香性越強。由數據可見，carborazine的pi芳香性雖然不及苯，但也相當顯著，而無機苯的芳香性極為微弱，接近非芳香性。sigma電子對芳香性的貢獻可忽略不計。

如《使用Multiwfn繪制一維NICS曲線并通過積分衡量芳香性》所述，對NICS_ZZ在垂直于環的方向上積分，即∫NICS_ZZ或稱integrated NICS (INICS)，是比NICS(1)ZZ還更為嚴格的基于磁屏蔽特征衡量芳香性的方法，因為它的結果不依賴于計算磁屏蔽張量的位置的選取。從上面表格的數據可見∫NICS_ZZ的結論與NICS(1)ZZ相一致，更進一步體現了之前結論的可靠性。∫NICS_ZZ計算過程中利用到的穿過環中心且垂直于環方向上的NICS_ZZ曲線可以繪制出來并進行直觀對比，如下所示，橫坐標是相對于環中心（零點）的位置。根據pi電子的NICS_ZZ曲線，可以清楚地看出carborazine的曲線與苯比較接近，這將carborazine顯著的pi芳香性特征體現得非常確切，而無機苯的pi芳香性相比之下顯得微乎其微，其曲線在全范圍都很接近0。三個體系的sigma電子的NICS_ZZ曲線幾乎完全重合，很嚴格地體現出它們的sigma芳香性基本沒有任何區別。

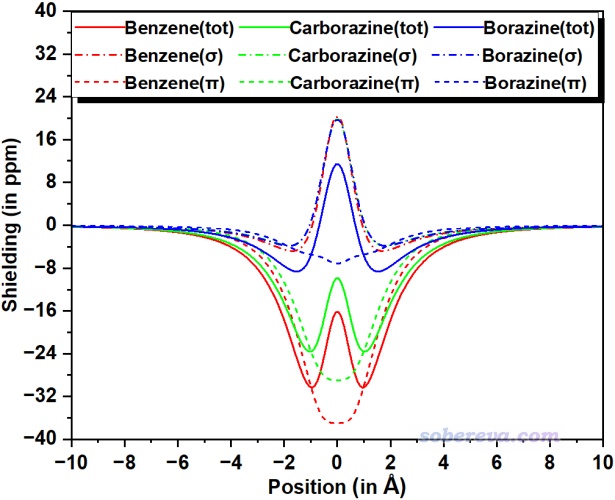
下圖左列是Multiwfn結合VMD繪制的ICSS_ZZ等值面圖，等值面數值為3 ppm，橙色和深藍色分別是對外磁場屏蔽和去屏蔽區域。從這種圖上能非常完整地了解體系的磁屏蔽特征。可見carborazine和苯一樣都是在分子外圍形成了環狀的去屏蔽區域，又一次體現出了carborazine類高度似于苯的顯著的芳香性，而無機苯的去屏蔽區域等值面則明顯顯得不夠連續，體現出其芳香性遠比carborazine弱得多。

上圖還給出了Multiwfn直接繪制的填色等值線圖，中列和右列分別是分子平面以及分子的側截面，顏色越紅和越藍分別對應相應位置的磁屏蔽和去屏蔽效應越強。可以看到carborazine在分子中心是磁屏蔽的，顏色和苯一樣是偏紅的，而borazine在分子中心卻是去屏蔽的，顏色偏藍，這充分反映了carborazine和苯在芳香性上是類似物，而無機苯可近似歸為非芳香性分子一類。

8 苯、無機苯和carborazine的感生電流

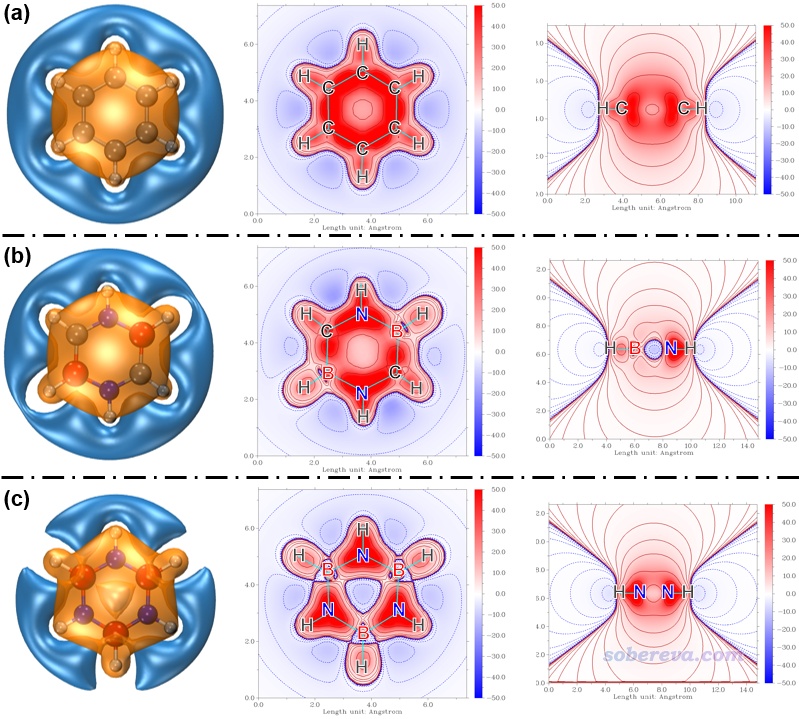
在外磁場作用下在環狀區域內離域的電子可以形成感生環電流，這是衡量電子離域性和芳香性的非常直觀的方法，其中AICD展現方式尤為常見，詳見《使用AICD 2.0繪制磁感應電流圖》（http://www.shanxitv.org/294）。本文對苯、無機苯和carborazine分別繪制了總的、sigma電子的和pi電子的AICD圖，如下所示，從AICD(pi)圖中箭頭標注的感生電流上可以清楚地看出carborazine形成了和苯一樣的貫穿整個六元環的顯著的感生電流，而無機苯則完全不具備這樣的特征。AICD圖進一步有力地體現出，carborazine和苯一樣都屬于芳香性物質，而無機苯是近乎非芳香性的，這和ICSS分析的結論一致，彼此相互印證。

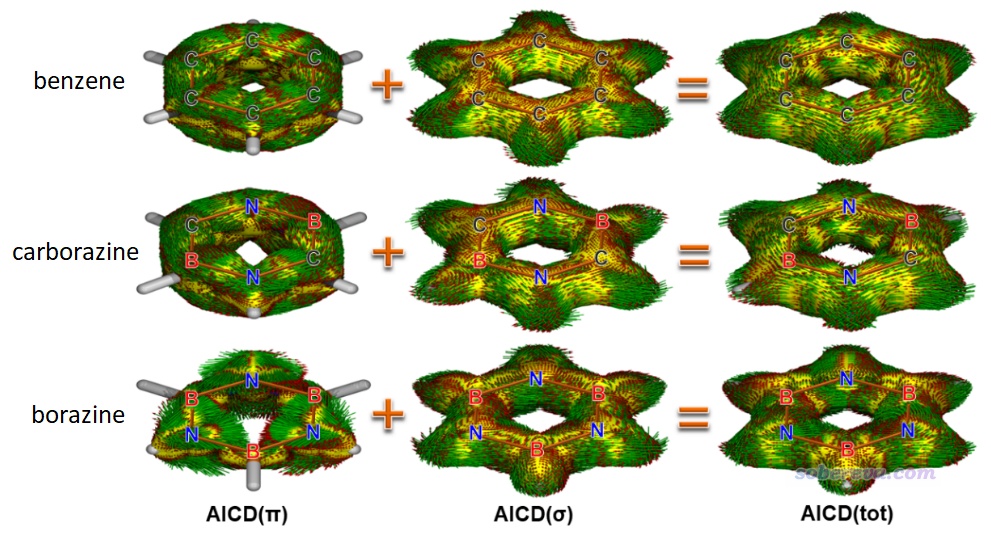
此文還使用《使用SYSMOIC程序繪制磁感生電流圖和計算鍵電流強度》（http://www.shanxitv.org/702）中介紹的做法用CTOCD-DZ2方法繪制了分子平面上方1 Bohr處的感生電流圖，如下所示，灰、紅、藍分別對應碳、硼、氮原子。由圖可見CTOCD-DZ2方法展現的感生電流圖和pi電子的AICD圖的現象很類似，而這種平面圖看得更清楚一些。此圖體現carborazine分子平面上方pi區域的感生電流的強度雖不像苯那么均勻，在硼上方相對弱一些，但終究還是形成了明顯的全局感生電流。而無機苯的感生電流則主要在氮原子周圍打轉，體現出pi電子主要都是定域在各個氮的局部原子空間里。

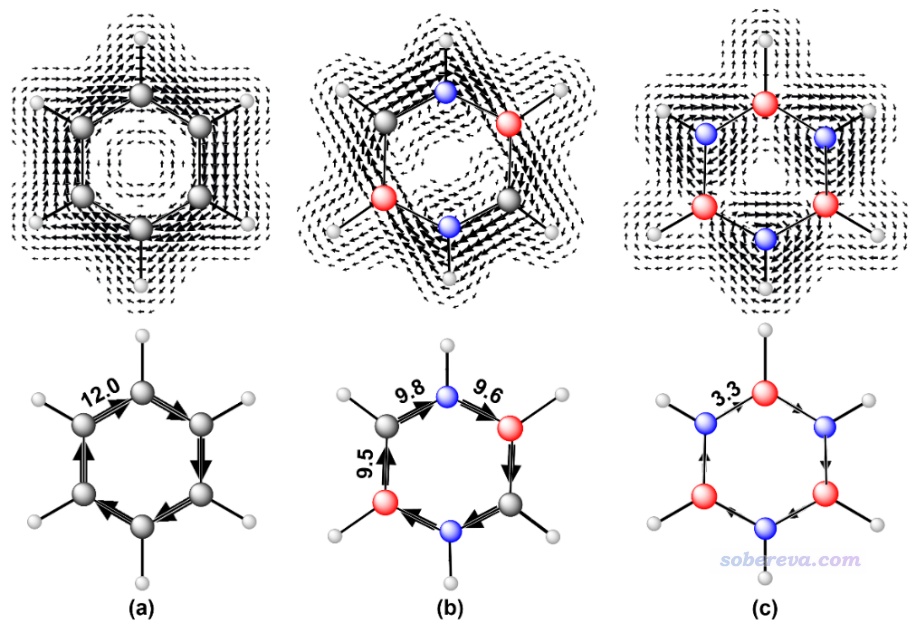
為了便于定量對比，此文還計算了六元環上各種鍵的電流強度（BCS）值，即在鍵中心位置垂直于鍵的平面上的感生電流的積分，結果如上圖標注的數值所示，單位為nA/T。可見carborazine的感生電流強度與苯相差并不懸殊，而無機苯則相當微弱。這從定量角度上進一步驗證了前面基于肉眼觀看感生電流圖所做出的結論。

值得一提的是，在《深入理解分子軌道對磁感生電流的貢獻》（http://www.shanxitv.org/703）中我給了計算感生電流的具體公式，假定只有HOMO-LUMO躍遷對感生電流有顯著貢獻，那么感生電流大小與HOMO-LUMO gap之間會有反比關系。在前面說過，carborazine的HOMO-LUMO gap明顯小于苯和無機苯，因此基于磁屬性和感生電流得到的關于carborazine的芳香性的強度會有一定程度的高估。但即便如此也不影響它具有明顯芳香性的結論，而且前面從多中心鍵級、LOL-pi等分析角度也全都體現了carborazine有遠強于無機苯的芳香性。

9 carborazine中的碳原子對硼和氮原子橋聯的重要意義

前面從各個角度極為充分、全面、嚴格地論證了carborazine具有無機苯不具備的顯著的芳香性，而二者的差異僅在于前者給后者的氮和硼之間引入了碳原子起到橋聯作用。為什么碳原子的橋聯對于提升芳香性有如此關鍵性的影響？此文將Multiwfn、NBO、VMD相結合繪制了前述三個體系的環上的各原子的對應2pz原子軌道的預正交自然原子軌道（PNAO）等值面的疊加圖，過程可參照《使用Multiwfn繪制NBO及相關軌道》（http://www.shanxitv.org/134）舉一反三，如下所示。可見2pz的空間延展程度是硼 > 碳 > 氮，這和電負性增大的順序相一致。氮和硼的軌道重疊頗差，電子明顯難以離域過去。而給二者之間插入的碳原子，增加離域路徑上的原子軌道重疊程度、降低相連原子的電負性不平衡性，明顯可以起到了幫助電子離域過去的“中介”，從而使得carborazine能夠具有無機苯不具備的顯著芳香性。之前筆者在《18碳環等電子體B6N6C6獨特的芳香性：揭示碳原子橋聯硼-氮對電子離域的關鍵影響》（http://www.shanxitv.org/696）介紹的文章中也使用了類似的角度進行分析。

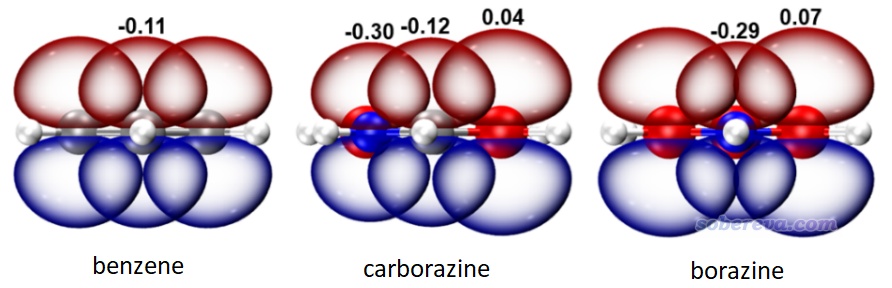
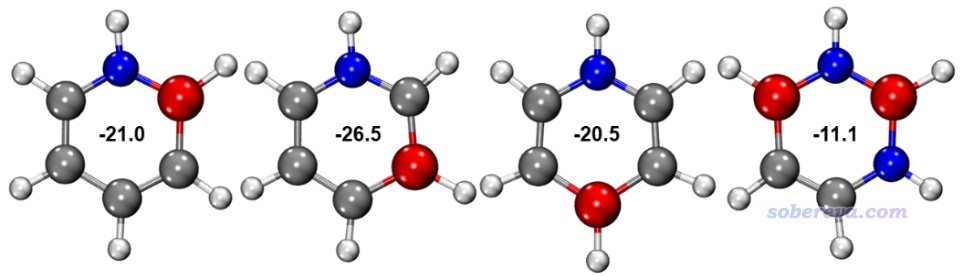
文章里還研究了其它4種苯的等電子體，以考察碳的數目和位置對芳香性的影響。它們的結構如下所示，NICS(1)ZZ也標在了圖上，注意carborazine的值如前所述是-23.1 ppm。通過對比可見，環上的碳原子數多不意味著芳香性就強，例如下圖第1、3個分子雖然有4個碳原子，但單從NICS(1)ZZ來看其芳香性還沒只有兩個碳的carborazine強。下圖第4個分子和carborazine的碳原子數一樣，但碳沒有插入在硼和氮之間，芳香性也遠不如carborazine強。而只有下圖第2個分子，碳橋聯了氮和硼，同時碳原子數比carborazine還更多，這才帶來了稍微更強的芳香性。這個對比體現出對只有硼、氮的環上引入碳，而且能起到對它們的橋聯作用時，才能顯著提升芳香性。

10 總結

本文介紹的Chem. Eur. J. 2024, e202403369一文十分全面透徹探討了互為等電子體的苯、無機苯（borazine，B3N3H6）和尚未實驗合成的carborazine（B2N2C2H6）的電子結構和芳香性的差異。此文的重點是綜合運用各種分析手段，充分論證了含有碳原子橋聯硼、氮原子特征的carborazine具有明顯的芳香性（盡管強度一定程度弱于苯），同時還嚴格地證明了無機苯的芳香性極弱，甚至很大程度上體現出非芳香性分子的特征。文章對此現象的本質從電子結構層面進行了詳細的分析和解釋。此文的研究工作對于化學家們更好地了解由碳、氮、硼構成的物質的電子離域性和芳香性有顯著的意義。

值得一提的是，此文的研究也是使用Multiwfn等程序做波函數分析深入剖析化學物質特征的非常典型的文章，可以作為波函數分析的很好的范例作為參考。此研究涉及的研究方法在前面提及的各種博文里有一些粗略、初步的介紹，通過量子化學波函數分析與Multiwfn程序培訓班（http://www.keinsci.com/WFN）可以一次性全面深入透徹掌握文中用到的一切波函數分析方法的背景知識和使用具體程序計算的方法，從而能順利地復現此文的研究并舉一反三探索更多的體系。

文/Sobereva@北京科音   2024-Oct-28

0 前言

18碳環以其獨特的幾何和電子結構，自從2019年在凝聚相觀測到后引發了化學界的巨大關注。與之相關的分子間相互作用文章已有不少，例如《全面探究18碳環獨特的分子間相互作用與pi-pi堆積特征》（http://www.shanxitv.org/572）介紹的Carbon, 171, 514-523 (2021)、《8字形雙環分子對18碳環的獨特吸附行為的量子化學、波函數分析與分子動力學研究》（http://www.shanxitv.org/674）介紹的Phys. Chem. Chem. Phys., 25, 16707 (2023)、《理論設計新穎的基于18碳環構成的雙馬達超分子體系》（http://www.shanxitv.org/684）介紹的Chem. Commun., 59, 9770 (2023)，等等。筆者迄今對18碳環及其衍生物的研究論文匯總和各種相關博文見http://www.shanxitv.org/carbon_ring.html（不斷更新）。

碳單環體系和富勒烯體系是碳元素的兩種關鍵的同素異形體，形狀截然不同，一個環形一個球形，而且由于二者都有pi共軛特征，理應存在pi-pi相互作用。這顯著的差異性和明顯的共性無疑使得碳環與富勒烯的相互作用非常值得進行細致、充分的探索。近期，北京科音自然科學研究中心（http://www.keinsci.com）的盧天和江蘇科技大學的劉澤玉在知名的Chem. Eur. J.（歐洲化學）期刊上發表了極為全面、系統、透徹的研究不同尺寸碳環（C18到C36）與不同數目C60富勒烯相互作用的理論研究文章，充分揭示了它們之間獨特的相互作用，包括強度、結構和本質，內容很新穎有趣，非常歡迎閱覽和引用：

Zeyu Liu, Tian Lu*, Theoretical Insight into Complexation Between Cyclocarbons and C60 Fullerene, Chem. Eur. J., 30, e202402227 (2024) DOI: 10.1002/chem.202402227
可以通過此鏈接免費在線閱覽：https://onlinelibrary.wiley.com/share/author/PJDSJZN8IMBAVDCCBXQS?target=10.1002/chem.202402227

此文不僅研究碳環與富勒烯相互作用本身，文章在分析思想和方法學方面對于其它分子間相互作用的研究也頗有借鑒意義，十分推薦對這類研究問題感興趣的讀者閱讀。此文充分運用了強大的Multiwfn（主頁http://www.shanxitv.org/multiwfn）波函數分析程序提供的豐富的弱相互作用分析功能，包括IGMH、sobEDA、范德華勢等，是Multiwfn研究弱相互作用問題的很好的范例。Multiwfn支持的弱相互作用分析功能在《Multiwfn支持的弱相互作用的分析方法概覽》（http://www.shanxitv.org/252）有概述，在量子化學波函數分析與Multiwfn程序培訓班（http://www.keinsci.com/workshop/WFN_content.html）的“弱相互作用的分析”部分有最全面透徹的講解和演示。

下面將對上述Chem. Eur. J.文章的主要內容進行深入淺出的介紹，便于讀者更容易理解文章的研究結果，同時額外附上許多分析和計算細節以幫助讀者能夠將文中的研究手段舉一反三運用到自己的研究中。原文里還有很多細節信息和討論，故請閱讀下文后閱讀原文。

1 碳環-富勒烯二聚體

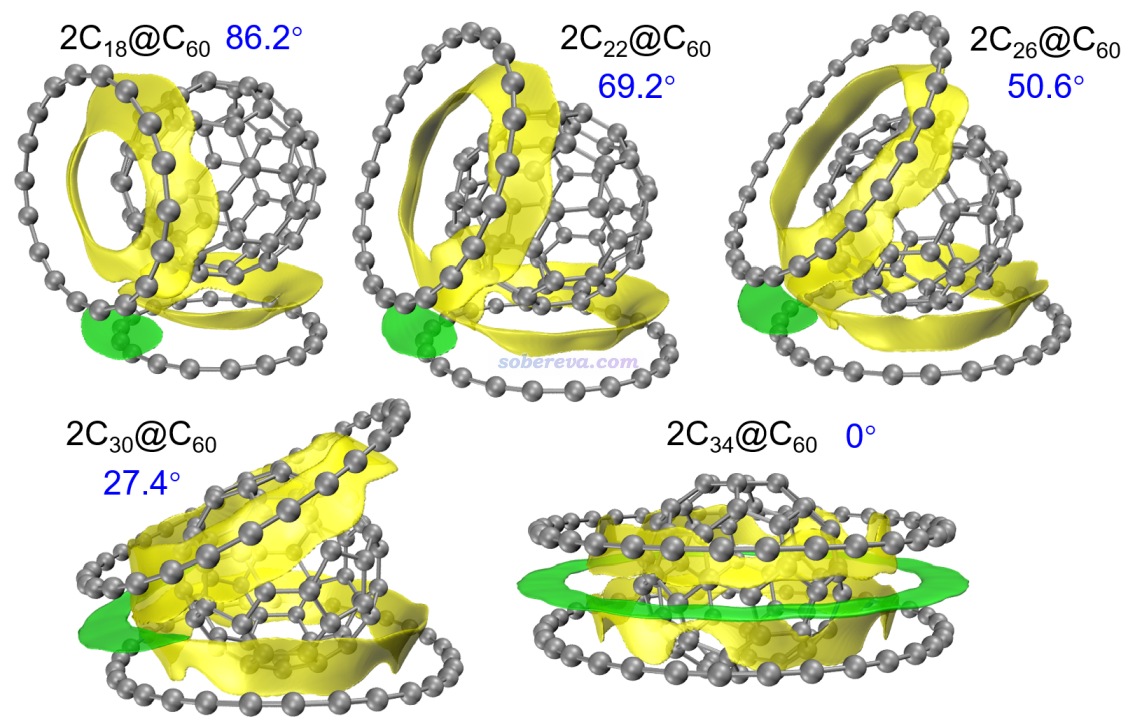
文章首先考察了碳環與富勒烯形成的二聚體結構。文中用Gaussian 16在ωB97XD/6-311G*級別下優化了碳環Cn (n=18, 20, 22, 24, 26, 30, 32, 34, 36)與富勒烯形成的二聚體C60@Cn，并確認了無虛頻。ωB97XD泛函曾用于http://www.shanxitv.org/carbon_ring.html里羅列的筆者的各種18碳環的研究中，不僅可以正確描述18碳環的幾何結構（見Carbon, 165, 468 (2020)中的方法對比測試），也能合理描述弱相互作用，故很適合用于優化涉及碳環的復合物。得到的二聚體中比較有代表性的5個如下所示。可以看到隨著碳環尺寸的增大，富勒烯逐漸陷入碳環中，到了C60@C34的時候富勒烯正好不偏不倚精確嵌入在碳環的正中央，富勒烯的中心和碳環的中心正好重合，這是一個完美的納米土星（nano-saturn）結構。而當碳環尺寸進一步增大到C36，為了最大化分子間相互作用，富勒烯的中心自發偏離了碳環的中心。

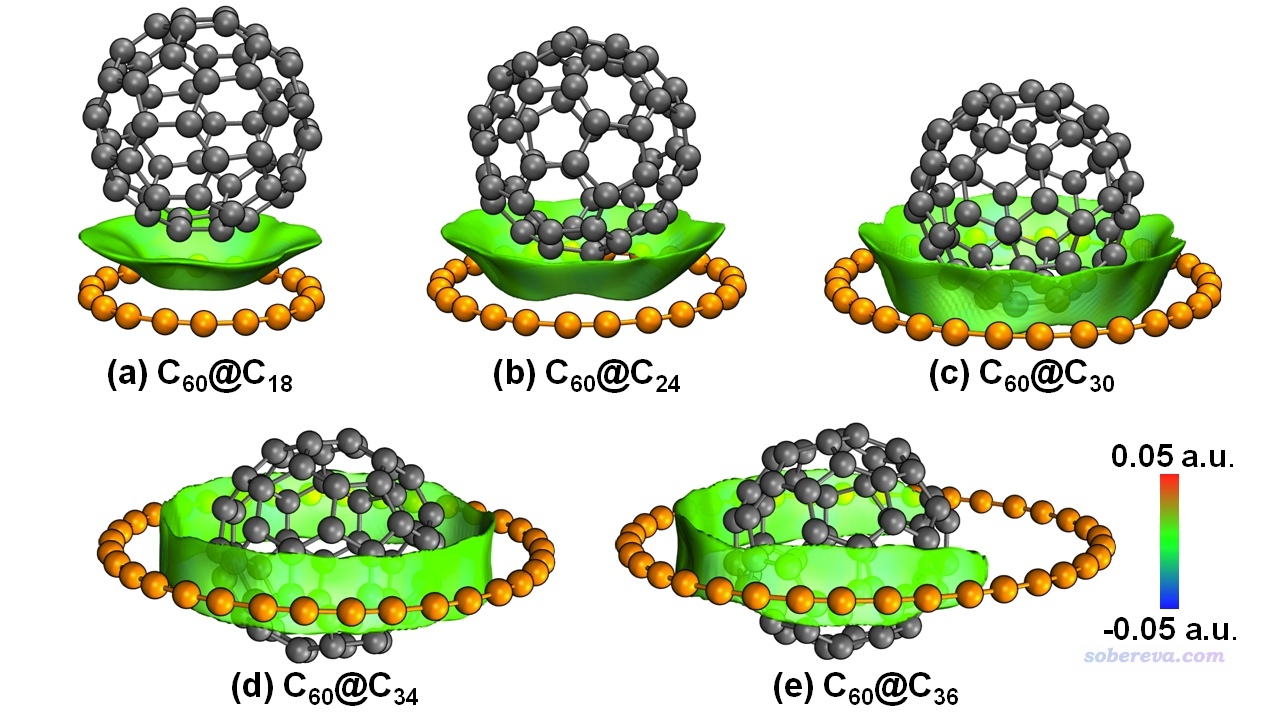
筆者提出的IGMH是目前非常流行、效果理想的可視化片段間相互作用的分析方法，見《使用Multiwfn做IGMH分析非常清晰直觀地展現化學體系中的相互作用》（http://www.shanxitv.org/621）和《一篇最全面介紹各種弱相互作用可視化分析方法的文章已發表！》（http://www.shanxitv.org/667）介紹的綜述。上圖的等值面是IGMH方法定義的sign(λ2)ρ著色的δg_inter等值面，描述富勒烯和碳環這兩個片段間的相互作用。圖中非常清楚直觀地展現出了碳環-富勒烯之間的相互作用區域。等值面幾乎都是綠色，說明相互作用區域的電子密度數值非常低，pi-pi相互作用區域普遍具有這種特點，再加上碳環和富勒烯的接觸面也正是pi電子分布的區域相互接觸，無疑富勒烯和碳環之間的結合是典型的pi-pi相互作用所驅動的。

為了嚴格考察碳環和富勒烯的結合強度，基于Gaussian優化的幾何結構，文中用ORCA程序精確計算了不同碳環與富勒烯形成二聚體對應的結合能，即E_bind = E(C60@Cn) - E(C60) - E(Cn)，其中E是電子能量，每個能量都在各自分別優化的結構下得到。計算級別用的是ωB97M-V/def2-QZVPP，ωB97M-V不僅像ωB97XD一樣是長程極限HF成份為100%的范圍分離泛函因而能夠合理描述碳環的電子結構，而且大量測試都體現了其計算弱相互作用能相當優秀，在《簡談量子化學計算中DFT泛函的選擇》（http://www.shanxitv.org/272）中以及北京科音中級量子化學培訓班（http://www.keinsci.com/workshop/KBQC_content.html）里的“弱相互作用的計算與相關問題”專題部分也專門說過這一點。def2-QZVPP是相當高質量的基組，算分子間相互作用能的BSSE問題小到可以忽略，在ORCA里利用RIJCOSX加速技術計算像C60@C36這樣約100個非氫原子體系的單點能完全算得動。此外，為了從熱力學角度嚴格考察C60@Cn二聚體形成的可能性，文中還計算了標況下的結合自由能，其中對電子能量的自由能熱校正量通過《使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據》（http://www.shanxitv.org/552）介紹的Shermo程序基于ωB97XD/6-311G*振動分析的輸出文件得到。如552博文所述，像這種含有大量很低頻的體系的自由能的計算一定要用Shermo支持的quasi-RRHO模型得到的自由能熱校正量，而切勿直接用Gaussian等程序基于RRHO模型給出的，否則低頻模式對熵的貢獻可能被高估得離譜，導致結合自由能誤差很大。另外，為了考察溶劑效應對結合的影響，文章還使用Gaussian的SMD溶劑模型按照《談談隱式溶劑模型下溶解自由能和體系自由能的計算》（http://www.shanxitv.org/327）說的做法獲得了水環境下的自由能，并求差得到了水中的結合自由能。計算結果匯總如下

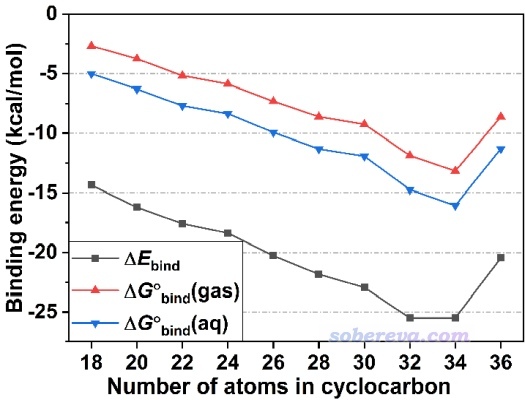
由上圖可見，從C18到C32，隨著碳環尺寸的增大，它與富勒烯的結合強度近乎嚴格地線性增強，這是由于二者間的接觸面積逐漸增大，這點從上文的IGMH圖的等值面面積的變化就可以清晰地反映出來。而從C34變成C36，結合強度反倒減弱了，這正如IGMH圖所示的，C36有的地方與富勒烯離得相對較遠、作用較弱，導致δg_inter等值面也沒有在相應區域出現。

上圖體還現出標況氣相的結合自由能和基于電子能量算的結合能的變化趨勢基本一致，但前者沒有后者那么負，這是因為結合過程中熵減小對結合造成了嚴重不利的影響。對比上圖中的紅線和藍線可見水溶劑環境下的結合自由能比氣相下的更負幾kcal/mol，說明極性溶劑會促使碳環與富勒烯的結合，這本質上就是疏水效應，眾所周知疏水效應會驅動非極性物質間在水中的結合。

很值得一提的是，文中發現碳環-富勒烯之間的δg_inter=0.002 a.u.的等值面面積與它們的結合能有頗好的線性關系，如下所示。因此IGMH圖像的等值面面積在某些情況下可以作為解釋或預測相互作用能的很好的描述符，這一點很值得在未來進一步探索。這種面積的計算方法見《計算IGMH等值面的面積和體積的方法》（http://www.shanxitv.org/738）。

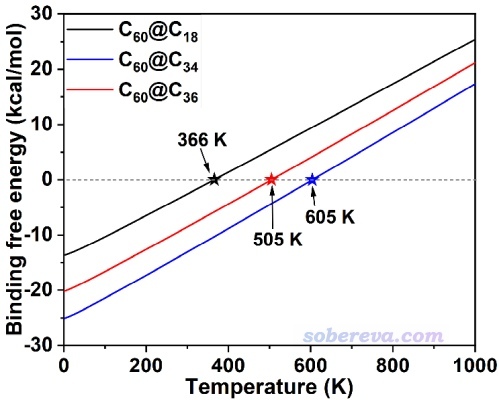
為了考察溫度對碳環-富勒烯結合的影響，以及探索結合的臨界溫度，文中利用Shermo程序做了自由能隨溫度的掃描，并進而得到了結合自由能與溫度的關系，如下所示。可見溫度越高越不利于結合，在氣相常壓下，C18碳環與富勒烯之間從366 K開始就無法結合了，而C34和富勒烯之間的二聚體在高達605 K以下都是可以形成的。C36的情況處于二者之間。

碳環與富勒烯的復合勢必造成單體的結構變化，由于單體結構相對于極小點結構改變導致單體的電子能量在復合過程中的升高稱為變形能。文中補充材料里的表S1給出了不同碳環與富勒烯結合時的碳環的變形能，發現C18到C34的變形能都<=0.3 kcal/mol，可以忽略不計，而C36的變形能則達到了1.0 kcal/mol，這一方面是因為這樣較大的碳環有足夠顯著的柔性，另一方面在于它與富勒烯之間的不對稱的相互作用（如全面IGMH圖所展示的），這造成了這種碳環在復合物中相對于圓形的極小點結構的不可忽略的形變。下圖是按照《在VMD中計算RMSD衡量兩個結構間的差異以及疊合兩個結構》（http://www.shanxitv.org/290）的方法繪制的C36在孤立狀態（紅線）和與富勒烯結合狀態（藍線）的疊加圖，可見富勒烯的存在誘使C36碳環被拉長了。

碳環與富勒烯的作用雖然形式上屬于“弱相互作用”類別，但結合強度真不是一般的強，而是相當的強！如《透徹認識氫鍵本質、簡單可靠地估計氫鍵強度：一篇2019年JCC上的重要研究文章介紹》（http://www.shanxitv.org/513）所列舉的，像是水二聚體這樣的一般強度氫鍵的結合能才-5 kcal/mol左右，而本文研究的與富勒烯結合最弱的18碳環，它與富勒烯的結合能都達到了-14.4 kcal/mol，將近三個普通氫鍵的強度。而且這比《全面探究18碳環獨特的分子間相互作用與pi-pi堆積特征》（http://www.shanxitv.org/572）提到的曾經筆者研究的兩個18碳環間的結合能-9.2 kcal/mol強得多，也比J. Chem. Theory Comput., 13, 274 (2017)高精度計算的兩個富勒烯之間的結合能-8.3 kcal/mol強得多！

2023年筆者提出的能量分解方法sobEDA和sobEDAw的詳細介紹見《使用sobEDA和sobEDAw方法做非常準確、快速、方便、普適的能量分解分析》（http://www.shanxitv.org/685），其中sobEDAw用于考察碳環+富勒烯的相互作用成份極為合適，速度足夠快而且結果也很準確。sobEDAw只對部分泛函擬合了參數，由于碳環體系需要HF成份較高的泛函才能正確描述，因此文中使用了HF成份達到50%的BHandHLYP泛函結合DFT-D3(BJ)色散校正和6-311+G(2d,p)基組做碳環-富勒烯之間的sobEDAw能量分解，并且考慮了counterpoise校正，結果是總相互作用能為-12.0 kcal/mol，其中靜電貢獻-8.4、交換互斥貢獻25.6、軌道相互作用貢獻-2.4、色散作用貢獻-26.8 kcal/mol。可見色散作用對碳環-富勒烯之間的吸引作用起絕對主導效果，靜電作用相對次要，而軌道相互作用可忽略不計。這完全符合pi-pi堆積的典型特征，在《全面探究18碳環獨特的分子間相互作用與pi-pi堆積特征》（http://www.shanxitv.org/572）介紹的Carbon, 171, 514 (2021)中使用sSAPT0/jun-cc-pVDZ級別對18碳環的pi-pi作用形成的二聚體做能量分解基本上也是這個情況。

此文還使用Multiwfn通過筆者提出的ADCH原子電荷計算方法，以及很常用的Mulliken方法，計算了C60@C18中18碳環部分的片段電荷。如果對原子電荷缺乏了解的話建議閱讀《一篇深入淺出、完整全面介紹原子電荷的綜述文章已發表！》（http://www.shanxitv.org/714）里提到的筆者的原子電荷綜述。這兩種方法給出的18碳環的電荷分別為0.015和-0.027，都十分接近于0，體現出碳環與富勒烯之間的基態的電荷轉移效應可以忽略不計。文中也用Multiwfn的主功能9的選項-1將18碳環和富勒烯分別定義成片段1和片段2，然后計算了它們之間的總Mayer鍵級，數值僅為可忽略的0.041，即基本沒有共享電子作用，再次體現出兩個分子間完全是非共價相互作用。如果讀者對鍵級不了解，建議看《Multiwfn支持的分析化學鍵的方法一覽》（http://www.shanxitv.org/471）中鍵級的相關部分。

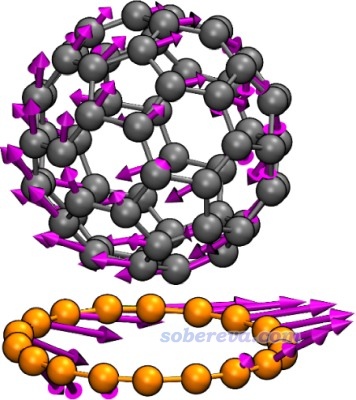
文中發現18碳環和富勒烯實際上有兩種極小點結構（見原文圖S1），次低的比最低的能量高0.9 kcal/mol，它們之間互變的過渡態的虛頻為9.8i cm-1，振動模式如下所示，可見明顯對應于富勒烯相對于18碳環的旋轉。在ωB97M-V/def2-QZVPP級別下計算出的正向和逆向勢壘分別為0.90和0.04 kcal/mol，極低的勢壘體現出復合物中富勒烯可以非常自由地旋轉。實際上pi-pi堆積作用的體系之間普遍容易發生滑移（如18碳環二聚體，在http://www.shanxitv.org/572里做了動力學模擬直接體現了這一點），因為滑移造成的能量變化很小。

2 碳環-富勒烯 2:1三聚體

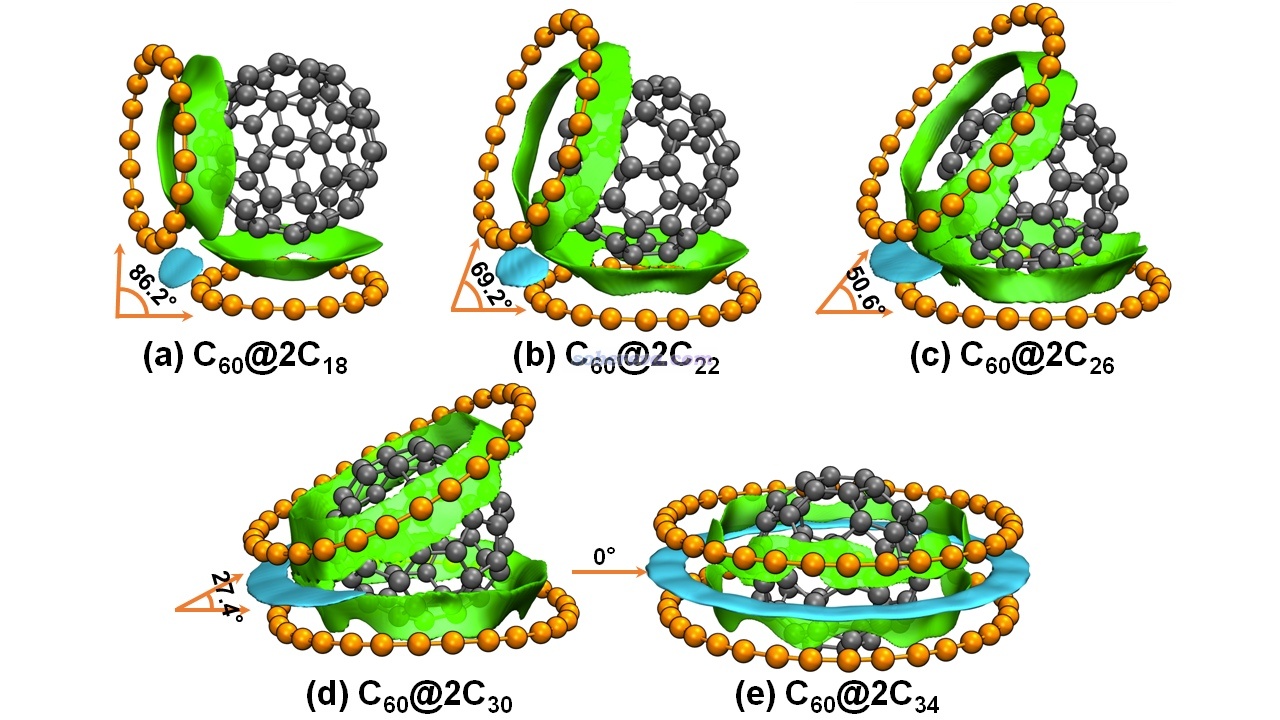
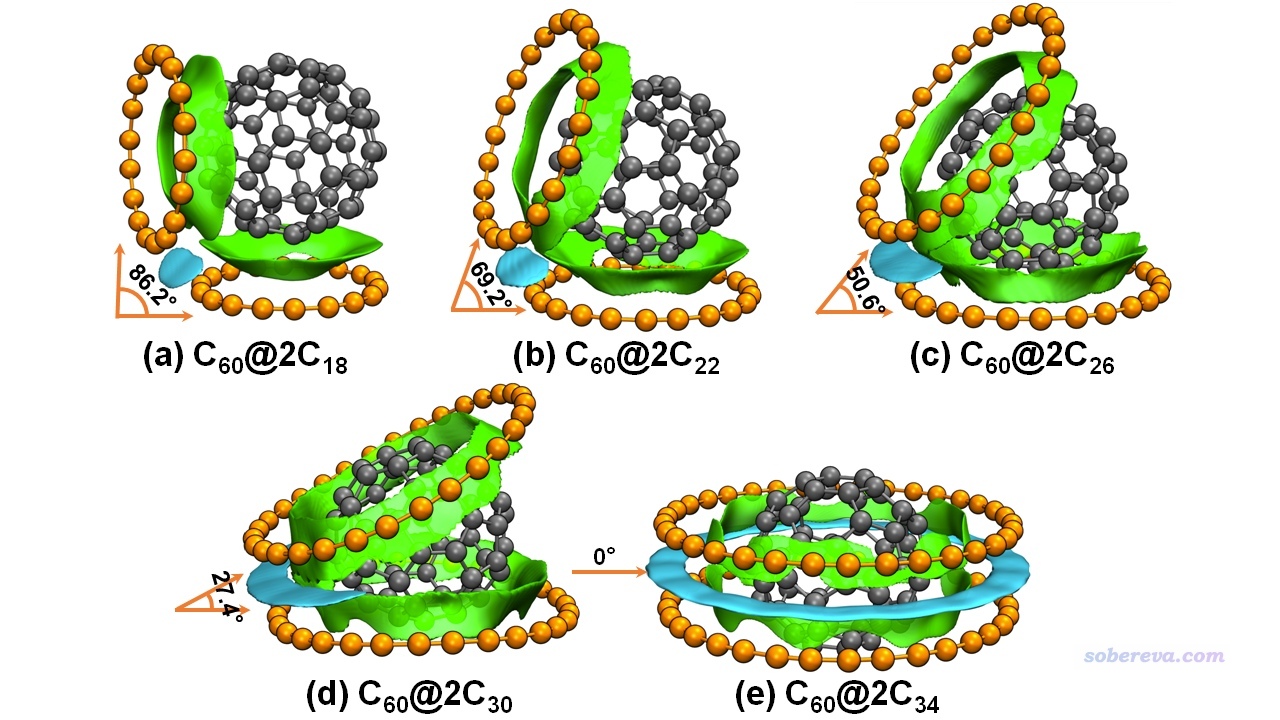
文章系統考察了一個富勒烯結合兩個碳環（C18至C34）形成的三聚體的結構，優化得到的結果如下圖所示。這種體系中既有碳環與富勒烯之間的相互作用，也有兩個碳環之間的相互作用，為了能直觀區分，這兩類相互作用的δg_inter等值面分別用綠色和青色著色，這樣的IGMH圖真是巨直觀！可以看到，隨著碳環的增大，兩個碳環間的夾角逐漸減小，富勒烯越來越多地被兩個碳環“吃”了進去，富勒烯始終與碳環保持著緊密的接觸和充分的pi-pi作用。當碳環大到C34時，兩個碳環之間完全平行并形成了全面的pi-pi相互作用，而且和http://www.shanxitv.org/572提到的18碳環二聚體一樣是較長的C-C鍵對著較短的C-C鍵，此時富勒烯已精確嵌入到了兩個碳環的正中間。

ωB97M-V/def2-QZVPP計算遠超100個非氫原子的體系時過于昂貴，因此文中在計算三聚體和更多聚體時在ORCA里使用的是ωB97M-V/def2-TZVP結合gCP方式的經驗性的BSSE校正，精度比ωB97M-V/def2-QZVPP差不了多少而耗時低得多得多。使用ωB97M-V/def2-TZVP+gCP，文中計算了富勒烯結合第一個碳環的結合能ΔE_1_bind，以及在此基礎上再結合第二個碳環的結合能ΔE_2_bind（即C60@Cn與Cn形成C60@2Cn的結合能），總的結合能（三聚體結合能）為ΔE_1_bind與ΔE_2_bind之和。結果如下圖(a)所示。可見隨著碳環增大，結合能越來越負、結合作用越來越強，而且ΔE_2_bind比ΔE_1_bind明顯更負，這體現出多個碳環與富勒烯結合的非常明顯的協同作用。如上面的IGMH圖所示，已有的一個碳環可以和另一個碳環形成pi-pi作用，而且碳環越大時pi-pi作用越顯著（青色等值面越來越大），這是為什么碳環越大時協同效應越強。

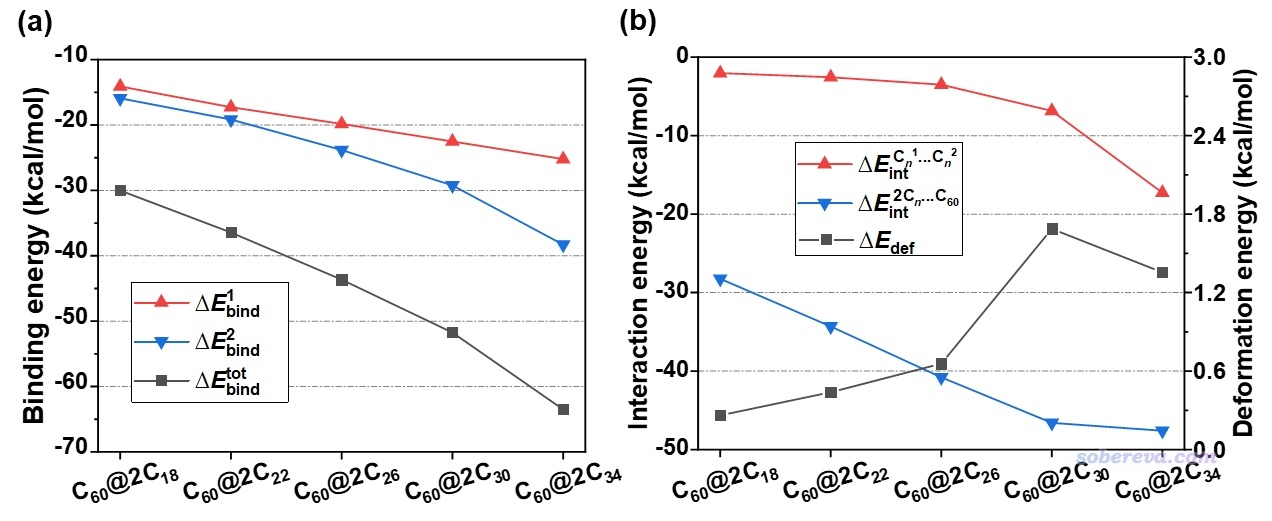
為了更進一步考察三聚體結構中不同片段之間的相互作用強度，此文還基于優化后的三聚體結構計算了片段間的相互作用能，如上圖(b)所示，兩個碳環間的相互作用能對應紅線，兩個碳環與富勒烯之間的相互作用能對應藍線。可見隨著碳環增大，碳環間的相互作用逐漸增強，特別是兩個C34碳環之間的相互作用格外強，這是因為如前面的IGMH所示，它們能形成完整的遍及整個碳環的pi-pi作用，而不再只是局部區域的pi-pi作用。還可見從C18到C30之間，碳環越大，由于可以和富勒烯相互作用的原子越多，碳環-富勒烯的相互作用越強，但是從C30到C34這種相互作用反倒稍微變弱了，這是因為在C60@2C34中C34與富勒烯的接觸不像C60@2C30中C30與富勒烯的接觸那么充分，這一點從IGMH圖上就可以明顯看出來，即C60@2C34中綠色的兩條環狀等值面明顯比C60@2C30的窄很多。這體現出恰當利用IGMH方法可視化分子間相互作用，甚至可以把不同體系間輕微的差異性也給明確揭示出來。《直觀解釋分子間相互作用如何影響不對稱催化：Nature Chemistry上一個很好的IGMH分析范例》（http://www.shanxitv.org/700）里的例子也同樣體現了這一點。

各個片段在結合成C60@2Cn三聚體過程中的總變形能如上圖的黑線所示，由于富勒烯的剛性很強，因此變形能基本都來自于碳環的變形。可見隨著碳環的增大，變形能也逐漸上升，這在于越大的碳環柔性越強。從前面的結構圖甚至肉眼都能明顯看出來C30碳環在三聚體結構中有明顯的彎曲。而C34的變形能則小于C30，這是因為C60@2C34復合物中的兩個C34基本是圓形、平面的結構，和孤立狀態結構特征相差較小，而且此結構中C34與富勒烯的相互作用沒有C30的那么強。

3 碳環-富勒烯 1:2三聚體

下面再來看一個碳環與兩個富勒烯結合成2C60@Cn（n=18到30）三聚體的情況。優化后的復合物結構和IGMH圖如下所示，綠色等值面展現富勒烯與碳環之間的相互作用，黃色等值面展現兩個富勒烯之間的相互作用。標注的d_min對應兩個富勒烯之間最近原子距離（可以將結構文件載入Multiwfn，進入主功能100的主功能21，輸入dist，然后依次輸入兩個片段里的原子序號得到此值）。由圖可見，從C18到C26碳環，碳環越大，由于對兩個富勒烯之間的接觸阻礙越小，富勒烯之間的距離越近、富勒烯之間的相互作用越顯著。碳環從C22變成C26時，富勒烯與碳環之間的IGMH等值面明顯變窄，體現相互作用明顯變弱，和富勒烯之間的相互作用強度的變化形成了此消彼長的關系。對于2C60@C30的情況，碳環與兩個富勒烯的相互作用不再對稱，上面的富勒烯歪到一側去了，與碳環的相互作用顯著小于下面的富勒烯，因此可以預料2C60@C30的穩定性明顯不及2C60@C26。

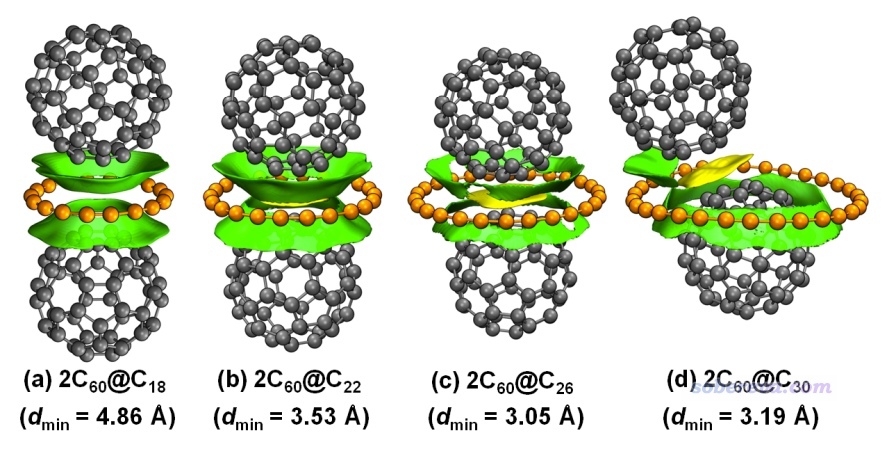
下圖(a)給出了2C60@Cn的三聚體總結合能（黑線），以及結合第一個和第二個富勒烯時候的結合能（紅線和藍線）。可見碳環越大，對第一個富勒烯的結合越強，這在前文的碳環-富勒烯二聚體的研究中已經說過。由于已有的富勒烯會對第二個結合的富勒烯產生吸引作用，對于2C60@C18、2C60@C22、2C60@C26，第二個富勒烯的結合能比第一個富勒烯的結合能更負，即兩個富勒烯與C18、C22、C26碳環的結合有明顯的協同效應。而對于2C60@C30，由于第一個富勒烯嚴重妨礙第二個富勒烯的結合，導致第二個富勒烯只能歪斜著與C30碳環發生較弱的相互作用，同時第二個富勒烯結合時還稍微削弱了第一個富勒烯與碳環的相互作用，因此第二個富勒烯的結合能只有第一個富勒烯結合能的一半。

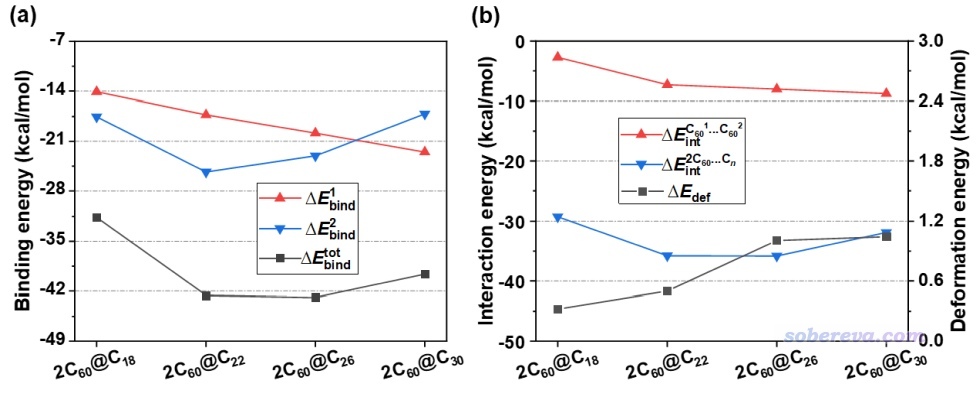
上圖(b)更進一步考察了2C60@Cn的三聚體中各個片段間的相互作用能。可見由于碳環越大、越不給富勒烯之間的接觸礙事，圖中紅線對應的富勒烯之間的相互作用能是隨著碳環的增大而越來越負的。圖中藍線體現C22和C26與兩個富勒烯的相互作用最強，而C30由于只能松散地與其中一個富勒烯相互作用，因此它與兩個富勒烯的總相互作用更弱一些。

根據以上信息，文中提出了新穎的“分子膠水”的概念。大小恰到好處的碳環，如C22，可以把兩個富勒烯特別牢固地粘在一起。C22對第二個富勒烯的結合能，也等價于C60@C22與一個富勒烯的結合能，達到了約-42 kcal/mol，這比起兩個富勒烯之間的結合能-8.3 kcal/mol強太多了，甚至都輕微超過了C-C單鍵鍵能的一半！！！

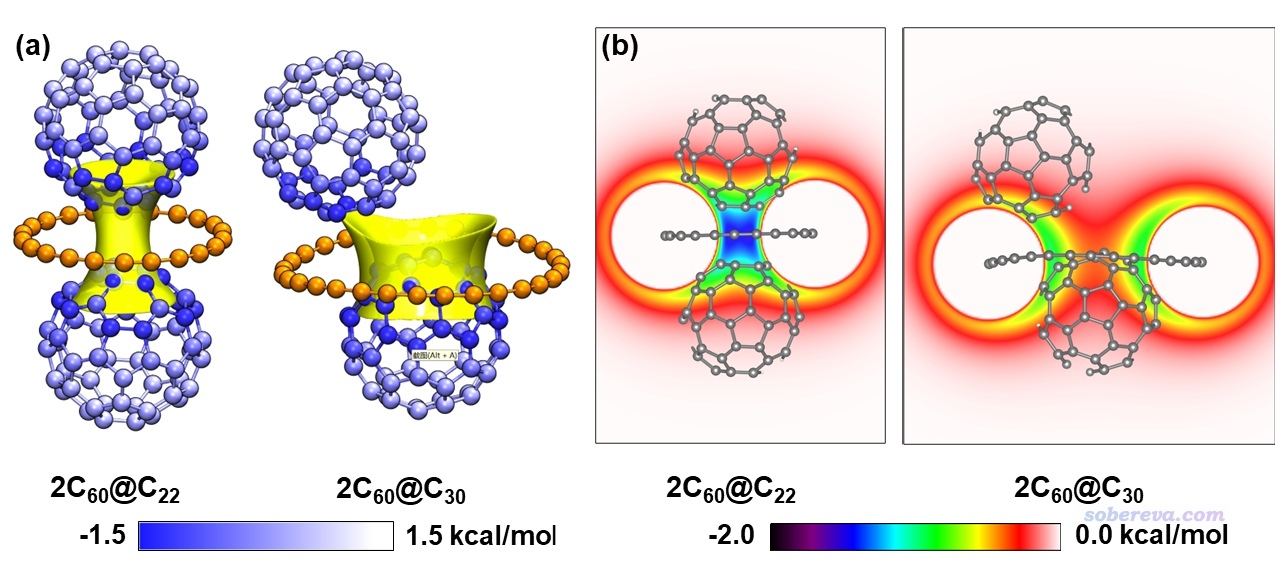
為了更充分地探究碳環對富勒烯結合起到的膠水作用，此文運用了《談談范德華勢以及在Multiwfn中的計算、分析和繪制》（http://www.shanxitv.org/551）中介紹的方法，基于GAFF力場參數繪制了2C60@C22和2C60@C30三聚體結構中碳環產生的范德華勢，以碳原子為探針原子，如下所示。圖(a)的黃色等值面對應范德華勢=-0.8 kcal/mol，富勒烯的原子按照原子所在位置的范德華勢著色，顏色越藍體現富勒烯的相應原子與碳環間的色散吸引作用越強。圖(b)是利用VESTA程序基于Multiwfn產生的范德華勢cube文件繪制的填色平面圖。由圖可見C22碳環的范德華勢最負的區域從碳環中心向上下兩側延伸出來，沒過了每個富勒烯大約1/3的區域，顯然C22碳環的這種范德華勢分布能恰到好處地把兩個富勒烯粘起來，是富勒烯之間最簡單且最完美的膠水分子！而碳環也不宜過大，如圖中C30的情況，雖然其范德華勢很負的區域能覆蓋下方的富勒烯將近一半的原子，但對上方的富勒烯的色散吸引則較為有限。盡管如此，C30對第二個富勒烯的結合能-17.1 kcal/mol仍然比兩個富勒烯之間的結合能-8.3 kcal/mol負得多。因此哪怕碳環偏大，照樣能促進兩個富勒烯的結合。

4 一個富勒烯最多能結合多少個18碳環？

從前面給出的兩個18碳環與一個富勒烯形成的復合物來看，富勒烯表面實際上還有空間可以結合更多的18碳環。那么一個富勒烯最多能結合多少個18碳環？多少個碳環才能令富勒烯的表面飽和？為了探究這個有趣的問題，文中根據碳環和富勒烯的結構，搭建了6個碳環均勻分布在富勒烯上下左右前后的結構并做了幾何優化。由于此體系多達168個碳原子，用ωB97XD/6-311G*優化和振動分析實在過于昂貴，所以這部分的計算對碳環用6-311G，而對富勒烯用6-31G。這么做的合理性一方面在于碳原子對于極化函數的要求遠低于雜原子，另一方面是以C60@C18進行測試，6-311G&6-31G優化的結果與6-311G*的結果的差異確實可忽略不計，分別如下圖的紅線和藍線所示（原文圖S4），可見幾乎完全重合。注意18碳環的基組不能再減小到6-31G，這點筆者在《我對一篇存在大量錯誤的J.Mol.Model.期刊上的18碳環研究文章的comment》（http://www.shanxitv.org/584）中專門指出過。

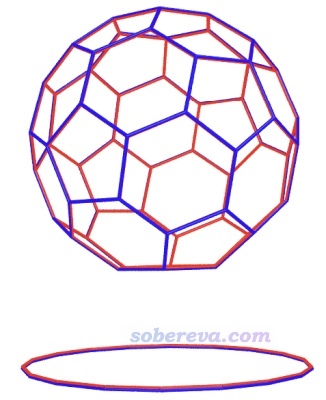
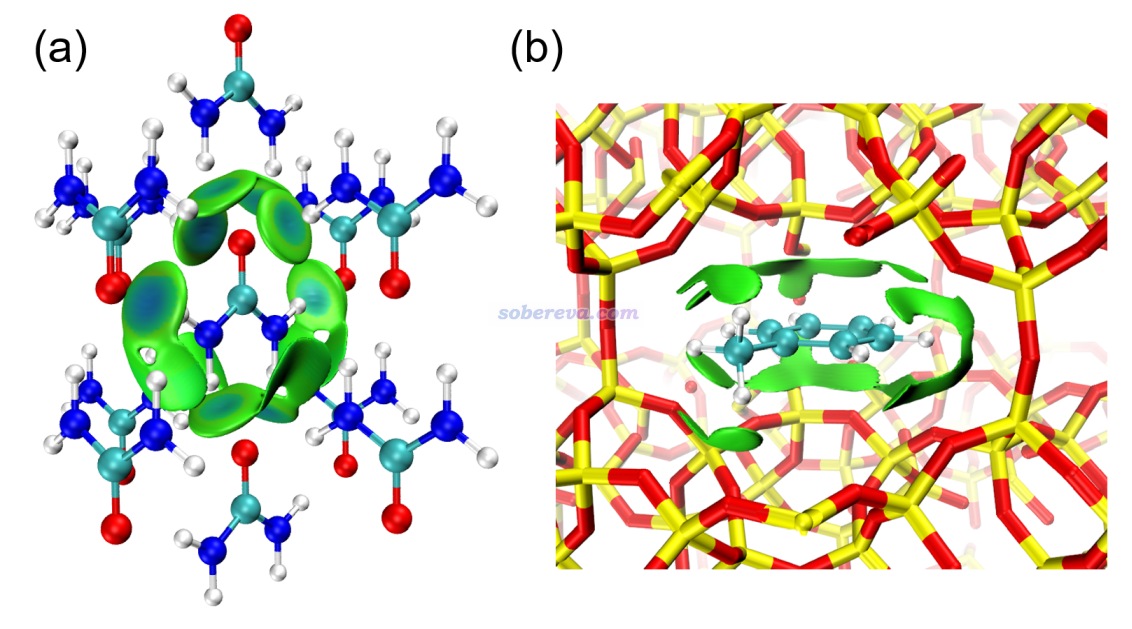
優化得到的富勒烯結合6個18碳環的結構如下圖(a)所示。為了清楚起見，在VMD程序里通過繪圖命令用黃色圓球把18碳環中心位置顯示了出來，并且把相鄰的黃球用藍線連了起來，由此可以清楚地看出6個碳環構成了一個包圍富勒烯的近乎理想的正八面體空間。下圖(b)是IGMH圖，依然是富勒烯與碳環之間的作用用綠色展示，碳環之間的作用用青色展示，可見這個C60@6C18結構中每個碳環都與富勒烯產生了非常顯著、充分的pi-pi作用，而且每一對相鄰碳環之間也產生了特別顯著的pi-pi作用，這是何等完美的結構啊！6個18碳環與富勒烯的結構匹配程度完美到令人驚嘆！

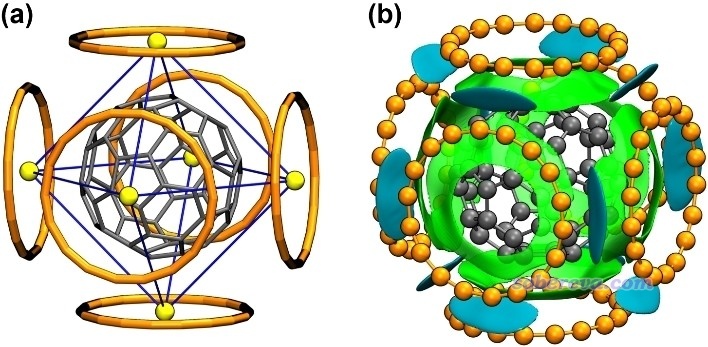
在ωB97M-V/def2-TZVP+gCP級別下計算的C60@6C18的總結合能高達-101.3 kcal/mol，已經達到了常規化學鍵的數量級！此體系中平均每個18碳環的結合能是-101.3/6=-16.9 kcal/mol，這比起C60@2C18中18碳環平均結合能-15.0 kcal/mol更負，體現出C60@6C18的形成過程的協同作用真是巨強。這在于此體系中每個18碳環都能同時與周圍四個18碳環充分地吸引。C60@6C18在氣相標況下的結合自由能為-13.4 kcal/mol，體現出此結構在熱力學上很容易自發形成。

基于C60@6C18的結構，文章還大膽地設想了富勒烯與18碳環形成的共晶的結構，示意圖如下所示（原文圖S4）。此結構里每個碳環、富勒烯都最大程度利用了自己的色散吸引能力與對方結合，因此應當是一個頗為穩定、大概率在未來能被實驗合成出來的晶體。

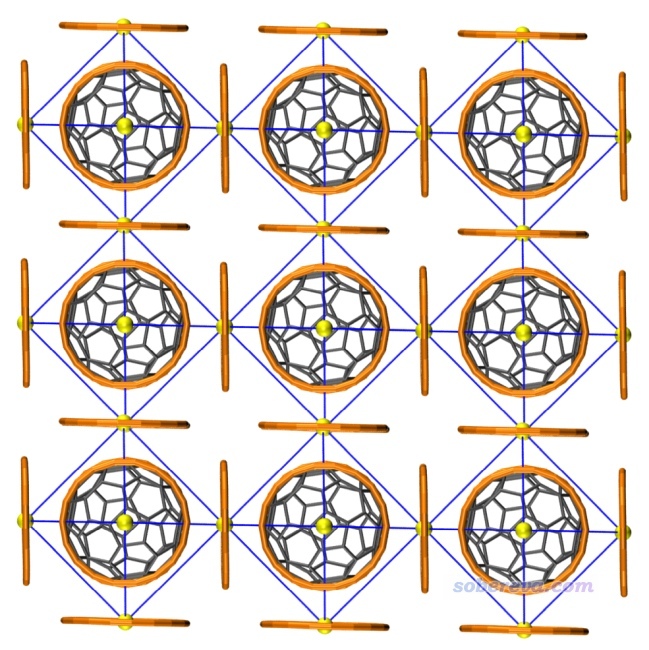
5 總結

本文介紹的Chem. Eur. J., 30, e202402227 (2024)一文通過嚴謹的量子化學計算并充分運用Multiwfn實現波函數分析，首次預測了各種尺寸碳環與不同數目C60富勒烯形成的復合物的結構，并深入探討了相互作用強度和本質。此文體現出富勒烯與碳環這兩種碳的同素異形體之間通過pi-pi作用表現出極強的親合性。碳環體系以其特殊的環形幾何結構以及獨特的兩套全局共軛的pi電子，還可以作為分子膠水將兩個富勒烯牢牢粘在一起。文章還證明了一個富勒烯最多能結合6個18碳環，而且結合過程中有顯著的協同性，結合越多越容易。因此靠富勒烯吸附碳環，或許在未來能成為一種富集富勒烯的手段。文章還預測了富勒烯與18碳環形成共晶的可能，在未來有可能能以這種形態將不穩定的18碳環穩定地儲存起來。

此文是通過理論計算研究新穎的分子間復合物的很好的例子，兼具重要的理論意義和實際意義。同時此文也是利用Multiwfn做波函數分析探究弱相互作用的很好的范例，把相互作用特征研究得十分通透，尤其是IGMH方法把富勒烯與碳環的復合物中的弱相互作用展現得超級生動直觀、一目了然，此文充分體現出掌握Multiwfn程序做波函數分析對弱相互作用研究的關鍵性價值！

另外，如果你對pi-pi研究感興趣，強烈建議閱讀《談談pi-pi相互作用》（http://www.shanxitv.org/737）。