正確地認識分子的能隙(gap)、HOMO和LUMO

正確地認識分子的能隙(gap)、HOMO和LUMO

First release: 2020-Mar-26 Last update: 2020-May-2

0 前言

筆者在QQ群里、論壇里答疑時經常看到有計算化學初學者、理論計算外行對gap、HOMO、LUMO的理解存在嚴重誤區，很多錯誤還存在各種文獻中，長期以來以訛傳訛，諸如什么“軌道能量差就是激發能”、“循環伏安法能測HOMO能級”等等。在此就寫一篇文章，讓缺乏理論化學知識的人能對分子的gap、HOMO、LUMO有個正確的認識，分清楚不同gap之間的區別，明白為什么軌道能量是不能實驗測定的，最后再專門說說與本文主題有關的Koopmans定理。

1 分子體系gap的三種類型

首先要搞清楚，孤立體系，比如分子、團簇，有三種gap（能隙），絕對不能混淆：

(1) HOMO-LUMO gap：定義是E(LUMO)減去E(HOMO)，顯然肯定是個正值。平時說分子體系的gap的時候，如果沒有前提，多數情況指的就是這種gap。

(2) Fundamental gap：定義是VIP減去VEA。其中VIP是vertical ionization potential的縮寫，中文一般叫垂直電離能，定義是VIP = E(N-1) - E(N)，這里E是電子能量，N是體系原本的電子數，N-1是電離掉一個電子之后的電子數。VEA是vertical electron affinity的縮寫，文中叫垂直電子親和能，定義是VEA = E(N) - E(N+1)，N+1是指體系額外獲得一個電子后的電子數。顯然，fundamental gap等于E(N-1) + E(N+1) - 2*E(N)。

(3) Optical gap（光學gap）：基態電子態通過吸收光子所能躍遷到的最低激發態對應的激發能。比如對于一般的有機染料分子，對應的就是S0態極小點結構下S0到S1態的垂直躍遷對應的激發能。由于躍遷禁阻而無法觀測到的最低激發態不算，比如對于單重態基態體系，雖然T1態比S1還要低，但不能把S0與T1間的能量差叫做optical gap，因為這是對稱禁阻的。

以上三種gap中，HOMO-LUMO gap是無法通過實驗測定的，因為HOMO和LUMO根本就不是真實存在的東西，詳見本文第4節，因此凡是見到有人說通過xxx實驗測了HOMO-LUMO gap，一律都是胡說八道，或者錯誤地解釋了實驗。由于VIP和VEA都是可以實驗測定的（氣相VIP可以通過光電子譜得到，氣相VEA可以通過電子附著光譜得到），因此fundamental gap是可以實驗測定的。Optical gap通過UV-Vis光譜就可以直接測定，相當于波長最大的吸收峰位置（其實這不嚴格，因為有時相鄰的激發態的吸收峰會顯著相互疊加，導致實際觀測到的一個峰可能對應不止一個激發態。另外還要考慮振動耦合問題，這影響峰位置，本文就不多說了，感興趣者可以看《振動分辨的電子光譜的計算》http://www.shanxitv.org/223。后文也忽略振動態的問題）。

所有以上三種gap都可以通過量子化學計算非常容易地得到。在基態極小點結構下，HOMO-LUMO gap用KS-DFT方法做個單點計算就有，optical gap用諸如TDDFT算一下激發態就有（見比如http://www.shanxitv.org/314），算fundamental gap只需要把N+1、N、N-1態的單點能都算出來代入公式即可。

Optical gap比fundamental gap數值肯定要低，差值稱為electron-hole pair binding energy。

老有初學者明明說的是分子體系，卻用帶隙（band gap）這個詞，這是大錯特錯。周期性體系才有能帶的概念，而分子體系根本都沒有能帶，何來帶隙？

感興趣的讀者可以看看《mind the gap》（Mater. Horiz., 1, 17 (2014)），只有兩頁，專門說了這三種gap。文中還提到，fundamental gap是對于分子體系而言的，對于周期性體系來說，band gap=fundamental gap=transport gap，但和optical gap不同，因為也相差著electron-hole pair binding energy。周期性體系不能說HOMO-LUMO gap，因為HOMO和LUMO從其名字上就知道這本來就是對于分子（或者說孤立體系）而言的，對周期性體系可以類比的概念是LUCO（最低非占據晶體軌道）和HOCO（最高占據晶體軌道），分別對應于導帶底和價帶頂的位置，差值就是band gap。

2 HOMO-LUMO gap與fundamental/optical gap的關系

分子的HOMO-LUMO gap雖然和fundamental gap、optical gap不等價，但可以視為二者的近似，在一定程度上有正相關性，下面具體說一下。

Koopmans定理認為VIP≈-E(HOMO)、VEA≈-E(LUMO)，因此VIP-VEA≈E(LUMO)-E(HOMO)，即fundamental gap≈HOMO-LUMO gap。雖然二者有相關性，但是絕對不要期望在定量數值上能有多好的對應關系。因為VIP≈-E(HOMO)這個關系對于常用泛函來說誤差是很大的，尤其是VEA≈-E(LUMO)這個關系極差，在本文第4節還會專門說。

不少搞實驗化學的，以及不少儀器分析、有機化學之類的書籍里，認為LUMO與HOMO間的能量差就對應于最低電子激發能，即把HOMO-LUMO gap和optical gap劃等號，這是大錯特錯！要明白，電子激發過程是從一個電子態（電子基態）到另一個電子態（電子激發態）的躍遷，而不是從一個占據軌道到一個非占據軌道的躍遷。電子態是真實存在的，而軌道只是虛構出來的概念。看過《電子激發任務中軌道躍遷貢獻的計算》（http://www.shanxitv.org/230）一文就知道，比如常用的算電子激發的TDDFT方法，把電子激發在數學上描述成各種各樣形式的軌道躍遷的線性組合。雖然對于某些體系，通過查看TDDFT的單激發組態函數的系數會發現，能量最低的電子激發方式確實可以近乎100%地通過HOMO->LUMO的躍遷來描述，但也絕對不能把這倆軌道的能量差（即HOMO-LUMO gap）直接當做激發能，因為二者之間還相差激子結合能。這里引用筆者講授的北京科音基礎量子化學培訓班（http://www.keinsci.com/workshop/KBQC_content.html）的幻燈片里的一頁來說明

上圖中的激子結合能絕對不能忽略，它導致HOMO-LUMO gap與TDDFT算的optical gap之間相差零點幾eV是非常正常的。還要知道，最低電子激發即便有一對軌道貢獻近乎100%，這對軌道也未必是HOMO和LUMO。比如反式偶氮苯，在基態極小點結構下用TD-PBE0/6-31G*下計算出來的S0→S1激發對應的是HOMO-1→LUMO躍遷，而S0→S2才對應于HOMO→LUMO躍遷，這是因為兩種電子激發的激子結合能的不同導致激發能與軌道能量差不滿足正相關性。另外，由于對稱禁阻，或者恰好最低激發態的振子強度就是特別小，實驗吸收譜上觀測到的最大波長的峰位置可能并非是最低激發態，換句話說，最低激發態是個暗態（dark state），這種情況下顯然就更甭指望optical gap能和HOMO-LUMO gap聯系起來。

雖然HOMO-LUMO gap原理上與optical gap不等價，對于實際體系，從統計結果上看關系如何？在J. Chem. Inf. Model., 57, 1300 (2017)中，作者計算了2248895個小分子體系的最低激發能與HOMO-LUMO gap，得到下圖

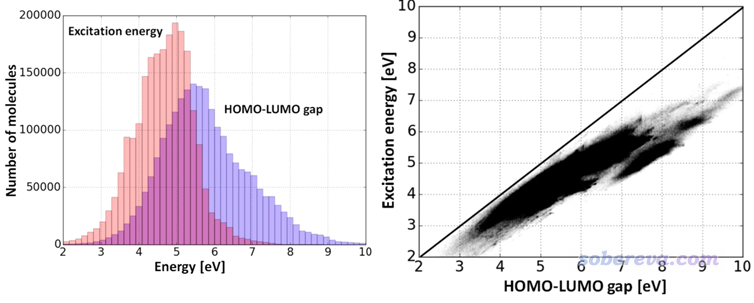
可見二者間雖然有正相關性，但是相關性比較弱，數據點分布相當分散。

在實際研究中，拿量子化學程序算出來的HOMO-LUMO gap去解釋理論計算或者實驗觀測到的fundamental gap、optical gap的趨勢，在一定程度上是可以的，但如果解釋不好，也絕對不要強求，否則就是強詞奪理了。而把HOMO-LUMO gap直接當做fundamental gap或optical gap來用，是絕對不能接受的！碰上稍微懂點理論計算的審稿人一定會挨批。

還要注意，計算的HOMO-LUMO gap受使用的DFT泛函影響非常大，通常是HF成份越高的泛函，算出來的HOMO-LUMO gap越大。從下圖筆者計算的數據中可以清楚地看到這一點。

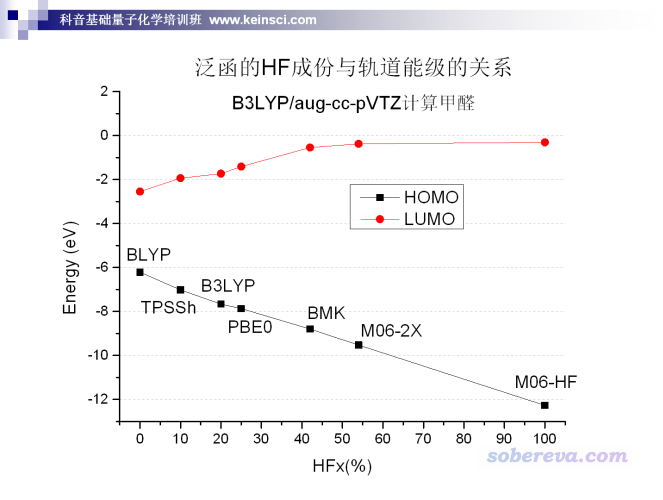
某種泛函算出來的HOMO-LUMO gap大小，和它計算出的fundamental gap或optical gap的準確性毫無必然關系。而且本身HOMO-LUMO gap也不是實驗可測的，完全不能以這個量的大小判斷泛函的好壞。

3 HOMO-LUMO gap的一些用處

HOMO-LUMO gap除了作為optical gap和fundamental gap的近似外，還有一些實際用處，在這里提一下。

寡聚物的HOMO-LUMO gap常被用于衡量分子的導電性。HOMO-LUMO gap越小，一般認為導電性越好。例如筆者和合作者在RSC Adv., 3, 25881 (2013)中研究了一系列寡聚物的能隙，如下所示，苯和萘以不同排列、不同比例進行組合，使體系展現出了不同的HOMO-LUMO gap。這體現出寡聚物像蛋白質一樣，通過序列可以決定其功能性（控制導電性）

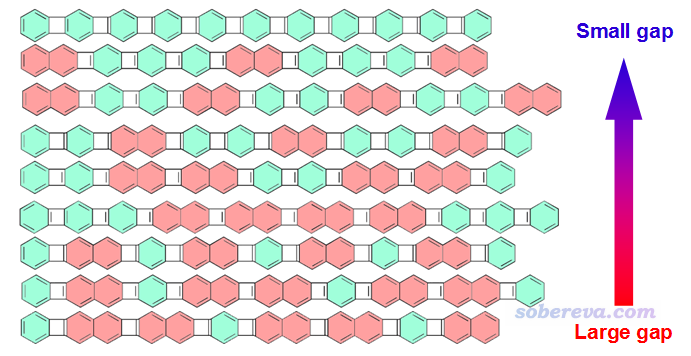
寡聚物的HOMO-LUMO gap和無限延展的聚合物的帶隙存在密切聯系，可以通過量子化學程序計算的HOMO-LUMO gap來外推出帶隙。下圖來自Acc. Chem. Res., 44, 14 (2011)

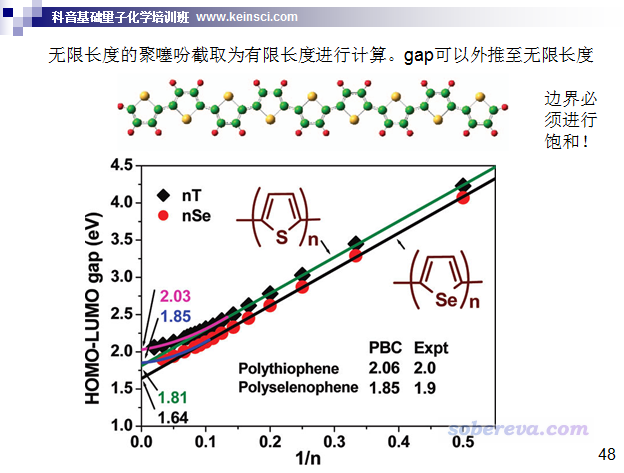
文中用B3LYP/6-31G*對不同單元數的噻吩寡聚物計算了HOMO-LUMO gap，并且外推到無窮長的數值，如圖中粉字所示，結果為2.03 eV，這和用周期性計算聚噻吩得到的帶隙2.06 eV非常相近。周期性體系的帶隙是可以直接實驗測的，實驗值是2.0 eV，可見理論計算的和實驗很相近。

這篇Acc. Chem. Res.文章和不少研究寡聚物的文章中都提到，B3LYP/6-31G*很適合算聚合物的導電性。另外，在J. Phys. Chem. Lett., 7, 1198 (2016)中，作者對于各種無機體系做了測試，發現B3PW91算帶隙算得很理想，平均誤差只有0.28 eV。由于B3LYP和B3PW91的特征相近，HF成份都是20%，因此此文的結論對于B3LYP也適用。雖然前面說了，分子體系的HOMO-LUMO gap是不可觀測的，但考慮到它與帶隙之間的關系，倘若非要說HOMO-LUMO gap拿什么泛函算比較合適，通常來說B3LYP或B3PW91是優先值得考慮的，對于算這個問題二者結果幾乎一樣，見比如RSC Adv., 3, 25881 (2013)文中圖2的對比。

概念密度泛函是研究化學反應活性和位點的一套重要理論，詳見《概念密度泛函綜述和重要文獻合集》（http://bbs.keinsci.com/thread-384-1-1.html）中的資料。在這個框架中有一個量叫軟度(softness)。軟度不是指體系的剛性大小，而是反映電子的活潑性、其分布的易變形程度。對于一系列類似體系（比如某些官能團不同、局部結構有差異，但主體特征一致），通常認為軟度越大，分子越容易發生反應。軟度的表達式為1=1/(VIP-VEA)，可見它等價于fundamental gap的倒數；而在Koopmans近似下，軟度直接等于HOMO-LUMO gap的倒數。這是為什么很多文章喜歡拿HOMO-LUMO gap說事，誰比較小就說誰的反應活性更高。這確實有一定依據，但一定要注意這種分析僅限于類似物，若用于對比兩個特征相差甚巨的分子的反應活性，那純屬偽科學。

有很多文章拿HOMO-LUMO gap衡量分子穩定性，誰的HOMO-LUMO gap越小就說誰越不穩定。這種說法相當粗俗，總是被用來瞎討論。要注意“穩定性”絕對不是一個簡單的詞。不穩定是指當前分子容易變成其它構型或物質，這對應于很多可能的過程，因此可以區分成化學穩定性、光穩定性、熱穩定性等等，顯然這絕對不是簡簡單單光靠一個HOMO-LUMO gap就能說明的。倘若是討論化學穩定性，并且不考慮另一種反應物的特征，且對比的一批分子之間有足夠相似性，那么拿HOMO-LUMO gap來說事還算說得過去。如果另一種反應物是明確的，并且你有能力用量子化學程序計算出反應勢壘，若發現HOMO-LUMO gap和勢壘有正相關性，那么值得在文章中說一說，但如果與勢壘沒有這種相關性，則體現出HOMO-LUMO gap把問題過度簡單化了，應當摒棄這種分析（如果強行分析，可能會被審稿人批，屆時更麻煩）。

HOMO-LUMO gap越小通常極化率也越大，這點也值得一提。這可以從完全態求和公式角度理解，詳見《使用Multiwfn基于完全態求和(SOS)方法計算極化率和超極化率》（http://www.shanxitv.org/232）。由極化率表達式可見，分母有一項是激發能，這和主導電子激發的兩個軌道間的能量差有相關性。HOMO-LUMO gap越小暗示著占據軌道與非占據軌道的能量差整體越小，進而傾向于令激發能也越小，故而極化率傾向于越大。

搞實驗的人很喜歡拿HOMO-LUMO gap說事，在這里告誡一下初學者，千萬不要盲目聽信已發表的文章里的HOMO-LUMO gap的分析，盡信文獻不如無文獻。文章中說得在理的可以吸取，而顯得莫名其妙的分析、不合基本化學邏輯的討論，則絕對不要輕信和效仿。如果以為已經發表的文章就都是正確的，那實在太天真了。

4 HOMO和LUMO能實驗測定么？

在化學領域里“循環伏安法測定的HOMO、LUMO是xxx”這種描述隨處可見，有些文章更是聲稱測量了軌道波函數并給出了圖像，甚至還發到了某些人夢寐以求的頂級刊物上。這類文章以訛傳訛程度之廣令人發指，明顯錯誤的東西反復出現在諸多研究者的視野里，令他們信以為真。這使得筆者在“波函數分析與Multiwfn程序培訓班”一開始就給出了兩頁ppt以正視聽：

分子軌道是不可測量的這一點，根本不需要什么復雜的理論知識就能明白。只要有理論化學最基本的常識，知道Fock和Kohn-Sham算符是什么，自然就明白分子軌道是理論上做了單電子近似才有的概念，是將分子波函數以簡化方式求解才誕生的，顯然是純粹人為虛構出來的產物。Hartree-Fock、半經驗、KS-DFT方法全都可以得到分子軌道，具體來說，分子軌道是人為定義的單電子有效哈密頓算符的本征函數的統稱。既然分子軌道在現實當中都不存在，談何實驗觀測？在原理上怎么可能實驗測定？顯然，那些號稱實驗上測定的分子軌道根本就不是分子軌道，而是對觀測到的數據的錯誤理解和解釋，將其錯誤地冠上了“分子軌道”的名字。

那些通過光電子實驗給出了“分子軌道”圖像的文章，實際上觀測到的是物理意義嚴格的Dyson軌道，仔細看看上面幻燈片里的文章就會了解得更多。分子軌道只不過很多情況是Dyson軌道的近似罷了。具體來說，對于靜態相關弱的體系，Dyson軌道與分子軌道定性一致；對于強相關體系（靜態相關強的體系，如雙自由基），Dyson軌道可能與分子軌道顯著不符，往往需要寫為多個分子軌道的線性組合才能定性描述出來。所以千萬不要把Dyson軌道與分子軌道混淆。只有當完全忽略電子相關以及軌道的弛豫，即Koopmans定理所假設的情況，那么Dyson軌道才正好是HF方法算的分子軌道。

那些搞電化學的人通過循環伏安法測的既然不是HOMO、LUMO的能量，那測的究竟是什么？看下面我總結的關系圖（引用的話請注明出處，即本文的網址）

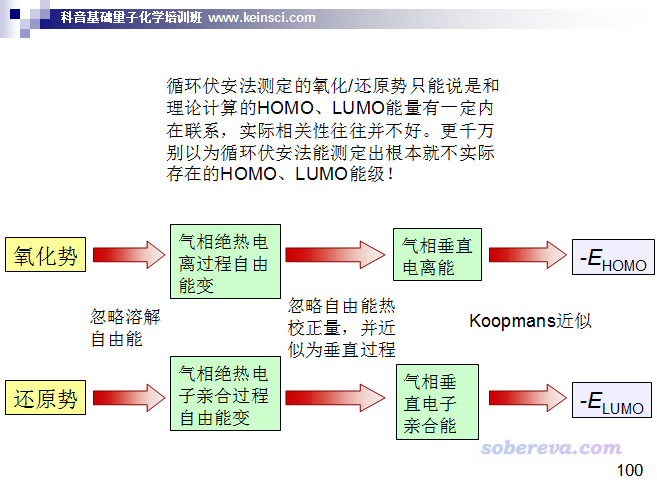
實際上，循環伏安法測的是溶液中的氧化勢和還原勢，這對應于電極反應過程的自由能變，離HOMO、LUMO能量隔著多達三層近似！顯然把溶液中的氧化勢和還原勢直接分別當成HOMO和LUMO能量的負值是非常荒唐的，只能說存在正相關性而已，而這相關性還不怎么樣。所以千萬不要以為自己做量子化學計算算出來的前線軌道能量和循環伏安法實驗數據對應得不好就以為自己算得不對。溶液中的氧化勢和還原勢都是可以通過量子化學方法（需要利用溶劑模型）計算出來的，這才和循環伏安法實驗真正有可比性（但想對應得很好仍然很不容易，因為對于離子體系，現有的最好的隱式溶劑模型算的溶解自由能的誤差也挺大，相關信息看http://www.shanxitv.org/327）。

光電子譜可以測定將體系各層（不限于最外層）電子電離走對應的電離能。有人說光電子譜測定的就是分子軌道能量，實際上這也是錯誤的。前面已經說了-E(HOMO)只不過是最外層電子的電離能（第一VIP）的近似，對于其它層的電子也是一樣。實際上，電離過程相當于N電子態躍遷到N-1電子態，由于電子相關作用，不能將這簡單當成是一個軌道上的電子電離掉；而且哪怕是忽略掉電子相關問題，即N與N-1態的躍遷就相當于掉了一個軌道上的電子，但這個電子走了之后由于其它電子感受到的外勢發生了變化，故其余的占據軌道會發生弛豫，也會導致體系能量進一步發生改變。顯然將電離各層電子對應的電離能直接當做是各個分子軌道的能量的負值是明顯錯誤的。

HOMO、LUMO不僅不可實驗測定，而且也不能通過諸如CCSD(T)、NEVPT2等高精度量子化學方法來計算，這是因為這些方法不是像HF、KS-DFT那樣是基于單電子近似框架的，方法本身也沒有定義有效單電子哈密頓算符，因此根本無法產生分子軌道。有些人可能會問“我用Gaussian做完CCSD(T)，不是給出了一批軌道能量么？”這實際上是做CCSD(T)電子相關計算之前做HF的那一步產生的HF分子軌道，根本不是什么“CCSD(T)的分子軌道”！在一些IF很高的非專業理論化學的期刊上，比如ACS Nano，居然也有作者寫“MP2計算的分子軌道能量是xxx”之類明顯錯誤的表述，真不知道審稿人都是什么水平、干什么去了。量子化學里有很多種軌道，不要和分子軌道混淆。比如MCSCF計算完給出的軌道是贗正則分子軌道，Gaussian里對MP2、CCSD等方法加上pop=NO關鍵詞給出的是自然軌道、做軌道定域化處理后得到的是定域化分子軌道（參看http://www.shanxitv.org/380）等等。它們都不是單電子有效勢算符的本征函數，不屬于分子軌道。本文說的泛函都是指雙雜化泛函以外的泛函，雙雜化泛函也是得不到分子軌道的，因為它包含類似MP2的一項，因此也脫離了單電子近似。量子化學程序做完雙雜化泛函計算后給你的軌道能量其實只是雙雜化泛函當中的雜化泛函那部分計算時產生的軌道，并非是雙雜化泛函級別的軌道。

5 關于Koopmans定理

前面已經多次提到Koopmans定理，但都沒有細說。為了令讀者了解得更透，這里專門詳細說一下，并且做一些額外的討論。

Koopmans定理的含義如今經常被廣義化，其1934年剛提出來的時候最初的說法是：分子體系的第一電離能等于HF方法的HOMO能量。當然，這段話是忽略了電子相關和軌道弛豫效應情況下的。根據J. Chem. Phys., 150, 074108 (2019)的大量測試，對各種價層電子電離的情況，HF的軌道能量的負值與實驗VIP偏離的絕對平均值為1.86 eV，若只考慮最外層電子電離的情況，則誤差為0.74 eV。可見至少對于最外層電離，即第一VIP，Koopmans定理能給出定性正確的結果。之所以HF方法精度很爛，但Koopmans定理表現得還不差，這被認為是忽略電子相關和忽略軌道弛豫效應帶來的誤差往往能很大程度抵消。

Koopmans定理在一些文章和書籍中也被擴展到LUMO的情況，說分子的第一（垂直）電子親和能等于LUMO軌道能量。但這個近似從實際結果上來看非常糟糕，完全沒有實用性。雖然占據分子軌道沒有嚴格的物理意義，但非占據分子軌道的物理意義明顯更差，而且能量和形狀對基組非常敏感。

Koopmans定理后來被用于DFT領域，為了區分，有時叫DFT-Koopmans定理。這個定理說的是：完全精確的交換-相關泛函做KS-DFT計算得到的HOMO能量等于第一VIP。這個關系可以證明是嚴格的，而非近似的。此處的第一VIP既可以是指以E(N-1)-E(N)方式算的，也可以是指實驗測定的，對于精確的泛函二者顯然是相同的（前提是排除了雜七雜八其它因素帶來的誤差）。

DFT-Koopmans定理對于LUMO并不適用，不能說精確泛函下KS-DFT計算得到的LUMO能量等于VEA。但是在精確泛函下VEA精確等于N+1電子態的HOMO能量的負值。因為-HOMO(N+1)=E(N)-E(N+1)，VEA(N)=E(N)-E(N+1)，故VEA(N)=-HOMO(N+1)。

DFT-Koopmans定理原本只是用于HOMO，但也有人用它把HOMO以下的軌道與更內層電子電離的VIP相關聯起來，確實對于某些泛函這個關系不錯，但即便對于精確的交換-相關泛函這也不是嚴格的。

即便有DFT-Koopmans定理將HOMO能量與實驗VIP聯系了起來，也絕對不要理解為“實驗可以測定分子軌道能量”，仿佛分子軌道能量是真實存在的東西，而應當說成“實驗可以測定精確的交換-相關泛函計算出的Kohn-Sham軌道能量”，即要強調實驗數據只不過是正好對應于特定情況下計算得出的某種純理論上定義東西。

由于精確的交換-相關泛函的形式是誰也不知道的，因此我們目前不可能直接基于Koopmans定理靠做個KS-DFT計算就得到嚴格精確的（第一垂直）電離能以及可能也很準確的更深層電子的VIP。

可能你會看到在一些地方有些人說Koopmans定理只對HF才近似適用、對DFT不適合。還有的人甚至說KS-DFT軌道沒有絲毫物理意義，理由是“違背了Koopmans定理”。這些亂七八糟或者嚴重歪曲的說法要么過時，要么根本沒有正確理解KS-DFT或Koopmans定理。實際上，不同的現有的泛函對Koopmans定理滿足得有好有壞，這和泛函的HF成份有關。HF成份較高的，以及一些長程校正泛函，其軌道能量的負值比起HF軌道的更接近實驗VIP。特別是Bartlett搞的QTP (Quantum Theory Project)為開頭的一系列泛函，對Koopmans定理滿足得比起現有的幾乎其它任何泛函都好（也明顯好于HF）。對價層電子電離，QTP17分子軌道能量的負值與實驗測定的VIP平均絕對誤差為0.5 eV，而換做是其它泛函，即便是表現相對較好（HF成份高達54%）的M06-2X，誤差也達到1 eV左右；如果是純泛函，誤差則高達4~5 eV。在計算內核電子的電離能方面，CAM-QTP(00)和QTP17根據Koopmans定理算的甚至比昂貴的IP-EOM-CCSD精度更高。

之前筆者在《使用Multiwfn繪制光電子譜》（http://www.shanxitv.org/478）一文中還提到了廣義化Koopmans定理，通過E(N-1)-E(N)方式算的第一VIP來試圖消除分子軌道能量與各層電子電離能的偏差，通過此處理，就可以直接用分子軌道能量較好地模擬光電子譜。顯然，對于QTP系列泛函來說，這種處理的必要性就沒有那么高了（但還是會有改進）。

由于分子軌道本來就不現實存在，所以原理上也沒有辦法判斷軌道能量算得準不準。不過，從實用角度出發，有研究文章通過讓占據軌道的能量的負值與電離能盡可能吻合來優化泛函參數。前面說的QTP17和CAM-QTP(00)泛函就是如此。還有其它一些文章，比如J. Comput. Chem., 21, 227 (2000)也是這么考慮，發現把B3LYP的雜化成份從20%提升到60%，就能讓軌道能量與實驗電離能吻合程度有幾倍的改進。通過這樣優化的泛函，就可以很省事地計算VIP，即只要在基態極小點結構下做一次單點計算，各層電子的VIP就全都能較好地得到了（這種做法的精度和可靠性，以及與其它各種方法的比較，看J. Chem. Phys. 150, 074108 (2019)中的測試）。泛函的ω參數的調控也很值得一提，這在《優化長程校正泛函w參數的簡便工具optDFTw》（http://www.shanxitv.org/346）一文中專門說了。這種做法是通過調節長程校正泛函的ω參數，盡可能令N和N+1電子態同時最大程度滿足Koopmans定理，這也是精確的交換-相關泛函應當滿足的條件之一。這樣的泛函在計算激發能、(超)極化率、fundamental gap、單-三重態激發態能量差等方面比起未經調控的泛函往往明顯更好，但缺點是不同體系最優ω參數不同，對每個被計算的體系都要優化一遍ω。

另外，也有文章通過利用分子軌道能量來較好計算VEA。例如J. Phys. Chem. A, 109, 8923 (2005)指出VEA可以近似計算為-E(LUMO)-E(HOMO)-VIP，相當于存在VEA+E(LUMO)≈-VIP-E(HOMO)的關系。至少對于B3LYP而言，通常-E(LUMO)>VEA、VIP>-E(HOMO)。對38個分子，在PBE/aug-cc-pVTZ下用這種方式算的平均絕對誤差為0.49 eV。楊偉濤等人對純泛函提出了一種非經驗的global scaling correction (GSC)方法，在Mol. Phys., 116, 927 (2018)里有介紹。將LUMO軌道波函數代入文中14式得到校正量Δε(LUMO)，然后VEA就可以計算為-[E(LUMO)+Δε(LUMO)]，這比基于純泛函通過E(N)-E(N+1)的標準方式算的更準確，不過算這個校正量的程序沒公開提供。