使用Multiwfn繪制光電子譜

使用Multiwfn繪制光電子譜

文/Sobereva@北京科音

First release: 2019-Apr-27  Last update: 2020-Sep-28

1 前言

波函數分析程序Multiwfn（http://sobereva.com/multiwfn）具有很方便、靈活、強大的態密度(DOS)繪制功能，在《使用Multiwfn繪制態密度(DOS)圖考察電子結構》（http://www.shanxitv.org/482）里有充分講解和示例。光電子譜（photoelectron spectrum, PES）的繪制原理和DOS圖頗為相似，而且需要繪制PES的人不在少數，經常有人問我怎么繪制，因此筆者在Multiwfn的DOS繪制模塊里專門加入了一個很方便的PES繪制功能，在此文專門介紹一下。注意只有2019-Apr-27及之后更新的Multiwfn才有繪制PES的功能。不了解Multiwfn的話強烈建議參看《Multiwfn入門tips》（http://sobereva.com/167）。

PS：在Multiwfn支持光電子譜繪制之后，很快就有不少文章使用Multiwfn的這個功能作圖發表文章了，比如Mater. Today Adv., 6, 100070 (2020)、J. Phys. Chem. C, 123, 28561 (2019)、Comput. Theor. Chem., 1170, 112635 (2019)、Int. J. Quantum Chem., 120, e26087 (2019)、Int. J. Quantum Chem., e26457 (2020)、New J. Chem. (2020) DOI: 10.1039/D0NJ03483E等。

2 光電子譜的繪制原理

光電子譜上的譜峰位置體現的是被光子打掉一個電子后的陽離子狀態的能量與原先中性狀態的能量差。根據打來的光子的能量不同，可分為紫外光電子譜(UPS)和X光光電子譜(XPS)，前者打來的電子能量低，電離掉的是價層電子；后者打來的光子能量很高，電離掉的是內層電子。假設體系是中性，則體系原先通常處于中性的振動基態，電離掉電子之后，體系可以處于陽離子態的不同振動態，因此PES是有精細結構的，體現振動耦合效應。但我們實際理論研究時為了省事，往往忽略掉核運動的量子效應（下文都是這樣考慮），而把電離假想為垂直過程，即電離過程中核坐標來不及改變，一直處于初態勢能面的極小點，此時PES上的峰位置就等同于垂直電離能(VIP)。后文我們說的所有電離能(IP)都是指VIP。因此，只要我們先對體系優化，然后算出來從體系各層電離掉電子對應的電離能，就能繪制出PES。

一般我們做電離能計算都是在中性的勢能面極小點下通過IP=E(cation)-E(neutral)得到，E是電子能量。但是這樣通常只能得到最外層電子電離的能量，而電離掉更深層電子的能量得不到，不過其它方法可以計算，比如OVGF、IP-EOM-CC、ADC等。

最最簡單的繪制PES的方法就是基于Koopmans定理。Koopmans定理非常知名，它說各層電子的電離能等于各個Hartree-Fock軌道能量的負值。注意這只是近似的關系，它忽略了電子相關和軌道弛豫問題，把電子態層面的問題簡化到了單電子近似得到的軌道層面上。光從第一電離能來看，HF軌道能量的負值只是其很粗糙的近似，而對于如今最常用的KS-DFT計算，這個近似往往更爛，但這點實際上具體取決于泛函的選用（諸如在特殊的QTP17等泛函下靠Koopmans定理得到的VIP相當不錯。而對于精確泛函，可以證明HOMO的能量和第一IP精確相等。有些人由于誤認為KS-DFT軌道對Koopmans定理滿足程度一定很差就因此信誓旦旦地鼓吹KS-DFT軌道缺乏意義、甚至不叫分子軌道，還引來不少點贊，真是...）。

HF如今誰也不用。而對于大家平時常用的那些DFT泛函，各個軌道能量對各層IP肯定有不同程度的偏離，而且一般偏離還挺明顯，這導致直接用KS-DFT軌道能量的負值繪制的PES和實驗對得可能較差。還有個定理叫Generalized Koopmans定理，可以很大程度上解決這個問題。這個定理把常規的通過E(cation)-E(neutral)方式計算的IP作為第一個IP，然后把HOMO以下的各個占據軌道相對于HOMO軌道的能量差的絕對值加上去作為第二IP、第三IP...換句話說，就是把所有軌道能量進行整體平移，使得IP與-E(HOMO)恰好相等，拿平移后的軌道能量的負值再來繪制PES往往就能和實驗對得不錯了。

在《正確地認識分子的能隙(gap)、HOMO和LUMO》（http://www.shanxitv.org/543）一文中，筆者還詳細介紹了QTP系列泛函。用QTP17泛函的話，軌道能級能比較理想地滿足Koopmans定理（無論是價層的還是內核的）。因此如果你基于這種泛函的軌道能級繪制PES的話，就不用著Generalized Koopmans定理了，直接基于Koopmans定理繪制即可（換句話說，在下文的例子中就用不著輸入平移值了）。在Gaussian中使用QTP17的方法見《Gaussian中非內置的理論方法和泛函的用法》（http://www.shanxitv.org/344）。

上面只是說了PES的峰的位置的確定方式，我們最終要得到的是能夠和實驗譜對照的PES曲線圖。具體產生的方式是給每個軌道一個強度值，然后通過Gaussian函數進行展寬（展寬出的峰的積分面積正比于強度值），再把所有展寬出的曲線疊加到一起來得到PES曲線圖。這個過程十分類似于《使用Multiwfn繪制紅外、拉曼、UV-Vis、ECD、VCD和ROA光譜圖》（http://sobereva.com/224）中介紹的基于量子化學程序計算的躍遷能量和強度數據產生各類光譜的過程，沒看過此文者強烈建議一看。一般都是將每個軌道的強度值定義為相同的數值，具體數值是多少無所謂，因為模擬的PES譜的整體強度大小不是我們關心的，縱坐標的具體數值都不需要標在圖上。展寬過程中有個重要的參數FWHM，決定了每個軌道展寬出的峰的半高位置處的全寬，數值越大峰越寬。在Multiwfn中，每個軌道強度默認為1，FWHM默認為0.2eV，但用戶也可以自己適當修改，來試圖使得模擬的譜圖和實驗譜對得更好。

3 用Multiwfn繪制光電子譜的基本過程

在Multiwfn里繪制PES很容易。輸入文件可以用fch/fchk、chk、molden、gms、Gaussian的pop=full的輸出文件。其中gms是GAMESS-US的輸出文件，用chk時需要設定formchkpath，詳見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://sobereva.com/379）里的說明。對于無法產生這些文件的量子化學程序，你也可以把軌道能級信息整理成手冊3.12.2節說明的文本文件格式，此文件也可以作為繪制DOS或PES的輸入文件使用。

載入文件后，進入主功能10，選擇子功能12進入繪制PES的界面，然后選擇0，PES圖馬上就蹦出來了。在這個界面里有很多選項可以調節作圖設定，一看提示就立馬明白，包括：
? 橫、縱坐標范圍
? 是否將橫軸左右反轉
? 是否顯示曲線和離散豎線
? 是否顯示Y軸的標簽和刻度
? 曲線和離散豎線的粗細
? 結合能的平移值，用于滿足Generalized Koopmans定理的目的
? FWHM值
? 曲線乘的系數。數值越小，則豎線相對于曲線來說越高

還可以在PES繪制界面選擇選項1把圖像保存。這種純曲線圖建議用pdf、svg、wmf這些矢量圖格式。pdf大家都熟悉，svg用網頁瀏覽器都能打開，而wmf適合嵌入word、ppt里面。啟動前在settings.ini里通過graphformat參數可以設置保存成什么格式。

如果你選擇繪制PES時屏幕上什么都沒出現，要么是你輸入文件有問題，可以在PES界面里選擇選項-2把所有占據軌道信息顯示出來檢查載入的數據有無問題；要么就是你的橫坐標范圍沒設合理，繪制的能量范圍內沒有任何軌道出現。

如果你想對不同的軌道定義不同的強度和FWHM值，可以在PES界面里選選項-3把數據導出成PESinfo.txt，手動對里面對應強度和FWHM值的列進行編輯，然后將這個文件作為輸入文件。

注意PES繪制界面雖然是通過DOS繪制界面進入，有些選項也比較類似，但是二者的參數大多不共享。在PES繪制界面里用的展寬函數只能為Gaussian函數，單位只能是eV。另外，對于非限制性開殼層波函數，雖然有alpha和beta兩套軌道，但是繪制PES時是不區分自旋的，兩套軌道都一視同仁。

4 實例：Cr3Si12-光電子能譜的繪制

在J. Phys. Chem. A, 122, 9886 (2018)一文中研究了Cr3Si12-等團簇，既測了這些體系的PES譜，又在PBE/6-311+G*下做了理論計算，并且通過上文提到的原理繪制了理論PES譜。本例就拿文中優化出的Cr3Si12-這個體系中的一個構型（文中稱為3A）來示例一下用Multiwfn繪制PES譜的過程。這個構型的笛卡爾坐標是直接從文中的補充材料中取的，因此這里就不再做優化了，本例用的計算級別也和原文保持一致。文中指出這個結構在PBE/6-311+G*下的電子態應為8B1（八重態，B1不可約表示），是D6d點群，體系結構如下：

 

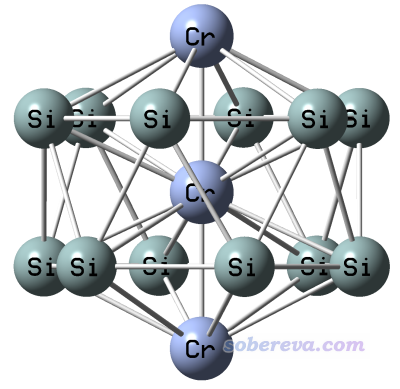
此體系用PBE/6-311+G*按照常規方式計算IP是2.56 eV。值得一提的是，對于這樣的陰離子體系，VIP一般被叫做VDE，即vertical detachment energy（垂直脫附能），體現陰離子脫掉帶的額外的一個電子需要的能量。

這里假定讀者是最常用的量子化學程序Gaussian的用戶。我們首先要基于文獻里優化好的結構算一次單點任務得到fch文件。然而筆者發現對這個體系直接用PBE/6-311+G*算單點時程序自動初猜的波函數是B2不可約表示，而且很難收斂。筆者略施小計，先在B3LYP/6-31G*下算了個單點，很容易就收斂了，而且最終波函數是B1。然后做PBE/6-311+G*計算，用guess=read讀取chk里的波函數當初猜，然后很容易就收斂到了B2態。相應的輸入、輸出文件，以及chk轉換出的fchk文件都可以在此下載：http://sobereva.com/attach/478/file.rar。

啟動Multiwfn，依次輸入
Cr3Si12-.fchk  //輸入實際路徑
10  //繪制DOS
12  //進入繪制PES光譜的界面
1   //顯示PES光譜

瞬間在屏幕上看到下圖，對應于基于Koopmans定理得到的PES圖

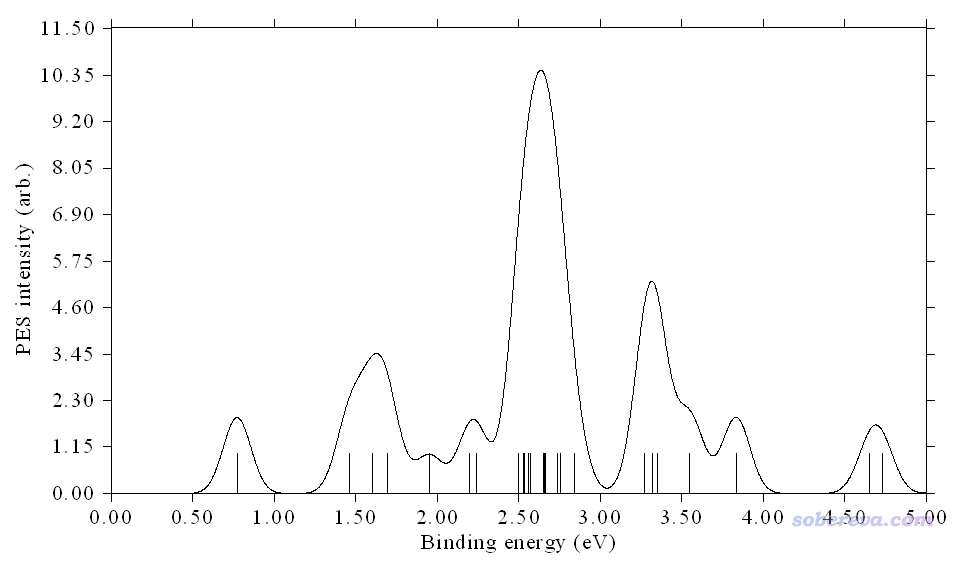
上圖中縱坐標的單位不用管，arb.是arbitrary，即任意的意思，只有曲線形狀、橫坐標位置有意義，也可以選擇一次選項13來把縱坐標上的數值和刻度給去掉。橫坐標對應結合能(binding energy)，可見默認繪制的是0~5eV區間。圖上每個豎線的橫坐標的位置對應分子軌道能量的負值，豎線高度對應強度值。

下圖是JPCA那篇文章里實驗測出來的

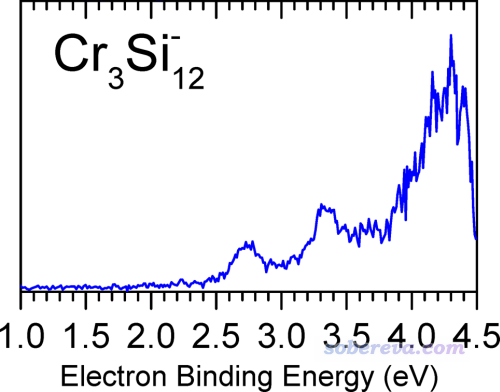
可見對于我們繪制的PES譜，即便只關注0~4.5 eV部分，也和實驗對得不好，第一個峰出現的位置明顯太早了，在0.75 eV左右，而實驗則是2.75左右。

為了修正這個問題，我們下面基于Generalized Koopmans定理再來重新繪制一次，相當于自行設定平移量，結合能加上這個量之后才會被用于繪圖。注意，在進入PES光譜繪制界面時，Multiwfn在文本窗口里已經給出了HOMO能量，為-0.7732 eV，這是alpha的HOMO和beta的HOMO中最大的值，可以當做不區分自旋時候的HOMO。JPCA文中在當前計算級別下算出來的VIP為2.56 eV，對結合能的修正量應當為這兩個量的相加，即2.56-0.7732=1.79 eV。

我們在PES繪制界面里輸入
3   //設定平移值
1.79
4  //設定橫坐標
1,4.5,0.5  //繪制1.0~4.5 eV范圍，標簽間隔0.5eV
1  //繪制光譜
立刻看到下圖

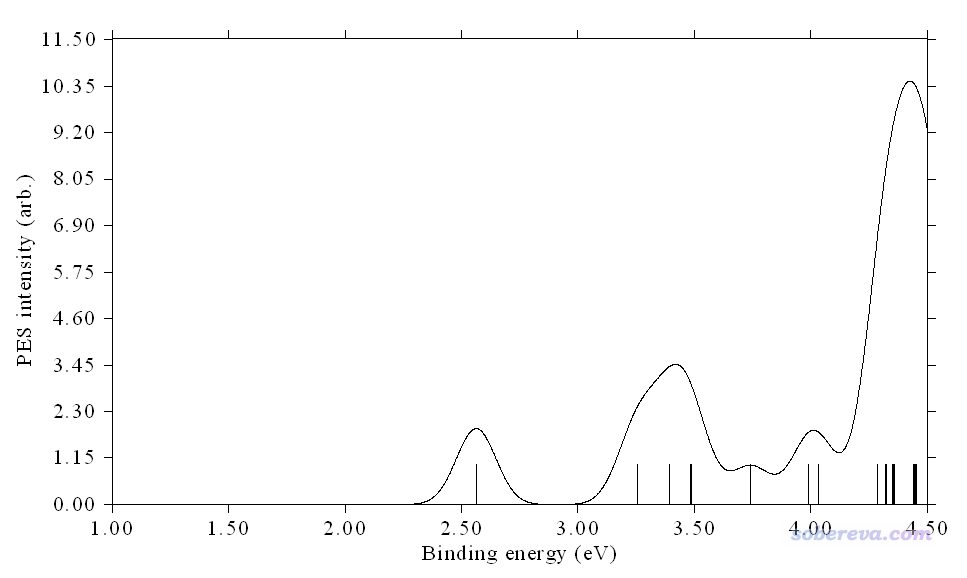
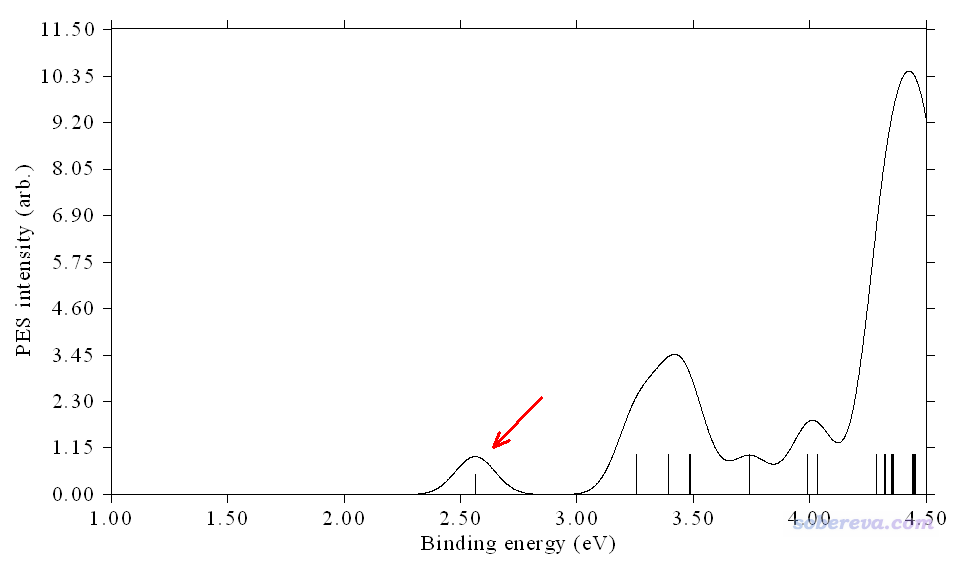
我們將上圖與實驗譜對照，發現雖然峰的位置仍有些許偏差，但整體已經高度相符了，不同區域曲線之間的相對高度也和實驗對應得很好，說明當前繪制的PES非常理想，也說明當前算的這個體系的結構正是實驗觀測到的實際結構。

下面，再演示一下如何自行修改軌道的強度值，假設我們的目的是讓圖上第一個峰對應的軌道強度值設為0.5，即默認的一半，從而讓峰的曲線高度降低。在PES界面里選擇-3，當前目錄下就出現了一個PESinfo.txt文件，含義在手冊3.12.2節已經說明了。從第三行開始，四列數據分別是軌道能量（原始值）、占據數、強度、FWHM。上圖中第一個峰對應的是能量最高的占據軌道，仔細看一下PESinfo.txt，會發現對應的是下面兩行，是二重簡并的alpha的HOMO軌道（其能量值的負值也正對應于一開始基于Koopmans定理繪制的圖里面第一個豎線位置）
         -0.773240    1.000000    1.000000    0.200000
         -0.773240    1.000000    1.000000    0.200000
我們手動將其內容改為
         -0.773240    1.000000    0.500000    0.200000
         -0.773240    1.000000    0.500000    0.200000
保存后，將這個PESinfo.txt作為輸入文件，和前面的步驟一樣基于Generalized Koopmans定理繪制光譜，得到的圖如下所示，可以看到確實第一個峰變低了，豎線高度只有原來的一半。