使用Multiwfn繪制態密度(DOS)圖考察電子結構

使用Multiwfn繪制態密度(DOS)圖考察電子結構

First release: 2019-May-14 Last update: 2023-Jan-28

0 前言

基于主流量子化學程序產生的波函數信息，使用Multiwfn可以對孤立體系非常簡單、快速、靈活地產生質量非常理想的態密度圖，對于分析化學體系的電子結構特征很有幫助。本文將介紹各類態密度圖（Total DOS、Partial DOS、Overlap population DOS、Local DOS）的原理，以及它們在Multiwfn程序中的繪制方法。DOS雖然是第一性原理計算范疇的重要概念，但本文對DOS的繪制只涉及量子化學計算范疇。

Multiwfn從很早期的版本開始就支持DOS的繪制，后來又不斷進行了改進和完善，如今已非常強大，顯著強于其它任何能繪制DOS的程序。Multiwfn的DOS繪制功能已經被大量發表的文章所使用，比如Carbon, 165, 461 (2020)、Chem. Asian. J., 16, 2267, (2021)、Carbon, 187, 78 (2022)、J. Comput. Chem., 38, 1574 (2017)、RSC Adv., 5, 78192 (2015)、Nature Communication, 8, 14551 (2017)、Phys. Chem. Chem. Phys., 19, 23373 (2017)、J. Phys. Chem. C, 119, 8349 (2015)、J. Phys. Chem. A, 121, 4009 (2017)、Chem. Eur. J., 24, 17046 (2018)等等等等，這些文章也可以當成例子。

本文的內容非常深入細致，如果你很急著作出TDOS/PDOS/OPDOS圖，可以先直接參考本文第3節的例子，之后若想全面了解Multiwfn的繪制DOS的功能，再看本文其它部分。本文內容對應Multiwfn官網上的最新版本，不要用太老的版本，否則情況和本文可能明顯不符！Multiwfn可在其官網http://www.shanxitv.org/multiwfn免費下載，相關基礎知識看《Multiwfn入門tips》（http://www.shanxitv.org/167）和《Multiwfn FAQ》（http://www.shanxitv.org/452）。

Multiwfn的DOS繪制模塊還能用于計算d-band center，對于討論過渡金屬表面化學吸附和催化問題很重要，見《用Multiwfn計算過渡金屬的d-band center（d帶中心）》（http://www.shanxitv.org/582）。

目前最新版Multiwfn可以基于第一性原理程序CP2K產生的記錄周期性體系波函數的.molden文件繪制各種類型的DOS圖，怎么用CP2K產生.molden文件參見《詳談使用CP2K產生給Multiwfn用的molden格式的波函數文件》（http://www.shanxitv.org/651）中的相關部分。特別注意計算時不要用OT，否則不產生軌道能量信息。而且應當讓CP2K計算出最低一批空軌道（默認只計算占據軌道）。

1 態密度的物理意義與種類

態密度（Density-of-states，DOS）是一個以能量為變量的函數。DOS(E)代表在能量為E的位置，單位能量區間內態的數目。“態”具體指什么，看這個詞具體用在什么地方。

一般說DOS這個詞較多的場合是第一性原理領域，此時的態通常指的是解KS-DFT方程得到的單電子軌道。第一性原理研究的主要是周期性體系，有k點的概念，不同k點處軌道能級也不同。第一性原理計算可以得到物理意義嚴格的DOS，即通過對k空間進行積分得到。

量子化學主要研究的是孤立體系（分子、團簇等），當使用DOS考察體系電子結構時，態指的是分子軌道（可以由HF、半經驗、KS-DFT等各種基于單電子近似的理論方法計算產生）。孤立體系計算的時候沒有k點的概念，算出來的軌道能級都是離散分布的，因此DOS這個詞對于孤立體系來說本身沒什么意義，畫出圖來的話，就是下面這樣，對應的公式也一起給出了（為了避免和后文說的其它類型的DOS混淆，這里用了Total DOS (TDOS)這個詞）。

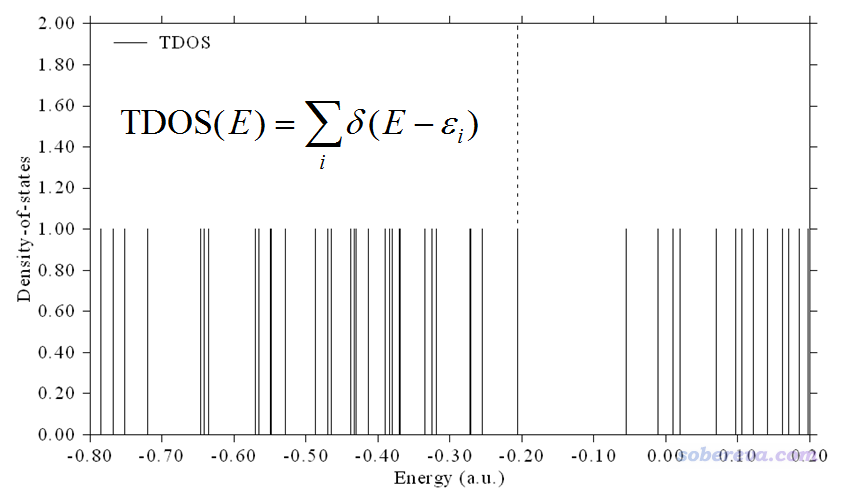
上圖中虛線位置是HOMO的位置，公式里ε是軌道能量，δ是狄拉克δ函數（不懂的話Google）。從上圖可見，孤立體系的TDOS圖本身只不過相當于在分子軌道能級位置畫一個豎線而已，這種圖一點意思也沒有，沒法傳遞出比軌道能級分布本身更多的信息。

如果通過一些函數將上圖中這些離散的豎線依次進行人為地展寬然后再累加，從圖中將可以一目了然地看到不同能量區域內軌道分布的密集程度，如下圖所示。注意這種展寬純粹是人為的，僅僅是為了便于直觀分析而做的，這樣得到的DOS曲線并不是像第一性原理計算那樣是以嚴格方式得到的。

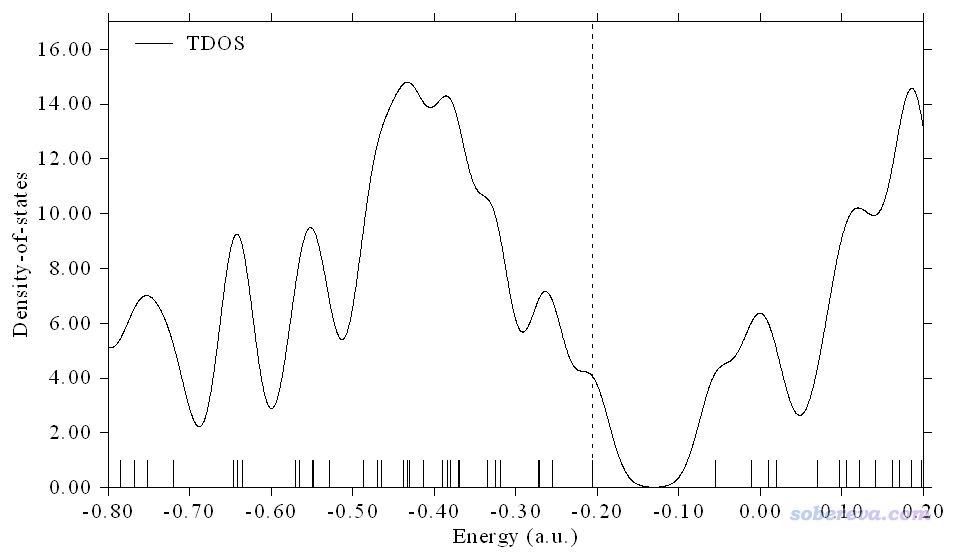
不同的展寬函數把離散的豎線展寬出的峰的形狀不同。繪制DOS時展寬函數一般用Gaussian函數，在Multiwfn里也允許用Lorentzian函數，或者二者混合產生的Pseudo-Voigt函數。函數表達式這里就不列出了，讀者可以在Multiwfn手冊里的介紹DOS繪制功能的3.12節中看到。不管用的是哪個展寬函數，都會牽扯到半高全寬（FWHM）這個參數，即豎線展寬出來的峰在高度一半的位置峰的寬度。顯然FWHM設得越大峰越寬，曲線看起來就越平滑、越連續，而FWHM越小則對峰的分辨率越高，繪制上圖用的FWHM為0.05 a.u.。FWHM這個值沒有什么物理意義，設多大是具有主觀任意性的，一般的設定標準是讓得到的圖適合、便于說明自己想說明的問題。下圖分別是FWHM改為0.1 a.u.和0.02 a.u.時候得到的圖。

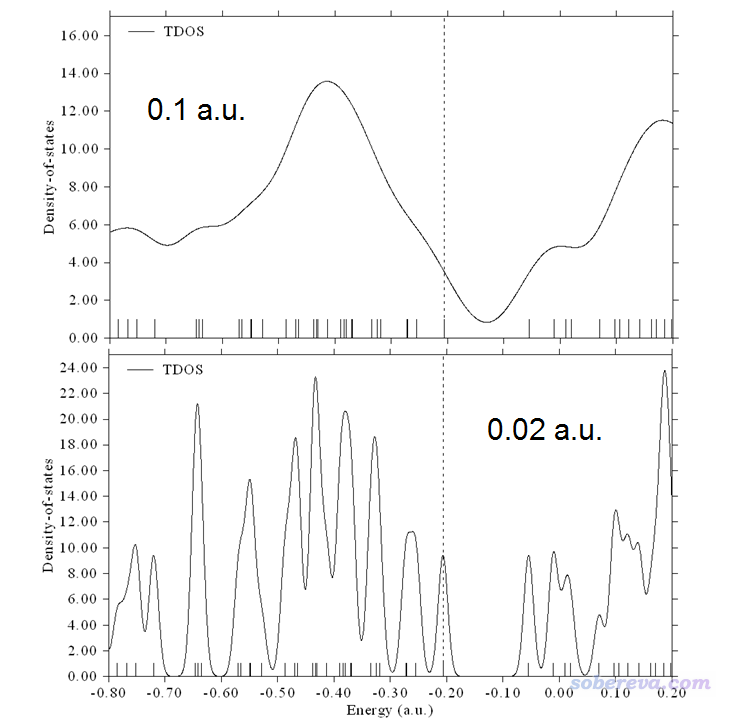
在《使用Multiwfn繪制光電子譜》（http://www.shanxitv.org/478）一文中，得到光電子譜(PES)的方式在本質上和上述繪制TDOS其實如出一轍。

還可以定義Partial DOS (PDOS)，可以叫做“局部DOS”或“分數DOS”，它體現的是特定的片段對TDOS貢獻的曲線。若恰當定義片段，通過PDOS圖就可以較好地把握不同能量區間的軌道的本質、主體構成。顯然，如果定義的所有片段的并集等于整個體系的話，那么每個片段的PDOS曲線累加在一起正好就是TDOS。對于某個片段A，其PDOS定義如下。其中F是展寬函數，Θ是軌道成份。

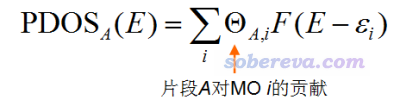
計算軌道成份的方法很多，詳見《談談軌道成份的計算方法》（http://www.shanxitv.org/131）和《分子軌道成分的計算》（http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract340458.shtml）里的介紹。在繪制DOS的功能中，Multiwfn支持Mulliken、SCPA、Hirshfeld和Becke方法計算軌道成份。

重疊布居DOS（Overlap population DOS，OPDOS）對于考察片段間的相互作用比較有用。筆者在《Multiwfn支持的分析化學鍵的方法一覽》（http://www.shanxitv.org/471）里專門介紹過什么叫Mulliken鍵級，這和重疊布居（Overlap population）是一碼事，可以體現原子間是成鍵作用還是反鍵作用，沒看過此文的話一定要仔細看一下。文中還提到，重疊布居可以精確分解為各個軌道的貢獻，將這個思想和DOS圖搞到一起，就是OPDOS的定義了。下式是片段A與B之間的OPDOS的表達式

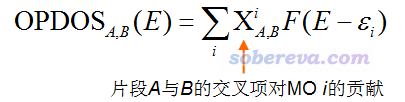
式中的那個Χ項，也等價于假設i軌道是占據的，然后這個軌道對片段A和B之間的重疊布居的貢獻量除以軌道占據數。在某個能量范圍，若OPDOS數值明顯為正，就說明這個能量范圍里的軌道如果被電子占據了的話，會對兩個片段間的結合起到積極貢獻，換句話說，這些軌道對這兩個片段而言是成鍵軌道；若數值為負，說明這些軌道如果被電子占據了的話，將對片段間的結合產生不利貢獻，相當于起到反鍵軌道作用。

雖然OPDOS確實能展現片段間相互作用的情況，但是由于Mulliken鍵級本身對鍵的強度反映不好，所以也別太把OPDOS當回事。而且，有彌散函數的情況下，OPDOS結果會很離譜，可能數據完全沒有意義。所以，若計算波函數時有彌散函數則不要討論OPDOS，若必須討論OPDOS且之前的計算用了彌散函數，應把彌散函數去掉算個單點重新得到波函數后再做分析。Multiwfn是分析成鍵問題的百寶箱，里面有大把方法可以很好地討論化學鍵特征，所以千萬別拘泥于拿OPDOS說事，強烈建議仔細看《Multiwfn支持的分析化學鍵的方法一覽》（http://www.shanxitv.org/471）。另外，之前筆者還見到有人試圖拿兩個片段各自的PDOS曲線討論它們的成鍵，以為在某些能量區間它們同時較大就說明二者間有成鍵作用，這明顯毫無意義，且不說它們是相位相同方式重疊還是相位相反重疊，首先這種情況都沒法體現這兩個片段間存在軌道重疊，因為PDOS圖根本都體現不出片段的軌道分布在三維空間中的什么區域。

還有一種DOS叫Local DOS，這個留到本文第4節專門介紹。

我們來看一個典型的DOS例子，是Multiwfn的原文J. Comput. Chem., 33, 580 (2012)里的圖，將二茂鐵的TDOS、PDOS、OPDOS繪制在了一起。為了便于說清楚軌道特征，一部分軌道的等值面圖是用Multiwfn的主功能0繪制出來后手動ps到恰當位置的。

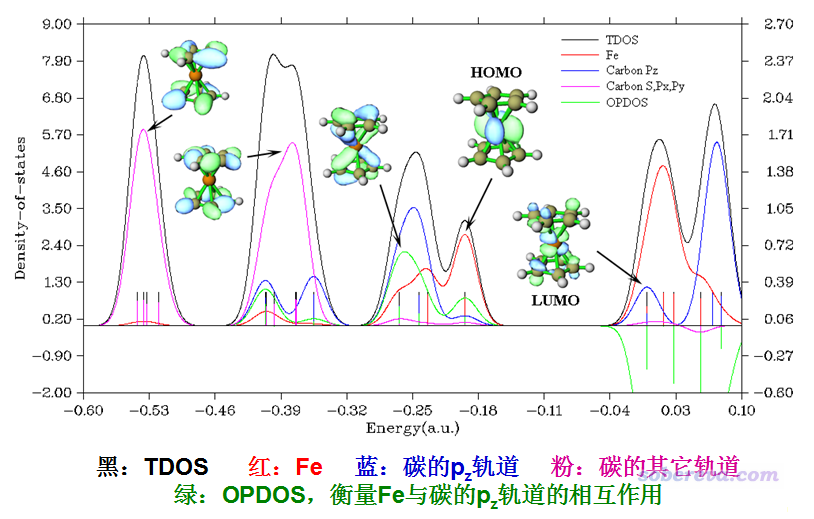
圖中左側是對應TDOS、PDOS曲線的軸，右側是對應OPDOS曲線的軸。DOS或OPDOS的數值的絕對大小是我們不需要關心的，刻度軸的標簽都抹掉也無妨，需要關心的僅僅是不同能量區間之間曲線的相對高度。為了便于直觀考察不同能量區間內軌道的本質，繪制時定義了三個片段：
? 片段1：Fe的所有軌道
? 片段2：碳的垂直于茂環的p軌道。由于茂環在XY平面上，因此它們也即碳的pz軌道，合在一起相當于茂環的pi軌道
? 片段3：茂環的碳的其它軌道，即s、px、py
由圖可見，對于能量比較低區間的軌道，諸如-0.53 a.u.的那一批，從圖上立馬就可以判斷出它們基本都是由碳的s、px、py軌道貢獻的，結合軌道等值面圖也看出確實如此。而對于能量為-0.25 a.u.附近的軌道，藍色曲線和紅色曲線都較高，說明這些軌道應當是由茂環的pi軌道與鐵的軌道混合產生的，確實從軌道等值面上也可以證實是由鐵的d軌道與茂環的pi軌道以相位相同疊加組合出的。在HOMO軌道位置，Fe片段的PDOS與TDOS非常接近，說明HOMO主要是由Fe的軌道構成的，茂環的參與較弱。我們再看綠色的OPDOS曲線。在比如-0.25 a.u.附近，綠色曲線明顯為正，說明這些軌道的存在對于茂環與鐵的結合起到積極作用，這也容易理解，畢竟是相位相同疊加，所以對于此二者而言起到的是顯著的成鍵軌道作用。對于非占據軌道區域，可見OPDOS曲線都為顯著的負值，這也就是說，如果它們被電子占了，傾向于讓茂環與鐵的結合散架。確實從LUMO的軌道圖來看，是Fe的d軌道與茂環的pi軌道以相位相反方式組合出來的，對它倆而言無疑起到的是反鍵軌道作用。

從上面這個例子看出，DOS圖很有助于清楚、直觀地討論化學體系的電子結構。雖然可能有人覺得，用Multiwfn方便的軌道成份計算功能（主功能8，操作見http://www.shanxitv.org/131和手冊4.8節的例子），批量計算片段對各個軌道的貢獻值也能得到本質上同樣的信息，但是這樣的話你得去分析一大堆數據，而且寫文章的時候得把一大堆數據堆上去，審稿人和讀者看著也累，遠沒有DOS圖一目了然、遠不如通過DOS圖討論起來方便。

2 Multiwfn中的DOS繪制功能

下面對Multiwfn的繪制DOS的功能做一下系統的介紹。

2.1 基本使用流程

將輸入文件載入Multiwfn，進入主功能10，然后會看到一個菜單，里面有很多選項可以調節作圖設定。設好后，按0，DOS圖馬上就可以顯示出來。關閉圖像后，會看到一個后處理菜單，里面又有很多選項來調節繪制參數，修改后可以選1 Show graph again重新繪圖查看當前的效果。

如果繪圖前不設定片段，則繪制出來的圖是TDOS。如果先用-1 Define fragments設定片段再繪圖，則繪制出來的是TDOS+PDOS。如果片段1和片段2都定義了，則這倆片段間的OPDOS會一同繪制出來。

2.2 輸入文件

.mwfn、.fch、.molden、.gms文件都可以作為輸入文件繪制TDOS、PDOS、OPDOS以及后文提到的LDOS，怎么生成它們見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379）。也可以使用Gaussian單點任務的輸出文件（必須帶著pop=full）作為輸入文件，但此時只能繪制TDOS。.wfn、.wfx格式不能作為輸入文件，因為這倆格式不包含空軌道信息。

為靈活起見，對于只需要繪制TDOS的目的，Multiwfn也支持通過文本文件作為輸入，自行把軌道能級等信息按照要求的格式寫進去即可，格式見手冊3.12.2。因此，原理上任意量子化學程序計算出的軌道能級都可以被Multiwfn展寬成TDOS曲線繪制出來。

2.3 DOS繪制界面里的選項

進入主功能10后看到的菜單里面的選項在這里說一下。一般來說默認選項下繪制出的圖不會恰好滿足需要，因此需要反復調節選項、反復作圖直到滿意為止。

-5 Customize energy levels, occupations, strengths and FWHMs for specific MOs：默認情況下，軌道能量、占據數都是從輸入文件里讀的，如果你想修改，可以用這個選項。默認情況下，每個軌道的強度值(strength)都為1，FWHM都是相同的，如果你想對不同的軌道進行獨立的設定，也可以用這個選項。展寬出的峰的積分面積與軌道的強度值是呈正比的。

-4 Show all orbital information：顯示所有軌道的能量、占據數、強度值、FWHM信息。

-3 Export energy levels, occupations, strengths and FWHMs to plain text file：把所有軌道的能量、占據數、強度值、FWHM信息導出到當前目錄下的orginfo.txt中。這個文件的格式是滿足作為Multiwfn繪制TDOS的輸入文件的要求的，因此你可以自行修改這個文件里的數據后作為輸入文件。

-2 Define MO fragments for MO-PDOS：這個選項專用于繪制一種我起名叫MO-PDOS的圖中涉及的片段，本文第6節會提到。

-1 Define fragments for PDOS/OPDOS：設定片段。這會在本文2.5節專門說。

1 Select broadening function：設置展寬函數。可以用Gaussian、Lorentzian和Pseudo-Voigt。

2 Set energy range：這用來設置繪制出的DOS圖的橫坐標，即能量下限、上限、標簽間隔。

3 Set full width at half maximum (FWHM)：設置展寬時用的半高全寬FWHM。

4 Set scale ratio for DOS curve：設定DOS曲線乘的系數。這個數值越小，曲線的數值顯然就越小，而離散的豎線相對于曲線就顯得越高。因此如果你覺得作出的圖里面離散豎線的高度相對于曲線太高或太低，可以用這個選項調節。

6 Choose orbital spin：對于非限制性開殼層波函數的情況才會看到此選項，用于選擇在繪圖時考慮哪些軌道。可以只考慮alpha軌道，或只考慮beta軌道，或alpha和beta軌道同時考慮。

7 Set the method for calculating PDOS：設定繪制PDOS時用的軌道成份的計算方法。

8 Switch unit between a.u. and eV：切換橫坐標的單位，默認是a.u.，對于能量而言就是指的Hartree，而eV也很常用。1 Hartree=27.2114 eV。

9 Toggle using line height to show orbital degeneracy：選此選項后，程序會讓你輸入能量閾值，當相鄰軌道能量差小于這個值的時候，程序將會把它們視為簡并，并且在DOS圖上通過豎線高度體現簡并度。一般就用默認的閾值即可。此選項可以結合TDOS、MO-PDOS圖使用，但在繪制PDOS圖時不能用。

在DOS繪制界面里經常要進行諸多設置才能達到最滿意的效果。為了避免日后重新繪制完全相同的圖（或在此基礎上進一步修改）時還得再重新輸入一遍設置，在DOS繪制界面里（不是后處理菜單）中，用戶可以直接輸入s（意為save）來將作圖設定、片段設定、軌道信息一起保存到一個用戶指定的文本文件里。日后再次啟動Multiwfn并載入相同體系后，進入DOS繪制功能，只需輸入l（意為load），然后選擇之前保存的狀態文件，就能立刻恢復先前的作圖狀態。

2.4 繪制PDOS用的軌道成份

繪制PDOS用的軌道成份的計算方法支持下面四種：
? Mulliken方法：此為默認。計算速度很快，但可能給出缺乏物理意義的結果（片段貢獻超過100%或為負值），對于空軌道的可靠性低于占據軌道，而且絕對不能用于有彌散函數的情況！
? SCPA方法：速度和Mulliken一樣快，相對于Mulliken方法唯一的好處是軌道成份不會算出來超過100%或負值，但其它問題仍在。
? Hirshfeld方法：基于Hirshfeld方式的實空間劃分來計算軌道成份，比Mulliken和SCPA方法更為昂貴，優點是對于空軌道和占據軌道都非常可靠、穩健，而且不怕彌散函數。
? Becke方法：和Hirshfeld方法各方面都差不多，結果一般也都相近，只不過對原子空間的定義不同。

使用Mulliken和SCPA方法時，定義片段時最小的單位是基函數，也因此可以等效實現把特定的原子軌道、特定角動量的軌道、原子軌道殼層等定義為片段，非常靈活。而Hirshfeld和Becke方法只能計算原子在軌道中所占成分，因此定義片段的時候最小單位是原子，而且此時無法繪制OPDOS。

2.5 片段的定義方法

進入前述的片段定義界面后，你會看到一個片段列表，有10個片段可以定義。定義幾個，PDOS就會繪制出幾條曲線。片段1和片段2同時定義時也同會對二者繪制OPDOS。

要定義哪個片段，就在這個界面里輸入哪個片段的序號即可，之后會開始片段的定義。如果比如2號片段已經定義了，輸入-2就可以把這個片段清空，使之處于未定義狀態。輸入兩個片段序號比如2,5可以交換兩個片段（這個設置是為了便于把想考察OPDOS的兩個片段切換到片段1和片段2）。如果你的片段定義比較復雜，以后還可能要用，可以輸入字母e將片段定義導出為當前目錄下的DOSfrag.txt，下次再進入這個界面時可以輸入i來從當前目錄下的DOSfrag.txt中導入片段定義，省得再重新設一遍了。

用Hirshfeld或Becke方法計算軌道成份時，設定片段的內容時就按提示輸入原子序號即可，比如1,3-5,12,15就代表把1,3,4,5,12,15號原子定義為片段。

用Mulliken或SCPA方法計算軌道成份時，片段里記錄的是基函數的序號。開始定義片段后，會看到一個命令很豐富的設定界面，值得細說一下。在這個界面里，你首先在屏幕上會看到一大堆命令的介紹以及用法示例。如果你想讓這些幫助信息重新顯示出來，可以隨時輸入help。下面對可以用的命令都解釋一下：
q：保存片段并離開定義當前片段的界面，屏幕上會提示片段里都加入了哪些基函數
list：顯示當前片段里包含的基函數序號
clean：清空片段。默認情況下，片段里是沒有內容的，如果之前已經對這個片段進行過定義，再次定義時原先那些基函數還會在，因此想徹底重新定義之前應當輸入clean清空一下
addall：將所有基函數加入這個片段，即這個片段等同于整個體系
inv：反轉定義。原先在片段里的基函數將不再片段里，而不在片段里的將被加入片段里
a：按照原子(atom)定義片段。比如a 2,5-8,12代表把2,5,6,7,8,12原子上的基函數都加入片段
s：按照基函數殼層(shell)定義片段。比如s 2,5-8,12代表把2,5,6,7,8,12號基函數殼層里的基函數都加入片段
b：按照基函數(basis function)序號定義片段。比如b 2,5-8,12代表把序號為2,5,6,7,8,12的基函數都加入片段
l：按照角動量定義片段。后面跟著角動量名字。比如l s,d就代表把s和d角動量的基函數都加入片段
da、db：分別按照原子序號和基函數序號來從當前片段中刪除基函數
cond：將滿足條件的基函數加入片段，條件包括基函數所處的原子的序號范圍、基函數所處的序號范圍、基函數類型（如S、Y、XZ）或者基函數所處的殼層的類型（如S、P、D）。只有同時滿足這三個條件的基函數才會被加入片段。如果想無視某個條件，設相應條件時輸入a（代表all）即可。

a、s、b、l這些命令若反復用多次，每次都會把滿足要求的基函數添加到片段，換句話說片段里包含的會是它們的并集。而cond這種方式加入的基函數是自己設的三個條件的交集。上面說到的所有這些往片段里加入基函數的命令都可以反復使用多次，效果是累加的（某些基函數加重復了也沒關系，程序會自動去除重復的）。

如果你想查看基函數、殼層、原子的對應關系和特征，隨時可以用all命令，會輸出諸如下面這些，此例是6-31G*用于HF分子。如果某個基函數已經在片段里了，前面會顯示星號。如果屏幕上顯示不全，參考手冊5.5節來加大窗口緩沖區。
Basis:     1    Shell:    1    Center:    1(H )    Type: S
Basis:     2    Shell:    2    Center:    1(H )    Type: S
Basis:     3    Shell:    3    Center:    2(F )    Type: S
Basis:     4    Shell:    4    Center:    2(F )    Type: S
Basis:     5    Shell:    5    Center:    2(F )    Type: X
Basis:     6    Shell:    5    Center:    2(F )    Type: Y
Basis:     7    Shell:    5    Center:    2(F )    Type: Z
Basis:     8    Shell:    6    Center:    2(F )    Type: S
Basis:     9    Shell:    7    Center:    2(F )    Type: X
Basis:    10    Shell:    7    Center:    2(F )    Type: Y
Basis:    11    Shell:    7    Center:    2(F )    Type: Z
Basis:    12    Shell:    8    Center:    2(F )    Type: XX
Basis:    13    Shell:    8    Center:    2(F )    Type: YY
Basis:    14    Shell:    8    Center:    2(F )    Type: ZZ
Basis:    15    Shell:    8    Center:    2(F )    Type: XY
Basis:    16    Shell:    8    Center:    2(F )    Type: XZ
Basis:    17    Shell:    8    Center:    2(F )    Type: YZ

上面顯示的X,Y,Z即PX,PY,PZ型基函數，XX,YY,ZZ,XY,XZ,YZ都是笛卡爾型D型基函數的標識，不懂的話看《談談5d、6d型d殼層基函數與它們在Gaussian中的標識》（http://www.shanxitv.org/51）。根據6-31G*定義，我們可以立刻判斷出哪些基函數對應哪些原子軌道。比如對于F，由于每個內層原子軌道用一個基函數描述，每個價層原子軌道用兩個基函數一起描述。因此你輸入b 3，就等于把1s原子軌道加入片段了；如果輸入b 4,8或者等價的s 4,6，就代表把2s原子軌道加進去了；如果輸入b 5-7,9-11或者等價的s 5,7，就代表把2p原子軌道加進去了；如果輸入b 12-17或s 8，就代表把給F加的d極化函數加進去了。

對于非Pople系列基組，往往基函數與原子軌道的對應關系沒法根據基組名字簡單判斷，但筆者也發明了一種簡單且普適的判斷方法，參見《利用布居分析判斷基函數與原子軌道的對應關系》（http://www.shanxitv.org/418）。

2.6 后處理菜單中的選項

在繪制出圖像并關閉圖像后，后處理菜單中也有很多選項可以設定繪制參數，這里把其中一部分提一下，其它的選項含義不言自明。

-1 Set format of saved image file：用來設置通過選項2保存出來的圖像的格式。對于除了二維LDOS（見后文）以外的DOS圖，由于圖中的主體都是線條，建議使用矢量格式，比如pdf、ps、wmf（可以嵌入Office的組件中）、svg（可以用網頁瀏覽器打開），這樣線條看著光滑且可以無損縮放。如果想修改默認的格式，可以改settings.ini里的graphformat。筆者強烈建議使用pdf格式（可以打開pdf后再截圖成為比如png、jpg等常用格式再嵌入文章里）。

1 Show graph again：后處理菜單修改過選項后，可以用這個選項重新繪制圖像檢查當前效果。

2 Save the graph to image file in current folder：將圖像文件保存到當前目錄，文件名前綴為DISLIN。如果不懂什么叫當前目錄，看http://www.shanxitv.org/237。

3 Export curve and line data to plain text file in current folder：這個選項可以把DOS曲線數據和離散豎線數據導出到當前目錄下的文本文件中，之后可以導入Origin之類程序中畫DOS圖，屆時有更多可調選項可用。

選項5~10：用來設定是否顯示TDOS、各個PDOS、OPDOS曲線和離散的豎線。

11 Set color for PDOS curves and lines：設定各個PDOS的曲線和離散豎線的顏色

12 Set position of legends：設定圖例的X和Y位置。X數值越大越靠右，Y數值越大越靠下。通過調節這個可以避免圖例把曲線擋住。用選項13也可以完全關閉圖例。

14 Set scale factor of Y-axis for OPDOS：對OPDOS設置倍數因子。OPDOS對應圖中右側坐標軸，其范圍是對左側坐標軸（對應于TDOS和PDOS）的范圍乘上這個倍數因子得到。因此通過設定這個值可以控制OPDOS曲線相對于TDOS/PDOS曲線的高低。

15 Toggle showing vertical dashed line to highlight HOMO level：默認情況繪制出的DOS圖上有個垂直的虛線，用來標注HOMO軌道的位置以便分清楚哪些DOS區域是占據的和非占據的。用這個選項可以關閉這個虛線的顯示。老有人以為這個虛線是費米能級的位置，這完全是誤解。費米能級是固體物理里的概念，對于孤立體系，費米能級本身就是個ill-defined的概念，對于孤立體系絕對不要用費米能級這個詞。

16 Set the texts in the legends：設置TDOS、各個PDOS、OPDOS顯示在圖例中的文字

選項17、18：設置DOS曲線和離散豎線的粗細。注意線條在屏幕上顯示的粗細可能和保存出的圖像文件里的粗細不同。

19 Toggle showing labels and ticks on Y-axis：用這個選項可以關閉縱軸上的標簽和刻度。前面說過，DOS圖中的絕對數值大小沒什么實際意義，不想顯示的話可以索性用這個關了。

22 Toggle drawing lines at bottom of curves：此選項很有用也很常用。默認情況下離散豎線是和曲線顯示在同一個坐標軸的，但有時候相互重疊可能看起來比較亂，而且豎線高度不很理想。選了這個選項后就可以把離散豎線作為額外的圖顯示在曲線圖下方，互不干擾。

3 TDOS/PDOS/OPDOS在Multiwfn中的繪制例子

下面給出幾個有代表性的DOS圖的繪制例子。這些例子顯然不可能把所有情況都體現，讀者務必將例子與上面介紹的原理和選項說明相結合，舉一反三。手冊4.10節還有更多的例子。下面例子用到的所有文件都可以在此下載：http://www.shanxitv.org/attach/482/file.rar，計算都通過Gaussian 16實現。

3.1 繪制二茂鐵的各種DOS圖

這一節我們以二茂鐵為例演示一下繪制TDOS、PDOS、OPDOS，復雜度由淺入深。這個例子的Gaussian輸入文件是本文文件包里的Ferrocene.gjf，可見關鍵詞是BP86/genecp opt，對Fe用的SDD贗勢基組，對茂環用的6-31G*。繪制DOS不需要用太高質量波函數，用這樣比較便宜的基組就夠了。計算產生的fch文件是文件包里的Ferrocene.fch。

3.1.1 繪制TDOS圖

我們先看怎么繪制最簡單的TDOS。啟動Multiwfn，載入Ferrocene.fch，依次輸入
10 //DOS繪制模塊
0 //繪制TDOS
馬上就看到下圖

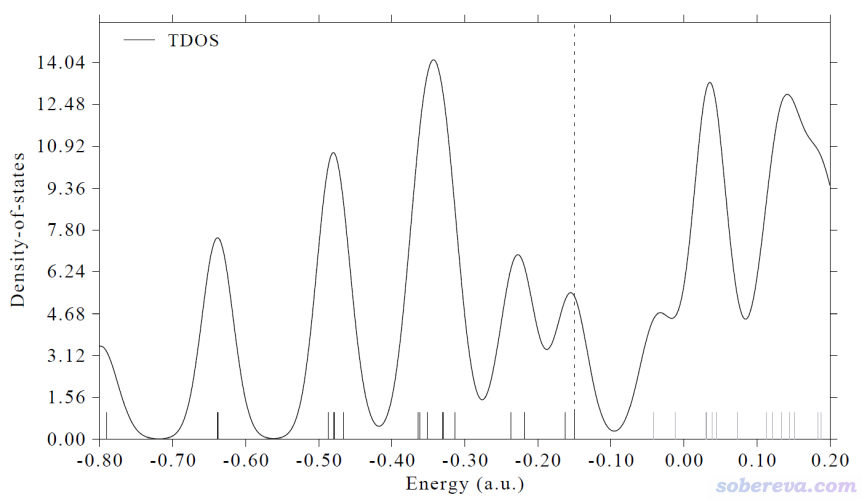
上圖中虛線標注了HOMO的位置，黑色和灰色豎線分別展現占據軌道和空軌道。

如果你想讓軌道的簡并度通過豎線高度體現出來，可以輸入
0 //從后處理菜單返回DOS繪制界面
9 //考慮簡并度
[按回車] //用默認的0.005 eV閾值。如果兩個軌道的能量差小于這個閾值就被認為是簡并的軌道
0 //繪圖
現在看到下圖，豎線高度對應右邊的坐標軸，可見很多軌道是雙重簡并的。當前體系是D5d點群，原理上就是有很多軌道會雙重簡并。

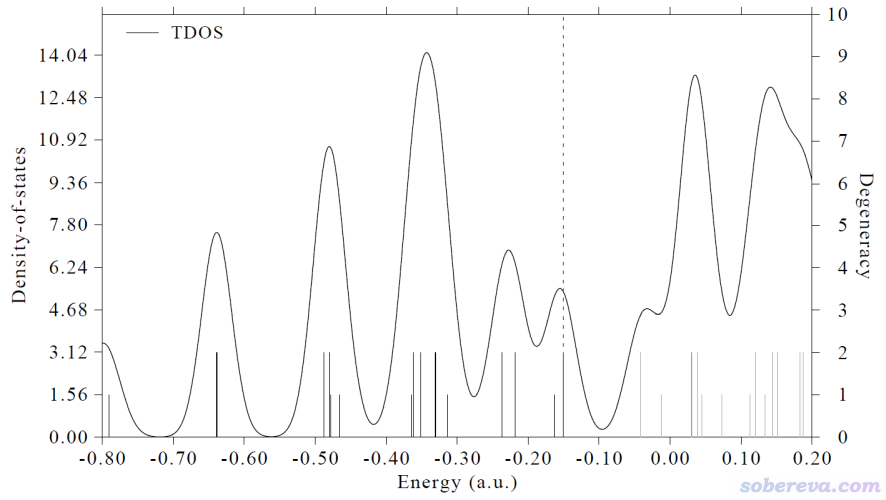
3.1.2 繪制TDOS+PDOS圖

下面我們把兩個茂環中的所有碳原子作為片段1來繪制它們的PDOS。為此我們需要先知道這些碳原子的序號，可以通過Multiwfn主功能0查看，但原子多的話一個一個記錄數字比較費事。一個簡單的做法是把Ferrocene.fch載入GaussView（筆者用的GaussView 6.0.16)，用Builder界面里的選擇工具把這些碳都選中成為黃色，然后進入Tools - Atom Selection界面，如下所示文本框里直接就顯示了這些原子的序號，將它們拷出來備用。

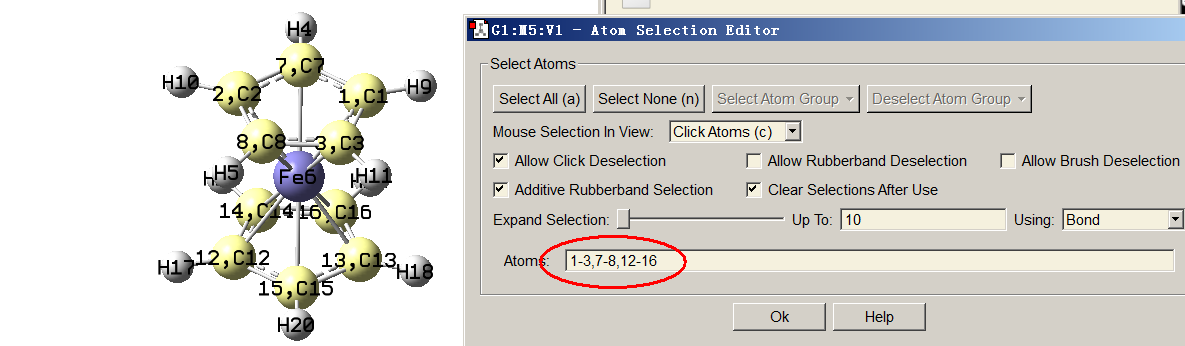啟動Multiwfn，依次輸入
o //載入上次載入的文件
10 //DOS繪制模塊
-1 //設置片段
1 //定義片段1
a 1-3,7-8,12-16 //將茂環上的碳加入片段
q //保存片段1
0 //退出片段設定界面
0 //繪制TDOS+PDOS圖

看到的圖像如下，紅色曲線就是茂環的PDOS。

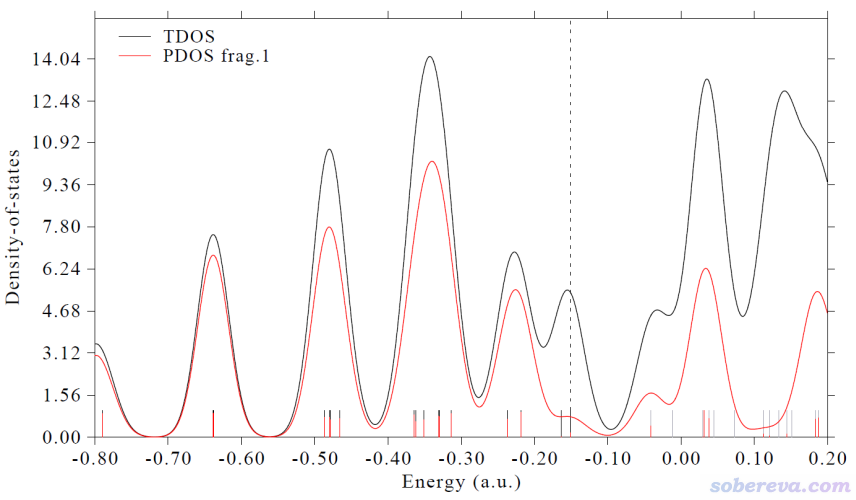
3.1.3 繪制TDOS+PDOS+OPDOS圖

這一節最后，我們畫個較復雜的，重現一下本文前面給出的二茂鐵的TDOS+PDOS+OPDOS圖。但由于計算級別和Multiwfn的版本與當時繪制那個圖的情況有所不同，所以結果得到的圖像不會完全相同。

接上一節，從后處理菜單退回到DOS繪制界面，然后依次輸入
-1 //定義片段
-1 //撤銷掉原先的片段1的定義（先進入片段1然后輸入clean命令清空片段也可以實現相同目的）
1   //定義片段1
a 6 //將Fe作為片段1
q //保存此片段
2   //定義片段2。我們要把所有碳的pz軌道加入
cond //以條件方式定義向此片段添加基函數
1-3,7-8,12-16 //茂環上的碳的序號
a //不對基函數序號范圍做限制
Z //必須是PZ型基函數，即垂直于茂環的P型基函數（Multiwfn主功能0里有笛卡爾坐標軸，一看就知道茂環正好是在XY平面上）
q //保存此片段
3   //定義片段3。我們要把所有碳的s,px,py軌道加入，需要重復用三次cond命令來實現（大家可以把下面這一串內容直接復制到Multiwfn窗口中執行，省得一行一行敲進去）
cond
1-3,7-8,12-16
a
S
cond
1-3,7-8,12-16
a
X
cond
1-3,7-8,12-16
a
Y
q //保存此片段
現在片段都已經定義好了，可以輸入e把片段設定導出到當前目錄下的DOSfrag.txt中，以便之后隨時在這個界面里通過輸入i來恢復之前好不容易設好的片段。然后輸入
0 //退出片段定義界面
2 //設定橫坐標能量范圍
-0.6,0.1,0.1 //能量范圍-0.6~0.1 a.u.，標簽間隔0.1 a.u.
0 //繪制TDOS+DOS+OPDOS
當前看到的圖像如下

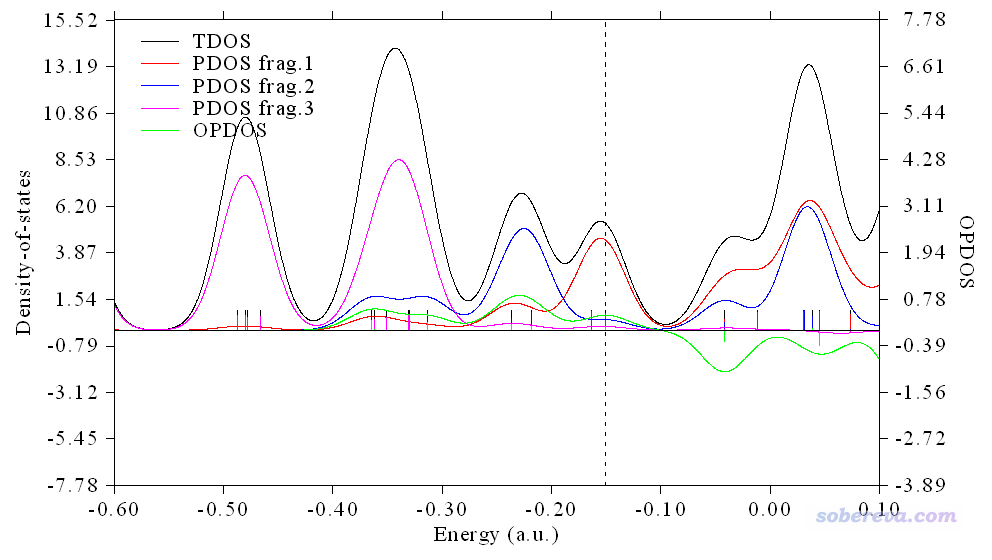此圖已經基本有模樣了，但還需要做一些調整。圖中顯得FWHM數值有點大，顯得本來挺大的gap看起來都有點連上了，而且縱坐標軸的范圍可以再改改，讓圖像主體區域更加充滿畫面。圖例的文字也需要設一下。關閉圖像并輸入0退回DOS繪制界面，然后依次輸入
3 //修改FWHM
0.03 //比默認值小一點
4 //修改DOS曲線乘的系數
0.05 //比默認值更小，以此讓離散的豎線相對于曲線變得更高點
0 //繪圖，并根據此時顯示的圖判斷Y軸范圍設多少最合適
關閉圖像后在后處理菜單輸入
4 //修改Y軸設定
-2,12,2 //下限、上限、標簽間隔
19 //取消顯示Y軸標簽和刻度，因為這些沒什么實際意義
16 //設置圖例文字
1 //設置片段1
Fe
2 //設置片段2
Carbon pz
3 //設置片段3
Carbon s,px,py
0 //返回
1 //重新繪圖
目前看到的圖像如下，已經令人滿意了。

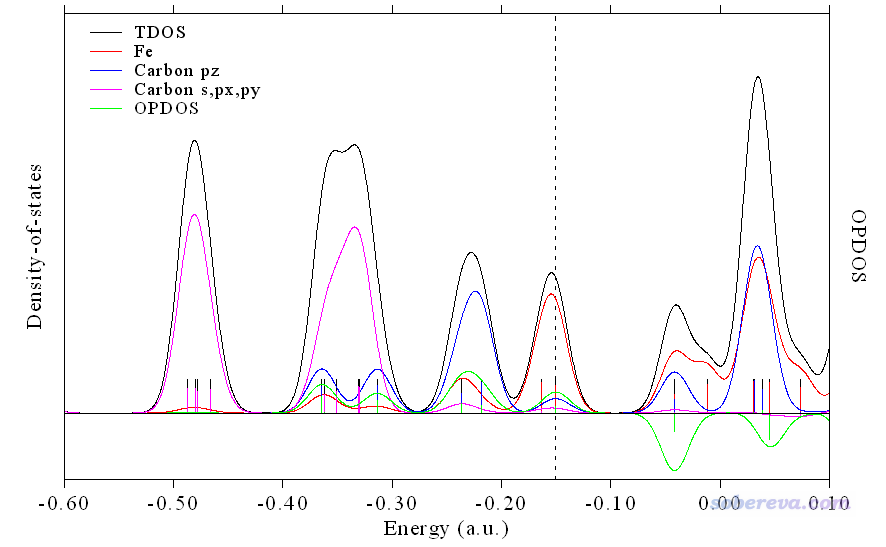
如果你吹毛求疵的話，還可以把圖例文字挪到圖的靠右側空檔比較大的地方，然后把Y軸上限再設小點以讓曲線看起來更高，做法是在后處理菜單輸入
12 //修改圖例位置的絕對坐標
1830 //圖例的橫坐標的絕對位置，越大越靠右。可以反復嘗試直到位置合適
[按回車] //原先圖例的縱坐標位置保持不變
4 //修改Y軸設定
-2,8.5,2 //下限、上限、標簽間隔
1 //重新作圖

你會看到此時屏幕上顯示的圖像已經挺完美了。我們可以導出為pdf格式，這樣線條會很光滑。輸入
-1 //修改導出文件的格式
7 //pdf格式
2 //將圖像文件保存
此時當前目錄下出現了dislin.pdf，此文件是本文文件包里的Ferrocene.pdf，效果如下，可以算是無可挑剔了

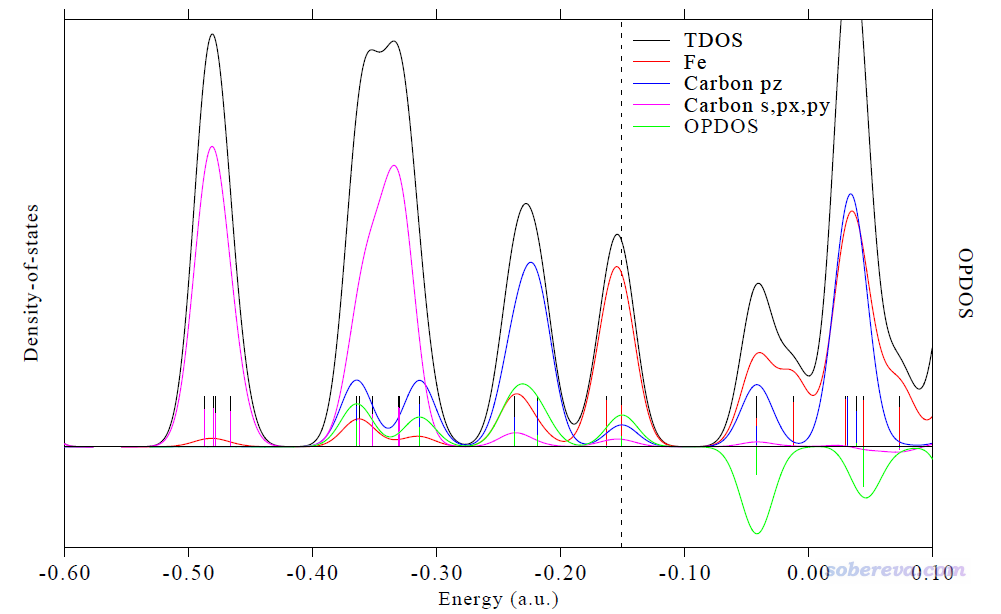
大家也可以自行把一些軌道的等值面圖ps上去。圖中每個豎線對應哪條軌道，通過DOS界面里-4 Show all orbital information把軌道信息都顯示出來，將其中的能量和DOS圖上豎線位置一對照便知。找到序號后，即可按照《使用Multiwfn觀看分子軌道》（http://www.shanxitv.org/269）中的做法方便、迅速地繪制出圖形。

值得一提的是，如果某個共軛環不是恰好平行于某個笛卡爾平面的話，是沒法把通過恰當選取基函數來試圖把這個環的pi軌道定義為片段的，因為此時pi軌道會由px,py,pz共同貢獻。如果被考察的環就一個，也可以用《調節平面分子間距的方法》（http://www.shanxitv.org/178）中的alignplane腳本讓特定的環平行于XY平面，然后算一次單點以得到fch文件，算的時候記得用nosymm關鍵詞避免體系被Gaussian調整到標準朝向。

3.2 繪制PhCz的DOS圖

PhCz是一個普通有機分子，B3LYP/6-31G*優化任務產生的fch文件是本文文件包里的PhCz.fchk，下面我們以它為例繪制一些DOS圖，這些圖沒多大實際意義，僅為了演示怎么操作用。

3.2.1 對不同角動量繪制DOS圖

這個例子中我們要繪制PDOS圖，要把所有原子的s、p、d角動量基函數分別定義為三個片段，并且把苯基上原子的p角動量基函數定義為第4個片段。

啟動Multiwfn，載入PhCz.fchk，然后輸入
10 //DOS繪制模塊
-1 //定義片段
1 //定義片段1
l s //把所有角動量為S的基函數加入此片段
q //保存片段1。接下來類似地把所有原子的p和d基函數分別定義為片段2和3
2
l p
q
3
l d
q
4 //定義片段4
cond //條件方式定義
22-25,27,29 //苯基上碳原子序號
a //對基函數序號范圍不做限制
P //基函數必須是P角動量
q //保存片段4
0 //返回DOS界面
8 //把橫坐標單位切換為eV
2 //設定橫坐標
-20,2,3 //范圍為-20~2 eV，標簽間隔3eV
0 //繪圖
關掉圖像后，輸入
9 //切換OPDOS曲線顯示狀態來將之隱藏。因為OPDOS不是我們目前感興趣的
10 //切換OPDOS離散豎線顯示狀態為隱藏
17 //修改曲線粗度
5 //比默認粗一點
4 //修改Y軸范圍
0,0.55,0.1 //設為0~0.55、步長0.1
22 //讓豎線顯示在曲線下方，這樣更清楚

然后在后處理菜單恰當設置圖例文字，最終得到的圖像如下：

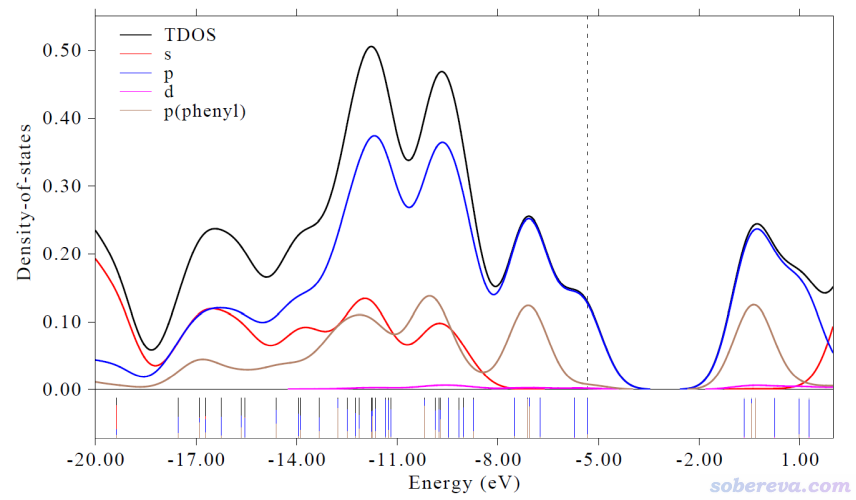
由此圖可以看到靠近HOMO和LUMO的那些前線分子軌道主要都是由p軌道貢獻的，s軌道只參與更低和更高的能級。d基函數對圖中展現的這些軌道參與程度極低，因為d對于這個體系而言是起到極化函數的作用，本身這個體系涉及的元素沒有d電子，所以d型基函數對占據軌道以及化學意義相對強一些的低階空軌道的貢獻必然很低。圖上還可以看出，對圖中涉及的能量范圍里的軌道，其中大部分都有苯基的顯著參與，不過對于HOMO和HOMO-1，苯基參與程度很低。

順帶一提，繪制當前這個圖的操作較多，建議畫完之后保存作圖狀態。也就是從后處理菜單返回DOS繪制界面后輸入s，然后輸入繪圖狀態文件的保存路徑，比如D:\PhCz_PDOS.dat。以后想重新作圖時，進入DOS繪制界面后輸入l，再輸入狀態文件的路徑即可恢復之前的作圖狀態。

3.2.2 基于Hirshfeld計算的軌道成份繪制DOS圖

前面的例子繪制PDOS圖的時候用的都是默認的Mulliken方法算的，此例我們基于Hirshfeld方法來計算軌道中原子所占成分。將要定義三個片段，一個是苯基，一個是分子中央的氮原子，其余原子定義為第三個片段。

啟動Multiwfn，載入PhCz.fchk，然后輸入
10 //DOS繪制模塊
7 //修改計算軌道成份的方法
3 // Hirshfeld。之后程序會把所有軌道的成份計算出來放到內存里備用
-1 //定義片段
1 //定義片段1
22-32 //苯基
2 //定義片段2
21 //氮原子
3 //定義片段3
1-20 //其余原子
0 //返回片段定義界面
0 //繪制TDOS+PDOS圖
關閉當前圖像。我們想讓離散的豎線不顯示，在后處理菜單中輸入
6 //關閉TDOS豎線
8 //設定PDOS豎線的顯示狀態
1 //關閉片段1的豎線
2 //關閉片段2的豎線
3 //關閉片段3的豎線
0 //返回
然后適當調節Y軸范圍、圖例文字、曲線粗細，可得下圖

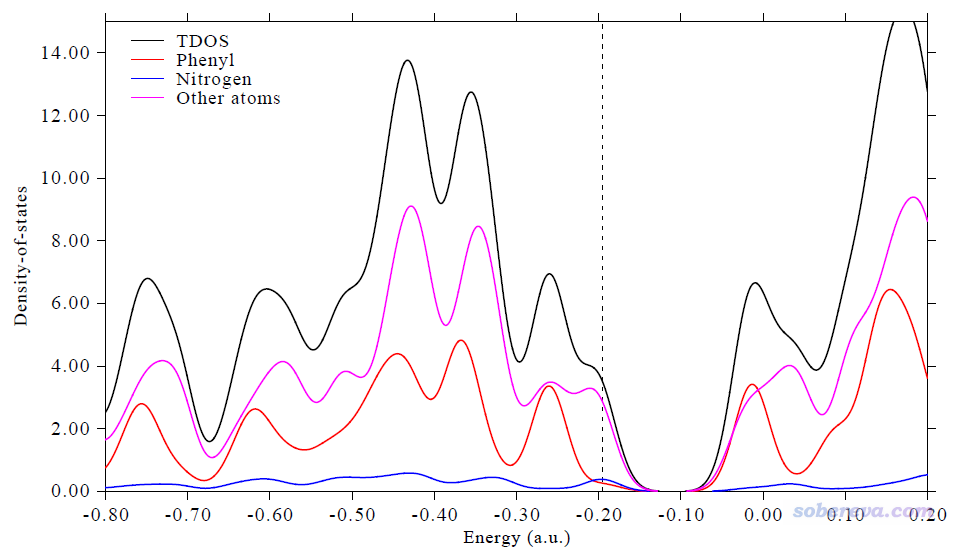
3.3 繪制開殼層體系Cr3Si12-團簇的DOS圖

前面考察的都是閉殼層體系，這里繪制一個開殼層體系Cr3Si12-。這個體系在《使用Multiwfn繪制光電子譜》（http://www.shanxitv.org/478）文中考察過，基態是八重態，PBE/6-311+G*計算得到的文件是本文文件包里的Cr3Si12-.fchk。這個體系里Si繞著排成一條直線的三個Cr分布。我們打算繪制TDOS，并且把三個Cr設為一個片段來同時繪制它的PDOS。由于計算時用了彌散函數，所以這次也必須用Hirshfeld或Becke方法計算軌道成份。

啟動Multiwfn并載入Cr3Si12-.fchk，然后輸入
10 //DOS繪制模塊
7 //修改計算軌道成份的方法
3 //Becke方法（用Hirshfeld方法也可以，結果相仿佛）
-1 //定義片段
1 //定義片段1
1,2,15 //三個Cr的序號
0 //離開片段設定界面
接下來做一些調整，都是我之前對此體系事先試出來的比較合適的設定
8 //切換橫坐標為eV
2 //設置能量范圍和標簽間隔
-7,2,1
3 //修改FWHM
0.3 //注意此時輸入的FWHM的單位應是eV
4 //設定曲線乘的系數
0.5
0 //畫TDOS+PDOS圖
此時看到的圖像如下。注意對于非限制性開殼層波函數，默認考慮的是alpha自旋，因此下圖的離散豎線、曲線體現的都只是alpha軌道，虛線也對應的是alpha的HOMO

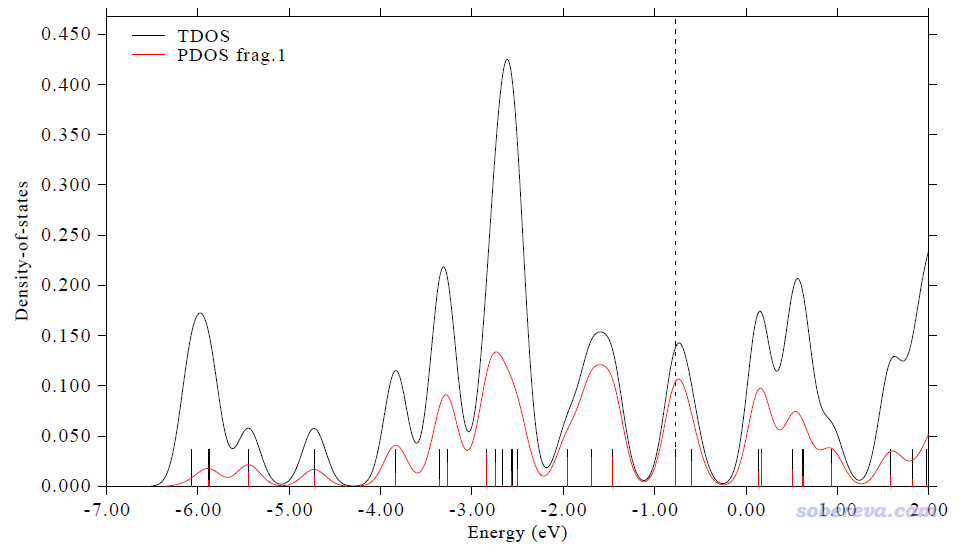
我們再來繪制beta自旋的圖。關閉圖像接著輸入
0 //退回到DOS界面
6 //設置考慮的自旋
2 //只考慮beta自旋
0 //畫TDOS+PDOS圖
此時看到的圖像如下，可見與alpha的圖像差異挺明顯，這說明此體系的這個電子態的自旋極化現象比較明顯，圖中的虛線對應的是beta的HOMO位置，可見比alpha的HOMO低不少。

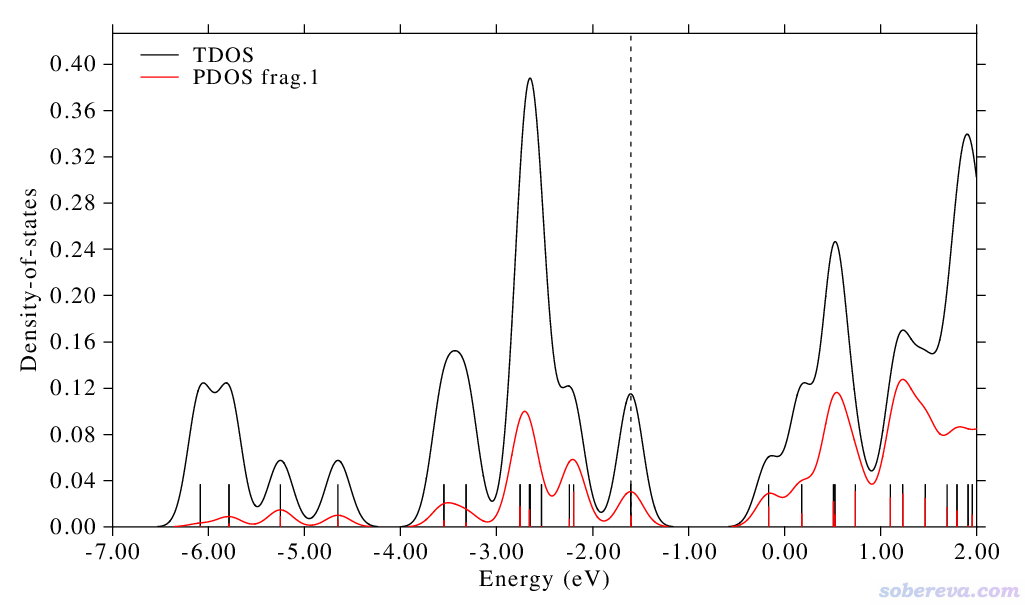
如果在選擇自旋的界面里選擇Both spins的話，繪制出的圖將把alpha和beta軌道一起考慮，得到的圖相當于上面兩幅圖的加和。

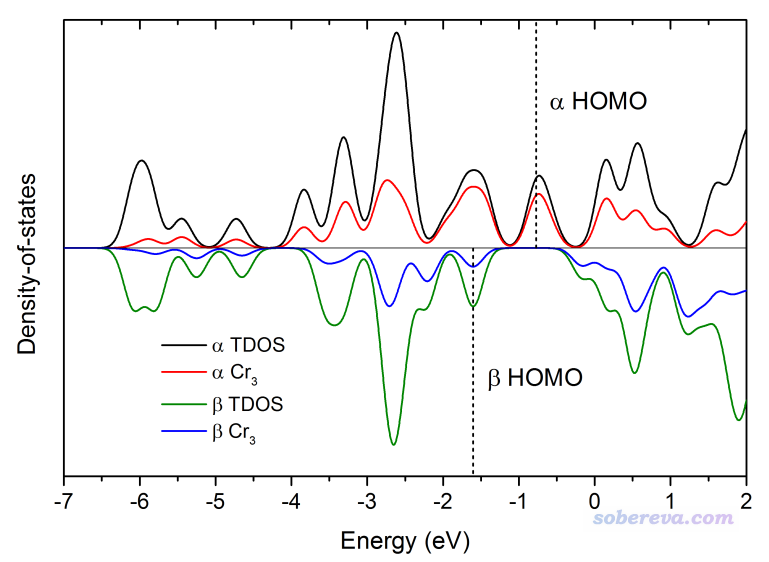
在很多文獻里，為了便于對比，往往是把alpha的圖繪制在上方，beta的圖反轉一下繪制在下方，這樣對比起來比較容易。這樣的圖在Multiwfn里沒法直接繪制，但是可以很容易地通過把數據導出，然后弄到Origin里繪制。下面來實際操作一下。

還是和之前一樣先把alpha部分的圖畫出來，然后在后處理界面里選擇選項3，此時如屏幕上的提示所示，當前目錄下已經產生了DOS_curve.txt和DOS_line.txt，分別記錄了曲線和離散豎線的X-Y數據點信息，這倆文件每一列的含義在屏幕上也提示得超級清楚。若將這倆文件弄到Origin里，用其中的數據繪制曲線圖，恰當設定后可以得到和Multiwfn繪制效果相同的圖。我們這里不打算把離散豎線在Origin里繪制出來，所以DOS_line.txt不用管，我們把DOS_curve.txt改名成alpha.txt。然后回到DOS繪制界面，把自旋切換成beta，也在后處理菜單導出這倆文件，并且把DOS_curve.txt改名為beta.txt。接下來，把alpha.txt和beta.txt全都拖入Origin導入。此時在alpha.txt和beta.txt各自的工作表里，第A列是能量，第B列是TDOS，第C列是第一個片段的PDOS。將beta.txt的表格里的D列內容定義為-Col(B)、E列內容定義為-Col(C)來實現曲線數據上下反轉的目的。然后繪制曲線圖，將alpha.txt里的A列作為X數據、將B和C列作為Y的數據加入，之后將beta.txt里的A列作為X數據、將D和E列作為Y的數據加入。然后我們可以再創建個額外的工作表，在里面填上適當內容，以使得對它們作line形式的圖時，Y=0的橫線、alpha HOMO位置、beta HOMO位置可以被顯示在圖上。其中alpha和beta各自的HOMO的能量在進入Multiwfn主功能0時文本窗口中直接就會提示。經過適當調整，最終得到的圖像如下，Origin的opj文件已經提供在了本文文件包里，如果有糊涂的，看一下這個文件必然就懂了。

4 關于Local DOS

TDOS體現整體的DOS，PDOS體現片段的DOS，而Local DOS (LDOS)則體現三維空間中某個點的DOS，因此也被叫做spatial DOS，其定義如下。注意，在一些書籍和文獻里，LDOS這個詞有時指的是前面說的PDOS。

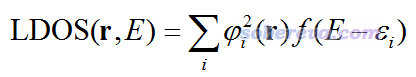
式中，r是三維空間的坐標矢量，φ是軌道波函數，取平方后就相當于這個軌道上電子的概率密度。三維空間某個特定的點的LDOS圖是個曲線圖，橫坐標是能量，圖中出現較高峰的地方，體現出某條軌道在r位置的概率密度較大，而且這個軌道的能量也差不多是這個能量。

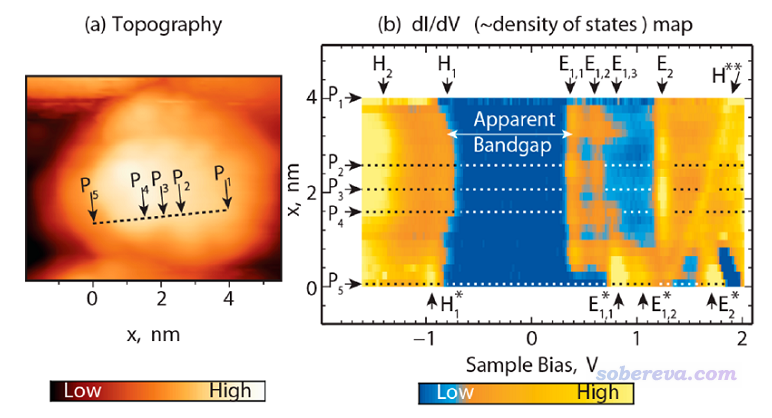
三維空間中某一條路徑上各個點的LDOS可以通過二維填色圖的形式展現，橫坐標是能量，縱坐標是與路徑始端的距離，LDOS值通過顏色的不同來體現，這可以稱作二維LDOS圖，這種圖對于解釋掃描隧道顯微鏡(STM)的數據有幫助，下圖出自J. Phys. Chem. Lett., 5, 3701 (2014)，三維空間中取的路徑如左圖所示，對應右邊LDOS圖的縱軸，其中5個有代表性的點被做了特別的標注。

5 Local DOS在Multiwfn中的繪制例子

這里我們用吡咯作為例子演示繪制LDOS。輸入文件是此文文件包里的pyrrole.fch，通過B3LYP/6-31G*優化任務得到。分子在X=0的YZ平面上，結構如下

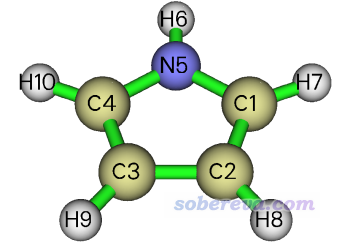
在Multiwfn載入文件后，進入主功能0時在屏幕上可以直接看到各個原子的坐標。1 Bohr=0.5292埃。
1(C ) --> Charge: 6.000000 x,y,z(Bohr):   0.000000   2.126932   0.626525
2(C ) --> Charge: 6.000000 x,y,z(Bohr):   0.000000   1.346889 -1.858520
3(C ) --> Charge: 6.000000 x,y,z(Bohr): -0.000000 -1.346889 -1.858520
4(C ) --> Charge: 6.000000 x,y,z(Bohr): -0.000000 -2.126932   0.626525
5(N ) --> Charge: 7.000000 x,y,z(Bohr):   0.000000   0.000000   2.120935
...略

5.1 繪制某個點的LDOS曲線圖

我們先來繪制氮的對位的兩個碳原子C2和C3連線中點在分子平面上方1 Bohr位置的LDOS圖。其X坐標顯然應為1或-1，Y坐標為(1.346889-1.346889)/2=0，Z坐標為(-1.858520-1.858520)/2=-1.858520。

啟動Multiwfn，載入pyrrole.fch，依次輸入
10 //DOS繪制功能
10 //對某個點繪制DOS
1,0,-1.858520 //X,Y,Z坐標（Bohr）
馬上看到下圖

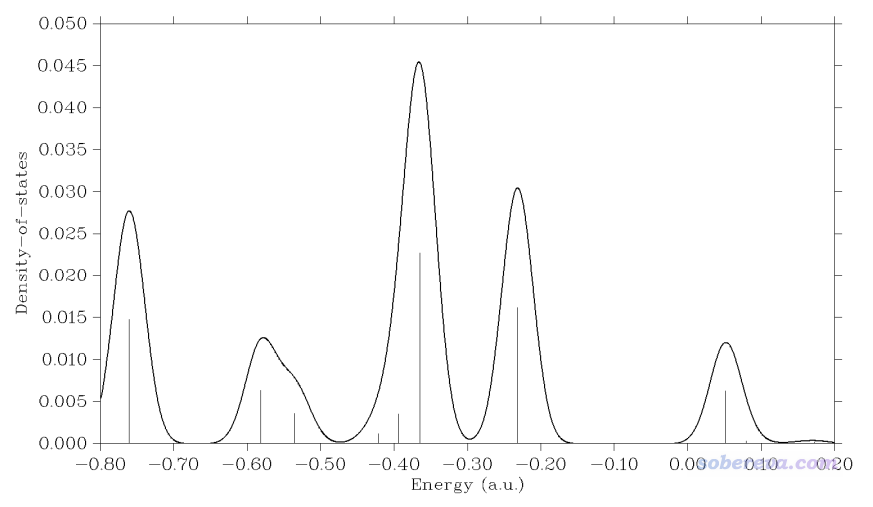從此圖我們可以了解到，有一條能量在-0.24 a.u.左右的軌道在當前考察的這個點有顯著分布，如果把軌道能量都列出來就可以找到它，實際上它是HOMO-1軌道，能量為-0.232 a.u.，如下圖左邊所示，確實在C2和C3中點上方的位置有顯著分布。下圖所示的HOMO軌道能量為-0.201 a.u.，由于在C2和C3之間正好有個節面，因此對當前位置貢獻為零，故在LDOS圖上看不到相應的峰。

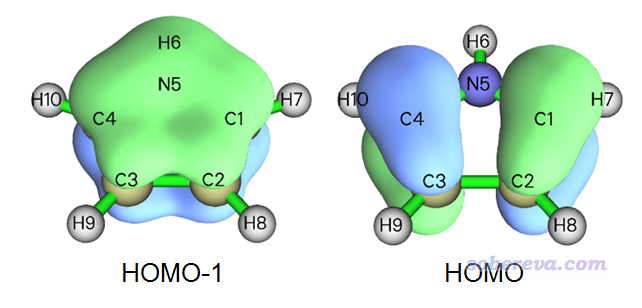
5.2 繪制一條線段上的LDOS填色圖

下面，我們將C2和C3上方1 Bohr的位置作為線段的兩個端點，繪制這條連線上的LDOS填色圖。啟動Multiwfn，載入文件，然后輸入
10 //DOS繪制功能
11 //繪制某條線段上的LDOS
1.000000 1.346889 -1.858520 //起點坐標，即在C2的坐標基礎上把X設為1 Bohr
1.000000 -1.346889 -1.858520 //終點坐標，即在C3的坐標基礎上把X設為1 Bohr
200 //連線上的點數。越大繪制耗時越高，而圖像越光滑。通常200個足夠光滑了
很快就看到了圖。但是我們還要做一些調節。關閉圖像后輸入
4 //設定縱軸相對于橫軸的比例
0.4 //讓縱軸長度是橫軸的40%
5 //設定色彩刻度軸
0,0.1,0.02 //讓色彩刻度數值顯得比較“整”
6 //設定左邊Y軸的標簽間隔
0.4
然后選1重新繪圖，得到下圖

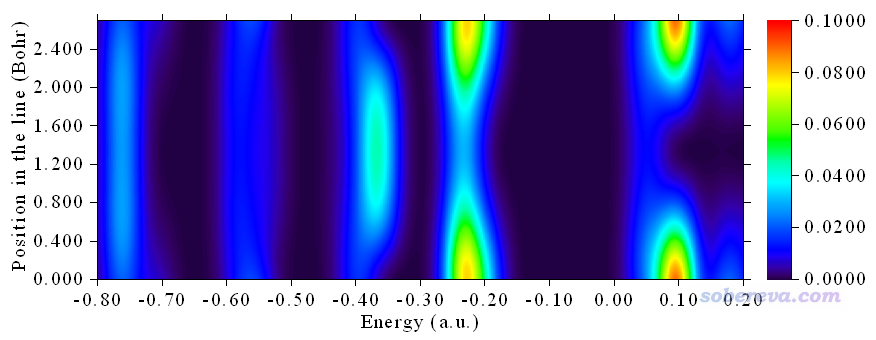縱坐標體現出了連線上的不同位置，顏色越紅LDOS數值越大。為了讓大家更好地理解這張圖的含義，我們關注一下橫軸為0.1 a.u.的那個位置，這個地方在接近兩個端點的地方LDOS較大，而在兩個端點中央區域LDOS幾乎為0。為什么會這樣？我們首先去找能量大約為0.1 a.u.的軌道，會發現是MO 21，是此體系的LUMO+2，其確切能量是0.0968 a.u.。下圖是用Multiwfn主功能0繪制的這個軌道的等值面圖。為了便于看得清楚，等值面用了透明，并且圖中把我們繪制LDOS定義的兩個端點位置用小球表示了出來，如箭頭所示。

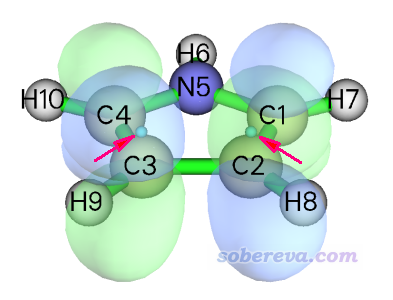
由圖可見，在小球的位置，軌道波函數的概率密度較大，這是為什么在端點附近LDOS數值較大的原因。而在兩個小球中央部分，是這個軌道的節面區域附近，顯然軌道波函數的概率密度很小，因而在LDOS圖上相應部分是深紫色。

6 MO-PDOS圖

前述的PDOS圖里面的片段對應的是分子片段、原子、基函數等，如果把片段定義為分子軌道，那就叫MO-PDOS了（這是我自己起的名字）。這種圖可以直觀展現不同的軌道所在的能級位置以及對TDOS的貢獻，而且可以通過豎線的高度體現軌道的簡并度。筆者就不在這里給出具體的繪制例子了，在手冊4.10.5節有非常詳細的示例。此例繪制的是18碳環體系，筆者對這個特別不尋常的體系做過十分廣泛的研究，非常歡迎查看：http://www.shanxitv.org/carbon_ring.html。18碳環的MO-PDOS圖如下

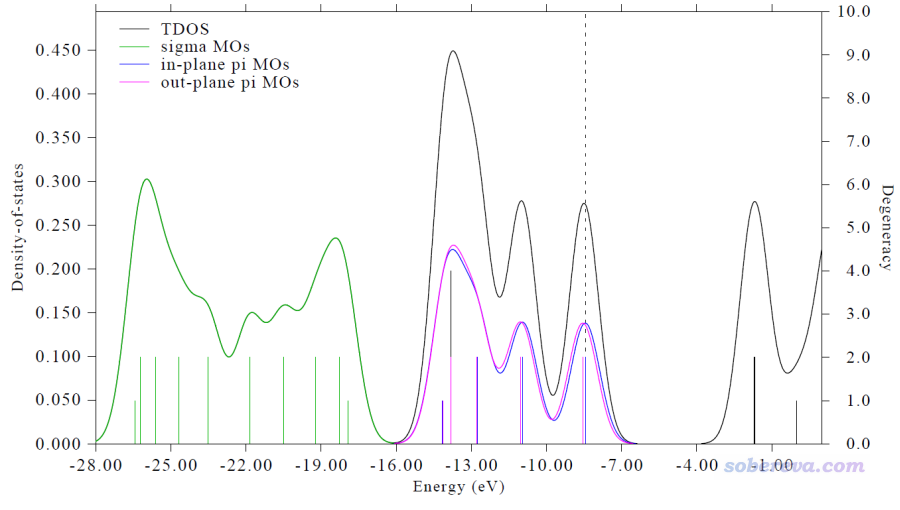
18碳環這個體系是D9h對稱性的，價層占據軌道分為三種：sigma軌道、平面內pi軌道、平面外pi軌道，繪制時將這三類軌道分別定義為了三個片段（序號通過Multiwfn主功能0觀看軌道圖形確定）。上面通過一張圖就清晰展示出這三類軌道的能級位置，以及TDOS是如何由這三類軌道各自的PDOS貢獻的。由于非占據軌道沒有被定義為片段，因此圖中的非占據軌道那部分區域的圖像和普通的TDOS相同。這張圖上價層占據軌道的豎線高度體現了軌道的簡并度，對應圖上右側坐標軸。可見大部分占據價層軌道是雙占據的，只有少部分是非簡并的（豎線高度只有一半）。

提醒：第一篇發表的使用MO-PDOS圖討論問題的文章是筆者發表的這篇18碳環的研究論文：Carbon, 165, 461 (2020) DOI: 10.1016/j.carbon.2020.05.023。使用MO-PDOS圖的用戶除了引用Multiwfn原文外，也請在文章當中引用此文。

7 總結

本文非常詳細地介紹了各種DOS的定義、物理意義、實用價值，并且介紹了Multiwfn繪制這些DOS圖的用法，并通過一系列實際例子展現了使用Multiwfn繪制DOS圖的強大、靈活和便利。顯然本文的例子不可能把Multiwfn的DOS繪制功能的一大堆選項的使用全都一一體現，讀者務必舉一反三，在領會本文介紹的內容、搞懂例子里每一步操作的目的后，靈活地將Multiwfn繪制DOS圖的功能用于自己實際問題的研究。在Multiwfn手冊4.10節還有其它DOS繪制的例子，感興趣的讀者可以看看。