談談5d、6d型d殼層基函數與它們在Gaussian中的標識

在含有d軌道的體系的高斯輸出文件中，有時會看到d軌道名以D 0, D+1, D-1, D+2, D-2標識，有人誤以為那些軌道就是指復數型真實原子軌道，這是個嚴重的誤區，下面將對此進行討論。

在高斯等量化程序中，對于非半經驗方法用的都是GTF(Gaussian type function)型實函數用來描述原子軌道，以解決雙電子多中心積分的麻煩，所以與復數型軌道完全無關。

最常用的高斯型函數是笛卡爾型高斯函數，通式為N*x^a*y^b*z^c*exp(-q*r^2)，N為歸一化常數，q為高斯函數的指數，r為以此基函數所在原子為中心的坐標向量。

對于描述d原子軌道，使用d型笛卡爾型GTF作為基函數，包含六種具體形式:xx,yy,zz,xy,xz,yz。例如xy型GTF，其通式中的a=b=1，c=0。然而這6種里面除了xy、yz、xz以外的其它三種笛卡爾型GTF并沒有與真實的實形式的原子軌道有直接的對應關系，波函數角度部分的行為明顯不一致。

還有一種球諧型高斯函數，也叫原子軌道型高斯函數，通式為N*r^n*exp(-q*r^2)*Y(θ,φ)，其中Y(θ,φ)就是類氫原子軌道的角度部分函數，與STO的區別是指數項的r變為了r^2。球諧型高斯函數與實型原子軌道角度部分行為一致，通過調整收縮系數調整徑向行為，就可以一一對應地近似描述實型原子軌道。

笛卡爾型GTF可以線性組合，使角度部分行為與球諧型GTF一致（盡管組合后的函數形式與球諧型仍不同），以用于合理描述原子軌道。對于d型軌道轉換比較簡單：xy、yz、xz這三種不變，其余三個變成了x^2-y^2、3*z^2-r^2、r^2。（注：r^2=x^2+y^2+z^2）。其中xy、yz、xz、x^2-y^2、3*z^2-r^2這5種就是組合出的d型球諧GTF，也叫純d型GTF，而r^2函數一般不用，它是一個特殊的球型GTF軌道，在某個徑向距離（取決于指數）附近函數值較大，而接近GTF的中心和遠離GTF時都很小，其投影地形圖如下所示：


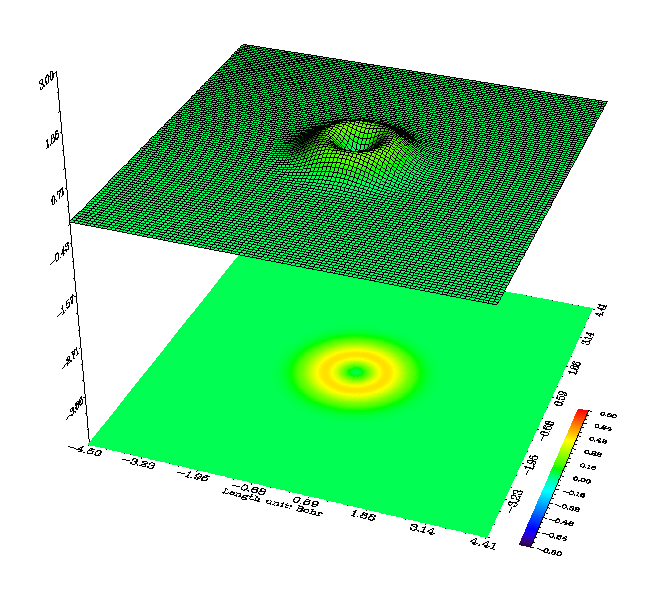
在高斯中，如果用了5d關鍵字，就會使用xy、yz、xz、x^2-y^2、3*z^2-r^2這5種軌道描述d軌道。這時輸出的d軌道符號會顯示D 0, D+1, D-1, D+2, D-2，但顯然這決不是指這樣由GTF組合出來的波函數的角動量z軸分量的本征值，也不是指這5個軌道用來對應地近似描述5個真實的復數型原子軌道。這樣的軌道符號沒有意義，還會引起嚴重混淆，它僅僅是做個標識罷了。
可以得到這樣的對應關系：

作為基函數的GTF   實型真實原子軌道符號   高斯中用了5d關鍵字后對d軌道的標識
3*z^2-r^2 ->dz^2     ->d 0
xz        ->dxz      ->d+1
yz        ->dyz      ->d-1
x^2-y^2   ->dx^2-y^2 ->d+2
xy        ->dxy      ->d-2

高斯一般默認使用6d關鍵字（在使用gen等關鍵字時往往默認為5d）。此時說明使用xx、yy、zz、yz、yx、zx這6種笛卡爾型GTF軌道，在輸出的d軌道符號中也對應地以xx、yy、zz、yz、yx、zx標識。在d軌道基函數不分裂情況下，描述d軌道的可獨立變分的基函數就相對于5d關鍵字時的5個增加到了6個，可看到輸出文件中basis functions的數目對應地增加了。但無論用5d還是6d，輸出文件顯示的原始基函數（primitive gaussians，即笛卡爾型GTF）的數目都一樣，這是因為5d的5個軌道仍需要有全部6種笛卡爾型d型GTF才能組合出來。比如對5d中的3*z^2-r^2函數來說，將其中r^2展開，可寫成N*(2*z^2-x^2-y^2)，即等于zz、xx、yy三種笛卡爾型GTF系數按照2:-1:-1組合并乘上歸一化系數，這個比值這是固定的，不會在計算過程中改變，某種意義上也可看作是CGTF（收縮型GTF）。

6d型軌道好處是方便編程，能夠直接計算各種積分。缺點很明顯，由于缺乏與真實原子軌道的對應關系，結果不像用5d的結果那樣方便分析。雖然這6個笛卡爾型軌道不直接對應于真實原子軌道，但在計算過程中經過變分，其結果同樣會展現出真實原子軌道的行為。這是因為以它們為基函數變分的結果，等價于對它們線性變換后的基函數變分的結果。前面已提到，6個笛卡爾型d型GTF線性變換后的6個函數其中的5個就是對應真實軌道的5d型軌道，只不過多增加了一個r^2軌道。換句話說，使用6d關鍵字，就是在5d型的基函數基礎上多添加了一個內部含有節面的s型GTF軌道，由于這個軌道與其它s軌道有不小重疊，會造成一定線性相關問題，所以并不會比5d的結果有多少改進。

7f與10f的關系與5d與6d的關系類似，對于g、h等更高角動量函數也有如上討論，笛卡爾型與球諧型GTF轉換關系將更為復雜，而且組合方法并不唯一（比如有所謂標準純f集、純f“立方”集）。計算時若同時含有d和f軌，用5d時應當結合7f，用6d時應當結合10f。順帶一提，6d軌道間不都是正交的，例如XX與YY，而5d軌道間都是正交的，同樣10f和7f的關系也是如此。