基于Fortran使用Levenberg-Marquardt算法做非線性擬合
基于Fortran使用Levenberg-Marquardt算法做非線性擬合
文/Sobereva@北京科音
First release: 2020-Mar-13 Last update: 2023-Jun-19
1 前言
非線性擬合在計算化學研究中用得非常多,比如自己用復雜函數擬合力場參數就需要用到。Fortran是科學計算領域用的最多的語言之一,本文就通過一個例子,講解如何通過Fortran非常容易地實現非線性擬合。
2 非線性擬合方法
做非線性擬合有很多種方法,比如可以用各種常規的非線性優化算法來實現,即通過不斷調整擬合系數來最小化誤差函數,誤差函數定義為所有擬合點上實際與擬合出的數據差值的平方和。可以用的這類算法很多,比如《L-BFGS-B局部極小化算法在Fortran中的使用簡例》(http://www.shanxitv.org/538)和《無需導數的局部極小化算法NEWUOA在FORTRAN中的使用簡例》(http://www.shanxitv.org/536)中介紹的方法。而用得最多,且擬合效率最高、效果最好的是Levenberg-Marquardt算法,具體細節大家看https://en.wikipedia.org/wiki/Levenberg%E2%80%93Marquardt_algorithm,這里就不多說了。大家只要知道這幾點就行了:
? 這是個迭代求解的算法
? 擬合出的結果依賴于初猜參數
? 此算法需要導數信息
Levenberg-Marquardt算法的代碼沒必要自己寫,因為有很多現成的庫可以用。其中MINPACK(https://people.sc.fsu.edu/~jburkardt/f_src/minpack/minpack.html)是一個Fortran 90語言的專門做最小二乘極小化的庫,其中就有子程序來實現Levenberg-Marquardt算法,另外它還能使用Powell方法求解非線性方程組。下面的例子我們就基于這個庫來實現擬合。
3 例子的背景知識
本文的例子是用Morse勢對乙烷碳碳鍵斷裂的柔性掃描曲線進行擬合。做掃描的方法參看《詳談使用Gaussian做勢能面掃描》(http://www.shanxitv.org/474)。用Gaussian做過掃描后,再用GaussView查看掃描曲線,在上面點右鍵就可以看到選項把掃描的點導出為.txt文件。
實際上這個擬合例子是筆者講的北京科音基礎量子化學班(http://www.keinsci.com/workshop/KBQC_content.html)中的,課上是講怎么用流行的Origin程序通過圖形界面操作來實現擬合,而這里我們改為使用Fortran程序來等價地實現。實際上Origin用的也正是Levenberg-Marquardt算法。
Morse勢的表達式在以下幻燈片里面給出了

下面是通過Origin擬合出來的結果。之后我們要將我們自己寫的代碼擬合出來的結果和圖中的對照
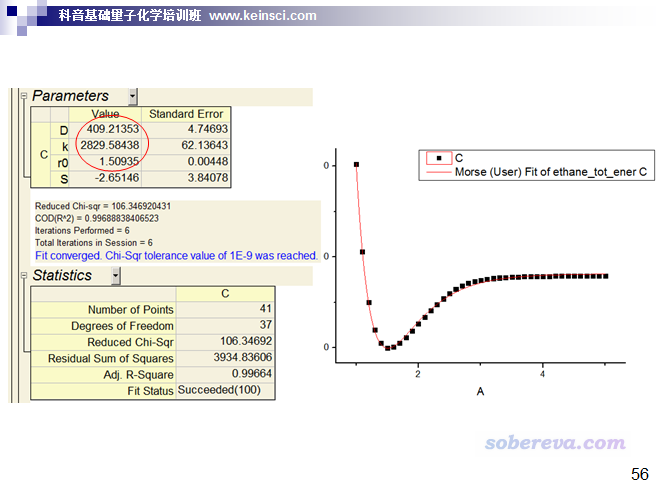
4 例子的代碼和解讀
乙烷碳碳鍵斷裂的柔性掃描的曲線的數據、本例的Fortran源代碼文件,以及筆者修改后的MINPACK庫的源文件都可以在這里下載:http://www.shanxitv.org/attach/541/file.rar。編譯很簡單,把兩個.f90文件放在一起即可編譯。
啟動后,程序會讀取當前目錄下的ethane_dissoc.txt文件,然后開始用Morse勢來擬合,之后輸出結果和擬合誤差統計信息。
例子的完整代碼如下:
!A code to illustrate how to use Levenberg-Marquardt method to fit
!Written by Tian Lu (sobereva@sina.com), last update: 2023-Jun-19
module fitting_module
integer,parameter :: maxdata=1000
real*8 x(maxdata),value(maxdata)
end module
program LMfit
use fitting_module
implicit real*8 (a-h,o-z)
integer,parameter :: nparm=4
real*8 parm(nparm) !D,k,r0,S
real*8 fiterr(maxdata),fitval(maxdata)
character c80tmp*80
external calcfiterr
open(10,file="ethane_dissoc.txt",status="old")
ndata=0
do while(.true.)
read(10,"(a)",iostat=ierror) c80tmp
if (c80tmp==" ".or.ierror/=0) exit
ndata=ndata+1
read(c80tmp,*) x(ndata),value(ndata)
end do
close(10)
write(*,"(i6,' data have been loaded')") ndata
value=(value-minval(value))*2625.5D0
tol=1D-7
maxcall=5000
parm(1)=300
parm(2)=2000
parm(3)=1.5D0
parm(4)=0
write(*,*) "Fitting via Levenberg-Marquardt algorithm..."
call lmdif1(calcfiterr,ndata,nparm,parm(:),fiterr(1:ndata),tol,maxcall,info)
if (info==1.or.info==2.or.info==3) then
write(*,*) "Fitting has successfully finished!"
else if (info==5) then
write(*,"(a,i7)") " Warning: Convergence tolerance has not met while the maximum number of function calls has reached",maxcall
else if (info==6.or.info==7) then
write(*,*) "Error: Tolerance is too small, unable to reach the tolerance!"
end if
write(*,"(' Fitting result:',/,' D=',f10.4,' k=',f10.4,' r0=',f10.4,' S=',f10.4)") parm(:)
write(*,"(' RMSE:',f12.4)") dsqrt(sum(fiterr(1:ndata)**2)/ndata)
call calcfitval(ndata,nparm,parm,fitval(1:ndata))
pearsoncoeff=covarray(value(1:ndata),fitval(1:ndata))/stddevarray(value(1:ndata))/stddevarray(fitval(1:ndata))
write(*,"(2(a,f12.6),/)") " Pearson correlation coefficient r:",pearsoncoeff," r^2:",pearsoncoeff**2
do idata=1,ndata
write(*,"(' r=',f8.4,' Inputted=',f10.3,' Fitted=',f10.3,' Error=',f10.3)") x(idata),value(idata),fitval(idata),fitval(idata)-value(idata)
end do
write(*,*)
write(*,*) "Press ENTER button to exit"
read(*,*)
contains
real*8 function stddevarray(array)
real*8 array(:),avg
avg=sum(array)/size(array)
stddevarray=dsqrt(sum((array-avg)**2)/size(array))
end function
real*8 function covarray(array1,array2)
real*8 array1(:),array2(:),avg1,avg2
avg1=sum(array1)/size(array1)
avg2=sum(array2)/size(array2)
covarray=sum((array1-avg1)*(array2-avg2))/size(array1)
end function
end program
!------ The routine calculates fitting error
subroutine calcfiterr(ndata,nparm,parm,fiterr,iflag)
use fitting_module
integer ndata,nparm,iflag
real*8 :: parm(nparm),fiterr(ndata),fitval(ndata)
call calcfitval(ndata,nparm,parm,fitval)
fiterr(:)=abs(fitval(:)-value(1:nparm))
end subroutine
!------ The routine calculates fitted function at given points
subroutine calcfitval(ndata,nparm,parm,fitval)
use fitting_module
implicit real*8 (a-h,o-z)
integer ndata,nparm
real*8 :: parm(nparm),fitval(ndata),k
D=parm(1)
k=parm(2)
r0=parm(3)
S=parm(4)
do idata=1,ndata
alpha=dsqrt(k/(2*D))
fitval(idata)=D*(1-exp(-alpha*(x(idata)-r0)))**2+S
end do
end subroutine
這個代碼內容很容易理解。整個代碼的核心是這一句:
call lmdif1(calcfiterr,ndata,nparm,parm(:),fiterr(1:ndata),tol,maxcall,info)
每個參數的含義如下:
lmdif1:MINPACK庫的做Levenberg-Marquardt算法擬合的子程序
calcfiterr:自寫的計算各個擬合點位置的誤差的子程序
ndata:數據點的數目
nparm:被擬合的參數數目
parm:被擬合的參數的數組。此數組的四個元素對應Morse勢當中的D,k,r0,S。其中S參數是用于對Morse勢進行上下移動的。本來Morse勢是沒有S這一項的,之所以弄這么一項是因為當前的掃描數據中并沒有一個點恰好落在勢能曲線真正的精確谷底位置(這需要優化來得到),所以擬合時應當允許被擬合的曲線整體上下移動,否則掃出來的勢能曲線的能量最低的那個擬合點就會誤成為Morse勢谷底位置
fiterr:達到擬合收斂時的calcfiterr返回的誤差數組
tol:收斂限,數值越小擬合精度越高,但耗時越高,越容易達不到收斂限
maxcall:最多可以調用calcfiterr子程序的次數,如果超過了maxcall還沒收斂,擬合就算失敗了。前面說過這個算法需要導數信息,具體來說是需要Jacobian矩陣(見https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant)。當前例子我們是讓MINPACK庫自動通過有限差分來計算Jacobian矩陣,因此就省得寫計算解析的Jacobian矩陣的代碼了。也因此,調用calcfiterr的次數并非等于Levenberg-Marquardt算法的迭代次數。maxcall不要設太小,免得達到此值時迭代還沒收斂;但也不要太大,免得白費了大量時間計算結果最后也沒收斂(往往是迭代過程中參數出現了震蕩等問題)
info:運行狀態信息,在MINPACK包的lmdif1子程序開頭的注釋中有詳細說明
被lmdif1所調用的子程序,即calcfiterr,包含的5個參數是固定的,必須有這個5個,而且數據類型必須和例子中的一致。ndata是數據點的數目,返回的fiterr是各個擬合點的真實值和擬合值之間的誤差,iflag不用管。可見calcfiterr子程序調用了calcfitval子程序計算基于當前參數和Morse勢的公式得到的各個點的擬合值,然后與真實值求了差值,lmdif1子程序就是根據這個誤差數組來優化參數的。由于傳入calcfiterr的信息里沒有擬合點信息,所以擬合點信息是通過fitting_module這個module來傳遞進來的。
本例的程序首先從當前目錄下的ethane_dissoc.txt中讀取所有數據點的位置到x數組、讀取數據值到value數組。此文件里是以a.u.為單位的電子能量,我們先轉換為以kJ/mol為單位,并且為了不讓轉換后數量級太大,給調整成以數值最低的擬合點為0點的情況。之后對擬合的運行參數進行設置,初始化擬合參數。在擬合之后,根據返回的info,輸出擬合情況。接下來把擬合出的四個參數值輸出出來,其中的S不用管,以后使用這個Morse勢時只考慮D、k、r0便夠了。之后給出誤差統計信息,RMSE即Root mean square error,數值越小擬合精度越好。calcfitval子程序計算各個擬合點的擬合值,用于之后計算真實值與擬合值的Pearson相關系數以及r^2。stddevarray函數是對傳進來的數組計算標準偏差,covarray函數是對傳進來的兩個數組計算協方差。
執行后輸出信息如下
41 data have been loaded
Fitting via Levenberg-Marquardt algorithm...
Fitting has successfully finished!
Fitting result:
D= 409.2492 k= 2830.1767 r0= 1.5093 S= -2.6847
RMSE: 9.7965
Pearson correlation coefficient r: 0.998443 r^2: 0.996888
r= 1.0000 Inputted= 1011.870 Fitted= 1016.567 Error= 4.697
r= 1.1000 Inputted= 529.142 Fitted= 529.802 Error= 0.660
r= 1.2000 Inputted= 250.526 Fitted= 244.665 Error= -5.861
r= 1.3000 Inputted= 98.450 Fitted= 89.974 Error= -8.476
r= 1.4000 Inputted= 24.984 Fitted= 18.107 Error= -6.876
r= 1.5000 Inputted= 0.000 Fitted= -2.560 Error= -2.560
r= 1.6000 Inputted= 4.375 Fitted= 7.171 Error= 2.796
r= 1.7000 Inputted= 25.963 Fitted= 33.789 Error= 7.826
r= 1.8000 Inputted= 57.081 Fitted= 68.672 Error= 11.591
r= 1.9000 Inputted= 92.888 Fitted= 106.447 Error= 13.559
r= 2.0000 Inputted= 130.356 Fitted= 143.887 Error= 13.531
r= 2.1000 Inputted= 167.625 Fitted= 179.163 Error= 11.538
r= 2.2000 Inputted= 203.599 Fitted= 211.340 Error= 7.741
r= 2.3000 Inputted= 237.685 Fitted= 240.048 Error= 2.363
r= 2.4000 Inputted= 269.599 Fitted= 265.257 Error= -4.342
r= 2.5000 Inputted= 299.236 Fitted= 287.134 Error= -12.102
r= 2.6000 Inputted= 324.266 Fitted= 305.952 Error= -18.314
r= 2.7000 Inputted= 342.488 Fitted= 322.026 Error= -20.462
r= 2.8000 Inputted= 355.783 Fitted= 335.683 Error= -20.100
r= 2.9000 Inputted= 365.529 Fitted= 347.236 Error= -18.293
r= 3.0000 Inputted= 372.714 Fitted= 356.976 Error= -15.738
r= 3.1000 Inputted= 378.049 Fitted= 365.165 Error= -12.884
r= 3.2000 Inputted= 382.043 Fitted= 372.034 Error= -10.008
r= 3.3000 Inputted= 385.058 Fitted= 377.786 Error= -7.272
r= 3.4000 Inputted= 387.355 Fitted= 382.596 Error= -4.760
r= 3.5000 Inputted= 389.115 Fitted= 386.612 Error= -2.503
r= 3.6000 Inputted= 390.465 Fitted= 389.962 Error= -0.502
r= 3.7000 Inputted= 391.508 Fitted= 392.755 Error= 1.247
r= 3.8000 Inputted= 392.332 Fitted= 395.082 Error= 2.750
r= 3.9000 Inputted= 392.993 Fitted= 397.019 Error= 4.026
r= 4.0000 Inputted= 393.524 Fitted= 398.631 Error= 5.107
r= 4.1000 Inputted= 393.955 Fitted= 399.971 Error= 6.016
r= 4.2000 Inputted= 394.320 Fitted= 401.086 Error= 6.767
r= 4.3000 Inputted= 394.638 Fitted= 402.013 Error= 7.375
r= 4.4000 Inputted= 394.915 Fitted= 402.784 Error= 7.869
r= 4.5000 Inputted= 395.149 Fitted= 403.424 Error= 8.275
r= 4.6000 Inputted= 395.348 Fitted= 403.956 Error= 8.608
r= 4.7000 Inputted= 395.522 Fitted= 404.398 Error= 8.876
r= 4.8000 Inputted= 395.668 Fitted= 404.765 Error= 9.098
r= 4.9000 Inputted= 395.784 Fitted= 405.070 Error= 9.286
r= 5.0000 Inputted= 395.873 Fitted= 405.324 Error= 9.450
可見擬合出的Morse勢參數和前面ppt中用Origin擬合出來的結果非常接近。r^2非常接近于1,而且所有點的相對誤差都不大,故擬合得相當成功。我們算出來的r^2也和Origin給的相一致。
筆者開發的波函數分析程序Multiwfn(http://www.shanxitv.org/multiwfn)的主功能300的子功能2專門用來將球對稱化的原子徑向密度擬合成多個Slater type orbital (STO)或多個Gaussian type function (GTF)的線性組合,其中就用到了本文的方法,但考慮的細節多得多得多,擬合的質量相當高。可以看Multiwfn手冊3.300.2節的詳細介紹以及4.300.2節的擬合例子,對代碼實現感興趣者可以看Multiwfn源代碼中的fitatmdens子程序。