無需導數的局部極小化算法NEWUOA在Fortran中的使用簡例

無需導數的局部極小化算法NEWUOA在Fortran中的使用簡例

文/Sobereva@北京科音  2020-Mar-1

1 NEWUOA簡介

數學上對多維函數做局部極小化的算法非常多，諸如simplex、BFGS、最陡下降法、共軛梯度法等等。NEWUOA（NEW Unconstrained Optimization Algorithm）是已故的劍橋大學教授Powell于2004年提出的一種不需要導數信息的非約束性局部極小化算法（這點類似于simplex），并且給了實現此算法的Fortran子程序，在此文介紹一下使用。

NEWUOA和其它極小化算法一樣需要進行迭代，而且結果依賴于初猜。它不需要導數的好處很明顯，很多情況函數是個黑箱，本身沒有解析導數，或者解析導數代碼很難寫，如果用有限差分來計算導數，一方面昂貴，一方面還有數值精度層面的問題。根據Experimental Comparisons of Derivative Free Optimization Algorithms一文的對比（Google一搜就有），相對于流行的BFGS方法（假設梯度通過有限差分得到），多數情況下NEWUOA效率更高，即收斂到極小點所需要計算函數值的次數更少。NEWUOA的原理我就不在這里介紹了，大家可以看https://en.wikipedia.org/wiki/NEWUOA。

Powell分享了他的Fortran77寫的NEWUOA程序，后來有人寫了Fortran95的wrapper（https://github.com/ralna/MJDP_software/tree/master/newuoa），我又進一步做了輕微修改使之用著更舒服，可以在這里下載：http://www.shanxitv.org/attach/536/newuoa_module.f90。下面就基于這個文件，通過兩個很簡單的問題示例怎么使用NEWUOA方法解決實際問題，你會發現超級容易。

2 例：二元函數極小化

本例我們求下面這個函數的極小點位置和函數值

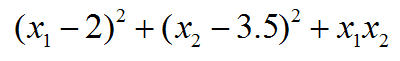
我們可以先自行求一下解析解。讓函數對x1和x2求導分別得0，聯立求解方程組，可知精確極小點位置是x1=1/3、x2=10/3。

極小化以上函數的最簡Fortran代碼如下

PROGRAM test_newuoa
use newuoa_module
implicit real*8 (a-h,o-z)
real*8,allocatable :: X(:)
external CALFUN

nvar=2
allocate(X(nvar))
X(:)=0
call newuoa_min(CALFUN, X, RHOBEG=0.1D0, RHOEND=1D-6, IPRINT=2, MAXFUN=50000)
END PROGRAM
        
subroutine CALFUN(X,F)
real*8 :: X(:),F
F=(X(1)-2)**2+(X(2)-3.5D0)**2+X(1)*X(2)
end subroutine

在編譯的時候要將上面的源文件和newuoa_module.f90放在一起編譯。newuoa_module.f90中定義了newuoa_module的module，并提供了包含newuoa_min在內的各種相關函數。運行期間newuoa_min會反復調用計算函數值的子程序CALFUN直到達到收斂。CALFUN這個函數的名字以及里面的參數名也可以用其它名字。

此例中，我們定義了含兩個元素的數組X，一開始我們給它賦的值是初猜值，在調用newuoa_min子程序做NEWUOA極小化后，X里記錄的就是我們要求的終值。CALFUN是計算被極小化的函數的數值的子程序，傳入X數組，返回函數值F，這個函數有且只能有這兩個參數。NEWUOA算法迭代過程牽扯到置信半徑(rho)，初值和終值分別由RHOBEG和RHOEND定義，它們直接影響收斂成功幾率以及總耗時。二者都為正，且顯然RHOEND<=RHOBEG。Powell建議把RHOBEG設為估計的參數最大變化量的十分之一。RHOEND控制最終X收斂時能達到的精度，顯然要求精度越高就應當被設得越小。IPRINT決定newuoa_min運行過程中在屏幕上輸出的信息量，0代表什么也不輸出，1代表只輸出最終結果，2代表運行過程中每當更新RHO的時候輸出到現在為止最佳的X及相應的函數值，3代表每次調用CALFUN的時候都輸出當前的X及對應的函數值。MAXFUN設的是最多調用CALFUN的次數，如果達到了這個值還沒正常結束就算失敗。

此例我們以X(1)=0、X(2)=0作為初猜，運行過程輸出的信息如下
  New RHO = 1.0000D-02     Current number of function evaluations =    17
  Least value of F =  3.918956916835460D+00
  The corresponding X array is:
   3.772896D-01   3.340358D+00

  New RHO = 1.0000D-03     Current number of function evaluations =    22
  Least value of F =  3.916670957635140D+00
  The corresponding X array is:
   3.356529D-01   3.331668D+00

  New RHO = 1.0000D-04     Current number of function evaluations =    26
  Least value of F =  3.916666676331397D+00
  The corresponding X array is:
   3.334374D-01   3.333242D+00

  New RHO = 1.0000D-05     Current number of function evaluations =    30
  Least value of F =  3.916666666692425D+00
  The corresponding X array is:
   3.333392D-01   3.333330D+00

  New RHO = 1.0000D-06     Current number of function evaluations =    33
  Least value of F =  3.916666666666715D+00
  The corresponding X array is:
   3.333336D-01   3.333333D+00

  At the return from NEWUOA     Total times of function evaluations =    37
  Least value of F =  3.916666666666666D+00
  The corresponding X array is:
   3.333333D-01   3.333333D+00

可見每次RHO更新時兩個X值都被輸出，且相應的函數值F也被輸出，迄今總共調用了多少次CALFUN也顯示了。到最后達到收斂時，X(1)=0.3333333、X(2)=3.333333，和我們前面手動求的解析解1/3和10/3精確一致。把這兩個值代入公式得到的值也正是最終顯示的3.916666666。

如果你想節約耗時可以把RHOEND設大，這樣正常結束時調用CALFUN的總次數會明顯變少，但會發現優化出的參數精度也有所打折扣。一般來說需要較精確結果時用1E-6是比較適合的。

當前被極小化的函數很簡單，所以用(0,0)這個初猜就得到了想要的結果，然而有時候被極小化的函數可能有不止一個極小點，如果想找全，或者找全局最低的，顯然就需要考慮不止一個初猜了。可以結合比如Differential Evolution (DE)等全局最小化算法使用，諸如J Cheminform, 8, 57 (2016)這篇文章就把DE和NEWUOA相結合來優化電負性均衡方法(EEM)電荷的參數。

3 例：單變量求解

本例我們要對下面的方程求解x

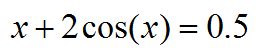
如果以極小化的思想來考慮，實際上這就等于對|x+2cos(x)-0.5|進行極小化。因此此例的代碼應當這樣寫：

PROGRAM test_newuoa
use newuoa_module
implicit real*8 (a-h,o-z)
real*8,allocatable :: X(:)
external :: CALFUN
  
nvar=1
allocate(X(nvar))
X(1)=0
call newuoa_min(CALFUN, X, RHOBEG=0.1D0, RHOEND=1D-6, IPRINT=1, MAXFUN=50000)

END PROGRAM

subroutine CALFUN(X,F)
real*8 :: X(:),F
F=abs(X(1)+2*cos(X(1))-0.5D0)
end subroutine

由于這次用了IPRINT=1，所以就只有最終結束時的信息輸出了：
At the return from NEWUOA     Total times of function evaluations =    24
Least value of F =  2.144288913097370D-08
The corresponding X array is:
-8.379604D-01

結果為x=-0.83796，此時方程的求解精度可見已經很好了，x+2cos(x)與0.5之間僅相差2.1442889E-8。

4 總結

本文簡單介紹了實現NEWUOA局部極小化算法的Fortran子程序的使用，通過實例，充分體現出使用這種算法相當便利，值得大家在平時的研究中嘗試使用。此算法不僅可以用于參數較少的情況，用于甚至含有幾百個參數的情況也同樣可以。但是參數越多時，達到收斂所需計算函數值的次數就會相應地明顯越多。另外，如果被優化的函數已經有解析梯度計算代碼了，那么NEWOUA的價值就不大了，因為此時用BFGS達到收斂所需的代價一般會更少。總的來說，筆者感覺此算法目前受到的關注程度相對于其價值來說還偏低，以后估計會受到越來越多的重視。順帶一提，Powell還開發過用于帶約束條件的無需導數的局部極小化子程序，見https://zhangzk.net/software.html。