振動分辨的電子光譜的計算
注:本文內容比較適合Gaussian09,而對于Gaussian16,本文的某些描述已經過時,做法也不是最好的。
振動分辨的電子光譜的計算
文/Sobereva @北京科音
First release: 2014-Feb-24 Last udpate: 2016-Apr-15
1 原理
表面上看,光電子能譜、UV-Vis都只是電子態之間的變化的光譜(本文只討論UV-Vis吸收光譜),吸收峰來自于電子態之間的躍遷。但是實際上每個電子態還對應諸多振動模式。比如從A電子態向B電子態躍遷的光譜,只要有對應頻率的光射進來,電子實際上就會從A的振動基態躍遷到B的各種振動態上,它們的躍遷能是不同的。因此,一個電子態躍遷的峰,如果將光譜分辨率增加來獲得精細結構,就會看到它是由許多與振動相關峰構成的。這稱為振動分辨的電子光譜(Vibrationally-resolved electronic spectra)。
在0K下體系會處于振動基態。而在有限的溫度下,A的振動激發態也會有一定分布,故也可以從A的振動激發態躍遷到B的各個振動態上。根據波爾茲曼分布,求出A的各個振動態的分布比例,將A的每個振動態向B躍遷的光譜進行權重疊加,就是實際溫度下觀測到的振動分辨的電子光譜。因此,振動分辨的電子光譜對溫度的依賴性是可以理論計算的。
理論計算振動分辨的電子光譜需要考慮|電子基態v=0>到各種|激發態v=?>的"電子+核"波函數Ψ間的躍遷,v代表振動量子數,0對應振動基態。在基態和激發態任務中做振動分析分別得到這兩個電子態下的各振動能級,并求差值,就得到了振動分辨的電子光譜中涉及的各種態之間的躍遷能。但光知道這是沒用的,為了做出圖來,我們關鍵要求的是每個這樣的躍遷的振子強度,這就要知道各個Ψ之間的躍遷偶極矩,振子強度正比于躍遷偶極矩的模方。在BO近似下,躍遷偶極矩<Ψ'|μ|Ψ''>可以分離為電子波函數φ和核波函數ψ部分:<Ψ'|μ|Ψ''>=<ψ'|μ_e|ψ''>,其中μ_e為電子躍遷偶極矩<φ'|μ|φ''>.
μ_e顯然是依賴于核坐標的,可以相對于激發態平衡結構進行Taylor展開,對它的處理導致了<Ψ'|μ|Ψ''>計算的三種方法:
(1)FC(Franck-Condon)近似:μ_e只取Taylor展開的第一項,因此μ_e是個常量,即激發態平衡結構時的電子躍遷偶極矩。對于亮態的研究,通常這個假設已經足夠給出合理結果了。
(2)HT(Herzberg-Teller)方法:只取Taylor展開的第二項,μ_e故為核坐標的函數。通常不單獨用這個方法,因為結果肯定和實際對不上,畢竟Taylor展開的第一項是最重要的。單獨使用HT的場合僅在于討論Herzberg-Teller效應對振動分辨的電子光譜的影響。不過,有的時候兩個態之間由于電子態對稱性的原因從電子躍遷偶極矩上看是嚴格躍遷禁阻的,但是若用比如HT方法把核振動也考慮進去后,兩個態之間躍遷偶極矩就不再為0了,這使得躍遷有一定(但很小)的幾率能夠發生。所以如果要研究很弱的躍遷,特別是暗態,必須考慮HT。
(3)FCHT方法:即FC和HT部分都算上,把Taylor展開的第一項(常數項)和第二項(一階校正)都考慮。這樣的結果適用范圍顯然比FC近似要寬。
PS:FC原理、FC因子(或稱FC積分)、FC近似不要搞混,雖然有關,但是具體說的問題不同。FC原理是指的電子躍遷過程很短暫,核坐標來不及改變。FC因子是指的基態振動波函數和激發態振動波函數之間的重疊積分的平方。而FC近似則是計算振動分辨的電子光譜中用到的躍遷偶極矩的一種簡化處理方式,假定μ_e為常量而不受核坐標影響。
非線型多原子分子中有3N-6個簡正振動模式,諧振子模型下它們之間可以視為獨立的,即體系振動波函數可寫為每種振動模式的波函數的乘積。若每個振動模式的振動量子數v都為0,那么體系就處于振動基態。如果一種振動模式v>0,或者多個振動模式同時v>0,那么體系就處于振動激發態。這部分詳細介紹可參見《淺談VSCF求解分子振動問題》(http://www.shanxitv.org/203)。由于v在諧振模型下是沒有上限的,再加上這些振動模式的激發態之間可以有各種組合,因此電子激發態的振動態數目甚巨,把基態到所有這些態的振子強度都考慮是不可能的,計算量太大。好在如果兩個態之間的FC因子如果很小,那么可知它們之間的躍遷偶極矩也會很小,因此對光譜圖沒什么影響,從而可以忽略。另外,也可以指定光譜的研究范圍,如果兩個態之間的能量差超過這個范圍,那么也不必去計算它們間的振子強度。FCClasses是一種系統的預先篩選方法,會事先進行估計,并對躍遷進行分類,只算對實際光譜重要的態之間的躍遷。篩選閾值對應于計算量,一般只需要通過調節要算的積分數目這一個參數就夠了,屬于黑箱方法。
2 利用Gaussian09進行計算
Gaussian09開始可以利用Freq關鍵詞計算振動分辨的電子光譜,其實就是把專門分析這個問題的FCClasses程序(http://village.pi.iccom.cnr.it/Software)給嵌入進去了。計算激發態的步驟用CIS或TDDFT都可以。雖然原理上計算振動分辨的電子光譜可以用非諧振模型,但是目前只支持諧振頻率下計算振動分辨的電子光譜,因為非諧振效應需要考慮三階或更高階導數,Gaussian的激發態計算做不到這一點(CIS能做二階解析導數,TD只能做一階解析導數)。
下面以苯甲醚為例進行說明如何計算S0->S1的振動分辨的電子光譜。
用下面的輸入文件優化S1激發態并做振動分析,saveNM關鍵詞使得激發態振動信息存到chk里,并且產生前面討論的FC方法計算μ_e時需要的激發態平衡結構的電子躍遷偶極矩。想要研究第幾個電子激發態,root就寫幾。
%chk=C:\gtest\anisole_exc.chk
# cis(root=1)/6-31G* opt freq=saveNM
anisole S1
0 1
C 2.28445000 0.32691600 0.00003800
C 1.34343300 1.38142800 -0.00010400
C -0.03741900 1.09055200 -0.00003400
C -0.44320000 -0.26595700 -0.00005800
C 0.49751700 -1.32326400 -0.00002000
C 1.87678500 -1.02037200 0.00017600
H 3.33003700 0.56133100 -0.00002300
H 1.67739200 2.39758400 -0.00018600
H -0.75550500 1.88022800 0.00018000
H 0.12880400 -2.32514600 -0.00027400
H 2.60234200 -1.80568700 0.00035800
O -1.73605800 -0.64937600 -0.00027400
C -2.82140400 0.30027500 0.00020300
H -3.71931200 -0.29382400 0.00075700
H -2.78766600 0.92165900 0.88463800
H -2.78859800 0.92139000 -0.88445500
然后用下面的輸入文件優化基態,并作基態的振動分析。freq=FC任務會使用FC方法基于當前的S0態的振動信息和剛才S1態的chk文件中的振動信息來計算S0的振動基態到S1的各個振動態之間的躍遷能、躍遷偶極矩,并換算成振子強度
%chk=C:\gtest\anisole.chk
# hf/6-31G* opt freq=FC nosymm
anisole S0
0 1
C -2.27936800 0.32609200 0.00008100
C -1.34379900 1.33903700 -0.00003400
C 0.01378100 1.05103000 -0.00016100
C 0.43663600 -0.26434700 -0.00020100
C -0.50250800 -1.28814500 -0.00003400
C -1.84702200 -0.99409200 0.00014300
H -3.32624700 0.55310300 0.00026000
H -1.66092300 2.36324200 0.00002000
H 0.71962800 1.85453200 -0.00023700
H -0.14729200 -2.29705700 -0.00003400
H -2.56259500 -1.79229300 0.00028200
O 1.75151800 -0.65529700 -0.00024100
C 2.80692300 0.31779600 0.00026800
H 3.72320000 -0.24943200 0.00040700
H 2.76733600 0.94326200 -0.88309400
H 2.76687800 0.94280000 0.88395800
C:\gtest\anisole_exc.chk //剛才的激發態freq=saveNM任務的chk文件
FC計算過程中,在輸出各種躍遷方式前會先輸出0-0躍遷(S0振動基態->S1振動基態)能量
Energy of the 0-0 transition: 47860.6879 cm^(-1)
實際上這個值只要自行把激發態和基態的包含ZPE的能量相減就能得到。激發態計算的輸出中會看到
Sum of electronic and zero-point Energies= -344.222064
基態計算的輸出中會看到
Sum of electronic and zero-point Energies= -344.440134
故(-344.222064+344.440134)*219474.6363=47860 cm^-1
輸出中諸如
Initial State: <0|
Final State: |15^2>
DeltaE = 1683.4671 | TDMI**2 = 0.1337E-01, Intensity = 0.4341E-01
就是指從S0的振動基態躍遷到S1的振動激發態的情況。這個振動激發態對應于15號振動模式處于v=2的情況。DeltaE是躍遷能,不是絕對值,而是相對于0-0躍遷能的數值。TDMI是躍遷偶極矩的模的平方。
再比如這種情況
Initial State: <0|
Final State: |26^1;17^1>
這里的S1的振動激發態是由26號振動模式處于v=1且17號振動模式也處于v=1的情況組合而成的。
最后Gaussian會輸出通過高斯函數展寬模擬出的光譜
+------------------+
| Final Spectrum |
+------------------+
Axis X = Energy (in cm^-1)
Axis Y = Intensity
------------------------------------------------------------
...略
47476.6879 0.247451D-02
47484.6879 0.311828D-02
47492.6879 0.391045D-02
47500.6879 0.488005D-02
47508.6879 0.606049D-02
47516.6879 0.748991D-02
47524.6879 0.921152D-02
...略
對這兩列數據用origin直接作圖即可,就是振動分辨的電子光譜了,如下圖黑線所示。圖中最高的峰對應于0-0躍遷。
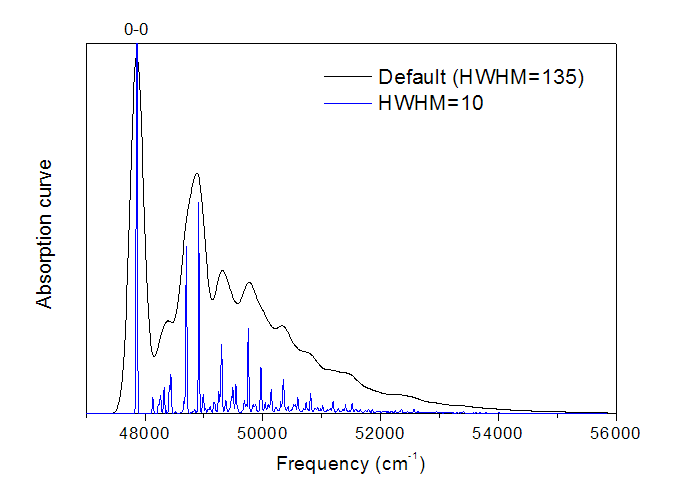
將實驗光譜和計算的光譜相互疊合,然后考察各種振子強度較大的躍遷方式的能量和強度,就能對實驗光譜的峰的本質進行指認了。
3 額外的參數
基態計算時如果用freq=(FC,ReadFCHT),則會讀取控制計算的額外參數,見Gaussian手冊Freq關鍵詞的末尾部分。比較重要的有
MaxOvr:激發態的振動量子數最大考慮到多少,默認是20。對于幾何變化較大的電子躍遷來說,會涉及到較高量子數的振動激發態,光譜范圍會比較寬,此時若不設大這個值,光譜就會不完整。
MaxInt:每一類躍遷要計算的積分數,以百萬為單位,默認為100,即10^8。FC/HT/FCHT計算的耗時不在于體系大小、基組、理論方法,而僅在于要算的積分數。因此這個值設得越大,所得光譜越準,但計算量也越大。
SpecHwHm:計算結果展寬成光譜時用的半高半寬,默認為135 (cm-1)。
PrtInt:默認為0.01,即曰如果躍遷模式的振子強度大于0-0躍遷的振子強度的1%,就在輸出文件中輸出這個躍遷模式。
DoTemp:光譜計算時是否考慮溫度,寫上DoTemp則考慮溫度。默認是0K下的,故初始態只考慮電子基態的振動基態。注意這個關鍵詞雖然存在,但是在Gaussian中并不生效。
NORELI00 SPECMIN=37900 SPECMAX=42000:這么寫代表只計算躍遷能為37900cm^-1到42000cm^-1的部分。
SPECRES:默認為8(cm^-1)。諸如上例的輸出看到的,47476.6879、47484.6879、47492.6879...彼此間間隔都是8。數值越小光譜精度越高,但是計算也會越耗時。
PrtMat:如果設為1,則會輸出Duschinsky矩陣J;如果設為2,則會輸出位移矢量K。
(注:Duschinsky旋轉或者稱Duschinsky混合效應表現的是電子躍遷使得基態振動模式發生了線性混合(旋轉)而產生激發態振動模式,表達為Q''=J*Q'+K。Q''_i和Q'_i分別代表電子激發態和電子基態的第i個簡正振動坐標。如果基態和激發態振動模式完全一致,則J是單位矩陣,表示沒有混合。J偏離單位矩陣若比較明顯,說明激發態振動模式需要通過基態振動模式的顯著的混合來表現)
這些額外參數在輸入文件中的位置是
[分子坐標]
空行
MaxInt=200 SpecHwHm=1 MaxOvr=100...
空行
[激發態chk文件路徑]
我們往往需要不同的上述參數下的光譜結果。在重新計算時,為了節約時間,可以用readfc來直接讀取chk文件里已經有的Hessian。例如,我們重新算上一節的例子,這次需要SpecHwHm設為10時的結果,輸入文件可以這么寫
%chk=C:\gtest\anisole.chk
# hf/6-31G* geom=check guess=read freq=(readfc,FC,readFCHT) nosymm
anisole S0
0 1
SPECHWHM=10
C:\gtest\anisole_exc.chk
將結果繪制的圖像,就是前面的圖中的藍線,可見細節變得更清晰了。可以認為HWHM越大,就對應于分辨率越低的光譜,曲線就越平滑,振動效應在光譜中表現得越模糊。如果HWHM設得很大,這部分吸收就連成一個大的吸收峰了,就不叫“振動分辨”的電子光譜了。
另外,眾所周知諧振頻率和非諧振頻率是有一定差異的,通常用頻率校正因子來修正諧振頻率。利用SclVec關鍵詞還可以對基態和激發態的諧振頻率進行校正,來近似得到非諧振模型的振動分辨的電子光譜,例子見Vibrationally-resolved electronic spectra in GAUSSIAN 09(idea.sns.it/files/idea/docs/vibronic_spectra_G09-A02.pdf)。具體來說是自己提供非諧振計算的電子基態的各個振動頻率(G09中支持PT2方法得到非諧振頻率),與當前的諧振模型計算的結果相除,就得到了每個振動模式對應的校正因子。通過基態的每個振動模式的校正因子,按照Duschinsky矩陣進行混合,就得到了激發態每個振動模式的校正因子了。當然了,直接對激發態做非諧振計算得到非諧振頻率顯然更準確,但是非諧振計算需要高階導數,對于激發態來說難于實現,所以只能用這種方法間接地通過基態頻率校正因子估算出激發態振動頻率的校正因子了。
4 其它
前邊討論的和G09默認計算的都是吸收光譜,G09也能算振動分辨的發射光譜。輸入文件和前面的例子一樣,但是第二步即基態計算時寫成freq(FC,emission),注意此時不支持HT、FCHT方法。G09也能算電離過程中的振動分辨的光譜,也就是把激發態計算改成陽離子計算即可。G09里CIS和TDDFT都能用于FC,但是HT或FCHT只能用CIS,而且做CIS時必須用freq=numer,因為只有這樣才會產生躍遷偶極矩導數信息。
對于很多體系,只要激發態和基態的平衡結構相差有些大,程序就會提示 ERROR: The Franck-Condon factor corresponding to the overlap integral between both vibrational ground states is too small: |<0’|0">|?2 = x。這可以用readFCHT讀取ForceFCCalc關鍵詞強行進行計算,默認是x<10^-4就不計算了。出錯的原因本質上是這種情況下FC方法不是很合用,幾何變化太大。