Multiwfn的軌道定域化功能的使用以及與NBO、AdNDP分析的對比
文/Sobereva @北京科音
First release: 2017-Jun-5 Last update: 2021-Sep-10
摘要:本文首先介紹分子軌道定域化的含義,然后介紹在Multiwfn中做軌道定域化的基本步驟。然后通過5個例子,講解如何基于定域化分子軌道討論、分析體系的電子結構,并且與流行的AdNDP方法和NBO方法進行對比。本文的實例體現出軌道定域化的重要應用價值,也鮮明反映出NBO分析對于電子結構復雜、牽扯多中心離域的體系結果經常不靠譜,一定要慎用,最好不用。
1 談談分子軌道的定域化
我們做一般量子化學計算產生的分子軌道叫正則分子軌道(Canonical MO),它們是Fock或者KS算符的本征函數,本征值就是軌道的能量。下面說的MO都是指正則分子軌道。MO往往有很強的離域性,也就是說往往MO涉及很多原子,因此與化學鍵沒法一一對應。所以,直接通過分子軌道討論成鍵問題,多數情況毫無用處。有不少文章、畢業論文擺出來一堆MO圖,但要么沒怎么討論(純粹是湊數據),要么就是瞎討論。例如,下面的圖是丁烷的兩個MO圖,完全離域在整個分子。顯然從這種MO圖上根本沒法直接對應眾所周知的此體系存在C-C、C-H sigma鍵的事實。
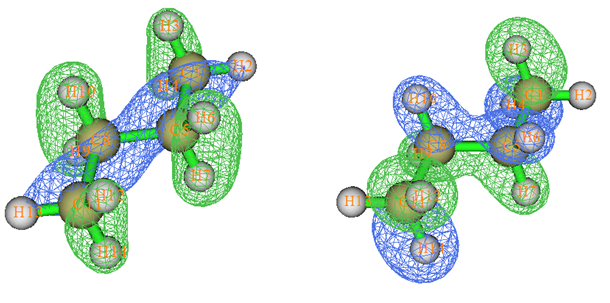
要想將軌道與化學鍵直接聯系起來,需要做軌道定域化,將MO變換成定域化分子軌道(localized MO, LMO)。軌道定域化相當于對占據的MO做酉變換,從而產生出相同數目的離域程度盡可能低的占據軌道。描述體系波函數的Slater行列式無論是由原先的MO所構成,還是由變換后的LMO所構成,所對應的體系各種可觀測量,如體系能量、電子密度、靜電勢等等,都是不變的。還有很多量雖然是不可觀測的,但也不受這種變換所影響,比如電子定域化函數(ELF)。
通常做軌道定域化只需要把占據軌道定域化,因為可觀測性質、成鍵問題等等都是只與占據軌道相聯系。如果也想把空軌道做定域化,那么也可以再把空軌道以相同方式做酉變換來得到離域程度盡量低的空軌道。將空軌道做定域化主要是用于一些基于定域軌道的電子相關方法,比如知名的但如今用處不大的Local MP2 (LMP2)。由于空軌道比占據軌道數目多得多,將它們也定域化耗時會增加甚巨,而且空軌道對我們分析體系的性質沒影響,所以通常我們只把占據軌道定域化就夠了。
軌道定域化有許多做法。比較知名的是
(1)Edmiston-Ruedenberg定域化:1963年提出。通過最大化軌道的自互斥能(亦即最小化軌道間的互斥能)來實現定域化。缺點是耗時很高,而且得算復雜的雙電子積分,而且又沒額外好處,故很不推薦。
(2)Boys定域化:1960年提出。應用比較廣泛,通過最小化軌道涵蓋的空間范圍來定域化。需要利用偶極矩積分。
(3)Pipek-Mezey定域化:1989年提出,它通過最大化Mulliken原子布居數的平方和達到定域化目的,編程實現頗為簡單,只需要重疊積分,而且耗時很低,被廣泛使用。后來還有人提出基于其它布居分析方法來做Pipek-Mezey定域化。
(4)NLMO定域化:NLMO的N是Natural的意思。這是NBO開發者提出的定域化方法,它將高占據(Lewis型)的NBO和低占據(non-Lewis型)的NBO以一定方式混合,從而得到整數占據的定域化軌道。由于得到NLMO軌道得先產生NBO,故此方法只有NBO程序,以及也同樣能做NBO分析的Molpro才支持。
以上方法計算過程需要迭代,迭代過程中不同軌道間不斷混合,最后使得目標函數被最大化或最小化。
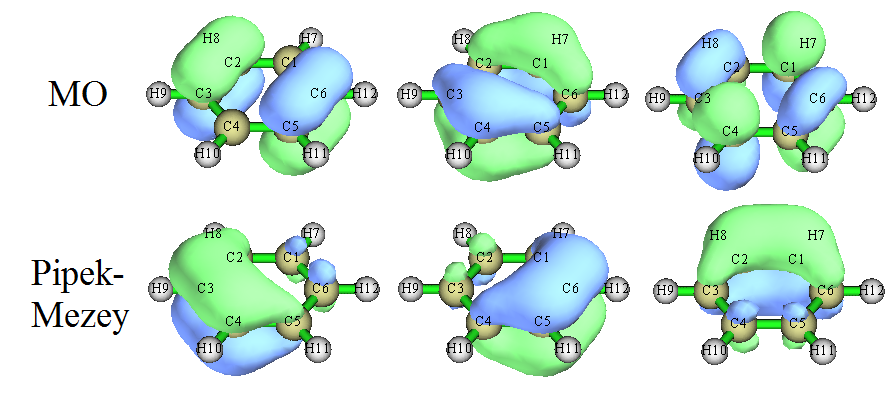
不同的軌道定域化方法得到的LMO圖形有一定差異。對于雙鍵的描述,不同方法差異很大,比如下圖是乙烯的C=C鍵,Pipek-Mezey產生的LMO保留了sigma和pi分離的特征,然而Boys定域化則是以兩個香蕉鍵來描述這個雙鍵。
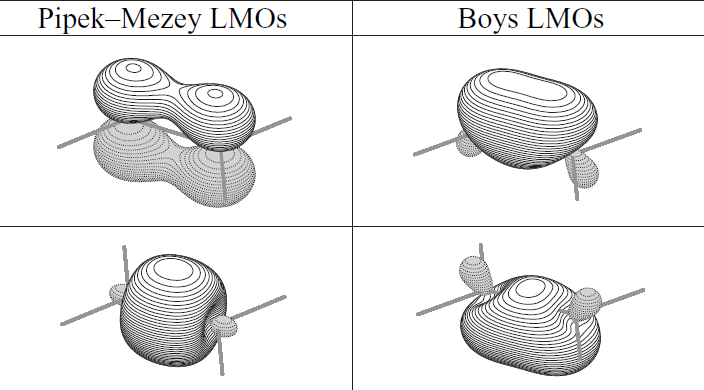
這兩種雙鍵的描述形式沒法說誰對誰錯,從物理角度上是等價的描述,但是顯然Pipek-Mezey方法更好一些,結果更符合化學觀念,更便于討論。
原始的基于Mulliken布居的Pipek-Mezey方法的一個缺點是不適合有彌散函數的情況,因為Mulliken布居在有彌散函數的時候結果缺乏意義。這點在《原子電荷計算方法的對比》(http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml)、《分子軌道成分的計算》(http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract340458.shtml)里面都談過。不過近年來也有人提出基于IAO (Intrinsic Atomic Orbitals)代替原始基函數來做Pipek-Mezey定域化的做法(得到的軌道稱為IBO),這使得彌散函數不會對結果有什么影響,因為IAO的意義和NBO框架中的極小集NAO很相似,從原始基函數變換成IAO的過程中已經把彌散函數的不良影響充分去除了。將其它不怕彌散函數的布居分析方法(如Hirshfeld、Becke)結合Pipek-Mezey方法使用也可以使定域化結果不會因為有彌散函數而受到不良影響。
眾所周知,NBO軌道的離域程度非常低,這點很像LMO。實際上從等值面圖形上會看到NBO比LMO的定域程度其實更高,但NBO的占據數卻不像LMO那樣是整數,因此NBO軌道不能算做LMO中的一種。實際上,將高占據的NBO和低占據的NBO混合成前述的NLMO之后,就會發現NLMO比對應的NBO的離域程度要高一些,而占據數也變成了LMO要求的整數。產生NBO的過程和Edmiston-Ruedenberg、Boys、Pipek-Mezey定域化方法有本質的不同,NBO軌道是搜索出來的。對于尋找雙中心、三中心軌道,NBO程序會循環不同的兩個或三個原子組合,檢驗對應的塊密度矩陣的本征值是否超過閾值來判斷算不算找到了它們之間的成鍵軌道,NBO程序里的具體實現其實比這里說的復雜得多,有興趣者可以看看NBO分析資料匯總里的文章:http://bbs.keinsci.com/forum.php?mod=viewthread&tid=102。需要特別強調的是,NBO的這種搜索方式非常不natural,對于成鍵方式典型的有機體系還行,但是對于電子結構復雜的體系嚴重不科學!試圖用NBO討論這些體系的電子結構特征完全是坑爹,經常會得到離譜的結論!有很多人拿著NBO輸出的荒謬的結果還各種胡亂討論一番,純粹是以訛傳訛。后文我們對比LMO和NBO軌道就會明顯看到這一點。
Multiwfn支持的AdNDP分析方法在《使用AdNDP方法以及ELF/LOL、多中心鍵級研究多中心鍵》(http://www.shanxitv.org/138)一文中做過充分介紹,強烈建議作者閱讀,本文不再詳述。AdNDP所做的事也是搜索出離域程度比MO更低的軌道,從而便于展現和討論體系中不同區域共享電子的情況。AdNDP既可以搜索出NBO那樣1~3中心軌道,也可以搜索出更多中心軌道,對這類軌道我管它叫半定域化軌道。AdNDP軌道占據數和NBO軌道一樣也不是嚴格整數,因此不屬于LMO的一種。下文的例子中,我們也會對比Pipek-Mezey方法產生的LMO與AdNDP分析結果的異同。
總的來說,按照軌道離域程度的上限由低到高,有這樣一個關系:NBO-LMO-AdNDP-MO。之所以說“上限”,是因為即便MO也并非都是離域的。比如算個水,就會看到能量最低的MO完全定域在氧上。
雖然LMO、NBO、AdNDP軌道都不是Fock或KS算符的本征函數,但是我們在單電子近似框架下仍可以討論這些軌道的能量,也就是把Fock或KS矩陣從原始基函數表象變換到相應軌道的表象下,此時對角元就是各個軌道能量,例如第i軌道的能量就是第i對角元,表達式是<φi|f|φi>,這里f代表Fock或KS算符。我們做NBO分析時看到的程序輸出的NAO、NBO、NLMO等軌道的能量,就是NBO對量化程序產生的Fock/KS矩陣做這么一個簡單的表象變換得到的。
2 在Multiwfn中做軌道定域化
Multiwfn做軌道定域化支持基于Mulliken、Lowdin和Becke布居的Pipek-Mezey方法,以及Foster-Boys方法。其中PM-Mulliken方法速度最快(對于只要求定域化占據軌道的情況,處理200個原子一般都沒問題),所以是默認的。PM-Mulliken和PM-Lowdin原理上不適合有彌散函數的情況,不過我實測發現有時候即便用aug-cc-pVTZ這樣帶彌散函數不少的基組,PM-Mulliken定域化占據軌道的結果還是基本合理的(但如果用d-aug-cc-pVTZ這樣帶巨量彌散函數的基組,PM-Mulliken是絕對不能用的)。如果由于特殊原因必須帶彌散函數,比如陰離子,或者被外電場極化得特別厲害的中性分子(比如《一篇文章深入揭示外電場對18碳環的超強調控作用》http://www.shanxitv.org/570文中就有這種情況),最穩妥的做法是改用PM-Becke或者Foster-Boys方法,這倆在原理上都完全不怕彌散函數,但它倆都比PM-Mulliken或PM-Lowdin昂貴得多。PM-Becke尤為昂貴,對于50個原子體系結合6-31G*的情況耗時就相當高了,而Foster-Boys雖然耗時不這么夸張,但是如前所述,沒法給出比較符合一般化學直覺的sigma-pi分離的定域化軌道。對軌道定域化方法的更多介紹、討論、實現細節的說明參見手冊3.21節。另:筆者發現對于個別特殊體系結合某些基組時,即便沒帶彌散函數,PM-Mulliken方法得到的定域化軌道也不太理想,此時用PM-Becke得到的結果明顯更好。所以當你覺得PM-Mulliken結果詭異的時候也可以嘗試改用PM-Becke。
Multiwfn可以在其主頁http://www.shanxitv.org/multiwfn免費下載。不熟悉此程序的請參看《Multiwfn入門tips》(http://www.shanxitv.org/167)、《Multiwfn波函數分析程序的意義、功能與用途》(http://www.shanxitv.org/184)。
把含有基函數信息的輸入文件(如fch、molden等,不清楚的話看《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》http://www.shanxitv.org/379)載入到Multiwfn里,然后進入主功能19就可以做軌道定域化。可以選擇只定域化占據軌道,還是把占據軌道和空軌道分別定域化。對于非限制性開殼層體系,程序會把alpha和beta部分分別做定域化。此功能不支持限制性開殼層波函數。
定域化過程中會顯示迭代細節,當Delta P降到設定的閾值以下時即宣告收斂。默認的閾值,以及默認的循環次數上限在這個功能的界面里會直接看到,可以自己設,一般不需要改。
默認設定下,當迭代收斂后,程序會通過Hirshfeld方法(不熟悉者看《談談軌道成份的計算方法》http://www.shanxitv.org/131)計算得到的LMO中的各個原子的成份,然后由此對LMO的特征進行指認,判斷是單中心、雙中心還是離域到更多中心的LMO,便于用戶快速找到自己感興趣的軌道。然后程序自動把波函數導出到當前目錄下的new.fch中。默認情況下,程序會再把這個文件載入,此時內存里的軌道波函數就變成了LMO了,可以直接做進一步分析,如考察軌道圖形、計算軌道成份等。注意此時LMO的占據數是對的,但能量還是原先MO的能量。
如果要得到LMO的能量,應當在軌道定域化界面里選擇-4 If calculating and printing orbital energies。計算LMO的能量需要利用Fock矩陣,你需要選如何獲得Fock矩陣,有兩個選項:
(1)直接基于分子軌道能量和系數矩陣反解出來Fock矩陣。通常建議用這個方式,最為省事。但是如果使用了大量彌散函數,量子化學程序可能會自動去除一些線性相關基函數,這個時候就沒法用這個做法了,只能用下面的方法
(2)從特定文件里讀取。可以從記錄Fock矩陣的文本文件里讀取,也可以從.47文件里讀取(Gaussian可以直接產生),也可以從ORCA輸出文件里讀取,等等,詳情見Multiwfn手冊附錄7。
為了便于展現LMO的分布特征,Multiwfn可以計算出所有LMO的中心位置并在圖上顯示出來,這使得哪里有LMO出現一目了然。第i個LMO的中心位置計算為<LMO_i|r|LMO_i>,r是電子坐標算符。
下面我們通過幾個實際體系,演示一下Multiwfn軌道定域化的使用,并對結果進行討論,與此同時還會與NBO或AdNDP軌道進行一些對比。在《使用Multiwfn通過LOBA方法計算氧化態》(http://www.shanxitv.org/362)這篇文章中使用的LOBA方法是基于定域化軌道的計算氧化態的方法,文中已經利用到了Multiwfn的這個軌道定域化功能,建議大家也看看。
下文涉及的各種文件都可以在此處下載:http://www.shanxitv.org/attach/380/file.rar。
本文使用G09 D.01計算。若未注明,NBO分析是用的G09自帶的NBO3.1做的。本文用的NBO6是2017年5月買的版本。
3 實例1:1,3-丁二烯
這個例子我們對1,3-丁二烯做分子軌道定域化分析,寫以下輸入文件
%chk=C:\butadiene.chk
# B3LYP/6-31G*
Generated by Multiwfn
0 1
C 0.60180003 1.75050480 0.00000000
H -0.32508753 2.31854834 0.00000000
H 1.52387750 2.32224216 0.00000000
C 0.60180003 0.41067144 0.00000000
H 1.55113518 -0.12465745 0.00000000
C -0.60180003 -0.41067144 0.00000000
H -1.55113518 0.12465745 0.00000000
C -0.60180003 -1.75050480 0.00000000
H 0.32508753 -2.31854834 0.00000000
H -1.52387750 -2.32224216 0.00000000
計算之后用formchk把chk文件轉換成butadiene.fch。然后啟動Multiwfn,輸入
butadiene.fch
19 //軌道定域化
1 //只定域化占據軌道
由于體系很小,一瞬間就算完了,經過了幾輪迭代就收斂到了要求的閾值了。屏幕上輸出了各個定域化軌道的基本特征以便于找到用戶感興趣的軌道,并且當前目錄下產生了new.fch,里面記錄了占據的LMO和非占據的MO。如屏幕的提示所示,Multiwfn已經又自動載入了此文件,所以當前內存里的占據軌道已經是定域化后的了。我們按0返回主菜單,然后進入選項0觀看剛得到的LMO。
把所有占據軌道,即1號到15號軌道挨個看一遍,先會看到各個收得很緊的內核軌道,然后是各種C-C、C-H sigma軌道,最后兩個軌道是邊緣的C=C鍵的pi軌道,如下所示:
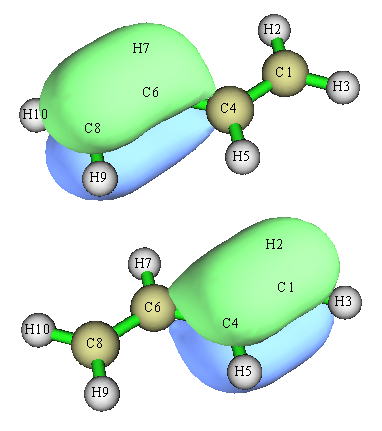
如果不做定域化,我們會看到占據的pi軌道是離域在分子整體,不好討論。從定域化后的這兩個pi軌道上,我們看出,兩邊的C-C之間有明顯的pi鍵。但是,這絕不意味著中間的C-C之間沒有絲毫pi鍵特征,如果我們用Multiwfn主功能9來計算Mayer鍵級(主要體現原子間共享電子對數)和拉普拉斯鍵級(看JPCA,117,3100的介紹),會看到中間的C-C鍵的這兩種鍵級分別為1.138和1.313,都大于1,因此兩種鍵級都表明中間的C-C并不僅僅有sigma鍵,還有一定的pi鍵特征。但如果計算邊緣C-C鍵的鍵級,則Mayer鍵級和拉普拉斯鍵級分別為1.872和1.917,接近雙鍵的形式鍵級2.0,說明其pi鍵特征遠強于中間的C-C鍵。
此例體現出,定域化軌道會著重把體系中最主要的共享電子的特征展現出來,而共享電子程度較弱的作用,就沒有相應的定域化軌道與之對應了,所以此例中間的C-C鍵之間沒有與之直接對應的pi型LMO出現。
根據上面算的鍵級值,我們知道并不是看到某兩個原子之間有N個定域化軌道,就代表這兩個原子間應當視為有N重鍵。上面的軌道等值面圖是在Multiwfn默認的isovalue值0.05下繪制的,如果我們把isovalue值設小一點,比如用gview默認的0.02,那兩個軌道圖就成下面這樣了
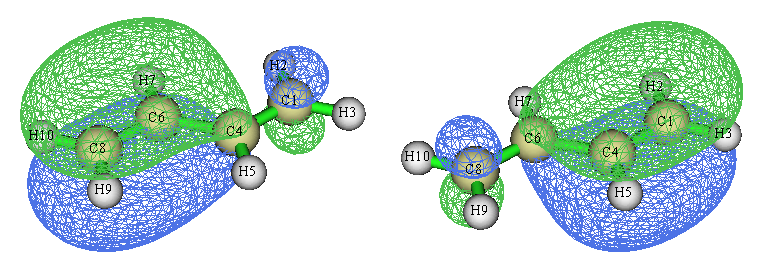
可見,這倆定域化軌道并不是100%定域在兩端的C-C鍵上的,只能說大部分對應兩端C-C鍵,而有小部分還是出現在中間C-C鍵的區域上,因此,它們在一定程度上對于中間的C-C鍵的鍵級是有貢獻的。相應地,由于這倆軌道上的電子對也并非僅被兩端的兩個碳原子共享,故不會對它們間的鍵級產生恰好1.0的貢獻。
實際上可以用Multiwfn做一下占據數擾動的Mayer鍵級分析,考察一下各個軌道對Mayer鍵級的影響。雖然Mayer鍵級并不能精確分解為軌道的貢獻,但這種占據數擾動的Mayer鍵級分析方法在實際中還是很有助于討論的。我們進入Multiwfn主功能9,選擇子功能6進入相應分析界面。我們先考察各軌道的存在對兩端的C6-C8鍵的Mayer鍵級的影響,故輸入6,8,看到結果
...(略)
11 2.00000 -0.39137 0.836985 -1.035523
12 2.00000 -0.38506 1.887136 0.014627
13 2.00000 -0.34441 1.869943 -0.002566
14 2.00000 -0.31993 1.014101 -0.858407
15 2.00000 -0.22908 1.948604 0.076096
結果表明,如果少了第11和14號LMO,C6-C8的Mayer鍵級將分別下降1.035和0.858。LMO11就是C6-C8間的sigma型LMO,LMO14就是主要涵蓋C6-C8區域的pi型LMO。可見,那個pi型LMO對C6-C8并沒法產生1.0的鍵級貢獻,而那個sigma型LMO則充分定域在C6-C8上,從而產生了1.0的貢獻。我們再輸入4,6考察各LMO對位于分子中間的C4-C6鍵的Mayer鍵級的影響,結果為
...(略)
13 2.00000 -0.34441 0.132491 -1.005149
14 2.00000 -0.31993 1.026398 -0.111242
15 2.00000 -0.22908 1.026398 -0.111242
數據也說明,13號LMO可以算是嚴格意義的C4-C6間的sigma軌道,產生鍵級貢獻約1.0。而LMO 14和LMO 15,即上面繪制的兩個pi型LMO,對于C4-C6的鍵級也有很少量貢獻。當前的例子表明,把LMO分布圖和Mayer鍵級放在一起,既能從圖形上直觀展現成鍵,又能從數值上定量討論成鍵,很有益處。ELF和LOL對于圖形化展現成鍵特征也極為有用,見《電子定域性的圖形分析》(http://www.shanxitv.org/63)。
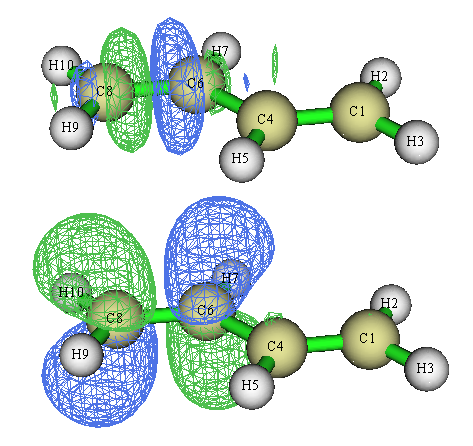
對于當前體系,進入軌道定域化界面后可以選2來讓Multiwfn同時對占據和非占據MO分別做定域化。占據軌道部分和上面得到的完全一樣,在非占據軌道當中我們可以找到sigma反鍵軌道和pi反鍵軌道,和我們根據結構化學常識所期望的圖形一致:
4 實例2:Li5+團簇
此例我們對Li5+團簇做LMO分析。上一節我們沒有讓程序產生LMO的能量,所以主功能0里顯示的能量仍然是原先的MO的能量,當前例子我們要讓Multiwfn把LMO的能量也產生,用到的Fock矩陣讓Multiwfn直接生成,這是最省事的。
啟動Multiwfn,依次輸入
Li5+.fch
19 //軌道定域化
-4 //讓Multiwfn做完定域化后計算LMO能量
1 //用基于MO的能量和系數矩陣反解出的Fock矩陣算LMO能量
1 //對占據軌道做定域化
定域化收斂后,輸出了LMO的能量信息,如下所示
1 Energy: -2.1347449 a.u. -58.0894 eV Type: A+B Occ: 2.0
2 Energy: -2.1347449 a.u. -58.0894 eV Type: A+B Occ: 2.0
3 Energy: -2.1347448 a.u. -58.0894 eV Type: A+B Occ: 2.0
4 Energy: -2.1213722 a.u. -57.7255 eV Type: A+B Occ: 2.0
5 Energy: -2.1213709 a.u. -57.7254 eV Type: A+B Occ: 2.0
6 Energy: -0.3037221 a.u. -8.2647 eV Type: A+B Occ: 2.0
7 Energy: -0.3037206 a.u. -8.2647 eV Type: A+B Occ: 2.0
當前內存中記錄的占據軌道的能量,以及導出的new.fch里的占據軌道能量都是這些新算出來的能量。由于這里沒對空軌道做定域化,所以它們的能量沒被輸出,內存里和new.fch里的空軌道的能量還是MO的。
從上面列的7個占據的LMO的能量來看,軌道分為三種,簡并度分別為3、2、2。我們用主功能0觀看軌道圖形,每種簡并的軌道只在下圖繪制其中一個,圖上標的是eV為單位的能量
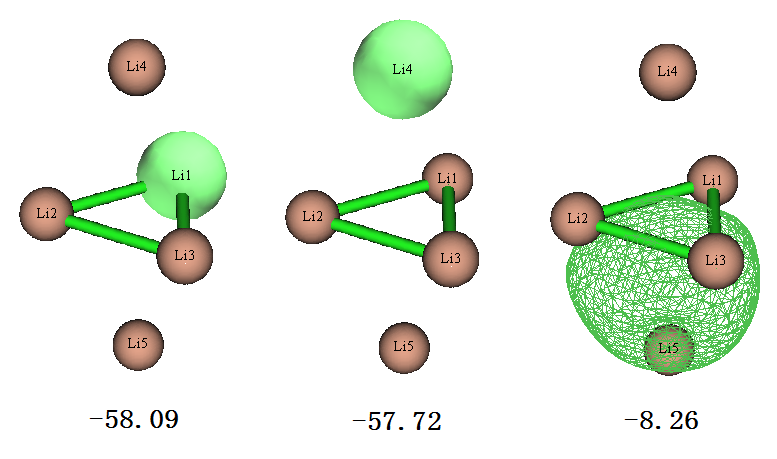
上圖第一個軌道是中間位置的Li的單中心軌道,由于其能量很低,很容判斷出這肯定是Li的1s軌道。上圖第二個軌道是上下兩端的Li的1s軌道,能量和中間的Li的軌道很接近,但畢竟所處的化學環境有所不同,所以軌道能量也有點差別。上圖第三個軌道是四個Li構成的4中心雙電子軌道(可標注為4c-2e),顯然是Li的2s電子構成的。由于本身單個原子的2s軌道能量就遠高于1s,所以這個由2s軌道組成的LMO的能量也比其它兩類LMO能量高一個數量級。
在前述的《使用AdNDP方法以及ELF/LOL、多中心鍵級研究多中心鍵》一文中我們用AdNDP方法也做過此體系的分析,得到的軌道圖形和LMO幾乎一模一樣。因此,對于一些簡單的體系,其實可以不必做操作相對麻煩的AdNDP,直接靠LMO就可以很好地討論電子結構了。
我們再看看如果對此體系做NBO分析產生的軌道是什么樣。我們用# b3lyp/6-311g(d) pop=saveNBO來計算,這樣算完了之后NBO軌道就被直接存到chk里了,轉換成fch后就可以直接用Multiwfn觀看NBO軌道了,詳見《使用Multiwfn繪制NBO及相關軌道》(http://www.shanxitv.org/134)。我們會發現能量最低的5個軌道,即Li的1s軌道,無論是軌道圖形還是軌道能量與Multiwfn的軌道定域化產生的結果十分一致,但價層NBO軌道就一塌糊涂了。從輸出信息中會看到除了CR型內核NBO軌道占據數幾乎是2.0的,其余的占據數不太接近0的NBO的占據數為
6. (0.55080) LP*( 1)Li 1
7. (0.36965) LP*( 2)Li 1
10. (0.55080) LP*( 1)Li 2
11. (0.36965) LP*( 2)Li 2
14. (0.55080) LP*( 1)Li 3
15. (0.36965) LP*( 2)Li 3
18. (0.61749) LP ( 1)Li 4
22. (0.61749) LP ( 1)Li 5
可見,NBO對價層電子,沒有給出任何成鍵信息,而假定每個原子上的價電子要么是孤對電子,要么是物理意義含糊不清的LP*電子。
默認情況下,NBO只能自動搜索單、雙中心軌道,實際上,如果用pop=nboread,然后在輸入文件末尾空一行寫上$NBO 3cbond $END,則程序還會自動搜索三中心軌道。然而,這么做了之后結果更詭異,軌道分布根本不滿足體系點群對稱性,對體系電子結構的描述完全錯誤。NBO會搜索出的兩個占據數為1.498的三中心軌道,圖形如下
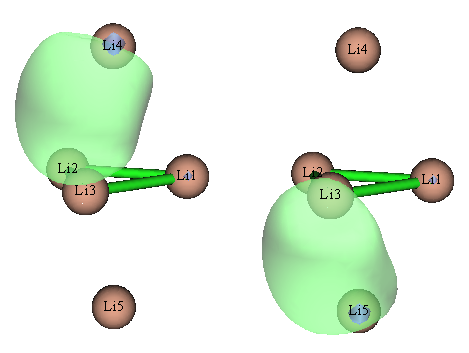
除了這兩個外,NBO還搜出Li1有兩個占據數分別為0.551和0.370的LP*軌道。
NBO6相對于NBO3.1在默認的軌道搜索規則上做了很大修改,但搞出來的NBO軌道也是完全沒法用來討論Li5+的成鍵本質。雖然NBO6已經允許在$CHOOSE中指定>3中心的定向搜索,但是卻不能自動搜索>3中心軌道。所以對于存在>3中心軌道的情況,NBO幾乎是沒有絲毫用處的,用了只會被誤導。若是信誓旦旦地拿這些NBO軌道去說事,明顯是坑爹。然而很多初學者缺乏最基本的理論常識,程序輸出什么結果就拿什么結果討論,胡亂解釋一番。盲目用NBO危害實在太大。
對此體系如果嘗試用NBO3.1做NLMO分析,程序會報錯,這是NBO3.1的bug所致。筆者也用NBO6做了NLMO分析,Li的2s軌道構成的NLMO軌道如下
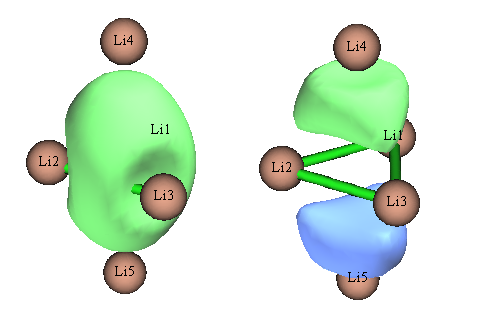
實際上,這正是Li5+能量最高的兩個占據MO的圖形,NLMO等于完全沒起到定域化效果!
5 實例3:OsO4
此例我們考察OsO4的LMO,并且也要得到軌道能量。可以使用與上一節相同的步驟在計算LMO的同時得到其能量,但這一節演示一下怎么從.47文件里讀取Fock矩陣。此體系的Gaussian輸入文件如下,算完了之后會產生C:\OsO4.47文件。
%chk=C:\OsO4.chk
# b3lyp/def2tzvp pop=nboread
B3LYP/def2TZVP opted
0 1
Os 0.00000000 0.00000000 0.00000000
O 0.98386911 0.98386911 0.98386911
O -0.98386911 -0.98386911 0.98386911
O 0.98386911 -0.98386911 -0.98386911
O -0.98386911 0.98386911 -0.98386911
$NBO archive file=C:\OsO4 $END
感興趣者可以用Multiwfn的子功能0觀看OsO4.fch里記錄的MO,會看到從MO圖形上根本討論不了此體系的成鍵特征,而必須做LMO。
啟動Multiwfn,依次輸入
OsO4.fch
19 //軌道定域化
-4 //計算LMO能量
2 //從一個文件里讀取Fock矩陣
OsO4.47 //輸入47文件的實際路徑,此文件里有Fock矩陣信息
1 //定域化占據軌道
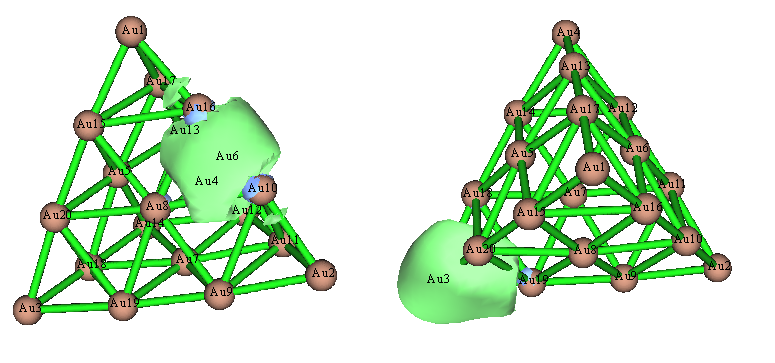
我們仔細觀看定域化后的占據軌道,會發現軌道是滿足體系對稱性的,Os和每個氧間都有兩個pi軌道和一個sigma軌道,并且還能看到每個氧都有一個孤對電子軌道和一個內核電子軌道。下面把Os與其中一個氧的三個成鍵軌道和那個氧的孤對電子軌道繪制出來,數值是軌道能量(eV):
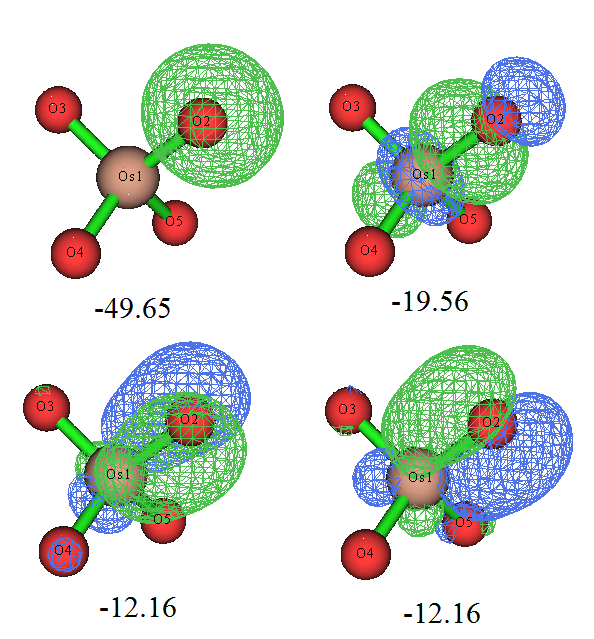
軌道圖形和我們期望的很一致,而且軌道能量也很符合化學直覺,即sigma軌道能量低于pi軌道。那個孤對電子軌道幾乎是球形的,如果用Multiwfn對它用Mulliken方法做一下軌道成分分析,也會看到它幾乎完全由S基函數構成,很容易理解這就是氧的2s軌道。本身由于2s軌道的能級顯著低于用于成鍵的2p,所以這個軌道的能量自然而然比sigma、pi軌道低得多。
雖然Os和每個O之間有3條成鍵LMO,但是也不代表它們的鍵級就是3.0,這只能認為是鍵級的上限。計算Mayer鍵級的話,發現Os和O之間的鍵級是1.720。如果同上一節做鍵級分解的話,會發現Os-O的sigma LMO對鍵級的貢獻是0.866,而每個pi LMO的貢獻僅有0.425,這可以認為這些pi軌道并不是在Os和O之間很充分共享的。我們可以在看軌道的時候把等值面數值加大,會發現在較大數值的時候,等值面幾乎都出現在氧上。如果我們用Multiwfn的主功能4對pi軌道作個填色+等值線的截面圖(相關操作參考手冊4.4節繪制平面圖的例子),可以將其分布特征看得更清楚,如下所示
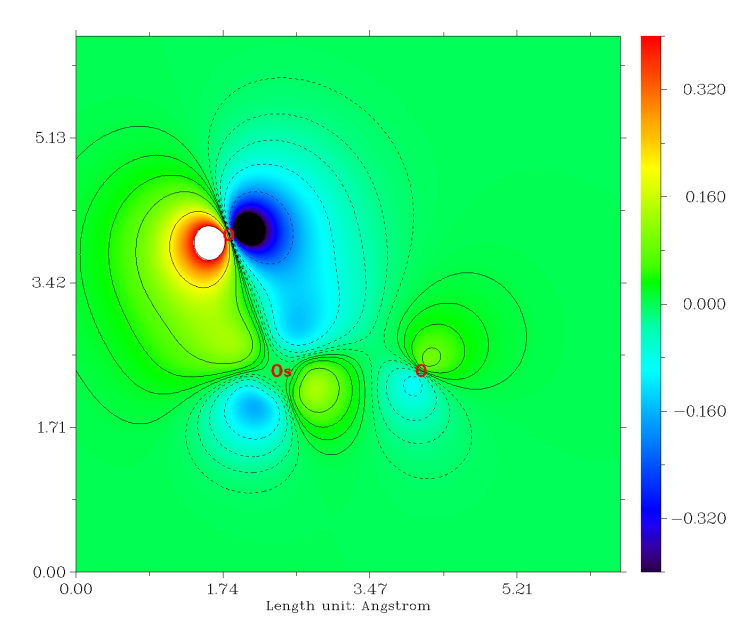
由圖可見,pi軌道大部分其實是分布在氧上的,只是一定程度上也離域到Os上,從而對O與Os的共價作用有所貢獻。如果用Hirshfeld方式做個軌道成分計算(做完軌道定域化后其實也自動在屏幕上輸出了),會發現O的貢獻高達71.7%,而Os只產生24.9%的貢獻。這么一分析,也很容易理解每個pi軌道對鍵級的貢獻是肯定達不到1.0的。
我們再看看用NBO3.1做NBO和NLMO會把這個體系描述成什么樣。做了之后會發現,大多數軌道和Pipek-Mezey定域化給出的軌道差不多,特別是NLMO與之相符得更好。但是,占據的NLMO以及高占據的NBO都有兩條軌道很離譜,見下
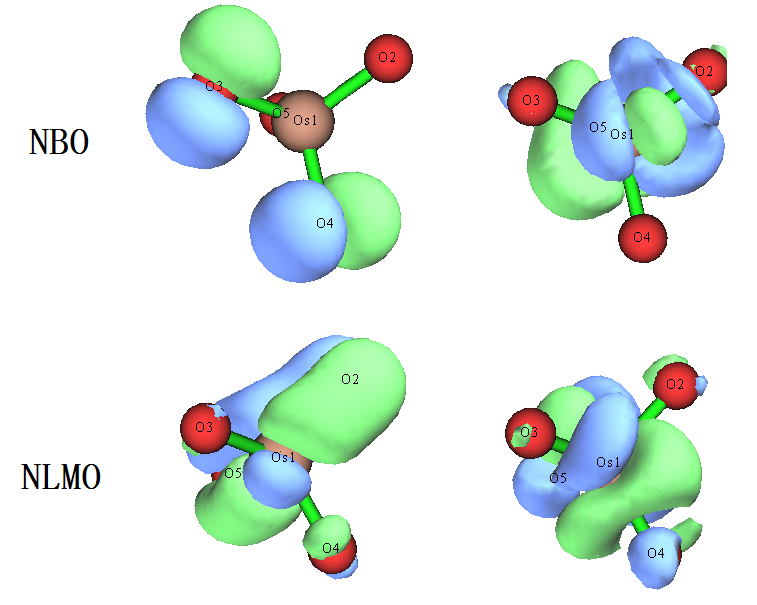
這些軌道完全沒合理體現出NBO和NLMO作為定域的軌道應有的特征,也和體系對稱性完全不符,結果根本沒法用!但其實這主要是NBO3.1搜索軌道算法很爛所致。
到了NBO6,情況得到了很大改觀。搜索出來的和每個氧的價電子有關的高占據數NBO如下所示,圖中數字是占據數
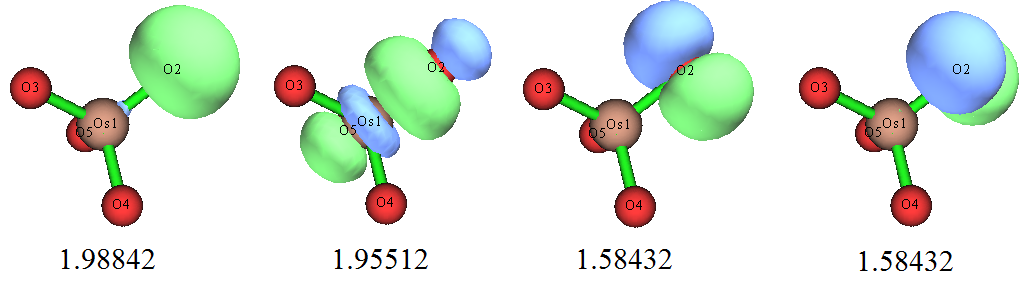
NBO6找出的這些軌道對每個氧都是一樣的,即起碼和體系對稱性相符了。然而,NBO把定域性給夸大了,之前展示的LMO軌道體現出氧與Os形成了兩個pi鍵,但在NBO里,這兩個pi鍵沒體現出來,卻被指認成了氧的孤對電子,其占據數僅有1.58,體現出這種軌道的物理意義不咋地,不夠convincing。此情況體現出NBO軌道搜索方法的內在弊端,即搜索方式、搜索閾值的設計有點太“任性”了,對于電子結構難以通過單一Lewis式描述好的情況,NBO軌道根本沒法如實展現出體系的電子結構,很容易誤導用戶。
NBO6給出的NLMO的圖形和Pipek-Mezey定域化方法得到的LMO十分一致,比NBO3.1給出的強太多,而且比NBO軌道物理意義明顯更好。因此對于電子結構復雜的情況,如果你死活非要用NBO程序不可,那么相對而言,應當用NBO6給出的NLMO來討論。
6 實例4:Au20團簇
Au20團簇的電子結構在前述的《使用AdNDP方法以及ELF/LOL、多中心鍵級研究多中心鍵》中已經充分研究過了,這里我們對Au20做Pipek-Mezey定域化軌道分析,只定域化占據軌道。操作過程和前述的一樣,就不再重述了。Multiwfn的輸入文件是文件包里的Au20目錄下的Au20.fch,在B3PW91/lanl2DZ下計算得到,由于體系比之前的大很多,所以定域化耗時也高了很多。
在AdNDP那篇博文里,無論是AdNDP軌道還是ELF等值面圖,都發現位于每個Au20頂角的四個Au原子間,以及每個棱中間的兩個Au原子之間存在顯著的共價作用。若我們觀看Pipek-Mezey定域化軌道,會發現得到了完全相同的結論,這兩種軌道如下所示
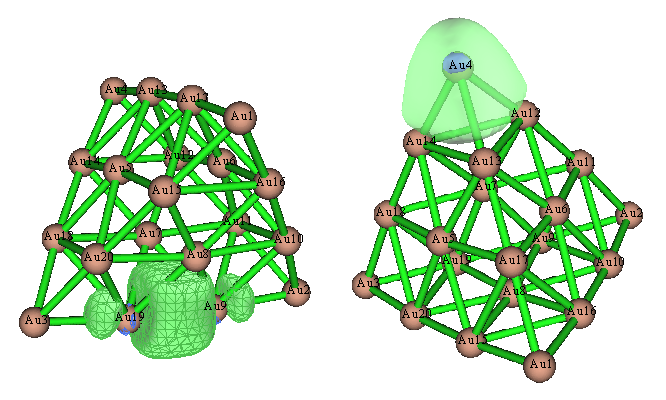
此例又一次表明,Pipek-Mezey定域化分析往往可以直接代替AdNDP分析。
由于前面我們看到NBO3.1分析往往極度不合理,這里我們就不再用NBO3.1分析了,直接看NBO6的結果。做NBO分析后,發現程序給出了一堆亂七八糟無意義的軌道,和實際電子結構完全不對應,列舉幾個:
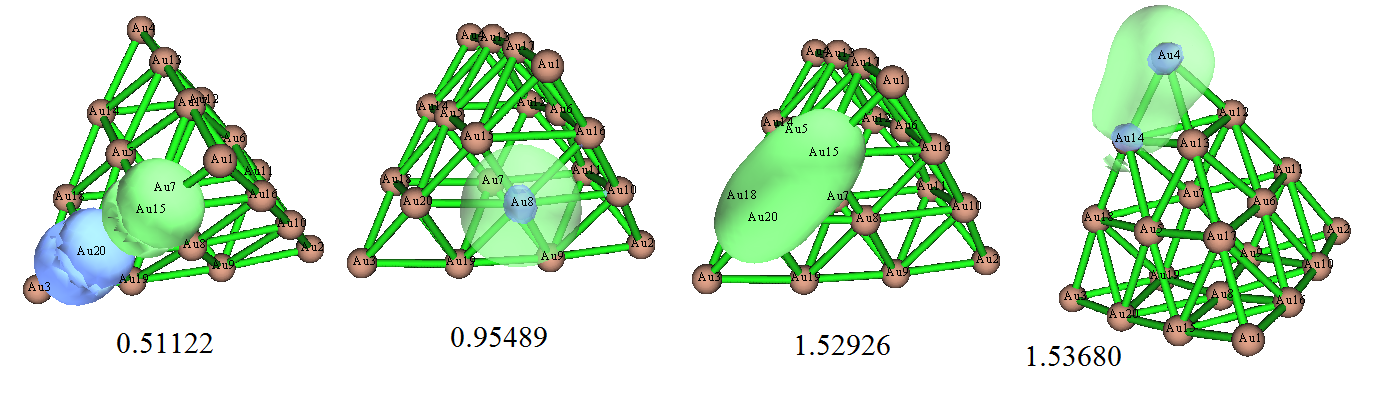
不僅形狀怪,毫無意義,它們的占據數離2.0也都差得較大,說明靠一套NBO軌道,根本沒法哪怕定性正確表現體系的電子結構。
再改用NLMO分析,發現這回結果定性正確了,圖景和Pipek-Mezey定域化軌道很相似:
上圖左邊那個軌道很正確,沒問題,但是上圖右邊那個NLMO還不很理想,因為其等值面形狀明顯是扭曲的,不符合體系的對稱性。之所以會這樣,是因為NBO程序沒法自動搜索>3中心的軌道,因此當前這個軌道是被當做Au3-Au19雙中心軌道來產生的。
7 實例5:苯與菲
在討論更復雜的菲之前,我們先看看苯的占據的pi型MO軌道和Multiwfn做定域化之后的相應軌道,如下所示
可見定域化明顯起到了效果,每個LMO的形狀都一致。由于苯的6中心pi鍵的離域特征非常強,因此即便定域化之后,而且哪怕等值面數值已設為0.05這樣挺大的值,還是看到每個LMO并不僅僅定域在兩個原子之間,而是同時一定程度離域到相鄰原子。因此這三個LMO合在一起,是可以表現出高度的六中心離域特征的。如果大家產生NBO軌道的話,則會發現這些軌道都被完全定域到雙中心了(但占據數僅為1.66),從而強行、誤導性地把體系電子結構描述成單雙鍵交錯的Lewis式。
然后我們再看菲的情況,此體系在《使用AdNDP方法以及ELF/LOL、多中心鍵級研究多中心鍵》中分析過。無論是ELF-pi、AdNDP還是本文用的LMO分析,都可以得到兩邊的六元環的共軛程度較高的結論。對應于右邊的六元環的pi電子的AdNDP和LMO軌道列于下圖
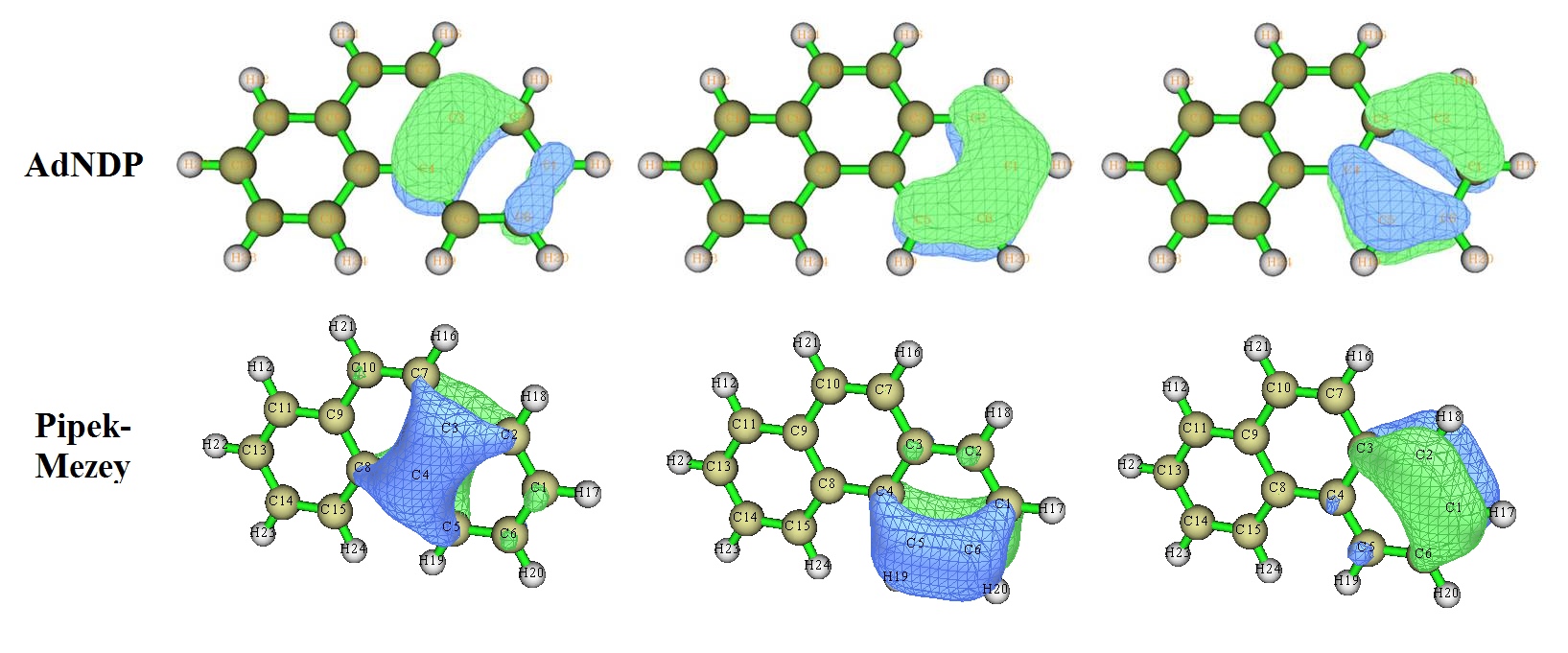
可以看到,無論是AdNDP還是LMO軌道,菲的兩端的六元環的與pi電子有關的軌道圖形都與芳香性很強的苯很形似,只不過受到實際化學環境的影響有一些變形而已。因此,我們可以得到菲的兩側的六元環的芳香性較強的結論。對此體系,用NLMO方法得到的LMO軌道和Pipek-Mezey方法得到的LMO軌道很相似。
而對于菲中間的六元環的芳香性,通過LMO的話不是很好討論。因為我們會發現還有個C7-C10之間的定域性pi軌道,如果和主要覆蓋C8-C9、C4-C3的定域性pi軌道放在一起的話,仿佛中間的六元環也有挺強芳香性。然而如果用AdNDP分析,在找六中心軌道的時候,就可以區分出芳香性差異了。當我們按照前述AdNDP的博文把sigma電子對應的軌道都挑走并從密度矩陣中扣除其貢獻后,對中心的六元環和兩側的六元環搜索六中心AdNDP軌道時,會發現對兩側的環找出來的三個六中心軌道占據數是2.000, 1.985, 1.821,而中間的環是1.994, 1.770, 1.684,從占據數上看明顯后者更小,即中間的環上電子離域程度不及兩邊的環。實際上,通過六中心鍵級、ELF-pi分析也都能得到相同結論。因此選出六中心AdNDP軌道時應該選邊緣環的。此例說明LMO分析在某些情況下并無法完全替代AdNDP分析。
8 直觀展現所有LMO的中心位置例子:多巴胺
前面提到Multiwfn可一次性把所有LMO的中心位置給出來,便于直觀地觀看產生的LMO都是怎么分布的,這樣也便于我們快速找到我們感興趣的LMO。注意,用PM定域化的話,C-C雙鍵會以sigma-pi分離形式展現,此時sigma-LMO的中心和pi-LMO的中心位置往往挨得很近,難以分辨,而FB定域化就沒有這個問題,每個雙鍵被描述為兩個香蕉鍵,其中心是明顯分開的。這里用多巴胺作為例子演示一下Multiwfn自動生成LMO中心位置的功能。由于多巴胺里面有芳環,如果用PM定域化的話,芳環里的有的C-C鍵會被傾向描述成sigma和pi兩個LMO軌道,因此這里用FB定域化以使得LMO中心位置總能分得開。
在Multiwfn里輸入:
dopamine.fch
19 //軌道定域化
-8 //啟用產生LMO中心位置的選項
-6 //修改定域化方法
10 //Foster-Boys
1 //定域化占據軌道(非占據的LMO的中心位置一般沒什么意義,無需考察)
如屏幕上的提示所示,在Multiwfn導出記錄了LMO的new.fch并把它再自動載入后,程序對每個LMO的中心位置進行了計算,并且把每個中心作為Bq原子(鬼原子)加入到了當前體系。同時在當前目錄下輸出了LMOcen.txt,其中記錄了各個LMO中心坐標,以及與新加入的Bq原子序號的對應關系。之后程序還問你是否做LMO的偶極矩分析,這里選擇n跳過。
現在進入主功能0,直接就能看到下圖了。由于Multiwfn已經自動將主功能0里的顯示風格設成了便于觀看Bq原子的特殊情況,所以圖像和平時在主功能0里看到的不同。
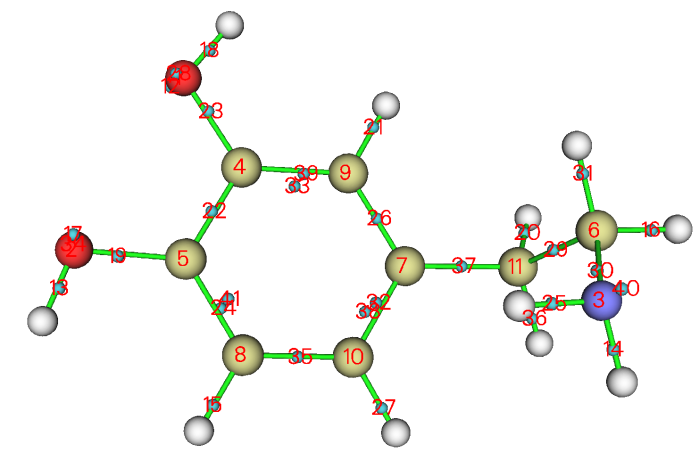
當前設定下此圖中Bq原子序號是從1開始排的,因此其序號正好和LMO序號直接對應,故各個LMO的位置從這張圖上一目了然。比如從這圖上我們可以看到LMO24和LMO41一起主要描述苯環上的一個C-C鍵,LMO40主要描述氮的孤對電子。將LMO40用0.1等值面顯示出來就是下圖(為了讓軌道等值面更平滑,已經在GUI菜單上的Isosur. quality里將格點數明顯設得更大)
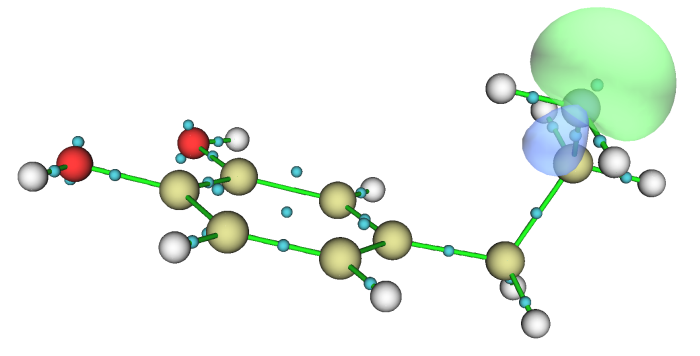
注意,當前體系里面加入的Bq原子由于沒有攜帶基函數,對于Multiwfn程序來講屬于“異常”狀態,因此對當前體系再進行波函數分析的話是沒有意義的,還可能導致Multiwfn崩潰。因此當前情況就看看結構和軌道圖就行了,不要再做其它波函數分析。
9 對LMO計算偶極矩考察鍵的極性
關于這點,原理請參閱Multiwfn手冊3.22節,實際例子參看手冊4.19.4節。從中可以看到通過在產生LMO中心位置后,再做一些額外考慮得到LMO的偶極矩后,就可以用來討論鍵的極性問題。
10 總結
Multiwfn的軌道定域化功能非常有用,得到的LMO軌道可以把體系中的關鍵電子結構特征通過大家熟悉的軌道模型很好地展現出來,對于分析電子結構非常有幫助。
對大量情況,軌道定域化分析其實可以代替比較麻煩、有較強任意性、需要化學直覺和使用經驗的AdNDP分析,得到的結果是定性一致的。雖然有些復雜情況,特別是牽扯到很多中心離域的問題,必須通過AdNDP才能找出理想的能恰當描述實際電子結構的軌道,但定域化軌道分析產生的軌道圖形,對于做AdNDP軌道搜索往往能提供一些有益的輔助和參考。
對于電子結構復雜、電子離域性強的體系,NBO分析有害無益,大多時候會給出定性錯誤的結論,如果基于其高占據軌道去討論問題,那純粹就是瞎討論,千萬別被坑了。NBO3.1對于復雜情況搜索出的無論是NBO還是NLMO,往往都是嚴重離譜的。NBO6使得結果合理性往往有明顯改善,其產生的NLMO基本合理了,和Pipek-Mezey軌道定域化的結果定性一致,但是給出的NBO軌道經常還是不足以定性正確描述體系電子結構。對于涉及到>3中心共享電子特征的體系,無論是NBO3.1還是NBO6,無論是NBO還是NLMO,都根本沒法用,因為NBO只能最多自動搜索3中心軌道。此時如果還試圖用NBO或NLMO討論,那純屬搞笑。
總之,討論電子結構復雜的,特別是牽扯多中心共享電子的體系,Multiwfn的軌道定域化分析很有用也很好用,有局限性的地方靠AdNDP分析也可以彌補,而NBO分析強烈不建議使用。NBO程序給出的NBO軌道比起LMO軌道其實也就一個好處,即可以通過考察E2討論超共軛,而基于LMO是沒法做E2的(可以證明數值精確為0)。不過,當NBO軌道本身就是定性錯誤時,E2分析也沒有絲毫意義。
除上述例子外,Multiwfn手冊的4.19節還有其它軌道定域化分析例子,包括分析SN2反應過程中LMO軌道的變化,以及通過LMO考察[Re2Cl8]2-中Re-Re四重鍵特征。在《談談18碳環的幾何結構和電子結構》(http://www.shanxitv.org/515)、《一篇最全面、系統的研究新穎獨特的18碳環的理論文章》(http://www.shanxitv.org/524)中筆者還利用定域化軌道考察了18碳環體系中被一些人誤當成是三重鍵的C-C鍵特征,對其真正的成鍵方式予以了正確的解釋。這些都十分建議一看。