Multiwfn波函數分析程序的意義、功能與用途
Multiwfn波函數分析程序的意義、功能與用途
文/Sobereva @北京科音
First release: 2013-Apr-29 Last update: 2019-Mar-18
前言:Multiwfn (http://www.shanxitv.org/multiwfn) 波函數分析程序的功能極其豐富,用途十分廣泛,用法十分靈活,所以絕大多數用戶可能不容易完全了解Multiwfn的全貌。雖然在J. Comput. Chem., 33, 580-592 (2012)筆者曾經對Multiwfn的各個方面進行過系統的介紹,但那篇文章對應于2.1.2版,而最新的Multiwfn版本早已比2.1.2版有了質的飛躍。為了幫助用戶全面認識Multiwfn,本文將對Multiwfn的功能和用途進行一個既系統又簡明扼要的概述。讀者如果對Multiwfn有任何問題歡迎到計算化學公社的Multiwfn專版討論:http://bbs.keinsci.com/wfn。Multiwfn也有專門的英文版論壇供世界各地的使用者交流:http://www.shanxitv.org/wfnbbs。
另外,北京科音自然科學研究中心(www.keinsci.com)也每年都會舉辦“量子化學波函數分析與Multiwfn程序培訓班”,詳細介紹請訪問北京科音網站的“科研培訓”欄目,由Multiwfn開發者全面講授波函數分析的理論基礎并結合大量實例介紹Multiwfn的使用方法,詳細內容見http://www.keinsci.com/workshop/WFN_content.html。未來的培訓班的舉辦時間在北京科音官網首頁的"科研培訓預告"一欄中會有體現。截止至2018年末此系列培訓已經成功舉辦了四屆。
1 波函數分析與Multiwfn的意義
量子化學本質上就是用基于量子力學的方法研究化學問題。通過現成的量子化學程序,在各種近似條件下求解薛定諤方程,就可以得到體系的波函數。波函數包含了體系中一切信息,可以視為是個黑箱,通過對波函數及其衍生信息(如電子密度)進行各種方式的分析,就可以從這個黑箱中提取各種具有化學意義的信息,使體系的內在特征能夠被我們透徹地認知,諸如原子間鍵的強度與本質、電子在體系中的行為和分布方式等,同時也可以預測當前體系如何與其它體系相互作用,諸如預測反應位點。波函數分析的意義可以用下圖來形象地描述
主流量子化學程序也可以給出體系的一些信息,如能量、穩定結構/過渡態結構、極化率、溶劑化能、NMR/IR/Raman/UV-Vis/ECD/VCD/ROA譜等,但這些信息不是基于直接對波函數分析而給出,故它們的計算一般不納入波函數分析范疇。
波函數分析是一大類分析方法的集合。實際上,眾所周知的前線軌道理論就是波函數分析方法的一種,它直接利用了前線軌道的波函數來分析化學反應性。量子化學界比較知名的兩大類分析方法,即Natural bond orbital (NBO)分析和Atoms in molecules (AIM)分析,都是波函數分析方法當中重要的組成部分。各種形式的布居分析、電荷轉移分析、電子定域性分析、鍵級分析、靜電勢分析等等,以及概念密度泛函理論的諸多內容也都屬于波函數分析的范疇,這些后文將會具體列舉。
波函數分析無疑是非常重要的。量子化學研究,特別是應用型的研究,決定研究價值的關鍵往往不在于計算過程,而在于分析得是否深入透徹,是否能給出足夠的分析依據來支持自己的結論,是否能通過詳細的分析發現新的問題并進而予以合理的解釋。然而,波函數分析的普及程度目前相當令人沮喪,這在我國尤甚。從很多文章以及網絡上的討論中可以明顯看出,很多量子化學工作者對波函數分析知之甚少,導致很多人研究體系時感覺沒得可分析,從而導致文章深度、檔次上不去。也有很多研究者則想要解釋體系的一些特點或論證一些設想(比如想說明哪個鍵比較強、電子躍遷到激發態后電荷是如何轉移的,想解釋為什么反應容易發生在某個位點),想去分析可是又苦于沒有手段。還有不少人,看過他人的文章,知道應該做什么方式的波函數分析,然而卻找不到現成、好用的程序來實現。
之所以意義重大、研究者們迫切需求的波函數分析的普及程度非常低,應用價值受到嚴重制約,主要有兩個方面的原因:
(1)長期以來量化教材當中很少有書對波函數分析進行介紹,書籍內容的取材往往比較陳舊和保守,也限于大多數作者的知識水平,波函數分析方法方面往往頂多也就是介紹一下半個世紀前就提出的Mulliken布居,導致量子化學初學者們連接觸波函數分析的機會都甚少。另外,雖然和波函數分析有關的文章數目甚巨,相關專著有不少,這個領域的研究從幾十年前起就一直十分活躍,然而迄今國內外沒有任何一本書籍對各種波函數分析方法進行全面而且深入淺出的介紹,資料過于零散,使得廣大量化工作者學習波函數分析比較困難。
(2)現有的波函數分析程序基本都存在一種或多種弊病,導致廣大研究者們很難將波函數分析方法付諸于實際研究。這些弊病包括:1.收費、不開源 2.計算速度慢而且沒有并行化 3.使用、操作十分復雜難懂,輸入文件編寫麻煩,輸出信息冗雜,不人性化,也沒有像樣的教程,更不提供技術支持 4.不夠靈活,無法通過調整設置滿足特殊研究需求 5.功能單一,每個程序往往只能實現很少的功能,缺乏整合性 6.作者別有用心,程序不公開發布,只給合作者用。另外值得一提的是,雖然各種半經驗/從頭算/第一性原理程序自身往往都帶有一定的波函數分析功能(特別是Mulliken布居分析幾乎都有),但是支持的分析甚少,而且往往不好用。
Multiwfn程序著眼于解決上述第(2)類當中的全部問題。雖然Multiwfn的開發目的有許多,但最主要的目的,是提供給廣大科研工作者一個免費開源,并且是世界上功能最全面最強大、使用最方便、最容易上手、計算速度最快、最靈活的波函數分析程序。Multiwfn程序從2009年11月發布的1.0版開始一直不斷開發至今,目前已經很成熟,已達到了預期目標,給波函數分析的普及和在實際研究中的應用掃除了重大障礙。如今Multiwfn的用戶已經遍及世界各地,除我國外還包括美國、墨西哥、歐洲各國、俄羅斯、印度、伊朗、日本等超過50個國家,已經被超過3000篇高水平SCI研究文章以及書籍所引用,其中有不少發表在Science、Nature、JACS、Angew、PNAS等頂尖刊物上。Multiwfn已經取得中華人民共和國計算機軟件著作權登記,登記號:2016SR010661。
Multiwfn的手冊編寫十分詳盡,費盡心血寫的600多頁的手冊中不僅介紹了程序的具體使用,還將程序各種功能涉及到的所有的理論進行了介紹,還包含了一百多個實際應用例子。結合筆者以往陸續在網上發布的一系列介紹各種波函數分析方法的帖子,其實已經解決了不少上述第(1)類問題。筆者日后將專門撰寫名為《量子化學波函數分析--原理與實踐》的書來徹底解決這類問題,其中將對各種主流的波函數分析方法進行全面系統的講解,盡可能壓低閱讀的門檻,同時結合Multiwfn等程序的具體操作步驟給出研究實例,使讀者明白波函數分析方法都有哪些、原理是什么、能解決什么問題、在實際研究中如何具體使用。想必此書出版后將會對波函數分析方法在我國的推廣有重大的意義。
2 Multiwfn的主要亮點
Multiwfn相對于其它種類繁多的波函數分析程序主要有以下幾大亮點:
(1) 功能非常全面。Multiwfn是迄今功能最全面最強大的波函數分析程序,它將各種波函數分析方法高度、有機地整合到了一起。除了幾個和NBO有關的分析外,所有最重要的波函數分析方法都可以僅靠Multiwfn一個程序來完成。Multiwfn的推出已經使得好幾十個波函數分析程序(不少還是收費的)徹底失去了存在價值。同時Multiwfn的許多功能都是獨一無二的,無法靠任何其它現有程序實現。
(2) 非常易于使用。Multiwfn程序是交互式程序,界面設計得十分周到并且高度智能化,用戶完全不需要像使用大多數量子化學程序那樣需要編寫復雜的輸入文件(關鍵詞還容易忘,老得查手冊很麻煩),而只要仔細按照屏幕提示一步步進行就行了,使用非常方便。大多數分析只需要敲幾個鍵就能輕松完成。另外,Multiwfn的輸出的信息簡明易懂,不會輸出一大堆只有內行甚至開發者才能搞明白的信息。Multiwfn主頁上還提供了非常豐富的資源,手冊也編纂得極盡周到詳細,可以幫助初學者很快入門。
(3) 高效。Multiwfn的開發過程特別注重提高運算效率以及降低內存的消耗。并且幾乎所有運算量大的部分都用OpenMP技術進行了并行化。對于計算較為耗時的波函數分析,Multiwfn的運算速度往往高于其它功能類似的程序一個甚至兩個數量級。
(4) 結果可直接可視化。對于需要可視化分析的波函數分析方法,Multiwfn會自動調用DISLIN圖形庫直接將結果繪制成圖像,這使分析過程大大簡化,這對于實空間函數的分析尤為重要,并且很多繪圖設定在Multiwfn中都允許由用戶自行調節。而大多數量子化學程序都做不到這一點,用戶往往得把數據進行處理后導入到第三方可視化程序里才能觀看,特別耗時、繁瑣。Multiwfn生成的圖像都可以直接導出到圖像文件,支持的格式豐富,包括ps、eps、png、pdf、wmf、gif、tiff、bmp。
3 Multiwfn的基本特征和使用方法簡介
初學者使用Multiwfn之前務必先閱讀一遍《Multiwfn入門tips》(http://www.shanxitv.org/167),其中對Multiwfn的基本信息和基本使用方法進行了完整的概括,本文下面只給出一些關鍵性的信息。
Multiwfn的主頁是http://www.shanxitv.org/multiwfn,所有Multiwfn版本的源程序、編譯好的可執行文件和手冊pdf文檔皆可從此網站免費下載,下載不需要注冊或申請。可執行文件的壓縮包很小巧,下載、傳播都很便利。
Multiwfn是跨平臺的程序,Windows版Multiwfn支持從WinXP到Win10的各個版本。程序不需要安裝,只要解壓后即可直接使用。源代碼可在Intel Visual Fortran下順利編譯。
Multiwfn也支持各種主流Linux發行版和MacOS。使用前需要按照手冊對系統進行配置,并且可能需要自行補全所需的庫文件。Linux和MacOS版Multiwfn源代碼可以在ifort>=12.0版下順利編譯(gfortran編譯器無法通過)。
Multiwfn的大部分功能是通過載入量子化學程序輸出的波函數文件來進行波函數分析。支持的波函數文件的格式豐富,包括:
(1) PROAIM波函數文件(.wfn)
(2) 擴展的波函數文件(.wfx)
(3) 格式化的Gaussian檢查點文件(.fch)
(4) Molden輸入文件(.molden)
(5) GAMESS-US和Firefly輸出文件(.gms)
由于Multiwfn支持的波函數文件格式豐富,它們又可以被各種主流量子化學程序所產生,因此Multiwfn具有很好的通用性。另外,Multiwfn還支持其它一些格式用于特殊類型的分析。例如如果所用的分析方法只依賴于原子坐標,那么可以使用通用的記錄坐標信息的格式.xyz、.pdb和.mol;對于繪制NBO、NLMO、NHO、NAO等NBO程序產生的各種類型的軌道,可以用NBO程序輸出的NBO plot文件(.31~.40);對于格點數據分析處理和可視化、盆分析等目的,可以用計算化學領域常用的格點數據文件格式.cub或Dmol3的.grd文件作為輸入。以上這些格式的介紹、產生方法詳見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。
Multiwfn的所有操作都是交互式的,大部分功能只要按照屏幕上的提示一步步進行即可,要輸入什么在屏幕上都會看到明確的說明。遇到問題時應先參閱手冊對功能的介紹,以及手冊中相關的例子,并舉一反三。手冊的內容超級詳細,十分簡單易懂,查閱很方便,章節結構在《Multiwfn入門tips》里有介紹。值得一提的是,Multiwfn的手冊絕不僅僅是一本手冊,它在很大程度上也是一本波函數分析書,把里面的原理介紹都搞懂,把例子都做一遍并且仔細領會,在波函數分析上就有相當的水準了。
Multiwfn也可以方便地通過重定向方式以命令行模式來運行,也可以直接編寫shell腳本來實現Multiwfn的批處理。方法在手冊附錄里有具體介紹。
4 Multiwfn的基本功能
4.0 Multiwfn支持的實空間函數
Multiwfn的眾多功能都與實空間函數密切相關,實空間函數在這里指分布在三維空間中的標量函數,它們在波函數分析中有重要價值,所以在介紹Multiwfn的功能前先將Multiwfn支持的實空間函數列舉一下。如果對它們不熟悉,可以參看手冊2.6節的簡要介紹。Multiwfn支持計算幾乎所有最重要的實空間函數,包括:
(1)電子密度
(2)電子密度的梯度
(3)電子密度的拉普拉斯函數
(4)軌道波函數。軌道可以是正則分子軌道、定域化軌道、自然軌道、NTO、NBO、NHO、NAO等,取決于輸入文件類型
(5)電子自旋密度或自旋極化參數
(6)電子的哈密頓動能密度K(r)
(7)電子的拉格朗日動能密度G(r)
(8)由原子核產生的靜電勢。如果用.chg文件(記錄了原子電荷數值)作為輸入文件,則對應的是原子電荷產生的靜電勢
(9)電子定域化函數(Electron localization function, ELF)。包括Becke和Tsirelson各自提出的形式。開殼層體系的Becke的ELF所用的具體形式是由筆者導出的,見《電子定域化函數的含義與函數形式》(物理化學學報,27,2786-2792)
(10)定域化軌道指示函數(Localized orbital locator,LOL)。包括Becke和Tsirelson各自提出的形式。關于ELF、LOL和電子密度拉普拉斯函數的簡介可參見《電子定域性的圖形分析》(http://www.shanxitv.org/63)
(11)局部信息熵
(12)總靜電勢(ESP)
(13)約化密度梯度(RDG)
(14)Promolecular近似下的RDG
(15)Sign(lambda2)*rho(電子密度Hessian矩陣第二大本征值的符號乘以電子密度)
(16)Promolecular近似下的Sign(lambda2)*rho
(17)電子的交換穴、相關穴、相關因子
(18)平均局部離子化能(ALIE)
(19)源函數(Source function)
(20)電子離域范圍函數(EDR)
(21)軌道重疊距離函數D(r)
(22)獨立梯度模型(IGM)的δg函數
Multiwfn還支持很多其它的實空間函數,請參閱手冊2.7節的介紹,共計100多個。比如Weizsacker泛函、局部溫度、平均局部靜電勢、形狀函數(Shape function)、勢能密度、能量密度、鍵的金屬性(Bond metallicity)、近似形式的DFT線性響應核、電子密度橢率、Fisher信息密度、位阻能密度、Pauli勢、相空間定義的Fisher信息密度(PS-FID)、SEDD、DORI、電子動量密度、電/磁偶極矩密度、局部電子相關函數等等。Multiwfn還可以計算大量LDA和GGA級別的DFT交換相關勢以及交換相關能密度(交換相關泛函的被積函數)。包括LSDA交換、B88交換、PBE交換+相關、PW91交換+相關、VWN5相關、P86相關、LYP相關、B97交換相關、HCTH407交換相關。
出于靈活性考慮,Multiwfn提供了一個自定義函數,用戶只要在程序源代碼的userfunc子程序里面簡單地填上代碼然后編譯,就可以讓Multiwfn直接分析和繪制用戶自行定義的實空間函數。
下面將Multiwfn的比較主要的功能依次進行簡要說明。限于篇幅,有大量功能、選項無法在此一一提及。
4.1 觀看分子結構并繪制軌道
載入含有分子坐標的文件(pdb、xyz等),在Multiwfn的主功能0里就能觀看分子結構。如果載入的文件包含波函數信息(wfn/wfx/fch/molden等),還可以觀看軌道等值面。如果載入的是格點數據文件(.cub或Dmol3的.grd文件),則可以直接觀看格點數據的等值面。
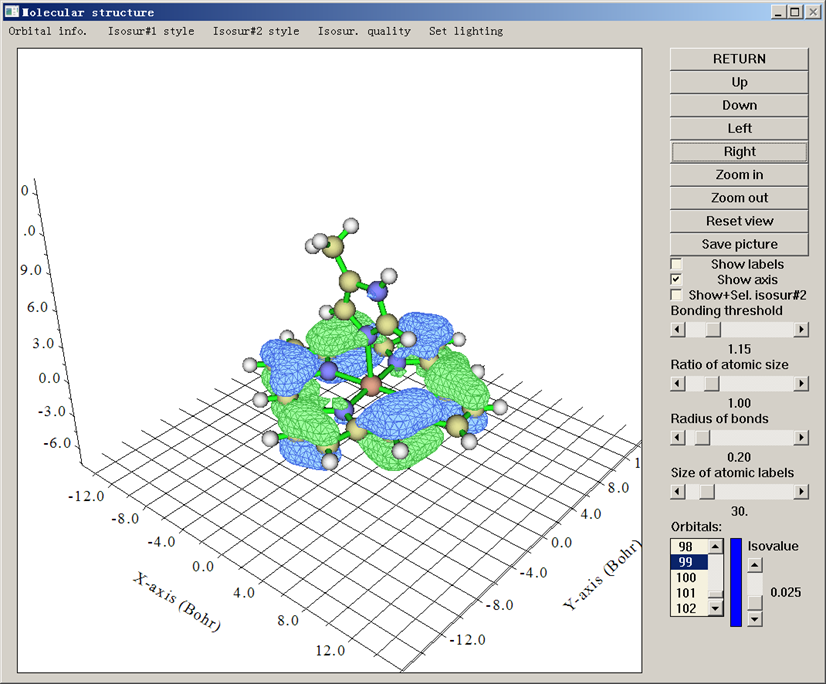
特別值得一提的是,Multiwfn顯示軌道等值面的速度飛快,對大體系甩GaussView幾條街。而且觀看軌道特別方便,想看哪個軌道直接在列表里一點就出現,調整等值面對應的數值(isovalue)只需要直接拉動滑條,遠比GaussView省事。Multiwfn還能同時顯示兩個軌道,分析軌道相互重疊問題的時候很有用。
Multiwfn可以方便地觀看NBO程序產生的各種軌道,包括NBO(自然鍵軌道)、NHO(自然雜化軌道)、NAO(自然原子軌道)、NLMO(自然定域化分子軌道),以及前頭帶P的類型,如PNBO(初自然鍵軌道)等,詳見《使用Multiwfn繪制NBO及相關軌道》(http://www.shanxitv.org/134)。而其它能觀看這些軌道的程序,如NBOView、Chemcraft都是收費的,并且功能和易用性上都不如Multiwfn。
等值面的顯示方式支持:不透明表面、網格狀表面、點狀表面、不透明表面+網格狀表面、透明表面。等值面和網格的顏色都可以任意設定。顯示分子結構時的原子尺寸、是否成鍵的判斷閾值、標簽大小等參數也可以自由調節。
4.2 計算實空間函數在一個點、一條線、一個面上和一個空間區域內的數值并繪圖
這幾種功能是Multiwfn最初版本就加入的,也是Multiwfn最核心、最強大的功能之一。
在主功能1里,用戶只要輸入一個點的坐標就能立刻將所有支持的實空間函數在此處的數值,連同指定的函數的梯度、Hessian矩陣一起輸出出來。而且這個點上的實空間函數值可以被分解成不同軌道的貢獻。
在主功能3里,用戶只要定義一條線的兩個端點的坐標,就能迅速將指定的實空間函數在這條連線上的變化作出曲線圖,并且還可以給出曲線上的極大極小點位置、特定函數值處的坐標位置。曲線的數據點也可以導出,供用戶在第三方程序如Origin里直接作圖。
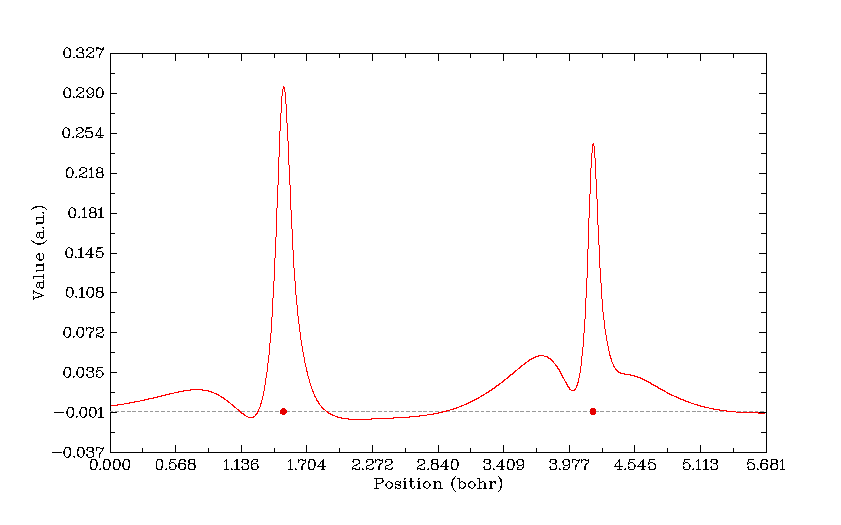
在主功能4里,用戶可以對指定的函數在指定的面上作圖。支持的圖形種類豐富,包括填色圖、等值線圖、地形圖(可以包含填色和投影效果)、梯度線圖、向量場圖。作圖不僅特別方便、速度很快,而且效果很好,有豐富選項可以用于調節作圖參數。還可以在圖上直接畫出分子范德華表面,顯示出拓撲分析的臨界點、拓撲路徑、盆分界線。平面上的數據也可以導出,便于用戶自行在Sigmaplot、matlab、surfer等程序里重新繪制。下面是幾個Multiwfn直接繪制出的平面圖的例子:
兩個NBO軌道的等值線圖,可以清楚地考察二者的重疊程度
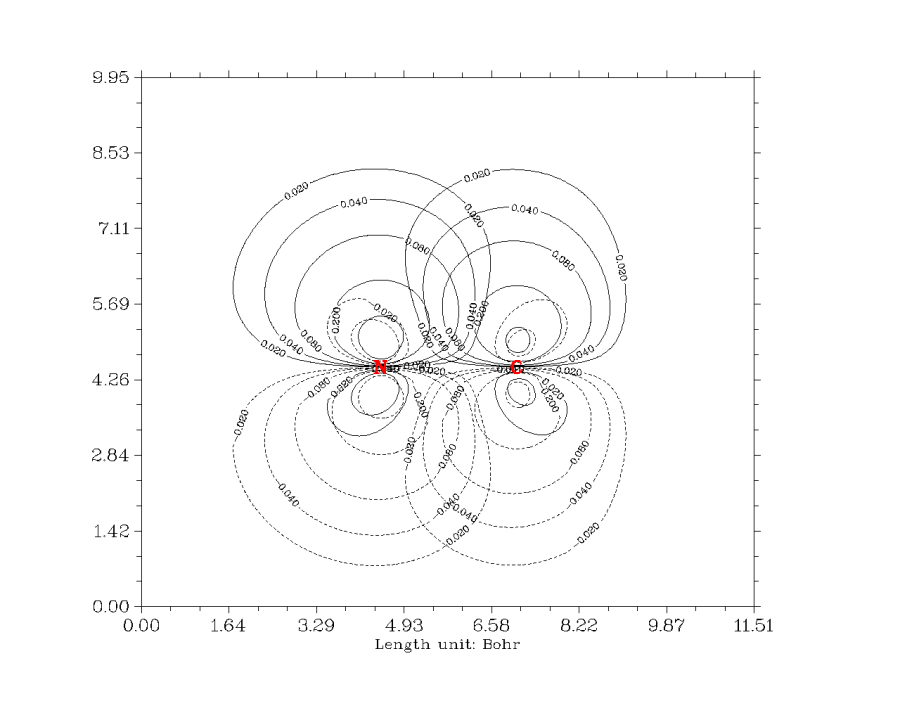
ClF3的靜電勢等值線圖,實、虛線分別代表正、負值。藍色粗線表示的是Bader定義的分子范德華表面(電子密度=0.001等值面)
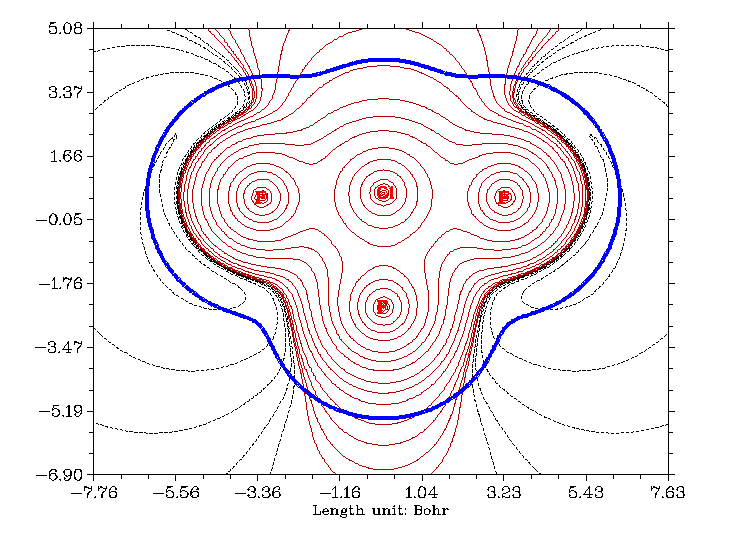
尿嘧啶的電子密度梯度場圖
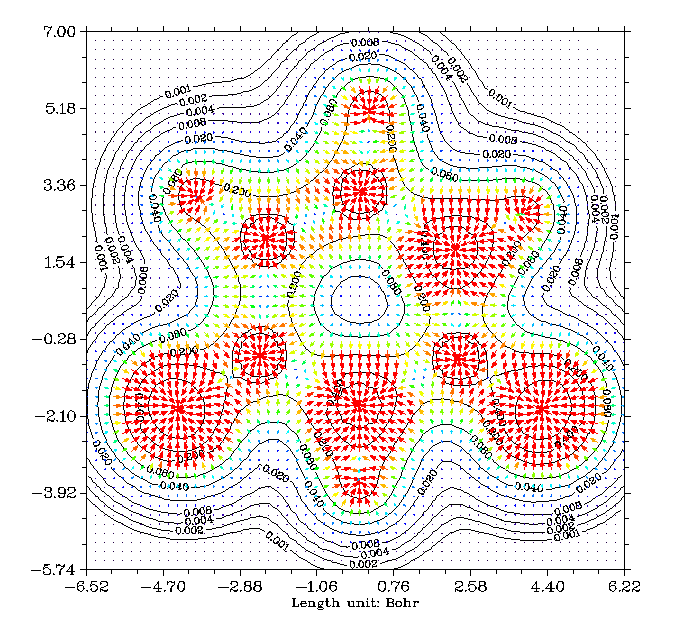
鎂卟啉的電子密度等值線圖+AIM臨界點、鍵徑和原子盆間面
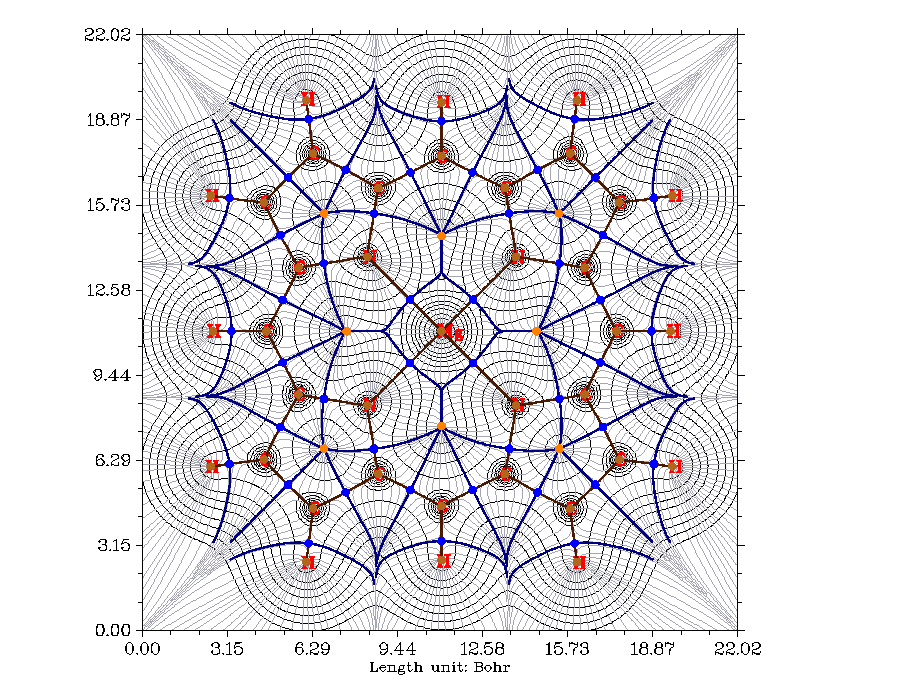
B13+團簇的LOL填色圖
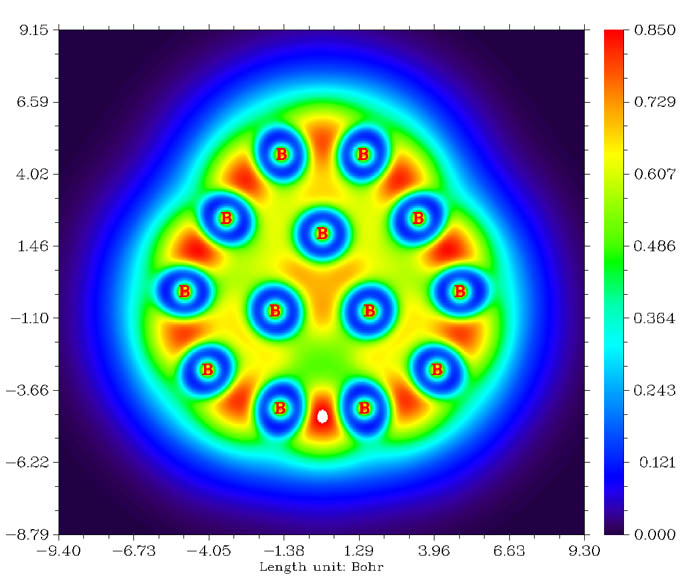
Li6團簇的ELF填色地形圖+投影。(Multiwfn的Logo就是來自Li6的ELF填色圖)
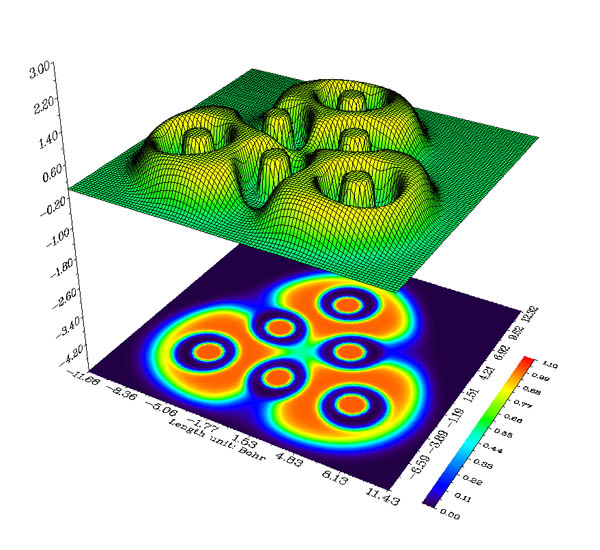
在主功能5里,可以計算指定實空間函數的格點數據,并且繪制等值面圖。格點的定義非常靈活方便,計算速度也遠勝具有相同功能的其它各種程序。格點數據既可以導出到文本文件也可以導出到Gaussian型cube文件中。也可以之后進入Multiwfn的其它功能對剛算完的格點數據進行進一步利用和操作。在主功能5里也可以計算指定一批數據點上的實空間函數,數據點坐標通過外部文本文件導入。
在計算直線、平面上以及空間區域內的實空間函數時,用戶可以設定“自定義運算”操作,來讓多個波函數文件對應的實空間函數相互運算。比如作密度差圖,只需先載入整體的波函數文件,然后設定它與哪些片段的波函數文件相減,然后在計算密度的時候就會自動依次算它們的密度并做差值。因此用Multiwfn計算諸如Fukui函數、雙描述符特別方便,詳情可參見《使用Multiwfn作電子密度差圖》(http://www.shanxitv.org/113)。當然,不只是密度差,也不光只是減法運算,Multiwfn可以直接讓任何支持的實空間函數對多個波函數文件進行加減乘除運算。另外,Multiwfn還可以直接得到promolecular屬性和deformation屬性。前者就是原子在自由狀態屬性的疊加,后者是指實際體系的屬性與promolecular屬性的差值。這里的屬性是指任意一種實空間函數,如果選的是電子密度,deformation屬性具體就是指電子變形密度,這對于分析原子形成分子時電子密度如何聚集、轉移十分有用。
如果產生相同體系不同坐標下的一批波函數文件(如對應IRC過程的每個點),以批處理方式調用Multiwfn對它們依次產生圖像,并結合做動畫的程序,就可以得到描述電子結構變化的動態圖像,對于分析反應過程內在機制很有幫助,詳見《制作動畫分析電子結構特征》(http://www.shanxitv.org/86)、《通過鍵級曲線和ELF/LOL/RDG等值面動畫研究化學反應過程》(http://www.shanxitv.org/200)。
4.3 拓撲分析
在AIM分析中,通常要對電子密度進行拓撲分析,包括尋找各種臨界點、產生拓撲路徑。Multiwfn不僅可以對電子密度做拓撲分析,還可以對ELF、LOL、電子密度拉普拉斯函數等實空間函數也進行拓撲分析。搜索臨界點和產生拓撲路徑速度非常快,顯著勝于其它有類似功能的程序。結果可以直接在圖形界面里可視化(如下圖所示),十分方便。還可以繪制出盆間分界面(interbasin surface)。每個臨界點上各種實空間函數的數值都能直接得到。臨界點和拓撲路徑可以靈活地自行修改、導入導出。Multiwfn還提供了其它很多附加功能,例如測量工具來獲得臨界點/原子核間的幾何參數、計算和繪制各種實空間函數沿著拓撲路徑的變化、計算基于BCP處的信息熵定義的芳香性指數、計算環臨界點位置上垂直于環平面的電子密度曲率以衡量芳香性。關于Multiwfn的拓撲分析功能的介紹具體可參見《使用Multiwfn做拓撲分析以及計算孤對電子角度》(http://www.shanxitv.org/108)。
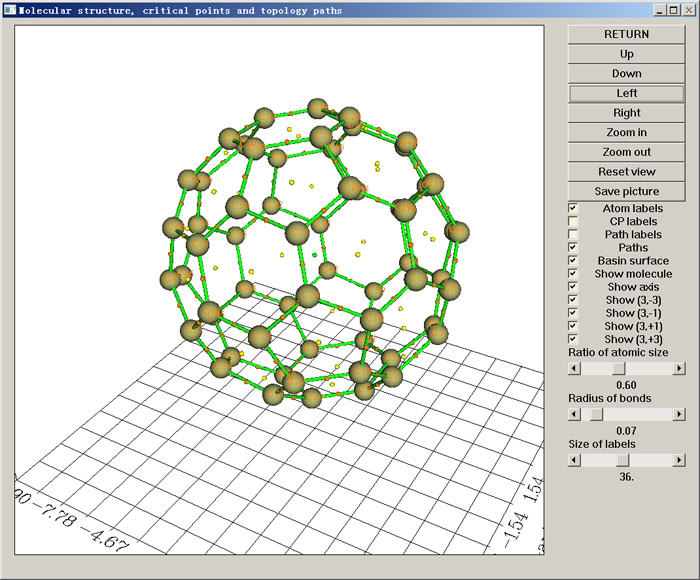
4.4 檢查和修改波函數
Multiwfn提供了許多選項對波函數進行檢查和修改。包括將當前波函數輸出為新的wfn文件;輸出GTF、基函數和軌道的信息;輸出系數矩陣、重疊矩陣、密度矩陣、不同類型的積分矩陣;交換、設定GTF的信息(所屬中心、系數、指數等);設定軌道的占據數和軌道類型;平移或平移+復制體系(后者可以用來近似地將單胞波函數擴展為超胞波函數);將某些原子從波函數信息中去除等。
對波函數進行修改后會直接影響實空間函數的計算結果,這對于一些特殊目的的分析十分有用,比如可以只考察某些原子、某些軌道(如pi軌道)上的電子產生的實空間函數。例如ELF-pi只考慮pi電子貢獻的ELF,有人通過它考察芳香性,本人也通過ELF-pi對寡聚物導電性進行過研究(RSC Adv.,2013,3,25881)。類似這樣的分析可以使用Multiwfn非常容易地實現。
4.5 布居分析與原子電荷計算
Multiwfn提供了豐富的布居分析與原子電荷計算功能,用于計算原子電荷或基函數/殼層上的電子占據數。支持的方法包括Hirshfeld布居、Hirshfeld-I布居、Voronoi變形密度布居(VDD)、Mulliken布居、Lowdin布居、修改的Mulliken布居(包括三種方法:SCPA、Stout-Politzer和Bickelhaupt)、Becke布居(包括經過原子偶極矩校正后的形式)、CHELPG和Merz-Kollmann(MK)擬合靜電勢電荷、CM5電荷、電負性均衡原理(EEM)電荷,以及本人提出的原子偶極矩校正的Hirshfeld方法(ADCH)。
Multiwfn中的Mulliken布居分析功能特別靈活,不僅可以得到基函數/殼層/原子上的電子布居數(開殼層體系會同時給出自旋布居),還可以得到原子間、基函數間的重疊布居以及它們自身的局域布居,并且結果還可以再進一步分解為每個軌道的貢獻。程序還可以給出每種角動量對布居數的貢獻。
雖然主流的量子化學程序如Gaussian也能計算CHELPG和MK電荷,但是Multiwfn在這兩個功能的實現上更為靈活,用戶可以任意設定擬合點的分布,還可以任意設定額外的擬合中心(為了準確描述分子間靜電相互作用,有時必須引入額外的非原子中心的點電荷)。這個功能還可以基于躍遷密度來做,得到的叫做TrEsp (transition charge from electrostatic potential)電荷。
此功能還可以基于原子電荷計算任意兩個給定的片段間的庫侖相互作用能。如果用的原子電荷是TrEsp電荷,則得到的就是兩個片段間的激子耦合能。
上述功能中ADCH方法是由筆者在J. Theor. Comput. Chem., 11, 163 (2012) (http://dx.doi.org/10.1142/S0219633612500113)中提出的。筆者在《原子電荷計算方法的對比》(物理化學學報, 28, 1-18 http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml)中對許多種計算原子電荷方法相比較,其中ADCH電荷展現出了非常優秀的性質,特別是能精確重現分子偶極矩,同時也有很好的靜電勢重現性。Multiwfn是唯一能實現ADCH方法的程序。
4.6 軌道成份分析
Multiwfn提供了多種方法進行軌道成份分析來得到各個原子軌道、殼層和原子對軌道產生的貢獻,并可以靈活地定義片段。支持的方法包括Mulliken、Stout-Politzer、SCPA、NAOMO、Hirshfeld、Hirshfeld-I和Becke。筆者寫的《分子軌道成分的計算》(物理化學學報,69,2393)是迄今第一個專門討論軌道成份分析方法的文章,其中對這些方法(除Becke以外)的原理進行了介紹并通過實例做了對比分析。NAOMO和Hirshfeld方法做軌道成份分析也是在這篇文章里首次明確提出的,并且目前只有Multiwfn能夠實現這兩種方法(注:NAOMO分析需利用NBO程序的輸出信息)。另外在《談談軌道成份的計算方法》(http://www.shanxitv.org/131)當中也對這些方法進行了粗略介紹,并給出了在Multiwfn中操作的實例。
另外,Multiwfn還支持利用定域化軌道的軌道成份的Localized orbital bonding analysis (LOBA)方法考察原子或片段的氧化態,見Phys. Chem. Chem. Phys., 11, 11297 (2009),這對研究配合物很有用,見《使用Multiwfn通過LOBA方法計算氧化態》(http://www.shanxitv.org/362)。
4.7 鍵級分析
Multiwfn支持的鍵級的計算方法眾多,包括:
(1)Mayer鍵級。這是目前最常用的鍵級。
(2)軌道占據擾動的Mayer鍵級。此功能用于分析各個分子軌道的電子對Mayer鍵級的影響(擾動),因此可以考察哪些軌道對鍵的強度影響比較顯著。
(3)Wiberg鍵級。此鍵級原始定義只能用于正交基,由于目前主流量化程序使用非正交基,Multiwfn會自動先做Lowdin正交化。在Multiwfn中Wiberg鍵級也可以基于NAO來計算,此時能夠將Wiberg鍵級分解為原子軌道對的貢獻,這對于考察原子軌道間相互作用對共價鍵的貢獻非常有幫助。
(4)多中心鍵級。這對于分析多中心鍵、芳香性極有用。Multiwfn最多支持到12中心,且可以自動搜索多中心鍵,還可以基于NAO軌道來計算。
(5)Mulliken鍵級,也稱Mulliken重疊布居數。Multiwfn可將它分解為軌道的貢獻。雖然Mulliken鍵級與鍵的強度關系符合得不佳,但是其數值可以為負值,以此表現出反鍵特征。
(6)模糊鍵級(Fuzzy bond order)。相當于模糊空間下計算的離域化指數。對于離子性不很強的鍵其結果和Mayer鍵級結果相仿佛,雖然計算會多耗時一些,但是對基組的敏感性顯著降低。
(7)Laplacian鍵級(Laplacian bond order, LBO)。這是筆者在J. Phys. Chem. A, 117, 3100 (2013)中提出的,基于對成鍵區域(模糊重疊空間)內的電子密度Laplacian的負值區域積分來獲得。LBO與鍵的強度有極好的對應關系,并且能清楚地反映出鍵的極性。
對于上述部分鍵級,Multiwfn還可以定義片段,來直接得到兩個片段的原子間的鍵級總和。
4.8 繪制態密度圖
雖然態密度(Density-of-states, DOS)一般是對于周期性體系來討論的,但是對于分子體系,將能級進行適當地展寬得到態密度,對于討論電子結構是很有益的。Multiwfn可以產生Total DOS (TDOS)、Partial (PDOS)、Overlap population DOS (OPDOS)。通過TDOS可以直觀地考察軌道在各個區域能量分布狀況,通過PDOS圖可以直觀地考察指定的片段對各個能量區域內的軌道的貢獻,而借住OPDOS圖可以直觀地了解不同能量區域的軌道對兩個片段間的結合能力(以Mulliken鍵級來表征)產生的影響。
對于PDOS和OPDOS,Multiwfn提供了十分靈活方便的界面用于定義片段。片段可以由基函數、殼層、原子以任意方式組合而成。片段可以一次性最多定義10個。Multiwfn也提供了許多選項用于用戶自行調節作圖設定,諸如展寬函數、半高寬(FWHM)等。
下面是Multiwfn產生的二茂鐵的TDOS+PDOS+OPDOS圖。其中定義了三個片段。從圖中可以一目了然地看到碳的px、py和s軌道主要貢獻的是低能態區域,-0.25 a.u.附近能態主要的貢獻者是Fe和碳的pz軌道,而HOMO則只由鐵所貢獻。OPDOS對應的是鐵與碳的pz軌道的相互作用,從其曲線上可以看到它對于二茂鐵的穩定性很重要,因為在占據軌道區域內OPDOS沒有負值而有明顯的正值,表現了鐵與碳之間的成鍵作用。在虛軌道部分,OPDOS全為明顯的負值,體現反鍵特征,這和軌道圖形上看到的特征是一致的。
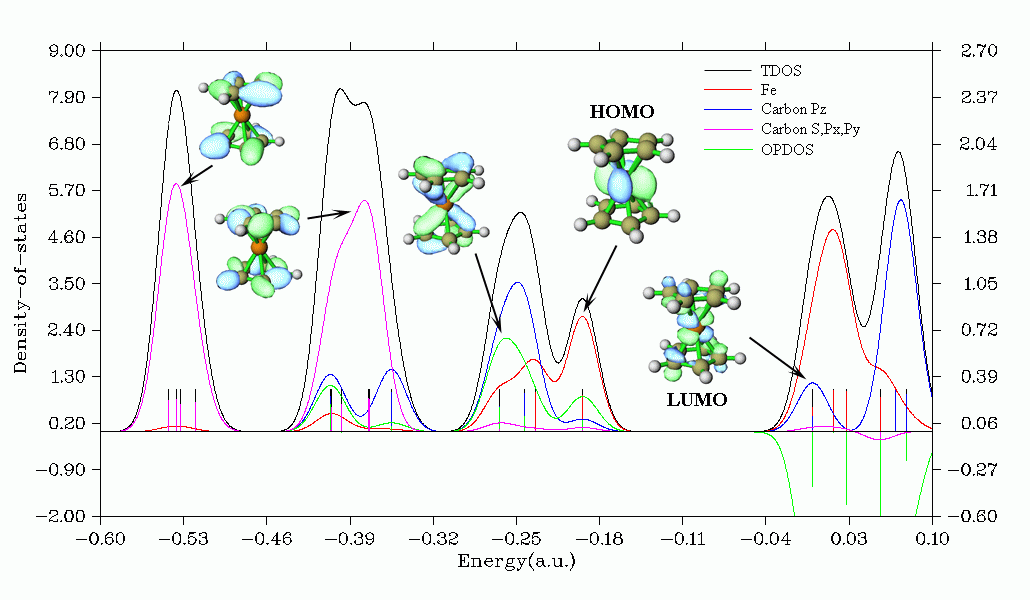
另外Multiwfn還可以研究Local DOS (LDOS),即通過繪制曲線圖考察三維空間中某個點,或者繪制填色圖考察三維空間中某條線上不同的點對于DOS的獻,由此可以理論模擬掃描隧道光譜(STS)。
4.9 繪制光譜圖
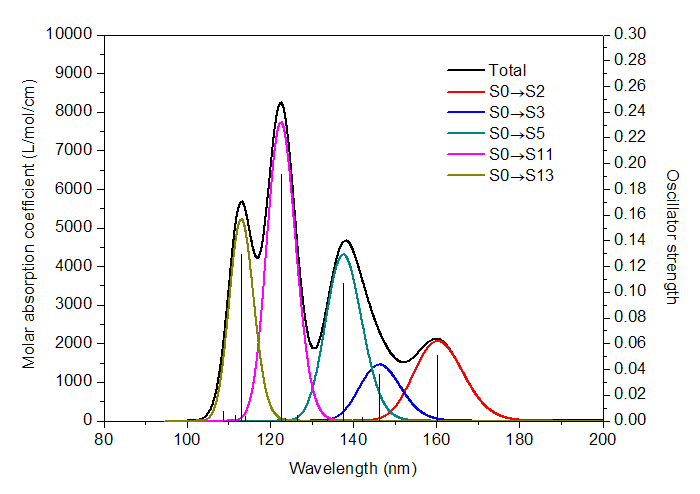
雖然繪制光譜圖不屬于波函數分析,但是是理論化學研究中常涉及到的,所以Multiwfn也具備這樣的功能,可以繪制IR、Raman(包括普通和預共振)、UV-Vis、ECD(電子圓二色譜)、VCD(振動圓二色譜)、ROA(拉曼光學活性)譜圖。激發能和強度數據可以從Gaussian、ORCA或Grimme的sTDA、xtb程序的輸出文件中直接讀取,也可以通過文本文件導入。諧振和非諧振的振動譜,以及考慮和不考慮旋軌耦合(SOC)效應的電子光譜都可以繪制。作圖的可調參數十分豐富(諸如可自行選擇展寬函數、可獨立設定每個躍遷的半高寬等),足以滿足專業用戶的需求,比Swizard、GaussSum等程序好用、強大得多。而且Multiwfn還能搜索出峰的精確位置、將峰分解為不同躍遷的獨立貢獻以便于指認峰的內在特征、繪制構象權重平均的光譜、同時繪制多個體系的光譜,這些是絕大多數繪制光譜圖的程序都不具備的功能。參見《使用Multiwfn繪制紅外、拉曼、UV-Vis、ECD、VCD和ROA光譜圖》(http://www.shanxitv.org/224)、《使用Multiwfn繪制構象權重平均的光譜》(http://www.shanxitv.org/383)。下圖是Multiwfn繪制的ECD譜圖
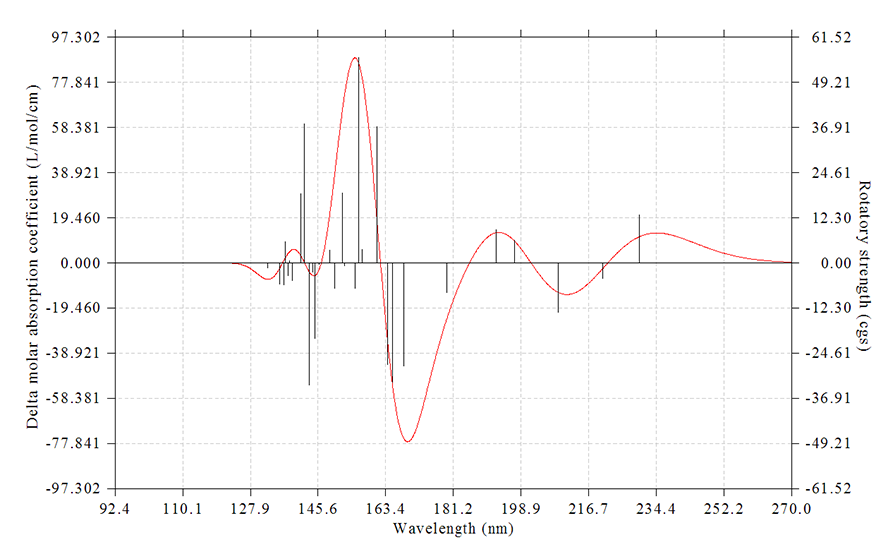
下圖是Multiwfn結合Origin繪制的乙酸的UV-Vis光譜,幾種主要的躍遷對光譜產生的獨立貢獻以不同顏色顯示
4.10 定量分子表面分析
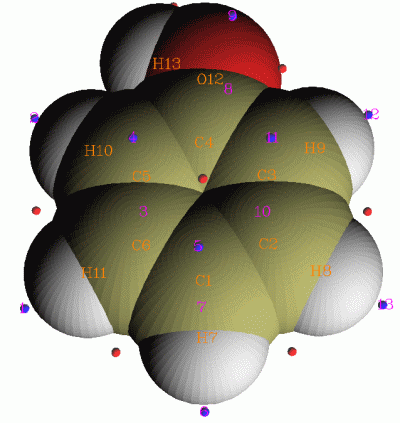
這里的“分子表面”是指電子密度等值面,比如0.001 e/bohr^3的表面常被用來作為分子的范德華表面,這是最初由Bader定義的。“定量分析”就是指的在這樣的表面上,對映射到上面的實空間函數進行定量的分析,諸如統計平均值、方差、不同數值范圍所占的面積大小,并且得到所映射的函數在分子表面上的極小值和極大值。雖然原則上各種實空間函數都可以作為映射到分子表面的函數,但通常只將靜電勢和平均局部離子化能(ALIE)映射上去。對靜電勢的定量分子表面分析對于預測分子間相互作用、通過QSPR(定量結構屬性關系)方式預測分子凝聚態性質十分有用,而對ALIE的分析則是一種很重要且很成功的預測親電反應位點的方法。例如下圖是Multiwfn產生的ALIE在苯酚分子表面上的極值點分布,極小點(藍球)清楚地表現了親電位點是在鄰對位。
Multiwfn的定量分子表面分析功能極為靈活、強大,不僅限于在電子密度等值面上分析靜電勢、平均局部離子化能等函數,還可以在任意實空間函數等值面上對任意實空間函數進行定量分析,比如可以在電子密度等值面上對福井函數的分布進行分析來討論反應位點。另外還具有獨創的局部分子表面分析功能,這種方法可以分析整個分子表面中的局部區域,可以有效地用于了解體系局部區域特點,比如討論體系內某個片段、某個原子對應的表面上的靜電勢。Multiwfn的這個模塊還能做Hirshfeld表面分析、繪制指紋圖形,這對于研究分子間,特別是在分子晶體環境下的相互作用很有幫助。
Multiwfn的定量分子表面分析模塊的部分介紹和一些應用實例可參見《使用Multiwfn的定量分子表面分析功能預測反應位點、分析分子間相互作用》(http://www.shanxitv.org/159),算法細節見J. Mol. Graph. Model., 38, 314 (2012)。
4.11 處理格點數據
Multiwfn的處理格點數據的功能源自于筆者早前開發的GsGrid程序,但它的開發早已終止,因為GsGrid的全部功能已被整合進了Multiwfn,同時做了不少擴充和完善。使用Multiwfn的這個功能前需要先載入cube或Dmol3的.grd文件,它們記錄了格點數據;也可以先用Multiwfn自身計算格點數據的功能產生格點數據,然后進入這個功能直接對其進行處理。
Multiwfn的處理格點數據功能包含眾多子功能:
(1)觀看格點數據等值面。
(2)將當前格點數據導出為cube文件。
(3)將一些格點的坐標和數值導出到文本文件。決定格點范圍的標準可以為:(a)所有格點 (b)接近某個平面的格點(特定的X/Y/Z平面或通過三個點來定義) (c)數值在指定范圍內的格點。
(4)設定遠離某些原子的格點的數值,可以由此屏蔽不感興趣的區域的等值面;設定遠離兩個片段間重疊區域的格點的數值,可以由此只保留重疊區域的等值面,對于RDG方法靠等值面展現弱相互作用區域比較有用,見手冊4.13.4節的例子。
(5)對當前格點數據進行運算(例如取絕對值、求對數、求冪),或者從cube/grd文件中載入另一套格點數據與當前格點數據相運算(相互加減乘除、求二者的平方和、取平均等等),由此產生新的格點數據。
(6)從cube文件中載入另一套格點數據并映射到當前格點數據中具有指定數值的格點上,并將坐標和數值輸出為文本文件。
(7)對格點數據范圍進行scale,以使得格點數據的范圍落在指定區間內。
(8)對指定數值范圍或空間范圍的格點數據進行統計,給出最大/最小值、平均值、均方根、總和、積分值、標準偏差、正值/負值/整體區域內數值的重心。
(9)繪制X/Y/Z方向的格點數據的積分曲線。如果當前的格點數據是片段密度差,那么這積分曲線也叫電荷轉移曲線,對于分析電荷轉移很有益,如JACS,130,1048。
4.12 自適應自然密度劃分(Adaptive natural density partitioning, AdNDP)
AdNDP在某種意義上是對NBO方法的擴展,可以得到“半定域化”軌道,它既不像分子軌道那樣一般會離域到整體,又不像NBO或傳統的定域化軌道那樣只分布在1~3個原子上,而是可以顯示出局部區域的離域特征,特別適合分析、展現多中心鍵,在研究團簇芳香性上已有大量應用。
Multiwfn是目前最強大的AdNDP分析程序。雖然AdNDP方法本身有一些人為性而不得不由用戶來干預AdNDP軌道的搜索,但是Multiwfn精心設計的界面已經將這個過程最大程度地便利化,并且可以直接觀看AdNDP軌道圖形,還能計算出AdNDP軌道能量。例如下圖是菲的邊緣的苯環上的三個六中心AdNDP軌道,展現了兩側的苯環的芳香性。
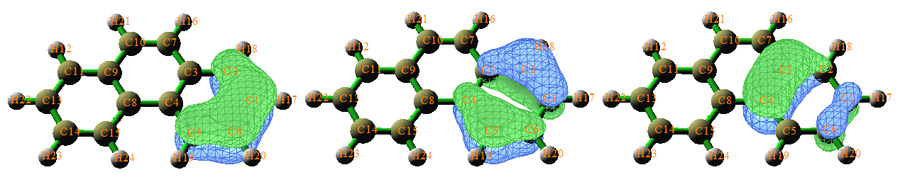
關于AdNDP方法在理論方面的介紹和討論,以及在Multiwfn中的實際操作,在《使用AdNDP方法以及ELF/LOL、多中心鍵級研究多中心鍵》(http://www.shanxitv.org/138)當中有詳述。
4.13 模糊空間分析
對體系中原子所屬空間的劃分有兩類,一類是離散式劃分,即原子間有明確的邊界,例如AIM的原子盆就是典型的一種;另一類是模糊式劃分,原子間沒有明確的邊界,而用平滑的權重函數來表示原子空間,越接近原子核則此原子的權重越大。模糊空間定義有很多,如Becke、Hirshfeld和Hirshfeld-I方法。在模糊空間下分析的好處之一是積分原子空間來得到原子的性質比較容易,這是由于邊界平滑所以容易積分得比較準確。Multiwfn的模糊空間分析就是用來計算各個模糊原子空間里的性質,來展現原子在分子中的特征。具體可以做以下分析:
(1)計算模糊空間以及模糊重疊空間內的任意實空間函數的積分值(模糊重疊空間是指兩個模糊原子空間之間重疊的空間)
(2)計算模糊空間內的電多極矩(即得到原子單極矩、原子偶極矩、原子四極矩和原子八極矩),以研究原子附近電子分布特征
(3)計算模糊空間內各個分子軌道間的重疊積分矩陣(也叫Atomic overlap matrix)
(4)基于模糊空間計算定域化指數(Localization index)、離域化指數(Delocalization index)和簡縮線性響應核(condensed linear response kernel)
(5)計算對位離域化指數(Para-delocalization index, PDI)、芳香波動指數(Aromatic fluctuation index, FLU)和對位線性響應指數(Para linear response index, PLR)用于研究芳香性
(6)計算多中心離域化指數用于研究多中心鍵
4.14 電荷分解分析(Charge decomposition analysis, CDA)
CDA用來將體系內兩個片段之間的電荷轉移進行分解,可以獲知各個分子軌道(或自然軌道)的形成導致電荷在片段間以什么方向轉移、轉移的量是多少,而非僅僅只得到一個整體轉移量。CDA對于分析金屬-配體間的電荷轉移極為有用,也同樣可以分析共價鍵相連的片段間的電荷轉移。Multiwfn的CDA模塊還可以給出各個片段軌道在復合物軌道中所占成分、給出不同片段軌道對兒對復合物軌道d,b,r項的貢獻、輸出片段軌道之間的重疊矩陣。Multiwfn的CDA功能可以定義無數個片段,而且支持后HF波函數,這是其它支持CDA的程序都難以做到的。
Multiwfn還支持擴展的CDA (Extended CDA)。CDA沒有明確將電荷轉移和電荷極化分開考慮,而ECDA則將它們分離開,排除了電荷極化效應對計算電荷轉移量的影響。
Multiwfn的CDA模塊不僅能做CDA分析,還能繪制軌道相互作用圖。下圖中是COBH3中CO(片段1)與BH3(片段2)之間的軌道相互作用圖,反映了片段的分子軌道如何構成復合物的分子軌道
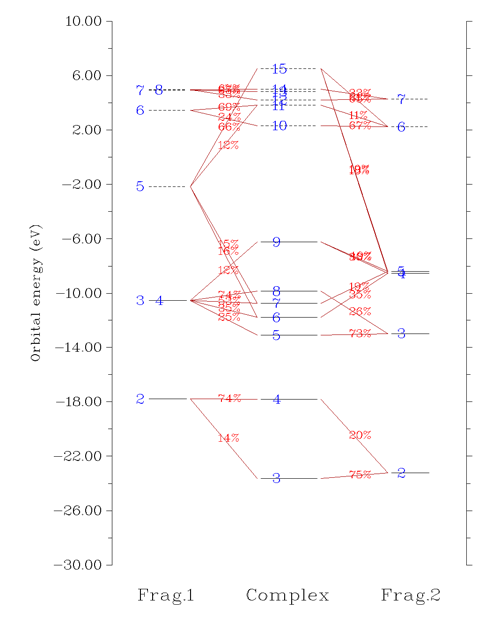
關于CDA的詳細討論以及在Multiwfn中的使用,見《使用Multiwfn做電荷分解分析(CDA)、繪制軌道相互作用圖》(http://www.shanxitv.org/166)
4.15 盆分析
Multiwfn的盆分析功能極其靈活、方便、強大和高效,所用的數值算法是基于立方格點的算法(見J. Phys.: Condens. Matter,21,084204)。不僅可以對電子密度尋找吸引子(也叫(3,-3)臨界點,即局部極大點)并產生相對應的盆,還可以對所有其它的實空間函數尋找吸引子并產生盆,諸如ELF、LOL、靜電勢,甚至于密度差等。每個盆都是體系中的一個局部空間,比如電子密度的盆對應于AIM原子空間,而ELF和LOL的每個盆則對應于一個電子結構的特征區域,如共價鍵區域、孤對電子區域、內核區域等。在產生盆之后,就可以直接觀看吸引子的位置和盆的范圍,例如下面的綠色區域代表了HCN中H的電子密度的盆:
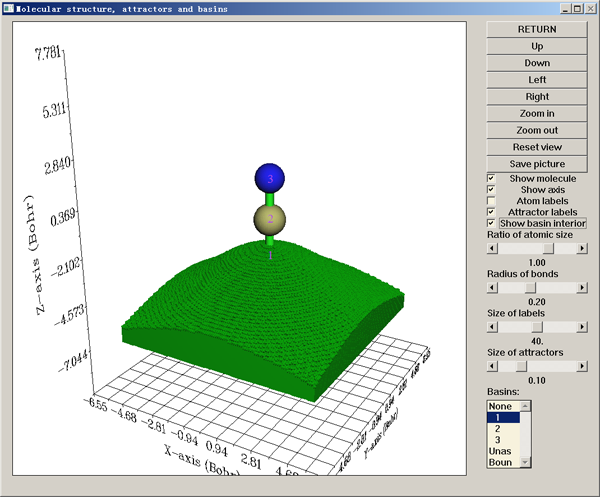
Multiwfn可以對各種函數的盆進行以下分析:
(1)在盆內積分任意實空間函數。
(2)計算盆內的電單極矩、偶極矩和四極矩。
(3)計算定域化和離域化指數并輸出盆區域內的軌道間重疊矩陣。
(4)計算原子對盆布居數的貢獻,例如考察成鍵的兩個原子對其ELF鍵盆布居數的貢獻以衡量極性。
Multiwfn產生盆所用的數值算法是基于立方格點的Near-grid算法,此算法實現方便,且適用于各種實空間函數。對于AIM盆的積分,單純基于立方格點積分精度不理想。為了進一步增加精度,Multiwfn中引入了本人提出的立方格點與原子中心格點混合積分方法,并且引入額外步驟使邊界格點的歸屬更為精確。
Multiwfn出于靈活、便利考慮,還提供其它一些選項,諸如測量吸引子/原子核間的幾何參數、將盆導出到.cub文件并將吸引子導出到.pdb文件便于用外部程序作圖。
關于盆分析的基本理論、算法和Multiwfn中的分析實例見《使用Multiwfn做電子密度、ELF、靜電勢、密度差等函數的盆分析》(http://www.shanxitv.org/179)。
4.16 電子激發分析
Multiwfn具備十分強大、全面的電子激發分析功能,可以把電子激發相關問題分析得淋漓盡致,其中很多方法都是Multiwfn獨家的。這部分功能在《Multiwfn支持的電子激發分析方法一覽》(http://www.shanxitv.org/437)當中做了非常全面的介紹,研究中涉及到電子激發計算的人請務必閱讀,你一定會發現Multiwfn在你的這方面研究是絕對不可缺少的利器!
4.17 軌道定域化分析
分子軌道有高度離域性,與化學鍵沒有直接對應關系。而將分子軌道做軌道定域化后,所得到的定域化分子軌道(LMO)就能夠與孤對電子、化學鍵直接聯系起來,討論許多化學上感興趣的問題。Multiwfn支持Pipek-Mezey(基于Mulliken或Lowdin布居)以及Foster-Boys方法做軌道定域化。使用例子見《Multiwfn的軌道定域化功能的使用以及與NBO、AdNDP分析的對比》(http://www.shanxitv.org/380)。
4.18 弱相互作用的圖形化分析
Multiwfn支持以下弱相互作用的圖形化分析方法,對于考察弱相互作用極為有用
(1)2010年楊偉濤課題組提出RDG(也叫NCI)方法。此方法在提出后迅速流行,已經成為研究弱相互作用最常用的方法之一,詳見《使用Multiwfn圖形化研究弱相互作用》(http://www.shanxitv.org/68)。
(2)在動態環境下(如分子動力學模擬)做平均RDG(aRDG)分析。這可以很好地、很直觀地考察實際環境下分子間在什么區域發生何種弱相互作用。例如可以考察苯-水混合體系中苯與水的弱相互作用。詳見《使用Multiwfn研究分子動力學中的弱相互作用》(http://www.shanxitv.org/186)
(3)DORI分析方法,這可以將體系中弱相互作用和強相互作用區域同時展現出來。詳見《使用DORI函數同時考察共價和非共價相互作用》(http://www.shanxitv.org/367)
(4)獨立梯度模型(IGM)。此方法可以任意設定片段,將片段間相互作用和片段內相互作用獨立展現出來,互不影響。還可以將原子和原子對對弱相互作用的貢獻定量化表達出來。詳見《通過獨立梯度模性(IGM)考察分子間弱相互作用》(http://www.shanxitv.org/407)。
4.19 其它實用功能
以上介紹的功能屬于Multiwfn的主功能。在Multiwfn當中還包括很多其它類型的分析,以及計算化學中會用到的實用功能,在此選擇其中一部分進行簡單提及
·同時計算兩個實空間函數的格點數據并繪制它們之間的散點圖。
·將fch文件里的密度矩陣轉化為對應的自然軌道,軌道還可以導出,這對于很多場合的計算和分析提供了很大便利。詳見《在Multiwfn中基于fch產生自然軌道的方法與激發態波函數、自旋自然軌道分析實例》(http://www.shanxitv.org/403)。
·基于蒙特卡羅方法計算分子范德華體積。見《談談分子體積的計算》(http://www.shanxitv.org/102)
·對任意實空間函數在整個空間范圍內進行積分。積分方法用的是Becke提出的對DFT交換相關泛函進行積分的方法,積分可以達到相當高的精度。結合Multiwfn提供的自定義函數,此功能十分靈活有用。比如自己提出一個新的相關泛函,那么在源代碼的自定義函數中填上自己的泛函的公式(計算密度、密度的梯度、動能密度在Multiwfn里都有現成的函數可以直接調用),利用此功能對自定義函數進行積分就能得到這個相關泛函所對應的相關能。
·計算非限制性計算的alpha和beta軌道間的重疊積分,這對于研究自旋極化程度是比較有用的。
·計算兩個軌道間的質心距離以及重疊程度,對于討論電子激發等牽扯到軌道對的問題十分有用,見《使用Multiwfn考察軌道間重疊程度和質心距離》(http://www.shanxitv.org/371)。
·監視Gaussian的SCF收斂過程并將收斂過程繪圖。這有助于了解收斂狀態,判斷是否應該停掉當前任務并重設關鍵詞重新計算。
·產生帶有片段組合初猜信息(由體系各個片段的波函數組成出的波函數)的Gaussian輸入文件。這對于產生高質量初猜波函數、計算自旋極化單重態體系很有用。基于此還可以進行比較簡單的能量分解,可以將“極化能”與“靜電能+交換能”二者從總相互作用能中分離開。
·將片段的波函數文件組合為體系的.wfn文件。利用這樣的.wfn文件,可以考察片段在相互作用之前ELF、LOL等函數的特征,也可以考察相互作用前后這些函數的變化,有助于討論片段間相互作用引起的電子結構變化。
·計算HOMA和Bird芳香性指數。HOMA是非常流行的基于結構的度量芳香性的指標。
·計算LOLIPOP,詳見Chem.Commun.,48,9239。這是一種基于對芳香環上方的LOL-pi值進行積分來衡量芳香體系pi-pi堆積能力的指標。
·計算分子間軌道重疊積分。這個積分與分子間電荷轉移能力密切相關。并且Multiwfn還能夠顯示二聚體內不同區域對分子間重疊積分的貢獻,這有助于指導設計高導電性的分子晶體。詳見《分子間軌道重疊的圖形顯示和計算》(http://www.shanxitv.org/163)。
·Yoshizawa電子轉移路徑分析,此功能基于Yoshizawa公式分析電子在平面共軛體系中可能的轉移路徑。原理見Acc. Chem. Res., 45, 1612 (2012)。
·自動檢測出pi軌道,批量設定它們或其它軌道的占據數。占據數設為0相當于此軌道在計算中被忽略,由此可以在各種Multiwfn的分析中去除sigma電子或pi電子的貢獻,對于計算ELF-pi、ELF-sigma等指標尤為方便。
·將函數分布擬合為原子的數值。這與MK擬合靜電勢方法很相似,但是被擬合的函數可以是任何其它實空間函數。
·輔助計算非平面體系的NICS_ZZ。雖然NICS_ZZ對于平面體系的計算很容易,但是對于非平面體系不易得到要計算的點的坐標,也難以得到垂直于環平面方向上的磁屏蔽值的分量,而Multiwfn的這個功能可以幫助解決這些問題。詳見《利用Multiwfn計算傾斜、扭曲環的NICS_ZZ 》(http://www.shanxitv.org/261)。
·計算等化學屏蔽表面(ICSS)。這在某種程度上可以視為是NICS的等值面,對于判斷哪些區域內外磁場存在屏蔽、去屏蔽效應,并由此考察體系的芳香性極為有用。詳見《通過Multiwfn繪制等化學屏蔽表面(ICSS)研究芳香性》(http://www.shanxitv.org/216)。
·計算并繪制實空間函數的徑向分布函數。
·在希爾伯特空間下計算原子偶極矩和鍵偶極矩。
·產生一批軌道的軌道波函數格點數據,便于在第三方程序中觀看軌道圖形。
·分析不同波函數當中的軌道對應性。例如對于一個分子,可以方便地考察MP2下的自然軌道是如何由HF下的分子軌道組成的。也可以研究兩個結構相似的分子的軌道間是如何轉換的。
·計算體系中原子間連接關系指數和原子的配位數。
·計算指定的一批原子的幾何中心、質心、轉動慣量、主軸、回轉半徑等基于幾何結構的信息,以及計算分子的直徑、分子的長寬高。
·計算體系中各種鍵的平均長度,這對于分析團簇特征很有用(例如JCP,111,1890)。
·計算軌道間的電偶極矩、磁偶極矩、速度、動能、重疊積分。
·計算各種實空間函數的中心和第一、第二極矩和回轉半徑。對于電子密度函數,第一、第二極矩就是電子偶極矩和四極矩張量的負值。
·將當前體系結構或者波函數導出為.xyz、.pdb、.wfn、.wfx、.molden、.fch、.47(獨立版NBO的輸入文件)格式。還可以根據當前結構對主流量化程序產生基本的輸入文件,包括Gaussian/GAMESS-US/ORCA/NWChem/MOPAC/PSI/MRCC/CFOUR/Molpro/Dalton/Molcas,其中對于GAMESS-US輸入文件還可以帶著$VEC字段作為初猜。因此Multiwfn可以作為非常方便的格式轉換工具,給研究者帶來了很大方便,有時甚至必不可少,比如ORCA用戶可以將得到的.molden轉化為.fch之后用Gaussian的cubegen工具進行一些計算,Gaussian的.fch文件可以用于給GAMESS-US提供初猜等等。詳見前述的《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》。Multiwfn還可以導出.pqr格式,可以載入進VMD程序,從而令原子根據Multiwfn算出的原子屬性值(比如原子電荷)進行著色來直觀展現數值大小,見《使用Multiwfn+VMD以原子著色方式表現原子電荷、自旋布居、電荷轉移、簡縮福井函數》(http://www.shanxitv.org/425)。
·計算鍵極性指數(Bond polarity index, BPI),這是在J.Phys.Chem.,94,5602(1990)中提出的基于原子平均價層電子能量衡量鍵的極性的指標。
·在一種實空間函數的域(被等值面包圍的區域)內對某種實空間函數進行積分,這兩個實空間函數可以是被Multiwfn支持的任意實空間函數。這對于討論原子間相互作用有益,比如有人就對能夠勾勒出弱相互作用區域的RDG函數的域內積分電子密度,從而討論弱相互作用強度。靈活利用這個功能還可以可視化分子孔洞、計算孔洞體積,見《使用Multiwfn可視化分子孔洞并計算孔洞體積》(http://www.shanxitv.org/408)。
·計算Matito等人在Phys. Chem. Chem. Phys., 18, 24015 (2016)中提出的衡量體系中動態、非動態和總電子相關大小的指數。
5 Multiwfn的用途
Multiwfn功能極多、用法靈活,所以有非常廣泛甚至數不盡的實際用途,不可能一次性全面概括,這一節僅列舉一些比較常見的應用,使讀者了解前述眾多的功能能發揮什么實際用處。此節所討論的分析方法都可以直接靠Multiwfn實現,細節在手冊中都有介紹,重要的應用在手冊或相關帖子里也都有實例,請自行查閱。很多文獻里的研究方法雖然在本文沒有提到,但是只要對Multiwfn的原理和操作領悟透徹,僅需稍作變通,自行寫一點處理腳本或稍微修改下Multiwfn的代碼就能輕易地實現。
5.1 觀看軌道
這已經在4.1節提到過了。Multiwfn觀看軌道又方便速度又快,還能支持NBO程序產生的軌道。不僅可以繪制軌道的等值面圖,還可以方便地作軌道波函數的各種類型的平面圖、曲線圖。
作等值面圖時如果想得到更好的顯示效果,還可以生成軌道波函數的cube文件,用第三方軟件如VMD來觀看。而平面圖、曲線圖則允許將數據導出,可放到諸如Sigmaplot、Origin、Surfer等程序里重新作圖并更靈活細致地調節作圖選項。
5.2 分析化學鍵
化學鍵的分析是Multiwfn的最主要用處之一。筆者專門寫了兩萬多字的大型文章介紹如何使用Multiwfn研究化學鍵問題,參見《Multiwfn支持的分析化學鍵的方法一覽》(http://www.shanxitv.org/471),本文不再累述。
5.3 研究化學反應過程
上述分析化學鍵的方法如果用到分析化學反應過程上,可以顯著加深對化學反應過程本質的認識。具體來說,就是取IRC路徑上的一些點,都繪制ELF、LOL、密度差圖等實空間函數圖形,討論這些函數隨反應過程的變化。也可以把IRC上所有點對應的函數圖形都作出來組合成動畫,見前述的《制作動畫分析電子結構特征》、《通過鍵級曲線和ELF/LOL/RDG等值面動畫研究化學反應過程》文中的例子。
同時也很建議將IRC上各個點的鍵級計算出來,并繪制出曲線圖(縱坐標是鍵級,橫坐標是IRC路徑上的坐標,同時把能量變化曲線也畫在上面),其中要考慮的鍵是反應過程中要斷裂的鍵和要形成的鍵。從圖上將可以清楚地看出隨著反應的進行,要斷的鍵的鍵級逐漸趨近于0,而新的鍵的鍵級逐漸增加,而過渡態的位置往往就在這兩套鍵級相交的位置附近。很多反應過程在過渡態附近都會出現多中心鍵特征,比如DA加成反應過程中就有一定的六中心鍵特征,對這種情況很建議也把多中心鍵級數值附在曲線圖上進行討論。另外還可以把諸如原子電荷數值、盆積分數值等性質在IRC上的變化曲線也繪制出來加以討論。
5.4 弱相互作用分析
這個主題在《Multiwfn支持的弱相互作用的分析方法概覽》(http://www.shanxitv.org/252)當中有全面的介紹,這里不再累述。
5.5 電荷分布分析
最簡單的表現體系中電荷分布的方式就是計算原子電荷,Multiwfn支持很多計算原子電荷的方法,各有特點,可參見物理化學學報,28,1的對比分析。對于Mulliken方法,Multiwfn還可以分析不同類型原子軌道上的電子占據數。原子電荷只能體現原子附近有多少電子,而更細致的研究就是計算前述的原子偶極矩、四極矩,前者可以展現出原子附近電子密度的極化方向和程度,后者可以展現出原子附近密度偏離球對稱的方式和程度。
通過盆分析功能得到ELF、LOL函數的盆,則可以將整個空間劃分為對應于不同電子特征的局部區域,如內核區域、孤對電子區域、共價鍵區域等,再對盆進行積分,就可以得到這些區域內的各種性質,如盆內的電子數、偶極矩、四極矩等等。這對于深入分析化學鍵和弱相互作用的特征也都是很有益的。特別是對應于成鍵的ELF盆內的偶極矩可以視為鍵偶極矩,在不少文章中都有討論)。可以參看前述的《使用Multiwfn做電子密度、ELF、靜電勢、密度差等函數的盆分析》的例子。另外還可以討論諸如體系不同區域的電子對分子總偶極矩的貢獻等問題,可參考JCC,29,1440文中的討論。
直接繪制電子密度圖、電子密度拉普拉斯圖顯然也是表征電荷分布的直觀的方法。
分析電子分布的方法也完全可以用來單獨分析alpha電子、beta電子或者自旋密度的分布。比如可以直接作自旋密度圖、通過Mulliken分析得到特定原子軌道上的自旋布居數、做盆分析/模糊空間分析得到特定區域內自旋電子數。這對于研究磁性體系、自由基體系是很有用處的。更多討論見《談談自旋密度、自旋布居以及在Multiwfn中的繪制和計算》(http://www.shanxitv.org/353)。
5.6 反應性、反應位點預測
預測反應位點的方法很多,比較重要的包括分析前線軌道成份、計算原子電荷、考察分子范德華表面上靜電勢以及平均局部離子化能的極值點分布、計算福井函數、計算雙描述符,還有人通過分析電子密度拉普拉斯函數的特征來討論被親核、親電進攻的位點和難易程度,如JPC,95,4698。這些分析方法在Multiwfn里全部能實現。有關的原理和操作可參見手冊4.A.4節、專門介紹各種反應位點預測方法的幻燈片Predicting reactive sites(http://www.shanxitv.org/234)、前述的《談談軌道成份的計算方法》和《使用Multiwfn的定量分子表面分析功能預測反應位點、分析分子間相互作用》。強烈建議一看的文獻是筆者撰寫的《親電取代反應中活性位點預測方法的比較》(物理化學學報,30,628 (2014)),其中對各種預測親電反應位點的方法進行了介紹和對比測試。
5.7 芳香性分析
Multiwfn支持的用來芳香性的方法多達十幾種,如AdNDP、ELF-sigma/pi、FLU/FLU-pi、PDI、多中心鍵級、HOMA、ICSS等等。原理與操作方法的介紹見《衡量芳香性的方法以及在Multiwfn中的計算》(http://www.shanxitv.org/176)和前述的《通過Multiwfn繪制等化學屏蔽表面(ICSS)研究芳香性》。另外,Multiwfn還提供了輔助計算非平面體系、扭曲環的NICS_ZZ的功能,見《利用Multiwfn計算傾斜、扭曲環的NICS_ZZ 》(http://www.shanxitv.org/261)。
5.8 電子躍遷分析
Multiwfn在電子激發分析上的極度豐富和強大,使用Multiwfn是電子激發問題研究中必不可少的。只要熟練掌握、靈活運用Multiwfn,在研究電子激發問題時會倍感如虎添翼,完全不愁不會分析、文章沒的可寫。在《Multiwfn支持的電子激發分析方法一覽》(http://www.shanxitv.org/437)中筆者對Multiwfn在電子激發研究中能做的所有分析做了全面匯總,經常研究電子激發的人請務必閱讀。
5.9 分子性質預測
Multiwfn可以計算分子體積、分子面積(由電子密度等值面定義)、分子表面上靜電勢的最大和最小值/平均值/方差/電荷分離程度/電荷平衡程度等分子描述符,利用它們來構建QSPR關系可以很好地預測分子凝聚相性質,如密度、升華焓、熔點、沸點、臨界壓力等。也可以用來構建定量結構活性關系(QSAR)來預測分子的生物活性。見《使用Multiwfn預測晶體密度、蒸發焓、沸點、溶解自由能等性質》(http://www.shanxitv.org/337)。
例如JPCA,110,1005就構建出一套關系可以成功地用來預測蒸發焓,即:delta_H_vap=a*sqrt(S)+b*sqrt(v*sigma2)+c,其中S是分子表面積,v是電荷平衡程度,sigma2是分子表面靜電勢的方差,a/b/c都是擬合得到的參數。
5.10 導電分析
如4.8節所述,Multiwfn可以通過基于對分子軌道能級進行展寬來得到TDOS,還能得到PDOS和OPDOS。從TDOS圖可以考察不同能量區域軌道分布的疏密,特別是Fermi能級位置,如果TDOS曲線有明顯的凹陷則意味著有相對較大的gap,導電性也相對較弱。通過PDOS可以考察TDOS的組成,在前線軌道區域有較大PDOS的片段內的原子與導電/電子激發有較密切的關系。
ELF-pi、鍵級等指標對于探討寡聚物的導電能力有直接幫助,例如文獻RSC Adv.,2013,3,25881給出了鍵級與寡聚物能隙之間的擬合關系,相關系數非常高。文章還基于ELF-pi分析了pi電子離域性與導電性的關系。
對于分子晶體或寡聚物體系,體系的導電能力和單體間電荷轉移積分有密切關系,而電荷轉移積分又與單體間的軌道重疊積分有很強的相關性。Multiwfn可以利用Gaussian輸出文件計算出單體軌道間重疊積分值。而且利用Multiwfn還可以以一種新穎的圖形化的方式考察單體間的交疊程度和交疊方式,重疊積分數值大小的成因可以一目了然地搞清楚,見前述的《分子間軌道重疊的圖形顯示和計算》。
Multiwfn的主功能100里的功能18可以幫助使用者基于Yoshizawa的公式(Acc.Chem.Res.,45,1612)獲知共軛體系內電子易于在哪些位點間轉移,見手冊4.100.18節的例子。
5.11 繪制光譜圖
如4.9節所述,Multiwfn可以基于量子化學計算數據產生可以與實驗圖譜相對比的IR/Raman/UV-Vis/ECD/VCD/ROA圖。雖然很多計算化學可視化程序也附帶了這一功能,但Multiwfn的靈活程度是絕大多數程序不能及的,而且提供了其它程序根本沒有的高級功能。詳見前述的《Gaussian中用TDDFT計算激發態和吸收、熒光、磷光光譜的方法》、《使用Multiwfn繪制構象權重平均的光譜》。
5.12 (超)極化率研究
如第4節末尾所述,Multiwfn在研究(超)極化率方面也極為有用,可以解析Gaussian程序的(超)極化率輸出并輸出平時研究中重要的量,可以基于完全態求和(SOS)計算(超)極化率,而且利用Multiwfn主功能3、4、5的自定義運算功能還能很方便地考察(超)極化率密度,這可以直觀、透徹地考察體系不同區域對(超)極化率的貢獻,也可以用于探討不同計算級別導致(超)極化率計算結果存在差異的內在原因,見《使用Multiwfn計算超極化率密度》(http://www.shanxitv.org/305)。
5.13 結構化學教學
給本科生講述結構化學的時候,將問題用直觀的圖形來展現遠比用復雜抽象的數學公式來討論更容易讓學生們理解、激發學習興趣。目前的結構化學的教學大綱普遍十分陳舊,筆者建議適當將簡單易懂又有重要實際意義的波函數分析理論適當引入課程。
Multiwfn在結構化學教學上有很多用處。例如講述原子殼層結構、討論原子軌道時,就可以利用Multiwfn方便地作出相應的圖形展現它們的特征。這個應用在《使用Multiwfn繪制原子軌道圖形、研究原子殼層結構及相對論效應的影響》(http://www.shanxitv.org/152)一文中有詳述。討論前線軌道的時候也可以用Multiwfn作出各種形式的圖來。
在討論共價鍵/離子鍵,非極性鍵/極性鍵的時候,就可以向學生們展示電子密度拉普拉斯圖或密度差圖,其物理意義對于量子化學外行人來說也很容易理解。在講述VSEPR模型的時候,可以展示電子密度拉普拉斯函數的(3,+3)臨界點位置(即此函數極小點的位置,這是電子凝聚程度局部最大的位置),這種臨界點位置和VSEPR模型描述的雜化方式有很好對應性。講述多中心鍵時建議結合多中心鍵級、AdNDP軌道圖以及ELF圖形來討論。在講述金屬配合物電子結構的時候,建議將CDA分析結果、CDA模塊繪制出的軌道相互作用圖連同軌道圖形展現出來。在講述氫鍵、范德華作用的時候,可以將上述RDG分析方法給出的圖形展現出來,既漂亮又易懂。
涉及到化學反應過程時,將前述的IRC路徑上的鍵級變化曲線,以及反應過程中ELF或密度差圖變化的動畫向學生們展示,必然會使學生們豁然開朗。
目前也已有文獻專門討論Multiwfn在結構化學教學中的應用,見《Multiwfn在分子軌道理論教學中的應用》(廣州化工,40,69)和《Gaussian和Multiwfn軟件在結構化學教學中的應用》(首都師范大學學報(自然科學版),33,23)。
5.14 其它
Multiwfn還有很多很多其它的應用,比如作為.fch、.molden、.wfn等格式文件到.wfn/.wfx/.pdb/.xyz/.molden/.gjf/.47等格式文件的格式轉換器、編輯和檢查波函數文件、監控SCF收斂、做簡單的能量分解、作為格點文件統計/處理以及相互運算的工具(諸如Gaussian的cubman程序完全可以被Multiwfn所替代)等等等等,請結合手冊介紹和例子自行探索。
Multiwfn還可以用來計算分子的直徑、長寬高,見《使用Multiwfn計算分子的長寬高以及顯示分子的主軸》(http://www.shanxitv.org/426)。Multiwfn與VMD結合還可以把分子的各種原子屬性以著色方式展現,用在自己的文章當中視覺效果很好,見《使用Multiwfn+VMD以原子著色方式表現原子電荷、自旋布居、電荷轉移、簡縮福井函數》(http://www.shanxitv.org/425)。
Multiwfn在理論化學計算方法的研究上也有很多用處。比如Science, 355, 49 (2017)中,作者利用Multiwfn研究了幾十種不同年代不同類別的DFT泛函對電子密度的描述精度,從而討論了DFT的發展方向。在PCCP, 18, 24015 (2016)和JCTC, 13, 2705 (2017)中Matito等人提出了分離動態和非動態電子相關的方法,而且還可以將他們在體系的不同區域的大小通過圖形化方式展現,這種分析方法在Multiwfn已經被支持,見手冊4.A.6節、3.200.15節的示例。
6 總結與展望
Multiwfn的推出大大拉低了波函數分析的門檻。以往許多十分重要的但只有專家們才會做的分析,如今變得可以被廣大量子化學工作者所方便地利用,在實際問題的研究中已產生了巨大價值。也正因為拉低了門檻,使不少原先被束之高閣少有人問津的卻又有重要實際價值的波函數分析方法進入了廣大量子化學研究者們的視野。波函數分析的概念、意義想必也因此更加地深入了人心。Multiwfn的開發不會終止,而是會不斷發展、完善,變得更強大、更高效、更好用,成為量子化學領域公認的世界第一的波函數分析程序。