衡量芳香性的方法以及在Multiwfn中的計算
補充:在此文撰文之后Multiwfn又支持了ICSS方法圖形化分析芳香性,極具實用價值,見《通過Multiwfn繪制等化學屏蔽表面研究芳香性》(http://www.shanxitv.org/216)。
衡量芳香性的方法以及在Multiwfn中的計算
文/Sobereva @北京科音
First release: 2013-Jan-23 Last update: 2021-Dec-26
摘要:本文首先先介紹芳香性的基本概念,然后對比較重要、目前比較流行的和近年來新提出的衡量芳香性的方法依次進行介紹,并談談筆者的看法。其中可以在Multiwfn程序中實現的方法會介紹操作過程。最后對實際應用中芳香性指標的選擇進行討論。
順帶一提,筆者對18碳環體系曾做過大量的理論研究,匯總見http://www.shanxitv.org/carbon_ring.html。其中有兩篇文章專門討論18碳環和18碳環衍生物C18-(CO)6的芳香性,綜合運用了本文中不少方法,十分推薦閱讀和作為范例引用,分別見Carbon, 165, 468 (2020) DOI: 10.1016/j.carbon.2020.04.099和Chem. Eur. J., 28, e202103815 (2022) DOI: 10.1002/chem.202103815,后者還有專門深入淺出的介紹文章:《深入揭示18碳環的重要衍生物C18-(CO)n的電子結構和光學特性》(http://www.shanxitv.org/640)。
1 什么是芳香性
芳香性是一個十分古老,重要,又含糊的化學概念。苯是最具典型的芳香性分子,也是芳香性的原型分子。與芳香性有關的文章近十幾年來增速十分迅猛,如今可以說已經過熱、被過分炒作。新的衡量芳香性的指標也不斷被提出,同樣在近年來增速迅猛,目前總計已有數十種。這些指標體現了芳香性的不同側面,其中絕大部分依賴于量子化學計算。芳香性難以給出一個確切、唯一的定義,實際上芳香性這個詞包含的內容被不斷地廣義化,以至于越來越不可能給出一個既簡單、精確又能被所有研究者接受的定義。芳香性分子在能量、結構、反應性、磁性質、電子結構等方面都展現出獨特的特征。對于大量芳香性體系,利用統計分析,可以發現它們總是同時具有很多特征,如:鍵長均衡化、電子呈高度整體離域性、外磁場下能形成整體誘導環電流、有較大離域化能、結構穩定等等,因此這樣來看只要考察某分子的某個方面特征就能衡量其芳香性高低。但是對于不少分子,它們具有的各種特征之間的相關性并不滿足上述大規律,這被稱為芳香性的多維性,因此為了合理地描述芳香性就不得不同時考慮數種基于分子不同性質的芳香性指標。
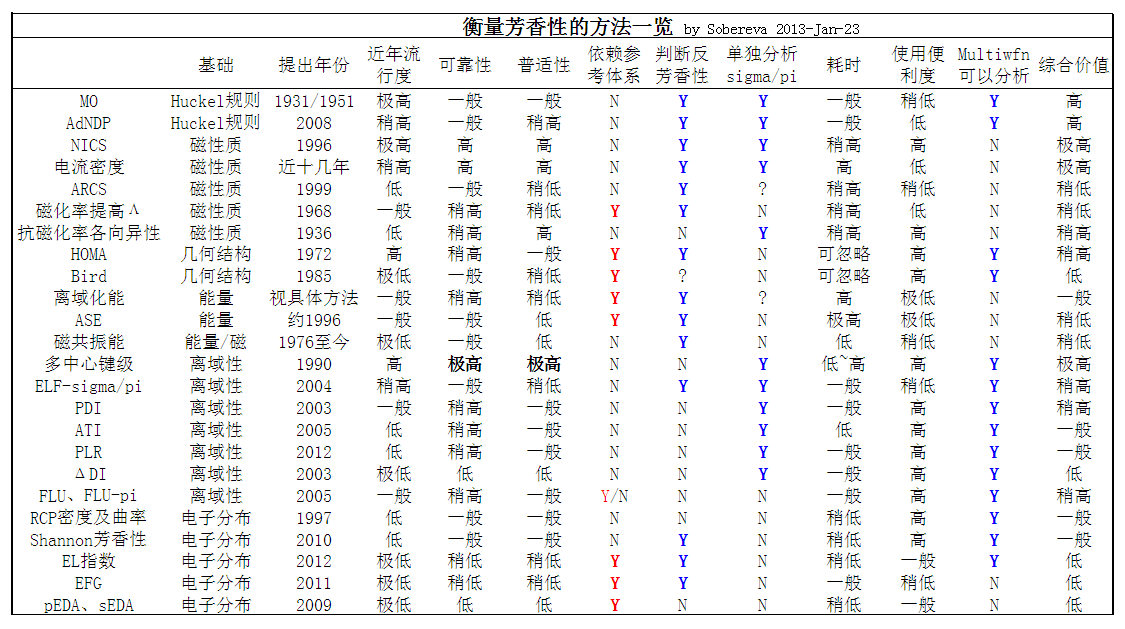
下面的表格列舉了芳香性、非芳香性和反芳香性體系一部分常見特征,有的內容并不很準確,僅供參考,取自Chem.Rev.,105,3716(2005)。
雖然芳香性這個話題越來越復雜化,不同研究者的觀點不同。一個經典、古老、被化學工作者所普遍認知的關于芳香性的說法是Huckel規則:環上的分子軌道若具有4n+2電子占據則環具有芳香性。但是這個說法比較狹義,從理論化學角度也沒觸及物理本質。如果要對芳香性的本質做一下解釋,那么寡人的觀點是:對于一個環,若電子能夠在整個環上高度離域,則環具有芳香性。雖然如上所述,芳香性具有多維特征,但很多都是外在表象,真正的源頭是電子的離域。若電子沒法在環上充分離域,那么芳香性就無從談起。
這里說的環是指電子的整體離域路徑構成明顯的環路,環的幾何結構可以偏離圓形,可以是扭曲的不在一個平面的。環形離域路徑不一定非得沿著分子的拓撲結構,比如某個局部結構是-C1-C2-C3-,若C1和C3離得近且軌道匹配,電子可以直接從C1跨過C2向C3離域;甚至還可以在分子片段間,乃至不同分子間有很強離域而構成整體環形離域路徑,這被稱為跨鍵或跨空間芳香性。另外還有很多文章研究球形芳香性,但這不屬于本文涉及范圍,相關綜述見Chem.Rev.,105,3613(2005)。
通常能夠明顯整體離域的是pi電子(絕大多數有機分子中sigma鍵定域性太強),這樣的芳香性就是pi芳香性。如果整體靠的是sigma電子,就叫sigma芳香性。如果又有pi又有sigma的貢獻,叫二重芳香性。雖然研究的最多的是有機分子的芳香性,但小的金屬團簇(或金屬和非金屬混合團簇)的芳香性,即全金屬(半金屬)芳香性也受到廣泛關注,對于這些體系sigma鍵的電子和delta鍵(d軌道構成)的電子和金屬芳香性密切相關,有的團簇有人指出同時具備sigma,pi,delta三重芳香性,有的有pi,delta二重芳香性,等等,種類繁多。對于過渡金屬團簇還可以利用f電子產生φ芳香性。
本文并非芳香性的綜述,不會去回溯芳香性的歷史,不會去列舉五花八門稀奇古怪的芳香性體系,不會去討論一些新奇的概念。本文的目的在于歸納、簡要介紹有歷史意義的、目前流行的和新提出的衡量芳香性的方法,并對之發表一些灑家的觀點。此文并非一覽無余地囊括所有已經提出的衡量芳香性的方法,因為數目太多,而且有很多實際意義不大,或者純屬跟風。對于那些能在Multiwfn程序中計算的方法本文會介紹操作過程。
Multiwfn可以計算大量考察芳香性的方法,包括:AdNDP、FLU/FLU-pi、PDI、ATI、PLR、HOMA、Bird指數、多中心鍵級、Shannon芳香性、LOL/ELF-sigma/pi、RCP處的電子密度及垂直于環平面的密度曲率、EL指數、AV1245、ICSS等。Multiwfn可以在此處免費下載:http://www.shanxitv.org/multiwfn,讀者請使用網站上的最新版本,否則可能與本文敘述的一些內容不符。如果你不了解Multiwfn,強烈建議參看《Multiwfn FAQ》(http://www.shanxitv.org/452)。如果你不知道什么時候該用什么格式作為輸入文件,或者不知道怎么產生要用的輸入文件的話,看《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。簡單來說,對于Gaussian的用戶而言,使用fch作為輸入文件可以用Multiwfn做本文提到的絕大部分分析。
由于基于Huckel規則判斷芳香性的方法屬于經典、有重大意義的方法,所以先在第二節對之進行介紹。之后,會按照基于磁性質、基于幾何結構、基于能量、基于電子離域性、基于電子分布的順序來介紹各種衡量芳香性的方法。最后,將對本文涉及的方法進行比較和總結,談談各種場合下筆者推薦的方法。
2 基于Huckel規則的方法
Huckel規則源自他在1931年的研究,但是直到1951年,Huckel規則在Doering的研究文章JACS,73,876中才被明確化為眾所周知的4n+2規則。Huckel規則原本是基于MO軌道來分析,但是碰到含有多元環情況通常就瞎了,此時需要基于AdNDP軌道才能分析局部的環的芳香性。
2.1 MO結合休克爾規則判斷芳香性
這種判斷芳香性的方法就是考察分子軌道(MO)圖形,找出環上的MO,如果這些軌道上總電子數滿足4n+2,則這個環具有芳香性。如果滿足的是4n,則具有反芳香性。
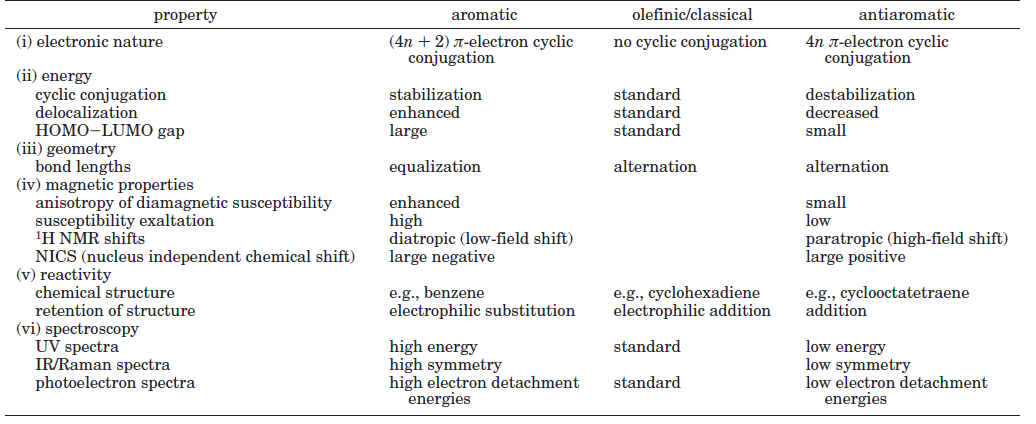
比如苯,以下是其雙占據的三個pi軌道圖,它們一起構成六中心的共軛環路,共6個電子,滿足4n+2,故具有典型的芳香性。
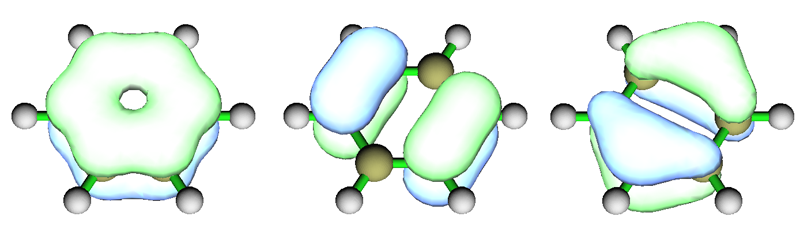
再看個復雜點的例子,中性狀態的Li7團簇。圖取自文獻。
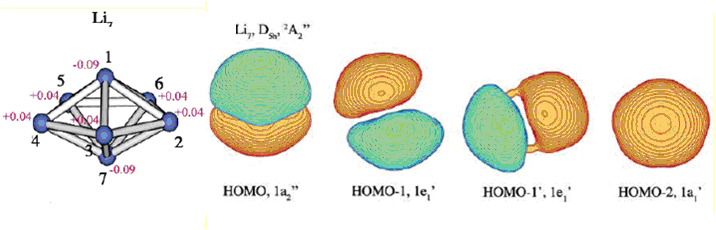
HOMO是構成pi芳香性的軌道。如果是兩個電子占據,即n=0,則將是典型的pi芳香性。但目前它只有一個電子占據(準確來講應當叫SOMO),因此比典型pi芳香性要弱,這可以算作是部分pi芳香性。HOMO-1、HOMO-1'和HOMO-2是構成sigma芳香性的軌道(軌道相位類似于苯的pi軌道),它們都被雙電子占據,n=1,故是完美的sigma芳香性。由于此體系sigma和pi都對芳香性有貢獻,所以算雙芳香性。
對于一個體系,若多種類型軌道都對芳香性有貢獻,則整體的芳香性會因累加而變得更強。如果有的軌道呈芳香性而有的呈反芳香性,則它們會彼此抵消,整體是芳香性還是反芳香性就看是誰起主導作用了。
不同電子態對應不同電子排布,因此也影響芳香性。例如某閉殼層體系單重態是4n反芳香性,如果把原先參與反芳香性的軌道上的一個電子電離掉,那么4n就被破壞了,從而反芳香性被大大削弱。如果這個電子被激發到相同環上的空軌道上,構成三重態,那么當前電子結構可以視為是本應構成4n+2的一批雙占據軌道中有目前兩個是單占據的(或者說,如果把這兩個單占據軌道都再補上一個電子就滿足了4n+2),故是不完美的4n+2,此時會有部分芳香性,即電子激發實現了反芳香性和芳香性的轉化。
正如Li7例子所示的,并非只有平面結構才能根據考察軌道來判斷芳香性。但是,用于結構復雜,特別是非平面的情況,這種根據MO分析芳香性的方式往往很不好用、很含糊、很麻煩。因為MO圖形往往較為復雜,有很多節點,涉及到體系諸多原子,時常沒法判斷哪些軌道是參與芳香性的;而且很多MO涵蓋的空間范圍廣(尤其是大體系),它們只是部分地參與構成某些環的芳香性,計算4n/4n+2時是否把它們算進去根本說不清楚,或者說這么判斷根本在原理上就行不通。而且,這種看軌道圖形數電子數的方法的判斷只是定性的,沒法定量地判斷芳香性的強弱。如今經常有文章利用這種方法討論芳香性,討論的結果令人匪夷所思。一方面是這種分析方法局限性太大,另一方面也是作者自身有問題,軌道選得莫名其妙,令人不禁覺得:憑什么把這些軌道算進4n/4n+2里?我不很鼓勵使用這種方法分析芳香性,或者至少也得結合使用一種可靠的能定量計算芳香性的方法。
Huckel規則是對一般體系來說的。對于Mobius型分子,即共軛環的鏈扭轉了(2M+1)*pi M=0,1,2...弧度的分子,滿足的是Mobius芳香性。相當于把Huckel規則反過來,即4n對應芳香性,而4n+2對應反芳香性。
2.2 AdNDP軌道結合休克爾規則判斷芳香性
上一節介紹的方法的主要局限性之一是MO離域性太強,即往往同時涵蓋很多原子。當體系原子較多,有很多環可能同時具備芳香性/反芳香性,就很難靠MO來判斷。例如菲就是這樣,沒法直接靠高度離域的MO來討論它的三個環的芳香性。這時需要使用AdNDP方法,原文見PCCP,10,5207(2008)。這種方法獲得的AdNDP軌道是“半定域化軌道”。AdNDP軌道既不像MO離域程度那么高,也不像傳統的定域化軌道定域程度那么強(但中心或雙中心軌道),而是介于兩者之間,既在一定程度上定域化,又能表現體系局部區域的離域性。關于AdNDP的原理和在Multiwfn中的操作另有一帖專門介紹,就不在這里詳談了,見《使用AdNDP方法以及ELF/LOL、多中心鍵級研究多中心鍵》(http://www.shanxitv.org/138)
菲的在邊緣芳香環上的pi型AdNDP軌道圖形如下:
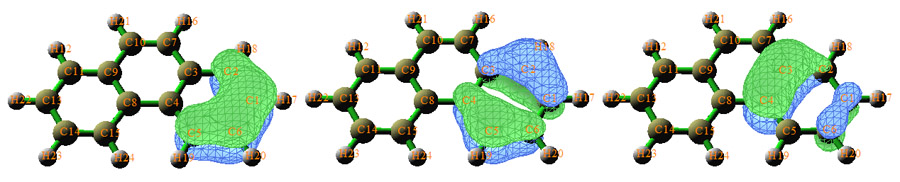
可見這三個軌道和苯的三個pi軌道很相似,因此它們構成了六中心共軛。這三個軌道占據數并非像苯一樣都是完美的2.0,而是在1.8~2.0之間,基本符合4n+2規則。這說明這個環雖然有明顯的芳香性,但是和苯相比要弱一些。假設基本符合的是4n規則,那么就是反芳香性。
如菲的例子所見,AdNDP方法很有用,不僅能考察局部的芳香性或反芳香性,還能根據占據數大致說明其程度的強弱。但是AdNDP的威力被某些文章作者(包括一些大牛)過分鼓吹、胡作非為亂發文章。AdNDP的最大軟肋就是搜索AdNDP軌道的過程對一些復雜體系任意性往往太強,人為干預太大,不同研究者可以得出不同結果,以至于,在JOC上某篇文章,coronene中心的根本算不上是芳香性(按照NICS還應該算反芳香性)的環居然被作者胡亂分析成芳香性。反正AdNDP的結果怎么解釋都有道理,別人也不好質疑,但是結果可靠性有多高(也即AdNDP搜索過程含糊性有多大),只有作者自己心里有數。寡人絕非不鼓勵用AdNDP,只是說,對于某些體系,如果用的過程中自己覺得心里很沒底,干脆就別用了,勿在文章中強詞奪理。目前亂用AdNDP分析芳香性的文章實在多得很,對于復雜的體系的分析結論,大家閱讀時不要不加懷疑地相信。如果某個體系的芳香性比較重要,筆者鼓勵大家自行重新找一遍AdNDP軌道以檢驗文章結論。
3 基于磁性質的方法
本節介紹的方法基于體系對外磁場的響應行為。
3.1 核獨立化學位移(NICS)及相關的方法
可以說NICS是目前用得最多、接受度最高的衡量芳香性的方法。原文是JACS,118,6317(1996),在Chem. Rev.,105,3842(2005)中有詳細的綜述,在Org. Lett.,8,863(2006)對幾種定義進行了對比分析。
NICS原始的定義是:環上重原子的幾何中心處的各向同性化學屏蔽值的負值,以ppm為單位。
因為考察的這個點不是原子核位置,所以叫“核獨立”。對于芳香性體系,一般這個屏蔽值是正值,即NICS為負,本質是因為外磁場導致的共軛環上的環電流產生的感生磁場會一定程度對外磁場有抵消(屏蔽)作用。對于反芳香性體系,環電流的感生磁場和外磁場方向相同,故會加強外磁場,所以這個屏蔽值為負,NICS即為正。
實際上,在實驗上也有類似于NICS的做法來測定芳香性,但用的是比較輕的原子核,諸如He_3、Li+離子、橋氫原子來作為探針,讓它們與芳香環構成復合物穩定在芳香環的面上,通過測定它們的化學位移就可以衡量環的芳香性。雖說這用的是實實在在的原子核來測定,但和NICS的思想本質是完全一致的。
多數成熟的量子化學程序都能很容易地計算NICS,這是NICS之所以這么流行的主要原因之一。這里以Gaussian計算菲的邊緣的環和中間的環為例來說明。獲得幾何中心的X、Y、Z坐標就是把環上重原子的X、Y、Z坐標分別取平均。假設邊緣和中央的環的幾何中心為(0.000000,-2.155707,-0.338053)和(0.000000,0.000000,0.859657),就在Gaussian輸入文件原子坐標后面寫上:
Bq 0.000000 -2.155707 -0.338053
Bq 0.000000 0.000000 0.859657
其中Bq代表虛原子,這使得Gaussian輸出這些位置的NMR信息。然后Route Section部分寫上NMR關鍵詞,以及所用理論方法、基組,然后開始運算即可。默認使用的是GIAO方法計算NMR,絕大部分文獻報道的NICS值都是這個方法計算的。如果用其它方法,如NMR=CSGT,當基組不很完備時結果會與GIAO的稍有不同。建議大家的研究文章中要注明計算NMR所用的方法,以便讀者重現。計算NICS用不著很高級別的方法和基組就能得到合理結果,通常用B3LYP/6-31+G*就可以。
從輸出文件中可找到這兩個環中心的NMR信息
25 Bq Isotropic = 8.7039 Anisotropy = 5.0411
XX= 12.0647 YX= 0.0000 ZX= 0.0000
XY= 0.0000 YY= 6.3843 ZY= -0.7977
XZ= 0.0000 YZ= -0.8627 ZZ= 7.6628
Eigenvalues: 5.9758 8.0713 12.0647
26 Bq Isotropic = 5.4377 Anisotropy = 3.7470
XX= 1.3628 YX= 0.0000 ZX= 0.0000
XY= 0.0000 YY= 7.0146 ZY= 0.0000
XZ= 0.0000 YZ= 0.0000 ZZ= 7.9357
Eigenvalues: 1.3628 7.0146 7.9357
其中3*3矩陣是磁屏蔽張量。之所以描述為張量的形式是因為電子對不同方向射來的磁場屏蔽強度是不同的。這個張量矩陣乘以外磁場矢量得到的矢量的負矢量就是感生磁場矢量。磁屏蔽張的對角元的平均就是Isotropic后面的值,也就是各項同性屏蔽值,這也是NMR實驗所對應的結果。邊緣環的NICS即是-8.7039,中央環的NICS即是-5.4377,由于都是負值表明都呈現芳香性;由于前者更負,所以表明邊緣的環的芳香性更強。
最初的NICS定義,也被稱為NICS(0),被指出在不少體系都不很適用。主要毛病是它取的是各項同性值,而非垂直于環平面的屏蔽張量的分量。然而只有這個分量值,才和環上離域的電子對應的環電流所產生的感生磁場直接相關,才真正能清楚地展現芳香性特征,這個問題在Org. Lett.,8,863(2006)有詳細討論。這篇文章推薦用NICS(1)_ZZ來衡量芳香性,筆者也確實發現這個指標遠比NICS(0)好得多得多。到現在仍有很多文獻沒完沒了地批判NICS,實際上批的都是NICS(0),大部分NICS(0)不適用的體系(諸如(HF)3環狀三聚體被NICS(0)誤判為芳香性)在NICS(1)_ZZ上都沒問題。奇怪的是,這些文獻總是無視NICS(1)_ZZ的存在卻緊咬著NICS(0)不放,簡直是莫名其妙。NICS(1)_ZZ就是指的在環平面上方1埃處(具體來說,是以環中心為起點向垂直于環平面方向挪1埃),垂直于環平面方向的屏蔽張量分量值的負值。假設分子平面是XY、YZ、XZ平面,那么這個分量值就是分別指的ZZ=、XX=、YY=后面的值。由于在環上方1埃處sigma軌道效應影響很小,所以NICS(1)_ZZ衡量的主要是pi芳香性。如果想在NICS框架內把sigma和pi對芳香性的貢獻單獨分析,可參見《基于Gaussian的NMR=CSGT任務得到各個軌道對NICS貢獻的方法》(http://www.shanxitv.org/670)和《將核獨立化學位移(NICS)分解為sigma和pi軌道的貢獻》(http://www.shanxitv.org/145)介紹的做法。
對于被研究的環不處在笛卡爾平面上,或者環是扭曲的情況,計算NICS(1)_ZZ是很麻煩的,不過Multiwfn有專門的功能來解決這個問題,見《利用Multiwfn計算傾斜、扭曲環的NICS_ZZ》(http://www.shanxitv.org/261)。另外值得一提的是,在RSC Adv.,6,23900(2016)當中作者對于非平面體系分別定義了NICS(1)和NICS(-1)兩個量,分別是凸面和凹面上方1埃處的NICS,還定義了幾個相關的量,比如NICS(1)av=[NICS(-1)+NICS(1)]/2用來衡量兩個面NICS的平均值、NICS(1)diff=NICS(1)-NICS(-1)用來衡量兩個面的NICS差值。文中指出體系的非平面性,以及手性,可能會造成兩個面NICS值的分裂,即NICS(1)diff不為零。文中還強調,NICS(1)和NICS(-1)兩個量衡量的是兩個面各自的芳香性,而不是環的芳香性,用這兩個值可以討論兩個面特征的差異性,比如反應性的不同。
計算NICS用的環中心怎么定義有含糊性,原文用的是幾何中心,若使用AIM理論定義的電子密度的環臨界點(RCP)在物理意義上更好一些,有文章(如DOI: 10.1002/wcms.1115)表明使用RCP比使用幾何中心在結果上更合理。RCP可以通過Multiwfn的拓撲分析功能很方便地得到,見《使用Multiwfn做拓撲分析以及計算孤對電子角度》(http://www.shanxitv.org/108)。對于計算幾何中心和質心,在Multiwfn也提供了一個小功能來實現,這比手算要方便。在啟動Multiwfn并載入含有分子結構信息的文件后(pdb/xyz/fch/wfn等等文件類型皆可),選100,再選21,然后輸入環上的重原子序號,如3,4,8,9,10,7,則它們的幾何中心和質心就會輸出出來。
在NICS的基礎上有人還做了進一步擴展,比如不僅僅考慮某個特定的點的屏蔽值,而是將磁屏蔽值作為一個實空間函數來考慮,通過繪制曲線圖、平面圖、等值面圖來研究以獲得更全面的信息,這叫ICSS,介紹和計算例子見《通過Multiwfn繪制等化學屏蔽表面(ICSS)研究芳香性》(http://www.shanxitv.org/216)。再比如NICS-rate方法(CPL,493,376(2010)),它以NRR(NICS-Rates Ratio)來衡量芳香性,NRR=|rate(Max)/rate(Min)|,這里rate(Max)和rate(Min)分別代表穿過環中心垂直于環平面的直線上NICS導數的最大值和最小值。
有人認為NICS不適合衡量尺寸不同的環的芳香性,但也有證據表明NICS對環的尺寸依賴性雖然有但是不太大。
3.2 磁感應電流密度與AICD
磁感應環電流在上一節已經提到了。當環上電子離域性很強,能在環上自由移動,類似于導體,外加磁場時就會像環形線圈一樣產感應電流,并且會在一定程度上抵消外磁場而表現抗磁性。感應電流方向如下所示
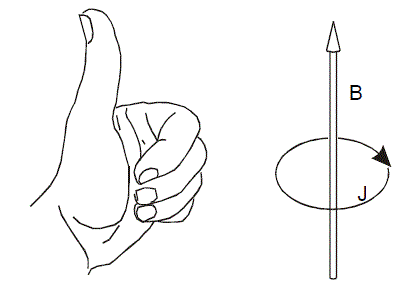
電流越強芳香性越強。如果感應電流的方向和左手定則相反,則會加強外磁場,表現出順磁性,說明環具有反芳香性,而且電流越強反芳香性越強。如果沒有產生明顯的貫穿整個環的感應電流,說明這個環是非芳香性的。
感應電流不同位置的強弱和方向可以通過作圖來直觀考察,也可以對某些鍵的截面進行積分來獲得電流大小的定量數據,這用GIMIC程序可以做到。AICD方法則是根據屏蔽張量矩陣元定義了一種實空間函數,它的數值越大的地方對應電流密度越大處。由于它是標量函數,所以可以很方便地通過繪制等值面圖來考察,并可以認為數值較大的等值面包含的區域內電子有較強離域性,其功能某種程度上類似于后面要提到的ELF。而且,這個實空間函數的二分點(詳見后文的ELF)大小表明了兩個區域間電子相互離域的程度。如果某處的AICD等值面只有將數值調得很大的時候才分離為兩個等值面,那么說明電子容易在這兩個等值所含區域間離域,環電流也容易通過,這對于證實是否有跨空間芳香性很有用,也是一種判斷芳香性強弱的定量指標。實現AICD方法有同名的程序,這程序可以將電流密度矢量直接標注AICD等值面圖上,考察感應電流分布十分方便,例如:
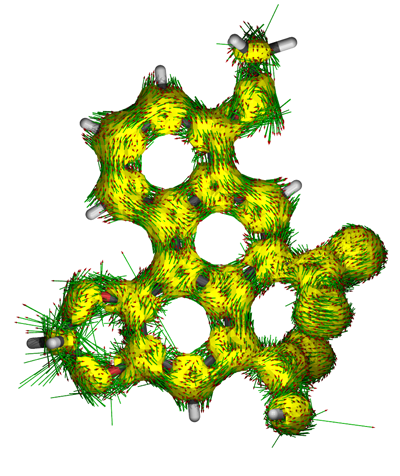
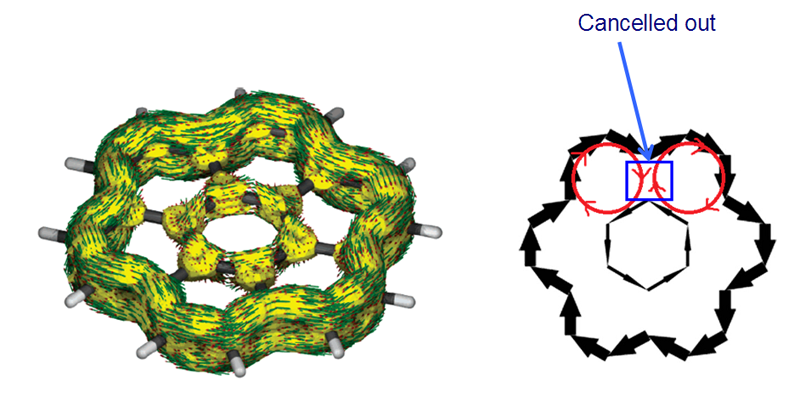
繪制感應電流密度圖是十分有用的方法,能讓電子離域路徑、芳香性/反芳香性/非芳香性區域很客觀地展現出來,但是對于較大的多環芳烴這樣有多個共軛環連續出現的體系分析起來容易造成誤導,內部電流密度的相互抵消導致一些環的芳香性特征在感應電流密度圖上被掩蓋掉了。如下圖所示的coronene,環電流在方向相反的地方抵消掉了(右圖只是簡化的示意,其實這么表示不嚴格),因此導致表面看起來仿佛6個外圍的六元環不是芳香環,而內部的環表現出反芳香性的假象。當芳香環數目更多,誤導性往往更強。
當外磁場方向與環垂直時,NICS_ZZ和磁感應電流密度在物理本質上有很直接的對應關系。如果看到某個環的環電流與左手定則相同/相反,那么表現在NICS_ZZ數值上也會是芳香性/反芳香性。這里NICS_ZZ未必是NICS(1)_ZZ,例如環電流是sigma電子貢獻的,那么考察NICS(0)_ZZ就比考察NICS(1)_ZZ更妥當,因為平面上方1埃處sigma電子的效應就比較弱了。由于感應電流密度圖分析方法用于分析較大的多環芳烴的芳香性上不很適合,這也導致NICS_ZZ不十分適合用于這類體系。
GIMIC相對于AICD的優點是:
(1)不僅支持HF/DFT,還支持后HF。特別是開殼層體系相關作用對電流密度影響強,尤為適合用CCSD。
(2)電流密度的分析能達到定量級別,比如對截面進行積分
相對缺點是
(1)對非平面體系可視化不方便
(2)沒法將電流密度分離為正則軌道的貢獻,因此不適合分析多重芳香性,特別是金屬芳香性體系的芳香性本質。而AICD則允許只考察指定的分子軌道產生的電流密度。
AICD和GIMIC筆者在《使用AICD程序研究電子離域性和磁感應電流密度》(http://www.shanxitv.org/147)和《使用GIMIC計算和分析磁感應電流密度》(http://www.shanxitv.org/155)中有過詳細介紹,建議大家一看。AICD和GIMIC程序最初版本用起來頗麻煩,后來都出了2.0版,可以基于最常用的Gaussian程序計算,相關操作在這里寫得非常詳細:《使用AICD 2.0繪制磁感應電流圖》(http://www.shanxitv.org/294)、《考察分子磁感生電流的程序GIMIC 2.0的使用》(http://www.shanxitv.org/491,含24分鐘演示視頻)。
除了前面已提及的AICD和GIMIC,還有一種CTOCD-DZ(continuous transformation of origin of current density-diamagnetic zero)方法也被不少研究者用于繪制感應電流密度,見JPCA,105,9553(2001)。此方法支持HF/DFT,并可以分解為軌道的貢獻。然而只有修改版的SYSMO程序能實現此方法,而此程序又不公開,所以這里就不多提它了。MRE是基于圖論和Huckel理論的計算感應電流的方法,這在后文有詳細介紹。
3.3 Aromatic ring chemical shieldings (ARCS)
按道理來說,先得已知感應環電流,才能得到感生磁場,才得到了磁屏蔽值。ARCS(PCCP,1,3429(1999))將這個過程反過來,先用量化程序算出穿過環中心且垂直于環的直線上各點的屏蔽值,以此為目標數據,通過擬合來得到感應環電流,并根據環電流大小和方向來判斷芳香性。ARCS的擬合模型用的是電磁學上最常見的無限細的圓環導體,其半徑也是被擬合的參數之一,通常比較接近于環的幾何半徑。
實際上ARCS方法和按照前面所討論的先計算電流密度再對某個鍵的截面進行積分來得到環電流數值在物理本質上并無差異,只是計算過程不同罷了。ARCS方法計算環電流有很大局限性,目前只能用于單個環,而且環必須接近圓形才行。如果將擬合的模型改為橢圓,倒也有可能用在諸如萘等鏈狀分子上得到分子整體的環電流。目前ARCS是對每個環用一個環形導線模型描述,但如果用多個,或許描述得更為細致,比如對于sigma+pi雙芳香性體系有可能同時擬合出sigma環電流和pi環電流。
原則上只要自己用的量化程序能算NICS就能靠ARCS方法得到環電流,某種程度上比分析感應電流密度方便點,不過擬合ARCS環電流的程序得自己寫,筆者認為其可靠性也不如直接分析感應電流密度。
3.4 磁化率提高Λ(Magnetic susceptibility exaltation)和抗磁化率各向異性
磁化率是順磁化率(正貢獻)和抗磁化率(負貢獻)之和,它們都用二階張量(矩陣)描述。
磁化率提高Λ(JACS,90,811(1968))主要用于實驗測定芳香性。假設化合物的各向同性磁化率為A,而對應的電子定域化的異構體的各向同性磁化率為B,則A減B就是Λ,體現了電子離域效應造成的額外的對磁屏蔽的效果。這里所指的磁化率是各項同性值,即磁化率張量對角元的平均值。Λ越負代表電子離域效應使實際體系磁化率降低得越多,芳香性越強;接近0代表非芳香性;越正代表反芳香性越強。Λ和NICS有很大雷同之處,物理本質也是相似的。從計算化學角度上看Λ沒什么價值,算起來也麻煩,算NICS就行了。
(注意此方法名字中的“提高”是指抗磁化率大小因電子離域導致的增加,增量越大也就是指抗磁化率數值變得更負,總磁化率更小。有些文中用到Λ時特意將名字中的Magnetic寫為diamagnetic以免混淆。另外注意,此方法的JACS原文及其它一些文獻中的Λ的數值的正負號與如今習俗是相反的)
抗磁化率χ的各向異性值Δχ自古就被用來衡量芳香性,因為其各向異性本質是由于環上電子離域性所產生的,和芳香性直接相關,這個概念的提出可以追溯到L.C.Pauling 1936年的文章JCP,4,673。Δχ=χ_11-(χ_22+χ_33)/2。這里χ_11、χ_22、χ_33指的是χ矩陣的絕對值由大到小的三個本征值,數值越負表明芳香性越強。χ也可以通過實驗或理論計算獲得。但是由于實驗上測定各向異性值需要先對化合物進行結晶,所以不如獲得Λ那么方便。
順磁化率/抗磁化率可以在Gaussian程序中通過NMR=Susceptibility計算。所得輸出文件中會有諸如這樣的抗磁化率信息
Diamagnetic susceptibility tensor (au)
XX= -263.8815 YX= 0.0000 ZX= 0.0000
XY= 0.0000 YY= -145.1938 ZY= 0.0000
XZ= 0.0000 YZ= 0.0000 ZZ= -136.8484
Isotropic diamagnetic susceptibility = -181.9745
由于當前體系是C2v對稱性,且計算時開啟了對稱性,使得輸出的抗磁化率張量直接就是對角矩陣,本征值就是對角元,故Δχ=-263.8815-(-145.1938-136.8484)/2=-122.8604 a.u.。如果矩陣不是對角化的,需要自行計算矩陣的本征值再算Δχ。
4 基于幾何結構的方法
本節介紹的方法只依賴于幾何結構信息,從鍵長的變化角度衡量芳香性。
4.1 Harmonic oscillator measure of aromaticity (HOMA)
HOMA是最為常用也是歷史十分悠久的基于幾何結構的衡量芳香性的方法。最初是在Tetrahedron Lett.,36,3839(1972)中定義的,后來在Chem.Inf.Comput.Sci.,33,70(1992)中被廣義化,表達式為
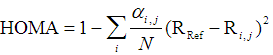
其中N是環上的原子數,i循環環上的每個原子,j是它的下一個原子,R是鍵長。α和R_ref都是事先計算好的常數,和鍵的類型有關,在原文中已提供,后者是理想的芳香性體系的平衡鍵長。HOMA的函數形式基于諧振勢,這是名字中Harmonic oscillator的由來。如果環上的所有鍵都和相應的R_ref相同,顯然體系就是理想的芳香性體系(例如苯),所以HOMA越接近1說明芳香性越強;若HOMA接近0,說明是非芳香性(α的確定方式就是使kekule結構的苯HOMA值精確為0);如果是負值,表現出鍵長極度不均衡,反映出反芳香性特征。
還有一些研究者在HOMA上動一些手腳,例如JPCA,107,7496(2003)中就把HOMA的鍵長替換為離域化指數,定義為θ指數;再比如Bultinck等人在J.Phys.Org.Chem.,18,706(2005)中提出的BOIA(Bond order index of aromaticity)定義為BOIA=1-(1/6)∑(B_i-B_ref),和HOMA主要差異也就是把鍵長替換為了鍵級。這類在HOMA上鬼鬼祟祟做一些小修改來得到新的芳香性指數的研究很無聊,非常沒創意,和HOMA定性結果往往也大同小異,筆者也就不屑于將之納入Multiwfn了。由于鍵級和模糊空間下的離域化指數在Multiwfn中都能算,因此θ和BOIA想算的話自己手算即可,也不麻煩。
在Multiwfn中提供了計算HOMA的工具,并且涉及到的參數都可以自定義。還是以菲為例,啟動Multiwfn后首先輸入包含菲的結構的文件,fch/wfn/wfx/pdb/xyz等等類型文件都包含分子結構信息所以都可以。然后選100,再選13進入HOMA計算界面。如果想自定義參數,就選1。按0可以開始計算,用戶需要輸入環上的原子序號,例如3,4,8,9,10,7(對應菲的中央的環)。這些原子必須依次相鄰,順時針還是逆時針順序都可以。之后結果馬上輸出出來,如
Atom pair Contribution Bond length
3(C ) -- 4(C ): -0.065698 1.427111
4(C ) -- 8(C ): -0.210455 1.458000
8(C ) -- 9(C ): -0.065698 1.427111
9(C ) -- 10(C ): -0.096016 1.435282
10(C ) -- 7(C ): -0.033673 1.360000
7(C ) -- 3(C ): -0.096016 1.435282
HOMA value is 0.432442
每個鍵的鍵長以及它對HOMA的貢獻值都會輸出。由于C4-C8偏離理想芳香鍵鍵長很大,導致HOMA值下降很多。接下來再計算邊緣的環,結果是0.855126,由于比中央的環更接近于1,所以明顯比中央的環芳香性更強。
HOMA的一個缺點是預先提供的參數比較有限,包括C-C、C-N、C-O、C-P、C-S、N-N、N-O,如果有其它元素參與就沒法用了。而且根本沒法用于研究諸如三個乙炔聚合形成苯環過程、Diels-Alder加成反應過程中芳香性的動態變化。HOMA的一個主要優點是只要有分子結構就行,不依賴于電子結構信息,計算量可以忽略不計。
4.2 Bird芳香性指數
Bird芳香性指數在Tetrahedron,41,1409(1985)當中被提出,表達式為
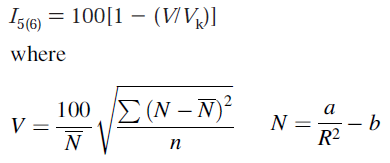
其中加和符號循環環上的每個鍵,R是鍵長,N是Gordy關系式計算的鍵級。N上帶一個橫杠是環上的鍵的N值的算術平均值。n是鍵的數目,V_K是參考值,對于五元環和六元環分別為35和33.2。a和b是Gordy關系式預設的參數,在Tetrahedron,57,5715(2001)當中給出了新的a和b參數。Bird芳香性指數越接近100,說明鍵的均衡性越好,芳香性越強。
Bird芳香性流行程度遠不及HOMA,且比起HOMA適用的元素類型更少,且只適合五、六元環。在Multiwfn中計算Bird的步驟和計算HOMA的步驟幾乎一樣,唯一不同的是,進入主功能100里的功能13后,不是選擇0,而是選擇2。利用選項3可以自定義各個元素之間的鍵的a、b值,利用選項4可以自定義V_k值。
5 基于能量的方法
本節介紹的方法基于能量標準來衡量芳香性。
5.1 離域化能及HOSE(Harmonic oscillator stabilization energy)
離域化能是指體系從定域化的電子結構(由Lewis式描述)轉化到實際的離域化的電子結構過程中的能量的變化。是否將幾何結構的變化對能量影響考慮進去,又可以分為垂直和絕熱離域化能。苯的離域化能就是從kekule式描述的三個雙鍵+三個單鍵轉變為實際的6個單鍵+1個六中心六電子大pi鍵的能量變化。芳香性越強,電子離域性越強,離域化能也就越大。
離域化能這個概念很好,但是計算時很困難。一方面是以什么結構Lewis結構作為參考標準的問題;另一方面更棘手,是用什么程序怎么實際去算的問題,下面談幾種可行的手段:
(1)離域化能在VB框架中稱為共振能(Resonance energy, RE)。價鍵理論(VB)用在計算離域化能很合用,因為VB計算時可以明確指定成鍵方式,因此能直接得到電子定域化狀態的能量。然后把所有可能的lewis結構在計算時一起考慮,對它們各自的系數變分,得到的就是在這些定域化狀態間相互共振的狀態的能量,這等同于電子離域狀態。將這個能量減去定域化狀態的能量即得到共振能。不幸的是VB在目前是比較小眾的計算方法,門檻略高。
(2)NBO的二階穩定化能(E2)分析。NBO是定域化的軌道,占據的NBO軌道與空的NBO軌道間的E2對應了電子從前者向后者的離域化造成的能量降低。把體系中各種與環上電子離域相關的E2都考慮進去,就能估計環上電子的離域化能。但是這個方法很不推薦,或者只能很定性地研究。因為E2不具備加和性,而且E2只是低階的微擾理論,而芳香環上電子的離域遠非“微”的級別。而且還有其它一些原理上的缺陷,這需要對NBO有一定認識才容易理解,這里就不多討論了。另外還有人用類似Fock矩陣元消除法來獲得穩定化能。
(3)BLW(block-localized wave function)方法。此方法原文見JCP,109,1687(1998)。這個方法是基于MO理論的,可以用在HF或DFT上。BLW方法是將體系的基函數劃分為位于特定片段上的數個子集,在SCF過程中只允許MO在這些子空間里分別展開。于是每個子空間里的MO是正交的,而每個子空間內的MO與其它子空間的MO是非正交的。利用BLW方法可以得到與lewis式對應的定域化的波函數,并得到對應的能量。令體系實際能量減去BLW波函數的能量就是離域化能。BLW可以結合GAMESS-US和XMVB程序計算,見http://wiki.lct.jussieu.fr/workshop/index.php/BLW。不過虞忠衡指出使用BLW計算離域化能有嚴重缺陷,見http://blog.sciencenet.cn/blog-94786-423823.html。虞忠衡也提出了計算穩定化能的方法,見其blog上一系列文章,這里就不多提了。
以上三種方法是基于電子結構的方法來計算垂直或絕熱離域化能。而HOSE(Harmonic oscillator stabilization energy)是基于幾何結構的變化按照諧振勢來計算絕熱離域化能,其表達式如下
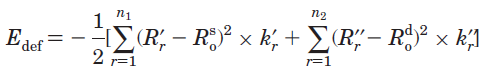
式中R'_r和R''_r代表實際分子中的pi鍵鍵長,n1和n2分別代表kekule式對應結構的單鍵和雙鍵的數目,k是力常數。因此HOSE描述了分子從實際幾何結構變化到Kekule式描述的電子定域化的幾何結構過程中所需的能量的負值,或者說是源自電子離域效應產生的實際結構相對于kekule結構的穩定化能。
關于計算離域化能其它的一些細節討論和歷史上的方法可參見Chem.Rev.,105,3773(2005)。
5.2 芳香穩定化能(Aromatic stabilization energy, ASE)
ASE和離域化能都是基于能量來分析芳香性的標準,體現電子離域導致的能量變化,但ASE的計算方法與之截然不同。ASE計算過程是構建一個開環的等鍵化學反應。反應能如果算出來是正值,即吸熱,說明體系是芳香性;如果是負,即放熱,說明是反芳香性。例如苯的ASE可按如下方式計算,能量是B3LYP/6-31G*下得到的
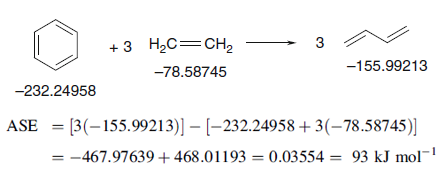
一般認為ASE>5kcal/mol就可以算是有芳香性了。計算ASE時構建的等鍵反應有任意性,不同的構建方式結果會有所不同,如果構建得不合適,甚至結果會不靠譜,詳見Computational Chemistry-Introduction to the Theory and Applications of Molecular and Quantum Mechanics 2ed(Errol Lewars)一書307頁的討論。
ASE最大的弱點就是計算極其麻煩。對于一個復雜的大體系,或者諸如金屬芳香性體系,構建一個合理、有意義的等鍵反應幾乎不可能。構建方式的不唯一性也導致不容易對不同文獻的結果進行對比。所以我不認為如今使用ASE討論芳香性有多大價值,除了對于簡單小體系。
5.3 磁共振能(Magnetic resonance energies, MRE)
MRE是一種計算ASE和環電流的方法,詳見JACS,128,2873(2006)、JPCA,111,8873(2007)。MSE基于圖論和Huckel理論,只要知道分子拓撲關系即可進行計算,計算時只需要一個參數即Huckel共振積分。此方法只能用于pi芳香性研究。
這個方法計算時要考慮體系全部可能的環路。比如菲不是只包含三個六元環路,而是包括三個六元環路、兩個10元環路和一個14元環路。對于每個環路,比如第i個環路,可以計算相應的A_i值,它為正值和負值說明這個環路的感應環電流起抗磁(電流方向符合左手定則)和順磁(電流方向與左手定則相反)作用。A_i也被稱為環路共振能(CRE),將當前體系的所有A_i加起來,得到的就是當前體系的MRE,可視為是離域化能。
根據I_i=4.5*I_0*A_i*S_i/S_0可以計算第i個環路的環電流,其中I_0是苯的環電流,S_i是第i個環的面積,S_0是苯環的面積。將所有環路的環電流累加到一起,就能繪制出整體感應電流圖。這和AICD那些方法得到的不一樣,那些方法可以得到空間中每個具體的點感應電流密度,而MRE的電流圖給出的只是每個鍵上電流大小和方向信息,如下所示。
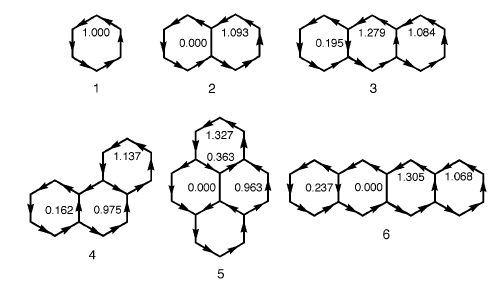
MRE方法的優點是不依賴于量化計算,不依賴于具體幾何結構,只根據拓撲關系就能迅速得到離域化能和感應電流分布。而且不像大多數芳香性判據那樣只能算每個小環的芳香性(比如對菲只能算三個六元環),而是可以研究體系中任意環路的穩定化能和環電流。此方法的缺點也很多,即只能用于平面pi體系、精度僅是HMO級別、不能用于非平衡構型或非基態或開殼層、體現不了鍵的拉伸產生的影響、不能用于諸如金屬簇等體系等等。MRE最適合的體系就是多環芳烴(可以含雜原子),特別是尺寸很大的情況。實現MRE的程序據筆者所知目前沒有公開的,不過估計也不會很難寫。
6 基于電子離域性的方法
本節介紹的方法都比較直接地與電子離域性相聯系。
6.1 多中心鍵級
多中心鍵級也叫多中心鍵指數,定義為
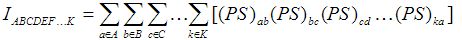
其中P是單電子密度矩陣,S是重疊矩陣,a,b,c...代表基函數序號,A,B,C...代表環上的原子序號,并且這些原子是按照在環中的連接關系相鄰的。
多中心鍵級理論依據強、普適性廣,是寡人強烈推薦使用的衡量芳香性的方法。它的數值越大說明芳香性越強。它也可以用在開殼層,只要把密度矩陣換成alpha和beta電子的密度矩陣分別計算,然后帶上特定系數相加即可。多中心鍵級的一個遺憾是沒法用來分析反芳香性,反芳香性的體系只是多中心鍵級很小而已,故和芳香性很弱的體系沒法區分開。
多中心鍵級可以在Multiwfn當中計算,考慮的原子數沒有上限。啟動Multiwfn后載入fch或molden等含有基函數信息的文件,然后選9,再選2,輸入環上的原子序號(必須在環上依次相鄰),如3,7,10,9,8,4,然后多中心鍵級數值會立刻輸出,輸入幾個原子序號就計算幾中心鍵級。注意順時針和逆時針輸入環上的原子序號的結果有時會有微小差異,原理上都對,取誰都可以,取平均值的話更為嚴謹(可以把settings.ini里的iMCBOtype設為1,此時給出的數據直接就是兩個方向輸入的計算結果的平均值)。
順帶一提,多中心鍵級的計算耗時原本是隨考慮的原子數增加呈指數型增長的,對于超過12個原子的情況即便在比較小的基組下也不可能算得動。盧天于2020年提出了一種多中心鍵級的超快計算方法,使得多中心鍵級的計算耗時隨原子數增加只是呈線性增長,用于含有幾十個原子的環也毫無壓力,這大大拓寬了多中心鍵級的應用范疇。2020-Sep-12及以后發布的Multiwfn版本支持了這個算法。
需要注意的是以一般方式計算多中心鍵級時切不可使用彌散函數,否則結果會缺乏意義。雖然也有諸如多中心離域化指數(Theor.Chem.Acc.,105,292(2001))等類似的指標能夠用來衡量芳香性,可以減小多中心鍵級的基組依賴性,尤其是能夠解決不適合彌散函數的問題,但計算明顯更費時。在Multiwfn中支持基于自然原子軌道(NAO)計算多中心鍵級,具體做法見Multiwfn手冊3.11.2節,此時計算的多中心鍵級就不怕彌散函數了,而且還有一個額外好處是計算結果與順時針還是逆時針輸入原子序號完全無關。
對于純平面體系,sigma和pi電子的多中心鍵級是可加和的,因此多中心鍵級可以分別研究sigma和pi芳香性。對于非平面體系,如果基于定域化軌道計算,也可以近似實現多中心鍵級對sigma和pi電子貢獻的分離,相關說明和例子看《在Multiwfn中單獨考察pi電子結構特征》(http://www.shanxitv.org/432)。
Bultinck等人的文章鼓吹計算多中心鍵級時應當將原子序號的各種置換組合都考慮進去,此時計算結果就完全和輸入的原子序號順序無關了。但這樣計算多中心鍵級非常耗時,而且此時的結果并不適合研究芳香性,因為反映的并不是沿著環的路徑的離域強弱,不過此時倒是適合研究某個簇狀區域的整體離域情況。如果想計算這種多中心鍵級,將settings.ini里的iMCBOtype設為2之后,照常計算時輸出的多中心鍵級就是這種了。詳見Multiwfn手冊3.11.2節。
6.2 ELF-sigma/pi和LOL-sigma/pi
電子定域化函數(Electron localization function, ELF)是Becke提出的衡量電子定域性的實空間函數,目前有極為廣泛的應用。此函數的在《電子定域性的圖形分析》(http://www.shanxitv.org/63)中從圖形的角度進行了介紹,在 物理化學學報, 27, 2786 (2011) 中作者對ELF的函數形式和物理意義做了詳細的討論,更多相關信息看“ELF綜述和重要文獻小合集”(http://bbs.keinsci.com/thread-2100-1-1.html)。可以認為,被數值越高的ELF等值面包圍的空間,電子越容易在這個空間內離域,同時越難離域到這個空間之外。
在JCP,120,1670(2004)中,作者提出了ELF-sigma和ELF-pi用于研究sigma和pi芳香性。前者就是在計算ELF時只考慮pi以外的軌道,后者就是計算ELF時只考慮pi軌道。注意哪怕是對平面體系,ELF也不能分解為ELF-sigma和ELF-pi的加和,但使用ELF-sigma和ELF-pi研究問題確實有實際價值,所以也就無視這個理論上的小缺陷了。
ELF等值面的數值(isovalue)取得越大,等值面內的空間(稱為域)就會越來越小。如果域內含有多個ELF極大點(叫可約域),則隨著isovalue的增加,這個連通的域就會逐漸分解為多個小的孤立的域,最終每個域內只包含一個ELF極大點(叫不可約域)。不同isovalue時苯的ELF-pi和ELF-sigma等值面如下圖所示
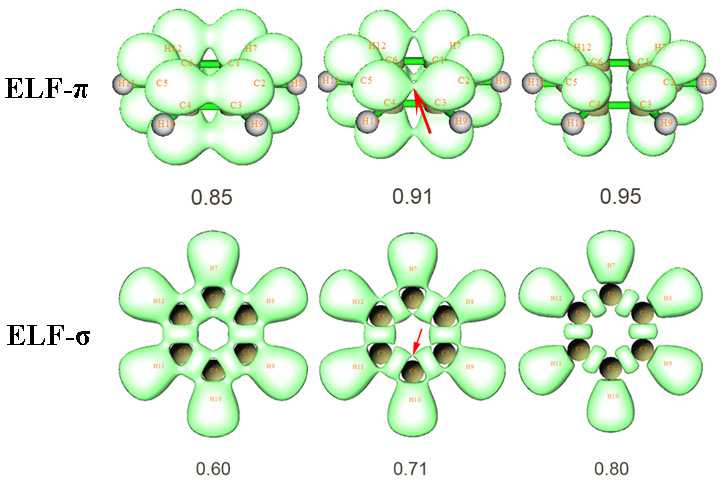
可見,對于ELF-pi等值面,當isovalue=0.91時,在苯環上方、下方對應離域pi電子的連通的可約域恰好要分解為六個碳原子上的不可約域,故0.91就是討論芳香性時候苯的ELF-pi值。紅箭頭所示的位置被稱為二分點(bifurcation point)。不同體系ELF-pi值不同,pi芳香性越強的體系ELF-pi可約域分解得越晚,即ELF-pi值越大。多數體系并非像苯這樣是每個鍵都對稱的,因此ELF-pi可約域在環上的某些鍵上分解得早,在有的鍵上分解得晚,ELF-pi應當取最先出現分解時的值,而最先分解處也對應了環共軛最弱的位置。
ELF-sigma函數在構成共價鍵的原子間總有極大點,對應一塊ELF-sigma值較高的區域。衡量芳香性所取的ELF-sigma值指的是環上的這些相鄰的高ELF-sigma區域之間的二分點,對于苯,就是上圖紅箭頭所示的位置。由于是在isovalue=0.71時恰好在此處從連通的可約域分解開來,因此苯的ELF-sigma值為0.71。
Chem.Rev.,105,3911(2005)中指出ELF-pi大于0.7的體系可以算作是有pi芳香性的,在0.11~0.35可以算是有pi反芳香性的。對于有機分子,ELF-pi和ELF-sigma平均值大于0.7可以算作有整體芳香性,小于0.55的體系可以算作有整體反芳香性。
在Multiwfn中計算ELF-sigma/pi的方法是:先載入含有波函數信息的文件,利用主功能100里的選項22把pi軌道占據數設為0(對于計算ELF-sigma來說),或把其余軌道占據數設為0(對于ELF-pi來說)。然后進入主功能5,選ELF,再選合適的格點設定(小體系通常選2即可,大一些的體系適合選3)。格點數據算完后選-1,在蹦出來的圖形界面里從小到大逐漸調節isovalue,直到ELF-sigma或ELF-pi等值面開始出現二分為止,就確定了ELF-sigma或ELF-pi的數值。另一種方法就是在設完占據數后用主功能2來進行拓撲分析找到精確的二分點位置,并獲知相應位置的ELF-sigma/pi值,這樣做沒有觀看等值面那樣直觀,但是結果更精確。非常具體的分析繪制ELF-pi的操作說明和示例見《在Multiwfn中單獨考察pi電子結構特征》(http://www.shanxitv.org/432)。
其實寡人并不完全贊同上述這種通過ELF-sigma/pi衡量芳香性的做法,因為只靠空間中個別的點的性質就斷定整個環的芳香性,這難免考慮得不夠周全,更合理的是諸如考慮一部分區域的ELF-sigma/pi。
在這里特別要指出的是,ELF-sigma/pi數值在目前的眾多文獻中十分混亂!問題極其嚴重!!!筆者發現很多文獻中的ELF-sigma/pi值根本沒法重現,有的明顯不合理。主要原因可能是那些作者用的程序和操作步驟可能有誤,更主要原因是對于復雜體系(對于苯的例子沒體現出來),會涉及到一大堆二分點,取哪個二分點來定義體系的ELF-sigma/pi值(尤其是ELF-sigma)是個很含糊的問題,不同研究者取的二分點經常不一致。這導致文獻中的ELF-sigma/pi值亂七八糟,有的體系的芳香性被明顯高估或低估。導致目前這種糟糕局面體現了ELF-sigma/pi這個研究方法本身的缺陷,而原作者一開始也沒嚴格地說清楚碰到復雜情況時該怎么選二分點。遺憾的是至今也沒有人撰文指出目前文獻中的ELF-sigma/pi值已經亂得一塌糊涂,導致鮮有人重視這個嚴峻問題,取二分點的標準始終沒能標準化。這樣下去早晚要出大麻煩。
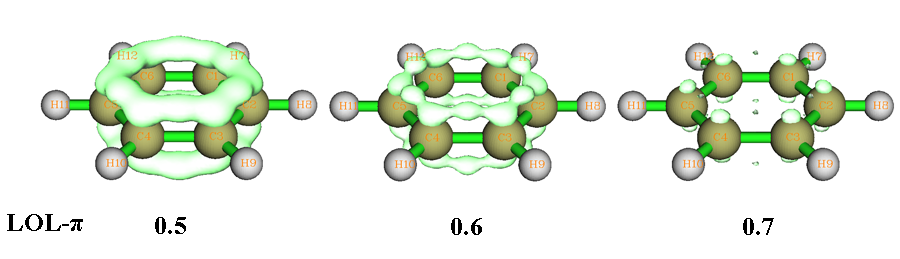
定域化軌道定位函數(Localized orbital locator, LOL)是Becke在J.Mol.Struct.(Theochem),527,51(2000)當中提出的和ELF在定義及實際功能上都十分相似的實空間函數。現在也有少數文章開始用LOL-sigma和LOL-pi來討論sigma和pi芳香性,例如PCCP,13,20584(2011),但是研究方法還沒標準化,還沒像ELF-sigma/pi那樣得到普遍認知。使用LOL代替ELF研究芳香性可能會有更好的效果。對于大量芳香性體系,LOL-pi不像ELF-pi那樣在pi鍵上有二分點,而是有局部極大值,直接對應了pi鍵,故分析比較便利(而ELF二分點的性質只能夠間接地展現pi鍵)。苯的LOL-pi等值面如下所示,pi鍵上的LOL-pi極大點在isovalue=0.7時很鮮明。通過對比也能看出LOL-pi的等值面不像ELF-pi那么鼓,延展不到氫那邊去,因此分析pi問題時顯得比ELF-pi更干凈清晰。
在Multiwfn里計算LOL-sigma/pi的過程和計算ELF-sigma/pi幾乎完全一致,唯一不同的就是選擇要算的實空間函數時選擇LOL而非ELF。
另外還有文章用其它能夠衡量電子定域性的實空間函數,如ELI-D來研究芳香性,但ELI-D函數定義比ELF/LOL更復雜,計算更耗時更麻煩,從結果上看也沒什么額外的好處,可以無視掉。
6.3 PDI和ATI
電子的交換相關密度Γ(r1,r2)依賴于兩個電子坐標,A、B兩原子間的離域化指數(DI)定義為∫∫Γ(r1,r2)dr1dr2,其中r1和r2分別是在A和B的原子空間內積分。實際計算中DI的公式可以寫為
DI(A,B)=2*∑∑√(η_m*η_n)*S_m,n(A)*S_m,n(B)
兩個加和號對應令m和n在所有分子軌道中循環。η代表軌道占據數,S_m,n(A)代表m和n號分子軌道在A的原子空間內的積分值。S稱為原子重疊矩陣(AOM)。DI最初的定義中原子空間用的是AIM原子空間,也叫原子盆。關于交換相關密度和離域化指數更具體的內容已經分別在Multiwfn手冊的2.6節的第17部分和3.18.5節進行了十分詳細、清晰的討論,這里就不重復了。可以簡單認為兩個原子間DI越大,那么電子在兩個原子間離域程度越高。
對于苯的DI研究發現,對位兩個原子間的DI明顯要比間位的大,盡管間位的兩個原子間離得更近。這表現出芳香環上電子離域的獨特特點。基于這一點,在Chem.Eur.J.,9,400(2003)當中作者提出了PDI來衡量六元環芳香性,也就是三個對位的DI值的平均值:
PDI=[DI(1,4)+DI(2,5)+DI(3,6)]/3
芳香性越強,對位的DI越大,PDI也就越大。PDI可以很好地反映化學反應進程中芳香性的變化,但主要缺點是沒法用于非六元環,以及沒法合理表現出環平面的扭曲造成的芳香性的減弱,比如苯環變成船型。也有文獻指出PDI對于帶很多正電荷的富勒烯,如C60(10+)的局部芳香性描述有錯誤。
對于平面體系,由于DI可以精確地分離為sigma和pi部分的加和,因此PDI也可以相應地分離為PDI-sigma和PDI-pi用于單獨研究sigma和pi芳香性。
在AIM原子空間中進行積分十分耗時,因為其邊界復雜,不容易得到較精確的積分值,這是為什么算AIM電荷很耗時的關鍵原因。相應地,在AIM空間中計算AOM也十分耗時,而DI的計算耗時幾乎全都花費在計算AOM上。所以使用AIM方式定義原子空間導致PDI的計算比較慢,尤其是對于大體系這更要命。模糊空間是另一類劃分原子空間的方式,相鄰原子空間之間是平滑過渡的,沒有明確的邊界。模糊空間有許多不同的具體定義方式,如Becke空間、Hirshfeld空間、ISA空間等。在模糊空間內對函數進行積分比較容易(通常用DFT的交換相關泛函的積分方法來做),因此在模糊空間下計算AOM可以使DI和PDI的計算很快地完成。在JPCA,110,5108(2006)中,作者證明使用模糊空間代替AIM空間來計算PDI研究芳香性是很合理的,這樣可以節省大量時間。
Mayer鍵級的計算比起在模糊空間下計算DI又進一步顯著節省了計算時間,在J.Phys.Org.Chem.,18,706(2005)作者提出可以將PDI公式里的DI替換為Mayer鍵級,此時的PDI被稱為ATI(Average two-center indices)。測試表明ATI和PDI(AIM空間下計算的)有很好相關性。實際上,如JPCA,109,9904(2005)所證明的,Mayer鍵級可以視為是希爾伯特空間下計算的DI,物理本質上沒有區別,所以有這樣好的相關性是很自然的事情。此文也證明了模糊空間下的DI和“模糊鍵級”(CPL,383,368(2004))是完全等價的。
注意AIM空間和模糊空間下計算DI對基組的敏感性都不高,雖然可以用,但沒必要用大基組,算PDI用6-31G*就夠了。由于DFT下的離域化指數的物理意義不清楚,所以原則上建議在HF下計算PDI。不過用雜化泛函時,從DI的數值結果上看倒也沒什么不妥,實際上很多文章用的就是在B3LYP下計算的DI和PDI。而Mayer鍵級對基組敏感性略大,尤其不適合在彌散函數存在的情況下計算,算ATI的話通常也用6-31G*就行了。
Multiwfn中計算模糊空間下的PDI的方法是:首先載入含有波函數信息的文件,然后選15進入模糊空間分析功能,然后選5。程序會先在模糊空間下計算AOM并產生各個原子間的DI值,然后用戶需要輸入環上的六個原子序號,如2,3,4,7,10,11,輸入順序需依照原子連接關系。然后PDI值馬上會輸出出來。Multiwfn默認用的模糊空間的定義是Becke所提出的。用戶也可以通過選項-1切換為Hirshfeld定義的模糊空間,但是它依賴于孤立原子密度,所以用戶得提供孤立原子的波函數文件,故略微麻煩,從結果物理意義上來講并不比Becke空間下計算的有顯著優勢。
Multiwfn中可以計算Mayer鍵級,方法是首先載入fch文件,然后選9再選1,此時大于默認閾值0.05的Mayer鍵級就會被輸出出來。如果沒有出現所要找的項,那么在啟動Multiwfn之前可以在settings.ini文件里將bndordthres閾值設很低,比如設為0,則所有Mayer鍵級都會輸出。程序也會問你是否將鍵級矩陣輸出出來,從鍵級矩陣里也可以直接找到所有原子間的Mayer鍵級。得到環上三個對位的Mayer鍵級后,取平均即得到了ATI。
對于平面體系,Mayer鍵級和DI都可以精確地分離為sigma和pi部分的加和。因此ATI和PDI都可以分離為sigma和pi部分以單獨研究sigma和pi芳香性。在Multiwfn中的做法是在計算PDI/ATI之前,按照前面提到過的,先用主功能100里的功能22來設定占據數,之后再照常計算PDI/ATI即可。
6.4 線性響應核和對位線性響應指數(para linear response index, PLR)
在密度泛函理論框架中定義了線性響應核(Linear response kernel, LRK),并且基于二階微擾理論可以得到閉殼層下KRL的近似形式:
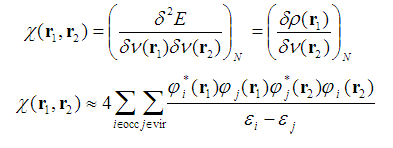
其中ε代表分子軌道能量,φ代表分子軌道波函數。occ和vir分別代表占據和空軌道。
LRK體現了在r2處對外勢的擾動產生的對r1處電子密度的影響值,某種程度上也表現了r1和r2處的電子耦合程度,這一點和自旋相同電子間的費米穴函數有相似之處。對于定域性較強的電子結構,比如烷烴,那么只有r1和r2較近時LRK才可能較大。而如果電子離域性很強,并且離域范圍明顯涵蓋r1和r2,那么哪怕r1和r2離得較遠,LRK數值仍然可能較大。由于LRK能用于探測離域程度,而離域又是芳香性的基礎,近來有人受這個啟發,利用LRK衡量芳香性。
直接用LRK圖形化分析很不方便,因為它是六維函數。在PCCP,14,3960(2012)中定義了Condensed LRK (CLRK),可以寫為
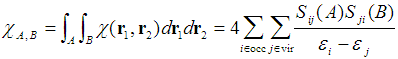
其中A、B代表原子空間,PCCP,14,3960(2012)中用的是Becke模糊空間。S是前面已提到的原子重疊矩陣。兩個原子間的CLRK定量地表現出兩個原子間相互作用強度,也隱含地表現了兩個空間內電子相互離域程度。形式上可以看出CLRK計算方式和DI十分類似,在doi:10.1039/C2CP43612D文中作者從數學上分析了二者間的密切關系。
類似于DI,在苯環上,也是對位間的CLRK比間位的大很多。因此基于CLRK,在PCCP,14,3960(2012)中進一步定義了對位線性響應指數(PLR)。PLR和CLRK之間的關系和PDI與DI之間的關系完全一致,也就是六元環當中對位間的CLRK值取平均,即
PLR=[χ(1,4)+χ(2,5)+χ(3,6)]/3。
在衡量芳香性問題上,現有的文章顯示PLR和PDI幾乎沒有差別,線性相關性高達R^2=0.96,缺點和優點完全一樣。由于CLRK也可以像DI那樣分離為sigma和pi部分,故PLR也可以分離為PLR-pi和PLR-sigma。PLR和PDI用誰都可以,但從計算量上來說,由于LRK要涉及到虛軌道,DI只涉及占據軌道,而虛軌道數目往往比占據軌道多很多,所以PDI比PLR更省時。PLR剛剛提出不久,在有更多文章表明PLR比PDI在某方面有顯著優點之前,在我看來只用PDI就行了。
在doi:10.1039/C2CP43612D中,作者也直接通過CLRK而非PLR來衡量芳香性,這樣就不局限于六元環。通過對不同四元環到八元環的體系的研究,作者提出一套假設:
(1)對于芳香性環體系,相對著的兩個原子間CLRK值為最大。比如六元環就是指1-4位原子間,七元環指1-4或1-5位,八元環指1-5位。
(2)對于反芳香性體系,相對著的兩個原子間CLRK值為最小(原文說的是“局部極小值”),并且雙鍵上的兩原子間CLRK值為最大。
如果芳香性/反芳香性來自pi電子,應考察的是CLRK-pi;如果是sigma電子,應考察CLRK-sigma。
CLKR和PLR都可以在Multiwfn中直接計算。首先載入含有基函數信息的文件如fch、molden(不能用wfn/wfx文件,因為其中無虛軌道信息),然后進入主功能15,選9即可計算并輸出CLRK矩陣。選10的話,會自動先計算并輸出CLRK矩陣,然后讓你輸入環上的原子序號,如3,4,5,7,10,11,需符合原子連接關系。然后PLR值立刻會立刻顯示出來。如果想只考察sigma或pi電子貢獻的CLKR或PLR,依然是先用主功能100里的22先設占據數后再做計算。
6.5 ΔDI
在Chem.Eur.J.,9,400(2003)中作者除了提出PDI用于衡量六元環芳香性,還提出了一種靠DI衡量五元環芳香性的方法,稱作ΔDI。如下圖所示,五元環的最典型Lewis結構式包含C-C單鍵和C=C雙鍵
令C=C雙鍵的DI減去C-C單鍵的DI,就是ΔDI。顯然,環的芳香性越強,單雙鍵的區別就越不明顯,因此ΔDI也越小。對于C5H5-,已經無法區分單雙鍵,所以ΔDI達到最小值0。通過測試發現ΔDI與NICS有一定相關性,但是也有少數體系二者相關性并不好。
原文計算ΔDI時用的是在AIM空間下計算的DI。在模糊空間下計算DI,或者改用Mayer鍵級來計算也都是可以的。文中也發現哪怕直接用鍵長求差值得到的Δr,也和ΔDI相關性很好。
ΔDI計算極其便利,但筆者認為ΔDI稱不上是很可靠的方法,關鍵一點是它只考慮了五元環的碳碳鍵部分,卻忽略了上圖中C-X鍵部分,這明顯很不周到。
6.6 FLU和FLU-pi
在JCP,122,014109(2005),作者提出了FLU(Aromatic fluctuation index)來衡量芳香性,它和HOMA挺類似,也是以理想芳香性環上的鍵的性質作為參考,來衡量實際的環上的鍵與它的偏離。相對于參考值偏離(波動)越大,說明芳香性越弱。FLU基于的是DI,既可以是AIM空間下計算也可以是模糊空間下計算,實際上換成Mayer鍵級估計也沒問題。FLU的定義如下:
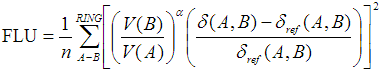
加和號循環環上所有鍵。n是環上原子數,δ(A,B)代表AB間的DI。δ_ref是相應類型的鍵的參考DI值,取自理想芳香性環(C-C、C-N、B-N鍵的參考值分別來自苯、嘧啶、borazine)。V代表原子價,對于閉殼層體系,V(A)也就是對B≠A的所有δ(A,B)的加和。當V(B)>V(A),α為1,反之為-1。將V(B)/V(A)引入式子中的目的是懲罰電子定域性較高的情況,而HOMA式子中沒有與之對應的項。
FLU可以用于任意尺寸的環。缺點是不適合用于非平衡狀態的體系,包括反應過程中芳香性的變化。更主要的缺點是引入了參考體系,這導致普適性差。
在同一篇文章中作者也提出了FLU-pi。和FLU的區別一方面是把所有DI值都替換為了DI的pi部分,另外就是把參考值換成了當前環上的所有鍵的DI-pi的平均值:
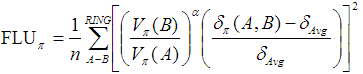
和FLU一樣,依然是數值越低表明芳香性越強。FLU-pi相對于FLU的好處是避免了引入參考體系而能夠適用于包含更多元素的體系,而缺點是FLU-pi只能用于平面體系,也只能體現pi電子芳香性。注意這里說的平面只是指所要研究的環是平面的,但不要求整個體系都是平面,因為利用軌道定域化方法,可以得到定域在感興趣的環上的pi軌道,而DI也是可以基于定域化軌道來計算的。
在Multiwfn中可以在模糊空間下計算FLU。首先載入含有波函數信息的文件,然后選15,再選6,程序就會先在模糊空間下計算AOM并輸出DI矩陣。然后用戶按照連接關系輸入環上的原子序號即可,FLU值和每個鍵對它的貢獻都會立刻輸出,由后者可以考察哪些鍵對芳香性有主要削弱效應。計算FLU所涉及到的參考值可以通過選項-4來設,默認參考值是筆者在HF/6-31G*下對苯、嘧啶、borazine計算的。如果用戶用的方法和基組與此有明顯不同,建議用戶自行用這些參考體系計算一下DI參考值并在計算FLU前輸入Multiwfn,否則FLU會有偏差(比如算得的苯的FLU將不是精確的0)。
在Multiwfn計算模糊空間下的FLU-pi的步驟是:首先載入含有波函數信息的文件,選15,再選7。待AOM和DI計算完畢后,輸入占據的pi軌道的編號,比如輸入17,20,21,然后再按照連接順序輸入環上的原子序號即可。讀者可以利用主功能0來圖形化觀察分子軌道以確定哪些軌道是pi軌道,也可以利用主功能100里的選項22,來讓程序自動找出pi軌道的編號(之后選0直接退回)。
目前FLU/FLU-pi都只對閉殼層進行了定義,在Multiwfn中也只能將它們用在閉殼層體系。如果讀者對PDI和FLU/FLU-pi有更多興趣,可參見綜述文章The Quantum Theory of Atoms in Molecules-From Solid State to DNA and Drug Design書中的第15章。對菲計算PDI、FLU、FLU-pi、PLR的例子已在Multiwfn手冊4.15.2節給出。
6.7 AV1245
2016年提出的AV1245可以視為是多中心鍵級的一個近似,目的是解決多中心鍵級因為算大環耗時太高而難以研究大環的芳香性的問題。AV1245在此文有專門介紹《使用Multiwfn計算AV1245指數研究大環的芳香性》(http://www.shanxitv.org/519),因此此處不再累述。AVmin與AV1245密切相關,它不是像AV1245那樣體現給定的環上的平均電子離域程度,而體現的是在環上離域程度最弱處的情況,即衡量的是離域的瓶頸位置,因此在衡量環的芳香性上有其獨特的意義。如前文所述,由于2020年Multiwfn引入的新的多中心鍵級計算代碼已可以非常快速計算哪怕非常大的環,因此AV1245已經沒什么實際意義了。
7 基于電子分布的方法
本節介紹的方法基于電子密度分布來間接地衡量體系的芳香性。
7.1 AIM環臨界點處電子密度及其曲率
在Can.J.Chem,75,1174(1997)當中,作者指出環臨界點(RCP)位置的電子密度和環的芳香性有對應關系。芳香性越強的環RCP處電子密度越大。而RCP的電子密度在垂直于環方向的曲率則與芳香性關系對應性更好,曲率越負(即RCP處電子密度在垂直于環方向上聚集程度越強),表明芳香性越強。
在Multiwfn中,這兩個量都可以直接輸出。首先將含有波函數信息的文件載入Multiwfn,選主功能2進入拓撲分析界面。通常只要依次選2、3、4即可找出所有電子密度臨界點,然后選0進入圖形界面查看環中心的RCP的編號。隨后選21,輸入RCP的編號,然后輸入三個原子的序號(如3,5,6)來定義環的平面,之后RCP處的電子密度連同它在垂直于這個面方向的曲率都會輸出出來。如果你不熟悉Multiwfn中的電子密度拓撲分析操作的話,建議參看http://www.shanxitv.org/108或手冊4.2節的例子。
注意不要用這種方法比較大小不同的環的芳香性,比如4元環和6元環比較芳香性沒有意義。因為環越小,高電子密度區域離RCP越近,必定RCP處電子密度數值越大,聚集程度越高。
7.2 Shannon芳香性
在PCCP,12,4742(2010)當中,作者提出了Shannon芳香性的概念,之所以叫做這個名字,是因為這個芳香性指標依賴于Shannon信息熵。其公式如下
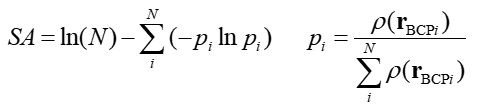
其中i循環構成芳香環的鍵上的AIM鍵臨界點(BCP),N是環上BCP總數,r_BCP是BCP的坐標。SA的加和符號里的項就是BCP處的電子的局部信息熵。Ln(N)對應于完美芳香性分子所具有的最大信息熵。芳香性越強,SA值越小,對于苯這樣的完美芳香性分子SA為0;反芳香性越強,SA就越大。小于0.003可認為具有芳香性,大于0.005可認為具有反芳香性。
在Multiwfn的拓撲分析界面里可以直接計算SA值。首先在主功能2里做拓撲分析找出BCP,然后選20,再把環上的BCP序號輸入進去即可,如輸入14,23,18,13,16,15。之后SA值會立刻輸出,每個BCP的局部信息熵也會一起輸出出來。
7.3 EL指數
在Struct.Chem.,23,1173(2012)中,作者提出了EL指數用于衡量芳香性,它基于BCP處電子密度的橢率。EL定義為:EL=1-c/n*∑|ε_i-ε_ben|
加和符號循環環上的每個BCP。ε_i是第i個BCP的電子密度橢率,ε_ben是理想芳香性體系(苯)的BCP的橢率。n是環上BCP總數,c是歸一化常數,目的是讓EL對于典型非芳香性體系的結果為0,即
c=n/∑|ε_i,nonaromatic-ε_ben|
其中ε_i,nonaromatic是非芳香性參考體系環上BCP的橢率。EL中這個體系取的是kekule形式的苯,其中單雙鍵鍵長來自(3E)-1,3,5-己三烯。
實際上EL和HOMA在形式上十分相似,主要區別就是把鍵長指標換成了BCP橢率而已,數值范圍依然是對于理想芳香性體系EL為1,非芳香性體系為0,反芳香性體系EL為負值。EL的基本思想是pi鍵越明顯,BCP處電子密度越偏離軸對稱分布,故此處電子密度橢率越大,于是用它來區分開普通sigma鍵和芳香環上的鍵。其實這種定義方式實在是了無新意。
EL雖然在原文中測了一些環狀不含雜原子的有機分子結果還不錯,但是缺點顯而易見。EL公式中的c和ε_ben是依賴于計算所用的理論方法和基組的,因此對于每種計算級別先得自己用己三烯和苯計算一下c和ε_ben才能用EL衡量別的體系,這挺麻煩。另外,由于引入了參考值,所以EL有和HOMA同樣的缺點,也就是研究的體系必須有對應的參考分子才行,而諸如金屬團簇,由于沒法找到合適的參考體系,EL就不能用。另外當鍵的極性較強,BCP處電子密度橢率變得不那么明確,EL也就不那么可靠。
總之筆者不認為EL是一個比較有理論意義或者有較大實用價值的方法,可靠性也還沒被廣泛檢驗。
計算EL所需的BCP處電子密度的橢率可以在Multiwfn里獲得。首先載入含有波函數信息的文件,用進入主功能2做拓撲分析找出BCP,然后選7,并輸入BCP對應的編號,就會輸出電子密度的Hessian矩陣和本征值。如苯的C-C鍵BCP:
Eigenvalues of Hessian: 0.3272716437E+00 -0.6439237628E+00 -0.5378860803E+00
令λ1和λ2代表絕對值最大和第二大的本征值,則橢率定義為ε=λ1/λ2-1,故此BCP處的ε=-0.64392/(-0.53788)-1=0.19744。而對于乙烷的C-C sigma鍵由于密度分布是軸對稱的,所以BCP處λ1=λ2,此時ε=0。
7.4 電場梯度(Electric field gradient, EFG)
靜電勢的負梯度是電場(矢量),電場的導數就是電場梯度EFG,是個二階張量。在J.Mol.Model.,17,2017(2011)里作者提出可以用化學鍵上的EFG的分量來衡量芳香性。EFG可以在空間任意一處計算,比較重要的是EFG(0),它指的是鍵的正中間處的EFG值,以及EFG(0.5),是以鍵的正中間為起點,向垂直于環平面方向上挪0.5埃處的EFG值。EFG(0)或EFG(0.5)和鍵的pi特征相關,比如乙烷、乙烯、乙炔、苯的C-C鍵的EFG(0.5)分別為0.9140、1.3874、1.8810、1.1986,可見pi特征越明顯數值越大,因此可以利用這個特點來衡量芳香性。
用EFG(0.5)衡量某個碳環的芳香性就是計算環上pi離域效應對環上所有鍵的EFG(0.5)值總和的影響,記為ΔEFG(0.5)。比如對于苯,EFG(0.5)總和為6*1.1986;它的電子定域化狀態是kekule式描述的三個雙鍵和三個單鍵,因此可以用三個乙烷的C-C鍵(EFG(0.5)總和為3*0.9140)和三個乙烯的C-C鍵(EFG(0.5)總和為3*1.3874)來描述,因此苯的ΔEFG(0.5)=6*1.1986-3*0.9140-3*1.3874=0.2874。再比如環丁二烯,環上EFG(0.5)總和為2*(1.3446+0.8262)=4.3416,減去兩個單鍵2*0.9140和兩個雙鍵2*1.3874,ΔEFG(0.5)算出來為-0.2612。ΔEFG(0.5)越正,說明芳香性越強,接近0說明是非芳香性,而為負值說明是反芳香性。ΔEFG(0)的計算方式和ΔEFG(0.5)完全一樣,將用到的EFG(0.5)值都替換為EFG(0)值即可。從DOI:10.1007/s11224-012-0097-9一文的討論來看,ΔEFG(0)比ΔEFG(0.5)顯得更可靠。
EFG值可以在Gaussian中方便地得到。在要計算EFG值的位置上定義一個Bq原子(類似于NICS的定義方式),然后寫上prop=EFG關鍵詞即可。在輸出文件末尾處可找到
Center ---- Electric Field Gradient ----
( tensor representation )
---- Eigenvalues ----
下面有Bq原子對應的值,如
13 Ghost -5.890022 2.881757 3.008266
14 Ghost -5.510474 2.741618 2.768856
在計算EFG(0)或EFG(0.5)時,取最后一列的值即可。
EFG方法衡量芳香性最大弱點是需要確定定域化Lewis結構,并且要有合適的參考體系來得到相應的定域化的鍵的EFG值,這使得它的適用范圍大大受限。
7.5 pEDA、sEDA
此方法名字中的EDA代表electron donor-acceptor,p代表pi,s代表sigma。這兩種描述符是在J.Phys.Org.Chem.,22,769(2009)中定義的,原本用于分析取代苯的電子結構,后來在DOI:10.1007/s11224-012-0097-9等文章中被用來研究芳香性。它們的定義為:
pEDA=∑π_i(取代苯)-∑π_j(苯)
sEDA=∑σ_i(取代苯)-∑σ_j(苯)
其中i、j分別循環取代苯和未取代苯的六元環上每個原子。π_i代表第i個原子上價層pz自然原子軌道(NAO)的布居數,σ_i是原子的價層s、px和py的NAO布居數的總和。這里假定分子平面處在XY平面上。pEDA和sEDA表現了由于取代基效應,使得pi電子數和sigma電子數偏離未取代狀態的量。pEDA、sEDA也可以用在其它類型環上研究取代基效應,比如吡啶,只要把公式中的苯環換成相應的環就行了。
NAO的布居數可以由NBO程序獲得。比如在Gaussian里,用pop=NPA關鍵詞就會調用NBO3.1模塊進行自然布居分析,給出NAO的布居數。
這個方法只適合研究取代基對芳香性的影響,不同類型的環的芳香性沒法比較。就算只考察取代基的影響,靠這兩個量來分析芳香性是否靠譜,筆者尚持懷疑態度。盡管某些文章號稱有成功的應用,并表示和其它個別芳香性指標有不錯相關性。
8 其它方法
共軛區域的幾何結構的平面性和這個區域的電子共軛程度、芳香性有很大關系。對特征相同的環,由于特殊因素使得它越偏離平面,pi共軛就會越大程度地削弱,導致芳香性越低。筆者提出了一種非常簡單、直觀、嚴格的方法展現平面性,可以直接通過Multiwfn很容易地計算,對于從平面性角度討論芳香性很有用處,參看《使用Multiwfn定量化和圖形化考察分子的平面性(planarity)》(http://www.shanxitv.org/618)。
有個芳香性分析方法叫CiLC(CI/LMO/CASSCF)。這個方法計算過程復雜,分析芳香性過程也十分麻煩,需要考察CI組態系數和組態構成來分析是否鍵的均衡性被很好地滿足以判斷芳香性。這方法對于更深入探究電子結構或許有價值,但分析過于繁瑣而對于分析芳香性沒多少實際應用意義。詳見JPCA, 104, 922 (2000)、JPCA, 106, 10370 (2002)、JPCA, 107, 9422 (2003)等文章。
除本文體提到的之外,還有一些其它的五花八門的衡量芳香性的標準,比如I_NB、I_NG(JPCA,111,6521),還有人用源函數(Source function)分析芳香性,但都沒什么意思,就不提了。
9 總結
一個完美的衡量芳香性的指標應當具備這些條件:(1)可靠性高(2)計算量小(3)不依賴于參考體系(4)普適性好,可以用于種類多樣的體系,如金屬/半金屬體系,任意尺寸的環,含任意元素、成鍵模式的體系。還應可以研究非平衡結構、不同電子態、不同外場環境下、化學反應過程中的芳香性(4)可以分離sigma和pi的貢獻(5)可以同時衡量反芳香性(6)操作過程簡便,有現成好用的程序可以支持。現有的各種芳香性指標互有優劣,沒有一個完全滿足這些條件。不過能滿足大多數條件的指標是值得推薦的。
以下是本文涉及的主要的衡量芳香性的指標的綜合對比。有些本文提及的方法,如LOL-sigma/pi、BOIA、HOSE、NICS-rate、θ指數、直接通過CLRK衡量芳香性、CiLC等等,要么目前用得很少,要么可靠性尚未檢驗,要么沒什么新意,故不值得一提,就沒列在表里。

注意本節的NICS是指RCP處NICS_zz(0)。FLU、FLU-pi、PDI、PLR、ΔDI都是指模糊空間下的。計算便利度是指使用Multiwfn程序的情況下。綜合價值指的是方法的重要性、意義,如果某方法的提出無關痛癢,那么綜合價值就比較低。耗時是指的計算芳香性指標本身的耗時,而諸如波函數計算、幾何優化階段的耗時不算在內。耗時是相對而言,對于小體系、中等基組的情況其實各種方法耗時都不大,但對于中、大尺寸體系或大量體系的計算就表現出明顯差異了。
這些方法中基于幾何結構的方法計算最為簡單,但局限性最大,由于沒有直接與電子相對應,沒法表現諸如不同電子態、外電場下的芳香性,除非在相應條件下先優化幾何結構。凡是依賴于參考體系的芳香性指標普適性都不很理想,用于金屬團簇、非平衡結構幾乎是不可能的。注意一些方法,如SA、Bird、FLU是基于鍵的均衡性來衡量芳香性,這類方法都有個通病,就是如果鍵的均衡性是來自于外因被迫產生的,那么就會明顯高估芳香性。例如coronene中央的環的六個C-C鍵的特征均等的,但這實際上是由于周圍六個環的對稱排列所致,因此如SA、Bird、FLU這類方法就會誤認為這個環的芳香性和苯一樣強。
對于一般的芳香性研究,筆者首推多中心鍵級或AV1245。如果需要研究反芳香性,首推NICS。這兩個方法的普適性、可靠性都令人滿意,計算NICS對于小體系耗時不多。由于一開始提到的芳香性的多維性,筆者推薦同時選用三種或更多的方法來考察芳香性,比如同時用多中心鍵級、NICS、PDI、FLU、HOMA來一起衡量。如果結論是一致的,表明結論十分可靠;如果結論有所不同,那么可以再進一步分析、解釋、探討。
如果想圖形化地考察芳香性,可以給出MO或AdNDP圖形,指出各軌道對芳香性/反芳香性的貢獻。也鼓勵給出ELF-pi、LOL-pi或AICD圖,電子離域路徑由此可以展現得十分直觀。