在Multiwfn中單獨考察pi電子結構特征

重要提示：本文介紹的方法筆者已經發表于Theor. Chem. Acc., 139, 25 (2020) DOI: 10.1007/s00214-019-2541-z，其中專門對pi電子結構分析的算法和應用做了詳細、深入的介紹和討論，給了許多應用例子，本文讀者看完后務必看一下這篇文章。使用本文提到的Multiwfn的功能的讀者，除了必須引用Multiwfn的原文以外，也務必同時引用上述文章。

2021-Sep-25注：筆者后來在Chemistry—Methods, 1, 231 (2021)中提出了IRI-pi分析方法，可以非常直觀地考察pi作用類型（單重還是雙重pi作用）以及pi作用強度，非常有實用價值，在《使用IRI方法圖形化考察化學體系中的化學鍵和弱相互作用》（http://www.shanxitv.org/598）做了介紹，對下文內容是重要的補充，請讀者務必一看。

在Multiwfn中單獨考察pi電子結構特征

文/Sobereva @北京科音

 First release: 2018-Aug-7  Last update: 2021-Oct-10

0 前言

對一些化學體系，特別是含有共軛特征的，我們往往只對其pi電子特征感興趣，因為pi電子特征直接影響體系很多方面的性質，比如芳香性、反應活性和反應位點等。考察pi電子特征有很多不同手段，比如計算ELF（電子定域化函數）和LOL（定域化軌道定位函數）、計算pi電子布居、計算pi鍵級等等。Multiwfn是分析電子結構最強大的工具，在Multiwfn中可以非常方便地對各種類型體系做各種形式的pi電子結構的分析，在本文就統一說一下。由于Multiwfn支持的分析方法極多，限于篇幅肯定不可能各種情況面面俱到都說一遍，希望讀者能充分舉一反三。

本文對應Multiwfn最新版本的情況，Multiwfn可以在其主頁http://www.shanxitv.org/multiwfn上免費下載。如果不了解Multiwfn，強烈建議參看《Multiwfn入門tips》（http://www.shanxitv.org/167）、《Multiwfn FAQ》（http://www.shanxitv.org/452），不知道怎么產生Multiwfn輸入文件的讀者應當看《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379）。

為了便于表述，本文簡單地把軌道分為pi軌道和sigma軌道兩種，只要不屬于前者的就算后者，哪怕這些軌道有的是并不是用于構成sigma鍵的內核軌道、孤對電子軌道。占據pi軌道的電子被稱為pi電子。本文用的.fch文件皆為Gaussian 16 A.03版在B3LYP/6-31G*級別下計算產生，結構也在同級別優化過。

本文用到的輸入文件皆可以在這里下載：file.rar。

順帶一提，Multiwfn也可以以軌道方式展現孤對電子，以及計算分子軌道、NTO等軌道中孤對電子所占成份，參看Multiwfn手冊4.200.6.2節的例子。

1 原理

在Multiwfn中，把sigma占據軌道占據數清零，而令pi占據軌道的占據數保持不變，那么接下來照常做的各種波函數分析就只由pi電子貢獻了，即體現的就是pi電子特征。反之，如果想只研究sigma電子，那么把pi軌道占據數清零而令sigma軌道占據數保持不變再做分析即可。并非Multiwfn里所有功能都可以這么分離sigma和pi電子的貢獻，但至少對所有三維空間函數的分析，以及本文提到的其它類型的分析，都是可以這么分離考察的。

在Multiwfn里，想修改軌道占據數，就進入主功能6的子功能26，根據提示選擇軌道、輸入要改成的占據數即可。要想找出來哪些是pi軌道，可以用Multiwfn的主功能0來依次觀看，參見《使用Multiwfn觀看分子軌道》（http://www.shanxitv.org/269）。然而，對于較大體系，軌道數目很多，這么憑肉眼去找是非常費時費力的。萬幸的是，Multiwfn專門提供了現成的功能，可以自動判斷出pi軌道并設定這些軌道或其它軌道的占據數，這使得單獨分析sigma和pi電子特征異常容易。對于純平面體系（即所有原子恰在XZ或YZ或XY平面）和非純平面體系，Multiwfn判斷pi軌道的方法截然不同，尤其是對后者Multiwfn有獨創的判斷方法，因此在下文中，純平面和非純平面體系會分別舉例。

另外，對于很多分析，對全部電子進行分析得到的結果并不等于單獨分析pi和sigma電子的結果，此時注定沒法嚴格精確做到分離sigma和pi的貢獻。而那些結果可以精確分解為軌道貢獻加和的分析方法，顯然都是可以精確分解為sigma和pi的貢獻的。對于常見的一些分析，情況是這樣的：
ELF：sigma和pi不可嚴格分離，即ELF-pi和ELF-sigma之和不等于ELF。對LOL也是如此。
電子密度（及其梯度、拉普拉斯）、電子對靜電勢的貢獻：可以嚴格分解為sigma和pi的貢獻
Mulliken鍵級、Laplacian鍵級：可以嚴格分解為sigma和pi的貢獻
Mayer鍵級、多中心鍵級：僅對于純平面體系才可以嚴格分解為sigma和pi的貢獻
電子布居數、自旋布居數：可以嚴格分解為sigma和pi的貢獻
至于其它以上沒有提及的分析，稍微推導一下公式，或者拿小體系測試一下，便知是否可以精確分離成sigma和pi的貢獻。

2 對純平面體系考察pi電子結構

下面舉一些例子演示怎么對純平面體系考察pi電子結構。

2.1 繪制菲的ELF-pi等值面圖以及計算ELF-pi二分點數值

ELF是極為重要的衡量電子定域性和離域性的三維函數，不了解此函數的人應當參看《ELF綜述和重要文獻小合集》（http://bbs.keinsci.com/thread-2100-1-1.html）。計算ELF的時候若只考慮pi電子，得到的就是ELF-pi，這對于考察芳香性十分有價值，有機體系的芳香性也都是因為pi電子多中心離域而產生的。在《衡量芳香性的方法以及在Multiwfn中的計算》（http://www.shanxitv.org/176）中筆者對ELF-pi有充分的介紹。

第一個例子，我們對一個典型的純平面分子菲繪制ELF-pi等值面圖。作為示例，首先我們用笨辦法，即人工挑pi軌道來實現pi軌道占據數的清零。啟動Multiwfn，載入本文文件包里的phenanthrene.fch，然后進入主功能0觀看軌道。從文本窗口提示的信息可知，第47號軌道是HOMO。因此我們把軌道切換到47，然后依次把軌道按照序號從大小進行觀看。只要發現pi軌道，就手動記錄下來編號。由于當前體系一共有14個碳原子，每個碳原子上有一個pi電子，而當前體系是閉殼層，因此一共有14/2=7個pi占據軌道，即曰當我們從47號軌道開始按照序號減小依次觀看軌道，總共找出來7個pi軌道時，就說明所有占據的pi軌道都已經找齊了。最后發現，這7個pi軌道編號是36,40,43-47。

之后，退出主功能0的圖形界面，依次輸入以下命令，就可以繪制出ELF-pi軌道圖形了
6  //修改波函數
26  //修改某些軌道的占據數
0  //選擇所有軌道
0  //把所選軌道占據數設為0
36,40,43-47  //pi軌道編號
2  //占據數設為2.0，即恢復這些pi軌道原先的占據數
q  //退回上一級菜單
-1  //退回到主功能菜單
接下來，按照正常的步驟繪制ELF等值面圖，得到的便是ELF-pi的等值面圖了。依次輸入
5  //計算格點數據
9  //ELF
2  //中等質量格點
-1  //觀看等值面圖
等值面數值設為0.7，顯示風格設為透明時看到的等值面圖如下所示（若你旋轉圖像，會看到ELF-pi在分子平面上有個節面）

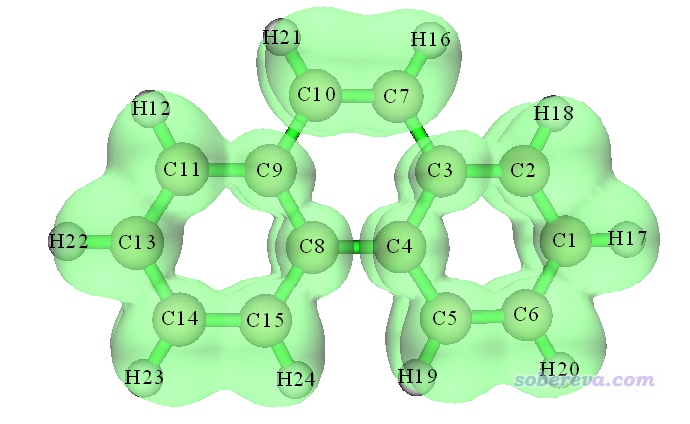
從這張圖可以看到，兩側的六元環上的ELF-pi等值面是連通的，但中間六元環上的ELF-pi不是連通的，在C9-C10、C3-C7、C4-C8的地方都斷開了，這體現出中央六元環上的pi電子六中心共軛程度明顯不及邊緣的六元環，因此芳香性不及兩側的六元環強。

一些文獻中對體系會用ELF-pi二分點數值來衡量芳香性強弱，這個值就是對應多中心共軛的ELF-pi等值面剛斷開時的等值面數值。我們仔細逐漸調節等值面數值，如下所示，會看到令中間六元環的ELF-pi等值面首次發生斷裂的等值面數值約為0.53，而兩側的六元環上的ELF-pi等值面首次斷裂的等值面數值約為0.765，這從定量角度上也體現出兩側六元環上的電子共軛程度明顯更強。

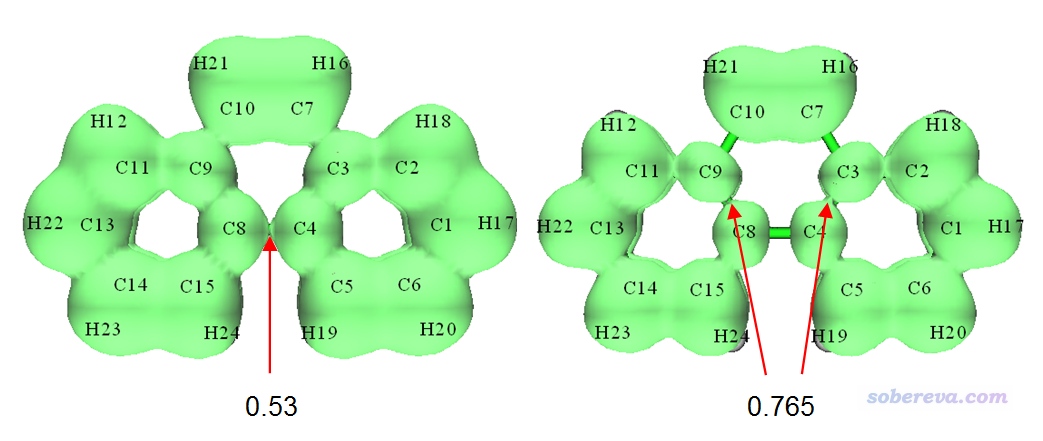
下面，我們來看如何讓Multiwfn自動找出來pi軌道并把其它軌道占據數清零，從而以明顯簡單得多的方式就能得到上面的圖。本例菲分子是個純平面分子，用Gaussian對它做計算時，哪怕輸入文件里它的結構是斜著的，由于Gaussian自動會把被計算的體系擺到標準朝向下，因此最終得到的fch文件里菲也會正好平行于某個笛卡爾平面。對于當前體系，你進入主功能0時，從屏幕上輸出的坐標就可以看到當前體系所有原子都在YZ平面上，X坐標皆為0。像這種情況，可以直接讓Multiwfn判斷pi軌道。Multiwfn用的判斷方法很簡單，當程序檢測到所有原子在YZ平面上時，如果一個軌道中S或PY或PZ型高斯函數的系數絕對值大于某個閾值，就認為這個軌道不是pi軌道，反之則是pi軌道。啟動Multiwfn后只需要依次輸入以下命令就可以實現pi以外軌道占據數清零的目的：
phenanthrene.fch
100  //主功能100
22  //自動檢測pi軌道并設定占據數
0  //讓程序自動判斷體系在XY、YZ、XZ中的哪個平面上
輸出信息如下所示
 This system is expected to be in YZ plane
 Expected pi orbitals, occupation numbers and orbital energies (eV):
    36      2.000000    -10.789622
    40      2.000000     -9.671071
    43      2.000000     -8.472032
    44      2.000000     -7.649069
    45      2.000000     -7.059917
    46      2.000000     -6.033737
    47      2.000000     -5.730233
    48      0.000000     -0.993257
    49      0.000000     -0.820463
...略
 Total number of pi orbitals:    56
 Total number of electrons in pi orbitals:   14.000000
 Total number of inner electrons:    28
即程序找出來56個pi軌道（包括占據和非占據的），上面一共有14個電子，同時提示體系內核電子數有28個（每個碳的1s上的兩個電子都是內核電子，當前14個碳，故2*14=28）。然后程序問你怎么處理這些軌道，屏幕上的提示寫得非常清楚：
1 把識別出的所有pi軌道占據數都清零
2 把其它軌道的占據數都清零
3 把價層pi軌道占據數清零
4 把除了價層pi軌道以外的軌道占據數清零
對于此例，我們為了獲得ELF-pi，就選2就行了（如果你的目的是獲得ELF-sigma，則顯然應該選1）。之后退回到主菜單，然后按上文的步驟利用主功能5照常繪制ELF，即可得到ELF-pi的圖。

如果你嫌調節ELF-pi等值面數值來找ELF-pi二分點數值的做法不夠精確，那么可以用Multiwfn強大的拓撲分析模塊來實現。此模塊做拓撲分析不僅可以用于電子密度從而實現Atoms in molecules (AIM)分析，對任何Multiwfn支持的實空間函數原理上也都適用。關于拓撲分析模塊的更多信息見《使用Multiwfn做拓撲分析以及計算孤對電子角度》（http://www.shanxitv.org/108）。我們對ELF-pi進行拓撲分析，找出來的(3,-1)型臨界點的位置和這個位置上的ELF-pi數值就分別對應于ELF-pi的二分點位置和此二分點的數值。

為了做ELF-pi拓撲分析，我們在按照如上方式把pi軌道以外的軌道占據數都清零并回到主菜單后，依次輸入
2  //拓撲分析
-11  //切換做拓撲分析的實空間函數
9  //ELF（如果想對LOL做拓撲分析，則此處選10）
6  //在球型空間內隨機撒初猜點做臨界點的搜索（這種搜索方式適合ELF-pi、LOL-pi、電子密度拉普拉斯函數等分布特征與電子密度相差較大的函數）
-1  //以每個原子核為中心的特定半徑（默認為3 Bohr）的球形區域內撒初猜點并開始搜索。默認每個原子附近撒1000個。當前體系共24個原子，因此共嘗試24*1000次臨界點搜索。此過程耗時較高需耐心等待
-9  //返回上一級菜單
0  //觀看臨界點
點擊圖形窗口右側的相應選項，把臨界點標簽和原子標簽顯示出來，把(3,-1)以外的臨界點都取消顯示，此時看到的圖如下所示（由于初猜點是隨機撒的，你運行此例得到的臨界點序號可能與圖中的不同）

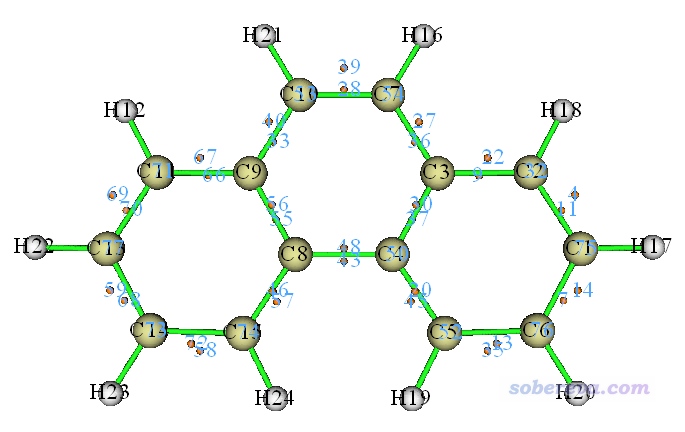
圖中每一個桔色小圓球對應一個(3,-1)，也即ELF-pi的二分點。可見諸如43和48號臨界點對應的就是C4-C8之間的二分點。如果要考察比如43號臨界點的ELF-pi的數值，就在圖形窗口右上角點擊RETURN按鈕關閉圖形界面，然后選擇選項7（查看臨界點屬性），輸入43，此時從屏幕上輸出信息中就能找到
Electron localization function (ELF):  0.5255798572E+00
即精確的二分點數值為0.525，和我們之前看圖肉眼判斷出的0.53幾乎精確一樣。因此，找ELF-pi二分點數值要求不高的時候直接看等值面圖就夠了，精度要求較高時則可以用很準確但耗時也較高的拓撲分析方式得到。

注：如果你關心的二分點在圖形界面里看不到，并且你確信那里應該有二分點，可能是隨機搜索的時候沒搜出來。可以重新進入選項6選-1再次搜索，然后再次進入圖形窗口檢查，直到搜出來為止。

還順帶一提的是，Multiwfn還可以把臨界點上的特定函數分解為各個軌道對其的貢獻。i軌道的貢獻等于把i軌道以外的軌道占據數清零后再計算的函數值。當然，只對那些可以精確分解為軌道貢獻的函數如電子密度，分解出的各軌道貢獻的加和才等于直接算出來的結果。比如我們想考察ELF-pi的43號臨界點處各個軌道對電子密度的貢獻，那么在拓撲分析界面依次輸入
7  //查看臨界點屬性
43d  //分解第43號臨界點的屬性
1  //分解電子密度
[直接按回車，考慮所有占據軌道]
此時如下所示，所有占據軌道對43號臨界點的電子密度的貢獻值和貢獻百分比全都得到了，其中44號起主導作用，貢獻了50%，如果你看軌道圖也會發現44號軌道顯著覆蓋了C4-C8之間的區域。Sum of above values就是指所有軌道貢獻加和，Exact value就是指直接算的結果，二者相同，體現了電子密度可以精確分解為軌道貢獻的事實。
 Contribution from orbital    44 (occ= 2.000000):      0.014123 a.u. ( 50.05% )
 Contribution from orbital    36 (occ= 2.000000):      0.010034 a.u. ( 35.56% )
 Contribution from orbital    47 (occ= 2.000000):      0.003773 a.u. ( 13.37% )
 Contribution from orbital    43 (occ= 2.000000):      0.000285 a.u. (  1.01% )
 Contribution from orbital    46 (occ= 2.000000):      0.000000 a.u. (  0.00% )
 Contribution from orbital    40 (occ= 2.000000):      0.000000 a.u. (  0.00% )
 Contribution from orbital    45 (occ= 2.000000):      0.000000 a.u. (  0.00% )
 Sum of above values:      0.02821475 a.u. ( 100.00% )
 Exact value:      0.02821475 a.u.

雖然也可以用這種方式將ELF-pi二分點上的ELF-pi值分解為軌道的“貢獻”，但由于ELF函數形式的原因，你會發現這樣強行分解成軌道貢獻并沒什么實際意義，所有軌道貢獻之和與直接算的值相差甚遠。

如果你退出拓撲分析模塊，然后如前述做法照常繪制ELF等值面圖，那么ELF-pi臨界點和等值面圖會顯示在一起，便于考察臨界點和函數分布之間的關系。下圖是ELF-pi=0.525的等值面，可見在C4和C8之間，等值面的二分位置正好和拓撲分析搜索出來的二分點相交

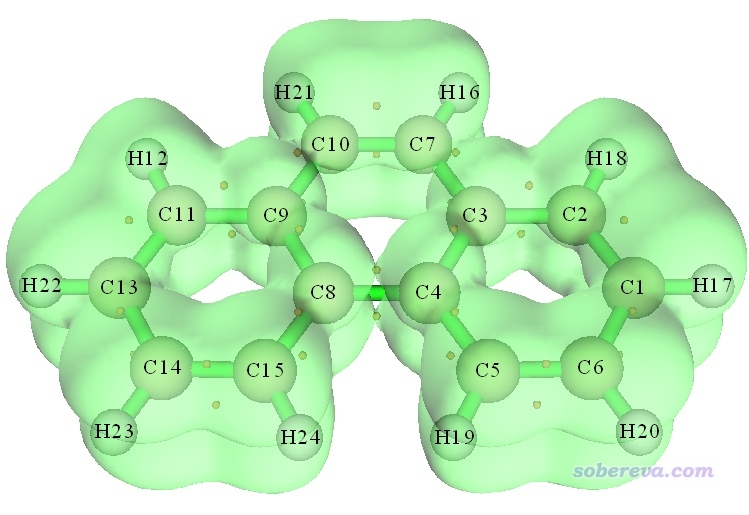
2.2 繪制卟啉分子平面上方1.2 Bohr處的LOL-pi的填色圖

LOL和ELF的函數分布特征非常類似，物理意義也很接近，在前述的ELF資源匯總貼里也有LOL的介紹，有時候LOL圖比ELF圖看著更清楚舒服。類似于ELF與ELF-pi、ELF-sigma的關系，對于LOL也可以繪制LOL-pi和LOL-sigma。本例我們繪制卟啉分子平面上方1.2 Bohr處的LOL-pi的平面填色圖，這樣可以非常清晰地展現卟啉分子中pi電子離域特征。這里用1.2 Bohr并沒有特別的理論依據，只不過經過測試發現這個距離的LOL-pi平面圖對pi電子特征展現得比較清楚。當然繪制LOL-pi等值面圖也可以，只不過對此例，等值面圖不如平面圖對LOL-pi分布特征展現得那么充分。

啟動Multiwfn，載入本文文件包里的porphyrin.fch，進入主功能0會看到所有原子都在X=0的YZ平面上，因此我們要繪制的應當是X=1.2 Bohr的YZ平面。接著在Multiwfn里輸入：
100  //主功能100
22  //檢測pi軌道
0  //自動檢測分子平面
2  //把pi軌道以外的軌道占據數清零
0  //返回主菜單
4  //繪制平面圖
10  //LOL
1  //填色圖
按回車用默認的格點數
3  //YZ平面
1.2  //X=1.2 Bohr
很快，平面圖就蹦出來了：

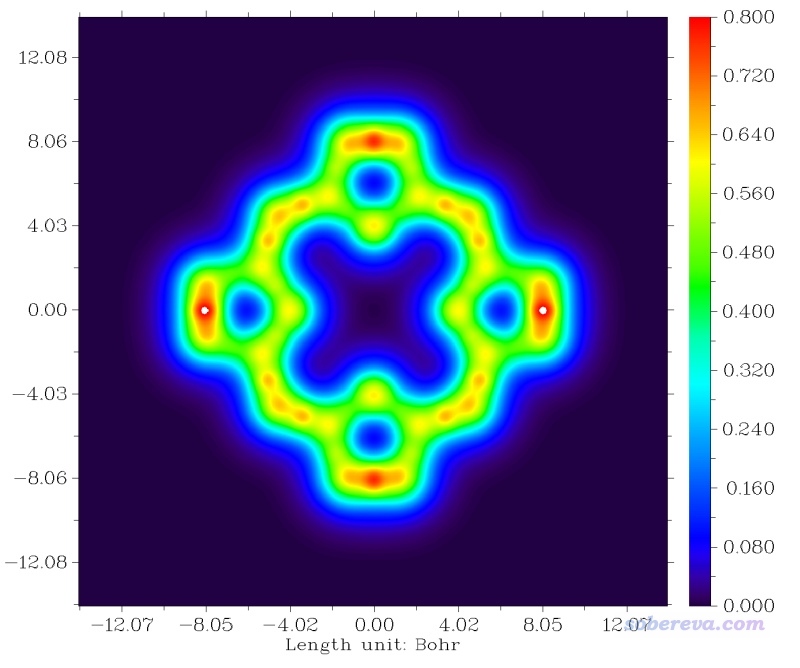
此時的圖像效果還不十分理想。我們需要修改作圖設定。關閉圖像，然后依次輸入
-8  //把坐標單位切換為埃，從而與習俗一致
-2  //修改坐標刻度間隔
2,2,0.1  //X,Y坐標刻度間隔為2，縱坐標刻度間隔為0.1
1  //修改色彩刻度上下限
0,0.66  //下限和上限
4  //顯示原子標簽
7  //以青色顯示
17  //修改顯示原子標簽的距離
2  //原子核位置距離作圖平面小于2 Bohr的原子都在圖上顯示出標簽（2 Bohr是隨意設的，對當前例子只要大于1.2 Bohr即可）
y  //距離超過2 Bohr的原子以較細字體顯示標簽（對于本體系設y還是n都不影響所得圖像）
8  //顯示化學鍵（程序按照原子核距離和原子半徑自動判斷是否成鍵）
14  //棕色顯示化學鍵
0  //保存圖像
此時當前目錄下就出現了名為dislin.png的圖像文件，如下所示

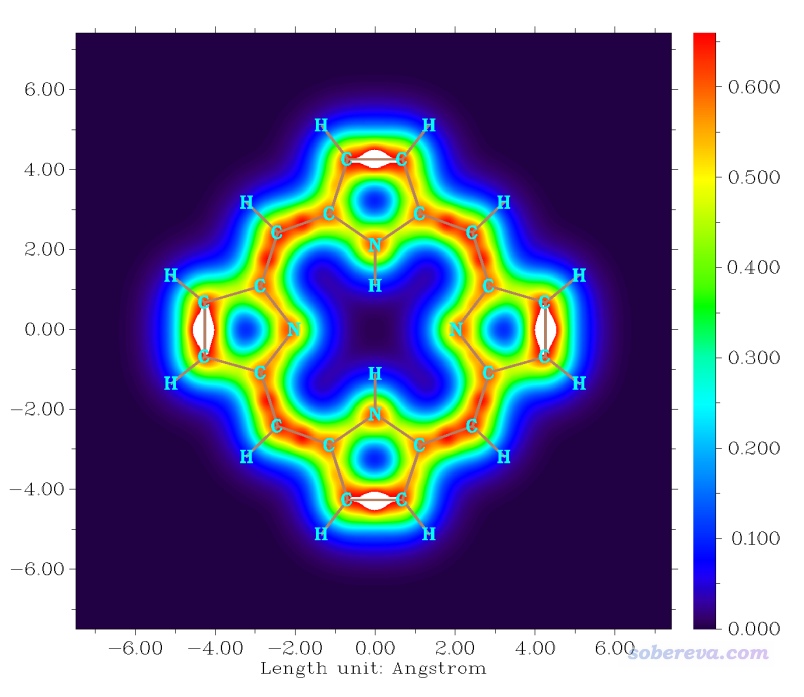
由圖可見，在左邊和右邊五元環的內側、上邊和下邊五元環的外側，LOL-pi較大數值區域連通成了一個大環，非常清楚地展現出了pi電子主要的離域路徑。如果你用AICD（http://www.shanxitv.org/294）或GIMIC（http://www.shanxitv.org/155）繪制磁感生環電流，會看到繞著pi電子離域的大環有顯著的環電流出現。如果你用Multiwfn通過ICSS方法（http://www.shanxitv.org/216）分析，也會看到那個大環內側的外磁場被顯著屏蔽，這都顯示出了卟啉分子顯著的芳香性。

2.3 計算苯酚的pi電子布居數和繪制pi電子密度分布圖

筆者在《親電取代反應中活性位點預測方法的比較》（http://www.whxb.pku.edu.cn/CN/abstract/abstract28694.shtml）中2.7節曾指出，利用pi電子分布可以考察親電反應位點。文中是考察垂直于平面的Pz軌道的布居數，實際上，如果把pi軌道以外的軌道占據數清零再做布居分析，得到的原子布居數直接就對應了原子的pi電子數。本例以苯酚為例來演示。

啟動Multiwfn，依次輸入
phenol.fch  //在本文的文件包里
100  //主功能100
22  //檢測pi軌道
0  //自動檢測分子平面
2  //把pi軌道以外的軌道占據數清零
0  //返回主菜單
7  //布居分析
5  //Mulliken布居分析
1  //輸出Mulliken布居數和原子電荷
n  //不輸出.chg文件

屏幕上看到的碳的布居數如下（看Population。Net charge對當前情況無意義）：
 Atom     1(C )    Population:    1.03706    Net charge:    4.96294
 Atom     2(C )    Population:    0.98865    Net charge:    5.01135
 Atom     3(C )    Population:    1.05314    Net charge:    4.94686
 Atom     4(C )    Population:    0.97316    Net charge:    5.02684
 Atom     5(C )    Population:    1.09090    Net charge:    4.90910
 Atom     6(C )    Population:    0.99054    Net charge:    5.00946
當前體系中，C3和C5是羥基的兩個鄰位碳，C1是對位碳，C2和C4是間位碳。由數據可見，鄰、對位碳上pi電子數比間位上的更多，暗示更容易發生親電反應，這和實驗結論是一致的。不過，實驗上對位產物比鄰位多，而當前結果與此矛盾，這和《親電取代反應中活性位點預測方法的比較》文中發現的情況相同，說明光靠考察pi電子分布量并不能完全說明問題。若用Multiwfn計算福井函數、雙描述符、平均局部離子化能等（如何在Multiwfn里實現參看Multiwfn手冊4.A.4節），結論都是對位比鄰位活性強，和實驗完全一致。

接著，我們可以再看看苯酚的pi電子密度等值面圖是什么樣，接著在Multiwfn里輸入
0  //回到布居分析界面
0  //回到主菜單
5  //計算格點數據
1  //電子密度
2  //中等質量格點
-1  //顯示等值面圖

等值面數值設為0.04時看到的等值面圖如下

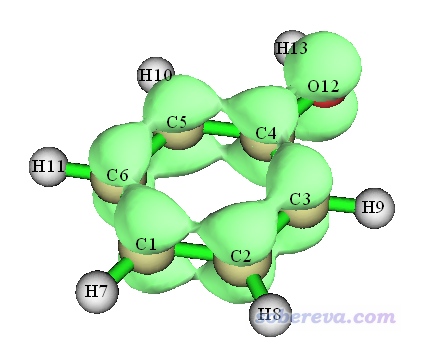
可見由于不同碳上帶的pi電子數差異不大，因此從電子密度等值面圖上看不出有多大差異。像這種情況，繪制分子平面上方比如1埃處電子密度填色圖，則可以看得清楚得多。

關閉圖形窗口，在Multiwfn里接著輸入
0  //回到主菜單
4  //繪制平面圖
1  //電子密度
1  //填色圖
按回車用默認格點數
0  //修改延展距離
1  //延展距離改為1 Bohr（因為pi電子分布區域在體系內側，作圖時不用在分子邊緣留出太大空隙）
1  //XY平面
1a  //Z=1埃
之后，在后處理菜單把色彩刻度下限和上限分別設為0和0.03，并且顯示出原子標簽，恰當設定坐標軸刻度等細節，最終看到的圖像如下

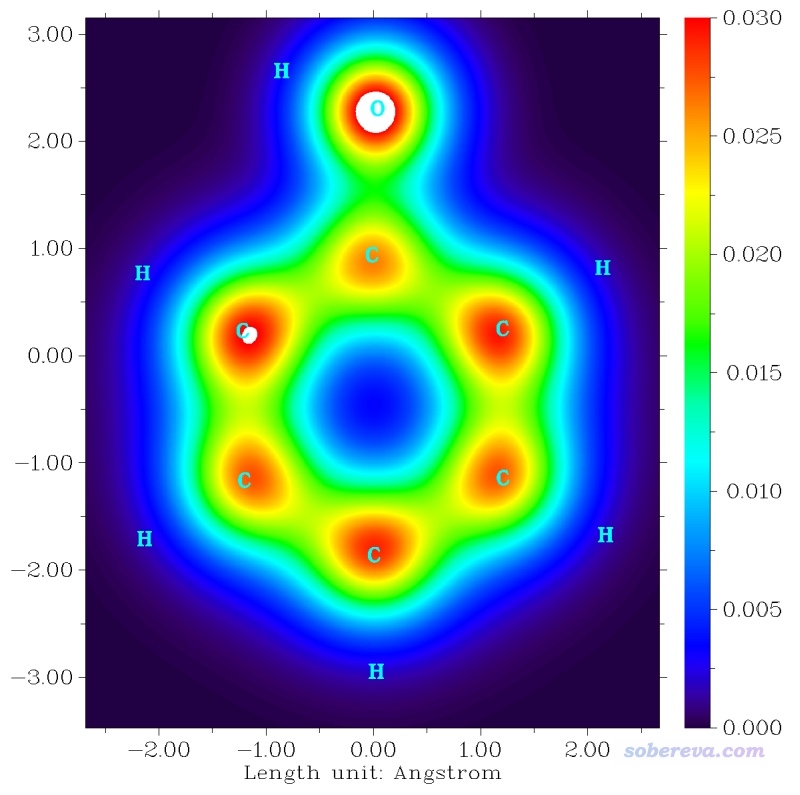
由圖明顯可見，在分子上方1埃的平面上，鄰、對位的pi電子密度大于間位的，因為桔紅色更深、范圍更大，這和我們做的pi電子布居分析結論一致。

2.4 計算菲的pi多中心鍵級

此節演示對菲計算pi多中心鍵級，從而考察菲的中間的芳環共軛程度高還是邊緣的芳環共軛程度高，看看能否進一步驗證ELF-pi的分析結論。多中心鍵級在前述的《衡量芳香性的方法以及在Multiwfn中的計算》和Multiwfn手冊3.11.2節都有介紹。

啟動Multiwfn，依次輸入
phenanthrene.fch
0  //在主功能0里觀看一下邊緣六元環和中間六元環的原子序號，按照逆時針或順時針順序記錄下來備用
100  //主功能100
22  //檢測pi軌道
0  //自動檢測分子平面
2  //把pi軌道以外的軌道占據數清零
0  //返回主菜單
9  //鍵級分析
2  //多中心鍵級
3,4,8,9,10,7  //中間六元環的原子序號
9,8,15,14,13,11  //邊緣六元環的原子序號
屏幕上顯示的中間六元環的計算結果為：
The multicenter bond order:    0.0237488557
邊緣的為：
The multicenter bond order:    0.0565680226
即邊緣的六元環共軛程度明顯比中間的六元環要高，多中心鍵級更大，和ELF-pi的分析結論相同。

如果要考察pi電子對應的Mayer鍵級也很容易，選擇0返回鍵級分析菜單，然后選1計算Mayer鍵級即可。會看到這樣的輸出
 The total bond order >=  0.050000
 #    1:         1(C )    2(C )    0.52086147
 #    2:         1(C )    4(C )    0.06618967
 #    3:         1(C )    6(C )    0.36615890
 #    4:         2(C )    3(C )    0.33674614
 #    5:         2(C )    5(C )    0.09901526
 #    6:         3(C )    4(C )    0.32998162
 #    7:         3(C )    6(C )    0.06162677
 #    8:         3(C )    7(C )    0.22763945
...
芳香環上的C-C鍵Mayer鍵級往往在1.5左右，即形式上類似于一個sigma鍵加上半個pi鍵。當前把sigma電子都扣掉了，因此剩下的C-C鍵的鍵級就變成零點幾了，其中有的大一些有的小一些。在本文的第一張圖，即ELF-pi=0.7的等值面圖上看到，C3-C7之間等值面是斷開的，而C3-C2和C3-C4等值面都是連通的，體現在pi電子Mayer鍵級上就是C3-C7鍵級小而C3-C2和C3-C4鍵級相對略大。

3 對非純平面的體系考察pi電子結構

3.1 基于LMO區分sigma和pi電子的原理

前面已經通過大量例子充分展現了怎么對純平面體系考察pi電子結構。對于非平面體系，分子軌道當中往往既有pi成份也有sigma成份，看似沒法嚴格把sigma和pi電子分離，但實際上，基于定域化分子軌道(LMO)，還是可以做到sigma-pi分離的。如果不熟悉軌道定域化這個概念，務必看《Multiwfn的軌道定域化功能的使用以及與NBO、AdNDP分析的對比》（http://www.shanxitv.org/380）。把分子軌道做軌道定域化轉化為LMO之后，根據結構化學知識，一般就可以輕易指認哪些是pi型LMO哪些是sigma型LMO。然而，當體系一大了，人工看軌道圖形來進行指認是很麻煩的事情。為解決此問題，筆者提出了一個自動檢測pi型LMO的方法并且實現在了Multiwfn里，在Theor. Chem. Acc., 139, 25 (2020)中筆者做了詳細介紹。這個檢測方法不復雜，原理如下：對每個LMO計算軌道成份，如果某個原子貢獻超過了某個閾值，那么這個LMO就被認為是單中心LMO（比如對應孤對電子的軌道、內核軌道等），應當被忽略。對剩下的軌道，假定對LMO貢獻最大的兩個原子是A和B，程序會計算0.7*R(A)+0.3*R(B)和0.3*R(A)+0.7*R(B)這兩個點處的軌道密度（即軌道波函數的平方），這里R是指原子核坐標。如果這兩個點的軌道密度同時都大于一個閾值，那么這個軌道就被認為是sigma型LMO，而其它的就被認為是pi型LMO。這種判斷方式的原理易于理解，如果這兩個點處的軌道密度特別小，就意味著這個軌道基本只體現pi特征，因為pi軌道在兩個原子連線上有個節面。這種判斷方法至少對于筆者測試過的各種有機體系是很合理、穩妥的，至于金屬團簇之類復雜情況還沒有充分測試過（如果不放心的話，可以在主功能0里看軌道圖形人工檢查一下自動找出來的pi型LMO對不對，如果有不合適的，就在主功能6的子功能26里通過手動修改軌道占據數使情況合理）。

注意，令Multiwfn做軌道定域化的時候必須是用默認的Pipek-Mezey方法來做，不能改用Foster-Boys方法來做，因為前者可以給出sigma和pi分離的LMO，而后者產生的多重鍵對應的LMO是sigma和pi混合的。默認的Pipek-Mezey是基于Mulliken布居實現的，此時基組最好不要帶彌散函數（對于定域化占據軌道但也不是一定不行，也可以實際試試效果）。如果有特殊原因必須帶彌散函數，并且發現默認的Pipek-Mezey得到的定域化軌道不好，建議改用基于Becke布居的Pipek-Mezey方法，但對于較大體系昂貴得多得多。

對于純平面體系，雖然也可以做軌道定域化、基于LMO來區分開sigma和pi電子，但是完全多此一舉，相對于直接基于分子軌道來區分不會有額外好處，分析結果也是相同的。

3.2 對苯甲酮繪制LOL-pi等值面圖

下面看一個對非純平面體系苯甲酮考察pi電子結構的例子。

啟動Multiwfn，依次輸入
benzophenone.fch  //在本文的文件包里
19  //軌道定域化
1  //對占據軌道做軌道定域化（非占據軌道對分析結果無貢獻，故不用對非占據軌道也做定域化）
100  //主功能100
22  //檢測pi軌道
-1  //當前內存里的軌道是定域化過的軌道
0  //開始檢測pi軌道。用屏幕上的選項可以修改判斷pi軌道的閾值，這里暫且不改
此時屏幕上提示了檢測出的pi型LMO的編號，一共發現了7個，接著輸入
2  //把其它軌道占據數清零
0  //回到主菜單
5  //計算格點數據
10  //LOL
2  //中等質量格點
-1  //觀看等值面圖
觀看到的圖像如下所示

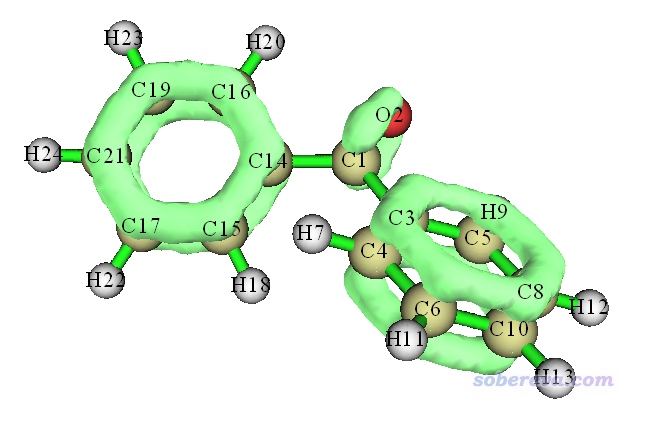
此圖和我們期望的一致，等值面把pi電子區域充分勾勒了出來，而sigma電子、孤對電子都沒有被體現。由于這個體系是非平面體系，不好選取作圖平面，所以就不用演示繪制平面圖了。

我們還可以像之前對純平面體系所做的那樣，繪制電子密度圖、做布居分析、計算pi鍵級等等。值得一提的是，對這樣非純平面體系計算Mayer鍵級、多中心鍵級，對sigma電子算的結果和對pi電子算的結果的總和，和直接對總電子算的結果是不同的，但差異一般不顯著。此體系的苯環的六中心鍵級計算結果為
考慮全部電子：0.0773346195
只考慮pi電子：0.0755099345
只考慮sigma電子：0.0024250360
將0.0755099345與0.0024250360相加結果為0.0779349705，和考慮全部電子時候的0.0773346195非常接近。

再對此體系的C=O鍵計算Mayer鍵級，結果為
考慮全部電子：1.81239410
只考慮pi電子：0.75232404
只考慮sigma電子：1.06873978
sigma和pi單獨算的結果之和為0.75232404+1.06873978=1.82106382，和考慮全部電子時的1.81239410也很接近。此例體現出，對非平面體系基于LMO劃分sigma和pi電子，計算的鍵級還是有近似可加和性的。

3.3 對螺烯局部繪制pi電子密度等值面圖

Multiwfn在基于LMO指認pi型LMO的時候能夠加約束條件，可以要求此LMO中貢獻最大的兩個原子必須屬于某個原子序號范圍。這個功能比較有用，比如我們想對一段DNA片段中的堿基部分繪制ELF-pi圖，而不希望磷酸基部分的pi電子也顯示出來，就可以利用這個約束設置。

下面我們對如下所示的螺烯繪制pi電子密度等值面圖，繪制的時候只繪制分布在中間四個六元環上的pi電子。

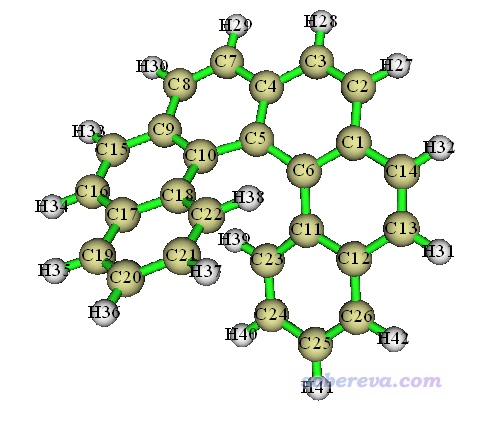
啟動Multiwfn，載入本文文件包里的helicene.fchk，然后依次輸入
19  //軌道定域化
1  //對占據軌道做軌道定域化
100  //主功能100
22  //檢測pi軌道
-1  //當前軌道是定域化過的軌道
5  //設定約束條件
1-18  //中間四個六元環的碳的編號（懶得自己記錄編號的話可以利用gview直接把選定區域的原子序號直接提出來，可參考https://www.bilibili.com/video/av26312703/里面的演示）
0  //開始檢測pi軌道
螺烯中間四個六元環一共有18個碳原子，它們上面共有約18個pi電子。屏幕上提示找出來了9個pi型LMO，正好對應18個電子，因此LMO肯定識別對了，也不用人工看LMO圖形檢查了。然后選2將其它軌道占據數清零，之后照常繪制電子密度等值面圖，結果如下圖左側所示。下圖右側是不做約束而繪制的所有pi電子的等值面圖。

 

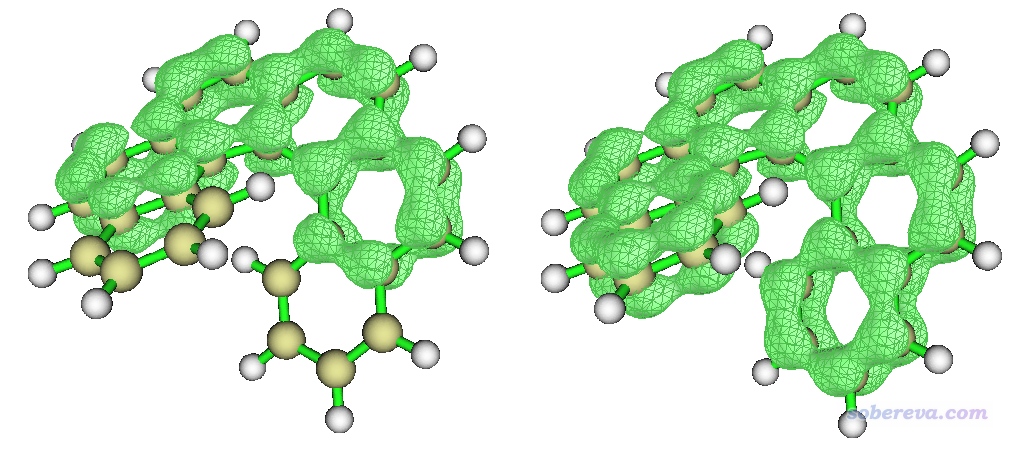
由于LMO的高度定域化特征，我們可看到上圖的左圖和右圖的中間四個六元環上電子密度分布特征完全相同。

3.4 對螺烯各個碳原子計算pi和sigma布居數

此例對螺烯各個碳原子計算pi和sigma布居數。判斷出pi型LMO后，把pi軌道以外的軌道占據數清零，再用Multiwfn做布居分析得到的顯然就是pi布居數了。類似地，如果把pi軌道占據數清零，再用Multiwfn做布居分析得到的顯然就是sigma布居數了（也包括內核電子。如果不想把內核電子算進去，手動再減去內核電子數即可）。正如計算原子電荷的方法很多，計算pi布居數的方法也很多，這里就用比較常用的、接受度也比較高、也不怕彌散函數的Hirshfeld方法來算。

啟動Multiwfn，載入本文文件包里的helicene.fchk，然后依次輸入
19  //軌道定域化
1  //對占據軌道做軌道定域化
100  //主功能100
22  //檢測pi軌道
-1  //當前軌道是定域化過的軌道
0  //開始檢測
螺烯一共有26個碳原子，屏幕上提示識別出的13個pi軌道上的pi電子數一共26個，即每個碳一個，顯然識別對了。然后輸入
2  // 把其它軌道占據數清零，
0  //返回主菜單
15  //模糊空間分析
-1  //修改空間劃分的定義
3  //用Hirshfeld劃分，而且是基于程序內置的自由原子密度
1  //對各個原子空間進行積分
1  //被積函數是電子密度

然后我們就得到各個原子上的pi電子數了，即下面輸出中的Value值
  Atomic space        Value                % of sum            % of sum abs
    1(C )            0.98589185             3.791847             3.791847
    2(C )            0.94199198             3.623003             3.623003
    3(C )            0.94339795             3.628411             3.628411
    4(C )            0.98692756             3.795831             3.795831
    5(C )            0.98574768             3.791293             3.791293
    6(C )            0.98389723             3.784176             3.784176
...略

對于這樣得到的pi布居數，也可以按照《使用Multiwfn+VMD以原子著色方式表現原子電荷、自旋布居、電荷轉移、簡縮福井函數》（http://www.shanxitv.org/425）介紹的方法進行著色來直觀展現。下圖是Theor. Chem. Acc., 139, 25 (2020)中我對碳納米管片段用這種方法繪制的pi電子布居數圖，不過pi電子數是Mulliken方法算的（主功能7里選主功能5，然后選1，讀Population），這比Hirshfeld方法快得多但怕彌散函數。

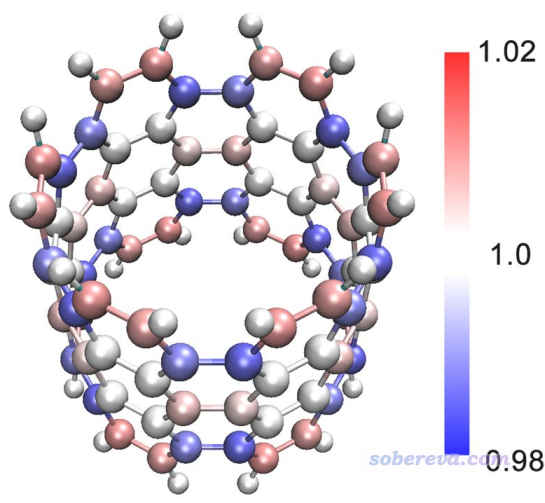
sigma布居數也類似地計算，這里就不再演示了。

4 使用VMD渲染得到更好效果

如果想得到比直接用Multiwfn顯示的等值面效果更好的圖像，強烈推薦按照《在VMD里將cube文件瞬間繪制成效果極佳的等值面圖的方法》（http://www.shanxitv.org/483）中的做法利用VMD腳本繪制。比如下圖是借助VMD渲染出來的對苯甲酮的LOL-pi等值面圖，效果絕佳，而步驟卻異常簡單！

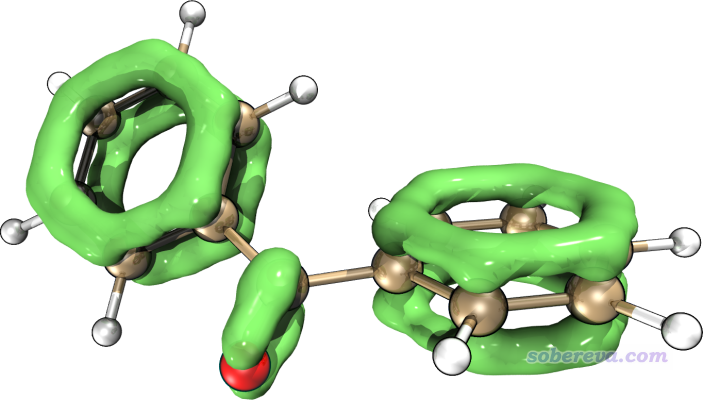
這里順帶給大家看一下筆者將本文的方法用到過的最大體系，[144]-annulene的效果。下圖是基于Multiwfn產生的LOL-pi格點數據，用VMD渲染后的等值面圖，可見非常理想地將這個巨大的共軛體系的pi電子共軛路徑十分清晰直觀地展現了出來！

下圖是筆者對手性共軛碳納米帶體系繪制的LOL-pi=0.4的等值面圖，可見等值面充分將pi共軛路徑展現了出來，圖像很漂亮。

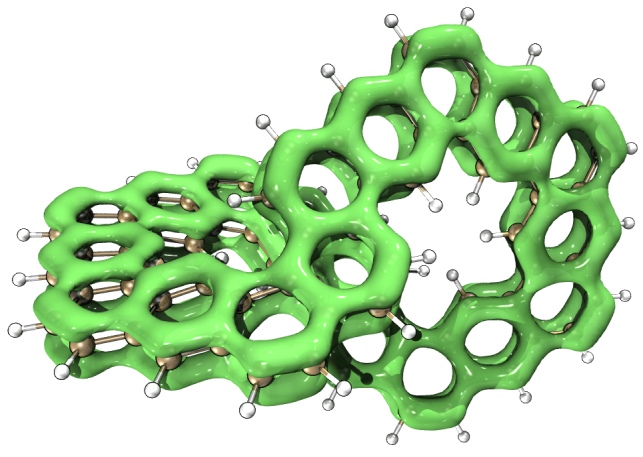
下圖的體系和上面的結構類似，但是邊緣有些碳是sp3雜化的，由圖可見在它們上面沒有LOL-pi等值面，清楚地體現出電子的pi共軛在這樣的地方被截斷了。

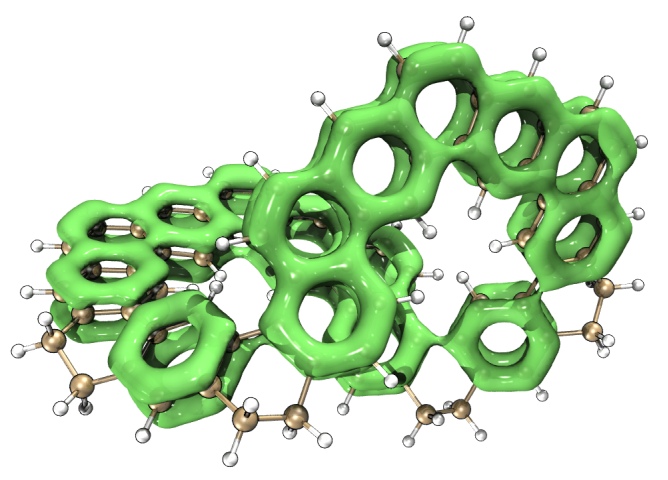
一篇Nature Communication文章（見http://bbs.keinsci.com/thread-29087-1-1.html）和一篇J. Am. Soc. Chem.文章（見http://bbs.keinsci.com/thread-29300-1-1.html）也都使用了上面介紹的方法繪制了LOL-pi等值面圖清楚地展現了pi共軛路徑。

5 總結&其它

pi電子在化學體系中有重要地位。本文充分演示了如何在Multiwfn中考察pi電子結構。雖然沒有示例怎么考察sigma電子結構，但想必仔細閱讀本文的人都知道怎么做，只不過就是讓程序識別出pi軌道后，選擇把pi軌道占據數都清零，然后照常分析即可。Multiwfn中對pi電子的分析絕不僅限于文中所列出的這些，希望讀者在理解本文例子的基礎上，充分靈活運用Multiwfn的各種分析功能，舉一反三，解決實際遇到的問題。

Multiwfn還可以計算任意類型軌道的pi成份，這個功能非常有用，在此帖專門做了介紹：《Multiwfn已支持計算任意軌道的pi成份》（http://bbs.keinsci.com/thread-13110-1-1.html），強烈建議一看！

在筆者的pi電子分析算法原文Theor. Chem. Acc., 139, 25 (2020) DOI: 10.1007/s00214-019-2541-z論文中，對于pi電子分析還有更多、深入、更充分的討論，并且給了更多例子，請讀者切勿忘記閱讀此文。

筆者在《談談18碳環的幾何結構和電子結構》（http://www.shanxitv.org/515）和《一篇最全面、系統的研究新穎獨特的18碳環的理論文章》（http://www.shanxitv.org/524）中專門考察了比較新穎的18碳環體系的pi電子結構，而且考察的不僅是常規的位于環上、下方的pi軌道，還考察了比較少見的在環平面上的pi軌道（in-plane pi軌道），此研究后來正式發表于Carbon, 165, 468 (2020)，里面還全面運用了其它方法分析了18碳環獨特的電子結構特征，十分建議一看。在《深入揭示18碳環的重要衍生物C18-(CO)n的電子結構和光學特性》（http://www.shanxitv.org/640）一文中還介紹了筆者發表的Chem. Eur. J., 28, e202103815 (2022)一文，其中也充分利用了LOL-pi非常清晰直觀地考察了C18-(CO)2、C18-(CO)4、C18-(CO)6的pi共軛情況的差異，也特別推薦一看。在《不尋常的環[18]碳前驅體C18Br6的電子結構和芳香性》（http://www.shanxitv.org/664）里介紹的Chem. Eur. J., e202300348 (2023) DOI: 10.1002/chem.202300348中還使用了LOL-pi考察C18Br6的電子結構。這幾篇論文都非常推薦作為LOL-pi的應用范例引用。

本文示例的都是DFT波函數。而后HF波函數（也包括其它各種多組態波函數）是以自然軌道形式記錄的，對純平面體系可也以按照本文第二節的做法照常區分sigma和pi軌道。而由于軌道定域化沒法用于后HF波函數，因此對于非平面體系的后HF波函數，一般是沒辦法區分sigma和pi軌道從而單獨考察sigma和pi電子特征的。但這也不是那么絕對，其實運用一些技巧也可以解決：
(1)對這樣的體系用DFT計算一次，得到LMO軌道，再用判斷軌道pi成份的功能判斷自然軌道的pi特征百分比，高于一定數值的就當做是準pi軌道
(2)對于比如甲苯這樣的體系，有三個準pi軌道離域在苯環上，可以讓程序自動挑出來。先令甲苯的苯環平行于XY平面（做法見http://www.shanxitv.org/178），然后用Gaussian單點計算的時候加上nosymm關鍵詞避免朝向被自動調整，將得到的波函數載入Multiwfn，用主功能6的子功能-4把甲基上的原子的GTF都刪掉，然后進入主功能100的子功能2，選擇0因為當前軌道是離域的軌道，然后選擇XY平面，再輸入兩個閾值（見屏幕上的提示，建議用自動推薦的），然后準pi型軌道編號就被找出來了。