使用Multiwfn做拓撲分析以及計算孤對電子角度
使用Multiwfn做拓撲分析以及計算孤對電子角度
文/Sobereva @北京科音
First release: 2011-Dec-1 Last update: 2020-Aug-10
波函數分析程序Multiwfn的拓撲分析模塊極為強大、高效、靈活而且普適,原理上可以用于各種實空間函數的拓撲分析,比如電子密度、ELF、LOL、電子密度拉普拉斯函數、軌道波函數等等。電子密度的拓撲分析也是Atoms in molecules (AIM)分析的最重要組成部分之一。本文將簡要介紹Multiwfn拓撲分析功能的基本使用方法。Multiwfn程序可以在其主頁http://www.shanxitv.org/multiwfn免費下載,相關入門知識參見《Multiwfn入門tips》(http://www.shanxitv.org/167)、《Multiwfn FAQ》(http://www.shanxitv.org/452)。
如果讀者不熟悉AIM,建議參看《AIM學習資料和重要文獻合集(http://bbs.keinsci.com/thread-362-1-1.html)里的資料。如果不熟悉ELF、LOL和電子密度拉普拉斯函數,建議參看《ELF綜述和重要文獻小合集》(http://bbs.keinsci.com/thread-2100-1-1.html)。在《Multiwfn支持的分析化學鍵的方法一覽》(http://www.shanxitv.org/471)中筆者對AIM拓撲分析在研究化學鍵上都能起到什么用處做了詳細說明,強烈建議一看。
1 拓撲分析簡介
限于篇幅,這里只是對拓撲分析做極簡單的說明,或者說是回顧。對于完全不了解AIM理論的人,不妨看看The Quantum Theory of Atoms in Molecules-From Solid State to DNA and Drug Design一書的第一章,對電子密度的拓撲分析有簡介、清楚、易懂的介紹,上面的文獻合集里有這一章。
實空間函數(以三維空間坐標為變量的函數)的拓撲分析主要是指獲取臨界點,以及獲得連接臨界點的拓撲路徑。電子密度的拓撲分析是由Bader首先提出的,是AIM理論中的重要組成部分,后來拓撲分析的思路又被Silvi、Savin等人用于分析ELF(電子定域化函數)。
臨界點(Critical point, CP)是函數的梯度的模為0的點,分四類,以(3,X)表示。假設實空間函數的Hessian矩陣(3*3的二階導數矩陣)的本征值有M個正值和N個負值,則X=M-N。
(3,-3)對應函數的局部極大點。對于電子密度函數,通常出現在離原子核很近的位置。對于ELF函數,通常出現在共價鍵區域、孤對電子區域、原子核處。
(3,-1)對應函數的二階鞍點。函數在一個方向曲率為正,另兩個方向為負。對于電子密度函數,通常出現在有相互作用的兩個原子之間,也被稱為鍵臨界點(BCP)。對于ELF函數,位置不甚確定,經常偏離兩個相關的(3,-3)的連線很多。
(3,+1)對應函數一階鞍點,如同勢能面上的過渡態。對于電子密度函數,通常出現在環體系平面中,如苯環的中心。對于ELF,(3,+1)和下面的(3,+3)通常較少討論。
(3,+3)對應函數的局部極小點。對于電子密度函數,通常出現在籠狀體系中,例如C60的中心。
尋找臨界點通常使用牛頓法。給出一個初猜點,通過反復迭代,就能找到與之最鄰近的臨界點。但牛頓法不一定每次都成功,有可能一直不收斂,也可能迭代過程中碰到Hessian矩陣為奇矩陣的情況,或者收斂到已找到的臨界點位置,此時就要嘗試從下一個初猜點開始了。初猜點與期望的臨界點位置越近越容易成功收斂到相應的臨界點。
電子密度函數的結構很簡單,一般都是在原子核處像一個山峰聳立,向著四周呈指數降低,典型體系的各種臨界點位置都能大致猜出來,正如上面已經提到的。尋找(3,-3)點的時候初猜點都選在原子核位置。尋找(3,-1)點的時候,初猜點都選在兩個原子或者兩個已找到的(3,-3)點連線的中點,在這個過程中也可能順便找到(3,+1)和(3,+3)點。另外也常常將三個原子或四個原子的幾何中心作為初猜,這分別適合進一步尋找尚未找到的(3,+1)和(3,-3)點。假設利用這幾種初猜方式還是沒找到一些期望的臨界點,但通過經驗可以估計出期望的點出現的大致空間范圍,那么就應當在這個空間范圍內設定一大堆初猜點來嘗試尋找那個臨界點。
對于ELF、LOL和電子密度拉普拉斯函數,尋找對應原子內核處的臨界點(對應高度定域的1s軌道電子)還是用原子核位置作為初猜。但是對于價層的ELF臨界點,由于其分布較難預料,而且數目眾多,最好的辦法就是直接在每個原子附近都設一大堆初猜點來尋找各個臨界點。不過,由于ELF臨界點太多而且分布太復雜,想找全所有臨界點絕非易事,所以,只要看到化學意義顯著的臨界點(所有的(3,-3),以及部分(3,-1))都已經找到了,臨界點的搜索就可以停掉了。除了牛頓法,還有一種基于立方格點的臨界點搜索方法,可以通過Multiwfn的盆分析實現,見《使用Multiwfn做電子密度、ELF、靜電勢、密度差等函數的盆分析》(http://www.shanxitv.org/179),此方法雖然可以保證把(3,-3)搜索全,但定位精度低(精度取決于格點間距)。
拓撲路徑是連接臨界點的路徑。一般比較關注的是(3,-1)與(3,-3)之間的路徑,沿著(3,-1)的Hessian矩陣本征值為正的本征向量方向分別向前和向后出發,順著梯度方向不斷前進就能找到兩個(3,-3),而經過的軌跡就是拓撲路徑。對于電子密度函數,這樣的拓撲路徑近似于化學鍵,因此稱為鍵徑。對于ELF,通過生成拓撲路徑則可以將(3,-1)與(3,-3)臨界點之間的關系清晰地表現出來。
2 電子密度拓撲分析在Multiwfn中的操作
這里先介紹電子密度拓撲分析的操作,輸入文件是Gaussian對多巴胺分子優化得到的wfn文件。用.fch、.molden等格式也都可以,只要用的文件含有GTF信息即可,詳見《談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。先啟動Multiwfn程序,然后依次輸入
examples/dopamine.wfn //此文件是程序文件包里自帶的
2 //拓撲分析功能
2 //以所有原子核作為初猜點,目的是尋找所有核臨界點
3 //以每一對距離不很遠的原子核連線中點作為初猜點,主要用來尋找鍵臨界點
8 //生成鍵徑
0 //觀看結果
此時文本界面會輸出所有臨界點和鍵徑的信息,最后提示你Fine, Poincare-Hopf relationship is satisfied,這是所有臨界點都已找到的必要非充分條件,如果這個條件沒滿足,肯定臨界點沒找全。同時蹦出來一個圖形界面。若點擊界面上的CP labels復選框即可把每個臨界點的編號也顯示出來。如下所示
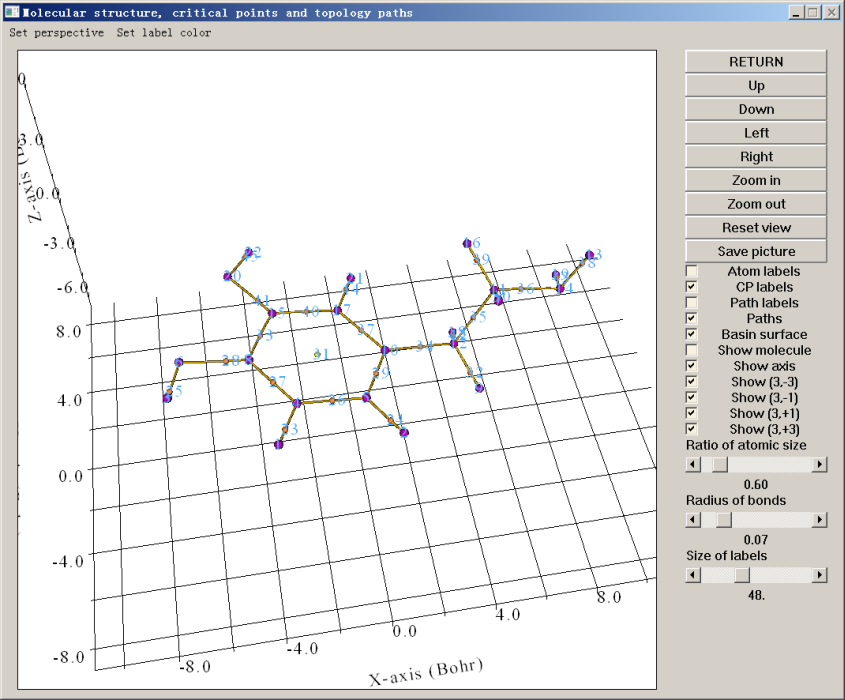
紫色的球是(3,-3),與原子核位置基本一致。桔黃色是鍵臨界點,黃色是環臨界點。棕色的線是鍵徑。通過圖形界面,可以選擇顯示哪些、不顯示哪些,以及旋轉縮放等操作。憑借化學直覺,以及Poincare-Hopf關系可知期望的臨界點都已經找到了,就沒必要再用選項4(三個原子中心作為初猜)、選項5(四個原子中心作為初猜)或選項6(在某個位置附近隨機設一大堆點)來進一步找臨界點了。
簡而言之,對于一般的體系,找電子密度的臨界點就是進入拓撲分析界面后,依次選2、3、4就行了,簡單至極!
值得說明的是Multiwfn的代碼經過充分優化,并且支持SMP并行,這使得其拓撲分析速度極快。在一般的主流四核機子上,上面的任務在Multiwfn里眨眼間就完成了。我曾比較過AIM2000和Multiwfn分析一個含900個高斯函數的C60體系,在四核并行的機子上,Multiwfn尋找臨界點的速度是AIM2000的約100倍,生成鍵徑速度是其將近30倍,而結果完全一致。AIMALL的速度比AIM2000要快,不過由于算法不很一致,也不好公平地比較,但從實際應用角度上來說,Multiwfn比AIMALL要快一個數量級。另外AIMALL的操作遠不如Multiwfn這種交互式程序便利,其結果可視化程序aimstudio還要收費。可以說,想要操作簡單、能直接可視化、免費而且速度飛快的AIM拓撲分析程序,Multiwfn是不二之選。
有些臨界點比較特殊,在默認的設定下,用選項2~5都找不到臨界點,這就需要人為調整一下參數了,在Multiwfn里提供了豐富的可調參數。一種典型的情況是重原子和氫連線上的鍵臨界點找不到,這就需要在參數設定界面中將Set scale factor for stepsize一項設低,建議設為0.5,然后再重新找臨界點。其它選項在Multiwfn手冊第三章的拓撲分析一節里都有說明。
有時候找不到臨界點是由于初猜位置不合適。初猜點越接近臨界點,就越有可能收斂到臨界點。對極個別體系,選項2~5的方式設定的初猜點可能都不合適,故而會漏掉某些臨界點,此時建議用選項6的方式設定初猜點。這種設定方式比較野蠻但是可靠強大。選項6會定義一個球心,然后讓指定數目(通常設幾百乃至上千)的初猜點隨機分布在球體中來尋找臨界點,只要能讓初猜點隨機分布的范圍能夠包含或者與潛在的臨界點位置比較近,通常就能將那些臨界點找出來。選項6的子選項1~6以不同方式定義這個球體的中心,10用來定義球體半徑,11用來設定將有多少個初猜點隨機分布在球體中,選0就開始執行搜索。如果選擇子選項-1,則用戶不必設定球心,球心會自動依次定義在每個原子核上,也就是說,每個原子附近都會分布一堆初猜點來搜索臨界點。如果用子選項-2,則球心會自動依次定義在指定的原子核上,而非所有原子核上。選項6這種搜索方式對于電子密度臨界點搜索用得機會不多,它最適合搜索ELF的臨界點,因為ELF比電子密度臨界點明顯多得多,分布更復雜,見下一節的例子。
Multiwfn還提供了一些選項用于分析、編輯結果。進入選項7 Show real space function values at specific CP or all CPs并且輸入臨界點的編號,就可以獲知這個臨界點的一切信息,包括Multiwfn支持的各種實空間函數的數值(如電子密度、拉普拉斯值、動能密度、勢能密度等)和電子密度的梯度以及Hessian矩陣,輸出信息例如(如果有看不懂的話,看Multiwfn手冊2.6、2.7節對實空間函數的介紹)
CP Position: -1.54802279321209 1.64407933432874 -0.36311758584834
CP type: (3,-1)
Density of all electrons: 0.3333962073E+00
Density of Alpha electrons: 0.1666981037E+00
Density of Beta electrons: 0.1666981037E+00
Spin density of electrons: 0.0000000000E+00
Lagrangian kinetic energy G(r): 0.1055976596E+00
Hamiltonian kinetic energy K(r): 0.3702940096E+00
Potential energy density V(r): -0.4758916692E+00
Energy density: -0.3702940096E+00
Laplacian of electron density: -0.1058785400E+01
Electron localization function (ELF): 0.9499848594E+00
Localized orbital locator (LOL): 0.8133846890E+00
...略
Multiwfn還可以將臨界點上的各種函數分解為各個軌道的貢獻(可以是分子軌道、定域化軌道等),看手冊4.2.4節的例子。
Multiwfn的拓撲分析功能可以說是驚人地靈活,本文限于篇幅就不詳細說了,相關詳細介紹在手冊3.14節都有。利用選項-9可以方便地計算臨界點間、原子間的距離、角度。用選項-4則可以導入導出已找到的臨界點、刪除或人為地增加臨界點。進入選項-5則可以顯示拓撲路徑的詳細信息(路徑軌跡的坐標、路徑長度等)并進行編輯和導入、導出,還能繪制各種實空間函數沿著鍵徑上的變化圖,見手冊4.2.3節的例子。Multiwfn還可以對特定或局部區域做拓撲分析,比如只對選定的分子范圍做拓撲分析、只得到連接兩個自定義片段間的鍵徑和BCP、只獲得對應弱相互作用(低電子密度)區域的臨界點和鍵徑等等,見手冊4.2.6節的示例。
除了尋找臨界點和生成拓撲路徑,Multiwfn的拓撲分析模塊還能生成并繪制盆分界面,對于電子密度分析,就對應于原子間分界面(Interatom surface, IAS)。在IAS面上沒有電子密度梯度線穿過,也稱零通量面(zero-flux surface),每個IAS都經過一個鍵臨界點。IAS將整個分子區域分隔成一個個原子空間,也叫原子盆。從拓撲分析主界面進入選項10后,輸入(3,-1)的編號,就能生成穿過這個(3,-1)的IAS。而在編號前加上負號,就說明將已經生成的穿過這個(3,-1)的IAS刪掉。如果當前尚未生成任何IAS,輸入0就可以生成所有IAS。如果已經有了IAS,輸入0就會刪掉所有IAS。下圖中生成了部分IAS
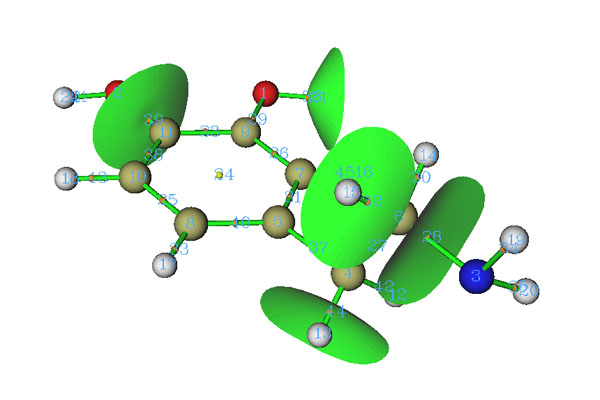
在Multiwfn手冊4.2.1節也有Multiwfn中做電子密度拓撲分析的例子,還有些額外的討論,強烈建議大家一看。
將Multiwfn與VMD相結合,可以非常簡單、快速地繪制出漂亮的含有臨界點、鍵徑、分子結構、臨界點編號的AIM拓撲分析圖,本文的讀者務必閱讀《使用Multiwfn+VMD快速地繪制高質量AIM拓撲分析圖》(http://www.shanxitv.org/445)并且認真觀看里面的演示視頻。把Multiwfn的拓撲分析數據搞到VMD里顯示比起在Multiwfn的圖形界面里看到的明顯更好,而且還可以完美解決一些用戶抱怨的在Multiwfn窗口里找臨界點編號時不容易轉到合適的視角的問題。
3 ELF拓撲分析在Multiwfn中的操作
這一節以苯酚為例演示一下對ELF的拓撲分析操作。在Multiwfn中對與ELF類似的LOL函數做拓撲分析也是同樣的步驟。啟動Multiwfn并輸入
examples/phenol.wfn
2 //進入拓撲分析模塊
-11 //清空已有拓撲分析數據并選擇新的實空間函數。默認的函數是電子密度
9 //選擇ELF
6 //在指定半徑和中心的球里隨機分布指定數目的初猜點來搜索臨界點
-1 //將每個原子核依次作為球中心。由于此分子有13個原子,如果提示中"Points:"此時顯示的是比如1000,總共就會以13*1000=13000個初猜點來找臨界點。在我的i7-2630QM機子上以四核并行模式運行,僅15秒鐘就完成了搜索。
-9 //返回上一級菜單
0 //觀看結果
你會看到結果遠比電子密度分析時復雜,總共找出了126個臨界點,很花哨。為了使結果更清楚,可以將意義不大的(3,+1)和(3,+3)臨界點通過右側復選框關掉。另外,原子球擋住了一些臨界點,將Ratio of atomic size滑動條拖到最小,原子球就不顯示了,分子此時相當于以棍棒模型顯示。如下圖所示。
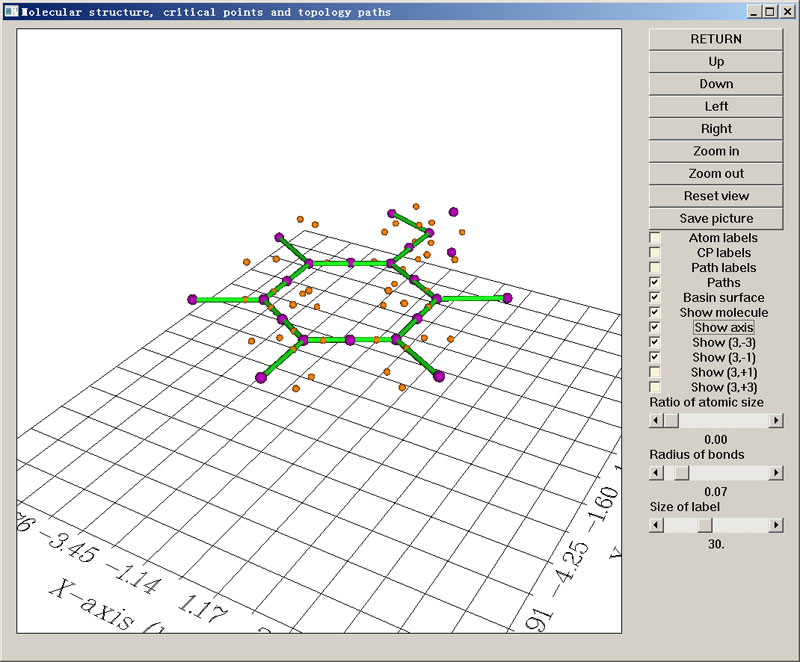
依然是每一個紫球對應一個(3,-3)。可以看到每個原子核都有一個(3,-3)(對于氫原子會偏離些)。如果你發現原子核處沒有紫球,說明它們搜索中漏過去了,可以用選項2以原子核位置為初猜再找一下,一般都能找到。C-C和C-O鍵之間都有紫球,這對應于共價鍵區域電子定域程度局部最高點。在氧原子旁邊還有兩個懸著的紫球,它們對應于氧的兩個孤對電子的電子定域性局部最大點。從位置上看,按照傳統雜化理論可以認為氧是處于sp3雜化狀態。
在顯示結果的時候,命令行窗口會提示Warning: Poincare-Hopf relationship is not satisfied, some CPs may missing,這表明這一次搜索并沒有將所有臨界點找全。不過沒有關系,因為從圖中可見所有有顯著化學意義的臨界點都找到了。如果你想徹底找全,那么就再次進入選項6,適當選擇參數后重新進行臨界點搜索,將會找出零星數個剩余的臨界點。徹底找全所有類型ELF的臨界點,對于不是很小的體系是很困難的事,一般沒有必要去做。對于最重要的臨界點類型,即(3,-3),基本上做一次每個原子周圍有1000個初猜點的搜索(即本例的操作)后就都能找到。
現在點RETURN關閉圖形界面回到拓撲分析主菜單,選8來生成(3,-1)和(3,-3)間的拓撲路徑,再次顯示結果,如下圖所示
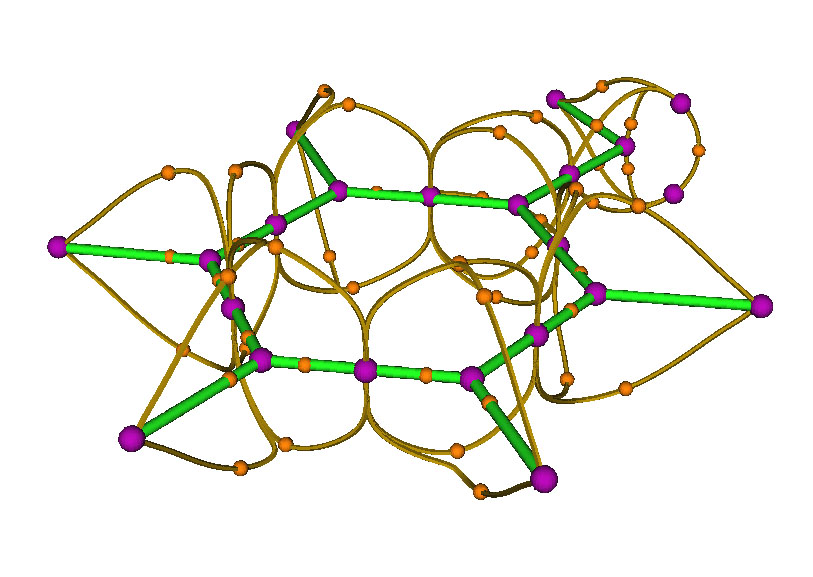
原本看起來數目眾多、很亂的桔黃色小球,即(3,-1)點,通過拓撲路徑與(3,-3)相連后,此時關系變得比較清晰了。
對于個別體系,有時候會發現本該出現的(3,-1)與(3,-3)間的路徑沒有出現,這很可能是因為生成拓撲路徑的默認參數不太適合。比較有效的解決方法是進入選項-2,將Stepsize設得小一些,比如將默認值減小一兩倍。注意路徑的最大長度是"步長*路徑的最大點數",如果生成路徑過程中,迭代次數超過了最大點數還沒遇見另外一個臨界點,就說明這次路徑生成失敗。因此,步長設小了,那么路徑最大長度就會減小,如果體系中有一些很長的路徑,這些路徑可能在此時就沒法生成了。因此減小步長的同時也應當同時加大路徑最大點數。步長越小越容易成功生成復雜的路徑(比如曲率特別大的路徑),但是由于需要加大路徑最大點數,這就會造成計算耗時越多。默認的路徑生成參數是折中考慮精度和效率的結果。
LOL和電子密度拉普拉斯函數與ELF有很大相似之處,此節的做法也同樣適合這兩種函數,只要在選項-11里選擇相應的函數然后以本例同樣的方法操作即可。另外還可以用這種方法來獲得軌道波函數的臨界點。
在《在Multiwfn中單獨考察pi電子結構特征》(http://www.shanxitv.org/432)一文中筆者還舉例演示了如何對ELF-pi進行拓撲分析,強烈建議一看。
4 談談孤對電子角度怎么算
好幾次看到有人問孤對電子夾角、二面角怎么算,由于Multiwfn的拓撲分析功能正好能解決這個問題,所以順便談談。如果對此問題沒興趣,可以跳過這節。
在討論怎么計算角度這個具體問題前,先要搞清楚孤對電子應該如何嚴格地描述。首先要明確的是,孤對電子本身不是可觀測的,只是個概念,也沒法唯一地去定義,只能說哪種方式的描述更有物理意義。一般意義上的孤對電子指的就是原子價層某局部空間內運動的兩個自旋互相配對的電子。一種將這個概念具現化的方法是軌道定域化方法,它通過對占據的分子軌道(往往有很強離域特征)進行酉變換,獲得能夠與化學鍵、孤對電子相對應的軌道,很大程度上重現了lewis模型。這類方法最大缺點是物理意義不嚴格,酉變換過程是隨意的,以什么標準去做酉變換因算法而異,不同的常用的定域化方法雖然能得到相似的圖景,但是在多重鍵、孤對電子的描述上卻可能很不相同,所以我并不建議用這類方式討論孤對電子。NBO也是屬于定域化軌道一類,雖然不是通過酉變換得到,但結果上看也通常差不多。從算法上NBO分析對孤對電子的描述在寡人看來也有點不合理性,在NBO分析中是先從密度矩陣的原子對角塊搜索完CR、LP型NBO才開始尋找雙中心NBO,等于說生成LP的優先級要高于雙中心NBO,然而實際上孤對電子和化學鍵是同時形成的,應當同步考慮。這也導致了NBO的孤對電子軌道看起來和雜化理論顯示的圖景不符。
下面是HF/6-31G*下的苯酚的16號和22號NLMO軌道圖形,以及兩個軌道波函數相加和相減后的圖形。順帶一提,NLMO是NBO分析方法框架內的一部分,它是由NBO進一步變換得到的,通常和NBO很相似,只是離域性比NBO稍大。NLMO也可以視為是直接通過對占據的分子軌道酉變換得到的。
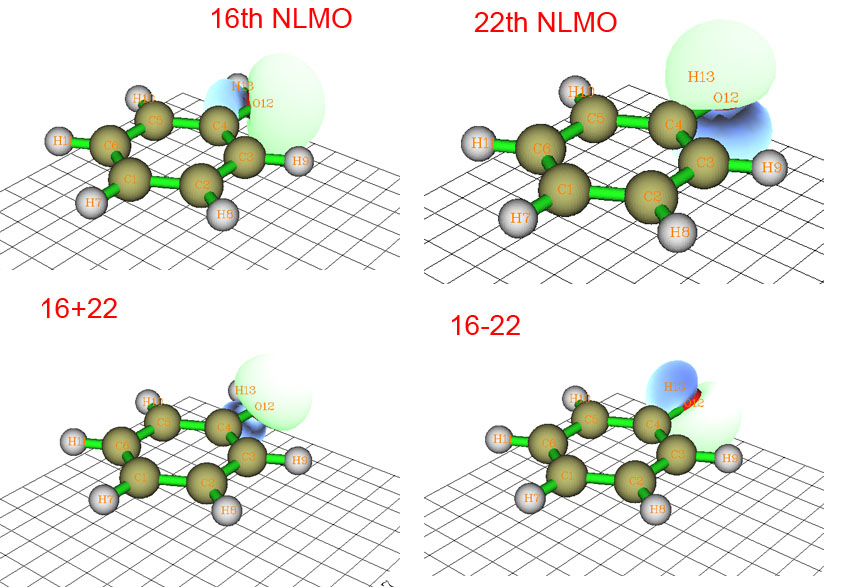
16和22號NLMO對應氧的孤對電子,乍看上去好像氧是sp2雜化,一個孤對電子在平面上,一個垂直于平面。但實際上我們可以將這兩個軌道人為地混合形成兩個新的軌道,即16+22和16-22(為了省事未考慮歸一化,這對定性分析沒影響)。這兩個新的軌道也可以說是對應孤對電子的,這樣一來氧就成了sp3雜化了,與ELF分析的結果一致。或許會有人問,將16和22號軌道那么混合有道理么?這樣混合是沒問題的,因為NLMO間都是正交的,因此16+22以及16-22軌道也與其它軌道正交,這等于是對占據軌道再酉變換一下罷了,完全是在軌道定域化的框架內允許的操作。所以說定域化軌道模型有嚴重的任意性,連孤對電子軌道都不能唯一確定,更甭提再進一步計算孤對電子角度了。
物理意義比較嚴格的是通過實空間函數分析,具體來說是ELF或LOL函數,結果通常較相似。電子密度拉普拉斯函數也能分析,但它與電子定域化的關系只是間接的,函數行為上也不如ELF和LOL舒服。ELF較大的區域,表明相應區域內的電子定域性較強,可以推斷電子的費米穴主要分布在這個區域內,即自旋相同電子間距離會較遠,而自旋相反的電子相對來說就容易呆在一起,即說電子在這個區域內配對,這正是孤對電子概念嚴格的物理解釋。如果對電子定域性問題想有進一步了解,可參閱筆者的《電子的定域性與相關穴》一文(http://www.shanxitv.org/94)。因此,位置適當的ELF較大的區域就可以說是孤對電子的區域,那么通過拓撲分析給出的ELF較大區域當中的極大點,就可以說是孤對電子出現位置的最大程度的抽象,利用這個點就可以很容易地計算出孤對電子角度了。
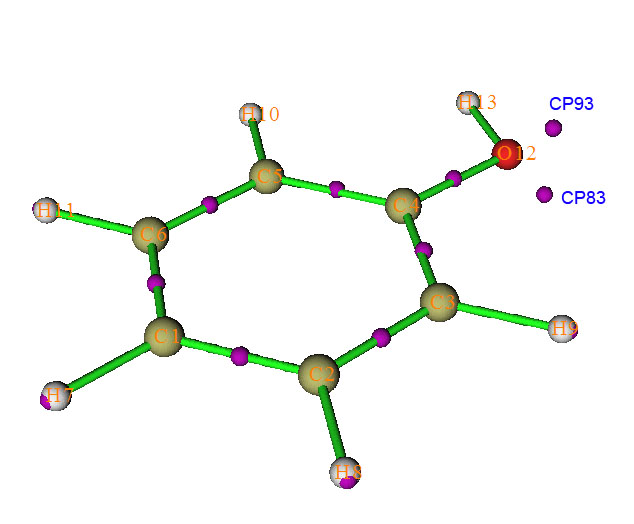
比如,按照第三節的方法找完臨界點后,我們想計算CP93-O12-CP83的夾角(標號見下圖。在圖形界面選擇CP labels就能顯示各個臨界點的編號),就在拓撲分析主界面里面選選項-9以進入角度測量的界面,然后輸入c93 a12 c83,結果顯示為88.228度。這里a代表angle,c代表critical point,a代表atom;想再測量CP83-O12-C4-C5的二面角就輸入c83 a12 a4 a5,結果是130.496度。按q可以返回主菜單。值得一提的是每次搜索臨界點給出的臨界點的編號可能不同,所以對一個體系重復分析時,每次都應在圖形界面里看清楚各個臨界點的當前編號。
我們也可以看看用LOL和拉普拉斯函數研究這個問題能得到什么結果。在拓撲分析的主菜單選擇-11然后選擇LOL函數,此時所有剛才ELF的拓撲分析會自動清空,然后重新搜索臨界點,我們會看到各個(3,-3)的位置和ELF分析時都差不多。再次計算氧的兩對兒孤對電子間的夾角,得到的結果是119.895度,明顯大于ELF給出的數值。改用電子密度拉普拉斯函數再算一次,結果是131.244度,更大了。按照一般觀念,孤對電子間相互互斥比較強,也應當大于sp3雜化的109度28分。結果在一定程度上顯示ELF可能會低估孤對電子的夾角。實際上有時低估得更厲害,乃至于LOL的結論是有兩對兒孤對電子出現的時候,ELF卻認為兩對兒孤對電子合在了一起。我的建議是使用LOL來研究孤對電子,LOL比ELF形式更簡單,計算速度稍快,而且一些文章指出LOL也能給出比ELF更清楚的化學圖景,而LOL在物理意義上也和ELF差不多。
還有一種展現孤對電子位置的方法是考察靜電勢極小點,在此文專門進行了介紹:《繪制靜電勢全局極小點+等值面圖展現孤對電子位置的方法》(http://www.shanxitv.org/493)。
5 臨界點與等值面圖
我們接下來將通過等值面圖討論ELF的域(Domain)、二分點(Bifurcation point)與(3,-3)及(3,-1)臨界點的關系,這有助于理解以及驗證拓撲分析的結果。
先按照第三節的過程搜索完ELF臨界點,然后直接退回到主菜單,并輸入以下命令
5 //生成格點文件
9 //ELF函數
2 //中等精度格點,對于小體系定性分析這就夠了。這時開始計算
-1 //顯示等值面
由于已經搜索過了臨界點,所以臨界點也在等值面圖上一起顯示了出來。拉動等值面數值的滑動條,可以看到隨著數值由小到大,等值面如下圖變化(藍色數字是等值面對應的數值)
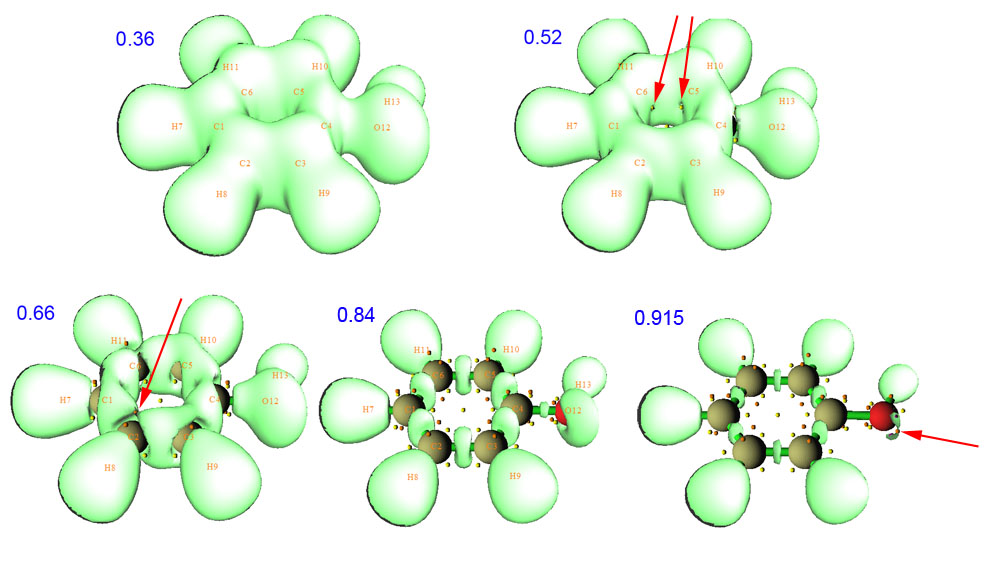
由圖可見,在數值很小時,等值面連成一個大域(或者叫做盆,是指等值面包含的封閉空間),也表明能超過這個定域性標準的區域非常廣。隨著數值增加,等值面開始逐漸減小。在0.52時,如紅色箭頭所指,恰好兩個(3,+1)剛剛出現。它們的出現容易理解,因為(3,+1)代表這個點在兩個方向上是函數值極小點,而另一個方向是極大點,由等值面隨數值的變化過程圖可以想象,那兩個作為極小點的方向就是順著等值面的兩個正交方向,而作為極大點的方向是基本上垂直于等值面的方向。進一步增加等值面數值,等值面會進一步萎縮,并且很多地方等值面開始分離,聯通的大域逐漸分解為小域。在0.66時,紅色箭頭所指的地方就是一個域開始二分的地方,稱為二分點,凡是這種地方都對應于一個(3,-1)點,而拓撲分析時獲得的相應(3,-1)點的ELF數值,也就正對應于ELF域在此處二分時的數值。等值面數值增加到比較高的情況,如0.84,從圖中可見ELF域已經充分分離了,對應每個成鍵區域以及氫的高定域性區域已經很清晰明朗,但是氧的兩對兒孤對電子的高定域性區域還是沒分開。繼續增加到0.915時,發現兩對兒孤對電子的域恰好分離開,紅箭頭指出了二分點。如果進一步增加數值,則每個域都只會進一步縮小直至消失,但不會在這個過程中二分成為更小的域,這種不能再二分的域稱為不可約域。每個不可約域里面都包含一個(3,-3)臨界點,對應于域隨著等值面數值增加越變越小最后消失的位置。
等值面圖比較直觀清楚,各個高定域性區域一目了然,通過不斷調節等值面數值,還可以直接確定出(3,-1)和(3,-3)的位置和這些臨界點的數值。但是等值面圖不便于準確地定量分析,無法得到很精確的臨界點的位置和函數數值。而且,這種找臨界點的方法也比較累,尤其是通過觀察等值面的變化來確定(3,+1)和(3,-3)臨界點是很困難的。直接用拓撲分析雖然準確快速,但電子結構復雜時,臨界點分布紛繁復雜,不能從圖上直觀地獲知各個空間位置電子定域性的大小、高定域性區域的分布范圍。所以,拓撲分析和等值面分析建議結合使用,前者用于精確定量分析,后者用于快速定性分析。另外,通過等值面圖觀察不可約域的位置,也有助于確定是否在拓撲分析中漏掉了一些(3,-3)臨界點,如果某不可約域的范圍內沒找到(3,-3),就應當在搜索設置中將球的中心設在那個區域,讓大量在球體內隨機分布的點作為初猜點來尋找那個(3,-3)。