生成富勒烯的螺旋算法簡介以及使CaGe中的編號與Fowler-Manolopoulos編號相符的方法

生成富勒烯的螺旋算法簡介以及使CaGe中的編號與Fowler-Manolopoulos編號相符的方法

文/Sobereva @北京科音   2011-Oct-4

近日有個網友，投了篇富勒烯包夾三金屬氮化物的文章。她用的富勒烯是CaGe生成的，編號用的是CaGe生成時的順序。然而審稿人要求必須使編號規則滿足IUPAC推薦的編號規則，即Fowler-Manolopoulos編號系統。經過探索，現在筆者已找到辦法讓CaGe的編號順序和Fowler-Manolopoulos編號系統對應上，將在此文介紹。在介紹具體做法前，將先順便介紹一下富勒烯的結構、螺旋算法以及spiral和CaGe程序。

1 富勒烯結構簡介

富勒烯(fullerene)是指由三價碳原子、只由五邊形和六邊形面構成的球狀多面體。最常見的那種C60，即足球烯，是富勒烯的一種。通過歐拉定理可以證明富勒烯都是由偶數個碳原子構成，五邊形一定有且只有12個。n個碳原子的富勒烯Cn包含n/2+2個面，n/2-10個是六元環。富勒烯沒有原子數上限，最小的是C20，因為再小的話面數將少于12個，也就不可能包含12個五邊形了。

IPR規則(isolated pentagon rule)是指富勒烯的五元環彼此之間不共點（與不共邊的條件是等價的）。不滿足IPR，即存在相連五元環的富勒烯是存在的，但符合IPR的富勒烯通常比不符合IPR的要穩定。最小的滿足IPR的富勒烯是C60的最穩定的異構體，即足球烯，再大的就是C70。

一定原子數目的富勒烯可以有很多異構體，不同異構體的原子間連接關系不同。下圖列出了各種碳原子數的富勒烯的可能的異構體數。由于所用的螺旋算法不能保證能找到所有可能的異構體，對于碳數多的富勒烯的異構體數可能比圖中的更多。另外，C22連一種異構體也沒有。圖中括號里是考慮了對應異構體的情況。

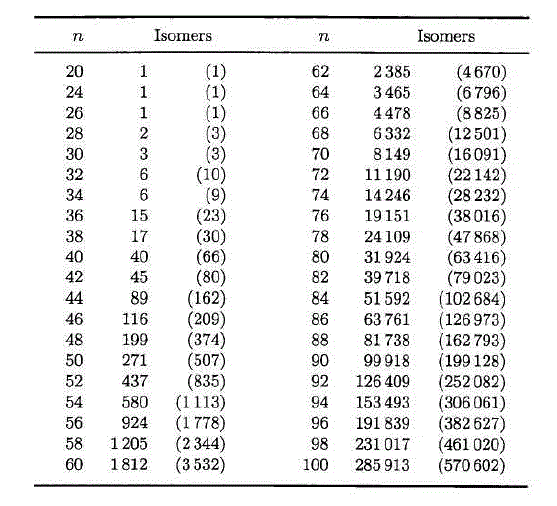
這些異構體中，只有極少數滿足IPR規則。例如C88的異構體中只有35個滿足IPR。

2 生成富勒烯的算法--螺旋算法簡介

生成富勒烯異構體，實際上也就是生成各種異構體中各個原子間的連接關系。連接關系可以以鄰接矩陣來表示，這是對稱矩陣，維度為n*n，若i,j原子相連接，則i,j矩陣元為1，否則為0。螺旋算法(spiral algorithm)是使用得最為廣泛的一種生成富勒烯異構體的算法，原理比較清楚形象，雖然不能保證一定能夠得到全部可能的異構體，但是對于380個原子以內的富勒烯是可靠的。螺旋算法比較適合低對稱性的多面體構造，由于富勒烯的異構體對稱性普遍很低，所以這種算法是適合的。螺旋算法在Fowler和Manolopoulos寫的AN ATLAS OF FULLERENES一書(1995)中的第二章有介紹，這里只是說說梗概。

富勒烯可以用平面圖來表示連接關系。例如下面的圖就是唯一滿足IPR的C60的異構體的平面圖（先別管曲線），每條直線都是一個C-C鍵，五元環、六元環都能看得很清楚。注意每種異構體雖然唯一地定義一種連接關系，但是平面圖的畫法并不是唯一的，比如滿足IPR的C60可以取一個六元環當成平面圖的中心，即下圖中間和右邊那種，雖然圖看起來和以五元環為中心時，即下圖中左邊那種不同，但是實際上是等價的。

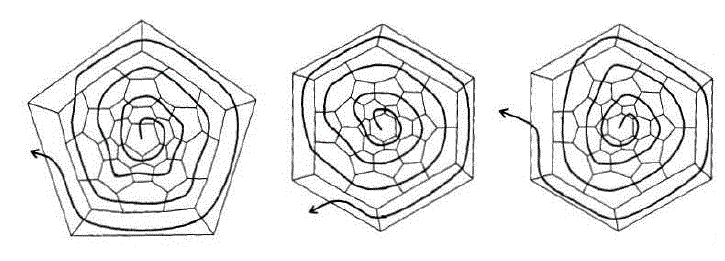
在說明怎么通過螺旋算法構建異構體前，先來看看如何將一個異構體進行解螺旋。解螺旋時，從平面圖的任意一個面開始（為了看起來方便通常取圖中間的），一圈一圈穿過各個面，就會得到一個螺旋序列，例如上圖左、中、右三種解螺旋路徑會分別得到下面這些螺旋序列
56666656565656566565656565666665
65655566656656656566566565656566
66565656566566565665665666565656
即如果穿過的是五元環，序列中就是5，若是六元環，就寫6。解螺旋的路徑不是隨意的畫畫圈就行。下一個要到達的面，必須緊埃著剛才的面，且同時挨著上一圈螺旋中第一個敞開的面。例如下圖中，當目前位置是紅點所在的面時，下一個面必須是藍點對應的面，因為藍點的面與剛才的紅點的面挨著（綠線），同時和上一個螺旋第一個開放的面挨著（黃線。第二個開放的面就是指黃線左邊的橫線）。紫色的面不能作為下一個面，因為雖然挨著紅點的面，但是不挨著黃線。解螺旋過程未必都能成功，有可能解到某個面時，發現無法找到滿足要求的下一個面，此時解螺旋宣告失敗。一種異構體，從某些面開始可以成功解螺旋（即所有面都能按要求地經過），而從某些面開始解螺旋則會失敗。可以證明最多有6n種可能的解螺旋路徑（包括對稱等價的路徑）。而一些原子數很大的富勒烯，如C380的一種異構體，甚至無法找到任何一種能夠成功解螺旋的路徑，此時，也就不可能按下文的過程通過螺旋算法來獲得這種異構體了，這就是為什么說螺旋算法不保證能找到所有異構體。

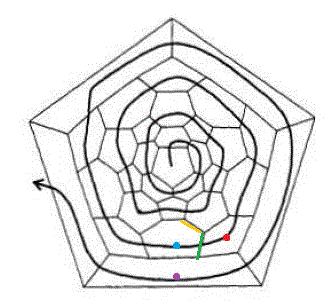
同一個異構體的各種螺旋序列是等價的，為了避免模糊性，就有必要從中選一個序列來唯一代表那種異構體，通常選擇序列對應的數值最小的那個序列，也叫正則(canonical)螺旋序列。因此，上面給出三種序列中第一種就是正則螺旋序列。

將解螺旋過程反過來，就可以構建異構體。首先，生成所有可能的螺旋序列。n個原子的富勒烯，由于有n/2+2個面，12個五元環，n/2-10個六元環，根據排列組合規則可知，總共有(n/2+2)!/12!/(n/2-10)!種排法。然后，依次嘗試將這些螺旋序列按照規則卷起來（解螺旋的逆過程），看看能否成功。所有螺旋中只有少數能夠通過這個檢測。剩下的螺旋序列中有大量是等價的，因此，需要再把成功卷起來的每種異構體再以全部6n種可能方式解開，找出等價的螺旋序列，并保留正則螺旋序列。這樣，尋找異構體的過程就結束了，我們得到了正則螺旋序列，也得到了相應的異構體的面之間鄰接關系。在上述過程中，可以很容易地將IPR作為限制條件，搜索出的異構體的數量將會大為減少，搜索速度也會大為加快。

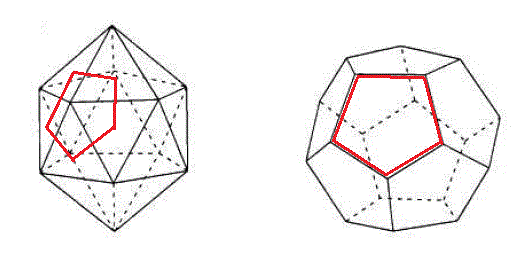
最后還要說一下dual(對偶)概念，會在下文用到。一個多面體的dual，就是將這個多面體的面替換成頂點，并根據原來的面的相鄰關系將這些頂點連接起來。例如下圖，左邊是20面體，它的dual就是12面體。由紅線所示，在左側的一些面的中間取一點，根據面相鄰的關系將點相連，就得到了dual的頂點和邊。也就是說，多面體的面之間的鄰接關系，實際上就是這個多面體的dual的頂點之間的鄰接關系，它們包含的信息是相同的。另外值得一提的是，對dual再取dual就恢復為原始多面體；dual中的面的邊數就是原始多面體相應頂點的價數（即那個頂點與多少個其它頂點相連）。由于在富勒烯中每個碳都與另外三個碳相連，所以Cn富勒烯的dual就是由n個三角形組成的多面體。

3 Fowler-Manolopoulos編號系統和spiral程序

富勒烯的異構體非常多，而且本身原子數也很多，因此如果不在文獻中使用一個標準的編號系統，會使交流變得很困難。Fowler-Manolopoulos編號系統是被廣為使用的，寫為Cn:xxxx形式。n是原子數，xxxx就是這種異構體在Fowler和Manolopoulos編纂的AN ATLAS OF FULLERENES一書的附錄中給出的生成富勒烯異構體程序中的生成順序。例如C60共有1812個異構體，符合IPR的唯一一種C60異構體在書中的程序中是最后一個輸出，因此這個異構體就叫C60:1812。

書里的程序在本文中將稱為spiral。這個程序功能遠沒有下面介紹的CaGe那么強大，而且速度頗慢，但是由于只有利用這個程序才能得到異構體的Fowler-Manolopoulos編號，所以十分重要。其它的生成富勒烯異構體的程序還有很多，但是由于使用的算法不同，而即便是使用了螺旋算法的程序，如著名的CaGe，由于在內部生成初猜的螺旋序列的順序不同，導致輸出的異構體的順序也和Fowler-Manolopoulos編號不符。如何找到CaGe輸出的異構體的序號和Fowler-Manolopoulos編號之間的關系（或者說spiral輸出的異構體的序號），就是后文要解決的。在此，首先介紹spiral程序的使用。

spiral的代碼和編譯好的可執行文件（Win32版）可以在這里下載：/usr/uploads/file/20150610/20150610015730_61465.rar
代碼主體是從那本書里搬下來的，為了能夠同時輸出異構體的指紋（根據鄰接矩陣生成的一個能夠唯一標識這種異構體的浮點數，詳見第五節），筆者在原始代碼的基礎上進行了改造，編譯時還需要blas和lapack庫文件，因為生成指紋時用到了lapack的對稱矩陣對角化子程序。編譯很簡單，比如在intel visual fortran里，把那四個.f90文件和blas、lapack庫文件都拖到工程的Source Files里，然后編譯即可；若是Linux下用ifort，就運行ifort -O3 *.f90 lapack.a blas.a -o spiral。

程序使用很簡單，每一步都有提示。
(1)首先輸入碳原子數以及是否需要滿足IPR。例如要生成C60全部異構體，符合與不符合IPR的都包括在內，就輸入60,0。
(2)選擇是否輸出異構體的指紋。如果輸入0，就不輸出指紋，也不輸出鄰接矩陣。如果輸入1或2，就輸出指紋，1代表生成指紋用的鄰接矩陣是富勒烯的dual的頂點的鄰接矩陣（或者說，是富勒烯的面的鄰接矩陣）；若是2，就代表用的是富勒烯的頂點的鄰接矩陣。
(3)如果上一步選擇了輸出指紋，則程序還會問你是否把鄰接矩陣也輸出出來。1代表輸出。輸出的鄰接矩陣是什么鄰接矩陣，對應于上一步選的是1還是2。

看個例子。這里要生成C36的全部異構體，并輸出各種異構體的頂點的鄰接矩陣的指紋，同時也輸出鄰接矩陣本身。于是就依次輸入
32,0
2
1
屏幕上立刻輸出總共找到的6種異構體
-----------------------------------------------------------------------------
       1   C2   1  2  3  4  5  7 12 14 15 16 17 18   16 x  2
       2   D2   1  2  3  4  5  8 12 13 15 16 17 18    8 x  4
       3  D3d   1  2  3  4  5  9 12 13 14 16 17 18    1 x  2,  1 x  6,  2 x 12
       4   C2   1  2  3  4  7 10 11 12 14 15 17 18   16 x  2
       5  D3h   1  2  3  4  7 10 11 13 14 16 17 18    1 x  2,  3 x  6,  1 x 12
       6   D3   1  2  3  5  7  9 10 12 14 16 17 18    1 x  2,  5 x  6
-----------------------------------------------------------------------------
第一列，即輸出序號，就是這種異構體的Fowler-Manolopoulos編號。第二列是點群。后面12個數字是螺旋序列中12個五元環所在位置。最后一塊是13C NMR信號，這里不做討論。
同時，各個異構體的頂點的鄰接矩陣輸出到了當前目錄的adjmat.txt里，比如第一個異構體的前四行是
01010010000000000000000000000000
10100000100000000000000000000000
01001000001000000000000000000000
10001100000000000000000000000000
....
說明其中第一個碳原子與2、4、7號碳原子相連，第二個碳原子與1、3、9號碳原子相連...
同時，當前目錄下fp.txt記錄了全部異構體的指紋，如下所示
           1  -7.27828597613050    
           2   41.8007533755431    
           3   41.7891354377565    
           4   23.6786023771991    
           5   43.7753607538324    
           6   48.6561193681689  

4 CaGe使用簡介

CaGe是Linux平臺下的歷史悠久的生成各種類型多面體結構的程序，還特別包括富勒烯、碳管等類型。該程序不僅可以生成結構，還可以通過基于java的圖形界面直接觀看結構，十分方便。生成速度也非常快，遠遠超越spiral。CaGe可以免費從http://www.mathematik.uni-bielefeld.de/~CaGe/下載。

在編譯CaGe前，系統里必須安裝JDK（僅安裝java運行環境，即JRE是不夠的）。
解壓CaGe安裝包后，在其目錄下運行./INSTALL，程序一般會說找不到java的路徑（哪怕已經將JDK安裝在了默認路徑下），于是輸入?然后輸入/usr讓程序在此目錄下自行尋找java路徑。在筆者的RHEL6-U1 64bit系統在安裝時已經裝了openjdk，于是安裝腳本找到了java的路徑是/usr/lib/jvm/java-1.6.0-openjdk-1.6.0.0.x86_64/bin，輸入1（對應于這個路徑的編號），CaGe就開始編譯了。

運行cage.sh就可以啟動CaGe的圖形界面。實際上也可以直接通過命令行方式調用結構生成器而不經過圖形界面。各種結構的生成器都在CaGe安裝目錄下的Generators目錄下，比如fullgen就是用來生成富勒烯的程序。

這里以觀看C60的異構體為例介紹使用方法。首先啟動圖形界面，選3-regular plane graphs，選fullerenes標簽頁，將最小和最大原子數都設成60，然后點next進入輸出方式的設定界面。將3D representation和2D representation都勾上，并都選擇為Viewer，選Start，就會如下圖看到平面圖和立體結構。實際上，CaGe是由很多模塊構成的，生成器模塊只生成鄰接關系，而所看到的平面和三維坐標是通過所謂的embed模塊通過讀取鄰接關系后轉化而成的。CaGe生成的三維結構并不是準確的，想獲得準確結構需要用量子化學方法優化。

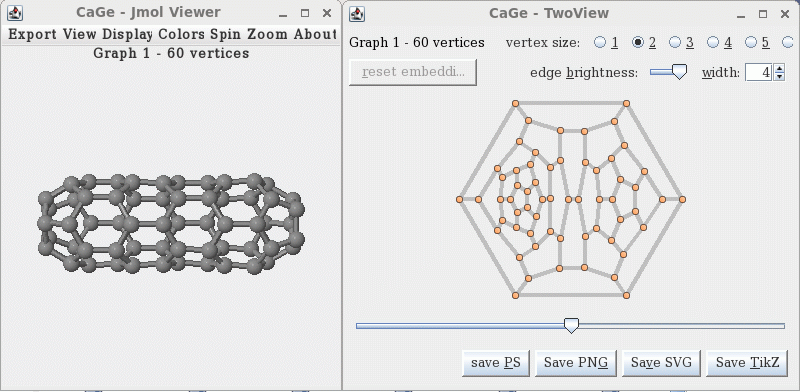
同時還出現一個窗口用于選擇要生成并顯示的異構體，如下圖。view/goto里填入指定數字就可以顯示指定序號的異構體。advance可以以1為步進或者以指定數目為步進顯示后續的異構體。點flow會尋找并顯示能夠生成的最后一個異構體，對于C60，就會最后在1812號停住。之前瀏覽過的異構體可以用review的左右按鈕來切換。注意異構體是在后臺按順序生成的，如果想瀏覽第m個異構體，那么程序就會把前m個異構體的鄰接關系在后臺全都生成出來（即generated所顯示的數量），并且接下來只能瀏覽編號大于m的異構體，而不能返回去瀏覽漏過去的編號小于m的異構體，除非某些編號小于m的異構體在之前已經瀏覽過（瀏覽過的異構體的平面和三維坐標會被記錄了下來，可以再次瀏覽）。看完后點exit可推出程序，cancel則返回主界面。

如果想一次將所有異構體的頂點的鄰接關系存到一個文件里，可以在設定輸出方式時勾上Adjacency information，并選擇File，format選writegraph，點start之后就會看到出現一個小窗口顯示生成到了多少，顯示finished時代表生成結束。這時可以檢查當前目錄下full_60.w0d文件，可以用文本編輯器打開，里面記載了各個異構體中每個原子和另外哪三個原子相連。
如果想把所有異構體的三維結構輸出到pdb文件里，則設定輸出方式時勾上3D representation，選File，Format選pdb。這樣得到的pdb可以用VMD等程序打開，每一幀對應一個異構體。

5 尋找CaGe的編號與Fowler-Manolopoulos編號的關聯

原理上講，可以通過修改CaGe的fullgen程序代碼讓其輸出的異構體序號滿足Fowler-Manolopoulos編號，但是這個程序里不僅注釋，甚至連變量名都是德文，而且代碼頗長，很難修改。因此，為尋找CaGe生成的異構體的編號與Fowler-Manolopoulos編號的關聯，應通過比較CaGe輸出的鄰接信息與Spiral輸出的鄰接信息來實現。顯然，最直白的比較方式就是比較鄰接矩陣，看看是否相同，相同則為同一個異構體。但是這樣做有兩個問題：(1)原子編號在CaGe里和spiral里通常不一樣，所以必須考慮以各種方式對行和列進行置換后再進行比較，這顯然太麻煩，而且十分耗時。(2)對于原子數多的情況，全部鄰接矩陣記錄下來的話會占很大硬盤。所以，筆者想出一個辦法，就是給每個異構體生成一個唯一的數字，可以稱之為指紋。通過比較指紋是否相同，來判斷異構體是否相同會有效率得多。

如果兩個異構體相同，無論原子編號是否一致，它們的鄰接矩陣的本征值是一定相同的（改變編號順序等于做矩陣的相似變換，這不影響本征值）。因此，可以用比較本征值來代替比較矩陣，問題大大簡化。然而本征值的數目也是很多的，為了比較更為方便，可以將矩陣的一串本征值壓縮成為一個稱為指紋的數。構建指紋的算法無窮多，但要求是必須能讓不同的異構體的指紋差異比較大，這樣一個異構體才能被一個指紋唯一、清楚地代表。筆者嘗試了不少構建方法，最后決定用這種形式：
nint(eig(1))-eig(1)+nint(100*(tmpval-nint(tmpval)))+sum(eig(N-5:N-3))
其中tmpval=10*(eig(2)+eig(7))，eig是本征值從小到大的序列，nint代表取浮點數最近的整數，N是總原子數。這種定義看似很詭異，的確，這是很隨意的，它確實能讓指紋差異較大。

（實際上，最好的辦法是直接比較異構體的正則螺旋序列是否相同，這才是最清楚、嚴格的指紋。然而CaGe并不能輸出正則螺旋序列，筆者也不打算修改CaGe使之能生成。）

介紹完原理，現在看看具體實現。下面是筆者編寫的adjmat2eig程序，它可以讀取CaGe生成的富勒烯的頂點的鄰接信息（.w0d文件），然后生成鄰接矩陣，之后計算指紋，最后與spiral生成的記載了指紋的文件進行比較，輸出CaGe的編號與Fowler-Manolopoulos編號的對應表。這個程序的源代碼文件和編譯好的程序(win32)可以由此下載：/usr/uploads/file/20150610/20150610015826_27110.rar。編譯時也需要blas和lapack庫。

這里介紹下這個程序的代碼
============================================================
program Adjmat2eig
implicit real*8 (a-h,o-z)
character*80 filename
real*8,allocatable :: adjmat(:,:),eigvecmat(:,:),eigvalarr(:),fp1(:),fp2(:)
integer,allocatable :: linkfound(:)
integer tmparr(4)

write(*,*) "Adjmat2eig"
write(*,"(a)") "Read adjacent matrix of vertices of fullrene outputted by CaGe (.w0d) and calculate eigenvalues then generate fingerprints"
write(*,*) "Written by Sobereva (sobereva@sina.com), 2011-Oct-3"
write(*,*)
write(*,*) "Input filename"
read(*,"(a)") filename
!讀取.w0d文件，其中記錄的必須是富勒烯的頂點的鄰接信息，而不能是其dual的頂點的鄰接信息。如果輸入的文件名叫result.txt，則直接從此文件中讀取指紋數據，而不利用鄰接關系重新生成
open(10,file=filename,status='old')
if (filename=="result.txt") write(*,*) "The fingerprints will be loaded from result.txt directly"
write(*,*) "Input number of atoms"
read(*,*) natom !富勒烯的原子數
write(*,*) "Input number of isomers recorded in this file"
read(*,*) nisomer !此文件內記錄的異構體數目
allocate(adjmat(natom,natom),eigvecmat(natom,natom),eigvalarr(natom),fp1(nisomer),fp2(nisomer),linkfound(nisomer))

if (filename=="result.txt") then
 do iso=1,nisomer
  read(10,*) nouse,fp1(iso)
 end do
 close(10)
 goto 1
end if

write(*,*) "If also output reformatted adjacent matrix? 0/1=no/yes"
read(*,*) ioutadjmat
!是否把由CaGe的.w0d文件轉化出的鄰接矩陣也輸出出來
if (ioutadjmat==1) open(11,file="isomat.txt",status='replace')
open(12,file="result.txt",status='replace')

write(*,*) "Please wait..."
do iso=1,nisomer
 adjmat=0D0
 read(10,*)
 do iatom=1,natom !讀取.w0d文件
  read(10,*) tmparr
  adjmat(iatom,tmparr(2:4))=1D0 !構造鄰接矩陣
 end do
 if (ioutadjmat==1) then
  write(11,"(a,i12,a)") "=========== isomer:",iso," ==========="
  do itmp=1,natom
   do jtmp=1,natom
    write(11,fmt="(i1)",advance='no') nint(adjmat(itmp,jtmp)) !輸出各個鄰接矩陣到isomat.txt
   end do
   write(11,*)
  end do
 end if
 call diagsymat(adjmat,eigvecmat,eigvalarr,istat,natom) !將鄰接矩陣adjmat對角化，eigvalarr是由小到大排序的本征值數組
 tmpval=10D0*(eigvalarr(2)+eigvalarr(7))
 fp1(iso)=nint(eigvalarr(1))-eigvalarr(1)+nint(100D0*(tmpval-nint(tmpval)))+sum(eigvalarr(natom-5:natom-3)) !生成指紋，fp1的第i個元素就是CaGe的第i個異構體的指紋
 write(*,*) iso,fp1(iso) !輸出到屏幕
 write(12,*) iso,fp1(iso) !也輸出到result.txt
end do

close(10)
close(11)
close(12)
write(*,"(a)") "Done! The results shown above have also been outputted to result.txt in current folder"
if (ioutadjmat==1) write(*,"(a)") "Reformatted adjacent matrix has been outputted to isomat.txt in current folder"
write(*,*)

1 write(*,*) "Make connection for the result with which file?"
read(*,"(a)") filename
!輸入另一個記錄了各個異構體指紋的文件的名字，注意格式必須和spiral輸出的fp.txt文件或者本程序輸出的result.txt一樣。此文件內異構體的數目也必須和前面輸入的一樣
open(10,file=filename,status='old')
do iso=1,nisomer !載入另一個文件記錄的指紋
 read(10,*) nouse,fp2(iso)
end do
close(10)
open(11,file="relat.txt",status='replace')
linkfound=0 !這個數組用于記錄當前文件（就是指.w0d文件或者一開始直接載入的result.txt）內的異構體序號與另一個文件內的異構體序號的對應關系
iwarndouble=0
iwarnlack=0
write(*,*) "The connection between isomers recorded in the two files"
write(*,*) "     Current file                   Another file"
do iso1=1,nisomer !依次選擇當前文件中的每個異構體的指紋，與另一個文件中異構體的每個指紋進行比較
 do iso2=1,nisomer
  if (abs(fp1(iso1)-fp2(iso2))<1D-10) then !判據。考慮到數值精度，如果兩個指紋間的差異小于1D-10就代表這兩個異構體等價
   if (linkfound(iso2)/=0) then !另一個文件記錄的第iso2號異構體此前已經與當前文件的一個異構體linkfound(iso2)有對應關系了，此時說明當前文件內iso1和linkfound(iso2)異構體的指紋太相近，導致都能對應上另一個文件中的iso2異構體的指紋。此時，需要調整指紋的生成算法（別忘了在spiral程序里也對應地修改算法，使二者一致），或者將差異的判據設得更嚴格
    warndouble=1
    write(*,"('Warning: The isomer',i12,' in another file has already linked to isomer',i12,' in current file')") iso2,linkfound(iso2)
    write(11,"('Warning: The isomer',i12,' in another file has already linked to isomer',i12,' in current file')") iso2,linkfound(iso2) !同時在屏幕上和relat.txt中顯示警告信息
   end if
   linkfound(iso2)=iso1
   write(*,"(i12,'           -------->',i12)") iso1,iso2
   write(11,"(2i12)") iso1,iso2 !同時在屏幕上和relat.txt中輸出對應關系
   exit
  end if
  if (iso2==nisomer) then !說明當前文件中第iso1號異構體在另一個文件中找不到等價異構體，即沒有相符的指紋。既有可能這是真實情況，也有可能是因為判據太嚴，且數值精度不夠，導致本來是等價構體的指紋間的差異大于判據。此時應放寬判據，但判據放得太寬，就容易導致不是等價的異構體因為指紋相近也被認為是等價的
   iwarnlack=1
   write(*,"(a,i12,a)") "Warning: Cannot find connection for isomer",iso1," of current file"
   write(11,"(i12,a)") iso1,"  ????????"
  end if
 end do
end do
close(11)
write(*,"(a)") "Done! The relationship shown above has also been outputted to relat.txt in current folder"
if (iwarndouble==1) write(*,*) "You may need to tighten the criteria for comparison"
if (iwarnlack==1) write(*,*) "You may need to lower the criteria for comparison"
write(*,*) "Press Enter to exit"
pause
end program

!下面這個子程序用來將lapack庫里面的DSYEV子程序重新封裝成簡潔形式，因為DSYEV的參數太多，使用不便。DSYEV用來將對稱矩陣對角化。如果istat不為0，說明子程序執行出錯。
subroutine diagsymat(mat,eigvecmat,eigvalarr,istat,nsize)
integer istat
real*8 mat(nsize,nsize),eigvecmat(nsize,nsize),eigvalarr(nsize)
real*8,allocatable :: lworkvec(:)
allocate(lworkvec(3*nsize-1))
call DSYEV('V','U',nsize,mat,nsize,eigvalarr,lworkvec,3*nsize-1,istat)
eigvecmat=mat
mat=0D0
forall (i=1:nsize) mat(i,i)=eigvalarr(i)
end subroutine

6 實例：尋找C88的CaGe的編號對應的Fowler-Manolopoulos編號

這里，我們將結合使用CaGe、spiral和Adjmat2eig程序來尋找CaGe生成的C88全部異構體的編號對應的Fowler-Manolopoulos編號。

首先，在CaGe里按照前文所述方法，生成C88全部異構體的鄰接信息，儲存到full_88.w0d，這個文件已經在Adjmat2eig程序壓縮包里面提供。然后，使用spiral生成C88全部異構體的指紋，即啟動程序后依次輸入
88,0
2
0             //鄰接矩陣沒必要輸出，所以選0
在筆者的機子上(i7-2630QM)經過20分鐘左右程序運行完畢。實際上，當程序輸出到81738時就可以停掉程序了，因為已知C88只有這么多異構體，這些異構體的指紋也已經同步輸出到了fp.txt。fp.txt已在Adjmat2eig程序壓縮包里面提供。

啟動Adjmat2eig，依次輸入
full_88.w0d
88   //原子數
81738  //文件中異構體數
0   //沒必要輸出鄰接矩陣。而且輸出的話很占硬盤，還降低程序運行速度
現在程序開始生成CaGe生成的異構體的指紋，生成完畢后，輸入
fp.txt
程序就開始將剛剛生成的指紋與fp.txt里的進行比較，同時在屏幕上輸出進程，這些內容也會輸出到當前目錄下relat.txt文件里。此文件里前幾行為
           1        3646
           2        4622
           3        4623
           4           4
           5           3
           6        3660
           7        3661
           8        3659
           9        3658
......
也就比如說，CaGe生成的第8號異構體，按照Fowler-Manolopoulos編號就應該寫為C88:3659。搜索一下relat.txt，發現沒有warning和???字樣，說明CaGe的每個異構體都完美地找到了對應的Fowler-Manolopoulos編號。