球諧型與笛卡爾型Gaussian函數的轉換關系
在筆者的《談談5d、6d型d殼層基函數與它們在Gaussian中的標識》(http://www.shanxitv.org/51)一文中曾簡要介紹了球諧型與笛卡爾型高斯函數的關系,本文是一些補充。
要提醒大家注意的是,球諧高斯函數與笛卡爾型的轉換關系對于d型是十分明確的,也是通用的。然而對更高角動量函數,在不同程序中用的關系往往不一致。在Gaussian中,f用的既不是所謂的“標準f集”,也不是“立方f集”,而用的是IJQC,54,83文中給出的形式。在Gaussian官方網站上介紹fch文件格式的頁面給出的球諧f函數的組合方式是錯誤的(頁面中寫的是ZZZ-ZRR,XZZ-XRR,YZZ-YRR,XXZ-YYZ,XYZ,XXX-XYY,XXY-YYY)。
筆者發現網上找不到很清楚的、帶歸一化系數的、包含高角動量的轉換表,給編程帶來不便,因此在這里總結出來。
以下是歸一化的實型球諧高斯函數向歸一化的笛卡爾型高斯函數的轉換關系(比如XYY,它的歸一化系數已經納入XYY這個符號當中了)。注意符號的表示,如√3/2=sqrt(3)/2,√(3/2)/5=sqrt(3/2)/5。
5D->6D:
!Used in all quantum chemistry codes
Sequence: XX,YY,ZZ,XY,XZ,YZ
D 0=-0.5*XX-0.5*YY+ZZ
D+1=XZ
D-1=YZ
D+2=√3/2*(XX-YY)
D-2=XY
7F->10F:
!f in Gaussian program
Sequence in .fch: XXX,YYY,ZZZ,XYY,XXY,XXZ,XZZ,YZZ,YYZ,XYZ
F 0=-3/2/√5*(XXZ+YYZ)+ZZZ
F+1=-√(3/8)*XXX-√(3/40)*XYY+√(6/5)*XZZ
F-1=-√(3/40)*XXY-√(3/8)*YYY+√(6/5)*YZZ
F+2=√3/2*(XXZ-YYZ)
F-2=XYZ
F+3=√(5/8)*XXX-3/√8*XYY
F-3=3/√8*XXY-√(5/8)*YYY
!Standard f set, normalization coefficient
!NBO程序里用這種形式,命名不同而已,f(c?)對應F+?,f(s?)對應F-?。如NBO輸出中的f(s2)對應這里的F-2
F 0=-3*XXZ-3*YYZ+2*ZZZ 0.240654032741774
F+1=-XXX-XYY+4*XZZ 0.281160203343101
F-1=-XXY-YYY+4*YZZ 0.281160203343101
F+2=XXZ-YYZ √3/2
F-2=XYZ 1
F+3=XXX-3*XYY 0.369693511996758
F-3=3*XXY-YYY 0.369693511996758
!Cubic f set, normalization coefficient
F(D1)=2*XXX-3*XYY-3*XZZ 0.240654032741774
F(D2)=-3*XXY+2*YYY-3*YZZ 0.240654032741774
F(D3)=-3*XXZ-3*YYZ+2*ZZZ 0.240654032741774
F(B)=XYZ 1
F(E1)=XZZ-XYY √3/2
F(E2)=YZZ-XXY √3/2
F(E3)=XXZ-YYZ √3/2
9G->15G:
!g in Gaussian program
Sequence in .fch: ZZZZ,YZZZ,YYZZ,YYYZ,YYYY,XZZZ,XYZZ,XYYZ,XYYY,XXZZ,XXYZ,XXYY,XXXZ,XXXY,XXXX
G 0=ZZZZ+3/8*(XXXX+YYYY)-3*√(3/35)*(XXZZ+YYZZ-1/4*XXYY)
G+1=2*√(5/14)*XZZZ-3/2*√(5/14)*XXXZ-3/2/√14*XYYZ
G-1=2*√(5/14)*YZZZ-3/2*√(5/14)*YYYZ-3/2/√14*XXYZ
G+2=3*√(3/28)*(XXZZ-YYZZ)-√5/4*(XXXX-YYYY)
G-2=3/√7*XYZZ-√(5/28)*(XXXY+XYYY)
G+3=√(5/8)*XXXZ-3/√8*XYYZ
G-3=-√(5/8)*YYYZ+3/√8*XXYZ
G+4=√35/8*(XXXX+YYYY)-3/4*√3*XXYY
G-4=√5/2*(XXXY-XYYY)
11H->21H:
!h in Gaussian program
Sequence in .fch: ZZZZZ,YZZZZ,YYZZZ,YYYZZ,YYYYZ,YYYYY,XZZZZ,XYZZZ,XYYZZ,XYYYZ,XYYYY,XXZZZ,XXYZZ,XXYYZ,XXYYY,XXXZZ,XXXYZ,XXXYY,XXXXZ,XXXXY,XXXXX
H 0=ZZZZZ-5/√21*(XXZZZ+YYZZZ)+5/8*(XXXXZ+YYYYZ)+√(15/7)/4*XXYYZ
H+1=√(5/3)*XZZZZ-3*√(5/28)*XXXZZ-3/√28*XYYZZ+√15/8*XXXXX+√(5/3)/8*XYYYY+√(5/7)/4*XXXYY
H-1=√(5/3)*YZZZZ-3*√(5/28)*YYYZZ-3/√28*XXYZZ+√15/8*YYYYY+√(5/3)/8*XXXXY+√(5/7)/4*XXYYY
H+2=√5/2*(XXZZZ-YYZZZ)-√(35/3)/4*(XXXXZ-YYYYZ)
H-2=√(5/3)*XYZZZ-√(5/12)*(XXXYZ+XYYYZ)
H+3=√(5/6)*XXXZZ-√(3/2)*XYYZZ-√(35/2)/8*(XXXXX-XYYYY)+√(5/6)/4*XXXYY
H-3=-√(5/6)*YYYZZ+√(3/2)*XXYZZ-√(35/2)/8*(XXXXY-YYYYY)-√(5/6)/4*XXYYY
H+4=√35/8*(XXXXZ+YYYYZ)-3/4*√3*XXYYZ
H-4=√5/2*(XXXYZ-XYYYZ)
H+5=3/8*√(7/2)*XXXXX+5/8*√(7/2)*XYYYY-5/4*√(3/2)*XXXYY
H-5=3/8*√(7/2)*YYYYY+5/8*√(7/2)*XXXXY-5/4*√(3/2)*XXYYY
注:盡管沒有明確的文檔介紹.fch中f以上角動量笛卡爾型函數的排列順序,只要自行用6d 10f pop=full結合高角動量基組隨便算一下,從輸出的分子軌道系數部分就能看到笛卡爾型函數的排列順序,正是本文所給出的。
在量子化學代碼里,將以上轉換關系(Gaussian程序里所用的轉換方式)寫成矩陣形式是便于使用的。
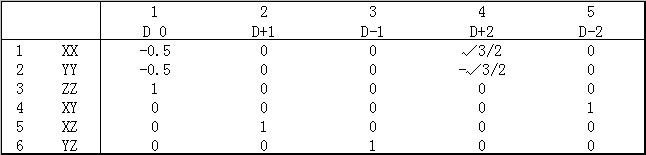

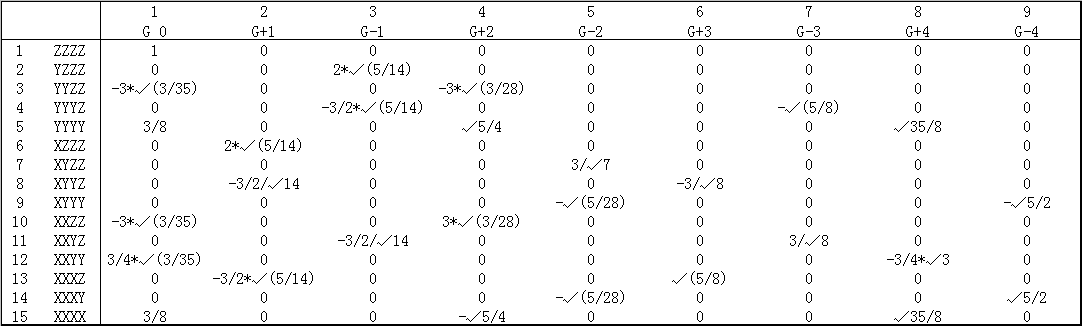
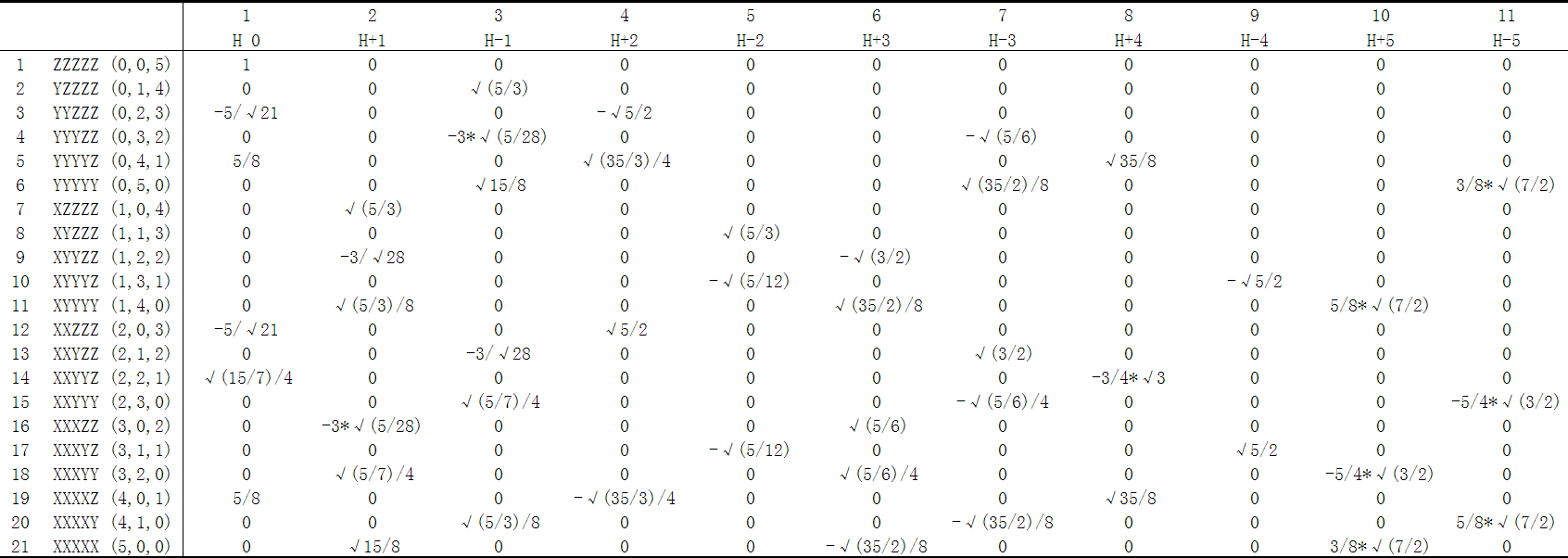
變量或數組后面5D和6D代表它對應球諧型和笛卡爾型(無論角動量的高低)。CObasa是系數矩陣,第n,i元素代表第i條軌道在n基函數上的展開系數,由于基函數數目與軌道數相同,所以是方陣。conv5d6d、conv7f10f和conv9g15g對應上面三個矩陣。以下Fortran代碼實際上是Multiwfn的readfch子程序里的一段。
ipos5D=1 !用于記錄當前位置
ipos6D=1 !同上
do ish=1,nshell !nshell是總殼層數
ishtyp5D=shelltype5D(ish) !shelltype5D將殼層編號轉化為球諧型的殼層類型
ishtyp6D=shelltype6D(ish) !同上
numshorb5D=type2norb(ishtyp5D) !獲得殼層內基函數數目
numshorb6D=type2norb(ishtyp6D) !同上
if (ishtyp5D==0.or.ishtyp5D==1.or.ishtyp5D==-1) then !S、P、SP殼層,不用變換,直接復制
!nbasis5D是球諧型高斯函數的數目,Cobasa6D之前已初始化為0,所以nbasis5D后面的列的元素都將是0。
CObasa6D(ipos6D:ipos6D+numshorb6D-1,1:nbasis5D)=CObasa5D(ipos5D:ipos5D+numshorb5D-1,:)
else if (ishtyp5D==-2) then !5D->6D
!CObasa5D的(ipos5D:ipos5D+4,k)列向量對應k軌道對當前D殼層的5個球諧型高斯基函數的展開系數,左乘變換矩陣conv5d6d,就能轉換成k軌道對相應的6個笛卡爾型高斯基函數的展開系數。將k替換為:,則所有軌道的展開系數被一次性轉換。
CObasa6D(ipos6D:ipos6D+5,1:nbasis5D)=matmul(conv5d6d,CObasa5D(ipos5D:ipos5D+4,:))
else if (ishtyp5D==-3) then !同上,這次是7F->10F
CObasa6D(ipos6D:ipos6D+9,1:nbasis5D)=matmul(conv7f10f,CObasa5D(ipos5D:ipos5D+6,:))
else if (ishtyp5D==-4) then !同上,這次是9G->15G
CObasa6D(ipos6D:ipos6D+14,1:nbasis5D)=matmul(conv9g15g,CObasa5D(ipos5D:ipos5D+8,:))
end if
ipos5D=ipos5D+numshorb5D !將讀寫位置移到下一個殼層的第一個元素
ipos6D=ipos6D+numshorb6D !同上
end do
笛卡爾型高斯基函數間的重疊矩陣(Sbas)很容易獲得,下面的代碼通過轉換矩陣將之轉換成球諧型高斯基函數的,從上面的注釋中應該容易理解代碼含義。基本原理是,設m:n代表一個D殼層內的全部基函數編號,Sbas(:,m:n)就代表這個6個笛卡爾型D基函數與全部笛卡爾型基函數間的重疊矩陣。令Sbas(:,m:n)右乘conv5d6d,則得到的就是變換出的5個球諧型D基函數與全部笛卡爾基函數間的重疊矩陣。因此,掃描Sbas的所有列,即循環每個殼層,將每個殼層右乘對應的變換矩陣,所得矩陣V中的i,j元素就是球諧型基函數j與笛卡爾型基函數i的重疊積分。然后,再類似地掃描V的所有行,即循環每個殼層,但改為左乘變換矩陣,所得的矩陣Sbas5D就是我們需要的球諧型高斯函數間的重疊矩陣了。下面的代碼為了緊湊將循環列和循環行這兩步揉在同一個循環里了。另外也沒有利用臨時矩陣V,而是每次乘完后直接賦值到原矩陣適當位置,這是因為球諧型高斯函數數目總少于笛卡爾型,所以賦值時不會把后面殼層的數據覆蓋掉。
ipos5D=1
ipos6D=1
do ish=1,nshell
ishtyp5D=shelltype5D(ish)
ishtyp6D=shelltype(ish)
numshorb5D=type2norb(ishtyp5D)
numshorb6D=type2norb(ishtyp6D)
!Now contract columns
if (ishtyp5D==0.or.ishtyp5D==1.or.ishtyp5D==-1) sbas(:,ipos5D:ipos5D+numshorb5D-1)=sbas(:,ipos6D:ipos6D+numshorb6D-1)
if (ishtyp5D==-2) sbas(:,ipos5D:ipos5D+numshorb5D-1)=matmul(sbas(:,ipos6D:ipos6D+numshorb6D-1),conv5d6d)
if (ishtyp5D==-3) sbas(:,ipos5D:ipos5D+numshorb5D-1)=matmul(sbas(:,ipos6D:ipos6D+numshorb6D-1),conv7f10f)
if (ishtyp5D==-4) sbas(:,ipos5D:ipos5D+numshorb5D-1)=matmul(sbas(:,ipos6D:ipos6D+numshorb6D-1),conv9g15g)
!Now contract rows
if (ishtyp5D==0.or.ishtyp5D==1.or.ishtyp5D==-1) sbas(ipos5D:ipos5D+numshorb5D-1,:)=sbas(ipos6D:ipos6D+numshorb6D-1,:)
if (ishtyp5D==-2) sbas(ipos5D:ipos5D+numshorb5D-1,:)=matmul(conv5d6dtr,sbas(ipos6D:ipos6D+numshorb6D-1,:))
if (ishtyp5D==-3) sbas(ipos5D:ipos5D+numshorb5D-1,:)=matmul(conv7f10ftr,sbas(ipos6D:ipos6D+numshorb6D-1,:))
if (ishtyp5D==-4) sbas(ipos5D:ipos5D+numshorb5D-1,:)=matmul(conv9g15gtr,sbas(ipos6D:ipos6D+numshorb6D-1,:))
ipos5D=ipos5D+numshorb5D
ipos6D=ipos6D+numshorb6D
end do
sbas5D=sbas(1:nbasis5D,1:nbasis5D)