繪制靜電勢全局極小點+等值面圖展現孤對電子位置的方法
2022-Jul-5重要補充:本文用的是盆分析方法得到靜電勢極小點的位置和數值,用Multiwfn的拓撲分析功能也實現同樣的目的,而且精度比用盆分析更高。如果你對精度有較高要求,應當用拓撲分析代替盆分析。具體例子參見《使用Multiwfn對靜電勢和范德華勢做拓撲分析精確得到極小點位置和數值》(http://www.shanxitv.org/645)。
繪制靜電勢全局極小點+等值面圖展現孤對電子位置的方法
文/Sobereva@北京科音
First release: 2019-Jun-24 Last update: 2020-Apr-13
1 前言
有人在計算化學公社論壇問下面這張圖怎么繪制(實際上是J. Comput. Chem., 39, 488 (2018)里的圖)
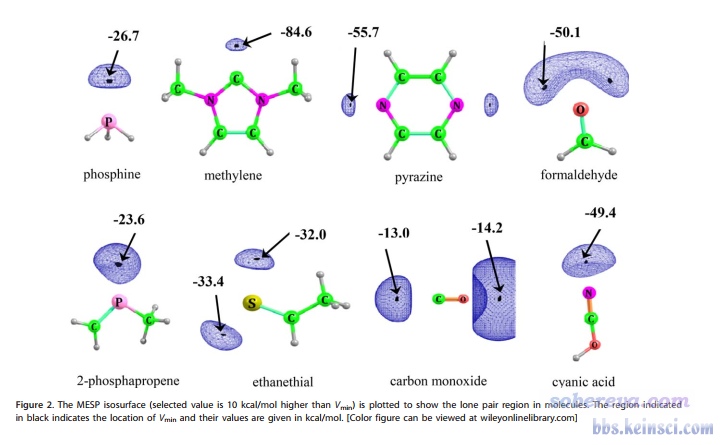
這張圖里面每個黑點是靜電勢的全局極小點,藍色網格等值面展現的是靜電勢的等值面圖,如圖題所示,等值面數值取的是比靜電勢全局最小點數值(Vmin)大10 kcal/mol的值。
孤對電子出現位置有不同方式可以考察,沒法說哪個是最嚴格的。比如可以用Multiwfn做軌道定域化分析看對應孤對電子的軌道質心位置來考察,見《Multiwfn的軌道定域化功能的使用以及與NBO、AdNDP分析的對比》(http://www.shanxitv.org/380);也可以通過對ELF或LOL函數繪圖或通過其臨界點位置考察,見《使用Multiwfn做拓撲分析以及計算孤對電子角度》(http://www.shanxitv.org/108)和《ELF綜述和重要文獻小合集》(http://bbs.keinsci.com/thread-2100-1-1.html)。Suresh的一些文章認為通過靜電勢全局極小點位置也可以展現孤對電子,如上圖所示,極小點連同周圍的靜電勢等值面也確實合理地把孤對電子出現區域展現了出來,與化學直覺一致。Multiwfn是分析靜電勢最強大、靈活的工具,下面就說一下怎么繪制上面那種圖。如果你對靜電勢了解甚少的話,建議看看《靜電勢與平均局部離子化能綜述合集》(http://bbs.keinsci.com/thread-219-1-1.html)里面的資料和筆者的相關博文。
本文使用乙硫醛作為例子,就是上圖第二行第二個。由于計算級別和原作者不可能恰好相同,所以結果也不可能精確相同。這里筆者用Gaussian在B3LYP/def2-TZVP下對結構進行優化并產生波函數,得到的fch文件在http://www.shanxitv.org/attach/493/file.rar里面。用其它的含有波函數信息的格式作為Multiwfn的輸入文件當然也可以,見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。為了加快靜電勢計算,強烈建議讓Multiwfn調用本機里Gaussian中的cubegen,做法見《Multiwfn現已可以調用cubegen使靜電勢分析耗時有飛躍式的下降!》(http://www.shanxitv.org/435)。
本文的Multiwfn用的是官網http://www.shanxitv.org/multiwfn上的最新版本(老版本可能不適用于本文的步驟)。VMD使用1.9.3版,可在http://www.ks.uiuc.edu/Research/vmd/下載。
2 在Multiwfn中的計算和繪制
首先需要用Multiwfn對乙硫醛做靜電勢的盆分析,從而得到全局極小點位置和數值,然后再繪制等值面。如果你不了解Multiwfn的盆分析功能的話,建議看《使用Multiwfn做電子密度、ELF、靜電勢、密度差等函數的盆分析》(http://www.shanxitv.org/179)。
啟動Multiwfn,輸入
ethanethial.fch //在本文文件包里
17 //盆分析
1 //生成盆并獲得極值點
12 //靜電勢
1 //當前對精度要求不高,選擇Low quality grid就夠了
如果你允許Multiwfn調用cubegen來計算靜電勢的話,一般Intel四核機子下不超過一分鐘就可以算完。從屏幕上可以看到如下極值點的信息,Value就是這些點靜電勢的值,單位是a.u.:
Attractor X,Y,Z coordinate (Angstrom) Value
1 -0.31737088 -2.08489274 -0.05291772 -0.04389250
2 2.64602171 -0.17985465 -0.05291772 -0.04492940
3 -1.90490263 0.13765170 -0.89960132 9.75537000
4 -1.48156083 0.66682895 -0.05291772 38.00920000
5 0.00013547 0.66682895 0.05291772 35.31730000
6 0.52931272 1.61934800 -0.05291772 7.39722000
7 -1.90490263 1.72518345 -0.05291772 6.35453000
8 0.84681907 -0.70903190 -0.05291772 86.36020000
9 -1.90490263 0.13765170 0.89960132 9.75537000
選擇選項0觀看極值點,恰當設置后會看到下圖。
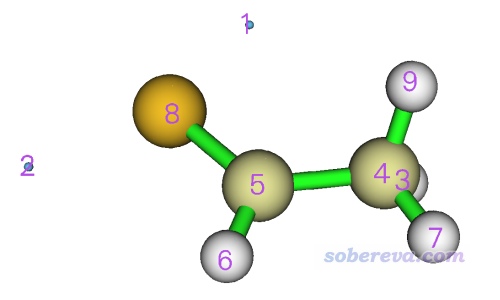
可見,有兩個靜電勢極小點(藍球),數值對應于上面看到的-0.04389250和-0.04492940 a.u.,乘上627.51 kcal/mol轉換單位后,數值是-27.5和-28.2 kcal/mol。然后點擊界面上的Attractor labels取消顯示極值點的標簽,然后輸入
-10 //返回主菜單
13 //處理格點數據的主功能
-2 //觀看等值面
此時圖形窗口里顯示的是內存里裝著的格點數據的等值面,即靜電勢等值面。
當前體系的Vmin是-0.04492940,比它靜電勢高10 kcal/mol的話就是-0.0449294+10/627.51 = -0.02899。將這個數值輸入當前窗口的Isosurface Value文本框里然后按回車,然后點擊Show both sign來避免顯示與之符號相反的0.02899 a.u.等值面。然后在菜單欄的Isosurface style里選Mesh。點擊Show atomic labels將原子標簽顯示在圖上,再選菜單欄的Other settings - Set atomic label type - Element Symbol。最后,點擊Save picture按鈕保存圖像文件到當前目錄,再自行把極值點的數值標上去,就得到了下圖
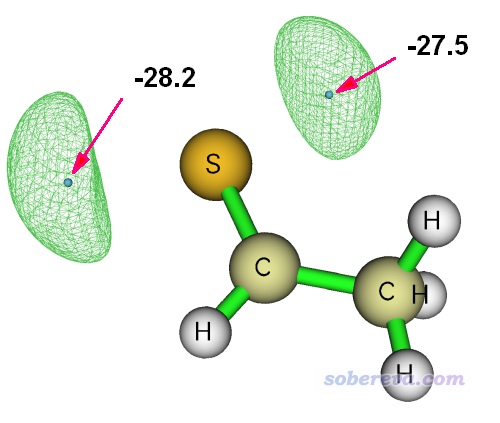
3 在VMD中的繪制
使用VMD來繪制往往可以得到比Multiwfn更好的效果,特別是對于大體系、需要精細調整視角的情況而言。接著上一節的例子,退出圖形窗口,在主功能13的界面中選擇0,然后輸入ESP.cub來把當前內存里的靜電勢格點數據導出為當前目錄下的ESP.cub(此文件也在本文的文件包里)。然后啟動VMD,將ESP.cub拖入VMD Main窗口載入之,進入Graphics - Representation,把Drawing Method切換為CPK,把Sphere Resolution設為22使得原子球更更滑。然后點Create Rep,并把選項設成下面這樣
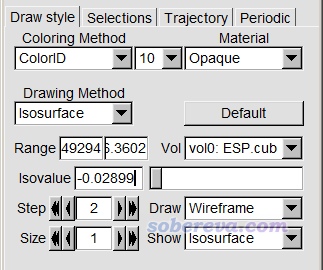
然后在命令行窗口輸入color Display Background white切換為白背景。之后輸入以下命令,在靜電勢極小點的位置繪制桔黃色小球,坐標就是之前Multiwfn做盆分析時候找出來的
draw color orange
draw sphere { -0.31737088 -2.08489274 -0.05291772 } radius 0.1 resolution 15
draw sphere { 2.64602171 -0.17985465 -0.05291772 } radius 0.1 resolution 15
現在看到的圖像如下所示,和Multiwfn顯示的完全一樣。可見無論是VMD繪制的還是Multiwfn繪制的,都明顯比原文的圖好看得多。
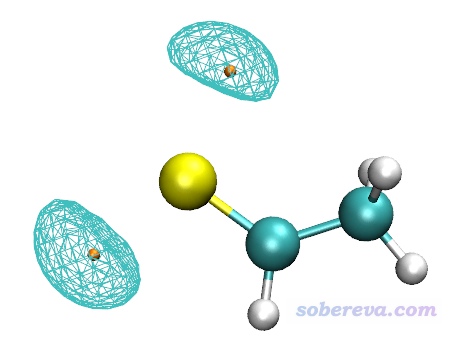
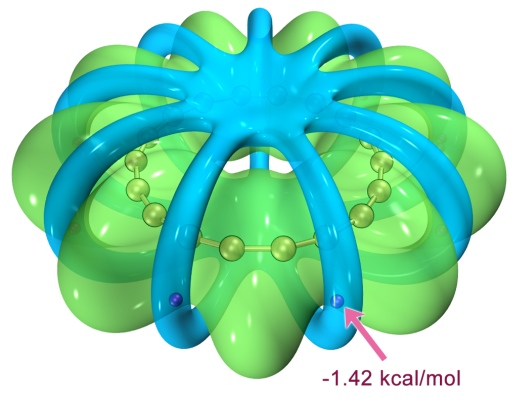
在VMD中,靜電勢等值面圖也可以通過《在VMD里將cube文件瞬間繪制成效果極佳的等值面圖的方法》(http://www.shanxitv.org/483)介紹的做法繪制,效果明顯更好,而且比上文的做法還省事,只需要在Multiwfn產生靜電勢cub文件后在VMD里運行一個我寫的繪圖腳本即可。在《一篇最全面、系統的研究新穎獨特的18碳環的理論文章》(http://www.shanxitv.org/524)介紹的文章中筆者研究了電子結構十分特殊的18碳環體系,其中在考察靜電勢分布特征的時候就用了此文的方法確定了靜電勢極小點位置并結合VMD進行了繪制,如下所示,可見效果極佳。綠色和藍色分別是靜電勢為正和為負的等值面,紫球是靜電勢最小點。很建議大家看看此文中對18碳環的靜電勢的相關討論。