使用Multiwfn對靜電勢和范德華勢做拓撲分析精確得到極小點位置和數值
使用Multiwfn對靜電勢和范德華勢做拓撲分析精確得到極小點位置和數值
文/Sobereva@北京科音 2022-Jul-4
0 前言
靜電勢和筆者在J. Mol. Model., 26, 315 (2020)中提出的范德華勢都是分析化學體系與其它分子相互作用的重要方法。靜電勢的極小點(指全空間內的極小點,而不是http://www.shanxitv.org/159和http://www.shanxitv.org/443等文章介紹的常被討論的分子表面上的靜電勢極小點)有重要的意義,比如J. Comput. Chem., 39, 488 (2017)指出靜電勢極小點能說明孤對電子位置、朝向,其數值和分子與其它Lewis酸的相互作用能有線性相關性。J. Phys. Chem. A, 123, 10139 (2019)還指出靜電勢極小點處靜電勢的Hessian矩陣本征值和體系的芳香性存在聯系。范德華勢在《繪制靜電勢全局極小點+等值面圖展現孤對電子位置的方法》(http://www.shanxitv.org/493)里有詳細介紹,它的極小點也有重要意義,其位置體現出體系在什么位置和探針原子的范德華凈吸引作用最強(這里說的“凈”是指交換互斥勢和色散吸引勢抵消后的凈效果),其位置和數值大小對于預測和解釋體系與其它分子的范德華作用出現的傾向性和強度極為重要。盡管范德華勢的等值面圖很直觀,但準確、定量對某體系內不同位點或者不同體系的類似位點間進行對比,還是要用到范德華勢極小點的具體數值的。
波函數分析程序Multiwfn(http://www.shanxitv.org/multiwfn)的盆分析模塊十分強大和普適,對任何三維實空間函數都可以基于均勻分布的格點數據搜索出函數的極大點和極小點的位置,并給出這些位置的函數值。之前筆者在《繪制靜電勢全局極小點+等值面圖展現孤對電子位置的方法》(http://www.shanxitv.org/493)中介紹了如何通過盆分析得到靜電勢極小點位置和數值,在《談談范德華勢以及在Multiwfn中的計算、分析和繪制》(http://www.shanxitv.org/551)也介紹了如何通過盆分析得到范德華勢的極小點位置和數值。靠盆分析考察靜電勢和范德華勢的極小點的關鍵不足在于定位精度很有限。盆分析給出的極值點位置的精度完全取決于格點間距,因為它給出的極值點對應的是某個格點。假設用的格點是立方格點,格點間距為d,那么盆分析給出的極值點位置的誤差最大可以達到(√3)/2*d。常用的格點間距在0.1~0.2 Bohr范圍,假設取0.15 Bohr,那最大定位誤差約0.07埃。對精度要求高的話這誤差就不算很小了。而如果通過減小格點間距來提升定位精度,一方面會造成計算格點數據耗時大幅增加(尤其是對昂貴的靜電勢來說),另一方面會導致儲存格點數據的內存占用量大幅提高,內存不夠的話Multiwfn就會崩潰。計算耗時和內存占量都是以格點間距的三次方呈反比的。
Multiwfn的拓撲分析模塊十分普適,原理上可以對任何三維實空間函數搜索各種臨界點。此功能最常被用來搜索電子密度的各種臨界點(即AIM拓撲分析干的事),也常用來搜索電子定域化函數(ELF)的極大點,見《使用Multiwfn做拓撲分析以及計算孤對電子角度》(http://www.shanxitv.org/108)。在本文,將介紹怎么利用Multiwfn的拓撲分析功能來搜索靜電勢和范德華勢的極小點。相對于靠前述的盆分析來找它們的極小點,本文的做法關鍵好處在于極小點定位精度相當高。拓撲分析模塊搜索極值點是通過各種局部優化算法實現的,定位精度原理上沒有上限,關鍵取決于你設的位移收斂限,對于靜電勢和范德華勢的極小點搜索通常設0.00001 Bohr,這絕對足夠精確了。另外,拓撲分析模塊搜索極值點時不會儲存占內存明顯的數據,因此也不必擔心對大體系做盆分析時內存不夠記錄格點數據的情況。拓撲分析的缺點是無法保證所有極大、極小點都能被毫無遺漏地找到。根據算法原理可知,盆分析所用的格點數據涵蓋的空間范圍里的極大、極小點位置一定能被(粗糙地)定位,而拓撲分析能找到哪些極值點,則取決于初猜位置是否恰當,這在后文會有更多說明。
下文第1、2節將分別給出通過拓撲分析模塊搜索靜電勢和范德華勢極小點的具體例子,第3節將會再介紹一種將盆分析和拓撲分析聯用的方法,雖然此做法步驟略多,但既可以保證極小點定位精度夠高,又可以確保所有極小點都找全。讀者請務必使用2022-Jul-4及以后更新的Multiwfn,否則情況將和本文所述不同。Multiwfn可以在http://www.shanxitv.org/multiwfn免費下載,不了解者參看《Multiwfn FAQ》(http://www.shanxitv.org/452)和《Multiwfn入門tips》(http://www.shanxitv.org/167)。如果讀者不怎么了解Multiwfn的拓撲分析功能,建議好好看看《使用Multiwfn做拓撲分析以及計算孤對電子角度》(http://www.shanxitv.org/108)以及Multiwfn手冊4.2節里的豐富的拓撲分析例子以了解一些必知必會的知識,相關常識性知識就不在本文累述了。
1 通過拓撲分析找靜電勢的極小點
這一節通過乙酰胺作為例子搜索它的靜電勢極小點。啟動Multiwfn,然后輸入
examples\CH3CONH2.fch
2 //拓撲分析
-11 //選擇被分析的函數
12 //靜電勢
注意,默認的拓撲分析搜索算法是Newton法,用這種方法可以搜索所有類型的靜電勢臨界點,包括(3,-3)、(3,-1)、(3,+1)、(3,+3)型,其中(3,+3)型臨界點相當于靜電勢極小點。而當前我們只需要搜索靜電勢極小點。為此,既可以用Newton法搜索出所有臨界點,然后只考察(3,+3)型臨界點,也可以改用專門搜索極小點的最陡下降法,它只會給出極小點。Newton法搜索靜電勢極值點的例子在Multiwfn手冊4.2.9節給出了,這里我們演示最陡下降法。接著輸入
-1 //修改臨界點搜索設置
12 //修改搜索算法
4 //最陡下降法
從當前菜單的選項3、4可以看到臨界點搜索的梯度模和位移的收斂限目前分別默認為1E-4 a.u.和1E-5 Bohr。對于當前的目的是比較適合的,定位精度足夠高了。接著輸入
0 //返回拓撲分析界面
6 //在球形區域內隨機撒初猜點方式搜索
11 //設置每個球內撒點數
10 //撒10個點
-1 //依次以每個原子核為球心撒位置隨機的初猜點并開始搜索
現在Multiwfn開始計算了,并且很快就算完。這里談一些細節問題。由于當前體系一共9個原子,因此會撒9*10=90個初猜點做最陡下降法找極小點。每個原子附近撒的初猜點越多,一次性找全所有極小點的概率就越大,但無疑耗時也越高(耗時和撒點數基本呈正比)。使用最陡下降法時,由于初猜點不會像使用Newton法時也有收斂到(3,+1)、(3,-1)、(3,-3)型臨界點的可能,再加上平均每個原子附近靜電勢極小點數目很有限,再考慮到靜電勢計算耗時頗高,因此撒點數不需要也不適合設太多,大多數體系像此例這樣每個原子周圍撒10個點就可以。如果根據化學直覺發現有的靜電勢極小點還沒找到,可以再次選擇-1再找一次,由于每次初猜點位置都是隨機的,可能再次找的時候就找到了。而如果想一次運行就盡可能找全,那可以每個原子球內撒的點數多設點,比如設50。還值得一提的是,如果當前體系較大,而你感興趣的靜電勢極值點只出現在少量原子附近,可以選-2來代替上面的-1,此時程序會讓你輸入只在哪些原子附近撒點,顯然耗時比在各個原子附近都撒點要低得多。
當前從屏幕上可以看到以下結果
Index Coordinate Type
1 0.61612569 4.34058094 -0.01350434 (3,+3)
2 -2.11862035 -1.61451335 -2.67603347 (3,+3)
3 -2.72454650 3.62685881 -0.00415595 (3,+3)
4 -2.01812136 -1.10844406 2.86125056 (3,+3)
Totally find 4 new critical points
由于這四個臨界點類型都顯示是(3,+3),因此總共找到了4個靜電勢極小點。
接下來看看這些極小點的分布。輸入-9返回拓撲分析界面,然后再選0,在圖形界面里右側點CP labels復選框把臨界點標簽顯示出來,此時看到的圖像如下
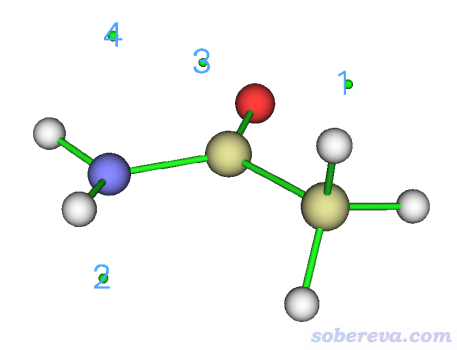
可見在氧的兩側各有一個靜電勢極小點,在氮的上下方也各有一個靜電勢極小點。假設想查詢上圖氮下方的2號臨界點的屬性,就點擊圖形窗口右上角的RETURN窗口關閉,然后輸入
7 //考察臨界點的屬性
2 //臨界點序號
然后看到的和靜電勢有關的信息如下
[無關信息略...]
ESP from nuclear charges: 0.7979843111E+01
ESP from electrons: -0.8016388860E+01
Total ESP: -0.3654574897E-01 a.u. (-0.9944604E+00 eV,-0.2293282E+02 kcal/mol)
Note: Below information are for total ESP
Components of gradient in x/y/z are:
-0.2849942504E-07 0.1657229909E-07 -0.1321709409E-06
Norm of gradient is: 0.1362204681E-06
Components of Laplacian in x/y/z are:
0.2959173774E-01 0.2559900521E-01 0.7778392722E-01
Total: 0.1329746702E+00
Hessian matrix:
0.2959173774E-01 0.2699237708E-02 0.2283944908E-02
0.2699237708E-02 0.2559900521E-01 0.5050204699E-02
0.2283944908E-02 0.5050204699E-02 0.7778392722E-01
Eigenvalues of Hessian: 0.2400095784E-01 0.3057397167E-01 0.7839974065E-01
Eigenvectors(columns) of Hessian:
0.4111466295E+00 0.9100899397E+00 0.5191098824E-01
-0.9090369814E+00 0.4050974512E+00 0.9771295428E-01
0.6789856765E-01 -0.8736335986E-01 0.9938598633E+00
Determinant of Hessian: 0.5753009073E-04
可見,此處靜電勢數值為-0.994 eV。如果考察上圖氮上方的4號臨界點,靜電勢數值只有-0.144 eV。這差異和氮的孤對電子分布有關。如果用Multiwfn繪制ELF等值面圖(參考Multiwfn手冊4.5節的海量例子),會發現在氮的下方孤對電子分布得相對更多一些,這也直接導致氮下方的靜電勢極小點的靜電勢更負。如果考察氧旁邊的靜電勢極小點,則會發現它們都能達到負二點幾eV,絕對值比氮附近的更大。這一方面在于氧在相應位置有顯著的孤對電子,而且氧又不像氮那樣旁邊有帶著顯著正電荷的氫。
上面的輸出中還給出了被考察的靜電勢極小點處的靜電勢的梯度(可見數值很接近0,這是極值點應滿足的條件)、靜電勢的拉普拉斯值、靜電勢的Hessian矩陣及其本征值和本征矢。三個本征值都為正,即各個方向靜電勢的曲率都為正,體現出這確實是靜電勢極小點。
最后,我們把靜電勢等值面給畫出來,并和靜電勢極小點位置進行對照,以更直觀地了解靜電勢分布特征。輸入以下命令
-10 //返回主界面
5 //計算格點數據
12 //靜電勢
2 //中等質量格點
-1 //觀看等值面
將等值面數值調到0.085 a.u.,可以清楚地看到靜電勢數值為-0.085 a.u.的兩個藍色等值面分別包圍了我們找到的氧旁邊的兩個靜電勢極小點,如下所示。這倆極小點也分別是這倆等值面內部空間里靜電勢最負的位置。如果把等值面數值改小,還可以再顯示出圍繞氮附近靜電勢極小點出現的等值面。
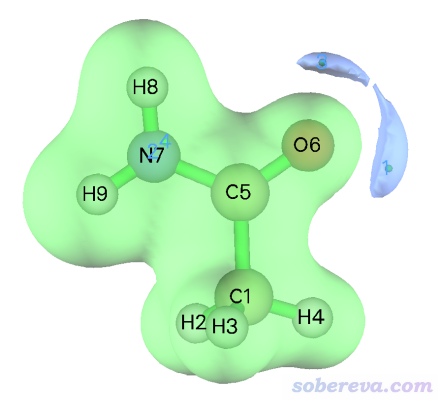
下面給讀者留個練習,對一氧化碳(examples\CO.fch)搜索靜電勢極小點,并且指出它們的靜電勢數值,判斷一氧化碳哪里靜電勢是最負的,并結合ELF圖對結果進行討論。
最后告訴大家一個技巧。前面演示的靜電勢極小點搜索過程做了不少設置,包括選擇被分析的函數、選擇臨界點搜索算法、設置撒點數、進入子功能6,這些都可以簡化為在拓撲分析界面里輸入vmin。即對一般情況,載入波函數文件后,搜索靜電勢極小點可以簡化為依次輸入:
2
vmin
-1
怕有讀者不知道,這里提醒一下,拓撲分析找到的臨界點都可以用拓撲分析界面里的選項-4里的相應子選項把臨界點導出為pdb文件,從而在VMD里繪制。
2 通過拓撲分析找范德華勢的極小點
范德華勢極小點也可以用最陡下降法找到。這里用金剛烷為例演示一下。范德華勢的探針原子用的是默認的碳。
啟動Multiwfn,然后輸入
examples\adamantane.xyz //B3LYP/6-31G*下優化的結構
2 //拓撲分析
-11 //選擇被分析的實空間函數
25 //范德華勢
此時如屏幕所示,程序自動把搜索用的算法設成最陡下降法了。進入選項6,從屏幕上的提示可見當前對每個球形區域內默認撒100個初猜點,這對于搜索范德華勢極小點通常是合適的。然后選-1在以每個原子核為中心的球形區域內撒點找極小點。很快,屏幕上會提示找到了27個(3,+3)臨界點,即極小點。
選-9返回拓撲分析界面,然后進選項0觀看臨界點,并把Ratio of atomic size設為4.0(此時的原子球半徑對應范德華半徑),并且也把Ratio of CP size設大到2.0使得極小點看得更清楚。當前看到的圖像如下所示,看起來很正常,合乎期望
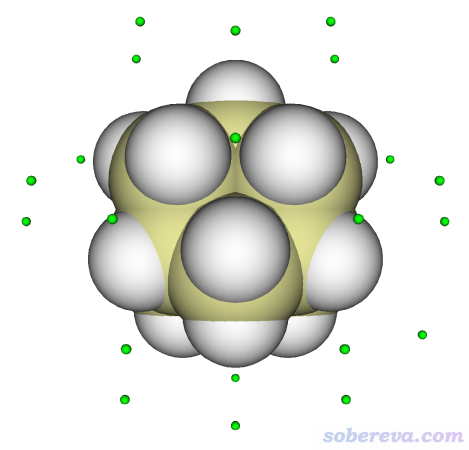
也可以像上一節例子那樣,進入選項7然后輸入臨界點序號來考察其屬性,從屏幕上的輸出中可以看到范德華勢的具體數值,以及它的梯度、Hessian信息。
下面把范德華勢等值面也顯示出來以更好地認識極小點的分布。返回Multiwfn主菜單,然后輸入
20 //圖形化分析弱相互作用
6 //觀看范德華勢
3 //高質量格點
3 //觀看范德華勢等值面
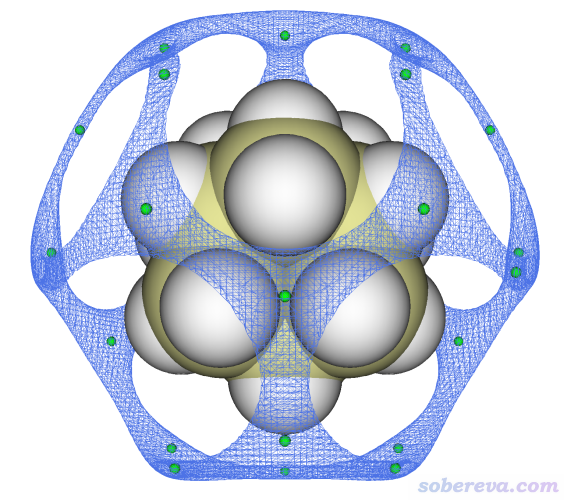
在出現的圖形界面里,把isovalue設為-0.7,取消選擇Show both sign復選框。在頂端的Isosurface style里把顯示風格設為mesh,再選Exchange positive and negative colors,看到的圖像如下所示,藍色等值面對應的是范德華勢為-0.7 kcal/mol的等值面
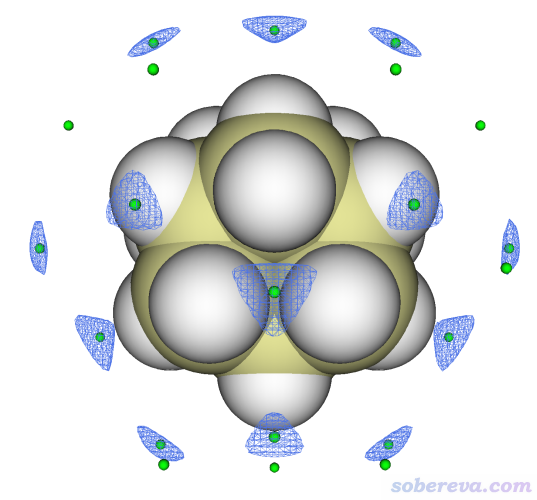
上圖的等值面和極小點的關系完全符合期望,證明極小點找得的確沒問題。此體系的范德華勢極小點有兩類,上圖中還有一類極小點沒被等值面包圍,這是因為它們的范德華勢比-0.7 kcal/mol更正。如果將等值面數值設為-0.62,則那些極小點也會被等值面包圍,如下所示
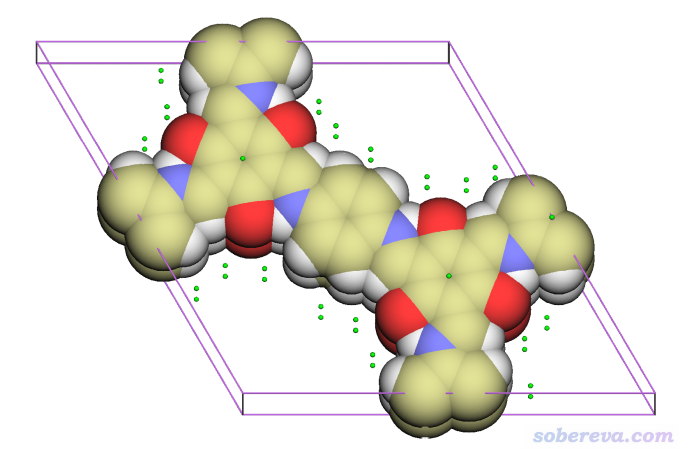
順帶強調一下,Multiwfn里范德華勢可以對周期性體系計算,而且拓撲分析也完美支持周期性體系,因此如果你的輸入文件能給Multiwfn提供盒子信息,比如cif等文件(詳見《使用Multiwfn非常便利地創建CP2K程序的輸入文件》http://www.shanxitv.org/587里的說明),就可以對周期性體系尋找范德華勢極小點,操作步驟和前面分析分子體系的情況精確相同。比如examples\COF_12000N2.cif是一個共價有機框架化合物的cif文件,用上面的步驟找范德華勢極小點的結果如下,可見很合理。這里用了正交視角,晶胞邊框也顯示了。
3 盆分析和拓撲分析聯用找極小點
這里再介紹一個盆分析與拓撲分析聯用找極小點的方法。具體來說,此方法是先用盆分析功能粗略定位極小點,然后以這些位置作為拓撲分析的初猜位置來找精確的極小點。由于此時的初猜離實際極小點非常近,而且又沒有遺漏,因此這種方法可以確保所有極小點都能精確找到。Multiwfn手冊里4.2.7節搜索自旋密度的臨界點就用了這種做法,《使用IRI方法圖形化考察化學體系中的化學鍵和弱相互作用》(http://www.shanxitv.org/598)里提到的IRI官方教程里搜索IRI-pi的極小點用的也是這種做法。如果你不了解Multiwfn的盆分析功能,用此方法前建議先看看《使用Multiwfn做電子密度、ELF、靜電勢、密度差等函數的盆分析》(http://www.shanxitv.org/179)。
什么時候適合用這種聯用的做法?實際上這種方法什么時候都可以用,而最有必要用的是極小點附近的函數分布是狹長的情況(形狀類似于很狹窄的山谷)。在這種情況下,最陡下降法特別容易震蕩,當隨機分布的初猜位置離極小點較遠時,可能得花好幾百步才能滿足收斂。這已明顯超過Multiwfn搜索臨界點的默認步數上限,因此搜索會失敗。雖然你也可以在拓撲分析界面的選項1里用相應子選項把步數上限設大,但是花大幾百步才收斂,對于靜電勢極小點搜索明顯不劃算。讓Multiwfn用Newton法搜索臨界點時震蕩問題遠沒最陡下降法嚴重,但如果此時極小點很多,想要找全的話需要令初猜點數目很多,對于靜電勢而言會導致搜索耗時頗高。這種情況明顯不如用盆分析+拓撲分析聯用的方法劃算和省心。下面要演示的對二茂鐵的靜電勢搜索極小點就是個很典型應當用聯用法的例子。
examples\ferrocene.mwfn是B3LYP/6-31G*&lanl2DZ計算得到的二茂鐵的波函數文件。啟動Multiwfn并載入之,然后輸入
17 //盆分析
1 //產生盆
12 //靜電勢
1 //低質量格點。對于粗略獲得靜電勢極小點的目的這樣的格點精度足矣
計算靜電勢格點數據耗時是比較高的,尤其是對大體系、大基組、CPU性能較弱的情況而言。如果你的機子里有Gaussian,可以讓Multiwfn調用cubegen更快地靜電勢格點數據,詳見http://www.shanxitv.org/435(這需要輸入文件是fch格式。當前是mwfn格式,可以先用主功能100的子功能2轉成fch,再用它作為輸入文件)。
算完后,可以進選項0看一下當前的靜電勢極值點分布情況,如下所示,藍球是極小點。在原子核位置附近還有靜電勢極大點,被原子球擋住了所以看不到。
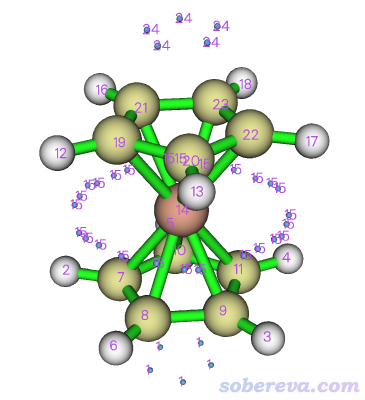
檢查沒問題后,關閉圖形窗口,選擇選項-4,再選3 Export coordinates and function values of all attractors as attractors.txt。然后當前目錄下就出現了attractors.txt文件,每一列的含義在導出文件時屏幕上提示得清清楚楚。
之后選-10從盆分析界面返回主菜單,然后輸入
2 // 拓撲分析功能
-11 //設置被分析的函數
12 //靜電勢
1 //從給定的一批初猜點搜索臨界點
4 //將txt文件里記錄的坐標作為初猜點
[按回車] //用將當前目錄下的attractors.txt
然后如屏幕上的提示所示,Multiwfn依次以attractors.txt里各個坐標當初猜尋找臨界點,很快就完成了。之后選0返回拓撲分析界面,再選0觀看臨界點,當前圖像如下。綠色是極小點,黃色和橙色分別是(3,+1)和(3,-1)臨界點。
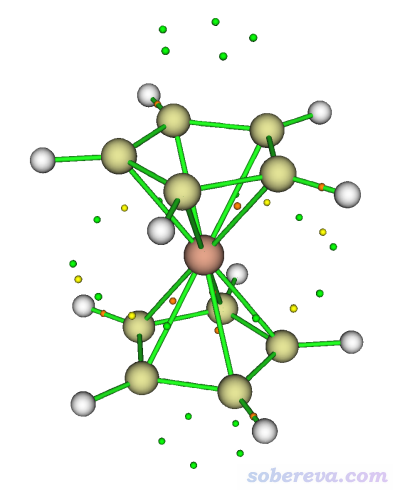
由于靜電勢極小點的分布完全滿足體系對稱性,所以憑直覺就知道所有極小點都找全了。感興趣的話還可以再結合等值面圖考察。為此,輸入
-10 //返回主菜單
13 //格點數據處理
-2 //觀看內存里格點數據的等值面(當前內存里的格點數據就是之前做盆分析時算靜電勢格點數據時留下來的)
把等值面數值設為0.025,用mesh方式顯示,現在看到下圖(由于我之前在拓撲分析功能的選項0的圖形界面里把(3,-1)和(3,+1)臨界點的顯示都關掉了,所以下圖只顯示了靜電勢極小點)
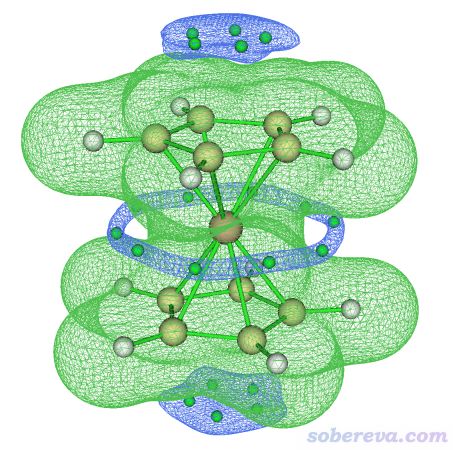
可見,體系上下兩端都有靜電勢為負的區域,這是由于茂環的豐富的pi電子對靜電勢明顯的負貢獻所致。每一塊這樣的等值面里都有5個簡并的靜電勢極小點。在體系中部,環繞著鐵原子還有一個大環狀的靜電勢為-0.025 a.u.的等值面,里面共有10個對稱分布的靜電勢極小點。這樣的靜電勢分布區域就是前面我說的狹長區域,最陡下降法往這里面的靜電勢極小點收斂時特別容易強烈震蕩。不按此例這樣通過盆分析+拓撲分析聯用的話很難將這些靜電勢極小點全都沒有遺漏地找全。
在《全面探究18碳環獨特的分子間相互作用與pi-pi堆積特征》(http://www.shanxitv.org/572)一文中給出了18碳環的靜電勢等值面圖(這篇博文里是用盆分析方式搜索的靜電勢極小點,因此定位精度略糙)。由圖可見,在碳環外圍繞著每個較短的碳碳鍵有環狀的靜電勢為負的區域,其中的靜電勢極小點也是屬于處在狹長山谷的情況,和上面的二茂鐵的例子一樣也應當用組合方法來定位極小點。
4 總結&其它
本文詳細介紹了使用Multiwfn的拓撲分析功能對兩個重要的函數,靜電勢和范德華勢,做拓撲分析尋找它們的極小點的過程。Multiwfn對任何函數都可以做拓撲分析尋找包括極大/極小點在內的各類臨界點,極其靈活、普適。只不過,對不同函數搜索不同類型的臨界點時,做拓撲分析的最佳流程可能不同。
Multiwfn手冊里還有多例子,例如4.2.11節介紹了怎么對《使用IRI方法圖形化考察化學體系中的化學鍵和弱相互作用》(http://www.shanxitv.org/598)里介紹的IRI函數做拓撲分析。很多弱相互作用是不存在鍵臨界點的,因此沒法用AIM拓撲分析根據相應的點的特征來考察,而所有弱相互作用總是有對應的IRI極小點,可以根據它的屬性討論弱相互作用。Multiwfn手冊4.2.7節還演示了對自旋密度做拓撲分析。Multiwfn甚至靈活到只要提供某個函數的格點數據文件就能對此函數做拓撲分析(基于B-spline插值出的函數),例如Multiwfn手冊4.2.8節給出了對密度差做拓撲分析的例子。按照《通過Multiwfn繪制等化學屏蔽表面(ICSS)研究芳香性》(http://www.shanxitv.org/216)和《使用AICD 2.0繪制磁感應電流圖》(http://www.shanxitv.org/294)介紹的方式產生的ICSS和AICD的格點數據,也同樣可以用Multiwfn做拓撲分析尋找精確的極值點以便準確地定量討論。注意,由于不同函數的分布特征不同,有時候需要恰當調節搜索設置才可能能成功搜索到臨界點,如搜索算法、收斂限、初猜方式等,必須在理解搜索原理的基礎上隨機應變。