利用Multiwfn計算傾斜、扭曲環的NICS_ZZ

利用Multiwfn計算傾斜、扭曲環的NICS_ZZ

First release: 2014-Nov-19 Last update: 2021-Oct-26

1 前言

NICS、NICS(1)_ZZ的定義在《衡量芳香性的方法以及在Multiwfn中的計算》（http://www.shanxitv.org/176）的3.1節有詳細介紹。NICS(1)_ZZ具體指的是垂直于環平面上方1埃處在垂直于環平面方向上的磁屏蔽值的負值。對于平面體系，這很好算，比如體系在XY平面上，那么先計算出環的中心，然后把坐標的Z值加1，放置個Bq原子（對于Gaussian來說），然后算NMR，讀取Bq原子的磁屏蔽張量的ZZ分量取負號即可。但是，被研究的環如果不在XY/YZ/XZ平面上，或者環本身就是扭曲的而非完美平面，那么計算NICS(1)_ZZ就很麻煩了，光是確定要計算的Bq原子的位置就不好搞。比如下面的例子，C36的一個異構體，假設要研究紅點標注的5,6,25,28,27,29這個六元環，它既是斜著的，又不是純平面。

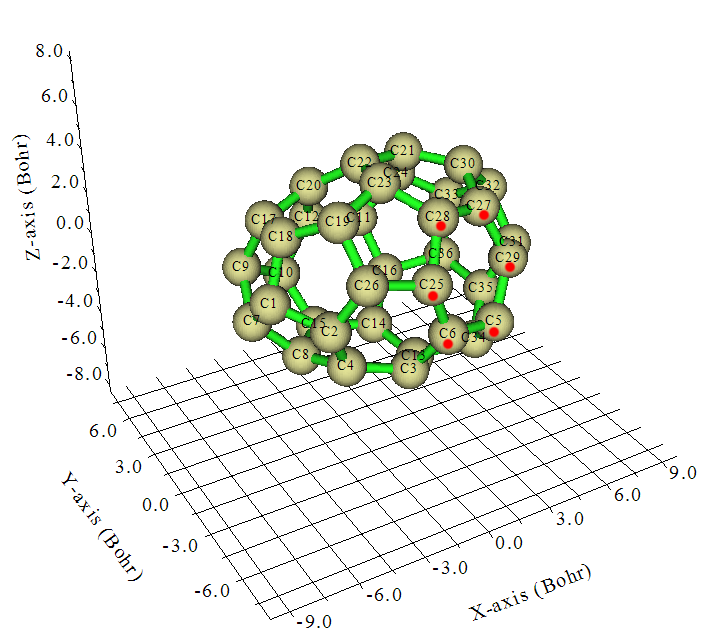
雖然也可以旋轉這個團簇，讓這個環正好基本平行于XY平面上，然后按照常規步驟算NICS(1)_ZZ，但是如果要研究的環很多，每研究一個環都這么轉一次結構，實在太麻煩。而利用Multiwfn (http://www.shanxitv.org/multiwfn)，則可以很方便地解決計算傾斜非平面環的NICS(1)_ZZ的問題。下面就以上面那個環作為例子，來演示一遍操作。

2 實例

C36的pdb文件，以及下文涉及的Gaussian的輸入、輸出文件可以在這里下載：http://www.shanxitv.org/attach/261/file.rar。

我們先計算出環中心。有很多方法計算環中心，兩種比較常用，其一是取環的質心，其二是取環的AIM理論中的環臨界點(RCP)位置。由于前者不需要波函數文件，有結構就行了，為了省事我們此例就用質心。后者也可以十分方便快速地通過Multiwfn的拓撲分析功能得到，可參見《使用Multiwfn做拓撲分析以及計算孤對電子角度》（http://www.shanxitv.org/108）。

啟動Multiwfn，輸入以下命令
Fullerene_No.1-C2.pdb // C36結構文件
100
21   // 計算各種基于幾何結構的屬性
5,6,25,27-29   // 組成環的原子的序號，這些原子將會被用來計算各種基于幾何結構的屬性
從輸出文件中我們看到了此環的質心
Center of mass (X/Y/Z):     0.96300000   -1.89100000    0.43750000 Angstrom

我們把質心坐標復制下來，然后輸入
q   //返回
24   //輔助計算非平面體系的NICS_ZZ
0.96300000   -1.89100000    0.43750000 //粘貼剛才的質心坐標
因為這個環本身不是完全平面的，因此也沒有辦法唯一地定義一個平面來代表它。但可以通過環上的原子根據最小二乘法擬合出一個最具有代表性的平面。因此我們輸入5,6,25,27-29，使Multiwfn根據環上的這些原子的坐標進行擬合。

屏幕上顯示
RMS error of the plane fitting: 0.194520 Angstrom
The unit normal vector is 0.31391747 -0.90899632 0.27419245

The X,Y,Z coordinate of the points below and above 1 Angstrom of the plane from
the point you defined, respectively:
0.6490825274 -0.9820036752 0.1633075459 Angstrom
1.2769174726 -2.7999963248 0.7116924541 Angstrom

告訴了平面的擬合誤差（如果平面本身就是純平的則誤差為0）、此平面的單位法向量，以及從剛才輸入的環中心沿著法向量向上和向下分別移動1埃后的坐標。這兩個坐標就可以設為Bq原子來計算NICS(1)_ZZ了。假設整個體系大體是個平面，那么用這兩個點的NICS(1)_ZZ值取平均是比較合理的。不過當前體系是籠狀體系，所以我們只應當取處在環外的那個點來算NICS(1)_ZZ。

建議先別關Multiwfn，因為待會兒還得把算好的Bq點的屏蔽張量輸進去。如果關了的話，之后還得重新做上述操作。

我們基于C36的結構創建一個Gaussian輸入文件，然后把剛才得到的1.2769174726   -2.7999963248    0.7116924541這個點作為Bq原子的位置，此時輸入文件如下（此文僅作為示例，純粹為節省計算量用STO-3G，實際研究中決不能低于6-31G*，否則結果沒法用）
# B3LYP/STO-3G NMR nosymm
[空行]
Generated by Multiwfn
[空行]
0 1
C     -3.06300000   -0.54400000    0.11800000
C     -2.20500000   -1.61200000   -0.25800000
...[略]
C      2.55900000   -0.14400000   -1.38400000
C      2.29700000    1.21800000   -1.08100000
Bq 1.2769174726   -2.7999963248    0.7116924541

用gview查看一下，可見Bq原子位置很合適，確實是在環平面上方1埃處

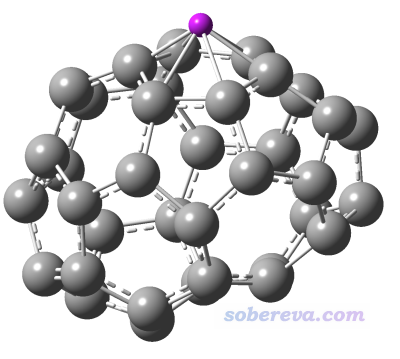
注意輸入文件里的nosymm很重要，如果不寫的話，Gaussian可能會自動旋轉體系到標準朝向下，導致垂直于環平面的方向在計算前后不同，Multiwfn也就沒法正確提取垂直于環平面方向的分量了。

用Gaussian計算此文件，看到NMR部分Bq原子的輸出
      37 Bq   Isotropic =    -6.1406   Anisotropy =    25.7238
   XX=     0.0370   YX=    -0.4791   ZX=    -1.2514
   XY=     3.5065   YY=   -23.1631   ZY=     7.3440
   XZ=     7.0901   YZ=   -35.5524   ZZ=     4.7043
   Eigenvalues:   -29.2734    -0.1570    11.0086

切換回Multiwfn窗口，將屏蔽張量依次輸入進去：
0.0370,-0.4791,-1.2514
3.5065,-23.1631,7.3440
7.0901,-35.5524,4.7043
（秘籍：想圖省事的話，把Gaussian輸出文件的屏蔽張量那三行一次性直接粘貼到Multiwfn窗口里也可以）

最后會顯示
The shielding value normal to the plane is -12.1124014284
The NICS_ZZ value is thus 12.1124014284
即NICS(1)_ZZ值為12.11（單位是ppm）。

其實本例在進入主功能100的子功能24之前可以不去特意用子功能21。因為當前用的環中心就是幾何中心，而且定義擬合平面用的原子就是環上的所有原子。對于這種情況，直接進入子功能24，讓你輸入環中心的時候直接敲回車，之后輸入環上的原子序號后，程序自動就會將這些原子的幾何中心作為環中心。

3 其它事項

對于平面上方和下方1埃處的NICS(1)_ZZ都需要計算的情況，你在輸入屏蔽張量的界面里，把平面上方1埃處的屏蔽張量粘貼進去，得到的就是上方1埃處的NICS_ZZ(1)，如果把下方1埃處的屏蔽張量粘貼進去，得到的就是下方1埃處的NICS_ZZ(1)。

順帶一提，雖然NICS(0)_ZZ我很不推薦，但如果非要算的話，步驟和上述一樣，只不過把Bq放在環中心即可。要計算比如NICS(5)_ZZ也可以，也就是把環中心坐標加上5*單位法向量，就得到了要算的垂直于平面上方5埃處的點的坐標。之后的步驟和文中一樣，輸入那個點的屏蔽張量即可。

如果要研究的環有多個，那么按照上述步驟，確定出各個環要計算的Bq原子位置，都寫進Gaussian輸入文件里，只需要Gaussian算一次即可，而不需要每研究一個環都單獨算一次。

1 前言

2 實例

3 其它事項

分類

友情鏈接

其它