CASSCF計算雙自由基以及雙自由基特征的計算
CASSCF計算雙自由基以及雙自由基特征的計算
文/Sobereva @北京科音 2014-11-24
1 前言
雙自由基就是指一個體系里有兩個未成對兒電子,它們的自旋相反,因此是單重態的體系。
普通的單重態體系是閉殼層的,所有電子都是配對兒的。最理想的雙自由基體系,是兩個自旋彼此相反的單電子之間完全不配對兒,二者的空間分布彼此完全分離。而多數雙自由基體系,情況介于二者之間,即兩個單電子之間部分配對兒,分布沒有完全分離。
本文主要討論的是Yamanaka等人提出的雙自由基特征y的計算。其數值從0到1,0對應閉殼層,越接近1說明體系雙自由基特征越明顯,1就是理想雙自由基。本文還順帶討論怎么用CASSCF計算雙自由基體系。
文中Multiwfn用的是撰文時最新版3.3.7(dev),計算用Gaussian09 B.01完成。Multiwfn可以在http://www.shanxitv.org/multiwfn免費下載。
2 CI波函數下的雙自由基特征
2.1 理論
在筆者《小談幾種量子化學方法對氫分子解離過程的描述》(http://www.shanxitv.org/59)一文中曾詳細介紹了CI、RHF、UHF、VB方法對氫分子解離成兩個氫原子過程的處理。文中提到,CI可以完美地描述這個過程。H2的CI波函數可以寫為
ψCI=c1*ψG+c2*ψD
其中ψG是基態組態,即兩個電子都占據H2的成鍵軌道(HOMO)的組態函數,ψD是兩個電子都激發到H2的反鍵軌道(LUMO)的組態函數。ψCI也可以等價地用兩個氫原子a、b的1s原子軌道來描述,記為Xa和Xb
ψCI=[(c1+c2)*(|Xaα Xaβ|+|Xbα Xbβ|)+(c1-c2)*(|Xaα Xbβ|-|Xaβ Xbα|)]/2
其中| |是slater行列式符號。諸如Xbα就代表Xb上占據α電子。
在H2平衡距離下,c1幾乎為1,c2幾乎為0。c1不完全為1是因為必須引入ψD才能體現電子動態相關。
在解離過程中,c1不斷減小,c2不斷增大。
當H2徹底解離為兩個相距很遠的氫原子后,成為完美的雙自由基體系,兩個氫原子各帶一個電子且彼此自旋相反,空間上完全分離。此時c1=1/√2,c2=-1/√2,兩個組態的權重(系數的平方)完全一致了。ψCI=(ψG-ψD)/√2這種波函數的形式不容易直接其物理含義,但是改寫為用原子軌道表示,即(|Xaα Xbβ|-|Xaβ Xbα|)/√2,意義一下子就清楚了,這是正是兩個氫原子各帶的一個電子所構成的單重態自旋匹配波函數。
可見,雙激發組態的權重c2^2越大,雙自由基特征越強,和基態組態權重c1^2相同時就是完美雙自由基。基于這個考慮,Yamaguchi在Chem. Phys. Lett., 33, 330 (1975)中將y=2*c2^2定義為雙自由基特征,完美雙自由基時c^2=1/2,故y恰為1。
2.2 CASSCF計算雙自由基C4H8實例
CI波函數描述雙自由基在形式上是完美的,實際中用的更多的是CASSCF波函數,即不光變分CI系數,還變分軌道系數。描述雙自由基至少用CAS(2,2),把那兩個單電子軌道以相位相同和相位相反方式組合構成的兩個分子軌道納入活性空間里,這樣才能產生合理描述雙自由基所需要的ψG和ψD。
解離后的H2可以說是最最最簡單、最完美的雙自由基的模型體系,實際的雙自由基體系還有許許多多其它的軌道,但是我們通常還是能從中找出與構成雙自由基直接相關的兩個分子軌道并將之納入活性空間的,很多情況下這兩個軌道就是HOMO和LUMO。比如C4H8這個體系,分子兩頭各缺一個氫,故必然是單電子出現的位點,在HF/6-31G*下計算后,HOMO和LUMO分別是(等值面數值為0.1)
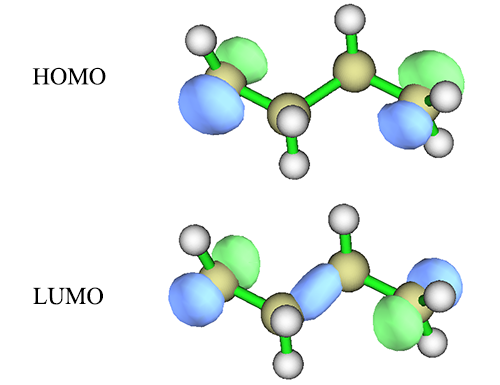
回想H2的成鍵軌道和反鍵軌道的形態,很明顯,這里HOMO就是分子兩端的單電子軌道以相位相同方式組合,而LUMO就是以相位相反方式組合產生的。因此將這兩個軌道弄進CAS(2,2)活性空間就可以至少定性正確描述這個雙自由基了。值得一提的是,LUMO軌道中在分子中間也出現了一坨,這和表現雙自由基關系不直接,但是問題不大,反正之后CASSCF還會對軌道變分。
這里我們就完整地算一下C4H8,看看它的雙自由基特征是多少。本文用的C4H8的結構:
C -0.74742092 1.77656753 0.00000000
H -0.62438907 2.32965189 0.92333358
H -0.62438907 2.32965189 -0.92333358
C -0.74742092 0.30933780 0.00000000
H -1.24978876 -0.09122321 0.88294562
H -1.24978876 -0.09122321 -0.88294562
C 0.74742092 -0.30933780 0.00000000
H 1.24978876 0.09122321 -0.88294562
H 1.24978876 0.09122321 0.88294562
C 0.74742092 -1.77656753 0.00000000
H 0.62438907 -2.32965189 -0.92333358
H 0.62438907 -2.32965189 0.92333358
整個過程是
第一步:#P HF/6-31G*
第二步:#P CAS(2,2)/6-31G* guess=read
我們做CASSCF時不需要調換軌道順序,因為HOMO和LUMO就是要用的兩個軌道。輸出的信息中看到
Configuration 1 Symmetry 1 10
Configuration 2 Symmetry 4 ab
Configuration 3 Symmetry 1 01
以及
( 1) EIGENVALUE -156.0256130028
( 1) 0.7961444 ( 3)-0.6051067 ( 2) 0.0000000 (
其中組態1就是ψG,組態3就是ψD。c1=0.7961444,c2=-0.6051067,故此體系的雙自由基特征=2*(-0.6051067)^2=0.732。
2.3 用UHF的自然軌道做CAS
也經常有人用非限制性計算(UHF/UDFT)得到的自然軌道作為CASSCF的活性空間的軌道算雙自由基,這種軌道稱為UNO (UHF natural orbital)。這里也用C4H8來演示一下。如果不熟悉怎么用非限制性計算來計算雙自由基,務必先看看《談談片段組合波函數與自旋極化單重態》(http://www.shanxitv.org/82)。
我們先看看UNO軌道形狀是什么樣。先用#P UHF/6-31G* guess=mix計算來得到對稱破缺波函數,此時UHF波函數就存到了check文件里,然后再用#P HF/6-31G* guess=(naturalorbitals,read,save,only)算一次。這說明,從check里讀取波函數(read),轉化成無自旋自然軌道(naturalorbitals),保存到check文件里(save),然后任務就停掉(only)。之后把chk文件轉化成fch,用文本編輯器打開fch文件,把第一行內容改為saveNO,再用Multiwfn打開此fch文件并進入主功能0。在圖形窗口上方選orbital info.-show all,我們看到UNO軌道信息
...[略]
Orb: 13 Ene(a.u./eV): 0.000000 0.0000 Occ: 1.996827 Type: A+B
Orb: 14 Ene(a.u./eV): 0.000000 0.0000 Occ: 1.996534 Type: A+B
Orb: 15 Ene(a.u./eV): 0.000000 0.0000 Occ: 1.996049 Type: A+B
Orb: 16 Ene(a.u./eV): 0.000000 0.0000 Occ: 1.123073 Type: A+B
Orb: 17 Ene(a.u./eV): 0.000000 0.0000 Occ: 0.876927 Type: A+B
Orb: 18 Ene(a.u./eV): 0.000000 0.0000 Occ: 0.003951 Type: A+B
Orb: 19 Ene(a.u./eV): 0.000000 0.0000 Occ: 0.003466 Type: A+B
...[略]
(注:如果不把fch文件開頭改成saveNO,那么占據數就會顯示到能量ene那列去,如果只是為了看軌道倒是無妨,但如果還想用Multiwfn計算性質,如密度、靜電勢、ELF等,結果就錯了)
從輸出信息中看到,<=15號的UNO差不多都是雙占據軌道,>=18號的幾乎都是零占據的虛軌道。而RHF計算時原本是HOMO和LUMO的16、17號軌道現在占據數明顯偏離整數,如下一節所示,這正是雙自由基體系的明顯特征。來看看它們的形狀
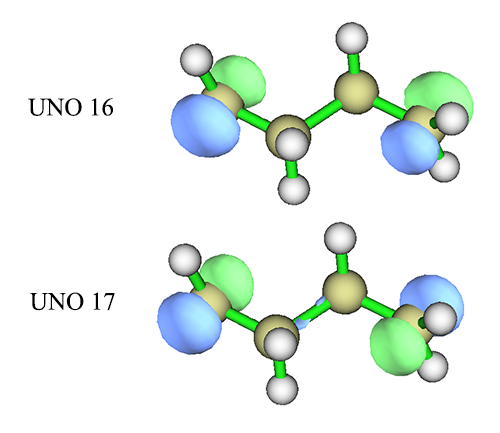
對比HOMO和LUMO的圖,會看到其實UNO 16和HOMO沒明顯差別,UNO 17和LUMO的主要差異在于分子中間的那一坨多余的區域沒了(isovalue設小后還是會看到它的存在,只不過數值減小了很多),因此更純粹地表現出分子兩端的單電子軌道的組合。對于其它體系可能分子軌道和UNO的差異更大,如果屆時從分子軌道中不好找出合適的用于CASSCF活性空間的軌道,就可以考慮用UNO。
接下來用#P CAS(2,2)/6-31G* guess=read做計算即可,這些UNO就被用作初猜軌道了,且UNO 16、17都處在活性空間。結果和上一節基于MO來做是一致的。
上面用UNO做CAS計算共經歷了三步:
#P UHF/6-31G* guess=mix
#P HF/6-31G* guess=(naturalorbitals,read,save,only)
#P CAS(2,2)/6-31G* guess=read
實際上可以化簡為兩步
#P UHF/6-31G* guess=mix
#P CAS(2,2,UNO)/6-31G* guess=read
這代表,做CASSCF的時候,先從check文件中讀取上一步的UHF波函數,自動轉化為UNO,然后再用它作為CASSCF的初猜。
這里都是假定與HOMO、LUMO編號對應的那兩個UNO是要被納入活性空間的,但如果和實際情況不符,要取的是別的UNO,那么應該用guess(read,alter)來調換UNO軌道順序,就像平時調換MO順序做CASSCF那樣。(無論是兩步方法還是三步方法,都是這么用alter調換UNO順序)
大家若有興趣,可以在CASSCF做完之后觀看一下chk里的軌道,會發現CASSCF優化出的16、17號軌道相較HOMO、LUMO,和UNO 16、17號在形狀上明顯更為接近,故此例使用UNO比用MO作為CASSCF初猜軌道可能更有優勢。不過,如果基于MO做CASSCF就能正常收斂,如C4H8,其實沒必要非得用UNO。
3 UHF波函數的雙自由基特征
這里只討論UHF的情況,UDFT的情況在處理上是完全一致的。
由于雙自由基是單重態的,直接用UHF的結果和RHF是相同的,必須用guess=mix等關鍵詞獲得對稱破缺解,這在《談談片段組合波函數與自旋極化單重態》(http://www.shanxitv.org/82)已經談了很多了,這里不再累述,只著重說說怎么計算UHF波函數的雙自由基特征。
UHF波函數下,雙自由基特征可以基于三種方法來計算:
(1)基于alpha和beta軌道重疊來計算
(2)基于<S^2>來計算
(3)基于UNO占據數來計算
對于H2這種理想體系,沒有其它軌道影響,這三種形式是等價的,而實際情況由于其它軌道的影響,三種方式計算結果會有一定的差異。下面就分別談談這三種計算方式,并且用C4H8作為實例。
3.1 基于alpha和beta軌道重疊來計算
UHF波函數中alpha軌道彼此間是正交歸一的,beta軌道彼此間也是正交歸一的,但是alpha和beta軌道之間并非總是正交歸一。對于雙自由基體系,我們可以看成RHF波函數原本的一個雙占據軌道(通常是HOMO)發生了分裂,形成空間分布并不重合的一個alpha軌道和一個beta軌道。二者空間分布分離越大,顯然雙自由基特征越強,這可以用它們重疊積分來衡量。
基于自旋投影UHF理論,Chem. Phys. Lett., 33, 330 (1975)中給出了UHF波函數雙自由基特征表達式
y=1-(2*T)/(1+T^2)
其中T是空間發生分離的那一對兒alpha和beta軌道間的重疊積分。這個表達式和前面的y=2*c2^2形式是內在對應的。
用Multiwfn可以計算這個重疊積分。我們先用#P UHF/6-31G* guess=mix計算體系得到對稱破缺波函數,并獲得fch文件,載入進Multiwfn后進入主功能100,再進功能5,選選項2,我們就得到了每個alpha軌道和序號對應的beta軌道的重疊積分:
...[略]
Overlap between the 13th alpha and beta orbitals: 0.986728
Overlap between the 14th alpha and beta orbitals: -0.961990
Overlap between the 15th alpha and beta orbitals: -0.995562
Overlap between the 16th alpha and beta orbitals: 0.042710
Overlap between the 17th alpha and beta orbitals: 0.149644
Overlap between the 18th alpha and beta orbitals: 0.939765
...[略]
(注:Multiwfn里beta序號在alpha序號之后。載入文件后屏幕提示從77號軌道開始是beta軌道,因此在主功能0看第16號beta軌道應該選77+16-1=92號軌道)
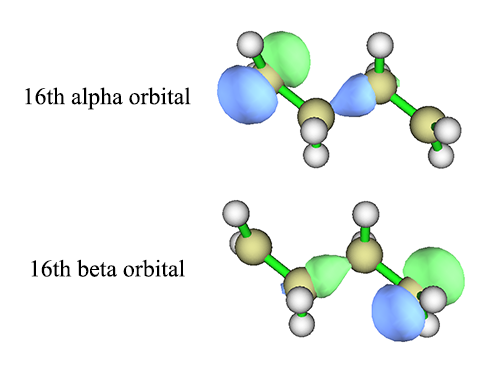
把T=0.042710代入y表達式,得到雙自由基特征為0.915,比2.2節基于CAS(2,2)波函數得到的0.732大不少。
3.2 基于<S^2>來計算
波函數的自旋平方算符期望值<S^2>和精確值S^2_Exact=S(S+1)之間有如下關系(見Szabo的Modern quantum chemistry p107)
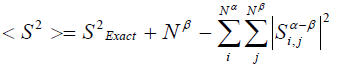
其中Nα和Nβ分別是alpha和beta電子數,S_ij是i號alpha和j號beta軌道重疊積分。由此式可見,如果每個alpha占據軌道都能和一個beta占據軌道唯一地匹配(積分值為1)而和其它的正交(積分值為0),那么<S^2>就是精確值S^2_Exact,RHF、ROHF波函數就屬于這種情況。而對于UHF計算,只要由于自旋極化導致alpha和beta占據軌道分布發生分離,那么<S^2>肯定會偏離精確值,這就是常說的UHF波函數的自旋污染問題。
假設只考慮對應單電子的那一對兒alpha和beta軌道而忽略其它的,上式可簡化為
ΔS^2=<S^2>-S^2_Exact=1-T^2
值得一提的是,雙自由基體系S^2_Exact=0,因此對于理想雙自由基,即T=0的情況,<S^2>應為1。
將T=√(1-ΔS^2)代入3.1節y的表達式,就可以得到基于<S^2>與精確值偏差量ΔS^2的雙自由基特征表達式
y=1-2*√(1-ΔS^2)/(2-ΔS^2)
不過這個式子往往沒法用。比如C4H8這個體系在#P UHF/6-31G* guess=mix計算后輸出的<S^2>=ΔS^2=1.0142,代入y表達式的話,根號里就成負值了。這是由于其它alpha和beta軌道間也出現了一定的分離,明顯影響了體系的<S^2>所致,只考慮一對兒alpha和beta軌道不合適。
3.3 基于UNO占據數來計算
重疊積分T和UNO占據數也有直接聯系。設只考慮對應單電子的那一對兒alpha和beta軌道而忽略其它的,則編號對應HOMO和LUMO的UNO的占據數(記為n_HOMO和n_LUMO)將分別為1+T和1-T,故T=(n_HOMO-n_LUMO)/2。因此,我們可以通過UNO占據數獲得T再獲得y。對于理想雙自由基,n_HOMO和n_LUMO都將為1。
2.3節中我們已經看到了C4H8的UNO占據數了,n_HOMO=1.123073,n_LUMO=0.876927,故T=0.123,y=0.758。和3.1節直接通過重疊積分算出來的0.915有不小差別,這是因為這里得到自然軌道占據數的時候把其它軌道的影響也納入進去了,結果倒是比較接近于CAS(2,2)得到的0.732。因此,如果不想做CAS,而想基于方便快速的UHF波函數來定量考察雙自由基特征的話,通過UNO占據數計算是比較理想的選擇。C4H8的0.7幾的雙自由基特征說明此體系是較明顯的雙自由基,盡管alpha和beta單電子分布還沒有完全分離,離理想雙自由基還有點距離。
實際上,只需要UNO占據數的話,并不需要2.3節那么多關鍵詞而且分兩步,只需要用#P UHF/6-31G* guess=mix pop=NO算一次就夠了,會看到這樣的輸出
16 17 18 19 20
Eigenvalues -- 1.12307 0.87693 0.00395 0.00347 0.00317
1 1 C 1S 0.01911 0.00845 -0.07955 0.10559 -0.08133
2 2S -0.04188 -0.01951 0.15207 -0.21148 0.16843
Eigenvalues便是這些UNO的占據數,即UHF無自旋密度矩陣的本征值。
4 雜談
相對于用CASSCF計算雙自由基,UHF雖然不如它準確,但好處是快、方便,而且有自旋密度,通過自旋密度能直接看到未成對兒alpha和beta電子分布,只要在Multiwfn里進入主功能5后選自旋密度然后按提示操作就能得到自旋密度等值面圖,單電子在什么位置一目了然。而CI波函數雖然精確、完美表現了兩個單電子處于自旋相反的狀態,但是卻得不到自旋密度。
如3.2節的<S^2>公式可見,只要用UHF描述雙自由基,就一定會出現自旋污染,而且對于理想雙自由基偏差值高達1.0,于是就總有人盲目地批判UHF/UDFT有自旋污染,好像偏差值這么大就根本不能用似的,這是大錯特錯!<S^2>與理想值偏差大,雖然意味著波函數與真實波函數偏差大,但并不意味著能量不合理!對于H2完全解離這樣的理想雙自由基,UHF和FCI結果是一致的,盡管前者表面上看自旋污染達到1.0已經大得要命了。自旋污染對于DFT波函數更是難以討論,本來DFT引入波函數的初衷就是為了獲得可靠的動能密度而不是構造真實的波函數,故不應當根據波函數的合理性來討論DFT結果的合理性。從實效上來講,UDFT計算雙自由基還是不錯的。