談談片段組合波函數與自旋極化單重態
談談片段組合波函數與自旋極化單重態
文/Sobereva @北京科音
First release: 2011-Apr-4 Last update: 2019-Apr-1
本文主要討論片段組合波函數的意義、用處,并結合實例介紹在Gaussian中的用法。由于片段組合波函數最重要用處之一就是計算自旋極化單重態體系,而且自旋極化單重態問題本身也很值得說說,所以將之一并討論。文末對初學者常問的“量子化學計算中如何設定原子/片段的電荷?”問題結合本文內容進行了討論。本文只涉及單行列式波函數(HF/KS-DFT波函數)。
1 片段組合波函數的含義
“片段組合波函數”具體來說是由整個體系內各個片段在孤立狀態時的波函數組合出的波函數。比如H2O---HF這樣的復合物體系,若將H2O和HF視為兩個片段,那么此體系的片段組合波函數就是由一個孤立的H2O的波函數和一個孤立的HF的波函數組合出來的。對于只由強化學鍵構成的體系也可以劃分,比如NH3BF3可以劃分成NH3和BF3。一個體系怎么劃分成片段要看目的是什么,要選擇最有意義的劃分,這在后文的例子中會體現出來。需要注意的是,所謂的“孤立狀態”是指片段內原子感受不到任何其它原子的情況,但是片段的結構和朝向必須與在分子中完全一致,否則組合出的波函數沒有意義。單行列式波函數情況下片段波函數很容易進行組合,這里介紹最簡單的方法。比如一個體系被5個基函數χ1,χ2...χ5所描述,也因此有5條分子軌道(本文分子軌道都是指自旋軌道,后同),前3條是有電子占據的。假設將此體系劃分為兩個片段A和B,分別以前2個和后3個基函數描述,也因此分別含2和3條分子軌道,并假設A中第1條和B中前2條分子軌道是占據的。A的第i條分子軌道寫為
ψA(i)=C_A(1,i)*χ1+C_A(2,i)*χ2,其中C_A(m,n)是第n條軌道向m基函數的展開系數。
B的第i條分子軌道寫為
ψB(i)=C_B(3,i)*χ3+C_B(4,i)*χ4+C_B(5,i)*χ5,其中C_B意義如同C_A
那么由A、B組合出的整體的波函數的5個分子軌道就可寫為
Ψ(1)=ψA(1)+0*χ3+0*χ4+0*χ5 //由A的1號軌道(占據)擴展
Ψ(2)=0*χ1+0*χ2+ψB(1) //由B的1號軌道(占據)擴展
Ψ(3)=0*χ1+0*χ2+ψB(2) //由B的2號軌道(占據)擴展
Ψ(4)=ψA(2)+0*χ3+0*χ4+0*χ5 //由A的2號軌道(虛)擴展
Ψ(5)=0*χ1+0*χ2+ψB(3) //由B的3號軌道(虛)擴展
可見,所謂的組合就是把片段的分子軌道的維數擴展到整個體系的情況然后放在一起而已。比如ψA(1)原先只用χ1,χ2,χ3表達,由于整體的軌道需要用1~5號χ一起來展開,擴展到整體后,即Ψ(1),就把χ4和χ5也加進去,其系數簡單地設為0。要注意的是空軌道和占據軌道順序不能錯,整體的前3條軌道是占據的,所以必須由A和B的占據軌道擴展得到,而這三條軌道間的順序是無所謂的。而整體的后2條是空的,就由A和B的空軌道擴展得到,同樣這兩條軌道間的順序是隨意的。
這樣組合成整體后,A的2個電子和B的3個電子在形式上構成了全同粒子,由于它們一起被整體的單行列式波函數所描述,所以它們之間滿足了反對稱原理。但是這個波函數中,A和B的軌道波函數(或者說其電子密度分布)仍然完全分別定域在A和B的區域內,因為它們在對方的基函數上系數是0。如果以這個片段組合波函數作為整體SCF計算的初猜波函數,這5個目前定域的軌道就有可能隨著迭代逐漸弛豫開,最終離域到整體各個部分上。
2 片段組合波函數的用處
片段組合波函數主要用途有三:(1)對于弱相互作用體系生成高質量初猜波函數。每個分子在復合物中的狀態與在孤立狀態下較為接近,所以如果已經有現成的單體的波函數,將之組合得到的復合物的初猜波函數質量會比直接讓量化程序初猜的要高,在計算時SCF所需迭代次數會減少,節約了時間。體系越大,相互作用越弱時優勢會越明顯。
(2)用片段組合波函數做為初猜的整體的SCF迭代過程正是電子密度在各個片段間轉移以及其分布發生極化的過程,所以用最后一輪迭代的能量減去第一輪迭代的能量就能獲知電子轉移和極化造成的能量降低。
(3)使波函數收斂到期望的態。SCF過程如同幾何優化,會收斂到離初猜最近的參數空間的極小點(和具體收斂方法的選擇有關),用默認的初猜波函數往往收斂不到能量最低的態或有特定特征的態,此時需要人為對其進行調整,例如常見的根據對稱性調換占據軌道與虛軌道,調整各片段的電荷和自旋方向構建整體初猜也是方法之一,這對于計算自旋極化的單重態特別有用,將在下面討論。
3 自旋極化單重態的含義
對于單重態,一般用限制性方法計算,即alpha和beta軌道完全匹配,自旋密度處處為0;對于多重態,一般用非限制性方法計算,即alpha和beta軌道允許不匹配,不匹配程度(或稱自旋極化程度)一般用它們之間重疊積分偏離1的程度衡量,這里暫不考慮限制性開殼層方法。還有一類特殊的單重態,即自旋極化單重態,它是指體系自旋多重度為1,但是自旋密度并不處處為0的態,有的地方alpha電密度大,有的地方beta電子密度大。計算這種態顯然不能用限制性方法,如果基態是這種態,則將得不到真正基態,而必須用非限制性方法。然而,直接用非限制性方法的結果和限制性計算是一樣的,因為量子化學程序會將這種體系按照一般單重態處理,默認的初猜波函數中alpha與beta軌道完全匹配,在迭代過程中由于并沒引入導致自旋極化的因素,所以即便允許alpha和beta軌道波函數相互獨立,收斂后的結果還是完全匹配的。因此,就必須人為地提供一個合適的自旋極化的初猜波函數才能收斂到真正基態。自旋極化單重態也經常叫對稱破缺態,這是因為對稱破缺態是指波函數對稱性低于當前分子結構的對稱性,自旋極化單重態總伴隨對稱破缺的出現,而出現對稱破缺又必然存在自旋極化,所以除了個例,二者指的是同一種態。在下文中涉及穩定波函數時“極化”和“破缺”不加區別地使用,只有在談到初猜時才會區分。遇見一個新穎的,且確定是單重態的體系,如果沒有經驗或證據判斷是否它的基態是自旋極化態,可以在限制性方法計算后進行波函數優化,程序會尋找能量更低的態,包括嘗試破壞對稱性,如果找到了(稱存在RHF->UHF不穩定性),說明自旋極化態才是基態。但是如果沒找到,也不能說非自旋極化態一定就是基態,波函數優化并不能保證獲得參數空間最小點,有可能通過調整初猜后能得到能量比非自旋極化態更低的自旋極化態。應指出的是未必得到了一個自旋極化態就能說它是基態,有的體系存在多個自旋極化態,比如雙核配合物體系中兩個金屬既可能是高自旋耦合也可以能是低自旋耦合。需要注意,本文在說到判斷基態時假設所用的理論方法是可靠的,基組有足夠質量,否則沒有意義,比如HF在小基組時有過度發生自旋破缺的傾向,而在一些純DFT泛函(如BLYP)下往往RHF穩定性過強,該破缺時卻又不破缺。
這里舉幾個重要的自旋極化單重態的例子:(1)雙自由基。兩個單電子間作用不強時單重態往往比三重態能量要低。比如·CH2-CH2-CH2·、·O-O-O·,兩邊的單電子自旋相反。(2)反鐵磁性耦合配合物。比如Mn2O2(NH3)8,基態是中性單重態,而兩個Mn(II)在形式上都有5個d單電子,且在二者上的自旋相反。(3)共價鍵被拉長的情況。在共價鍵處于平衡位置附近體系可完全以限制性波函數描述,而當拉長到一定距離后(稱為不穩定點),對稱破缺態的能量將比非破缺態要低。(4)矩形有限尺寸石墨納米帶,見后文的例子。更多的例子參看《談談自旋密度、自旋布居以及在Multiwfn中的繪制和計算》(http://www.shanxitv.org/353)和《詳談使用Gaussian做勢能面掃描》(http://www.shanxitv.org/474)。
4 計算自旋極化單重態的方法
用HF、DFT計算自旋極化單重態需要在非限制性計算時給出一個合適的自旋極化、對稱破缺的初猜,方法有很多,這里談一下方法。(1)混合HOMO與LUMO
電子密度的極化可以視為占據軌道與虛軌道混合產生的,所以讓初猜出現自旋極化就是讓初猜的alpha密度和beta密度發生不同的極化,最簡單的方法是通過HOMO與LUMO軌道混合來實現,這一般也使其對稱性得以破壞。在Gaussian中可以用guess=mix關鍵詞實現。通過UHF/STO-3G下H2分子很容易說明其原理,這里鍵長設為1.5埃,已經超過了不穩定點。使用guess=only pop=full會看到初猜中alpha和beta軌道彼此都是相同的,兩個基函數上系數在HOMO相等而在LUMO上相反,軌道對稱性符號也給了出來。
1 2
(SGG)--O (SGU)--V
Eigenvalues -- -0.28527 -0.05493
1 1 H 1S 0.63075 0.82022
2 2 H 1S 0.63075 -0.82022
使用guess(mix,only) pop=full會看到HOMO與LUMO混合后的初猜
Alpha Molecular Orbital Coefficients:
1 2
O V
Eigenvalues -- -0.28527 -0.05493
1 1 H 1S 1.02598 0.13398
2 2 H 1S -0.13398 -1.02598
Beta Molecular Orbital Coefficients:
1 2
O V
Eigenvalues -- -0.28527 -0.05493
1 1 H 1S -0.13398 1.02598
2 2 H 1S 1.02598 -0.13398
此時是對稱破缺的,對稱性符號不再顯示,且alpha和beta軌道不再相同。通過觀察可知是這些軌道是這樣由原先HOMO與LUMO混合而得的:
ψα_HOMO=ψ_HOMO+ψ_LUMO
ψα_LUMO=ψ_LUMO-ψ_HOMO
ψβ_HOMO=-(ψ_LUMO-ψ_HOMO)
ψβ_LUMO=-(ψ_HOMO+ψ_LUMO)
注意系數必須經過重新歸一化。例如對于ψα_HOMO,將ψ_HOMO和ψ_LUMO的系數加和后為(1.45097,-0.18947),通過iop(3/33=1)的輸出可知兩個基函數的重疊積分為0.256786,所以此時ψα_HOMO的模方的全空間積分值為1.45097^2+(-0.18947)^2-2*1.45097*0.18947*0.256786=2.00002,故ψα_HOMO的歸一化系數為1/√2.00002,將1.45097和-0.18947都乘上此值就得到了歸一化后的ψα_HOMO,與Gaussian輸出中一致。
用默認初猜時UHF的收斂結果中Mulliken自旋密度布居在兩個氫上都為0,且Mulliken總密度布居也都為0。這是由于在初猜中alpha占據軌道和beta占據軌道等價,且在兩個氫上系數相等,由于迭代中沒有引入破壞對稱和非自旋極化的因素,在收斂時仍然會保持這種狀態。使用guess=mix后收斂到了對稱破缺態,自旋布居分別為0.862525和-0.862525。從前面列的系數可見,初猜中alpha和beta電子分布已經不相等了,前者和后者分別主要聚集在第一個氫和第二個氫上,而且的確對稱破缺態是能量最低的態,所以最終會收斂到這種態。當然,如果鍵長沒有超過不穩定點,即對稱態是最穩定的,那么即便用了guess=mix,經過迭代后還是收斂到對稱態,和使用RHF結果一樣。
PS:還可以討論一種假想態,盡管在無外電場時它不會在實際出現(此時也收斂不到這種態),即對稱破缺但不自旋極化的態。對于H2,也就是讓ψα_HOMO=ψβ_HOMO=ψ_HOMO+ψ_LUMO,ψα_LUMO=ψβ_LUMO=ψ_LUMO-ψ_HOMO,此時自旋密度各處皆為0,但是電子聚集在第一個氫上。以它為初猜在UHF迭代后,由于沒有引入導致自旋極化的因素,得到的還是RHF那樣的對稱、非極化態。當然還可以考慮自旋極化而對稱的初猜,比如alpha密度集中在兩個氫中央,而beta密度均等分布在H2的兩個端點區域,在迭代后還是也得不到期望的態,因為對稱性不會自發地破壞。所以guess=mix的關鍵有兩點,一是使HOMO與LUMO混合而破壞初猜對稱性,二是對于alpha和beta軌道采用不同方式混合,以使初猜出現自旋極化。
guess=mix的使用很傻瓜化,在很多時候都能收斂到期望的自旋極化單重態,每次碰見一個新體系時可以先用它試一下,但它并非總是奏效,屆時需要其它方法構建更接近期望的態的初猜。
(2)利用片段組合波函數
這種方法雖然沒(1)方便,但是可以人為控制,效果往往更好。從09版開始,Gaussian可以直接生成片段組合波函數,結合GaussView使用起來很方便,用法將在下面介紹。注意Gaussian用的組合方法和前述并不完全相同,但意義類似。
通過筆者開發的Multiwfn(http://www.shanxitv.org/multiwfn)可以將多個算好的片段的輸出文件里的波函數信息按照前述方法進行組合,并生成一個整體帶有初猜波函數信息的Gaussian輸入文件,初猜波函數在任務開始時會被guess=cards關鍵詞讀取。具體詳見Multiwfn手冊3.100.8節,利用這個做法還可以實現做能量分解的目的。
(3)利用stable=opt關鍵詞
還有一種計算自旋極化單重態的方法是用stable=opt關鍵詞,代表程序會自動做波函數穩定性測試,如果發現不穩定,就通過特殊的算法試圖優化到更穩定的波函數。比如體系實際上是雙自由基,但是目前是使用對應計算閉殼層的關鍵詞計算,算完之后通常stable測試會表示此波函數不穩定,自動優化出來的波函數通常就對應于當前體系的基態波函數,也即自旋極化單重態波函數了。此做法比起guess=mix耗時得多,但得到對應基態的自旋極化單重態的幾率往往更大。注意stable=opt也不是什么時候都奏效。另外,stable=opt和做幾何優化的關鍵詞opt完全八竿子打不著,前者優化的是當前結構下的波函數,后者優化的是幾何結構。
一般來說,算自旋極化單重態體系,我比較建議先嘗試比如# UB3LYP/6-31G* guess=mix nosymm stable關鍵詞,因為又快又省事,如果提示波函數是穩定的,而且自旋密度確實不是處處為0(怎么繪制自旋密度看http://www.shanxitv.org/353),那就OK了。如果提示不穩定,改用# UB3LYP/6-31G* guess=mix nosymm stable=opt再試,一般都能成功找到最穩定基態對稱破缺波函數。這里nosymm要求Gaussian計算時不利用對稱性,碰見有對稱性的體系的時候這么做會更穩妥。但對于像反鐵磁性耦合這種配合物體系,我更建議用片段組合波函數的做法,這樣可控性更強。片段組合波函數的用法下文有具體例子。
5 使用Gaussian通過片段組合波函數計算自旋極化單重態實例
構建的片段組合波函數應當盡可能接近預期的態,這樣才能收斂到且較快地收斂到相應態。這里先以計算C2h對稱性的單重態雙自由基·CH2-CH2-CH2-CH2·為例來說明這一點以及在Gaussian中的操作,實際上此例用guess=mix也能實現目的。這里假設結構式左邊的小點是alpha單電子,右邊的是beta單電子,因此為了構建合適的初猜,就要讓左邊的·CH2-CH2-片段富集alpha電子,應當在計算它時讓它帶著兩個未成對alpha電子。因為這樣可以期望其中一個alpha電子定域在小點那里,而另一個alpha電子定域在劃分片段時斷裂的C-C鍵的位置。同理對于右邊的-CH2-CH2·片段,就讓它帶著兩個未成對的beta電子。這樣兩個片段波函數組合在一起時,按照價鍵理論的觀點,未成對的alpha和beta電子在劃分片段處就恰好接上而恢復C-C鍵了,而左右兩個小點處就正好是一個alpha一個beta電子了,非常理想。首先在GView里編輯好分子結構,然后進入Edit-Atom Group,將兩個片段的Atom Tags、Spin Mult.、Unpaired Spins改成圖中這樣
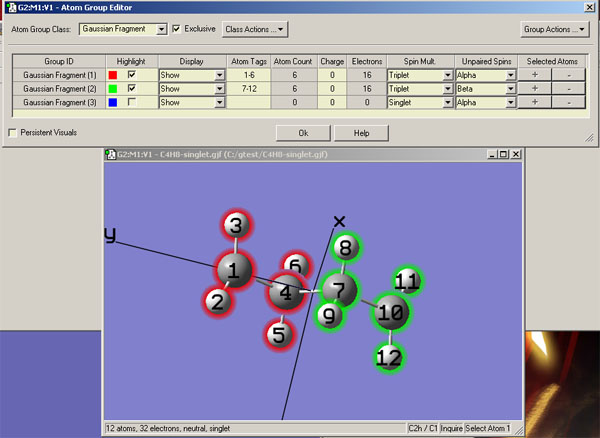
然后保存成gjf文件。適當修改后,最終輸入文件如下。
%chk=C:\gtest\C4H8-singlet.chk
# ub3lyp/6-31g(d) guess(fragment=2)
[空行]
Title Card Required
[空行]
0 1 0 3 0 -3
C(Fragment=1) 0.09727146 1.92239482 0.00000000
H(Fragment=1) 0.47392697 2.13428940 0.97885116
H(Fragment=1) 0.47392697 2.13428940 -0.97885116
C(Fragment=1) -0.55878611 0.59240328 0.00000000
H(Fragment=1) -1.16892856 0.49566725 0.87365029
H(Fragment=1) -1.16892856 0.49566725 -0.87365029
C(Fragment=2) 0.55878611 -0.59240328 0.00000000
H(Fragment=2) 1.16892856 -0.49566725 -0.87365029
H(Fragment=2) 1.16892856 -0.49566725 0.87365029
C(Fragment=2) -0.09727146 -1.92239482 0.00000000
H(Fragment=2) -0.47392697 -2.13428940 -0.97885116
H(Fragment=2) -0.47392697 -2.13428940 0.97885116
其中guess(fragment=2)說明體系包含兩個片段,并且執行生成片段組合波函數任務。每個原子所屬片段在原子名后面的括號里指定。也可以將所屬片段序號寫在坐標后面,比如 H -0.47392697 -2.13428940 -0.97885116 2。
0 1 0 3 0 -3部分代表:總電荷 總自旋多重度 片段1電荷 片段1自旋多重度 片段2電荷 片段2自旋多重度,如同Counterpoise任務的寫法。由于逗號和空格都是允許的分隔符,為了清楚起見,也可以寫為0,1 0,3 0,-3。如果片段的自旋多重度前面沒寫符號,就被認未成對電子是alpha自旋,如果寫了負號,就代表是beta自旋。此例片段1和2的未成對電子分別是兩個alpha和兩個beta,即自旋磁量子數分別是1和-1,兩片段組合在一起時相互抵消為0,故整體的自旋多重度為1。
Gaussian生成片段組合波函數的任務開始后,主要有以下步驟:
1 初猜整體波函數并做分析,但是不迭代
2 初猜片段1的波函數,進行SCF迭代,然后做分析
3 初猜片段2的波函數,進行SCF迭代,然后做分析
... (如果有更多的片段,將它們都類似地做完)
4 將片段波函數組合,然后寫入chk文件
如果運算開始時看到讀取電荷和自旋多重度時提示Charge and multiplicity card seems defective,但自己確信輸入是正確的,就不用管它。當程序提示Counterpoise: doing MCBS calculation for fragment X的時候,就說明開始處理第X個片段了。如果將此例的guess(fragment=2)寫成guess(fragment=2,only),則代表對每個片段都只初猜而不做SCF迭代,最后將各個片段的初猜波函數直接組成整體波函數,這樣可以明顯省時,但得到的整體波函數質量會差一些,不過一般來說并沒什么問題。所以我比較建議每次都寫上only。
現在開始計算自旋極化單重態·CH2-CH2-CH2-CH2·波函數。可以重新編輯一個新輸入文件,也可以直接把上面的輸入文件的route section改成
# ub3lyp/6-31g(d) guess=read nosymm
并進行運算(其它的都無需改動)。guess=read說明計算時從chk文件中讀取片段組合波函數作為初猜,nosymm讓程序在迭代過程中允許波函數對稱性的改變。迭代結束后,會看到Mulliken自旋布居在兩邊的碳上分別接近1和-1,說明這正是所希望的態,從Multiwfn繪制的自旋密度的等值面圖上能更直觀地驗證(等值面0.025,綠色和藍色分別代表正值和負值):
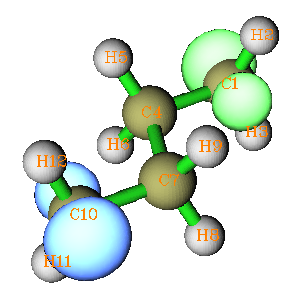
如果希望對自旋極化單重態進行優化,就直接在計算整體時寫上opt即可。默認情況是計算下一步結構時的初猜使用上一步結構的收斂波函數,因此自旋極化狀態會一直傳遞下去,除非優化到某步時波函數收斂到了非自旋極化狀態。上例可以加上stable關鍵詞確定波函數是否穩定,通過檢驗,收斂的波函數是穩定的。如果在RB3LYP下,或者直接用UB3LYP但不特意調整初猜,就會提示波函數存在不穩定性,如果用stable=opt讓程序自動找穩定波函數,最后也可以得到期望的自旋極化單重態,但是耗時遠比直接給出合適的初猜多得多。
筆者在《詳談使用Gaussian做勢能面掃描》(http://www.shanxitv.org/474)文中給出了好多個對共價鍵拉伸使之解離為雙自由基過程的計算例子,強烈建議大家仔細看看,即便你要做的不是掃描任務,看那些例子也會顯著加深對自旋極化單重態計算的理解。
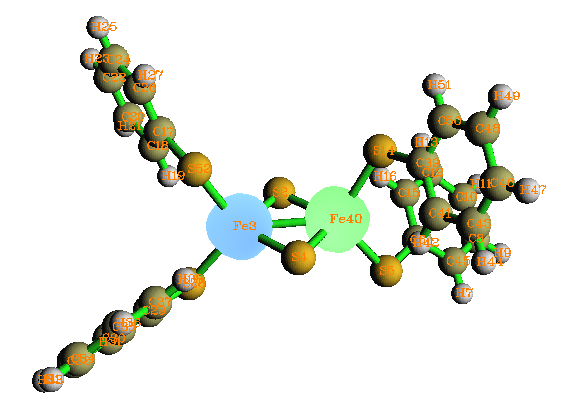
計算反鐵磁性配合物的片段設定稍復雜些,在官方網站有計算Mn2O2(NH3)8的實例http://gaussian.com/afc。另一個例子是Gaussian自帶測試任務中的test780,在手冊的Guess關鍵詞末尾也介紹了,這里稍微解析一下其片段設定的原理。這是個Fe2S2結合四個S-R配體的體系,兩個鐵被兩個硫橋連接。在片段設定中,兩個Fe被定義為兩個片段,電荷設為+3,自旋多重度分別設為6和-6,對應于5個alpha和5個beta自旋d電子;由于兩個硫橋不相連,所以定義為兩個獨立的片段,每個硫橋在形式上從兩個Fe獲得各一個電子,故電荷和自旋多重度都為-2和1。四個S-R定義成四個獨立片段,由于整體的電荷為-2,Fe2S2部分的電荷為+2,所以四個S-R配體電荷應為-1,此時電子為偶數個,又由于S-R與自旋極化沒直接關系,故自旋多重度設為1。最終得到的收斂波函數下的自旋密度圖如下,不同自旋的單電子的確富集在了兩個Fe上。
最后一個例子是矩形有限尺寸的石墨納米帶(GNR),它是一個矩形石墨片,邊界由氫原子飽和,當它的長寬大到一定尺度后,基態就成為自旋極化單重態,有興趣的讀者請參閱Phys.Rev.B 77,035411。能夠出現自旋極化單重態的最小的GNR稱Bisanthrene,它的基態自旋密度圖如下(泛函用的是HSE06,在Gaussian中寫作HSEh1PBE。6-31G*基組):
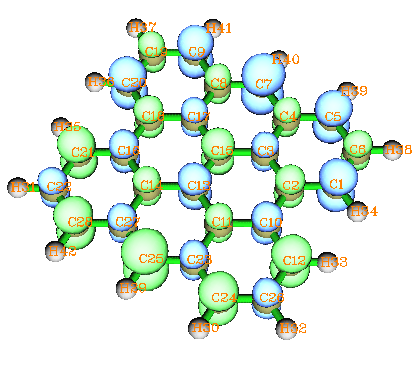
這種體系在設定初猜片段時似乎難以入手,不同自旋區域不相連而且數目眾多。實際上初猜沒必要很完美,往往只要引入一個對稱破缺及自旋極化的“因素”即可,隨著迭代的進行,破缺和極化因素將自動擴散,最終波函數將調整到最佳狀態。比如此例,可以只定義兩個片段,隨便取一個碳原子作為第一個片段(比如取C16),電荷設0,自旋多重度設成3,其余原子作為第二個片段,電荷和自旋多重度為0和-3。然后按照本節第1個例子的方法計算即可。為了節省生成片段組合波函數的時間,可以寫上SCF=sleazy,因為Gaussian默認用的是SCF=tight,往往比SCF=sleazy多花一倍時間迭代,而初猜波函卻又沒必要收斂得很精確。或者也可以嘗試直接在guess里寫上only省得對片段做SCF迭代了。順帶一提,此例直接用簡單的guess=mix經測試也能達到目的,可以省去生成片段組合波函數的步驟和時間,所以我建議總是先試試guess=mix,不行再考慮別的。
6 談談“量子化學計算中如何設定原子/片段的電荷?”
經常看到初學者在群里或論壇里問這個問題,鑒于此問題與本文有一定關系,就在此談談。問這種問題屬于量子化學知識完全沒有入門。
嚴格來說,量子化學計算中沒法設定原子/片段的電荷。因為在量子化學角度,所有原子/片段構成一個整體,薛定諤方程的求解是對整體而言的,沒有任何一個原子/片段是孤立的。從密度泛函的角度看,SCF迭代過程就是整體的電子密度的弛豫,是從不真實、非基態的分布調整到真實的、基態的分布的過程。雖然從技術上,利用拉格朗日乘子方法,可以使迭代過程中保持某個原子或片段的電荷為期望的數值(對于DFT而言也叫CDFT,詳見《談談約束性DFT (CDFT)》http://www.shanxitv.org/271),但是這樣做沒有太強的物理意義,并不能得到基態的能量和波函數。有些人受了形式電荷的誤導,以為原子電荷(或者分子復合物中的某個分子的凈電荷)應為整數,以為也只有算出來也是這樣時才正確,于是試圖這樣設定原子/片段電荷,實際上這樣做與初衷恰恰相反。實際電荷到底是怎么分布的,是做過量子化學計算得到了波函數/電子密度,然后再進行布居分析才知道的,顯然不是人為事先設定的。另外,計算出來的原子電荷和化合價、氧化態這樣經典概念的數值肯定會有很大偏差,看此文開頭的討論:《使用Multiwfn通過LOBA方法計算氧化態》(http://www.shanxitv.org/362)。
有人以為利用片段組合波函數的方式可以達到限定原子/片段的電荷及其上電子自旋的目的,于是在片段設定中將相應原子或原子團設為某種電荷和自旋多重度,實際上如上所述,這種想法本身沒有物理意義,而且將這樣的片段組合波函數作為初猜在實際計算中也達不到目的。比如前面提到的Fe2S2結合四個S-R配體的例子,盡管初態將Fe的電荷設為形式電荷+3,自旋多重度設為6,但SCF收斂后Fe的Mulliken電荷僅為+1.1,有3.3個未成對電子,說明Fe在此配合物中帶+3電荷、存在5個未成對d電子只不過是人為臆測罷了。在SCF迭代過程中,電子分布不斷弛豫,有不少電子從周圍轉移到了Fe(3+)上,并且有不少單電子從Fe上轉移走。當然有人會說Mulliken布居不合理,但是無論哪一種有一定根據、基于波函數及衍生性質(如電子密度、靜電勢)的布居方法都不可能得到那種臆測的結果。