談談約束性DFT (CDFT)

談談約束性DFT(CDFT)

First release: 2014-Dec-29 Last update: 2023-May-17

1 原理

經常有人，特別是初學者會問量化計算中如何設定原子的電荷，他們想讓某些原子或片段的電荷成為理想的整數。會問這個問題，大多都是對量化計算原理沒搞透徹所致，筆者在《談談片段組合波函數與自旋極化單重態》（http://sobereva.com/82）一文的最后一節對此有過專門的討論。一些初學者誤以為通過設定初猜、利用gview里的片段設定就能達到目的，顯然是錯誤的，不管初猜怎么定義，如果在SCF過程中不加約束的話，迭代至收斂后的電荷分布會和預期的初猜有明顯不同。若想令最終的電荷分布與自己設定的一致，唯一辦法就是在SCF迭代中進行約束，通常用的是拉格朗日乘子方法。對于DFT而言，這叫做約束性DFT(Constrained DFT, CDFT)，已經被廣泛使用。

如今CDFT的標準實現方法是在PHYSICAL REVIEW A 72, 024502 (2005)中提出的。它在對能量變分時引入拉格朗日乘子Vc使得電子分布與期望的狀態一致，這等價于在KS算符中額外引入了一個外勢項Vc*w(r)，其中w(r)是用來定義約束的權重函數。比如令w(r)為A原子的權重函數用來定義A原子所屬的空間范圍，那么就可以設定約束令w(r)*ρ(r)的全空間積分等于人為指定的A原子的電子數。在SCF迭代求解過程中，軌道和Vc交替優化。即每一步，先在當前的軌道下優化Vc直到滿足預設的約束條件，然后用Vc再構建KS算符產生新的軌道，如此往復。CDFT的過程，既可以看成是在約束條件下尋找能量最低的解，也可以視為尋找一個外勢，最終得到的是在這個外勢下的基態的解。

CDFT不僅可以約束某些原子的布居數等于特定值，也可以讓自旋布居數，即alpha和beta電子數的差值等于特定值（對alpha和beta布居數分別做約束），或者讓兩個片段間的電子布居數或自旋布居數的差值恰為特定值。權重函數也可以有多種選擇，而且原理上可以同時設定多個約束。

用CDFT時切不可盲目，一定要搞清楚原理，弄清楚自己使用CDFT的目的何在、所設定的約束有什么物理意義。CDFT用對了可以討論一些常規方式DFT計算研究不了的問題，比如討論某些電荷轉移、電子離域問題，但用得不合理得話只會得到毫無意義的結果。

2 NWChem中CDFT的使用

CDFT在NWChem、CP2K、Q-Chem、CPMD、GPAW、BigDFT、OpenMX等程序中都已經實現了。由于Q-Chem是收費的，下面就用免費的NWChem來演示一下CDFT。本文使用的是NWChem 6.5，編譯方法可參考《NWChem 6.6編譯方法》（http://www.shanxitv.org/270）。順帶一提，CP2K的CDFT功能明顯更為強大，對孤立體系和周期性體系都能用，可以計算CDFT下解析受力因而可以在CDFT下容易地做幾何優化和動力學，支持更穩健的Hirshfeld和Becke原子空間劃分方式，能基于CDFT得到的兩個單體間電荷轉移前后的兩個透熱態波函數計算單體間的電子耦合，支持做CDFT-CI，等等。筆者講授的北京科音CP2K第一性原理計算培訓班（http://www.keinsci.com/workshop/KFP_content.html）里對CDFT的背景知識有深入講授，對CP2K做CDFT給出了豐富的講解和例子，對CDFT感興趣者推薦參加。

NWChem里實現CDFT很簡單，在dft...end段落中加上比如cdft 2 5 charge 0.5 pop becke即設定2~5號原子的Becke原子電荷之和為0.5。也可以寫諸如cdft 2 5 10 13 charge 0.5 pop lowdin來讓2~5與10~13的Lowdin電荷差值為0.5。如果設定自旋布居數約束，把charge改為spin即可。NWChem的CDFT效率比較好，不比普通DFT計算多耗時多少。

注意計算原子電荷（或布居數）的方法很多，比如《原子電荷計算方法的對比》（http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml）一文就討論了很多種。因此，對于同一個約束條件，使用不同的布居分析方法最終得到的波函數并不相同。NWChem的CDFT支持Mulliken、Lowdin和Becke三種布居方法。默認是Lowdin，雖然從原理上并不比Mulliken可靠，但用在CDFT上比Mulliken要好不少，CDFT原文中也說了Mulliken布居下結果有問題。至于Becke布居，并不是嚴格定義的方法，它的合理性和銳度參數k以及選用的原子半徑密切相關，我不清楚NWChem內部是怎么具體設的，因此懷疑其可靠性。注意，Mulliken和Lowdin方法都不適合含有彌散函數的情況，此時要么去掉彌散函數，要么就只能用不怕彌散函數的Becke布居了。

碰見CDFT不收斂時，建議在dft...end里加入一行convergence nolevelshifting，如果還不行，可以嘗試其它布居方法，或者改改約束方式，或者改改基組和泛函。

NWChem中對電荷約束可以做幾何優化（且是解析梯度），對自旋約束不行。NWChem可以施加多個約束，不過正常收斂的幾率很低。使用Becke布居時，對于有對稱性的體系，如果計算時出現vectors were symmetry contaminated
，需要用noautosym關鍵詞避免使用對稱性，否則結果可能有問題或無法正常結束，使用Becke布居時幾乎總要加noautosym。用Becke布居時有時候并行運算沒法正常結束，此時應改用串行計算。

3 實例1：乙酸鈉

這是個最簡單的例子。我們先用以下輸入文件用NWChem算一下乙酸鈉在B3LYP/6-31G*下的能量以及原子電荷。結構已在此級別下優化過。
start
geometry
C                  0.00000000    0.52007900    0.00000000
O                 -1.13032800   -0.06349600    0.00000000
O                  1.11739200   -0.09103900    0.00000000
C                  0.03308100    2.04494400    0.00000000
H                  0.58076900    2.39854700    0.88048700
H                  0.58076900    2.39854700   -0.88048700
H                 -0.97577100    2.46220700    0.00000000
Na                -0.02552400   -1.94665100    0.00000000
end
basis
* library 6-31G*
end
dft
xc b3lyp
mulliken
end
TASK dft

得到的能量為-390.839634985795，Na的Lowdin布居數為10.63，對應于原子電荷為11-10.63=0.37。其數值與傳統化學概念上Na為1.0電荷相差不少，說明Na并沒有把一個電子完完全全給了CH3COO-，或者說CH3COO-的電子有一部分轉移向了Na+離子。

然后在dft...end當中插入
convergence nolevelshifting
cdft 8 8 charge 1.0
再次運算，從輸出文件中也可以看到此時Na的Lowdin布居數為10.0，即原子電荷確實為設定的1.0。并且能量為-390.589504441073，比之前沒加約束時高了656.7KJ/mol。

如果想優化的話，把TASK dft改為TASK dft optimize即可。

可見，我們可以通過CDFT和常規DFT計算的能量差，來討論離子之間或分子之間，電荷發生一定幅度轉移前后能量改變了多少。

4 實例2：叔丁基碳正離子

叔丁基碳正離子，即C(CH3)3+這個體系，一般畫結構式的時候正電荷都畫在中間的碳上，并認為這個碳用sp2雜化，垂直于碳平面的p軌道（以下簡稱pz軌道）是空著的。實際上這種說法完全忽略了三個甲基的電子向那個空pz軌道的離域。我們這里也算算玩玩。

運行以下輸入文件做常規B3LYP/6-31G*計算。體系結構已在此級別下優化。
start
charge 1
geometry
C                  0.00000000    0.00000000    0.00000000
C                  0.00000000    1.46600800    0.00000000
H                  0.58581400    1.81844700    0.86660600
H                  0.58581400    1.81844700   -0.86660600
H                 -0.99127200    1.92058400    0.00000000
C                 -1.26960000   -0.73300400    0.00000000
H                 -1.16763900   -1.81875900    0.00000000
H                 -1.86772800   -0.40189400    0.86660600
H                 -1.86772800   -0.40189400   -0.86660600
C                  1.26960000   -0.73300400    0.00000000
H                  1.28191500   -1.41655300    0.86660600
H                  1.28191500   -1.41655300   -0.86660600
H                  2.15891100   -0.10182600    0.00000000
end
basis
* library 6-31G*
end
dft
xc b3lyp
mulliken
end
TASK dft

能量為-157.554198182446，中心碳的Lowdin電荷為+0.30，可見，把1個正電荷畫在中心碳上的做法和實際的差距很大，那個正電荷明顯沒有完全定域在中心碳上。

然后在dft...end當中插入
cdft 1 1 charge 1.0
再次運算，看看人為讓一個正電荷定域在中心碳上的結果怎樣。結果為-157.460833435721，能量比不加約束時高了245.1KJ/mol。可以說，三個甲基的電子向中心碳離域，使得能量降低了245.1KJ/mol。此例表明恰當地利用CDFT可以用來計算離域化能。

需要特別注意的是，不同布居方法下得到的結果差異可能很大。比如此例，三種布居方法結果分別為
Mulliken -157.551751877858
Lowdin -157.460833435721
Becke -157.460056500370
Lowdin和Becke的差異不大，但Mulliken的數值卻不太合理，能量僅比不加約束時高了6.4KJ/mol，明顯偏小了。

CDFT計算時雖然使得中心碳的電荷為理想化的+1，但是，此時中心碳的pz軌道并非是空著的。如果在dft...end中使用
mulliken
print "mulliken ao"
來查看每個基函數的布居數的話，就會看到CDFT計算后中心碳的兩個pz基函數的Lowdin布居數之和為0.237，遠非為0，盡管比普通計算時的0.437有所減小。原理上講，CDFT也能使得某些基函數的布居數為指定的值，但是NWChem的CDFT尚不支持這種約束方式。

順帶一提，如果就是想考察周圍原子向中心碳的空pz軌道的離域的話，可以用NBO分析，計算當前體系會看到中心碳有個占據數為0.409的LP*軌道，這就對應于那個空pz（由于周圍電子已經明顯向此軌道離域了，所以其占據數遠比0大）。從E2分析中可以看到這三個甲基中都有兩個C-H鍵的BD軌道向此LP*有很強的超共軛作用，每對兒的E2作用能皆為11.5kcal/mol。雖然E2是不能簡單相加的，但是如果姑且這么算一下，3*2*11.5*4.186=288.8KJ/mol，倒也和CDFT給出的離域化能在數量級上相仿佛，但我認為有這種程度的相符多半是巧合。

5 實例3：LiF

這次我們計算LiF，令Li的Lowdin電荷逐漸從0變為1，步長0.05，看看能量是如何變化的。手寫那么多輸入文件顯然麻煩，我們用shell腳本來實現。把以下內容拷貝到一個文本文件里，然后執行之。

for ((i=0;i<=20;i=i+1))
do
chg=`echo "$i*0.05"|bc`
file=`printf "%4.2f\n" $chg`
echo processing $chg...
cat << EOF > LiF.nw
start
geometry
Li 0.00000000 0.00000000 1.52885
F 0.00000000 0.00000000 0.00000
end
basis
* library def2-svp
end
dft
XC b3lyp
convergence nolevelshifting
cdft 1 1 charge $chg
end
TASK dft
EOF
nwchem LiF.nw > $file.out
done

執行過后，就出現了0.00.out、0.05.out ... 1.00.out一系列文件，文件名就是約束的Li的電荷。然后運行
grep "Total DFT energy" *.out |tee t.txt
把t.txt用ultraedit等程序的列模式進行編輯，去掉多余的列，然后導入到origin里作圖，得到下圖（沒有0.9的值是因為此時計算沒有收斂）

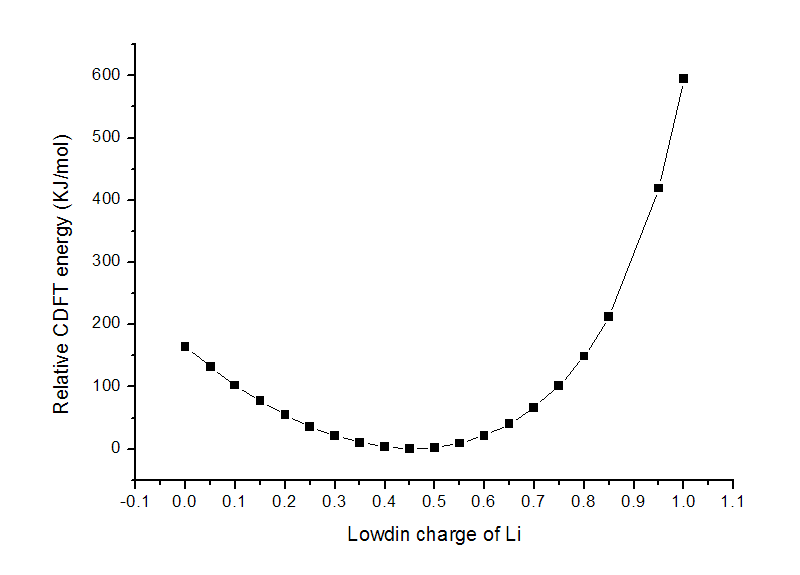
這個LiF體系正常DFT計算下Li的Lowdin電荷為0.46，這個數值也正是圖中的最低點，約束設定的電荷偏離這個值越大，顯然能量也越高，圖中很好地表現了這點。

如果將Li的電荷約束為1.0并進行優化，鍵長會由1.52885埃增加到1.84477埃。雖說經過優化，CDFT能量有所降低，為-107.12133927a.u.，但也比不加約束時在平衡結構時的-107.33859717a.u.要高得多。

6 實例4：C4H8雙自由基

雙自由基的對稱破缺DFT計算，在《談談片段組合波函數與自旋極化單重態》（http://sobereva.com/82）談了很多了，CASSCF計算在《CASSCF計算雙自由基以及雙自由基特征的計算》（http://sobereva.com/264）中也談了很多了，都用到了C4H8雙自由基這個例子，不熟悉的話建議先看看。

C4H8雙自由基直接用對稱破缺B3LYP/6-31G*計算的話，末端兩個碳的Lowdin自旋布居分別為0.919和-0.919。這里我們通過CDFT計算，讓這兩個碳原子自旋布居數之差恰為2.0。運行以下輸入文件。odft必須寫，否則會被當成閉殼層單重態計算。由于是對稱破缺計算而當前體系又有對稱性，故應當寫noautosym避免使用對稱性。
start
geometry noautosym
C                 -0.74400100    1.78566400    0.00000000
H                 -0.60282700    2.33865300    0.92499500
H                 -0.60282700    2.33865300   -0.92499500
C                 -0.74400100    0.30988100    0.00000000
H                 -1.25452600   -0.08746700    0.88463900
H                 -1.25452600   -0.08746700   -0.88463900
C                  0.74400100   -0.30988100    0.00000000
H                  1.25452600    0.08746700   -0.88463900
H                  1.25452600    0.08746700    0.88463900
C                  0.74400100   -1.78566400    0.00000000
H                  0.60282700   -2.33865300   -0.92499500
H                  0.60282700   -2.33865300    0.92499500
end
basis
* library 6-31G*
end
dft
xc b3lyp
odft
mulliken
cdft 1 1 10 10 spin 2.0
end
TASK dft
此例約束了兩個末端的碳的自旋布居之差為2.0，由于體系本身就是對稱的，這使得其中一個碳的自旋布居數恰為1.0，另一個為-1.0。從輸出的Lowdin自旋布居上可以確認這一點。

我們也可以通過設定多個約束讓體系末端兩個CH2的自旋布居數分別為1和-1，即約束設定改為
cdft 1 3 spin 1.0 pop becke
cdft 10 12 spin -1.0 pop becke
（Mulliken和Lowdin布居時這種約束設定下無法正常計算，故改用Becke布居）

7 實例5：H+ H-體系

最后，我們用CDFT和背景電荷兩種辦法計算一下H+ H-這個體系，相距5埃。NWChem輸入文件如下
start
geometry noautosym
H 0.00000000 0.00000000 0.00000000
H 0.00000000 0.00000800 5.00000000
end
basis
* library 6-31G*
end
dft
xc b3lyp
cdft 1 1 charge -1
end
TASK dft

結果為-0.567651263156。

然后在Gaussian里，計算H-體系，在與之距離5埃處放一個單位正電荷，輸入文件如下
#p b3lyp/6-31G* charge

test

-1 1
H 0. 0. 0.

0. 0. 5. 1.0

結果為-0.5676521。可見，用CDFT計算H+ H-和計算H-但在附近放一個質子，兩種方式計算結果是等同的，也體現了CDFT的合理性。