電子定域性的圖形分析
注:在撰寫本文后筆者還撰寫了大量與ELF有關的文章,連同其它各種ELF相關資料,可以在這里訪問:“ELF綜述和重要文獻小合集”(http://bbs.keinsci.com/thread-2100-1-1.html)
電子定域性的圖形分析
文/Sobereva @北京科音
First release: 2010-Jun-13 Last update: 2012-Oct-24
摘要:本文回顧了電子定域性分析的基本問題,介紹了拉普拉斯值函數、ELF函數、LOL函數的基本概念,利用一些實例介紹了這三種函數能夠說明的問題以及如何對分子進行分析。同時穿插介紹了函數繪圖的方法和經驗,最后給出利用Multiwfn (http://www.shanxitv.org/multiwfn)生成函數圖像的簡單例子,便于讀者將圖形化分析方法投入實際應用。希望本文能對推廣分子圖形化分析起到一定作用。
1. 電子定域性分析雜談
波函數分析是計算量子化學方法中重要卻常被忽視的一個領域,現在更多的人著眼于能量、幾何結構、光譜等性質的計算。然而,為了獲得精確的屬性值而同時不得不“附帶”得到的精確波函數卻往往被忽視掉。波函數無異于一個黑箱,蘊含著分子一切信息,計算出來的分子性質是已經從中被提取的部分,然而還有無窮未被挖掘的信息,若不利用明顯是巨大的浪費。波函數分析的目的是從波函數及衍生信息中提取易于被人所理解的概念,是有助于從更深層次認識分子本性的一大類方法,它既包含理論,又包含“技術”,也就是如何具體下手去解釋計算結果。波函數分析的范疇并沒有具體的定義,我認為它應包括拓撲分析(如AIM)、布居分析、鍵級分析、屬性分解分析(如能量分解、電荷轉移分解,軌道成分分解)、軌道定域化分析、圖形化軌道相互作用分析(如前線軌道理論)、概念密度泛函理論等內容。然而絕大部分量化教材里缺乏單獨的章節介紹這些方法,是不應該的,很多初學者遇到相應問題也毫無思路,例如總有人問怎么求每個原子軌道對某個軌道的貢獻(多數人都說用系數的平方,以訛傳訛)。
化學鍵、孤對電子、sigma/pi/delta鍵、軌道雜化、lewis結構、VSEPR這些經典理論誕生于大半個世紀前,屬于“概念化學”范疇。這些模型化的表述從當今量子化學角度看似乎缺乏根據,是一些很粗俗的觀點,但實際上它們并非是完全人為臆斷的,它們從量子化學的角度是可以找到充分依據的,定域化分析正是力圖通過波函數或其衍生信息還原這些信息。當然我們也不能固步自封,憑借量子化學的威力,在不失傳統概念簡潔、形象的優點下,可以得到更多的信息,比如精確的定量數據,還可以將應用范圍擴展到難以通過經驗分析的體系,比如團簇。目前已有不少軌道定域化方法力圖實現這樣的目的,其中很多是根據一定規則令原本離域的正則HF/DFT占據軌道作酉變換獲得定域化軌道(LMO),常用的比如Boys、Edmiston–Ruedenberg、Pipek–Mezey定域化方法,NBO分析盡管原理不同,但從目的上也可以歸為這類。然而如何變換成LMO的方法不是唯一的,由此產生一些矛盾。比如雙鍵,有的方法能得到sigma和pi鍵形狀的LMO,然而有的方法卻得到兩個香蕉鍵。再比如苯環,lewis共振結構至少能寫出兩種,究竟LMO該表示哪種結構?可能分子取向、構型稍稍變化一點,根據程序的判斷LMO就從描述一種共振式突然變成描述另一種共振式了,這樣的不連續描述若用在某些場合會造成問題,而且從概念上也莫名其妙。
還有一類方法是使用實空間坐標為變量的函數來描述電子定域性特征,這不需要明確地計算定域化軌道,因而避免了上述問題。這些函數將復雜的3N維波函數所攜帶的關鍵信息約化、抽象成三維函數,從這些函數在分子附近空間中各點的數值可以分析分子各個位置定域性特征的強弱,使化學鍵、孤對電子、原子殼層這樣電子定域性強的區域充分凸現出來。
PS: 回想基態電子密度包含了分子一切信息,利用各種形式的實空間函數,不僅可以做定域性分析,還有可能將構成分子各種屬性的因素皆以圖形化方式清晰、生動地展現出來,并由此總結出普遍規律用于分析未知分子的性質,這將有重要的意義。探索、發展這樣的函數,可能是潛在的熱點。然而現在多數人還是熱衷于計算各種分子各種屬性的數值,追求精確到小數點后的位數,這實屬“暴力”的研究,理論研究應當比這更美。
另外,軌道定域化方法依賴于對基組的選取,假設用非定域的基函數,例如平面波、多項式函數,乃至離散的格點描述,由于無法直接變換成定域軌道,軌道定域化方法就不適用了,盡管也有人用正交投影的方法投影到原子中心的基組來解決這個問題,卻不可避免地造成波函數質量的降低。基函數無非只是數學工具,依賴于它的軌道定域化方法從根本上缺乏物理意義。而使用函數的描述形式就避免了這一問題,只依賴于空間各點屬性的值,而不管這是以何種數學形式表達的,無論對于適合定域基函數描述的分子體系還是適合離域基函數描述的周期性體系,這類方法都同樣適用。
一般通過作圖來研究實空間函數數值的分布情況,表現切面上的情況主要通過填色圖(也稱贗色圖)、等值線圖、梯度線圖、地形圖(Relief map)。曾經作這些圖操作十分復雜,缺乏簡單、通用、免費、小巧、快速的軟件,Multiwfn徹底解決了這一問題,使函數圖形化分析變得十分容易,從1.4版開始加入了更多的函數,包括下文的ELF和LOL函數。下文的曲線、切面圖都是通過由Gaussian計算波函數并載入Multiwfn后直接獲得的。函數的三維空間分布一般通過等值面圖、顏色映射等值面圖(一般將屬性映射到電子密度等值面)研究。做這樣的圖需要先計算格點數據,它包含了離散化的空間上各點函數的數值。格點數據可以由Multiwfn等程序生成,并且可以直接預覽等值面。Multiwfn也可以將格點數據導出為cube文件,進而由第三方可視化程序觀看。GaussView、Chemcraft、VMD等都支持Cube文件。
下文主要談談這類實空間函數中的拉普拉斯值函數、ELF和LOL函數。
2. Laplacian函數
拉普拉斯值函數的值被定義為r處電子密度Hessian矩陣的跡,也就是拉普拉斯算符作用到電子密度的結果,亦即電子密度在三個正交方向曲率和。一般這三個正交方向就是指X,Y,Z方向,由于可以對Hessian做酉變換來旋轉坐標系而保持跡不變,所以三個正交方向是任意的。在AIM理論的鍵臨界點位置,可以將坐標系變換為一個平行于和兩個垂直于鍵軸的方向而使其意義更明顯,其各自的曲率在AIM分析中有重要意義,但本文不考慮拉普拉斯值的具體成分而只考慮總數值。拉普拉斯值函數在某處為正,說明此處電子密度以發散為主;若為負,說明以聚集為主。非極性共價鍵、孤對電子處由于電子呈聚集狀態,因而它們都處于負值區域;極性鍵也有電子凝聚區域,相對于非極性鍵發生了偏移、變形。對于這樣由價層電子聚集產生的效應稱為VSCC(Valence Shell Charge Concentration)。對于閉殼層鍵(離子、氫鍵、VDW鍵)則不出現電子凝聚的成鍵區域。通過觀察拉普拉斯值可以了解分子的特征,這比直接觀察電子密度圖清晰得多,電子密度從整體看都是以原子為中心向四周呈指數形衰減,成鍵、孤對電子引起的電子密度聚集僅能微弱影響這個總趨勢,從電子密度圖上很難分辨其效應。而求電子密度二階導數就能將這樣細部信息鮮明地展現出來,如同信息的放大鏡(有興趣可以做一下比如8*exp(-7*x)+exp(-10*(x-0.5)^2)的函數圖和它的二階導數圖來對比一下)。
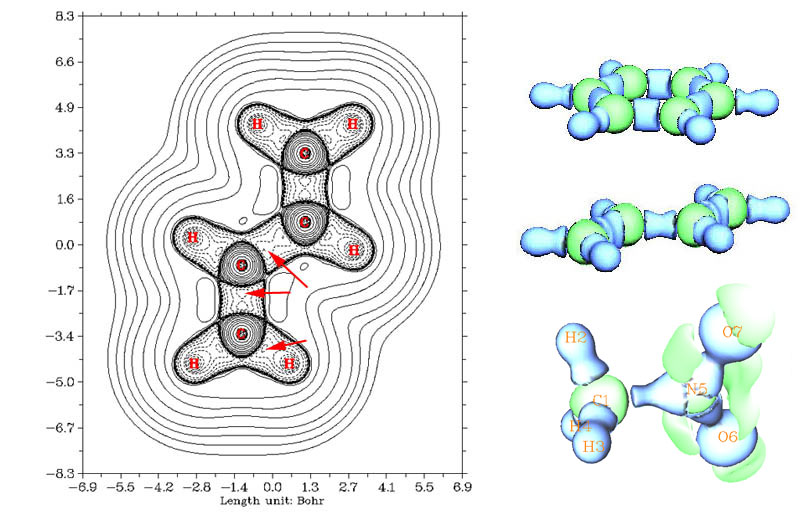
上圖的右上是苯分子的拉普拉斯等值面圖,這是由Multiwfn生成此屬性的格點文件后直接顯示出來的,藍色為負值,綠色為正值。可見分子的整體輪廓被等值面勾勒了出來,成鍵區域處拉普拉斯值為負。原子由于具有殼層結構,在每個殼層之間都有拉普拉斯值數值為正的區域,C原子處顯示的綠色球層就是這個區域。H是比較特殊的原子,僅有單個質子,其電荷與電子的束縛作用并不足以構成具有獨立特征的區域,無法形成殼層結構,甚至可看成質子化的孤對電子,所以與成鍵區域連為一體而沒有截面,對于ELF/LOL函數,氫原子也表現這樣特征。
圖的右側中央是1,3丁二烯的拉普拉斯等值面圖(這三幅圖等值面并不一樣,沒有完全的可比性),眾所周知中間的C-C鍵比兩端的C-C鍵要弱,從圖上也能看出這一點,兩邊的C-C呈橢圓形而中間的C-C鍵類似于柱形,這是因為兩邊的C-C鍵中的pi鍵更強所致。左圖是此分子平面的等值線圖,能更清楚地反映細節,箭頭所示的是鍵之間的拉普拉斯值函數極大點所在區域(此處等值線為-1.19)。中間的C-C sigma鍵之間有兩個成鍵極大點,兩個成鍵極大點中間存在鞍點。兩邊的C-C鍵距離更近,成鍵極大點之間也更為接近,對于乙炔,C-C鍵更短,中間只有一個極大點。這與后文ELF/LOL函數的情況有所不同,ELF/LOL函數描述的sigma鍵總是只有一個極大點。
右下方的圖是CH3NO2的拉普拉斯值為0.5的等值面圖。由于N的電負性比C大很多,所以可以看到C-N鍵對應的電子密度聚集區域很大程度向N偏移。
用拉普拉斯值函數分析定域性問題的缺點是數值范圍不確定,需要反復調整作圖的數值范圍,遠沒有ELF、LOL函數有確定的[0,1]區間那么方便。拉普拉斯值在原子內層區域數值波動極大,而且與價層區域不在一個數量級,做填色圖的時候原子內層很不好看,做地形圖時還必須將其數值在某處截斷。雖然大部分能夠用ELF、LOL分析的體系用拉普拉斯值函數也能分析出相似的結論,但是對具有定域性特征的區域分辨能力比ELF和LOL偏弱,有時不很明顯,甚至幾乎無法分辨,有文章指出拉普拉斯函數沒法展現出價層主量子數很大的原子的殼層結構。拉普拉斯值函數難以凸顯的特征都能用下面的ELF、LOL函數很好地表現。
3. ELF(Electron Localization Function,電子定域化函數)
ELF是個三維實空間函數,數值范圍在0至1之間。簡而言之,數值較高的ELF的等值面包圍的區域,電子在里面定域性較強,不容易跑出去,相對地,電子能夠容易地在這樣的區域內隨意運動(在此區域里隨意離域)。在那些ELF數值較低的區域,電子定域性弱,即如果把電子放在那里,就很容易離域到其它區域去。能跑到以及容易跑到哪里,可直接通過考察費米穴的分布來衡量。
三維的ELF是對六維的費米穴函數簡化而來的,使電子定域性、離域性更易于圖形表現。弄清楚了如何通過費米穴衡量定域性、離域性,才能抓住ELF的最本質思想。Bader在這方面做了關鍵性的工作。詳細討論可參考《電子的定域性與相關穴》(http://www.shanxitv.org/94),下面只是簡單說說ELF的思想。
ρ_cond(r1,r2)稱為條件電子對兒概率,代表已經知道有一個電子出現在r1處(稱參考點),在r2處出現另一個相同自旋電子的概率,是電子對兒密度ρ(r1,r2)除以ρ(r1)的值。可以將之變換為ρ_cond(r,s),稱為球形平均電子對兒概率,代表令r為參考點,以其為中心在半徑為s的球面上出現相同自旋電子的概率。將ρ_cond(r,s)對s做Taylor級數展開并截取第一個非零項就定義了D(r)函數,代表在r附近出現另一個自旋相同電子的概率,它在r處的值越小被認為r處電子定域性越強。D(r)的值一定大于等于0,為0時則表明完全定域。D(r)是三維函數,比六維函數ρ_cond(r1,r2)或四維函數ρ_cond(r,s)更易于考察。
D(r)的具體表達式為D(r)=1/2*∑[i]N(i)*|▽ψ_i(r)|^2 - |▽ρ(r)|^2/(8*ρ(r)),這里N(i)為第i條軌道軌道占據數,▽為梯度算符,ψ_i是第i條軌道波函數(后HF波函數時為自然軌道),ρ(r)是總電子密度函數。根據Savin等人對其的解釋,其中1/2*∑[i]N(i)*|▽ψ_i(r)|^2是當前體系動能密度函數(也稱G(r)或梯度動能密度),|▽ρ(r)|^2/(8*ρ(r))是Weizsacker泛函,表現了沒有Pauli互斥時,如同玻色子體系的動能密度,因此D(r)本質上體現的是由于Pauli互斥造成的超額動能密度,也稱Pauli動能密度,體系超額動能密度越低的區域定域程度越高。用D(r)描述電子定域情況有不妥之處,因為其數值越小代表越定域,這和觀念相反,而且它的數值沒有上限,觀察時不便。所以Becke等人將之變換后定義了ELF函數,ELF(r)=1/(1+(D(r)/D_0(r))^2),這樣就把數值投影到了[0,1]區間,且數越大表明定域程度越高。這樣將D(r)變換為ELF(r)的方式本身是任意的,并沒有確定的物理含義。式中D_0(r)=3/10*(3*pi^2)^(2/3)*ρ(r)^(5/3),是Thomas-Fermi均勻電子氣動能泛函,是人為引入的參照標準,因此ELF本質上是對定域程度的相對度量而非絕對度量標準。
關于ELF的物理意義的更深入和詳細的探討,以及對于開殼層體系的正確形式,參見《電子定域化函數的含義與函數形式》的討論(物理化學學報,27,2786-2792 (2011))。
ELF函數的定義略有缺陷,當r趨近于無窮時,D(r)會漸進地接近0,所以在遠離分子的位置ELF會等于1,成了完全定域的情況,這顯然不對。但由于D_0(r)具有ρ(r)^(5/3)的行為,往往消失得更快,所以(D(r)/D_0(r))^2在遠處一般為無窮大,故ELF在遠處一般還是會等于0。然而有時D(r)比D_0(r)更早地接近0,此時ELF在分子外部區域還是會等于1。為了避免這種情況,可以在D(r)上加入極微小量,比如10^-5,這樣可確保(D(r)/D_0(r))^2在電子密度已經很小的分子外部區域變得很大(因為D(r)至少有10^-5),故一定能令ELF(r)等于0,這只對分子內部區域ELF函數產生微不足道的影響。
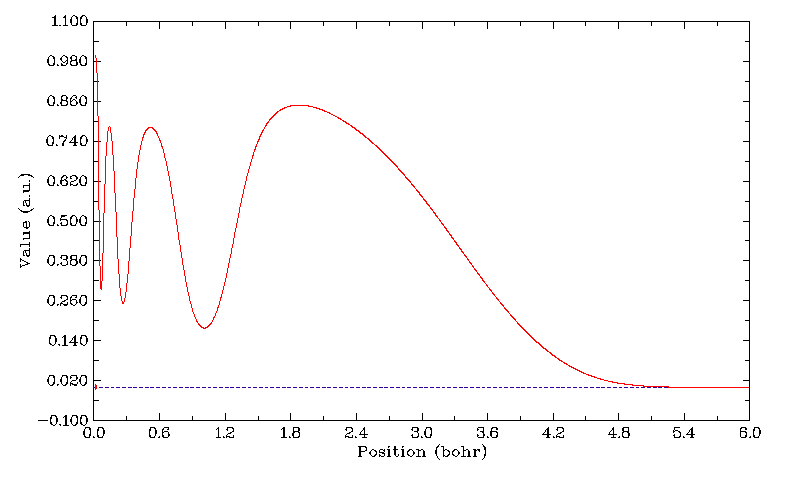
從化學體系的ELF函數分布上可以清晰地看到原子殼層結構、孤對電子、化學鍵等特征。下圖為Kr (cc-pVTZ)的從0到6波爾半徑的ELF函數曲線,可見主量子數為1,2,3,4的四個殼層清晰可見,若只是考察總電子密度的變化則只能看到呈指數衰減的曲線,獲得不了任何細節信息。如果以曲線各個極小點對應的球面此對空間進行劃分,并分別積分其中的電子密度,就能得到每個殼層內的布居數,數值近似等于相同主量子數原子軌道上電子數的加和值,差異來自軌道隧穿效應,而在量化中近似等于軌道指數處在相應殼層范圍內的基函數的布居數加和。
下圖中間的圖是吡嗪(C4H4N2)分子平面ELF函數的地形圖+投影圖,投影圖部分單獨拿出來就是填色圖。可見C-N、C-C化學鍵、N的孤對電子(與C-H區域形狀較像)都清楚地顯示了出來。
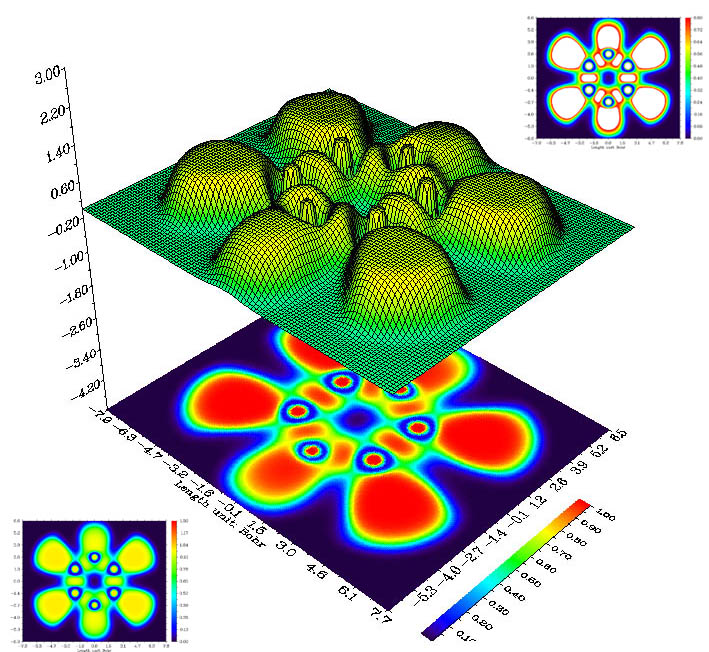
這里順便說一下填色圖的色彩刻度的設置問題。填色圖就是根據每個點數值大小,用色彩刻度條上對應數值的顏色顯示,最常用的色彩刻度從下限到上限是由藍變綠再變紅,類似彩虹。色彩刻度的上下限的設定是任意的,這會影響到圖上格點的顏色,設置標準的關鍵是要清晰地反映數據的差異。此圖將色彩刻度設為了0~1,這一方面是因為ELF函數數值在0~1范圍內,但最主要是因為在0~1范圍內填色圖能比較清晰地反應各個定域化區域。左下角的圖是將色彩刻度改為0~1.3的圖,原本在紅色區域(數值接近1)的位置都變成了黃色,成鍵區域與綠色區域不易區分,給人的感覺不夠明顯。右上角是將刻度設為0~0.8,那些超過0.8的數值通常就被自動設成了白色,這樣0.8~1.0部分的數值變化就沒法分辨了。所以上下限的設置應當比較接近數據集數值主體部分的上下限,這樣就能充分利用各種顏色將不同數值區域的點分開。從經驗上看,對于ELF函數的填色圖適合用0~1的范圍,但對于某些分子應進行適當調整,對于LOL函數用0~0.75比較好。
下圖是HCN分子在Chemcraft下做的ELF函數等值面圖,格點為80*80*150,由內往外的等值面分別為0.97、0.87、0.5。可以看出N的孤對電子以及H附近定域程度最高;隨后是一個sigma鍵和兩個pi鍵,在圖中合在一起呈現環形等值面,盡管這看似與一般觀念上sigma鍵和pi鍵的形狀很不像,但實際上是等價的。繼續降低等值面數值后pi鍵等值面范圍擴大,成為血小板形狀。
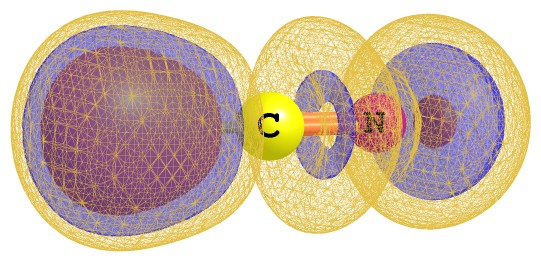
類似這樣結合不同透明度、不同顏色、不同顯示方式,可以同時在一張圖里不受影響地表現多層等值面,表現豐富的信息。在Chemcraft里每繪制完一層點一下keep this surface,則已繪制的層會一直保留,不受之后操作的影響,調整設置后繪制新的層,反復如此就可以實現這樣的效果。保存圖像不宜直接截圖,應當用file-save image保存,或者用View-draw export picture再截圖,這樣就會使用抗鋸齒技術使邊緣和線條平滑,尤其是用網格線表現等值面的時候效果會好很多。
對ELF函數也可以進行類似AIM的拓撲分析,是對AIM分析的推廣,由此可以比圖形化觀察更細致地定性或定量對體系進行分析以得到更多信息。ELF拓撲分析也有ELF函數的極大點(也稱點吸引子)、極小點、臨界點、零通量面這樣的概念。零通量面劃分了盆,不僅包括AIM原子盆那樣空間中的一團的形狀,還有環形、球層等形狀。此外還多了一些額外概念,環吸引子就是比如前面在HCN中看到的C-N三鍵的圓環,球吸引子就是例如Kr徑向ELF函數曲線中每個極大點所對應的一層球面。f-localization domain是指ELF函數值為f的等值面包含的空間區域,域內各點數值都大于f,若只包含一個吸引子稱之為不可約的,否則稱為可約的,對于可約的定域性化域,當f逐漸加大并超過某一個值后就會分裂為多個包含更少吸引子的定域化域。對于HCN的例子,若將等值面數值進一步降低,三個彼此不相接觸的不可約域就會擴張并連通成一個可約域。隨f的加大,由最初包含整個分子的可約域最終分裂為各個不可約域的過程可以繪制成樹狀圖。
這些概念對分析問題很有用處。按Bader的分類化學鍵可分為共享電子相互作用和閉殼層相互作用兩大類,前者包括共價、金屬鍵;后者包括離子鍵、氫鍵、二氫鍵、范德華鍵。Silvi和Savin在Nature 371 (1994) 683指出,對于前一類,在兩個原子(氫原子除外)的鍵徑總會出現至少一個用于成鍵的點吸引子或環吸引子(不參與成鍵時的孤對電子、內層電子的吸引子不算成鍵吸引子);而對后一類不出現這樣的情況。這樣的規則與前述拉普拉斯值函數的情況很類似,本文各個例子也都驗證了這一規則,這給成鍵的分類提供了明確依據,極大點的數值也可以評估鍵的強度。對共價鍵的盆空間內的電子密度進行積分能夠用于了解有多少電子用于形成此鍵。比如Theor.Chem.Acc.108 (2002) 150~156文中就以兩金屬原子間是否存在ELF函數極大點判斷它們是否有直接的共價鍵作用,并且根據積分Sc-Sc鍵的盆內電子數推斷出除了3d以外,3s、3p也參與了成鍵。還有人系統地研究了原子電負性大小對某一f值的f-定域化域體積的影響,發現與VSEPR的假設比較吻合,并且指出鍵的盆布居數與相連的兩原子電負性有相關性,鍵的極性越大,盆布居數越小于2,詳見The Quantum Theory of Atoms in Molecules-From Solid State to DNA and Drug Design第六章的討論。
Multiwfn可以對電子密度、ELF、LOL等各種各樣的實空間函數進行拓撲分析和盆分析,見《使用Multiwfn做拓撲分析以及計算孤對電子角度》(http://www.shanxitv.org/108)和《使用Multiwfn做電子密度、ELF、靜電勢、密度差等函數的盆分析》(http://www.shanxitv.org/179)。
4. LOL(Localized orbital locator,定域化軌道指示函數)
Schmider和Becke在J.Mol.Struct.(Theo) 527 (2000) 51-61中定義了LOL函數γ(r),γ(r)=t(r)/(1+t(r)),t(r)=D_0(r)/(1/2*∑[i]N_i*|▽ψ_i(r)|^2)。可見t(r)就是均勻電子氣動能密度與當前實際體系動能密度的比值,某處動能密度相對于均勻電子氣越小,γ越大,定域性越強。所以LOL和ELF引入D_0作為參考函數以獲得相對值,是為了令體系各處動能密度的差異更顯著地表現出來,否則結果很難考察。將t(r)變換為γ(r)則是為了使數值在[0,1]區間內。
LOL函數的本質也可以與軌道定域化方法進行比較來說明,t(r)具有軌道酉變換不變性,即是說用MO軌道或是定域化后的軌道其結果是一致的,因此這里假設軌道已經是定域化的。成鍵軌道波函數極大點的梯度為0,因而動能密度1/2*∑[i]N(i)*|▽ψ_i(r)|^2很小(由于定域軌道交疊很小,可把加和號去掉而只保留此成鍵軌道),導致t(r)很大,γ(r)接近于1,由于軌道波函數是平滑變化的,故軌道波函數極大點附近的數值也很大。而在軌道交疊處,軌道波函數梯度較大,致使t(r)分母較大,t(r)的值較小,所以γ(r)也很小。這就是為什么成鍵區域LOL的值較大,而在定域性強的區域相交處值較小。Burdett等人也在J.Phys.Chem.A 102 (1998) 6366-6372中從類似的軌道波函數的角度對ELF函數的意義進行了分析。
由于LOL與ELF本質上都是對動能密度函數不同形式的反映,所表現的信息是相仿佛的。實際上由于存在這樣的關系:h_bar^2/(4*m)*▽^2*ρ(r)=2*G(r)+V(r),V(r)為勢能密度(總為負值),拉普拉斯值越小動能密度G(r)往往越小,所以拉普拉斯值函數的結論與LOL/ELF函數也很相似。用LOL能給出與ELF定性一致的結果,此文對ELF與LOL的討論也是可以互相套用的。總體來說LOL給出的圖形比ELF的圖形更為明晰,更容易分析,而且函數形式更簡單,也沒有像ELF在遠距離時數值可能成為1的情況。所以拉普拉斯值函數、ELF、LOL這三者中最推薦使用LOL進行分析。
下圖是乙烯的LOL函數圖,格點為120*120*80,用Chemcraft繪制,填色圖顏色范圍為-0.05~0.7,等值面為0.5。同時取了兩個切面顯示填色圖,由于乙烯有pi鍵,所以在垂直于分子平面方向比平行于分子平面方向紅色區域更大。結合藍色小點表現的等值面更清楚地顯示出pi鍵的空間形狀,由于LOL值為0.5時正是體系動能密度等于相同密度下均勻電子氣時的值,所以常用0.5的等值面來劃分成鍵區域。Becke提出可以將0.5等值面以內的體積作為計算鍵級的依據。
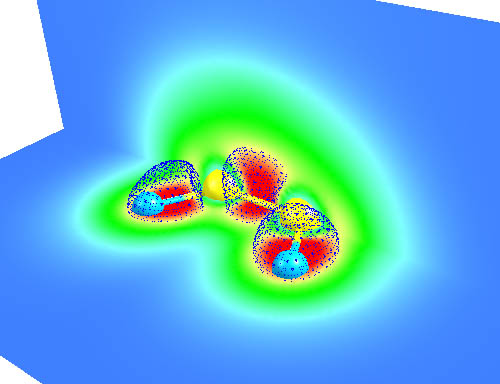
下圖是ClO分子的LOL填色圖,黑線代表LOL函數為0.51的等值線。上面是Cl下面是O。Cl的內部第一殼層(中心圓點)、第二殼層(黃圈)都明顯地展現出來,并且它們并未參與成鍵而變形,表現了內層電子的惰性。分子中間成鍵區域,以及原子旁邊的孤對電子也都清晰地顯現了出來。
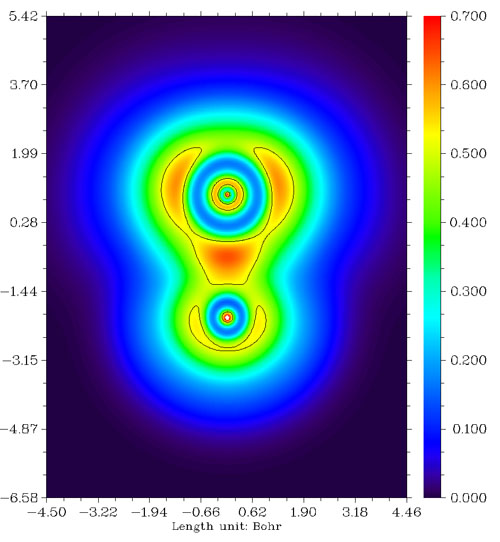
我們來看看F2分子、CH3F分子與LiF分子的LOL圖,依次如下所示。
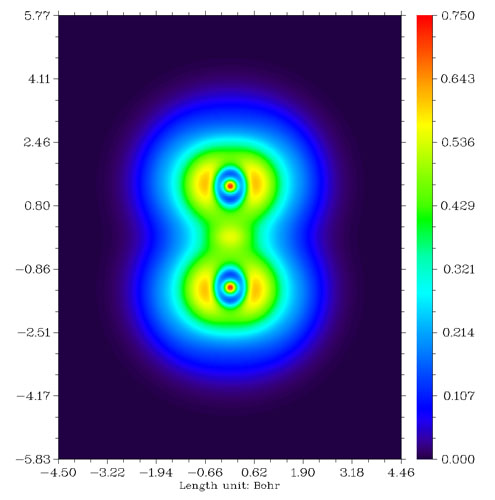
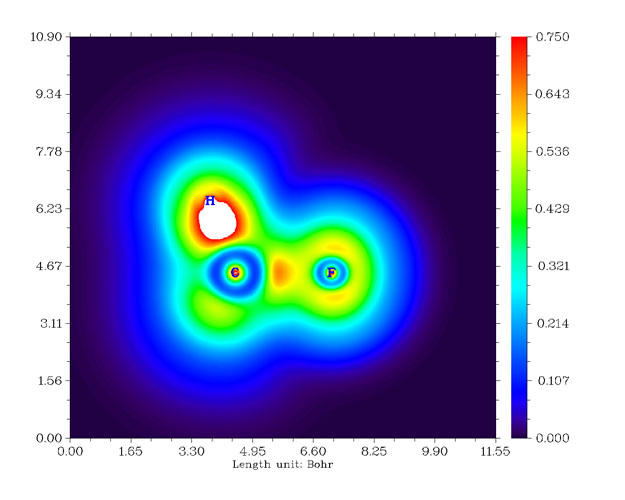
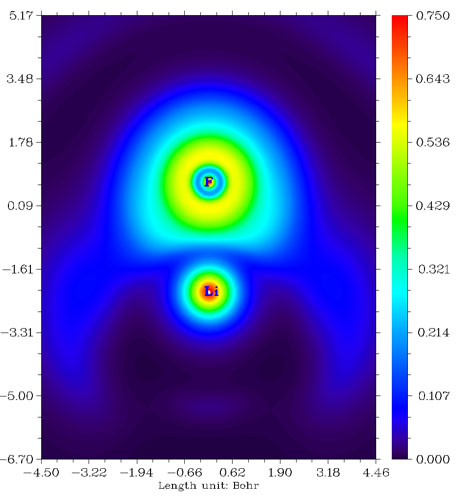
從F2的圖上看,兩個F之間高定域性區域很微弱,比起CH3F中的C-F鍵弱很多。這是由于F-F鍵本質上并不是共價鍵,而是典型的電荷轉移鍵,詳見Chem.Eur.J.,11,6358-6371的討論。由這種鍵連接的原子之間并不會像普通共價鍵一樣有明顯的電子聚集,也不會有定域性較高的區域。電荷轉移鍵比一般的共價鍵要弱,例如F-F的鍵能153KJ/mol明顯小于C-H鍵的平均鍵能485KJ/mol。CH3F中的C-F鍵是典型的極性共價鍵,兩原子間有一塊定域型較高的區域。LiF是典型的離子鍵,電子幾乎全被F吸走而形成滿殼層的F-,F-附近LOL函數值分布基本接近球對稱,只因為Li+的正電荷極化效果略有變形而已。由于二者之間主要靠靜電力束縛而沒有共價相互作用,故二者間沒有出現LOL函數較大的區域。
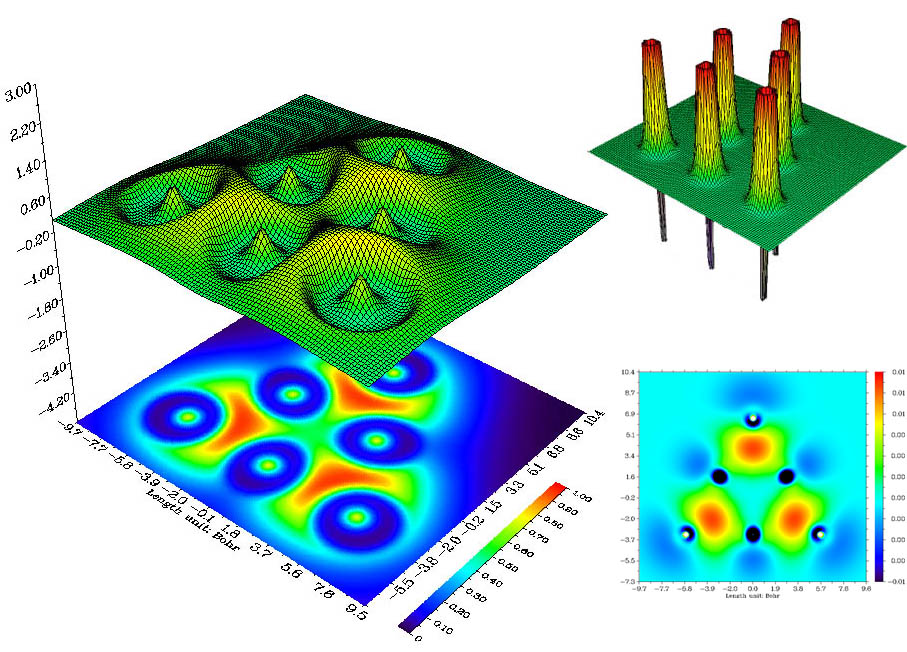
上面的例子憑經驗都能猜到原子間是如何成鍵的,然而對于新穎、復雜的情況,就必須借助ELF或LOL分析了,例如6個Li組成的團簇,憑經驗難以分析,而通過LOL函數圖(下圖左側)這個問題變得顯而易見。從圖中可見每個角上的Li與它相鄰的兩個邊上的Li形成了很強的三中心鍵。而圖中右上角的拉普拉斯值函數地形圖并沒有給予我們任何有用的關于成鍵的信息,各個Li之間拉普拉斯值幾乎為零,所以用拉普拉斯值函數分析成鍵問題不如LOL。這實際上與Li之間電子密度太小有關,必須將拉普拉斯圖的Z軸上下限設得非常小才能看出端倪,缺乏固定的數值范圍令拉普拉斯值分析很不方便。圖中右下角是這個體系的密度差圖,紅色和藍色分別代表孤立原子形成體系后電子增加和減少的區域。由于此體系密度差數值非常小,為了表示清楚,色彩刻度的Z軸上下限已設得非常小,可見Li背后的電子在形成強三中心鍵的區域富集,而三個處在邊上的Li之間電子沒有發生富集。對這個體系進一步進行Mayer鍵級分析,發現處在邊上的Li與相鄰的處在角上的Li之間的鍵級為0.386898,而處在邊上的Li與另一個處在邊上的Li之間的鍵級為0.165081,從LOL圖上可見,前一種成鍵方式跨越紅色區域程度很大,而后一種情況跨越程度很小,這在一定程度上解釋了Mayer鍵級的結果。這個問題還可以進一步與多中心鍵級分析結果相比較。
ELF/LOL不僅可以用于討論分子的靜態特征,還能用于研究化學反應過程,通過觀察反應路徑中成鍵區域和孤對電子的出現、消失、范圍和形狀的變化,可以得到很多重要的結論,限于筆者時間和精力不在此舉例,十分建議閱讀LOL函數原文中的幾個例子,其中包括SN2反應、水分子解離、HCN異構化、1,3丁二烯環化反應。
計算上述函數所用波函數質量會對結果有所影響。不要使用極小基,這樣的基組變分自由度太小,缺乏柔性,價層區域的實際情況難以正確描述。至少使用雙分裂價+極化函數級別的基組,6-31G*是比較適合的,對于陰離子、弱相互作用、激發態體系需要加上彌散函數,這樣才能較好描述距原子核較遠處的信息。然而再大的基組沒有必要,上述函數的空間分布不像能量等屬性對基組那么敏感,6-31G*一般已經足夠,試圖加大基組對結果影響微乎甚微。對于大體系如果用6-31G*基組仍然困難,可以使用混合基組,只在感興趣的區域用大基組。從計算方法看,使用后HF波函數顯然最好,但考慮計算時間,通常使用DFT波函數就可以。是否使用含電子相關作用的方法計算波函數對分析上述函數一般不會有定性影響,HF波函數也是完全可以的。但如果要求分析的精度比較高,比如幾種分子的上述函數差異很小,卻需要從這微小的差別中分析它們的不同點,或者要求準確的定量數據,比如求函數極大點的位置和數值或者計算f定域化域的體積,則應當使用更高質量的波函數。
上述函數也可以用于配合物體系,這總要涉及到贗勢。利用上述函數分析化學上感興趣的區域并不需要全電子基組,使用贗勢會雖然使得原子內部區域函數值為0,也因此不會顯示殼層結構,但價層的行為是完全正確的,感興趣的區域一般只與這部分相關,所以不必擔心贗勢會造成問題。選用的贗勢應當包含亞價層電子,因為亞價層軌道會在一定程度上延展到價層區域。特別是有些分子,比如Li6Ca2[Mn2N6]的Mn的內層電子也涉及成鍵[Angew.Chem. 110 (2000) 1667],或者分子處于電離態而使內層電子直接暴露,必須明確考慮亞價層的影響。如果必須要用全電子基組的話,也可以在幾何優化的過程中使用贗勢來節省時間。
5. 使用Multiwfn繪圖簡單實例
ELF/LOL函數的意義顯著,分析方法容易掌握,適用性廣泛,熟練運用可以使文章增光添彩,值得大力推廣,也很值得作為黑箱方法納入普通化學教材。當然ELF/LOL分析若要普及開來必須有方便的程序,Multiwfn正符合要求。下面是使用Multiwfn獲得ClF3分子在分子平面內LOL函數填色圖以及等值面圖的具體步驟,操作一遍就會發現這十分容易。此例只是Multiwfn的最基本的應用之一,其它功能請參閱程序手冊和《Multiwfn波函數分析程序的意義、功能與用途》(http://www.shanxitv.org/184)。
Multiwfn需要利用.wfn或.fch文件中的波函數信息進行計算。首先用GaussView生成ClF3的輸入文件,并在Route section部分寫上out=wfn,在分子坐標末尾空一行寫上.wfn文件輸出的路徑。也就是例如下面這樣,用Gaussian執行之:
=====================
# B3LYP/6-31G* opt out=wfn
Title Card Required
0 1
Cl 0.00000000 0.00000000 -0.32113636
F -1.57000000 0.00000000 -0.32113636
F 0.00000000 -0.00000000 1.24886364
F 1.57000000 0.00000000 -0.32113636
c:\ClF3.wfn
[空行]
[空行]
=====================
這樣就得到了優化后的ClF3的波函數文件。先做填色圖,啟動Multiwfn,按照以下順序依次輸入,//后面是注釋。
c:\ClF3.wfn //輸入文件名
4 //選擇繪制平面圖
10 //選擇LOL函數
1 //選擇填色圖
按回車 //兩個方向格點數,越大越精細。按回車代表用默認設定(200,200)
3 //選擇YZ平面
0 //設定YZ平面是X=0的YZ平面,也就是分子平面
立刻圖像就顯示出來了。然而圖像對比度顯得不高,成鍵區域特征區分得不是很清楚,這是因為默認的色彩刻度范圍偏大所致,所以需要進行調節。在圖上點擊鼠標右鍵關閉圖像,然后輸入
1 //設定色彩刻度范圍
0,0.7 //色彩刻度上下限為0,0.7
-1 //重新顯示圖像
結果如下圖所示。
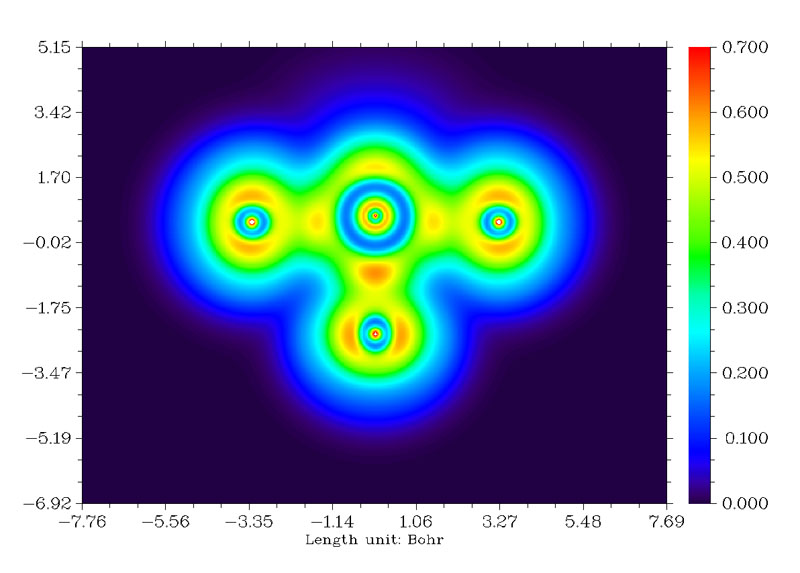
從圖中可見,在赤道上的F(圖中下方的F)與Cl的成鍵比軸向的兩個F與Cl更強,有更顯著的電子定域性區域。如果進行Mayer鍵級分析,會發現軸向的F與Cl的鍵級為0.7168,而赤道的F與Cl的鍵級為0.8367。另外,優化出的結構中軸向的F-Cl鍵長為1.7288埃,而赤道的F-Cl鍵長更短,為1.6517埃。都與LOL函數的結論十分吻合,即赤道的F-Cl鍵更強。
在圖像上點擊右鍵來關閉圖像,之后輸入0可以將此圖像保存到當前目錄下的以DISLIN為前綴的.png圖像文件中。
做等值面圖需要先用Multiwfn計算格點文件,啟動Multiwfn然后依次輸入:
c:\ClF3.wfn
5 //計算格點文件
10 //選擇LOL函數
2 //中等質量格點
現在格點開始計算。計算速度取決于總格點數和高斯函數數目,數目越多計算越慢。Multiwfn計算ELF/LOL函數格點數據速度很快,遠勝于Checkden、DGrid等程序。計算完畢后選-1可以預覽等值面,將isovalue稍微調大至0.53,顯示的圖形如下圖所示。從中能看到Cl的兩個孤對電子。而F的孤對電子組成了環形等值面。
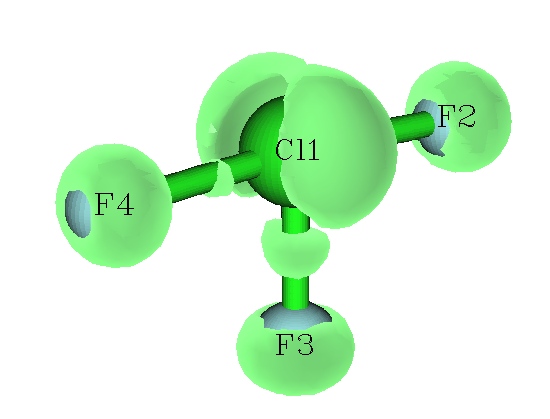
點擊Return關閉窗口后,可以選2將格點數據保存為cube文件,之后可以用第三方可視化工具,如VMD、molekel、gview、chemcraft等工具觀看等值面。