使用Multiwfn計算(超)極化率密度
2019-Aug-24補充:本文介紹的是考察某個笛卡爾軸方向的(超)極化率密度,如果你想考察體系偶極矩方向的(超)極化率密度,最好先旋轉體系使得偶極矩平行于某個笛卡爾坐標軸,具體做法見《讓體系(躍遷)偶極矩平行于某個笛卡爾軸的方法》(http://www.shanxitv.org/507)。
(超)極化率密度對于研究考察(超)極化率的本質特征非常有益,可以圖形化直觀展現體系不同區域對(超)極化率的貢獻。將超極化率密度作出圖來放到論文里,可以給(超)極化率計算文章增色很多,討論能夠更深入。本文就介紹一下什么是(超)極化率密度,以及具體怎么用Multiwfn去計算。Multiwfn可在http://www.shanxitv.org/multiwfn上免費下載,不了解著建議閱讀《Multiwfn入門tips》(http://www.shanxitv.org/167)。Gaussian使用G09 D.01。本文涉及的輸入文件都可以在此下載:http://www.shanxitv.org/attach/305/file.rar。
筆者的許多文章都利用了(超)極化率進行分析,是這種分析方法的很好的應用實例,非常歡迎大家閱讀和作為范例引用:
J. Comput. Chem., 38, 1574 (2017)
Carbon, 165, 461 (2020)
J. Phys. Chem. C, 124, 7353 (2020)
J. Phys. Chem. A, 124, 5563 (2020)
J. Phys. Chem. C, 124, 845 (2020)
Carbon, 187, 78 (2022) 介紹:《理論設計由18碳環與鋰原子構成的電場可控的光學開關》(http://www.shanxitv.org/630)
Phys. Chem. Chem. Phys., 24, 7466 (2022) 介紹:《深入揭示18碳環的重要衍生物C18-(CO)n的電子結構和光學特性》(http://www.shanxitv.org/640)
本文先介紹基本概念,然后用個很簡單的小分子甲醛來演示怎么計算第二超極化率密度。
1 基本概念
不了解(超)極化率及其在Gaussian中的計算的話可以先看這里的簡單介紹《使用Multiwfn分析Gaussian的極化率、超極化率的輸出》(http://www.shanxitv.org/231)。對體系偶極矩向外電場進行Taylor展開得下式

對電子密度函數也可以向外電場進行Taylor展開,其中ρ(n)體現出電子密度對外場的n階響應。其中ρ(0)就相當于無外場時的電子密度分布。
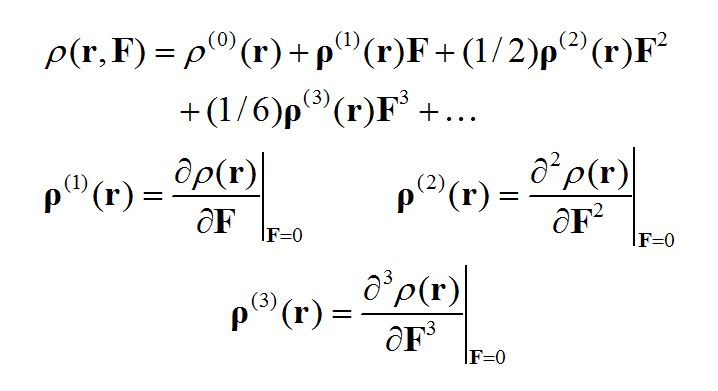
基于偶極矩(電子貢獻的部分)與電子密度的關系,進行對比我們就知道各階(超)極化率和ρ(n)是怎么對應的。通過ρ(n)可以考察體系不同區域對(超)極化率數值的貢獻,這被稱為(超)極化率密度。
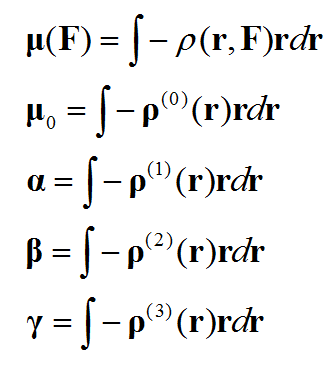
計算不同的(超)極化率密度過程大同小異,本文我們只討論計算和繪制上面列出的階數最高的,即第二超極化率密度。搞明白這個后繪制極化率密度、第一超極化率密度也就是小菜了,舉一反三即可,計算公式在文末給出了。
第二超極化率密度ρ(3)是三階張量函數,第二超極化率γ是個四階張量,我們不可能把每個分量都討論一遍,否則太費勁。我們這里只關注最重要的一個分量,zzzz。具體寫出來是這樣:
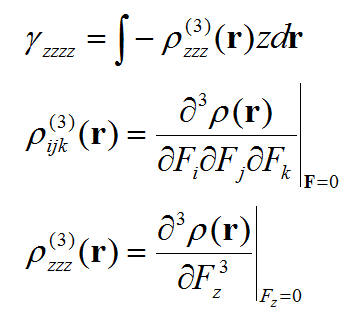
我們一旦把ρ(3)zzz這個函數圖形繪制出來,就能考察體系不同區域對γzzzz的貢獻了。計算這個密度對外場z分量的三階導數我們需要用有限差分的方法。具體計算公式如下所示
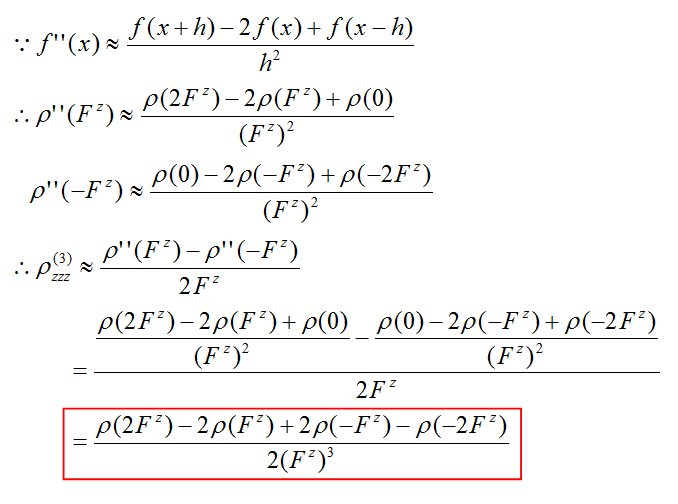
圖中開頭的是有限差分求二階導數的公式,我們將它代入有限差分求一階導數的公式就得到了有限差分求三階導數的公式。最后的紅框就是我們實際通過做密度差以及密度和求ρ(3)zzz的公式了。括號里的Fz代表在z方向外加微量電場(數值大小對應差分步長)時的結果。差分步長過大過小都會造成結果精度的下降,根據測試用0.003 a.u.左右比較不錯。
利用Multiwfn的實空間函數自定義操作功能,結合Gaussian等程序產生的波函數文件,就可以很容易地根據上式得到ρ(3)zzz圖像了。下面我們用甲醛作為實例來演示計算。
2 計算γzzzz
討論ρ(3)zzz前,我們先用Gaussian把γzzzz給算出來,當然這一步不是必需的。既然討論的是分量,就必須把分子朝向先明確了。本文用的示例分子甲醛的朝向如下,結構已在B3LYP/TZVP下優化。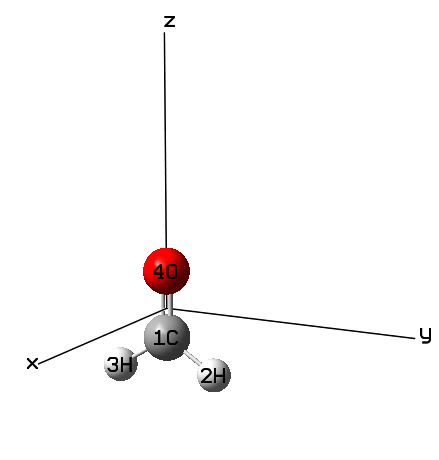
算γ的輸入文件如下。這會基于HF的解析三階導數做一次有限差分得到γ對應的四階導數。
# HF/aug-cc-pVTZ polar=gamma
B3LYP/TZVP opted
0 1
C 0.00000000 0.00000000 -0.52710800
H 0.00000000 0.93885600 -1.11413900
H 0.00000000 -0.93885600 -1.11413900
O 0.00000000 0.00000000 0.67386600
0.0
末尾的0.0代表外場為0,即我們計算的是靜態的γ。顯然用HF算超極化率肯定不準,但本文只是示意而已所以無所謂。從結果末尾可見γ的zzzz分量為0.145571D+04 a.u.,即1455.71 a.u.。
3 產生波函數文件
下面我們獲得不同大小外電場下的波函數文件。雖然一般加電場計算的時候都要用nosymm避免Gaussian把分子自動調整到標準朝向下(否則實際外加電場方向將和期望的不符),但當前例子里的坐標已經是在標準朝向下了,所以不用寫nosymm。
我們總共要得到四個波函數文件,分別是外場為-2Fz、-Fz、Fz、2Fz的情況。這里我們用0.003a.u.外場為步長。我們先計算-2Fz,于是外場就是-0.006a.u.,對應field=z+60關鍵詞(提醒一下,Gaussian中field關鍵詞定義的外場方向和一般定義是反過來的)。輸入文件如下:
# HF/aug-cc-pVTZ field=Z+60 out=wfx
B3LYP/TZVP opted
0 1
C 0.00000000 0.00000000 -0.52710800
H 0.00000000 0.93885600 -1.11413900
H 0.00000000 -0.93885600 -1.11413900
O 0.00000000 0.00000000 0.67386600
C:\H2CO-2FZ.wfx
算完上面這個任務后,改成field=Z+30再次計算得到H2CO-FZ.wfx,改成field=Z-30得到H2CO+FZ.wfx,改成field=Z-60得到H2CO+2FZ.wfx。這樣所需的四個外場下的波函數文件就都齊了。
實際上Gaussian能產生的.wfn、.wfx、.fch都可以作為Multiwfn的輸入文件,結果都一樣。但是當外場很小時(特別是小到0.001 a.u.程度時),可能是因為.wfn格式的數據記錄有效位數相對有限的原因,結果和.wfx偏差較大,所以這里用數值記錄精度更高的.wfx格式,當然用fch也是可以的,記錄精度同樣很高。
4 通過自定義運算獲得ρ(3)zzz
Multiwfn的主功能3、4、5,即繪制曲線圖、平面圖、等值面圖的功能都可以設定對實空間函數的自定義運算,作密度差是其最常見的應用,有興趣可以看《使用Multiwfn作電子密度差圖》(http://www.shanxitv.org/113)。本文算ρ(3)zzz是自定義運算的一個很特殊也很能證明其價值的應用。我們按照ρ(3)zzz計算公式的分子定義自定義操作的運算順序,然后除以分母就行了。啟動Multiwfn,然后依次輸入
C:\H2CO+2FZ.wfx //首先載入ρ(3)zzz計算公式的分子中的第一項ρ(2Fz)
5 //計算格點數據并顯示等值面
0 //自定義操作
5 //接下來對5個文件進行操作
-,C:\H2CO+FZ.wfx //公式中的-2ρ(Fz)項,通過減兩次來表現
-,C:\H2CO+FZ.wfx
+,C:\H2CO-FZ.wfx //公式中的2ρ(-Fz)項,通過加兩次來表現
+,C:\H2CO-FZ.wfx
-,C:\H2CO-2FZ.wfx //公式中的-ρ(-2Fz)項
1 //電子密度
2 //中等質量格點
然后程序開始計算密度數據并按照上述定義的規則進行運算,算完之后,我們要讓格點數據除以分母,即2(Fz)^3項。對于當前情況,這一項是2*0.003^3=0.000000054。接著輸入
6 //除以某個值
0.000000054
-1 //觀看等值面
在蹦出的圖形窗口中將isovalue設大一些,這里設為0.5,如下所示
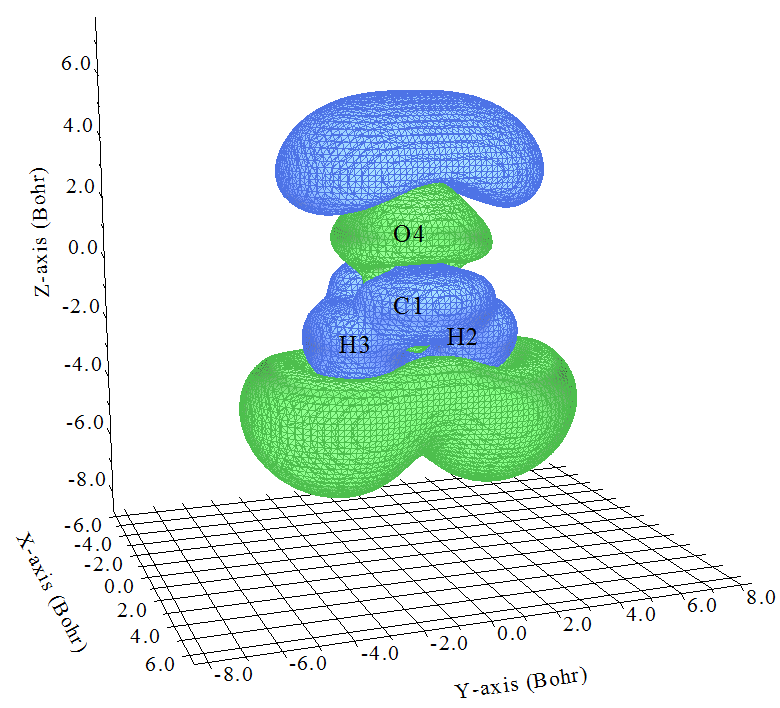
這就是ρ(3)zzz啦!第一節已經給出了ρ(3)zzz和γzzzz的關系,即各個位置的ρ(3)zzz乘上相應位置的-Z再全空間積分就是γzzzz,因此我們容易想象體系不同位置對γzzzz的貢獻。比如在原點附近(大約C=O中央),Z接近于0,所以這部分區域即便等值面挺大,即ρ(3)zzz數值不小,在乘了-Z后對γzzzz的貢獻也不會太大。而O的上方有一大塊藍色(負值)等值面,Z的數值也不小,和-Z相乘后肯定那部分電子對γzzzz有較大正貢獻。在兩個H下方有一大塊綠色(正值)區域,那部分Z為不小的負值,故乘上-Z后也對γzzzz有較大正貢獻。
這么考察還稍微有點費勁,我們可以把已經得到的這個ρ(3)zzz乘上-Z之后再考察圖形,這樣就能更直觀看到不同位置的貢獻了,因為直接一積分就是γzzzz了。我們可以用Multiwfn的格點數據處理功能實現。我們關閉圖形窗口,然后輸入
0 //返回主菜單
13 //處理格點數據
11 //對格點數據進行操作
20 //乘上坐標變量(此功能在2015年9月13日及之后更新的Multiwfn版本中才有)
Z //乘上Z坐標
11 //對格點數據進行操作
5 //乘上個常數
-1 //乘以-1。此時格點數據就相當于-Z*ρ(3)zzz的格點數據了
-2 //觀看等值面
數值為1.0的等值面如下所示
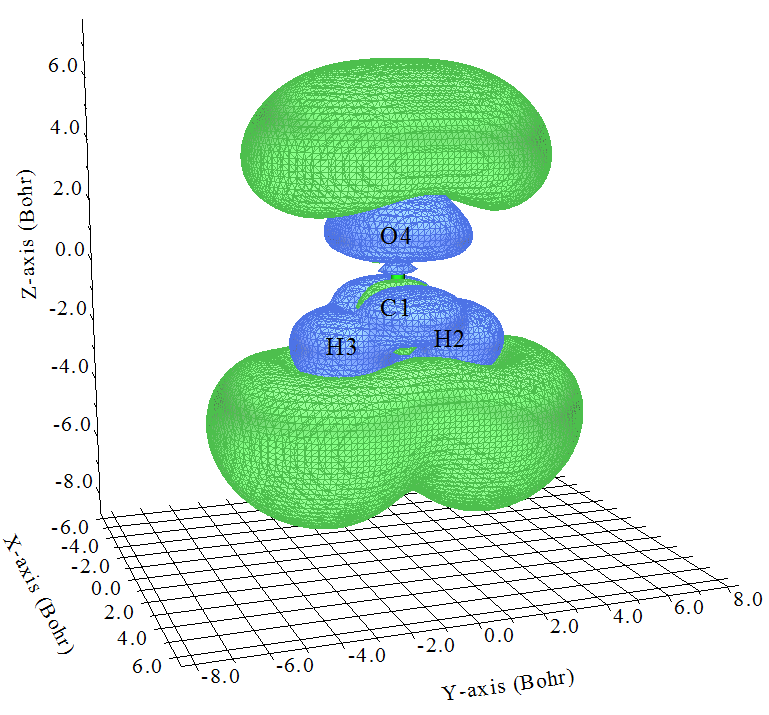
這下考察起來更容易了,也就是圖中綠色等值面越大的區域對γzzzz的貢獻越正,藍色等值面越大的區域對γzzzz的貢獻越負。可見,在分子價層區域,基本上都是負貢獻,而在O、H外圍區域有著很大的正貢獻,并且顯然明顯超越了負值區域,這是為什么當前體系的γzzzz是一個很大正值(前面計算結果為1455.71 a.u.)。對于一個較大體系,通過這么張圖,立刻就能解釋清楚γzzzz為什么大或者為什么小,為什么正或者為什么負,各個區域貢獻一目了然,太爽啦!放到論文里自然會加分。
這張圖也引出一個很重要的問題,也就是計算γ的基組一定要有充足的彌散函數!!!如果沒有彌散函數,那么可以想象,上圖中分子邊緣彌散程度較高的綠色區域就沒法合理描述,此時γzzzz肯定會被低估,甚至為負值!為了證明這點,我們在cc-pVDZ下進行計算,結果僅為26.4 a.u.,而在6-31G*下計算,結果為-108.85 a.u.,連符號都錯了。而加入彌散函數成為6-31++G*后,結果為726.27 a.u.,雖然定量上很爛,但趨勢基本對了。
不同的基組下、不同的理論方法下,γzzzz不同,顯然-Z*ρ(3)zzz也相應地不同,因為后者全空間積分就等于前者。因此,我們也可以通過比較-Z*ρ(3)zzz圖來考察為什么不同基組、不同的理論方法下結果有異。我們還可以用一個高精度級別下計算的-Z*ρ(3)zzz和一個較爛級別下計算的-Z*ρ(3)zzz作差值圖(用Multiwfn主功能13的子功能11做兩個格點數據間的相減運算即可),馬上就能知道較爛的級別是因為在什么區域描述不好而導致結果不好。此時誤差就不再僅僅是一個數值了,我們可以洞察內在真相。
-Z*ρ(3)zzz的積分是γzzzz,我們也可以很容易地通過數值驗證這一點。關閉剛才的圖形界面,然后進入選項17,再輸入1,就得到了當前格點數據在全空間中的統計信息,其中
Integral of all data: 1429.5132718689
就是基于立方格點積分的結果。這個值和我們第二節通過導數方法得到的γzzzz值1455.71 a.u.很接近。如果我們之前在計算格點數據時在設定格點的界面中將延展距離設大到10 Bohr,并且用更好的格點(high quality grid),則結果為1459.43 a.u.,非常接近導數方法計算的結果了。
5 繪制ρ(3)zzz和-Z*ρ(3)zzz的平面圖
我們也可以利用Multiwfn的主功能4十分容易地繪制ρ(3)zzz和-Z*ρ(3)zzz的平面圖,自定義運算的設置方式完全一樣。我們先繪制甲醛分子平面上的ρ(3)zzz等值線圖。
C:\H2CO+2FZ.wfx
4 //繪制平面圖
0 //自定義操作
5 //有5個文件將要與當前文件相運算
-,C:\H2CO+FZ.wfx
-,C:\H2CO+FZ.wfx
+,C:\H2CO-FZ.wfx
+,C:\H2CO-FZ.wfx
-,C:\H2CO-2FZ.wfx
1 //電子密度
2 //等值線圖
[回車] //用默認的格點設定
0 //調整延展距離
10 //設為10 Bohr
3 //YZ平面
0 //X=0
關閉圖像,然后選
-7 //將數據乘上個值
18518518.5185185 //即分母0.000000054的倒數
-1 //重新繪圖
結果如下,實線和虛線分別代表正值和負值部分。后處理菜單還有大量選項可以調節繪圖效果。
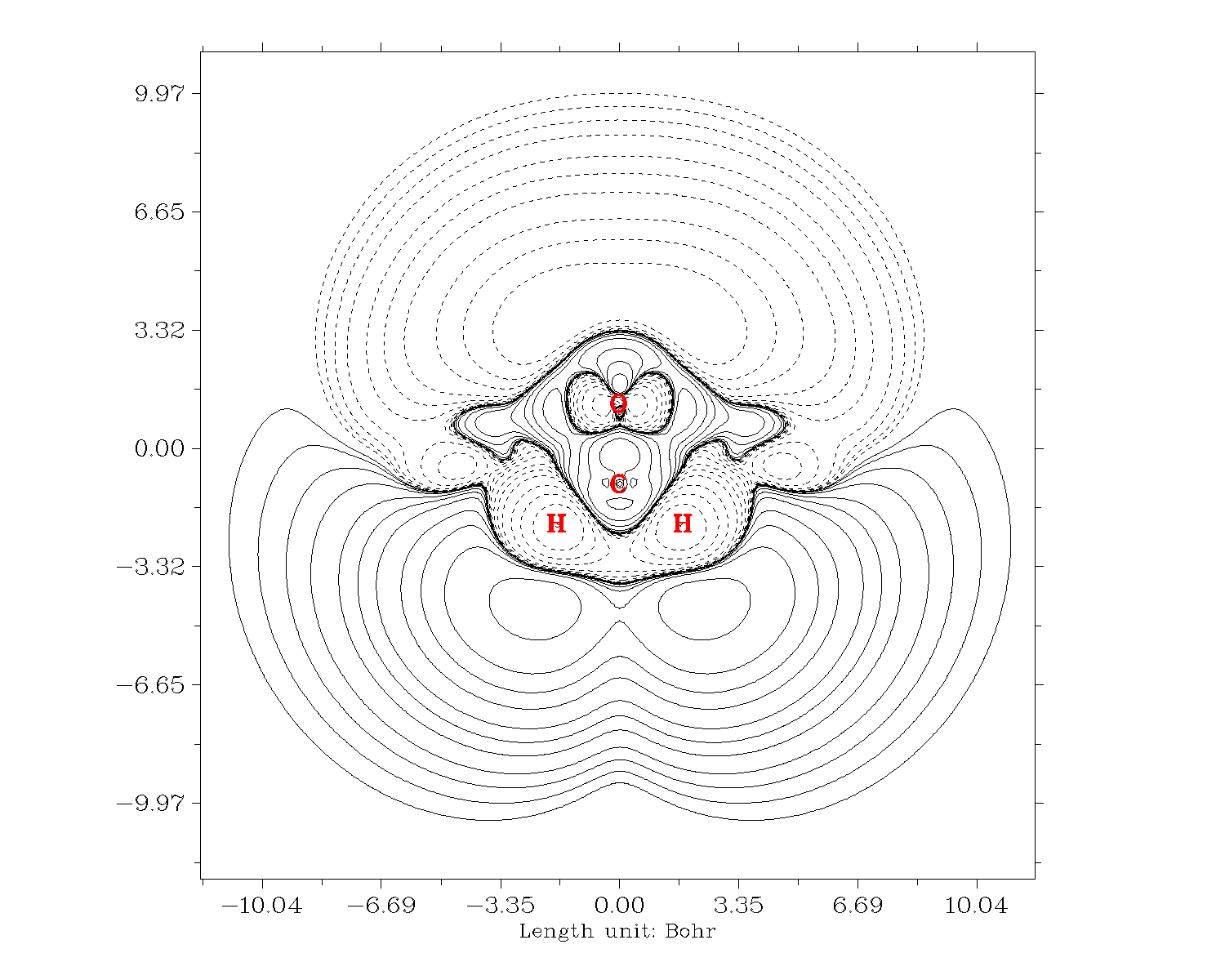
再來繪制-Z*ρ(3)zzz的等值線圖。關掉Multiwfn,把settings.ini的iuserfunc設為23,因為從手冊2.6節可以看到設為23時用戶自定義函數等價于-Z*ρ(r),因此我們直接對用戶自定義函數進行自定義操作就直接得到了-Z*ρ(3)zzz。繪圖步驟和上面一樣,唯一不同的是選擇實空間函數的時候選100(用戶自定義函數)。結果如下
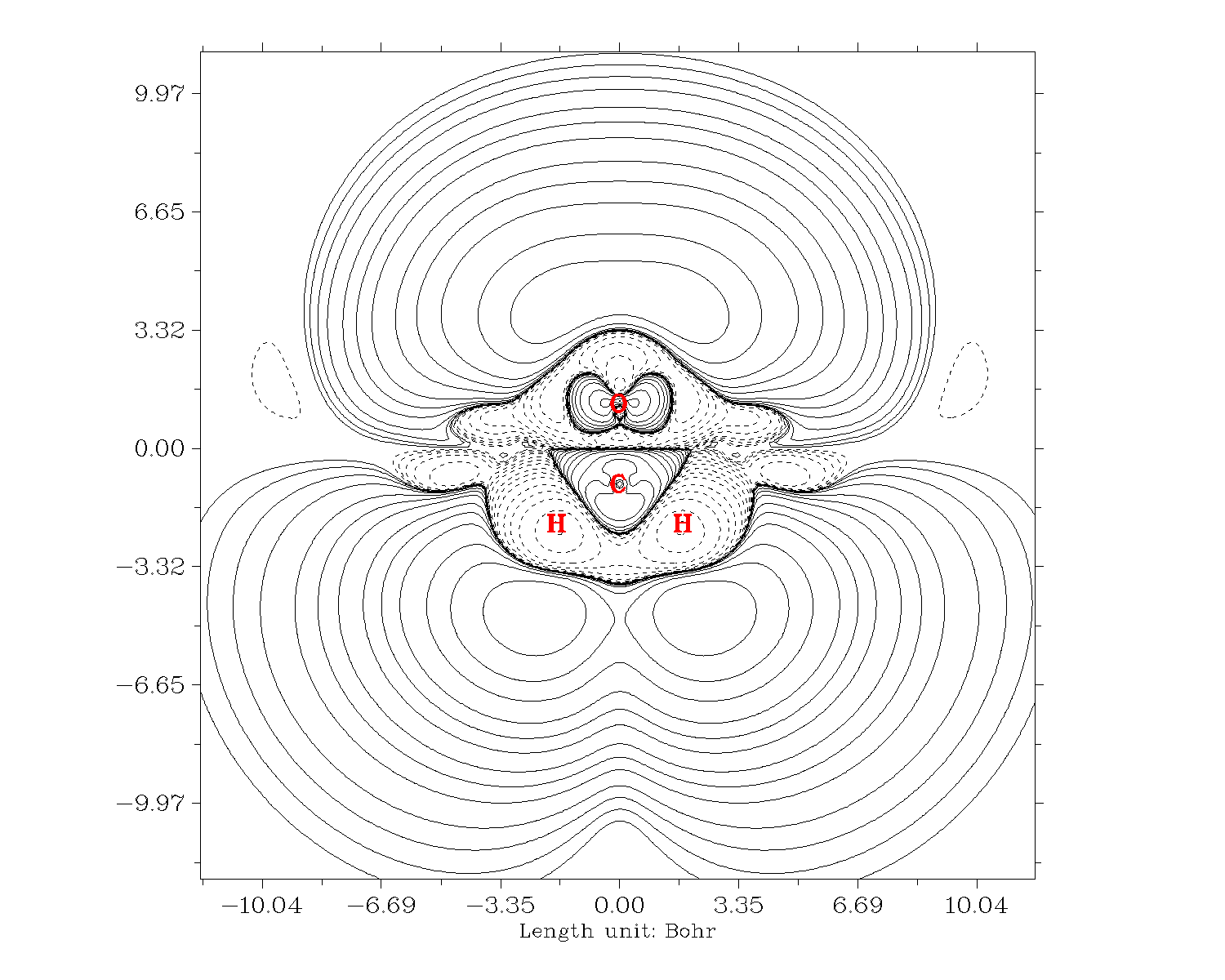
也可以作成填色圖+等值線圖,繪圖類型選繪制填色圖然后后處理菜單再把等值線打開就行了:
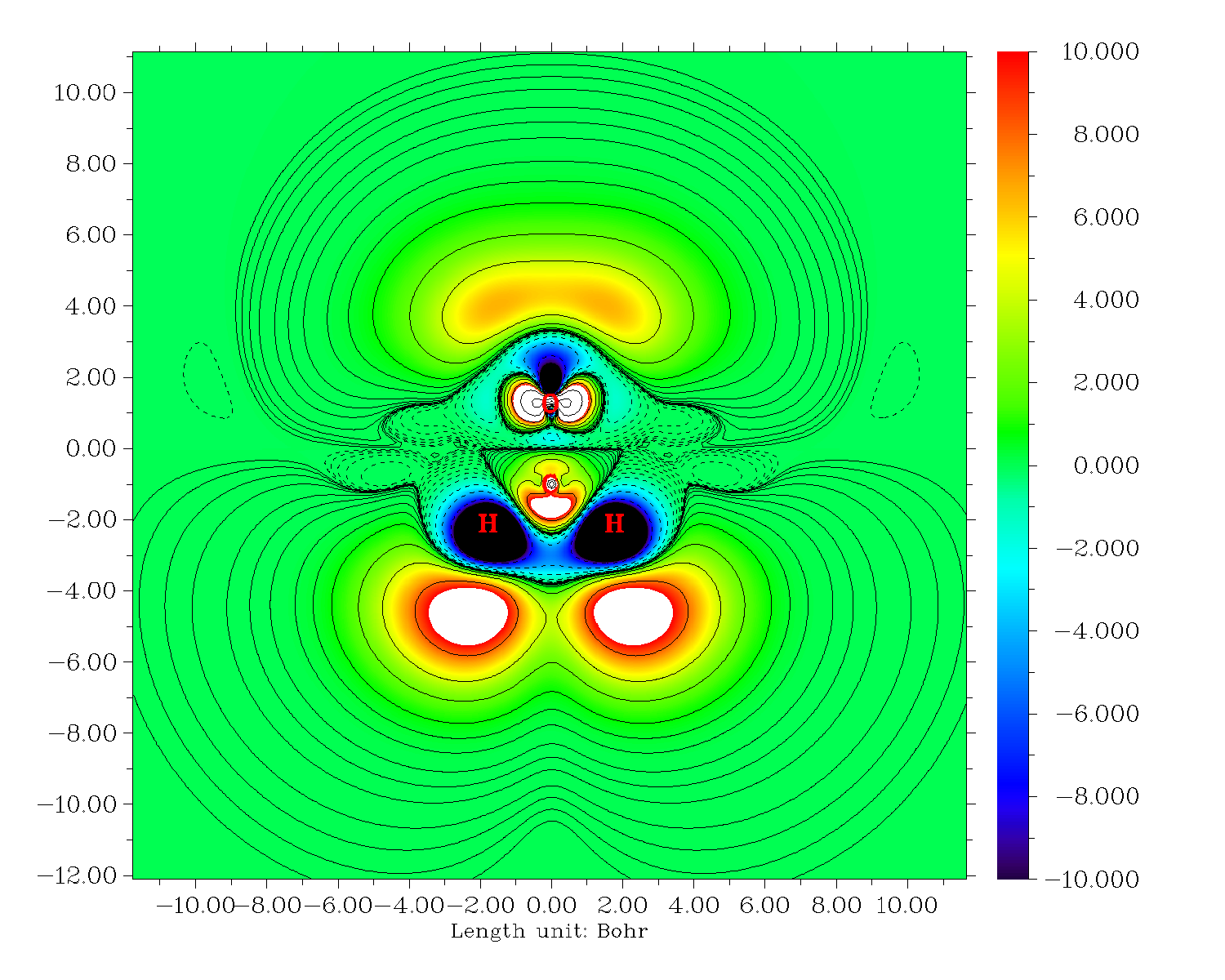
6 快速導出ρ(3)zzz和-Z*ρ(3)zzz的格點數據
在前述分析中的主功能5的后處理菜單中,以及在主功能13中,都有相應的選項將當前內存里的格點數據導出成cube文件,便于進一步通過第三方可視化程序如VMD去繪制等值面圖等等。由于一套計算流程的操作步驟較多,可能有人嫌每次輸入麻煩,其實可以通過以重定向方式運行Multiwfn來使得整個過程方便許多,這方面更多信息見手冊5.2節。
建立一個文本文件,比如叫hyperdens.txt,里面是在Multiwfn中為了產生ρ(3)zzz和-Z*ρ(3)zzz的cube文件所需要敲入的每一條命令。此文件在本文的文件包里已經提供了。首先確保前述的.wfx文件都已經放到C:\下了,hyperdens.txt放到Multiwfn當前目錄下了,然后在命令行窗口里運行Multiwfn < hyperdens.txt,則程序hyperdens.txt里每一行命令就會傳遞給Multiwfn。很快,當前目錄下就產生了density.cub,這是ρ(3)zzz的cube文件,也產生了-Zrho3zzz.cub,這是-Z*ρ(3)zzz的格點文件。
7 計算原子對超極化率的定量貢獻
可能有人想分析各個原子對超極化率的定量貢獻,實際上這可以通過在原子空間內對超極化率密度進行積分得到,這里演示一下。首先我們把settings.ini里的iuserfunc的數值設為-1并保存文件,之后Multiwfn里第100號實空間函數將對應于基于內存里的格點數據進行插值得到的函數。
啟動Multiwfn,載入-Z*ρ(3)zzz的格點文件(比如上一節產生的-Zrho3zzz.cub就是),然后依次輸入
15 //模糊空間分析
1 //在原子空間內進行積分。目前默認用的原子空間劃分方式見選項-1中的文字提示
100 //此函數目前對應于基于-Z*ρ(3)zzz的格點數據插值出來的函數
輸出信息為
Atomic space Value % of sum % of sum abs
1(C ) 80.42330427 5.643648 5.643648
2(H ) 428.30264522 30.055833 30.055833
3(H ) 428.19625953 30.048367 30.048367
4(O ) 488.10117815 34.252152 34.252152
Summing up above values: 1425.02338717
Value下面的值就是各個原子的貢獻值,同時程序還給出了對總值的貢獻比例,可見處在體系中央的碳貢獻不大,但邊緣的H、O貢獻都很大。所有原子加和值為1425.023,這和之前在主功能13里基于立方格點積分得到的1429.513略有偏差,這是正常的,畢竟積分方式不同。通過效仿本節的做法,還可以計算原子對ρ(3)zzz的貢獻。
附錄
