使用Multiwfn圖形化研究弱相互作用

后記：后來又寫了《用Multiwfn+VMD做RDG分析時的一些要點和常見問題》（http://www.shanxitv.org/291），是對本文內容的極其重要的補充，務必在看完本文后閱讀！另外也推薦之后閱讀《繪制有填色效果的用于弱相互作用分析的RDG散點圖的方法》（http://www.shanxitv.org/399）、《使用Multiwfn研究分子動力學中的弱相互作用》（http://www.shanxitv.org/186）、《使用Multiwfn做aNCI分析圖形化考察動態過程中的蛋白-配體間的相互作用》（http://www.shanxitv.org/591）。后來Multiwfn已經完美支持了對周期性體系做RDG分析，研究周期性體系的人一定要看此文：《使用Multiwfn結合CP2K通過NCI和IGM方法圖形化考察固體和表面的弱相互作用》（http://www.shanxitv.org/588）。

后記2：2021年筆者提出了IRI方法，詳細介紹和實例見《使用IRI方法圖形化考察化學體系中的化學鍵和弱相互作用》（http://www.shanxitv.org/598）。IRI與RDG在展現弱相互作用方面效果是等同的，而IRI有個關鍵性的好處是可以把化學鍵作用區域一起直觀地展現出來！因此可以一目了然地圖形化考察體系當中存在的所有類型相互作用，極有價值，讀者務必仔細看一下這篇IRI的介紹文章。由于IRI可以展現更豐富的信息，所以筆者建議使用IRI代替RDG！

2022年筆者又提出了IGMH方法，詳細介紹和實例見《使用Multiwfn做IGMH分析非常清晰直觀地展現化學體系中的相互作用》（http://www.shanxitv.org/621）。IGMH極其靈活，可以任意定義片段來專門圖形化考察片段間和片段內的弱相互作用，還能給出原子和原子對對片段間相互作用的貢獻，而且不像RDG等值面那么容易出現鋸齒，因此IGMH比RDG強大得多！由于有了IGMH和IRI，本文介紹的RDG方法如今已經基本沒有什么用處了，如果沒有特殊原因，不建議用RDG方法！

非常推薦閱讀《一篇最全面介紹各種弱相互作用可視化分析方法的文章已發表！》（http://www.shanxitv.org/667）介紹的筆者的綜述文章，其中對NCI、IRI、IGMH及相關方法有非常深入透徹的介紹并給了大量應用例子。

注：本文是啟發式文章，幫助你從本質理解RDG方法的原理和細節，要讀就讀完整，絕對不要斷章取義，更絕對不要才讀了前幾節就急急忙忙算！如果你特別著急要算出結果，建議別看此文，而直接看Multiwfn手冊3.23.1節的例子，寫得明顯更簡練、直白，并且吐血建議直接看這個演示視頻：《使用Multiwfn做NCI分析展現分子內和分子間弱相互作用》（https://www.bilibili.com/video/av71561024），幾分鐘之內就能學會操作！ 

使用Multiwfn圖形化研究弱相互作用

文/Sobereva @北京科音
First release: 2010-Aug-28  Last update: 2020-Jun-10

楊偉濤課題組2010年在名為Revealing Noncovalent Interactions (JACS,132,6498-6506)一文中提出了一種的可視化研究弱相互作用的方法，稱為RDG或NCI方法。其概念簡單清晰，具有廣泛意義，很有實用價值，本文目的之一在于介紹、推廣這一方法，但與原文的角度有一些不同。本文目的之二就是結合實例介紹Multiwfn做這種分析時的操作方法。能實現這種分析的程序已有不少，Multiwfn是其中最快、最好用、功能最強大的，讀者完全不需要考慮用任何其它程序。

這種分析方法的研究對象從距離上講是中、長程相互作用，屬于弱相互作用范疇，包括諸如氫鍵/鹵鍵/二氫鍵/pi-pi堆積/普通范德華作用等，也能展現位阻作用。雖然原文作者稱這種研究方法的對象是非共價相互作用，筆者認為稱為弱相互作用更為妥當，文中將使用這種稱呼。弱相互作用相關的基本知識在《談談“計算時是否需要加DFT-D3色散校正？”》（http://sobereva.com/413）一文中有講解和辨析。

本文所用的Multiwfn是免費、方便、靈活且功能最為強大的波函數分析程序，可以從http://www.shanxitv.org/multiwfn下載最新版本，入門資料見《Multiwfn入門tips》（http://www.shanxitv.org/167）、《Multiwfn FAQ》（http://www.shanxitv.org/452）、《Multiwfn波函數分析程序的意義、功能與用途》（http://www.shanxitv.org/184）。

本文介紹的方法僅僅是Multiwfn支持的一大波弱相互作用分析方法當中的一種，Multiwfn還能實現很多非常有價值的弱相互作用分析，見《Multiwfn支持的弱相互作用的分析方法概覽》（http://www.shanxitv.org/252）。

本文用到的所有輸入文件可在此下載：http://sobereva.com/attach/68/file.rar。

1. 用RDG函數等值面顯示弱相互作用區域

此方法的主要目的在于凸顯出體系中涉及弱相互作用的區域，以便直觀地了解到分子中哪些區域與弱相互作用有關。也就是定義一個實空間函數，使其數值能夠區分開體系中具有不同特征的區域。此方法使用的是約化密度梯度函數(Reduced density gradient, 下文稱RDG)，其表達式為1/(2*(3*π^2)^(1/3))*|▽ρ(r)|/ρ(r)^(4/3)，其中▽是梯度算符，|▽ρ(r)|即電子密度梯度的模。實際上前面的常數項（其值為0.16162）可以忽略掉，只考察|▽ρ(r)|/ρ(r)^(4/3)部分。一個分子體系主要由以下四部分構成：

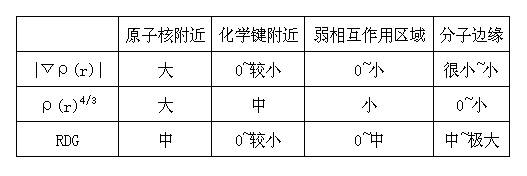
圖1

表格中的大、小的標準比較模糊，只是定性的。如果我們想要找弱相互作用區域，利用RDG函數的數值大小差異就可以將“原子核附近”和“分子邊緣”區域去掉，但“弱相互作用區域”和“化學鍵附近”的RDG函數值、|▽ρ(r)|值都比較小，區分不開，但ρ(r)存在一定差異。所以，結合使用RDG函數和ρ(r)函數，就可以確定分子中哪些區域涉及弱相互作用。

如果設定立方網格，使網格中的點能夠覆蓋整個體系，做這些點上ρ(r) vs. RDG的散點圖，就可以把上述概念圖形化且定量地表述出來。下面來做甲烷二聚體的這種圖。

首先要產生Multiwfn可以識別的含有波函數信息的輸入文件，Multiwfn支持的這樣的文件的類型很多，比如wfn、mwfn、fch、molden等等，詳見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》（http://www.shanxitv.org/379），用哪種文件做RDG計算結果原理上都一樣。此例我們用Gaussian跑一個甲烷二聚體來得到wfn文件，關鍵詞寫# B3LYP/6-311G* opt em=GD3BJ out=wfn，坐標后面空一行寫上.wfn文件的輸出路徑。此任務代表使用B3LYP-D3(BJ)/6-311G*級別對甲烷二聚體進行優化，最終結構對應的波函數將產生為.wfn文件。附件里的methanedimer.gjf是已寫好的，用Gaussian執行后得到methanedimer.wfn。

先把multiwfn目錄下的Settings.ini里的RDG_maxrho設為0.0（注意等號后面要留空格。改這個僅限此節的例子，幫助你由淺入深啟發式了解RDG方法的原理，此節例子算完后應把它的數值改回默認值0.05，其原因看了后文就會明白）。然后啟動Multiwfn，依次輸入：
c:\methanedimer.wfn   //輸入文件的路徑
100   //功能100，其中包含Multiwfn中比較雜的功能
1    //繪制“函數1 vs. 函數2”散點圖并生成相應格點文件
1,13  //輸入函數1和函數2的序號，分別作為散點圖的橫軸和縱軸。在Multiwfn支持的函數中ρ(r)是第1號，RDG函數是第13號。
2   //用中等質量的網格，總共約512000個點，x,y,z方向的具體點數通過使x,y,z方向格點間距相等來自動確定。網格的區域自動往分子外延展6 bohr。
現在開始計算格點數據。格點數越多、體系所含Gauss函數越多，計算速度越慢，計算時間與二者都成正比。計算完畢后，輸入
4   //設定散點圖X軸
0,0.35 //X軸上下限的值
5   //設定散點圖Y軸
0,2 //Y軸上下限的值
-1  //繪制散點圖
很快ρ(r) vs. RDG的散點圖就彈出來了，如圖2左圖所示。在圖上點右鍵可以關閉，然后選功能1可以將圖保存到當前目錄下。如果對圖的效果不滿意，可以選功能2將數據導出到當前目錄下output.txt，然后用origin、sigmaplot等程序作散點圖。如屏幕上提示所示，其中前三列是數據點的坐標，后兩列是兩個函數的值，將后兩列分別作為散點圖的X和Y軸數據即可，注意要調節好坐標軸范圍。使用Origin基于Multiwfn的輸出文件繪制散點圖的過程我錄制了一個視頻，不會操作者可以參考下，見https://www.bilibili.com/video/av27535384/。

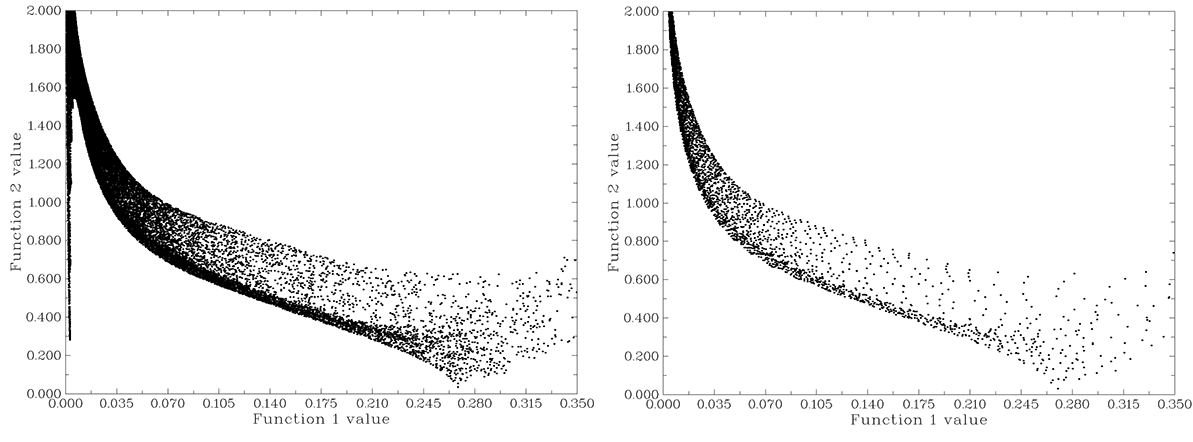
圖2

按上述步驟繪制甲烷孤立狀態的散點圖得到圖2右圖（設定網格時選3，用高質量網格）。從圖2可以看出，體系中存在與不存在弱相互作用時散點圖最主要區別在于圖中最左側是否有一個豎條，在原文中這被稱為spike。這個豎條上的點正是弱相互作用區域“RDG數值為0~中，ρ(r)^(4/3)數值為小”所對應的點；在右側也有一個區域RDG 值接近0，這是C-H鍵區域“RDG數值為0~較小，ρ(r)^(4/3)數值為中”所對應的格點；圖中坐標軸范圍的更右側就是原子核附近區域的點；圖中左上角的尖峰再往上繼續延伸就是分子邊緣的區域，雖然離分子越遠的地方|▽ρ(r)|和ρ(r)^(4/3)都越小，但后者比前者減小得更快，所以離分子越遠RDG值越大，并直至無限大，可自行調整坐標軸觀看。不同體系的散點圖的成鍵、原子核附近、分子邊緣區域都是類似的，一個體系中是否含有弱相互作用，就是看在ρ(r)較小區域是否有spike出現，這是此分析方法的要點。當然，網格不能太稀疏，如果在弱相互作用區域恰好沒有點，spike也不會出現。

接下來，要用等值面確定這些對應于弱相互作用區域的點在實空間上的位置。在計算完格點后的那個菜單中，輸入7，然后輸入想看的等值面數值就可以觀看第2個函數（即RDG函數）的等值面。其0.5的等值面如圖3左圖所示

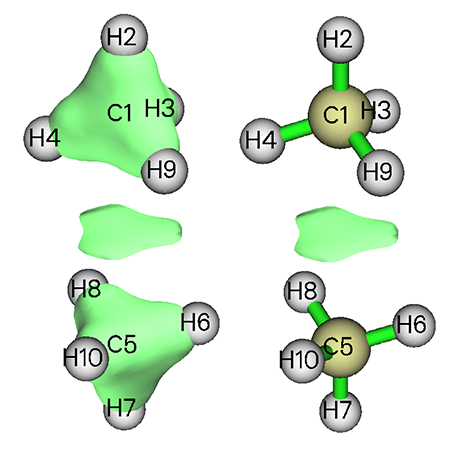
圖3

圖上在兩個甲烷中間出現了封閉的等值面，描繪的正是二者間的范德華作用，但是在分子上也出現了三角形封閉的等值面。這是因為成鍵區域和弱相互作用區域的RDG函數數值范圍有很大程度的重疊，如果在圖2左圖上做一個y=0.5的直線，會發現這條直線不僅貫穿spike，還貫穿成鍵區域，所以相應的RDG=0.5的封閉等值面不止一個，而在成鍵區域附近也會出現。這也是前面所說，必須再通過ρ(r)函數區分開成鍵和弱相互作用區域。

屏蔽掉成鍵區域，也就是將ρ(r)值稍微大一些的區域，比如ρ(r)=0.05以上的RDG函數的數值設得很大，比如設成100，這樣在散點圖上y=0.5的直線就不會經過那個區域了，等值面也就只剩下弱相互作用區域。具體做法是在之前的菜單中選擇-3，然后輸入0,0.05，再輸入100，這就表明將ρ(r)的范圍在[0,0.05]以外區域的點的RDG函數數值設為100。重新繪制散點圖，得到了圖4的結果，等值面也變為了所期望的圖3右圖的情況。

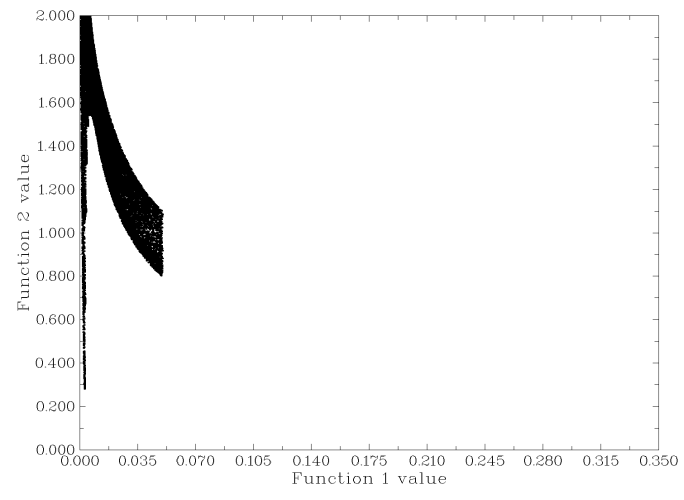
圖4

一般來講，觀看RDG函數一般觀看的是0.5的等值面，這沒有什么嚴格的物理意義，只是等值面大小比較適中。由于弱相互作用區域的ρ(r)一般不會越過0.05，散點圖上y=0.5的直線在ρ(r)<=0.05的區域內也只與spike相交，所以每次作弱相互作用等值面圖時沒必要再考察散點圖，只需直接將ρ(r)>0.05的點的RDG函數值設為較大數值就行了。由于這個步驟經常要做，為了方便，Multiwfn在settings.ini里面有一個RDG_maxrho參數，凡是涉及到計算RDG函數的功能，只要某個點的ρ(r)大于這個參數，這個點的RDG值就自動被設為100，這個參數默認被設定為0.05。所以用戶就不需要再考慮屏蔽掉成鍵區域了，這已由Multiwfn自動完成。當然，在后文中作完整的散點圖時、或者就是想通過RDG函數研究成鍵區域時，應當關閉這個功能，將RDG_maxrho設為0.0就代表關閉此功能。

2. 合理地設定網格

Multiwfn計算格點時默認將網格根據原子x,y,z坐標的最大值和最小值往外延展6 bohr，留出一定余地，避免等值面被截斷。不過，對于通過RDG函數顯示弱相互作用區域來說，這顯得浪費了，因為弱相互作用區域是在整個體系內側，這就導致很多格點白白用于描述沒用的區域。如果格點質量不夠高，作一些弱相互作用等值面還會有麻煩，比如直接用中等質量格點作苯二聚體的弱相互作用區域RDG=0.6的等值面會得到圖5左側結果，可見薄片狀等值面千瘡百孔，與原文中的圖明顯不同，這是因為這個區域格點太稀疏，對RDG函數描述得不夠精細。

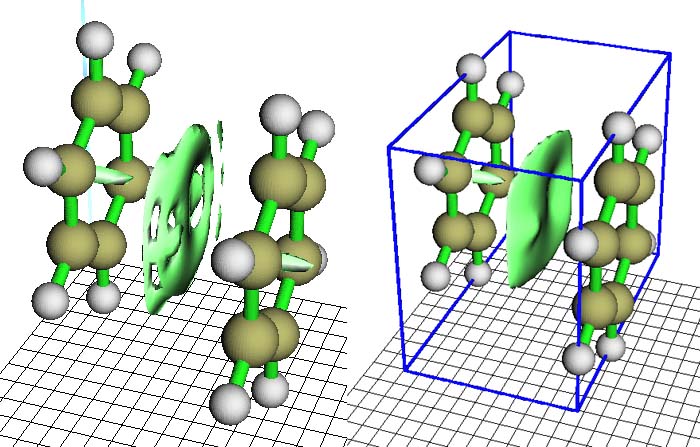
圖5

如果將原本被浪費掉的格點利用起來，加強對分子內部區域的描述，將得到更好的等值面。下例將繪制苯二聚體弱相互作用等值面，并自定義延展距離。由于此例只對RDG函數感興趣，用Multiwfn的功能5（計算格點文件并顯示等值面）即可，不需要像前例中用功能100中的子功能1同時把ρ(r)也算出來。啟動Multiwfn進行如下操作：

benzenedimer.wfn //已在附件中，幾何結構來自原文補充材料，為B3LYP/6-31G*波函數
5  //功能5
13  //RDG函數
-10  //設定延展距離
0  //延展距離為0 bohr，即網格范圍緊貼著體系。此時會看到功能-10條目上顯示的current:變為了0。
2  //用中等質量格點
4  //設定等值面數值
0.6  //等值面數值設為0.6
-1  //觀看等值面
此時圖像顯示出來，如圖5右側所示，點擊Show data range復選框可以用藍線顯示格點數據涵蓋的區域。點Return關閉圖像后，選功能2，格點文件就會被輸出到當前目錄下的RDG.cub中。

由于總格點數沒變，但涵蓋的空間范圍減小了，所以數據點更密，對弱相互作用區域描述得更精確，等值面的窟窿都不見了，好看了許多，很直觀地表現出兩個苯之間的π-π相互作用區域。如果點擊界面右側的Show data range，會用藍框將網格包含的范圍顯示出來。雖然苯分子之間相互作用好看了，但是由于網格沒有延展，導致苯環中間的體現位阻效應（見后文）的梭形的等值面被截斷了一半。此例之所以觀看的不是0.5的等值面，是因為0.5的等值面上也有窟窿，將等值面數值加大可以使等值面范圍擴張，補上窟窿，使圖像好看。

當然，絕不意味著有窟窿就說明是格點不夠精細所致，因為等值面隨數值由小到大的變化過程是：一堆點->一堆小等值面->帶窟窿的大等值面->沒窟窿的面，如果等值面數值取得較小，必然帶窟窿。用Multiwfn繪制此體系的對稱平面上的RDG函數填色圖將易于理解這一點。在Multiwfn里輸入以下命令即可繪制。為得到完整的圖，先把RDG_maxrho設為0.0（別忘了當前例子做完之后一定要改回默認的0.05）。

benzenedimer.wfn
4  //功能4，繪制平面圖
13  //RDG函數
1   //填色圖
按回車使用默認的格點數(200,200)
0  //設定延展距離。默認延展4.5 bohr，對于RDG函數偏大了
2   //改為只延展2 bohr
1  //繪制XY平面
0  //XY平面的Z值為0
圖像很快就彈出來了。如下圖所示

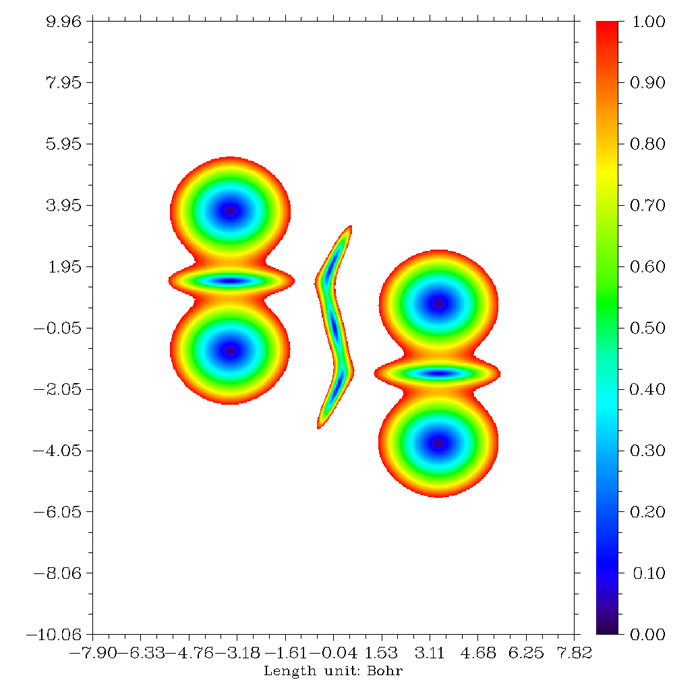
圖6

在分子邊界以外沒有弱相互作用的區域RDG值很大，遠超過1，這樣區域都顯示為白色。圖中央的區域正是描述苯二聚體弱相互作用區域扁片等值面的截面，如果等值面的數值不夠大，等值面只能包圍每個藍色區域，顯然彼此不相連，如果增大到對應綠色區域的值，孤立區域將會相連接，構成整個扁片等值面。如果繼續增大到紅色區域對應的值，則苯環中間代表位阻效應區域的等值面將與分子相連而無法區分。

由于原子間存在弱相互作用時（嚴格來說是指能被RDG函數等值面表現出來的作用）它們的距離一般不會太遠，所以一般能猜到哪些區域可能有弱相互作用，而且有時人們只對諸多弱相互作用區域中的某個一感興趣，此時網格只需要覆蓋那個小區域即可，即便網格點數較少，由于密度大，所以也能描述得較精確，可以節省計算時間。然而確定網格空間位置比較麻煩，Multiwfn在網格設置中提供了一個選項方便研究局部弱相互作用。例如圖7中苯酚二聚體之間只有一小塊區域相接觸，若將網格中心設定在1號和14號原子之間，然后向四周延展一定距離，網格就能覆蓋弱相互作用區域。

phenoldimer.wfn //已在附件中，幾何結構來自原文補充材料，波函數在B3LYP/6-31G*下產生
5 //功能5
13 //RDG函數
7 //將兩個原子的中點作為網格中心
1,14 //兩個原子序號分別為1和14
40,40,40 //由于網格范圍小，用較少的格點數就夠了
3,3,3 //各個方向延展距離皆為3 bohr
4 //設等值面
0.5 //設等值面數值為0.5
-1 //觀看等值面
此時得到圖7的結果。

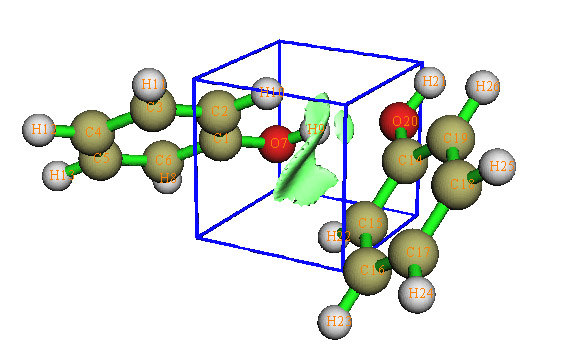
圖7

3 判別弱相互作用的強度與類型

這種分析方法不僅可以指出哪里存在弱相互作用，還可以可視化地了解弱相互作用的強度與類型。

弱相互作用強度一般以相互作用能來衡量，但這是一個全局的量，應用到可視化分析中必須通過局域函數（實空間函數）。在AIM理論中，弱相互作用的臨界點的ρ(r)是衡量相互作用強度的重要指標之一，其數值和鍵的強度存在正相關性，因而也被用來定義鍵級。實際上，此文的分析方法在某種程度上可以視為AIM方法的擴展，RDG封閉的等值面一般包圍著相應的臨界點，如果某個弱相互作用在其臨界點處ρ(r)較大，由于ρ(r)的連續性，一般在周圍區域ρ(r)也會較大。所以，將ρ(r)的數值大小以不同的色彩映射到RDG等值面上，相互作用的強度就一目了然。

ρ(r)只能反映出強度，但類型需要由sign(λ_2)函數來反映，這個函數是電子密度Hessian矩陣的第二大的本征值λ_2的符號，在AIM理論中鍵臨界點的sign(λ_2)=-1，環、籠臨界點的sign(λ_2)=+1，在接近臨界點的區域其值與臨界點處一般相同。可以將sign(λ_2)函數用不同色彩投影到RDG等值面上，用來表現某一個區域的相互作用類型。

若將ρ(r)和sign(λ_2)函數相乘而得的sign(λ_2)ρ函數投影到RDG等值面上，則弱相互作用的位置、強度、類型都能一目了然地顯現出來。

原文中色彩刻度被設為藍->綠->紅，色彩刻度一般設為[-0.04,0.02]或[-0.03,0.02]，對于個別體系為了色彩效果更好，可以進行調整。不同顏色所代表的ρ(r)、λ_2數值以及所對應的相互作用類型可以用下面這個圖來表示（對應的高清圖是Multiwfn目錄下的examples\RGB_bar.png，筆者允許大家在自己的文章里直接使用這個圖，請屆時引用http://www.shanxitv.org/598里介紹的IRI方法的原文，IRI原文里面有和這個差不多的色彩刻度圖）

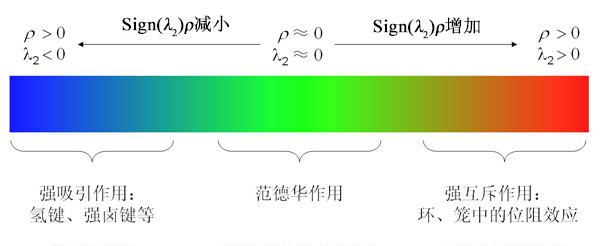
圖8

藍色區域ρ(r)大、sign(λ_2)=-1，表現較強、起吸引作用的弱相互作用，符合這個特征的最常見的就是氫鍵，還包括較強的鹵鍵等作用。當然如果把ρ(r)更大的，即成鍵區域也算進去，其等值面也是藍色。綠色區域的ρ(r)很小，說明相互作用強度很弱，范德華作用區域符合這個特征。由于這樣區域電子密度很小，λ_2的符號較為不穩定，所以可正可負。紅色區域ρ(r)較大、sign(λ_2)=+1，對應于在環、籠中出現的較強的位阻效應區域（也被稱為nonbonded overlap），產生張力，因而紅色等值面周圍原子間起互斥效應。

圖9是甲酸二聚體的sign(λ_2)ρ vs. RDG的散點圖和填色等值面圖。如果將這個散點圖的左邊折疊到右邊去，就還原為ρ(r) vs. RDG圖。

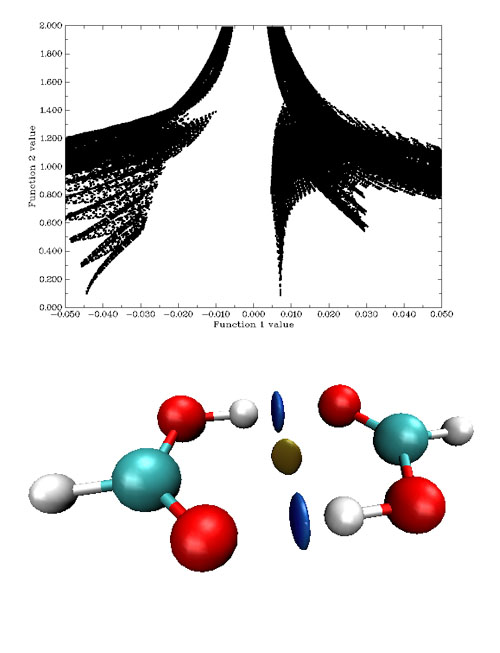
圖9

散點圖左邊的spike的sign(λ_2)ρ很負，對應很強的氫鍵，因而相應的等值面為藍色。這個spike在散點圖上看起來像是一條一條地有規律地組成的，并不致密，這是因為落在這個空間區域的格點偏少，由于格點是均勻、規則地以立方形式排列的，所以函數值變化起來比較有規律，如果增加這個區域格點密度，這個spike會更為致密。右側的spike的sign(λ_2)ρ為較小正值，對應于圖中棕色圓片等值面，體現了微弱的位阻效應。比較下面的例子會看到，這種靠弱相互作用結合的復合物，即便之間有位阻效應出現也不會太強，否則將不足以被弱相互作用抵消掉。至于只靠范德華這種很弱作用力結合的復合物，在平衡狀態下不會有位阻區域產生，除非是很強的范德華作用，如π-π堆疊，才可能有微弱的對應位阻效應的區域出現。下面的例子是鄰氯苯酚

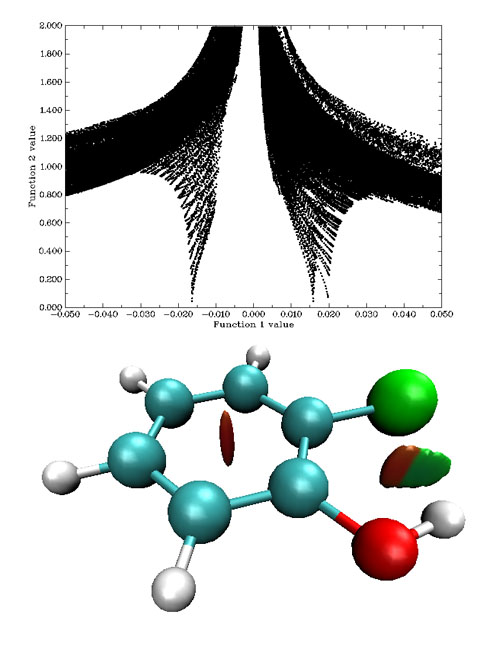
圖10

在苯環中間有紅色梭形區域，體現較強位阻效應，對應散點圖最右邊的spike。羥基與氯原子之間RDG等值面一小半橘紅色，一大半綠色，在散點圖上分別對應著spike尖端x值約為+0.016和-0.017的spike。如果橫坐標不是sign(λ_2)ρ而只是ρ(r)，則這兩個spike是合并在一起的，無法區分究竟代表什么類型的作用，而引入sign(λ_2)使其本質一目了然。這個等值面說明羥基與氯原子間既存在著位阻效應，也存在著弱氫鍵作用，互斥和吸引效應并存。如果做AIM分析，會發現橘紅色區域里面是一個(3,+1)臨界點，綠色區域里面是一個(3,-1)臨界點，兩個臨界點擴展后連成一個等值面，但各自區域的特征仍然能夠靠顏色分辨。

估計會有人存在疑問，羥基與氯原子之間有一大半區域是綠色，從色彩刻度條上看應該對應范德華作用，為何說是弱氫鍵？一方面，從散點圖上看，范德華作用的spike尖端的ρ(r)不會達到這么大，在原文中作者建議將是否ρ(r)小于0.005作為相互作用是否屬于范德華作用的評判標準。另外O-H----Cl這樣的構成也符合形成氫鍵的條件。這種情況實際上理應顯示成淡藍色，但由于色彩刻度上下限的設定有一定隨意性，導致同一個色彩刻度范圍未必對每個體系都很合適。如果不同體系不用同一個上下限，在橫向比較作用強弱的時候又會缺乏基準，而且需要每次手動調整，略微麻煩，一般來說還是按照原文，色彩刻度統一使用[-0.04,0.02]范圍為好。但遇到顏色與期望的差異較大時，最好還是看看散點圖上相應spike的位置來確認。色彩刻度的隨意性是這種分析方法的一個弊端，不同色彩刻度下得到的此體系的等值面如下圖所示，差異是很明顯的。另外屏幕對比度、可視化程序中分子與光源的相對朝向等諸多問題都可能影響色彩，給定量比較帶來些麻煩。

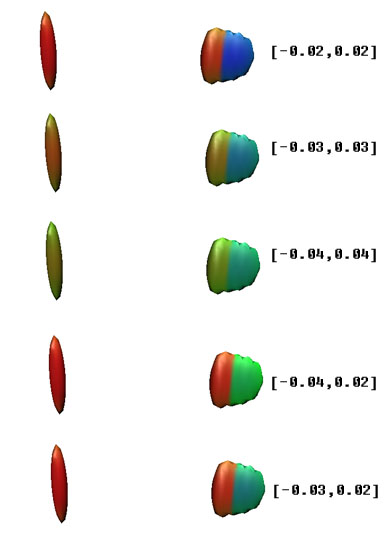
圖11

下圖的四個體系分別是：1. 環氧乙烷與氟化氯通過鹵鍵形成的復合物 2.二環[2,2,1]庚烷 3.gauche構象的苯乙胺 4.直立構象的甲基環己烷。這些留給讀者自行分析，在原文的補充材料中也有很多例子，值得一看。

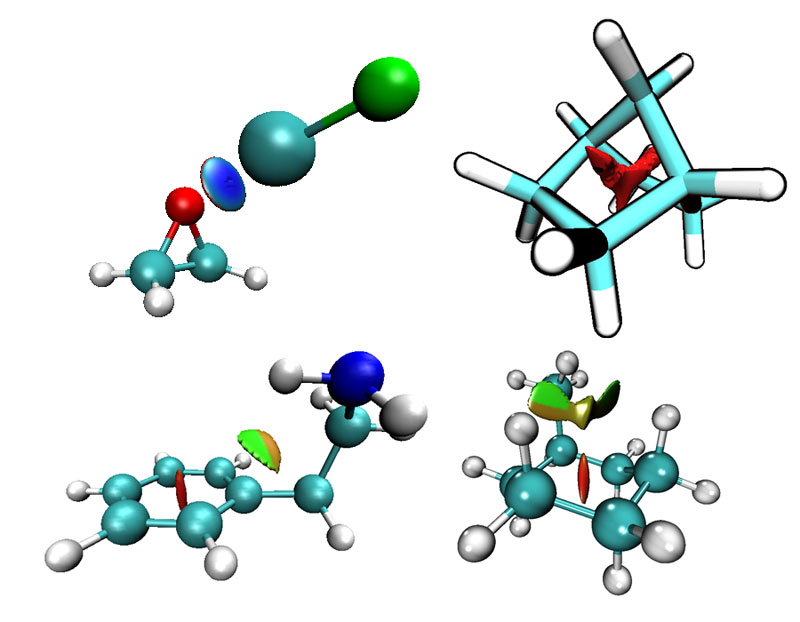
圖12

4 實例

這里以苯酚二聚體為例介紹如何繪制sign(λ_2)ρ函數填色的RDG等值面圖。如果你已做了前面的例子，注意檢查一下RDG_maxrho是否已經改回原先默認的數值0.05了。

phenoldimer.wfn  //文件名
100  //功能100
1    //繪制“函數1 vs. 函數2”散點圖并生成相應格點文件
15,13  //sign(λ_2)ρ是第15號函數，RDG是第13號函數
-10  //設定延展距離
0  //延展距離為0 bohr
2  //用中等質量格點
當選取的函數1和函數2分別為sign(λ_2)ρ和RDG時，散點圖的x,y坐標軸范圍會分別自動調到[-0.05,0.05]和[0.0,2.0]，所以直接用功能-1就能看到合適的散點圖了，如下圖上方所示。之后選擇選項3將函數1和函數2的高斯類型格點文件輸出到當前目錄下func1.cub和func2.cub。

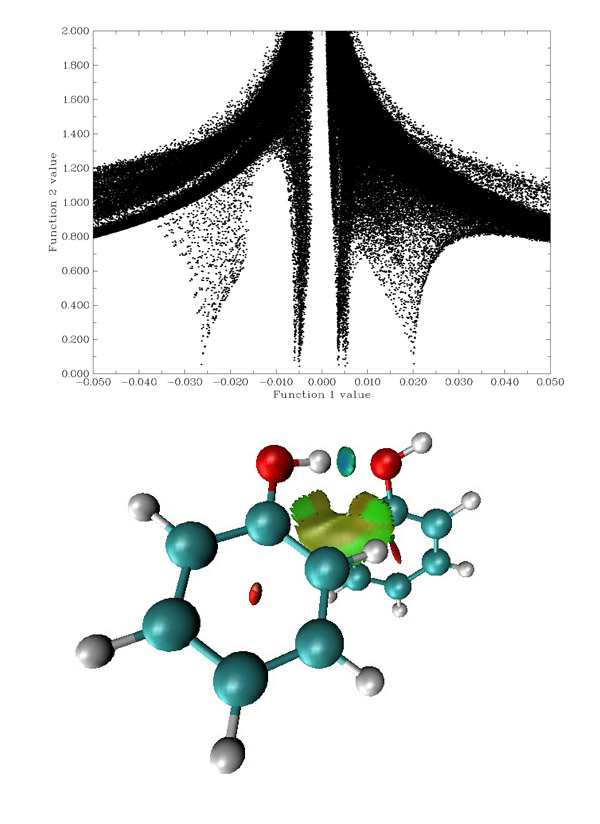
圖13

雖然能顯示高斯類型格點文件的等值面的程序很多，但支持將一個函數數值用不同顏色填到另外一個函數的等值面上的可視化程序比較有限，常用的GaussView雖然支持，但操作不便而且不夠強大。VMD是觀看、分析分子動力學結果最重要的軟件之一，它在映射顏色和顯示等值面方面也很好用，等值面又光滑又有光澤，填色的色彩變化細膩，調整等值面也比較容易，而且運行流暢。VMD可以免費在http://www.ks.uiuc.edu/Development/Download/download.cgi?PackageName=VMD下載。

首先安裝VMD，然后將func1.cub和func2.cub復制到VMD安裝后的目錄下，即vmd.exe所在路徑。然后在此目錄下編寫一個文本文件，后綴為.vmd，比如ltwd.vmd。在里面填上如下內容：
mol new func1.cub
mol addfile func2.cub
mol delrep 0 top
mol representation CPK 1.0 0.3 18.0 16.0
mol addrep top
mol representation Isosurface 0.50000 1 0 0 1 1
mol color Volume 0
mol addrep top
mol scaleminmax top 1 -0.04 0.02
color scale method BGR
保存文件后，啟動VMD，選File-Load State，選擇ltwd.vmd，圖13下方的圖就顯示來了。若想把背景改成白色，選Graphics-Colors-Display-Background-8 White。圖中的彎曲的片狀等值面邊緣略有鋸齒，可以通過增加此處格點密度來改善。從顏色上可看出，彎曲的片狀等值面描述的是二聚體之間范德華作用，但部分區域也有微弱的位阻效應。圓片等值面只有中間呈藍色，說明H與O之間形成了氫鍵，但并不像甲酸二聚體的氫鍵那么強。

VMD里面每個操作對應一條語句，載入.vmd本質上就是讓.vmd文件中的語句全部執行，這就免得每次都手動執行載入文件、設定參數的一系列繁瑣步驟。比如mol new func1.cub的含義就是讀入當前路徑下func1.cub文件（默認的當前路徑一般就是vmd.exe所在路徑），mol scaleminmax top 1 -0.04 0.02代表將1號representation（對應于顯示填色等值面的那個圖層）色彩刻度的下上限分別設為-0.04和0.02，color scale method BGR代表將色彩刻度由小到大設為藍->綠->紅。將背景設為白色的命令是color Display Background white，若將此命令添加到.vmd里面就能在載入.vmd文件時順便執行，使背景自動設為白色。這些命令在VMD手冊上都有解釋。這些命令也可以在VMD的控制臺下直接運行，控制臺通過Extensions-Tk Console進入，比如想把色彩刻度改為從-0.05到0.05，就在控制臺執行mol scaleminmax top 1 -0.05 0.05。有很多命令在VMD的GUI上有相應的選項，其中有些通過GUI操作會容易得多，比如調整等值面數值，可以在Graphics-Representations里面的列表中選定第二個顯示模式（即Style為isosurface的那個），然后將下方Range的下上限分別設為比如0和1，點回車，之后拉動滑條就能在0~1范圍內改變等值面。

另外，Chemcraft也可以實現相同功能，對初學者來說使用更簡單，不過效果不如VMD，而且收費。使用方法：
先打開func2.cub，再點左下角Add cube，選擇func1.cub。將Contour value設為0.5，敲回車，然后點Show isosurface。然后把Map other:選為2，再把Values range分別填-0.04和0.02，敲回車。

如果你想讓散點圖也有填色效果，便于將散點圖的spike和等值面圖通過顏色相互對應，判斷spike對應的等值面位置，用gnuplot可以很容易做到，看此文：《繪制有填色效果的用于弱相互作用分析的RDG散點圖的方法》（http://sobereva.com/399）。

這種分析方法也可以用于分析晶體間內部弱相互作用。雖然Gaussian的PBC功能并不給力，但是簡單的PBC計算還是可以勝任的。由于Gaussian的PBC計算是以高斯型函數作為基函數，所以波函數信息可以直接被Multiwfn讀入并進行分析。這里將以金剛石晶體作為例子。

還是先獲得波函數文件。Gaussian的輸入文件就是壓縮包里的pbc_diamond.gjf。運行之后，用formchk將.chk轉化為.fch文件。當然，用.wfn作為Multiwfn的波函數輸入也可以。由于計算的是素晶胞，波函數信息也只含有兩個碳原子的，獲得的等值面顯然體現不出周期性，然而計算復晶胞又太費時。在Multiwfn里提供了一個晶胞波函數平移復制功能，可以將這素晶胞波函數信息擴展為足夠大的復晶胞波函數。復制次數越多，體系中高斯函數越多，計算格點時越慢，為避免計算格點時間太長，這里只向各方向平移復制兩次。

啟動Multiwfn后輸入：
c:\pbc_diamond.fch
6 //修改波函數功能
32 //平移復制體系
4.7523,0,0 //第一個平移向量。平移向量在輸出文件中的PBC vector段落，或者查看.fch中的Translation vectors字段。不要用輸入文件中的平移向量，因為Gaussian可能自動改動坐標，平移向量也就變了。
1 //單位為bohr
2 //復制兩次。接下來再對另外兩個方向做相同的平移復制。
32
2.3762,4.1156,0
1
2
32
2.3762,1.3719,3.8802
1
2
0 //平移復制已完畢，保存當前波函數到當前目錄下new.wfn，也就是壓縮包中的pbc_diamond_dup.wfn。

由于得到的體系是斜著的，把所有原子都納入立方網格中必將造成很多格點落在體系外而浪費掉。實際上只要取體系中間一個原子（28號）作為網格中心，然后向四周延展一些距離，所得等值面就足夠體現周期性了。現在生成格點文件，依次輸入
pbc_diamond_dup.wfn
100
1
15,13
7  //用兩個原子的中點作為網格中心
28,28   //當輸入的兩個原子序號相同，則以此原子為中心向四周延展。Multiwfn默認延展距離是6 bohr，對此例子比較合適，不用修改。
80,80,80  //各方向格點數
6,6,6 //各方向延展距離皆為6 Bohr
算完后，用功能3保存格點文件，按照上例方法，用VMD顯示結果如下。可見，由于碳原子間距離較近，原子空穴間充滿紅色等值面，體現很強的位阻效應。

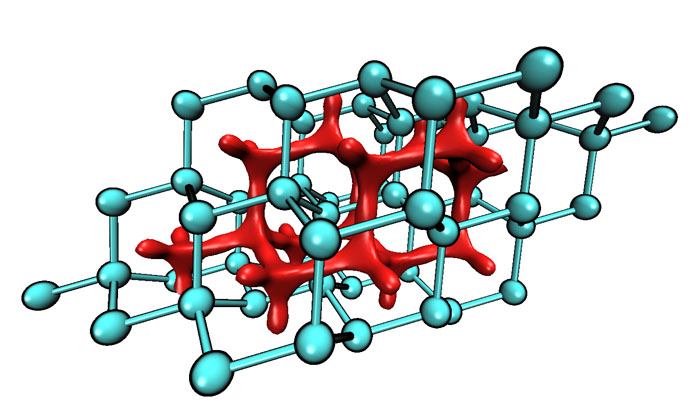
圖14

5 波函數質量產生的影響

在前面的例子中用的是B3LYP波函數，必定有人會認為用B3LYP計算以范德華作用為主的弱相互作用體系很不合理，但實際上計算能量的精度和計算電子密度的精度沒有必然關系，原文作者認為使用這種分析方法時用B3LYP/6-31G*級別的電子密度就夠了，這樣計算量也小，而且改為更昂貴的MP2/6-311+G**后等值面并沒有什么改變。甚至電子密度粗糙到只用自由電子密度疊加（promolecular近似的密度）都能得到定性合理的結果，所以這種分析方法對電子密度的質量很不敏感，使之用于大體系成為了可能。

6 Promolecule近似及對結果產生的影響

使原子坐標保持在形成分子時的狀態，將自由原子密度疊加得到的密度稱為Promolecule密度，可以視為在形成分子前，電子密度尚未馳豫的電子密度。構建這種密度不需要量子化學計算，只要有分子結構文件和自由原子密度就能十分容易地構建。由于在弱相互作用區域Promolecule密度和實際密度差異并不像在成鍵區域那么顯著，Promolecule密度在此分析方法中可以近似代替實際電子密度，等值面的基本形狀不會有太大差異，但是定量上，也即等值面細部特征會有一定差異，因為電子密度馳豫后會在吸引作用區域聚集，尤其是會在位阻效應區域疏散以減小斥力，位阻效應越強，改變量越大。

原子在自由狀態的真實電子密度是球對稱的，但是對于比如基態氧原子，p軌道一個是雙占據兩個是單占據，量化算出來的電子密度不是球對稱的，這將導致分析結果出現不應有的取向性，所以需要將之球對稱化。球對稱化方法不是唯一的，比如可以簡單地對三個p軌道占據數取平均，也有人利用GVB方法解決，原文的方法是用s型STO函數擬合B3LYP/6-31G*原子密度，第一、二、三周期的原子分別用1、2、3個STO擬合，以對應殼層數。這不僅解決了球對稱問題，還有另一個好處，就是描述原子密度的函數大大減少了，6-31G*描述氧原子用28個GTO，而擬合后只用2個STO，這使得計算RDG函數、sign(λ_2)ρ的速度也大大加快。實際上STO用的少主要在于雙電子積分時的困難，由于STO能正確地表現原子軌道波函數隨r增大的收斂行為和原點處Cusp的特征，如果研究內容不涉及到雙電子積分，比如這種只依賴ρ(r)的分析方法，用STO又便宜又好。

在Multiwfn中使用Promolecule密度計算RDG與sign(λ_2)ρ函數，只需在選擇要計算的函數的界面中選擇后面帶著"with Promolecule approximation"的相應函數即可。對于前三周期的原子，使用的是原文通過STO擬合的原子在自由狀態下的密度。而對于其它元素，原文沒有對密度進行擬合，并且本人發現對超過第三周期的元素通過STO也幾乎沒法擬合好。于是在Multiwfn中它們的密度通過對程序內置的高精度計算的原子的電子密度進行插值來得到，最高支持到Ra。超過Ra的元素暫時不支持promolecular近似。由于Promolecular近似下做計算不涉及到波函數信息，只要將分子結構傳遞給Multiwfn就可以，所以既可以通過.wfn、.fch等文件將分子結構傳入Multiwfn，也可以通過Multiwfn支持的.pdb、.xyz等文件導入分子結構。在Promolecule近似下苯酚二聚體的散點圖和等值面圖如下所示

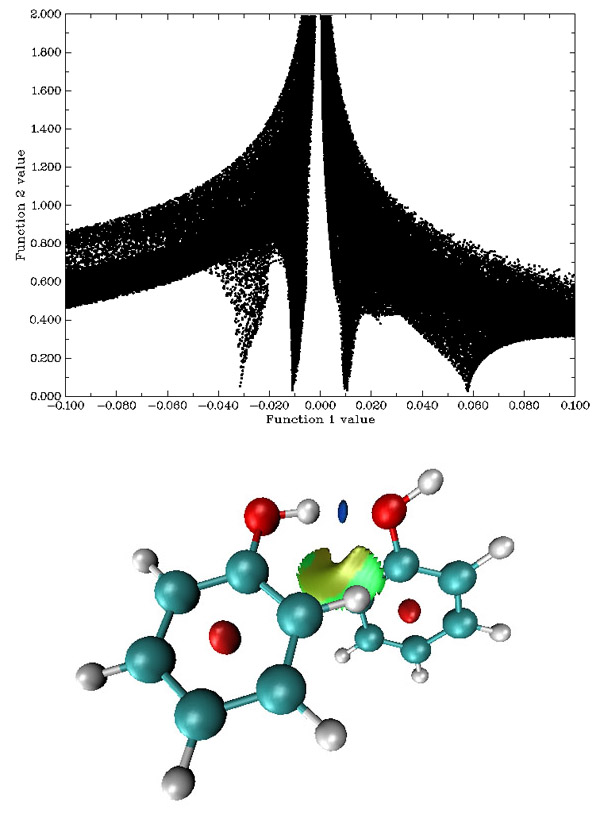
圖15

與B3LYP/6-31G*波函數下的散點圖相對比，在Promolecule近似下，主要區別是對應位阻效應的spike明顯靠右，這說明芳香環中間的電子密度在形成分子后顯著降低以減小互斥效應。并且Promolecule的散點圖整體分布比較靠下。所以在觀看Promolecule近似下的等值面就必須用與之前不同的等值面數值和電子密度屏蔽范圍，如果仍只保留sign(λ_2)ρ在[-0.05,0.05]區域，則最右邊的spike將會被截掉很大部分；如果觀看的等值面仍為0.5，則y=0.5的直線在散點圖中將與一大片范圍相交。所以建議保留sign(λ_2)ρ在[-0.1,0.1]區域的點，并觀看RDG=0.25的等值面，這樣只有這四個spike對應的區域被保留了下來，并且y=0.25的直線只與它們相交。這樣得到的填色等值面如圖15下方所示，色彩刻度范圍設為了[-0.04,0.03]，可見和B3LYP/6-31G*下的圖沒有太大差別，只是芳香環中間的梭形區域變成橢圓。

雖然靠實際電子密度分析時需要保留的sign(λ_2)ρ的范圍有比較通用的值[-0.05,0.05]，但是在Promolecule近似下情況比較復雜，spike的位置變化范圍較大，應保留的范圍不好確定，所以最好每次都考察一下散點圖確定保留范圍。在Multiwfn中默認的保留范圍是[-0.1,0.1]，可以通過修改settings.ini里的RDGprodens_maxrho參數來改變，當sign(λ_2)ρ小于-RDGprodens_maxrho或者大于RDGprodens_maxrho的點的RDG值將被自動設為100。若此參數設為0.0，則不自動作屏蔽。

7. 用于生物大分子體系

由于在Promolecule密度下就能得到可靠結果，計算函數時速度很快，也不再需要量子化學軟件計算波函數，使得這種分析方法又快又方便，能夠容易地用于蛋白質、核酸等生物大分子體系。

此例將繪制DNA雙螺旋結構的某一部分的RDG填色等值面圖。由于這種分析方法所用的分子結構應當盡量接近平衡構型，獲得這樣的結構最簡單的方法就是從RCSB數據庫(http://www.rcsb.org/pdb/home/home.do)里面找相應的晶體結構，然后加氫。也可以自行建立DNA結構，這樣序列可以自定義，可以用比如Ambertools里的NAB工具實現，之后再做能量最小化。附件里的DNA.pdb是已建好的含10個腺嘌呤-胸腺嘧啶堿基對兒的DNA片段，已通過Amber在ff99SB力場、GB溶劑模型下優化，細節見http://ambermd.org/tutorials/basic/tutorial1/。為了視覺上比較清楚，將要研究的區域是分子結構邊緣區域，如下圖灰色方框所示。其中黃色圓球所示的是第84、565號原子，將它們的中點作為網格中心并往外延展一定區域就能使網格涵蓋感興趣的范圍。如果不清楚延展多少比較合適，可以先設定一個預期的延展范圍，然后用粗糙格點計算一下，看看延展范圍是否合適，再做高質量格點的計算。

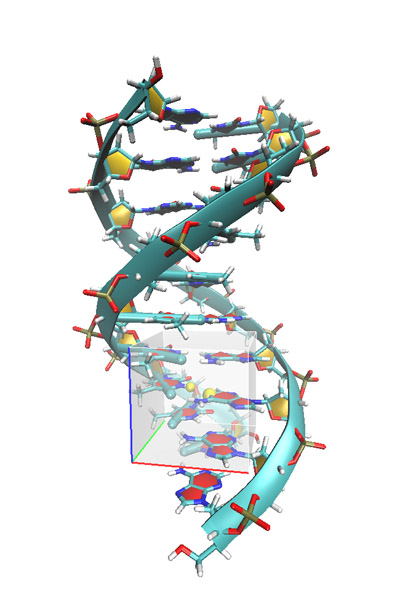
圖16

操作步驟如下
DNA.pdb //此文件已在壓縮包里。假設讀入某個pdb文件時提示發現未知元素，說明原子名有問題，應進行修改。
100 //功能100
1 //子功能1
16,14 //Promolecule近似下的sign(λ_2)ρ函數與RDG函數
7 //通過兩原子中心定義網格中心
84,565 //兩原子序號為84和565
120,120,120 //由于網格范圍較大，所以用較多格點
9,9,9  //各方向延展9 Bohr
現在開始計算，計算完畢后選3將格點文件導出并用VMD作圖，如圖17所示。若有興趣也可以看一下散點圖，由于網格內涉及的弱相互作用較多，所以spike比較多。

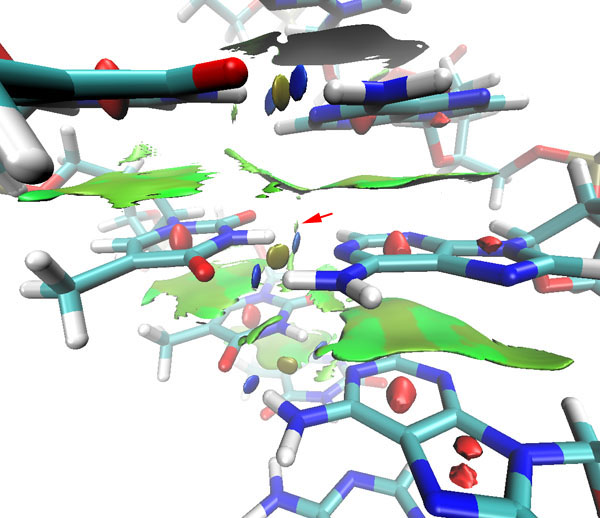
圖17

從RDG的填色等值面圖上看，上下相鄰的堿基之間存在著π-π堆疊作用。腺嘌呤和胸腺嘧啶之間形成的兩條氫鍵很清楚地通過兩個藍色圓片顯現出來，在之間還存在著土黃色圓片，對應著很弱的位阻效應。紅色箭頭所指的是C-H---O氫鍵，其強度已稱不上是氫鍵，只是范德華作用的級別。

8. 原子密度cutoff對速度的影響

在Promolecule近似下計算每個格點RDG和sign(λ_2)ρ函數時原本會計算所有原子的電子密度的貢獻，當體系較大、原子較多時，比如上面例子中的體系，耗時會比較長，除非人為地將不感興趣的區域原子刪掉，但操作麻煩，還可能帶來截斷誤差。為了進一步加快Promolecule近似下的計算，在Multiwfn中使用了原子密度cutoff的方案，對于C、H、O、N原子（由于它們最為常見），如果其電子密度在當前要算的格點位置上的數值小于1E-5，則忽視掉它，判斷標準是事先推算的距離判據。這使得計算大體系時速度顯著提升，對結果不會產生能查覺得到的影響。如果出于特殊原因想關掉此設定，在settings.ini里把atomdenscut設為0即可。

使用i7-2630QM的CPU，計算高質量格點下苯酚二聚體RDG和sign(λ_2)ρ函數的總耗時：
B3LYP/6-31G*波函數 33s
Promolecule近似 1s
可見使用Promolecule近似時比使用B3LYP/6-31G*波函數時速度提升了30倍，如果基組更大，提升幅度會更大。

計算前文DNA例子的情況：
Promolecule近似 54s
Promolecule近似+原子密度cutoff 8s
由于體系越大，能夠少算的原子就越多，原子密度cutoff帶來的加速越明顯。如果不做cutoff，在計算DNA下側的格點時還得計算所有在DNA上側原子的貢獻，白費很多時間。

9. 用RDG等值面研究成鍵

筆者曾在《電子定域性的圖形分析》（http://sobereva.com/63）一文中介紹了拉普拉斯值函數、ELF函數、LOL函數，這三個函數對研究成鍵、孤對電子、原子殼層結構很有用處，但是無法用于弱相互作用分析，RDG函數分析方法是對它們重要的補充，使可視化分析能涵蓋更廣的范圍。實際上，RDG函數對成鍵分析也有一定用處，從散點圖上看，成鍵區域可看做是ρ(r)比較大的spike，在圖上做橫線也會與這個spike相交，因而不對ρ(r)的范圍做屏蔽時也會在成鍵區域出現RDG等值面。具體的分析將另文討論，這里只以典型分子吡嗪作為例子，圖18上半部分是吡嗪的RDG=0.2的等值面圖，下半部分是LOL=0.6的等值面圖。可見，RDG函數等值面也描繪出了化學鍵，但是形狀基本是以鍵軸為對稱的，并且沒像LOL等值面體現出共軛π鍵，另外RDG等值面沒有描繪出氮原子的孤對電子區域。所以，RDG等值面圖雖然可以用于分析成鍵，但并不能體現出像ELF、LOL函數那么豐富的特征，有一定局限性。

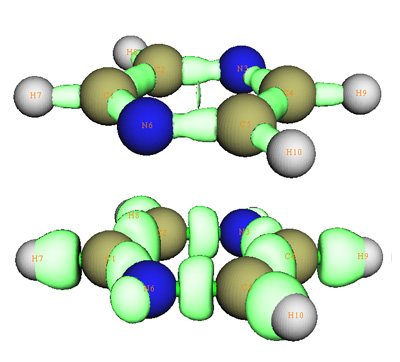
圖18

吡嗪分子平面的RDG函數圖如下所示，由此圖可以想象RDG等值面輪廓隨等值面數值由小到大是如何變化的，最初等值面是從最黑的（RDG=0）位置開始出現，也相應于AIM的臨界點。黑線表示的是0.2的等值線，可以與上面等值面圖相互對照。

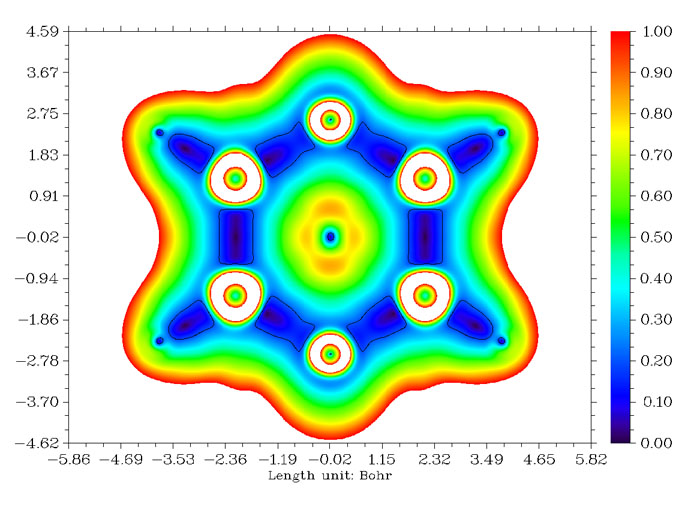
圖19

由于在形成分子后，電子密度在成鍵區域變化較大，所以用此方法研究成鍵問題時不要使用Promolecule密度。

10. 填色等值面的藝術

在各種各樣的體系中，使用不同的函數，通過調整等值面、色彩刻度、顯示方式，多個等值面再加以組合，時常會得到一些漂亮的圖形（盡管圖形未必有什么物理意義），能夠激發想象力，在比如設計Logo時往往能從中獲取靈感。如同分形一樣，這是科學與藝術的結合。舉一個偶然發現的不錯的例子：

首先確認settings.ini里RDGprodens_maxrho已設為了0.1，也即默認值，然后在Multiwfn里輸入：
benzene.wfn  //已在壓縮包里
100
1
16,14
-10
2   //網格延展2 bohr
4   //由用戶輸入各方向格點數，網格范圍涵蓋整個分子。
150,150,100  //X,Y,Z方向格點數，因為苯分子在XY平面，Z軸長度短于X,Y，所以Z方向格點數少些
3  //保存格點文件
然后用VMD顯示RDG填色等值面圖，等值面用0.47，材質用Glossy，色彩刻度設為[-0.04,0.06]，得到下圖，像什么東西請大膽發揮想象。

圖20

之前都是做ρ(r)或sign(λ_2)ρ vs. RDG的散點圖，在Multiwfn里也可以做其它函數之間的散點圖，偶爾也會遇到有趣的圖，記得曾做過一個大抵是ELF、LOL函數與RDG間的散點圖，十分像鷹的頭部。

11. 其它問題

11.1 RDG等值面的含義

要注意，有RDG函數等值面的區域說明一定有某種不很弱的相互作用跨過這個區域，但兩個原子間如果沒有RDG等值面，決非兩原子間不存在相互作用。例如范德華作用雖然隨r^-6減小，衰減得比較快，但分子離得很遠時并不是完全沒有范德華作用，此時RDG等值面卻不會出現。比較甲烷二聚體在平衡狀態下和拉遠時（碳原子間相距10埃）兩個碳原子直線上RDG函數的變化可以了解其原因。

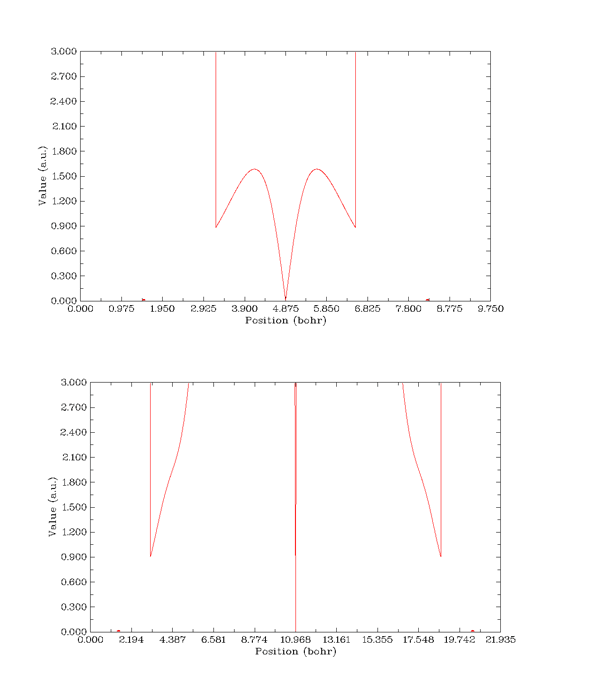
圖21

由于已將電子密度在0.05以上的區域的RDG值設為100而屏蔽掉，所以圖的兩側沒有顯示。X軸上的紅點代表碳原子的位置。在圖21的上圖所示的平衡狀態時，甲烷分子中間RDG函數曲線有個V字型區域，最下端為RDG=0，即AIM臨界點。做一條y=0.5的橫線，與RDG曲線的兩個交點之間有一定距離，所以能看到一定大小的RDG=0.5的等值面。前面已經提到，由分子邊緣開始往外越遠的地方RDG數值越大，所以在兩分子遠離狀態時，兩分子中間會夾著一塊RDG值很大的區域，雖然臨界點肯定仍然存在，但是V字型區域已經變得非常窄，與y=0.5的兩個交點幾乎碰上，所以從等值面圖上看不到這過于微小的等值面。

由于靜電作用能隨r^-1衰減，衰減速度較慢，對于帶有凈電荷的分子間相互作用，在遠距離時即便相互作用可能并不小，但出于同樣原因也不會顯示出等值面。

11.2 坐標應處于平衡狀態

要注意使用這種分析方法時體系坐標應當處于，至少是接近平衡狀態，否則將會得到明顯錯誤的結論。例如下圖

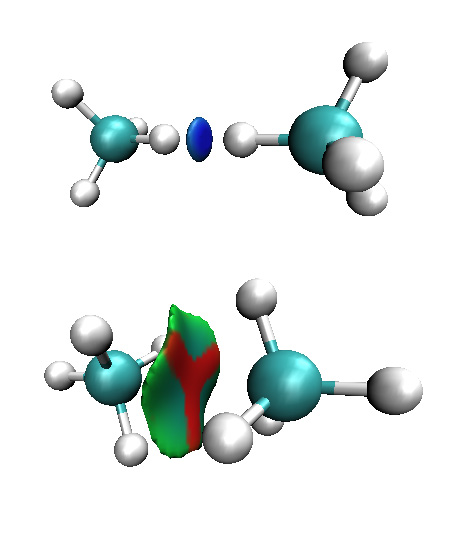
圖22

令兩個甲烷分子的C-H鍵對著對方，然后使之離得很近，從圖上看形成了很強的吸引作用。若以另一種朝向相互接近，當很近時弱相互作用等值面上出現了紅色區域，顯示強烈位阻效應。這兩個圖都沒正確表現出甲烷二聚體之間是通過范德華作用結合的，尤其前者完全是誤導。不真實的結構在關鍵位置產生了不真實的密度，不真實的密度就導致分析結果不真實。所以直接搭建的初始結構應當進行優化再做分析，即便是很大體系也至少要在合適的力場下做分子力學級別的優化。所有基于圖形化分析方法，也包括AIM分析，都要注意這點。

11.3 spike、等值面與AIM臨界點的關系

本文在介紹RDG填色等值面方法時將spike、等值面與AIM臨界點聯系地進行了討論。但要注意，有些時候散點圖上spike并不接觸x軸，所以相應的等值面也不是從臨界點擴張而來，比如前文例子中直立構象的甲基環己烷的甲基與環己烷之間的位阻區域內部就沒有臨界點，然而所示的填色等值面卻很迎合我們的期望結果，說明了其合理性。這種情況并不少見，將另文討論。

11.4 RDG填色等值面分析中所謂的“位阻效應”

關于這種分析所顯示的位阻效應值得再具體說一下。一般說的位阻效應是指每個原子都會占據一定空間，除了成鍵原子外，其它原子不會從以任何方向、任何形式與之靠得太近，否則會導致能量升高并產生斥力，只有當某種其它因素存在，強到能克服斥力時，體系才能在位阻效應存在的情況下保持穩定。這種情況一般就是指以成鍵方式（如苯環）或者以較強的弱相互作用方式（如甲酸二聚體）構成帶有張力的環或籠，這種情況在位阻效應產生的區域λ_2總是大于0，所以RDG填色等值面圖分析方法指出在紅色或偏紅色區域是存在位阻效應的地方。然而，這話不能反著說。因為存在位阻效應的區域的等值面未必λ_2一定大于0，所以未必會被填上紅色或者偏紅色。例如在圖22中，兩個氫原子之間距離過近，產生了位阻效應，由于二者中點存在(3,-1)，故附近區域λ_2<0，所以等值面顯示為藍色，表示為成鍵，這顯然是錯誤的。當然，圖中的情況由于不是平衡結構因此結論沒有意義，但假設有某種形式的外力能夠維持這種狀態穩定，即這種狀態就是當前最穩定的狀態，RDG填色等值面分析就給出了錯誤的結論。但這種例子極少，所以不必太擔心，只要明白這種分析方法體現的位阻效應究竟是什么含義就行了。

11.5 RDG中ρ(r)^(4/3)的含義

實際上，|▽ρ(r)|并不一定必須除以ρ(r)^(4/3)才能區分分子邊緣和弱相互作用區域，也可以將ρ(r)^(4/3)改成比如ρ(r)、ρ(r)^(5/3)，相應的散點圖如下所示（摘自原文的補充材料，注意系數1/(2*(3*π^2)^(1/3))沒有被乘上）

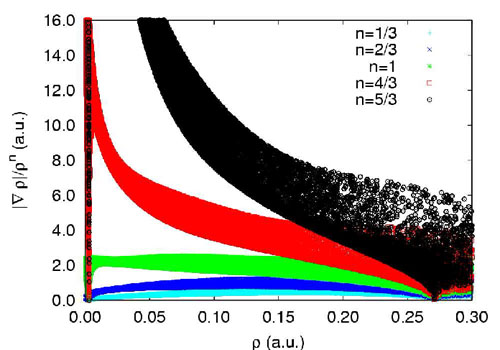
圖23

n=5/3時，雖然也很好地區分開分子邊緣與弱相互作用區域，但是數值范圍太大，顯示合適的、相同大小的等值面需要比RDG等值面用更大的函數數值。n=1時，由于遠離分子時ρ(r)的收斂速度不像ρ(r)^(4/3)那樣快，所以散點圖中對應分子邊緣區域的左上角的峰沒那么明顯。如果繼續減小n，則弱相互作用與分子邊緣區域就難以區分，數據點都一起縮到圖中左下角。RDG函數原本是用在GGA密度泛函中表達電子密度梯度項，這也正是其名字的含義，之所以不是|▽ρ(r)|而要除以ρ(r)^(4/3)，是為了消掉|▽ρ(r)|的量綱，使梯度的模成為無量綱的量。而RDG函數，即n=4/3的情況用在分析弱相互作用上最合適，是屬于巧合。

12. 總結

RDG填色等值面分析方法是十分方便、有用的分析方法，原理簡單易懂、適用范圍廣，在Promolecule近似下只需要提供分子坐標就能很快地得到結果，值得大力推廣。Multiwfn對這種分析方法投入實際應用提供了極大便利，操作傻瓜化，不涉及到任何復雜的理論、概念。此方法也存在一些不足，也因此可能有進一步改進或發展的余地，比如等值面數值的選取、色彩刻度的上下限設定有一定隨意性，那么是否有可能將這種分析定量化？其等值面面積和包圍的體積是否也有一定意義？此分析方法的提出純粹是從可視化便利的角度出發的，是否能找出其背后與ELF/LOL等函數的理論聯系，進而組合、衍生出一個能分析更廣泛問題的函數？筆者曾在《電子定域性的圖形分析》一文中淺談了實空間函數圖形化分析方法的優點，本文的RDG填色等值面分析方法進一步顯現了這類分析方法的用處，這類方法在未來必將得到進一步發展，并逐漸流行起來，也希望讀者多加實踐。