使用Multiwfn繪制原子軌道圖形、研究原子殼層結構及相對論效應的影響

使用Multiwfn繪制原子軌道圖形、研究原子殼層結構及相對論效應的影響

文/Sobereva @北京科音 2012-Jul-9

1 前言

這個帖子主要介紹怎么用Multiwfn程序（http://www.shanxitv.org/multiwfn）結合Gaussian繪制各種類型的原子軌道圖形，包括角度和徑向部分，在繪制過程中能加深一些對原子軌道的理解，如原子軌道間的正交性和鉆穿效應。本文繪制軌道并不是像一般教材中通過原子軌道波函數的解析形式來繪制的，解析的方式可以用matlab、mathematica等程序繪制，本文是通過Multiwfn靠Gaussian輸出的單原子體系波函數信息繪制的。在繪制過程中可以使沒用過Multiwfn的人熟悉Multiwfn的基本繪圖操作，對于有一定經驗的用戶也能學到一些特殊技巧。文中還將利用Multiwfn簡要討論相對論效應對軌道徑向分布產生的影響，讀者可以同時了解到在Gaussian中使用全電子標量相對論計算的基本方法。最后還將通過繪制各種實空間函數展現原子各個主層特征。本文介紹的方法和作出來的圖對于講授結構化學課程的老師也我想比較有用，很適合向學生們展示一些基本概念。本文用的Multiwfn為2.4版，Gaussian為G09 A02。

實際上，原子軌道只有對于類氫原子體系（一個核+單個電子）才是物理意義嚴格的，對于多電子原子體系，原子軌道模型只是近似的描述，但還是很合用的。類氫原子軌道波函數是徑向部分波函數與角度部分（球諧函數）的乘積。比s角動量更高的原子軌道有的角度部分是復數，復數型原子軌道難以圖形表示，用起來也不方便，因此一般都是將復數型原子軌道線性組合成實數型來用（它們將不再是Lz算符的本征函數而沒法討論磁量子數）。本文說的原子軌道都是指實數型原子軌道，教科書上的原子軌道圖形也一般是實型的。而本文所謂的真實原子軌道，則是指實數型的類氫原子軌道。

2 繪制s,p,d,f,g角動量原子軌道的角度部分圖形

這里我們先不考慮徑向部分，假定是個任意的常數，這里先來通過繪圖將s,p,d,f,g角動量原子軌道的角度部分表現出來。s,p,d角動量的原子軌道圖形想必大家已很熟悉，但是f、g的圖形可能不少讀者還不怎么印象深刻，此節將繪制它們。我們先建立一個Gaussian輸入文件，內容如下。使Gaussian運行它后每個“分子軌道”都對應一個原子軌道，這樣用一般方法觀看分子軌道就等于觀看原子軌道了。
%chk=c:\gtest\atom.chk
#p hf/gen pop=full guess=(cards,only,save)

Atom

1 1
H

H 0
S 1 1.0
0.1 1.
P 1 1.0
0.1 1.
D 1 1.0
0.1 1.
F 1 1.0
0.1 1.
G 1 1.0
0.1 1.
****

25(f2.0)
-1
1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.0.
0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.1.
0

這個輸入文件看起來可能覺得比較古怪，這里進行解釋。
Gaussian用的是高斯函數作為基函數，高斯函數又細分為笛卡爾型高斯函數和球諧型高斯函數，后者的角度部分和真實原子軌道的角度部分是一一對應的，所以我們應當用球諧型高斯函數。對于此例自定義基組的情況，默認就是用球諧型高斯函數，不必手動加5d 7f關鍵詞。對于這個問題的更細致討論見《談談5d、6d型d殼層基函數與它們在Gaussian中的標識》（http://www.shanxitv.org/51）和《球諧型與笛卡爾型Gauss函數的轉換關系》（http://www.shanxitv.org/97）

這個體系電子數為0，即質子體系。通過自定義基組方式，給這個質子加上從s到g角動量基函數各一個，比如
D 1 1.0
0.1 1.
就代表加上指數為0.1（因為我們這一節忽略原子軌道徑向部分，所以此值是隨意取的）的d殼層的共5個基函數，且每個基函數都只含一個高斯函數。當前體系總基函數數目是1+3+5+7+9=25個。

但是我們并不能在自定義基組后直接就這么計算，否則從pop=full輸出的信息會看到“分子軌道”中存在基函數的混合，繪制“分子軌道”圖形就不能對應于原子軌道圖形了，所以我們必須寫上guess=(cards,only,save)并自行設定初猜。其中cards代表自行從輸入文件后面讀取初猜的分子軌道系數，而不用程序自動給的初猜；only代表不做迭代，否則又會引起基函數的混合；save代表將初猜波函數寫入chk文件中（默認對于only任務是不寫入）。

25(f2.0)代表自行寫的初猜信息是每行25個值（恰好每行代表一個分子軌道的25個基函數的系數，比較清晰易讀），而且每個值用fortran語言的f2.0浮點格式（占兩個位置，即一位整數和一個小數點符號自身的占位，比如3.1415就會表示成3. ，這樣雖然精度極低但對于目前問題最適合，十分緊湊）。后面的-1代表用自己設的初猜替換所有軌道的初猜。接下來就是自己設的初猜軌道系數了，我們要讓i號“分子軌道”正好對應i號基函數，因此只有對角線系數為1其余為0。輸入文件末尾的一個0代表自定義軌道初猜信息已經寫完了。

pop=full其實沒有意義，只是這將便于從輸出文件中檢查每個“分子軌道”的組成，看看是否如預期的每個“分子軌道”只在一個基函數上有值且系數為1，即基函數沒有發生混合。

用Gaussian計算這個任務，然后將chk用formchk轉換為fch文件，然后啟動Multiwfn，輸入fch文件的路徑，然后選0，通過點擊彈出的圖形界面右下角的分子軌道標號就可以看相應分子軌道，在此例中即原子軌道的圖形了。在點擊一個軌道標簽后，也可以用鍵盤的上下鍵切換，在瀏覽一批軌道時比用鼠標點更為方便。

建議在啟動Multiwfn之前將Multiwfn目錄下的settings.ini里的aug3D參數從默認的6調大到10，然后保存，這樣可以避免以較小isovalue顯示外層原子軌道等值面時在邊緣被默認的比較窄的格點數據空間范圍所截斷。在Multiwfn中觀看原子軌道時建議將isovalue從默認的0.05減小到0.03，否則原子軌道的一些特征表現不出來。

這里我們隨便選一個軌道，比如15號軌道，從pop=full給出的信息中看到這個軌道對應于F+3，注意這個絕非代表磁量子數為3的f軌道。根據《球諧型與笛卡爾型Gauss函數的轉換關系》一文提供的信息，我們知道這個軌道用笛卡爾形高斯函數表示為√(5/8)*XXX-3/√8*XYY，可想而知這個軌道是處在XY平面上的。

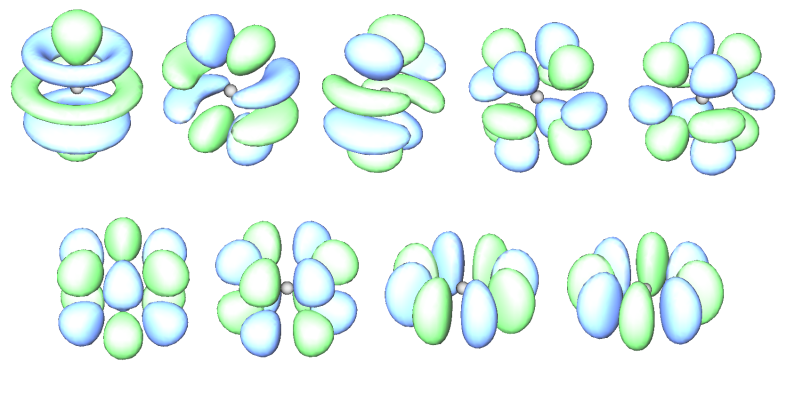
下圖將f原子軌道和g原子軌道等值面圖形匯總：

7個f （10~16號軌道）

9個g （17~25號軌道）

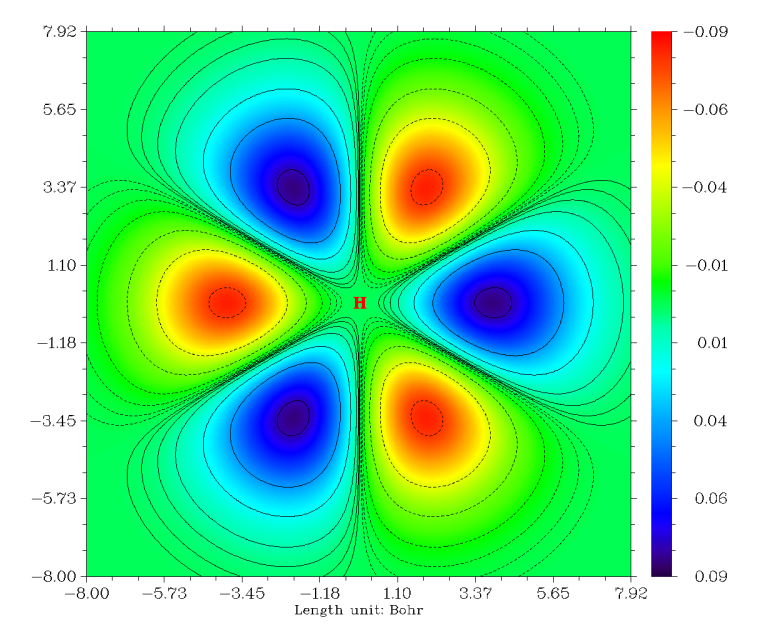
下面我們用Multiwfn作軌道的平面圖，這里以第15號分子軌道為例，在Z=0的XY平面上作圖最能充分表現它的特征。如果已經打開了Multiwfn，先將它關閉，然后在settings.ini里將idelvirorb值從默認的1設為0，然后保存。默認的1代表在一些可能比較耗時的任務中刪掉fch文件中的前10個虛軌道以外的虛軌道以節約計算時間，但是刪了虛軌道就達不到本文目的了，所以將此參數改為0并保存，以避免Multiwfn這么做（以后的Multiwfn版本中這個設定有可能還會改變，注意參見手冊和此參數在settings.ini里的注釋）。啟動Multiwfn，依次輸入
o //直因為之前已經輸入過一次當前體系的fch文件的路徑了，所以這次直接寫字母o就可以打開上一次載入的文件
4 //作平面圖
4 //要作的函數為軌道波函數值
15 //作第15號軌道
1 //填色圖
直接敲回車用默認的格點設定200,200
0 //設定作圖延展距離，默認的延展距離對于此例偏小，會看到軌道外部被截斷
8 //設延展距離為8 Bohr
1 //作XY平面
0 //Z=0
圖像立刻彈出來，但是基本是綠色，看不出什么特征，這是因為默認的色彩刻度范圍太大，不適合當前情況。遂在圖上點擊右鍵關閉之，選1，輸入-0.09,0.09修改彩刻度上下限。如果想讓圖像上同時出現等值線，可以再選選項2。最后選-1重新作圖，得到下圖（關閉圖像后選0可以將圖保存為當前目錄下的文件名以DISLIN開頭圖形文件）

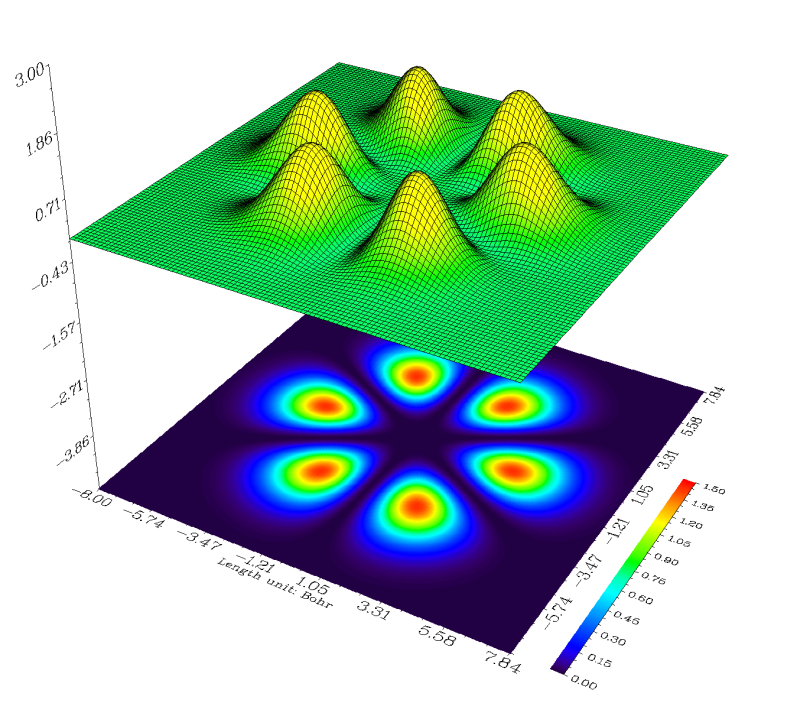
我們接下來繪制這條軌道的電子密度的地形圖+投影圖。雖然目前它是空軌道（其它軌道也都是空著的），但是我們可以通過修改波函數信息來設它為雙占據。選-5從剛才的后處理界面退回到主界面，依次輸入
6 //修改波函數
26 //設定軌道占據數
15 //選15號軌道
2 //占據數設為2（雙占據軌道）
q //退回
-1 //退到主菜單。由于其它軌道都是空軌道，目前只有15號軌道有電子占據，因此照常作密度圖時，就等于只作15號軌道的密度圖了
4 //作平面圖
1 //電子密度
5 //地形圖+投影圖
直接敲回車用默認格點設定100,100
1 //XY平面（由于之前已經調整了延展距離，所以這次不用再設一遍）
0 //Z=0
圖上幾乎一片空白，顯然默認設定不適合當前體系，所以我們還要調整。在Multiwfn目前版本繪制地形圖時，地形圖的Z軸范圍不允許改變。明顯是因為當前的Z軸范圍過大（-4到3），而僅這一條軌道的密度太小，所以圖上基本是個平面而看不出什么。從命令行窗口中看到這個平面上數據最大值僅為0.01439，因此可以將這個平面上的數據值擴大100倍，在目前的Z刻度范圍下就能明顯看出不同位置的差異了。點Return關閉圖形窗口，選-7，然后輸入100，就將這個平面數據乘上了100（可以反復這樣操作乘多次，直到效果滿意位置），然后選-1重新作圖，雖然可以看到地形圖比較合適了，但是投影圖的刻度范圍不很合適，有很大部分是白色，即超過了色彩刻度的上限，因此我們關閉窗口，選1然后輸入0,1.5修改投影圖的刻度，之后再選-1重新作圖，效果就很令人滿意了，此軌道上電子密度大的區域就像橘子瓣一樣：

雖然wfn文件也是最常用來作為Multiwfn波函數輸入文件的格式，但是對上文的情況不能用wfn而必須用fch。因為wfn文件的標準格式不允許記錄空軌道，而且最高角動量只支持到f，在帶有g角動量基函數的情況下若試圖讓Gaussian輸出wfn文件就會報錯。

用上文的方法原則上也可以看比g更高角動量的原子軌道圖形，但Multiwfn目前版本最高角動量只支持到g，想看更高角動量的話可以用gview，但用起來就沒Multiwfn方便了。

3 繪制原子軌道徑向部分圖形

雖然Gaussian程序用的高斯函數的徑向行為和真實原子軌道的徑向部分差異很大（尤其是高斯函數在核中心處沒有所謂的cusp，隨徑向距離衰減得也過快），但是只要基組比較大，通過變分過程，最終大量高斯函數的線性組合是可以基本正確表現出原子軌道的徑向行為的。

當出現多個角量子數相同的原子軌道殼層時，為了滿足波函數的正交性，徑向波函數會出現波節。對于相同角動量的原子軌道，主量子數越大的波節越多。通過解析推導的類氫原子軌道徑向部分公式可知，波節數=主量子數-角量子數-1，例如4s就會有4-0-1=3個波節。上一節的例子，在自定義基組時每種角動量都只有一個殼層，因此徑向部分看不到波節，而本例我們不用虛構的體系，而研究Kr的原子軌道。Gaussian的輸入文件如下。雖然第四周期已經有一定的相對論效應了，但這里暫不考慮。為了研究各層軌道，不能用贗勢而需要用全電子基組，流行的def2-TZVP的全電子基組版本恰好最大能支持到Kr（從Rb開始def2-TZVP就只有贗勢基組版本了）。由于Gaussian沒內置def2-TZVP，所以要去BSE網站（https://www.basissetexchange.org）上拷貝下來。
%chk=c:\gtest\Kr.chk
#p b3lyp/gen pop=full

Kr at B3lyp/def2-TZVP

0 1
kr

Kr     0
S   8   1.00
600250.9757500              0.23740610399E-03
89976.6507810              0.18410240539E-02
20476.8142250              0.95795580699E-02
   5796.1554078              0.39020650488E-01
   1887.5913196              0.12772645628
    679.11458519             0.30596521300
    264.38244511             0.44857474437
    104.88368574             0.24722957327
S   4   1.00
    641.47370764            -0.26745279805E-01
    199.57524820            -0.12571122567
     33.545462954            0.56483736390
     14.683955144            0.55972765539
S   2   1.00
     22.603101860           -0.25298771800
      4.0650682991           0.70992159965
S   1   1.00
      1.9611027060           1.0000000
S   1   1.00
      0.52465147979          1.0000000
S   1   1.00
      0.19332399511          1.0000000
P   6   1.00
   3232.9589614              0.24885607974E-02
    765.96442694             0.20379007428E-01
    246.33940810             0.96977188584E-01
     92.365283041            0.28199960954
     37.199509551            0.45116254358
     15.172166534            0.24917131496
P   4   1.00
     60.931321698           -0.22173603519E-01
      9.4792600646           0.32838462778
      4.2564686326           0.58124997120
      1.9729313762           0.32863541783
P   1   1.00
      0.76337108716          1.0000000
P   1   1.00
      0.30943625526          1.0000000
P   1   1.00
      0.11569704458          1.0000000
D   5   1.00
    186.41760904             0.86120284601E-02
     55.274124345            0.60394406304E-01
     20.283219120            0.21181331869
      8.0884536976           0.40366293413
      3.2214033853           0.42402860686
D   1   1.00
      1.1952170102           1.0000000
D   1   1.00
      0.6480000              1.0000000
D   1   1.00
      0.2510000              1.0000000
F   1   1.00
      0.6280000              1.0000000
****

由于s原子軌道是球對稱的，研究它不需要考慮角度部分，所以為了方便這里主要研究各層s軌道。上面這個輸入文件算完后，通過觀看軌道圖形可知fch文件中1、2、6、15號“分子軌道”就分別對應于1s、2s、3s、4s原子軌道。

我們先繪制4s原子軌道波函數的徑向部分。啟動Multiwfn，載入Kr.fch后，依次輸入
3 //繪制曲線圖
4 //繪制的是軌道波函數
15 //15號軌道，即4s
2 //自行輸入空間中兩個點作為曲線圖的兩個端點位置
0,0,0,4,0,0 //第一個點的xyz坐標為0,0,0，即原子核處。第二個點為4,0,0，因此也就是繪制r=0~4 Bohr徑向范圍的4s原子軌道波函數值。圖像立刻蹦出來，如下所示

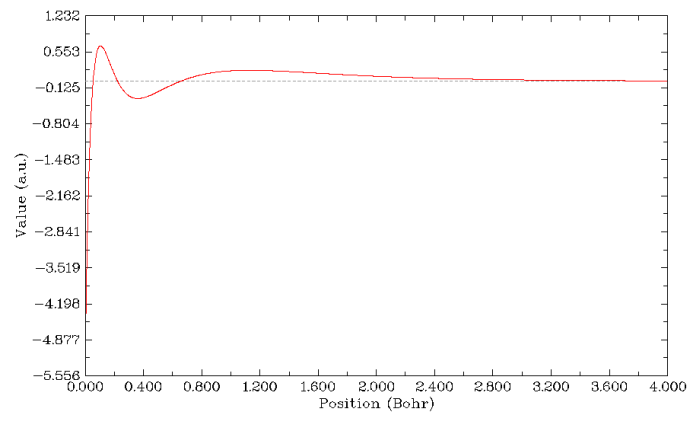
我們看到，曲線與y=0的橫線有三處交點，也就是三個波節。關閉圖像后，選7，輸入0，程序就會找出與y=0的交點（波節位置），位置是徑向距離為0.05480 Bohr、0.22239 Bohr、0.65715 Bohr處。

選2，可以將曲線的數據導出到當前目錄下line.txt文件中。此文件有5列，前三列是數據點的x,y,z坐標，第四列是當前點距離自行輸入的第一個點（即0,0,0）的距離，第5列是函數值。注意此文件中的長度單位都是埃，而不是Multiwfn程序內部用的Bohr。將這個文件導入到第三方繪圖程序，比如sigmaplot、origin當中，就可以直接用它們作圖，它們提供了比Multiwfn內部繪圖功能更豐富的選項。繪圖時就將line.txt的第四列和第五列作為曲線圖的X、Y坐標就行了。由于settings.ini文件中num1Dpoints參數在目前版本中默認是3000，所以Multiwfn在繪制曲線圖時會計算3000個點（這個精度一般足夠了），均勻分布在自己設的兩個空間坐標之間，也因此導出的line.txt包含了這3000個點的數據。

把line.txt改名為4s.txt。然后使用完全相同的方法，在Multiwfn里把1s、2s、3s的原子軌道在徑向的變化都計算并導出，并且分別重命名為1s.txt、2s.txt和3s.txt。把總共四個.txt一起放到Origin里作曲線圖，結果如下所示：

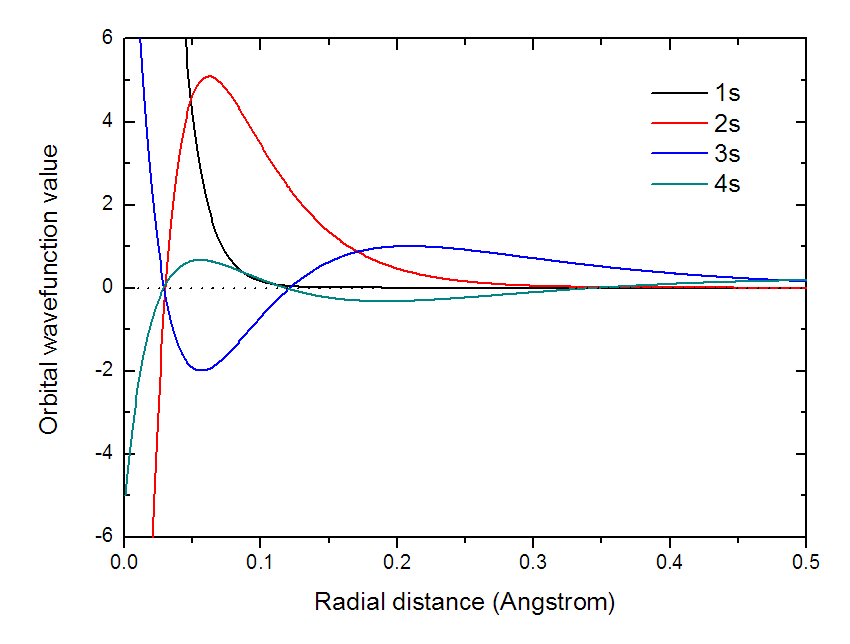
可見主量子數越大，波節越多。每個s軌道間都有波函數值符號相同和相反的部分，因此乘積在不同位置有正有負，這是這些s軌道間彼此正交，重疊積分都為0的根本原因。

更進一步，我們討論一下這些s原子軌道在徑向上電子密度的分布。根據Born概率解釋，i軌道的電子密度函數ρ_i就是其波函數的模的平方，即|ψ_i|^2。由于s軌道是球對稱的，因此4π*r^2*ρ_i這個函數表現的就是以核為中心半徑為r的無限薄球層內的i軌道的電子數，這也叫做電子的徑向分布函數。對這個函數從0積分到無窮遠就是i軌道上的電子占據數。

4π*r^2*ρ_i這個函數并沒有正式地出現在Multiwfn支持的實空間函數列表里，因為它對于研究分子體系沒什么用。想繪制它，一種方法是將line.txt導入進origin這樣的程序，在空白的列上做簡單的函數運算。筆者用的是Origin8，將前面計算4s軌道波函數輸出的line.txt文件直接拖進origin窗口之后，D列就是徑向距離（埃），E列就是相應處軌道波函數值。新建一列（F列），令這列數值的表達式為4*3.1415926*Col(D)^2*2*Col(E)^2/0.5291772^3。這里除以0.5291772^3是為了將原子單位的密度值e/Bohr^3變為e/Angstrom^3，因為我們將要做積分，必須和徑向坐標的長度單位對應；而Col(E)^2前面的乘的2是因為這個軌道是雙占據。令D列對F列作曲線圖，就會看到圖上有四個峰和三個低谷，展現了4s軌道的波節特征。選Analysis-Mathematics-Integrate-Open Dialogue，將D列和F列作為Input的X和Y，點OK，會出現一個新窗口，從中可見area = 1.9960884487804，十分接近此軌道期望的電子占據數2，

另一種繪制4π*r^2*ρ_i的方法是利用Multiwfn的自定義函數(user function)功能。這需要修改源代碼，其實十分簡單。打開Multiwfn的源代碼文件function.f90，搜索tion userfunc找到這個函數的代碼位置，在里面寫上userfunc=4*pi*fdens(x,y,z)*(x*x+y*y+z*z)，其中fdens是計算總電子密度的函數（按照前一節的做法，在Multiwfn里先將i軌道以外的軌道占據數設為0，那么之后fdens算的就是i軌道的密度了）。改過之后重新編譯Multiwfn，之后每當在Multiwfn里選擇實空間函數時選擇User defined function，就代表選擇了自己編寫的這個函數了。實際上，為了繪制4π*r^2*ρ_i我們不必改代碼重新編譯，因為如果你用的是2.4版Multiwfn，從userfunc這個函數的代碼中會恰好發現一行if (iuserfunc==6) userfunc=4*pi*fdens(x,y,z)*(x*x+y*y+z*z)，這本來是作為啟發用戶編寫自定義函數的示例代碼，而我們現在可以直接在Multiwfn中用它，也就是把settings.ini里的iuserfunc設為6，那么User defined function對應的就是4π*r^2*ρ函數。注意在以后的版本中不一定4π*r^2*ρ還對應于iuserfunc=6的情況，畢竟這不是Multiwfn中的正式支持的函數，用戶應自行看看相應Multiwfn版本的userfunc函數的代碼。

歸納一下，為了繪制4s軌道的電子徑向分布函數，最簡單的方法是先把settings.ini里的iuserfunc設為6，保存。然后啟動Multiwfn，輸入Kr.fch的路徑，然后依次輸入
6 //修改波函數
26 //修改軌道占據數
0 //選擇所有軌道
0 //所有軌道占據數設為0
15 //選擇15號軌道(4s)
2 //15號軌道占據數設為2
q //返回
-1 //退回到主菜單
3 //繪制曲線圖
100 //用戶自定義函數
2 //自行輸入兩個點的坐標定義作圖空間范圍
0,0,0,4,0,0 //兩個點的坐標

立刻得到如下圖像

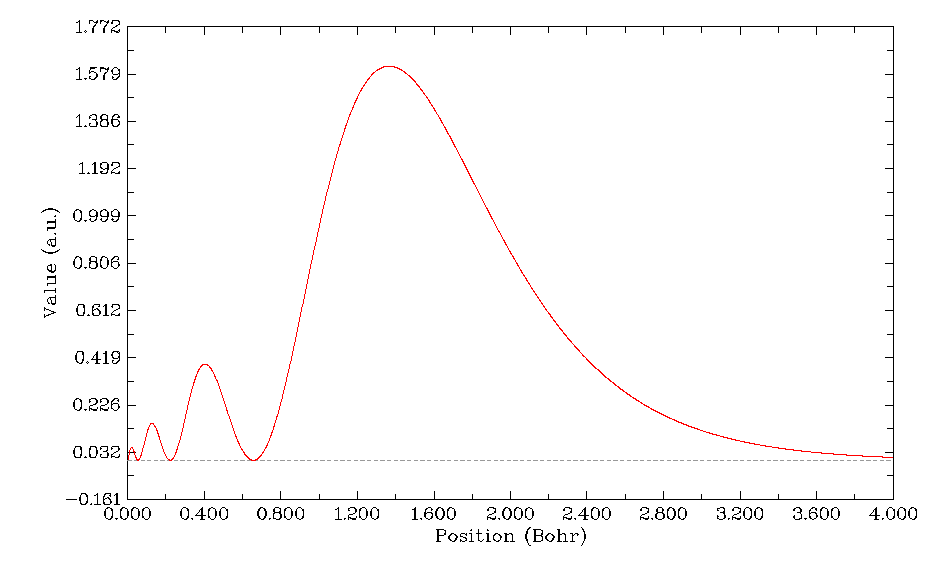
可見4s軌道的電子徑向分布函數的主峰在r=1.4 Bohr附近，也就是說這個軌道的電子大部分幾率都處在這個位置附近的球層內。雖然從前面作的4s軌道徑向波函數圖可以看到4s軌道在原子核附近的波函數的模平方（電子密度）比在其它徑向區域都大得多，但是由于原子核附近r小，因此4π*r^2項比較小，故4s的電子在離核較近的區域的平均數目其實很小。但是比主峰離核更近的那3個峰對應的球層內的平均電子數畢竟還是不可忽略的，由于電子在這個區域離核近因此受到的核吸引勢更強，導致了4s軌道的能量降低，這就是結構化學書里所謂的鉆穿效應。對于主量子數同為4但角量子數越高的原子軌道，由于波節數越少，電子徑向分布函數離核近的小峰也就越少，因此鉆穿效應越弱，能量比4s越高。

控制臺上會輸出積分值Integration value: 0.19960963D+01，很接近2，這和前面用origin積分出來的軌道的電子數結果1.9960884487804十分相符。Multiwfn內部用的是梯形法積分曲線面積。

4 相對論效應對徑向分布函數的影響

本例通過繪制Hg的電子徑向分布函數，展現相對論效應對原子軌道的影響。對于第四周期（K到Kr這一行）的原子相對論效應雖然重要但并不是必須考慮的，而對第五周期及更重的原子，相對論效應就不能忽略，Hg就是典型。下面是本例的Gaussian輸入文件。
%chk=c:\gtest\Hg.chk
#p b3lyp/gen int=dkh2 IOP(3/93=1)

Hg at B3lyp/SARC int=dkh2 IOP(3/93=1)

0 1
Hg

!from JCTC, 4, 908
Hg 0
s 6 1.0
   1778058.5043390000      0.1096336834
   790248.2241510000     -0.0573465500
   351221.4329560000      0.2087189001
   156098.4146470000      0.0637773176
   69377.0731760000      0.3818268624
   30834.2547450000      0.4512486959
s 1 1.0
   13704.1132200000      1.0000000000
s 1 1.0
   6090.7169870000      1.0000000000
s 1 1.0
   2706.9853270000      1.0000000000
s 1 1.0
   1203.1045900000      1.0000000000
s 1 1.0
   534.7131510000      1.0000000000
s 1 1.0
   237.6502890000      1.0000000000
s 1 1.0
   105.6223510000      1.0000000000
s 1 1.0
    46.9432670000      1.0000000000
s 1 1.0
    20.8636740000      1.0000000000
s 1 1.0
     9.2727440000      1.0000000000
s 1 1.0
     4.1212200000      1.0000000000
s 1 1.0
     1.8316530000      1.0000000000
s 1 1.0
     0.8140680000      1.0000000000
s 1 1.0
     0.3618080000      1.0000000000
s 1 1.0
     0.1608040000      1.0000000000
s 1 1.0
     0.0714680000      1.0000000000
p 5 1.0
   24956.6090260000      0.0179823881
   9982.6436100000      0.0188261927
   3993.0574440000      0.0932014721
   1597.2229780000      0.2560497643
   638.8891910000      0.7278258904
p 1 1.0
   255.5556760000      1.0000000000
p 1 1.0
   102.2222710000      1.0000000000
p 1 1.0
    40.8889080000      1.0000000000
p 1 1.0
    16.3555630000      1.0000000000
p 1 1.0
     6.5422250000      1.0000000000
p 1 1.0
     2.6168900000      1.0000000000
p 1 1.0
     1.0467560000      1.0000000000
p 1 1.0
     0.4187020000      1.0000000000
p 1 1.0
     0.1674810000      1.0000000000
p 1 1.0
     0.0669920000      1.0000000000
d 4 1.0
   1928.0943100000      0.0085722969
   701.1252040000      0.0450687967
   254.9546200000      0.2462324063
   92.7107710000      0.8046951098
d 1 1.0
    33.7130080000      1.0000000000
d 1 1.0
    12.2592750000      1.0000000000
d 1 1.0
     4.4579180000      1.0000000000
d 1 1.0
     1.6210610000      1.0000000000
d 1 1.0
     0.5894770000      1.0000000000
d 1 1.0
     0.2143550000      1.0000000000
d 1 1.0
     0.0779470000      1.0000000000
f 4 1.0
   96.6910160000      0.0585925893
   32.2303390000      0.2859731314
   10.7434460000      0.5719543263
   3.5811490000      0.3784947224
f 1 1.0
     1.1937160000      1.0000000000
f 1 1.0
     0.3979050000      1.0000000000
g 1 1.0
     1.2895000000      1.0000000000
****

此例的標量相對論效應通過DKH2 (Douglas-Kroll-Hess 2nd order)計算表現，IOP(3/93=1)是將Gaussian在相對論計算中默認的有限大小核模型改為多數量化程序用的點核電荷模型（大多數全電子相對論基組一般也都是針對點核電荷模型所提出的）。此例用的是SARC全電子基組專門適合DFT結合DKH、ZORA標量相對論計算，基組尺寸不很大且效果好，所以計算很容易。由于Gaussian沒內置它，BSE上也沒有，所以需要自行下載原文JCTC, 4, 908的補充材料，適當修改基組定義的格式然后用自定義基組的方式在Gaussian中使用。下面所說的不考慮相對論效應就是指將int=dkh2關鍵詞去掉后的計算結果。

用Gaussian計算此輸入文件后，通過觀看軌道，會發現不考慮相對論效應時1s,2s,3s,4s,5s對應的軌道編號分別為1,2,6,15,31,40。考慮相對論時由于發生了不同角動量軌道的相對能量變化，1s,2s,3s,4s,5s會分別對應1,2,6,15,24,40號軌道。（軌道總是按照能量從低到高編號）

相對論效應會使得1s軌道電子質量加大，減小其軌道尺寸，核電荷越大效應越明顯。由于外層的s軌道要與內層的s軌道滿足正交性，因此尺寸也會收縮。我們這里將繪制2s和3s原子軌道的電子徑向分布函數，看看考慮相對論后其分布是否確實收縮了。

先作不考慮相對論的2s軌道圖。我們按照與上一節同樣的做法，將所有軌道占據數都先設為0，然后把第2號軌道（2s）占據數設為2。回到主菜單后用主功能3作自定義函數的曲線圖（需確認iuserfunc參數目前仍設為了6，這時自定義函數才是電子徑向分布函數）。但是這回兩個端點設為0,0,0和0.6,0,0，因為2s和3s主要分布區域不太廣，徑向距離繪制0~0.6 Bohr就夠了。作完圖后，還是將曲線數據導出到line.txt，并改名為2s-nonrel.txt。然后，我們在相同的菜單內選擇選項6來尋找這個曲線上的極值點位置，這樣便于定量比較，settings.ini中num1Dpoints數值越大，算的點數越多，極值點的位置定位得越精確。程序會找出2個極大和2個極小點，我們只把函數極大值點的位置記錄下來。（如果作圖范圍比較大，比如徑向距離作到最大4 Bohr，會導致找出更多的極值點，但它們的函數值都非常小而不必考慮，這是由于與外側其它軌道相互作用而產生大量波節引起的）

接下來再把不考慮相對論的3s軌道，和考慮相對論時的2s、3s軌道的電子徑向分布函數圖都繪制出來然后導出到文本文件中，并且把極大值位置找出來并記錄。

我們把極大點位置匯總一下進行比較，第一列是徑向位置（Bohr）
不考慮相對論的2s原子軌道：
0.009400 Value:    0.74260372D+01
0.068600 Value:    0.28417400D+02
不考慮相對論的3s原子軌道：
0.009200 Value:    0.16238938D+01
0.055400 Value:    0.44666662D+01
0.186000 Value:    0.13213276D+02

考慮相對論的2s原子軌道：
0.006400 Value:    0.11038074D+02
0.059000 Value:    0.30805834D+02
考慮相對論的3s原子軌道：
0.006200 Value:    0.24480813D+01
0.047000 Value:    0.49772027D+01
0.167200 Value:    0.14286290D+02
很明顯地看出，考慮了相對論后徑向分布函數每個峰極大點的徑向位置都變小了，表明軌道收縮了，和預期的一致。我們把已導出的4個文本文件中的徑向分布函數數據一起放在Origin里作圖來圖形化地比較，如下所示

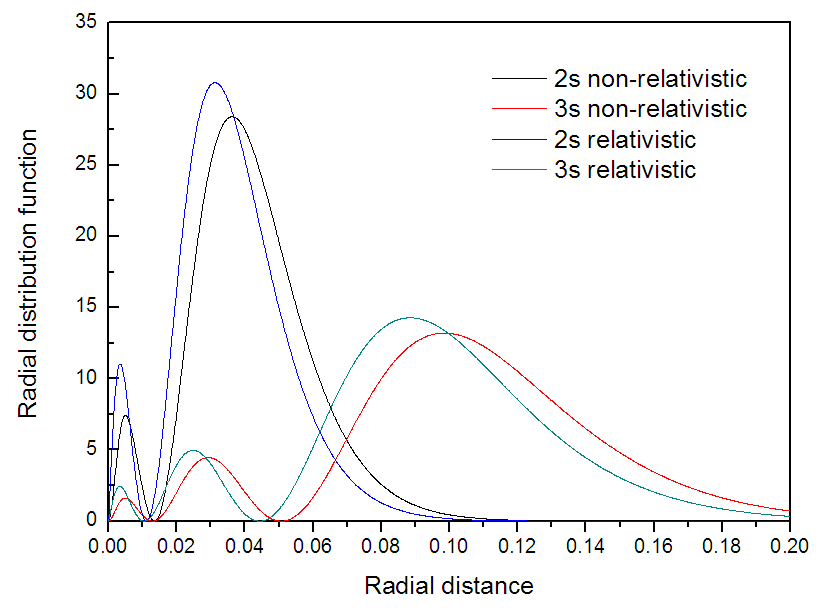
從圖上看非常明顯，相對論效應導致原子軌道電子徑向分布函數分布的收縮。

5 研究原子殼層結構

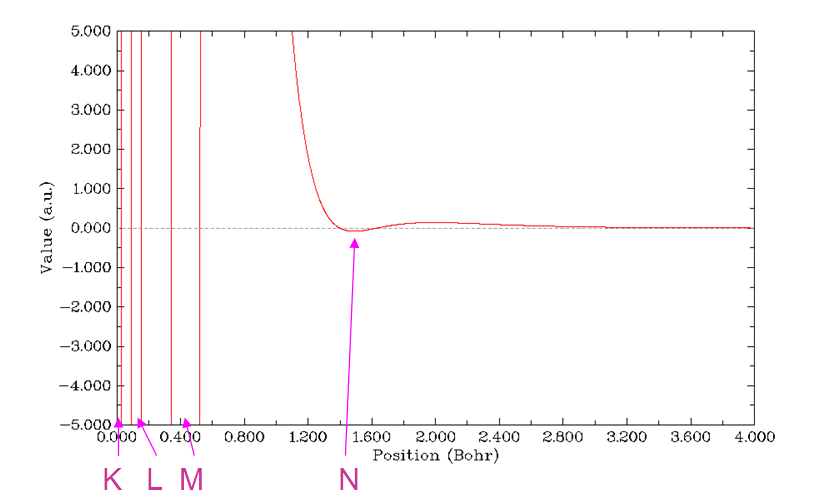
前面討論的都是單獨的原子軌道，本例我們更進一步，以Kr原子為例，介紹一下如何用Multiwfn描繪原子主殼層結構，即常說的K、L、M、N殼層。Kr的fch文件還是用上文的那個。

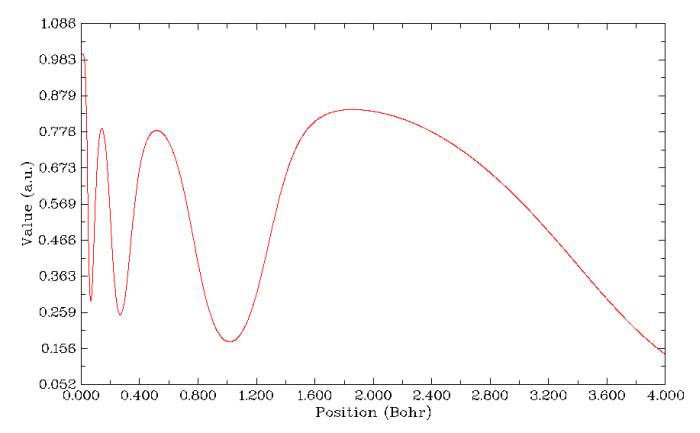
ELF（Electron localization function）專門用來展現電子高定域性區域，也可以展現原子殼層結構，因為每個殼層空間內電子的定域性相對較強，換句話說，每個殼層里的電子與殼層外的電子的交換的幾率較低。還是按照前幾節的方法繪制徑向圖，選擇函數的時候選9，即ELF，繪制范圍為r=0~4 Bohr。結果如下所示。總共出現了四個峰，對應于Kr的K、L、M、N四個殼層。利用前面已經用過的Multiwfn的搜索曲線極大極小點功能，可以定量地給出每個殼層的徑向位置。

LOL（Localized orbital locator）與ELF在物理意義和實際功能上都很類似，因此結果很類似。在繪制徑向圖過程中選第10號實空間函數就可以繪制出來，如下所示

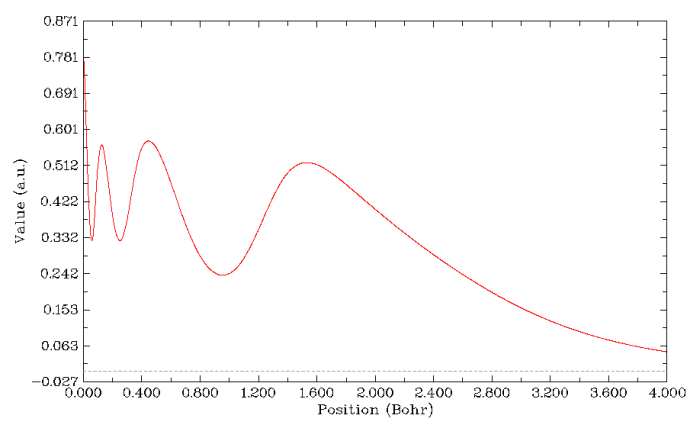
電子密度的拉普拉斯函數也曾是常用于展現原子殼層結構的函數。因為在每個殼層范圍內電子是相對聚集的，所以電子密度拉普拉斯為負值的區域就是各原子殼層范圍。在繪制徑向圖過程中選擇實空間函數時選10就可以繪制出來。但是由于此函數范圍太大，默認的曲線圖Y軸上下限范圍也太大，看不出應有的殼層結構特征，因此應當關閉彈出來的圖像，選3，輸入一個稍微合適的Y軸范圍，如-5,5，得到下面的圖。拉普拉斯值圖看起來略費勁，因為每個峰函數值大小差得非常多，沒法用一個刻度軸完整表現，所我在圖上標注了一下。可以看到N殼層的負值已經很不明顯了，實際上拉普拉斯函數辨別殼層的能力也就如此了。有文獻表明對于原子序數大于40的原子，拉普拉斯函數就沒法再辨別出原子殼層了。

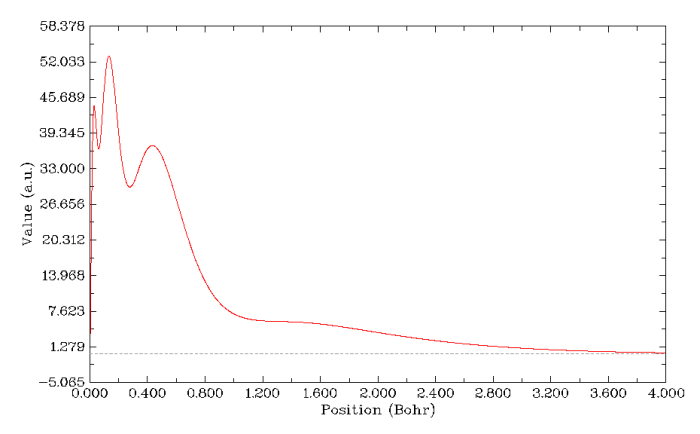
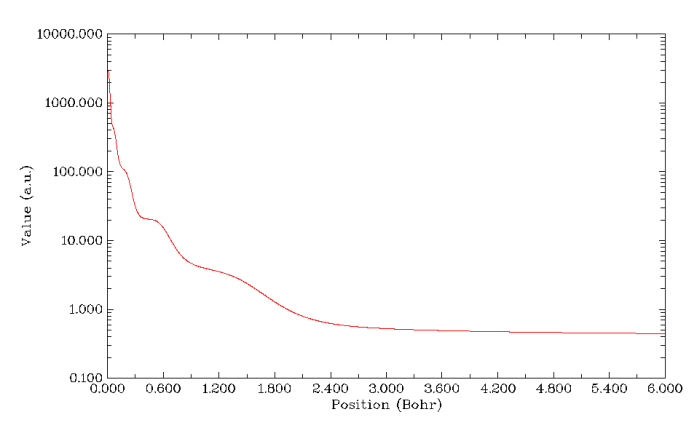
電子徑向分布函數也能表現原子殼層結構，這也是結構化學教科書上講原子結構時常出現的圖。怎么作電子徑向分布函數圖在前文已經詳細介紹了，這次作圖也是用同樣的方法，但不必再事先修改軌道占據數了，直接作圖得到的就是整個原子的電子徑向分布函數圖，如下所示。這個圖上清楚地顯示了K、L、M殼層電子對應的三個峰，但是N殼層就完全顯示不出來了，這據說和軌道的鉆穿效應有關。這表明電子徑向分布函數只能比較好地研究前三周期的原子結構。

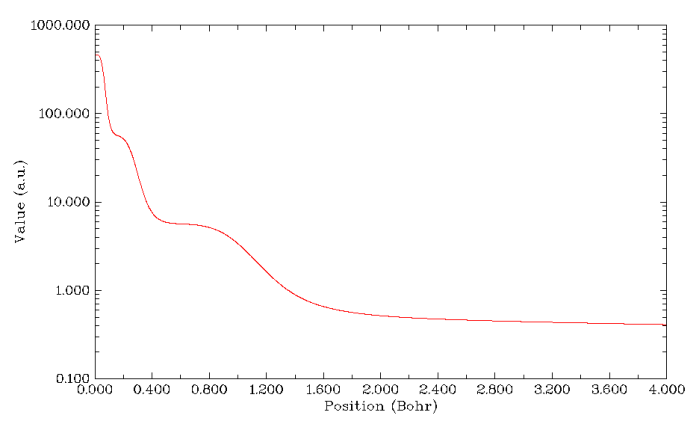
平均局部離子化能可以間接地反應出原子殼層結構，這個函數可能大家不熟悉，我以后會再專門詳談，讀者若感興趣可參見J.Mol.Model,16,1731和Theoretical Aspects of Chemical Reactivity一書的第8章的綜述。還是繪制徑向圖形，選擇實空間函數時選擇18，就得到了平均局部離子化能隨徑向距離的變化。默認的線性刻度軸對表現這個函數不太好，因此圖像彈出來后先關掉它，選8改用對數刻度軸，輸入-1,3（即10^-1到10^3區間），再選-1重新繪圖，結果如下。曲線的每個平臺代表一個殼層，而平臺之間的拐點代表殼層間的分界位置。這個圖有四個臺階，三個拐點，因此Kr的四個殼層都被表現出來了。

本文展示的最后一個有辨別原子殼層能力的函數是V(r)/ρ(r)，其中V(r)代表靜電勢。對于中性原子，V(r)和ρ(r)都是單調下降的函數。它們相除時，由于每個殼層內電子比較富集，ρ(r)在殼層范圍內會體現一定主導性，因此在殼層處這個函數曲線會產生凹陷，由此可以展現殼層結構。而每個凹陷中間夾著的峰自然就可以用來分辨相鄰的殼層，研究表明峰的位置和電子徑向分布函數極小點位置是有對應關系的。V(r)/ρ(r)也被稱為平均局部靜電勢，這個函數不是Multiwfn正式支持的函數，繪制它可以用Multiwfn先把靜電勢和電子密度隨徑向距離的變化分別計算并導出，一起讀入origin這類程序里手動相除并繪圖；另一個辦法就是像第3節討論的那樣修改userfunc函數的代碼，寫上userfunc=totesp(x,y,z)/fdens(x,y,z)，重新編譯Multiwfn，到時候作圖時選用戶自定義的函數即可。實際上，這個函數也是像4π*r^2*ρ函數一樣作為用戶編寫userfunc函數的示例代碼出現了，看代碼就會理解，只需要將settings.ini里的iuserfunc改成8，則用戶自定義函數就直接成了V(r)/ρ(r)了，而無需自己改代碼再編譯。作這個函數隨徑向距離變化的圖，結果如下所示。從圖可見Kr的K、L、M、N殼層都可以辨別出來。注意在原子核中央處有一個很小的峰，圖的最右邊平緩下降也算一個“凹陷”。

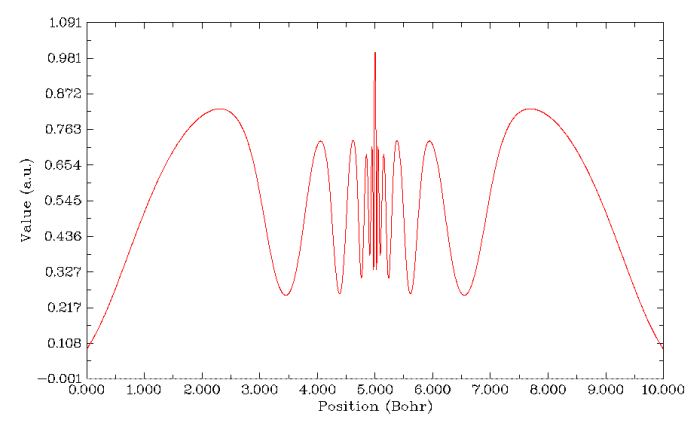
目前鮮有文章研究Rn這么重原子的殼層結構，辨別這樣的原子所有的殼層（K,L,M,N,O,P）是對上述函數更嚴峻的考驗，這里做一個簡單的測試，由于電子密度拉普拉斯函數和電子徑向分布函數在Kr上已經敗下陣來，M和N已經很難分辨開，這里就不再考慮。

支持到Rn這么重的元素的全電子基組可選余地相對有限，雖然也有不少五花八門的不出名的全電子基組可用，但獲取不便，修改成Gaussian能認的格式也有點麻煩。用Gaussian自帶的UGBS基組總是出現積分精度測試通不過的問題，雖然SCF=novaracc、int=ultra、guess=indo等選項有時能解決，但往往最終還得被迫靠int=noxctest來強行繞過精度測試，但結果多少讓人心有余悸。知名的ANO-RCC基組很適合后HF方法計算，但基組過大算起來很慢。前面提到的SARC系列基組又便宜又好但目前不支持主族元素。本節并不打算考慮相對論效應，因為這對此節研究的問題本質沒太大影響，所以這里使用周期表涵蓋全面，專為HF非相對論計算優化的WTBS基組，它是極小基，算起來相對較快，基組定義從BSE網站上就能得到，輸入文件就不再列出了，route section部分就是#P HF/Gen。

先做ELF的圖。為了圖像看起來更清楚，這回不是從核中心作圖，而是橫跨Rn原子，線段兩端位置為-5,0,0和5,0,0。如下圖所示。圖上總共有11個峰（注意辨別K殼層在中心的一個峰和L殼層在兩側對稱的峰，它們挨得很近），Rn的6個殼層都完美地展現出來，說明ELF對于展現原子殼層結構是最佳選擇。LOL也能得到很類似的圖。

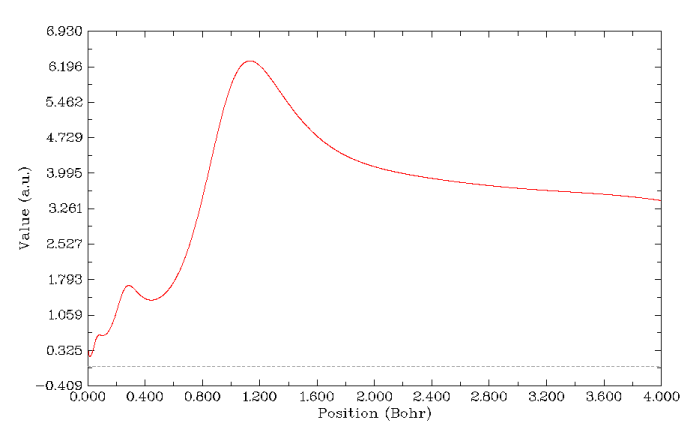
繪制平均局部離子化能隨徑向距離的變化，也能看到6個平臺，以及分離它們的5個拐點，因此這個函數對于解釋Rn的殼層結構也適用。但是看起來明顯不如ELF圖清楚容易辨別。

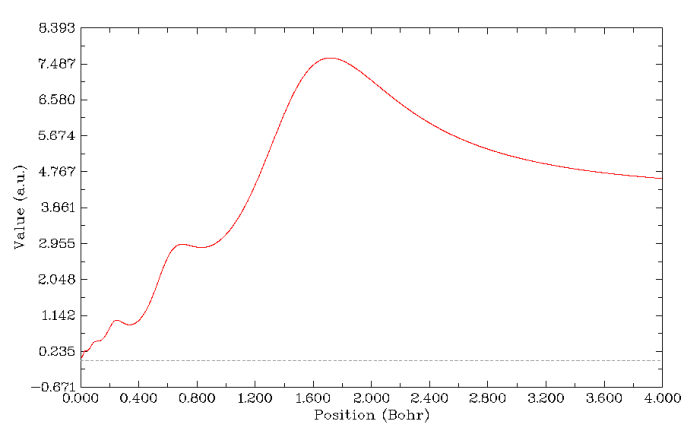
再來繪制V(r)/ρ(r)的圖。因為此體系高斯函數較多（是前面Kr體系的6倍），計算靜電勢又很耗時，所以得多等一會兒，普通的四核機子上要花好幾分鐘。如果想省時的話就把settings.ini里的num1Dpoints改小幾倍來減少計算的點數，其實有500個點一般也足夠精細了。結果如下所示，也能看到對應K,L,M,N,O,P這6個主層的6個凹陷（圖中最右側算一個。注意在核中心有個極微小的峰），說明此函數對辨別原子殼層結構的能力還是可以的。不過還是不如ELF圖分析起來方便，而且計算慢幾個數量級。

6 總結

本文利用Multiwfn結合Gaussian繪制了原子軌道的角度和徑向部分圖形、展現了軌道間的正交和鉆穿效應、分析了相對論效應的影響，最后還用不同方式描繪了原子的殼層結構。結果既很好地還原了教科書上關于原子結構的經典概念，又體現了量子化學計算的意義。本文只是Multiwfn全部功能的一小部分的應用實例，但讀者應該已經感受到Multiwfn操作簡單，功能強大，而且靈活自由。Multiwfn的各種各樣的應用實例都已在手冊第四章給出，在Multiwfn的主頁上的other resources一欄里面也有寡人寫的一系列中文的Multiwfn專題應用的帖子，比如分析多中心鍵、分析弱相互作用、做密度差圖等等，通過這些文章不僅能進一步了解Multiwfn的應用，還能同時了解到很多波函數分析方法的原理。