使用Multiwfn預測晶體密度、蒸發焓、沸點、溶解自由能等性質
使用Multiwfn預測晶體密度、蒸發焓、沸點、溶解自由能等性質
文/Sobereva @北京科音
First release: 2016-Jun-21 Last update: 2020-Jan-7
利用分子表面積、體積,連同基于分子表面上靜電勢分布定義的各種指標(統稱為GIPF描述符),如靜電勢極大、極小點數值、靜電勢的方差和平均值等等,可以用來預測分子凝聚相的各種性質,不少文獻給出了專門的預測公式。本文就專門說說怎么使用Multiwfn程序預測這些性質。很多文章理論研究自行設計的新分子時都是利用Multiwfn來進行這種預測。本文說的分子表面都是指電子密度=0.001 a.u.的等值面,分子范德華體積指的是其中包含體積。
閱讀后文之前一定要先閱讀《使用Multiwfn的定量分子表面分析功能預測反應位點、分析分子間相互作用》(http://www.shanxitv.org/159)以及Multiwfn手冊3.15.1節了解一些基本知識。Multiwfn可在http://www.shanxitv.org/multiwfn免費下載。不了解Multiwfn的話建議看看《Multiwfn入門tips》(http://www.shanxitv.org/167)和《Multiwfn波函數分析程序的意義、功能與用途》(http://www.shanxitv.org/184)。
1 分子晶體密度預測
討論分子晶體密度預測方法的文章很多,本文用的方法和這四篇相關,有興趣可以看看:(a)Rice et al., J. Phys. Chem. A, 111, 10874 (2007):這篇提出了可以把分子范德華體積換算成密度量綱來預測晶體密度。共測試了289個體系,包含180個普通中性分子、38個高氮分子、71個離子晶體,發現對于只含CHNO的中性體系預測得挺準。不過對于含其它元素的,以及離子晶體誤差大一些。
(b)Politzer et al., Mol. Phys., 107, 2095 (2009):這篇提出了對(a)文中方法的改進,預測公式引入了范德華體積以外的描述符。對一批只含CHNO的中性分子,用文中的(7)式預測的晶體密度的平均絕對誤差為0.036 g/cm^3,比只依賴于分子范德華體積進行預測誤差小了30%。
(c)Politzer et al., Mol. Phys., 108, 1391 (2010):這篇提出專門適合預測有機離子晶體密度的公式,這對于研究炸藥之類很有用。
(d)Rice et al., J. Comp. Chem., 34, 2146 (2013):這篇用了較大的測試集測試Politzer在上兩篇文章里提出的密度預測公式,測試結果證實將分子表面靜電勢相關的描述符引入預測公式確實對提高精度有幫助。
下面我們就結合具體例子介紹下利用Multiwfn預測晶體密度的操作。
1.1 中性體系
上面的文章(b)里推薦的預測中性體系密度的公式為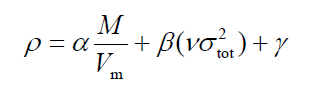
我們用著名的炸藥RDX(渾名黑索金)作為中性體系的例子。PS:《重裝武器》里的手斧貌似就是RDX。其實驗晶體密度有的說是1.806有的說是1.82g/cm^3。其結構式為:
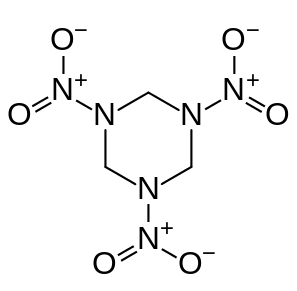
我們使用和Politzer用的相同的級別B3PW91/6-31G**用Gaussian對這個體系進行優化,然后將所得chk文件轉換為fch文件。啟動Multiwfn,輸入此fch文件路徑,之后輸入12進入定量分子表面分析功能,再輸入0用默認設定進行計算。默認情況下分子表面用的就是電子密度=0.001 a.u.的等值面,和前面幾篇文章一致。算完后得到如下結果:
Volume: 1379.32761 Bohr^3 ( 204.39531 Angstrom^3)
Estimated density according to mass and volume: 1.8045 g/cm^3
Minimal value: -20.75385 kcal/mol Maximal value: 45.96479 kcal/mol
Overall surface area: 729.58496 Bohr^2 ( 204.30463 Angstrom^2)
Positive surface area: 398.13142 Bohr^2 ( 111.48817 Angstrom^2)
Negative surface area: 331.45354 Bohr^2 ( 92.81646 Angstrom^2)
Overall average value: 0.00982246 a.u. ( 6.16369 kcal/mol)
Positive average value: 0.03289853 a.u. ( 20.64416 kcal/mol)
Negative average value: -0.01789579 a.u. ( -11.22978 kcal/mol)
Overall variance (sigma^2_tot): 0.00049125 a.u.^2 ( 193.43735 (kcal/mol)^2)
Positive variance: 0.00041232 a.u.^2 ( 162.35692 (kcal/mol)^2)
Negative variance: 0.00007893 a.u.^2 ( 31.08042 (kcal/mol)^2)
Balance of charges (nu): 0.13485811
Product of sigma^2_tot and nu: 0.00006625 a.u.^2 ( 26.08659 (kcal/mol)^2)
Internal charge separation (Pi): 0.02598527 a.u. ( 16.30602 kcal/mol)
第一行告訴你電子密度0.001a.u.等值面內部的體積,即范德華體積是204.39531 Angstrom^3,下一行告訴你把這個數據直接按照M/Vm等效地換算為密度結果是1.8045 g/cm^3。雖然計算方式如此簡單,但是結果和實驗值符合得極好!具體換算過程是:1埃=1E-8cm,每個RDX分子所占體積是(1E-8)^3*204.39531 cm^3,每個RDX分子質量為222.11634/6.02214179E23 g,因此密度為222.11634/6.02214179E23/(1E-24*204.39531)=1.8045 g/cm^3。
Multiwfn輸出的Product of sigma^2_tot and nu就是上面說的νσ2tot。我們按照前面圖中的公式,把分子表面上靜電勢的影響也考慮進去再進行計算,密度為
0.9183*1.8045 + 0.0028*26.08659 + 0.0443 = 1.77 g/cm^3
結果相對于實驗值的差異反倒比直接用M/Vm來計算大了點。但光從這一個例子不能說考慮了靜電勢的影響后結果會變差,根據文章測試從統計來看還是有改進的,只不過正如Politzer文章里說的,對于M/V結果恰好挺準的時候,考慮靜電勢的校正項反倒會令結果略微惡化。
1.2 離子體系
對于離子晶體,直接按照M/Vm方式預測密度會有較大誤差,在前述文章(c)中作者提出按照這種方式來預測: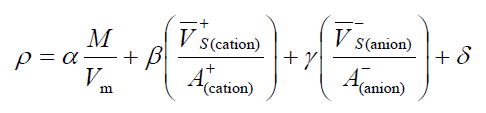
β后面括號中的分子代表陽離子的分子表面靜電勢為正的區域的平均靜電勢,分母為這些區域的面積;γ后面括號中的分子代表陰離子的分子表面靜電勢為負的區域的平均靜電勢,分母為這些區域的面積。在B3PW91/6-31G**下,當靜電勢以kcal/mol為單位,面積以埃^2為單位,密度以g/cm^3為單位,向實驗數據擬合的參數為α=1.0260, β=0.0514, γ=0.0419, δ=0.0227。根據文中的測試,按照這個公式預測密度平均絕對誤差僅為0.033g/cm^3。
下面我們就用1:1型離子晶體疊氮化銨(陽離子NH4+,陰離子N3-)示例一下,其實驗密度為1.346g/cm^3。用B3PW91/6-31G**分別對NH4+和N3-優化,得到fch文件,載入Multiwfn后也是先輸入12再輸入0。NH4+的結果為
Volume: 202.60123 Bohr^3 ( 30.02241 Angstrom^3)
Estimated density according to mass and volume: 0.9977 g/cm^3
Minimal value: 164.83607 kcal/mol Maximal value: 180.62353 kcal/mol
Overall surface area: 169.42489 Bohr^2 ( 47.44381 Angstrom^2)
Positive surface area: 169.42489 Bohr^2 ( 47.44381 Angstrom^2)
Negative surface area: 0.00000 Bohr^2 ( 0.00000 Angstrom^2)
Overall average value: 0.27371398 a.u. ( 171.75826 kcal/mol)
Positive average value: 0.27371398 a.u. ( 171.75826 kcal/mol)
Negative average value: NaN a.u. ( NaN kcal/mol)
Overall variance (sigma^2_tot): 0.00004471 a.u.^2 ( 17.60463 (kcal/mol)^2)
Positive variance: 0.00004471 a.u.^2 ( 17.60463 (kcal/mol)^2)
Negative variance: 0.00000000 a.u.^2 ( 0.00000 (kcal/mol)^2)
Balance of charges (nu): 0.00000000
Product of sigma^2_tot and nu: 0.00000000 a.u.^2 ( 0.00000 (kcal/mol)^2)
Internal charge separation (Pi): 0.00567588 a.u. ( 3.56167 kcal/mol)
這里Positive surface area就是前面提到的分子表面上靜電勢為正值區域的面積,Positive average value就是這個區域的靜電勢平均值。
N3-的結果為
Volume: 365.13961 Bohr^3 ( 54.10812 Angstrom^3)
Estimated density according to mass and volume: 1.2896 g/cm^3
Minimal value: -139.23748 kcal/mol Maximal value: -131.34857 kcal/mol
Overall surface area: 259.87905 Bohr^2 ( 72.77356 Angstrom^2)
Positive surface area: 0.00000 Bohr^2 ( 0.00000 Angstrom^2)
Negative surface area: 259.87905 Bohr^2 ( 72.77356 Angstrom^2)
Overall average value: -0.21750181 a.u. ( -136.48456 kcal/mol)
Positive average value: NaN a.u. ( NaN kcal/mol)
Negative average value: -0.21750181 a.u. ( -136.48456 kcal/mol)
Overall variance (sigma^2_tot): 0.00001397 a.u.^2 ( 5.49999 (kcal/mol)^2)
Positive variance: 0.00000000 a.u.^2 ( 0.00000 (kcal/mol)^2)
Negative variance: 0.00001397 a.u.^2 ( 5.49999 (kcal/mol)^2)
Balance of charges (nu): 0.00000000
Product of sigma^2_tot and nu: 0.00000000 a.u.^2 ( 0.00000 (kcal/mol)^2)
Internal charge separation (Pi): 0.00311483 a.u. ( 1.95459 kcal/mol)
這里Negative surface area就是前面提到的分子表面上靜電勢為負值區域的面積,Negative average value就是這個區域的靜電勢平均值。
總體積是陰、陽離子體積的加和,即30.02241+54.10812=84.13053埃^3。總相對原子質量是18.03846+42.02010=60.05856,只按照M/Vm來估算的話密度就是60.05856/6.02214179E23/(1E-24*84.13053)=1.185g/cm^3,和實驗值偏差較大。
若代入到前面考慮陰陽離子表面靜電勢的式子,結果為
1.0260*1.185 + 0.0514*(171.75826/47.44381) + 0.0419*(-136.48456/72.77356) + 0.0227 = 1.346 g/cm^3。絕了!這結果和實驗值驚人地吻合!當然這次純屬是撞大運,對于其它體系還是會有一點誤差的,不過至少例證了這種預測方法是頗準的。
順帶一提,在《詳談Multiwfn的命令行方式運行和批量運行的方法》(http://www.shanxitv.org/612)中詳細介紹了如何將上面的數據提取過程和預測公式的計算包裝成腳本,從而對某個分子的波函數文件可以實現一鍵密度預測,建議看看。
2 蒸發焓、升華焓預測
在J. Phys. Chem. A, 110, 1005 (2006),作者給出了預測含CHNO的分子的蒸發焓和升華焓的公式。蒸發焓公式為: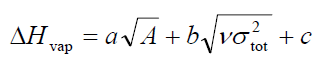
升華焓公式為:
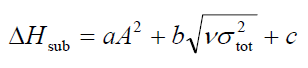
其中a = 0.000267,b = 1.650087,c = 2.966078。根據文中測試RMS誤差為2.1 kcal/mol。
這里我們還用RDX為例子。這次我們在Gaussian里直接用# B3LYP/6-311++G(2df,2p)//B3LYP/6-31G**作為關鍵詞進行計算,將結果轉化成fch文件,還是按上一節做分子表面靜電勢分析。由于本次fch文件里的基組比上一節的6-31G**大了許多許多,所以Multiwfn計算靜電勢的耗時會頗長,一般Intel 4核得約20分鐘。如果嫌慢就按照一開始說的方法通過設置cubegenpath參數來讓Multiwfn自動借用cubegen來計算靜電勢就行了,耗時會少一個數量級以上。Multiwfn給出的結果如下:
Volume: 1440.01752 Bohr^3 ( 213.38863 Angstrom^3)
Estimated density according to mass and volume: 1.7285 g/cm^3
Minimal value: -19.99318 kcal/mol Maximal value: 50.00839 kcal/mol
Overall surface area: 749.90235 Bohr^2 ( 209.99408 Angstrom^2)
Positive surface area: 416.24686 Bohr^2 ( 116.56101 Angstrom^2)
Negative surface area: 333.65549 Bohr^2 ( 93.43307 Angstrom^2)
Overall average value: 0.01158552 a.u. ( 7.27003 kcal/mol)
Positive average value: 0.03455435 a.u. ( 21.68320 kcal/mol)
Negative average value: -0.01706890 a.u. ( -10.71091 kcal/mol)
Overall variance (sigma^2_tot): 0.00051831 a.u.^2 ( 204.09253 (kcal/mol)^2)
Positive variance: 0.00044197 a.u.^2 ( 174.03591 (kcal/mol)^2)
Negative variance: 0.00007633 a.u.^2 ( 30.05662 (kcal/mol)^2)
Balance of charges (nu): 0.12558124
Product of sigma^2_tot and nu: 0.00006509 a.u.^2 ( 25.63019 (kcal/mol)^2)
Internal charge separation (Pi): 0.02653619 a.u. ( 16.65172 kcal/mol)
這里看到,根據M/Vm估出來的密度是1.7285 g/cm^3,明顯不如上一節B3PW91/6-31G**估出來的接近實驗值,所以絕非用大基組結果就好,因為其中有誤差抵消的巧合在內。
代入到蒸發焓的公式,結果為2.130*sqrt(209.99408)+0.930*sqrt(25.63019)-17.844=17.73 kcal/mol。
代入到升華焓的公式,結果為0.000267*209.99408^2+1.650087*sqrt(25.63019)+2.966078=23.09 kcal/mol。此值和實驗值26.8 kcal/mol比較接近,說明預測準確度還成。
在Int. J. Quantum Chem., 105, 341 (2005)中Politzer等人通過向NIST查到的30個實驗蒸發焓和66個實驗升華焓擬合了標況下的蒸發焓和升華焓的預測公式,平均誤差分別為2.0 kcal/mol和2.8 kcal/mol。相對于前述JPCA那篇的公式關鍵好處在于適用的元素更廣,可用于含有C、H、O、N、F、Cl、S體系的。公式如下,每一項的單位和上述相同
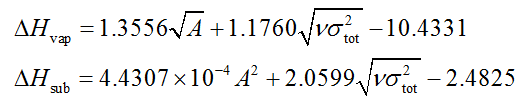
大家感興趣的話可以用Politzer的式子也預測一下RDX的升華焓和蒸發焓。注意他們在擬合參數的時候是在B3PW91/6-31G**進行的,所以大家還得在這個級別下再做一次表面靜電勢分析。
3 沸點和臨界性質
在J. Phys. Chem., 97, 9369 (1993)中作者給出了預測有機分子沸點和臨界溫度/體積/壓力的公式。預測沸點的公式如下: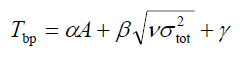
我們用上面的式子對苯的沸點進行預測
Overall surface area: 420.87971 Bohr^2 ( 117.85834 Angstrom^2)
Product of sigma^2_tot and nu: 0.00001021 a.u.^2 ( 4.01847 (kcal/mol)^2)
代入公式,得2.736*117.85834 + 33.31*sqrt(4.01847) -72.05 = 317.18K。其實驗沸點為353.3K,偏離實驗有點大。可能原因一方面是那個預測公式可靠度本身就有限,而且當年計算條件落后,它們擬合參數用的級別太爛;另一個可能原因是他們用的STO-3G*、STO-5G*直接在Gaussian09里面用時并不是對應的他們當時實際用的基組(這倆基組帶星號具體代表什么,文中并未說明,不知是什么鬼,實際上在G09中對STO-nG帶星號和不帶是完全一樣的)。
再來算個乙酸的
Overall surface area: 308.13678 Bohr^2 ( 86.28710 Angstrom^2)
Product of sigma^2_tot and nu: 0.00013329 a.u.^2 ( 52.48615 (kcal/mol)^2)
結果為2.736*86.28710 + 33.31*sqrt(52.48615) -72.05 = 405.35K,和實驗沸點391.1K比較接近。
4 溶解自由能
溶解自由能通過隱式溶劑模型很容易計算,見《談談隱式溶劑模型下溶解自由能和體系自由能的計算》(http://www.shanxitv.org/327)。而在J. Phys. Chem. A, 103, 1853 (1999)中作者提出了對有機分子預測水中的溶解自由能(水合自由能)的公式: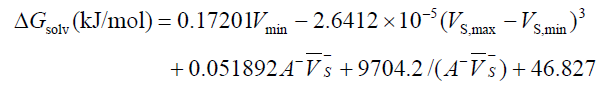
靜電勢單位都是kcal/mol。其中的參數是對于B3P86/6-31+G**級別優化和波函數分析的情況向實驗來擬合的。式中Vmin是指整個三維空間中靜電勢最小的數值,Vs,max和Vs,min分別是分子表面上靜電勢最大和最小點數值。A-是分子表面靜電勢為負值區域的表面積,Vs-上面帶一個橫杠是指靜分子表面靜電勢為負值區域的靜電勢平均值。
這里用苯酚作為例子預測其水合自由能。對它在B3P86/6-31+G**下優化和做定量分子表面分析,結果如下
The number of surface minima: 3
# a.u. eV kcal/mol X/Y/Z coordinate(Angstrom)
1 -0.02708400 -0.736993 -16.995483 0.144864 -1.152264 1.957787
2 -0.02708765 -0.737093 -16.997774 0.177172 -1.141436 -1.956363
* 3 -0.04117381 -1.120396 -25.836976 1.510535 3.362206 0.028759
The number of surface maxima: 5
# a.u. eV kcal/mol X/Y/Z coordinate(Angstrom)
1 0.02554682 0.695164 16.030883 -3.342025 -2.278454 0.048218
* 2 0.08663577 2.357479 54.364812 -1.946071 3.097000 0.021567
3 0.02200159 0.598694 13.806218 0.069391 -4.282483 0.042709
4 0.02253021 0.613078 14.137932 3.338105 -2.322365 0.021761
5 0.01865089 0.507517 11.703623 3.449724 1.099448 -0.000188
這里可知Vs,max和Vs,min分別是54.364812和-25.836976 kcal/mol。
預測公式涉及的分子表面上的靜電勢相關的量為
Minimal value: -25.83698 kcal/mol Maximal value: 54.36481 kcal/mol
Negative surface area: 242.41979 Bohr^2 ( 67.88446 Angstrom^2)
Negative average value: -0.01748812 a.u. ( -10.97397 kcal/mol)
為了獲取Vmin,我們要計算涵蓋整個分子三維空間的靜電勢格點數據,找到其中最小點數值。啟動Multiwfn并載入輸入文件后,進入主功能5,選擇靜電勢,再選擇Medium quality grid。算完后,屏幕上會看到極小點數值和位置
The minimum is -0.59120100E-01 at 1.82413 5.61762 -1.15668 Bohr
這個靜電勢值-0.05912 a.u.轉換下單位就是-0.05912*627.51=-37.098 kcal/mol。
將上面的量代入到預測公式里,得到的水合自由能為0.17201*(-37.098) - 2.6412E-5*(54.364812+25.836976)^3 + 0.051892*67.88446*(-10.97397) + 9704.2/(67.88446*(-10.97397)) + 46.827 = -24.86kJ/mol。這個值和實驗值-27.67 kJ/mol有不到3 kJ/mol的偏差,精度還算可以。而文獻中這個體系按照預測公式算出來是-26.45 kJ/mol,和實驗值只差一點幾kJ/mol。之所以這里計算結果和文獻里不同,一方面是Gaussian程序版本不一樣,另一方面是Multiwfn和他們當年用的程序在分析分子表面時用的算法、數值設定有差異(Multiwfn的絕對更準),還有一方面是獲得Vmin的方式不同,這對結果影響不小。他們擬合的參數確切來說只是對他們當年用的具體計算方式才是最合適的。
5 其它
分子體積、表面積連同分子表面靜電勢定義的描述符還能用來預測許多其它性質,例如一級/二級/三級/四級胺的pKb:J. Chem. Inf. Model. (2020) DOI: 10.1021/acs.jcim.9b01173
C60在不同溶劑中的可溶性:J. Phys. Chem., 99, 12081 (1995)
有機分子融化熱、表面張力、液體/晶體密度:Chem. Phys., 204, 289 (1996)
有機分子在明膠中的擴散系數:J. Phys. Chem., 100, 5538 (1996)
不同陰離子與NH4+、Na+、K+形成的晶體的晶格能:J. Phys. Chem. A, 102, 1018 (1998)
還有其它亂七八糟的性質如粘性等也可以這么預測。在J. Mol. Struct. (Theochem), 425, 107 (1998)等文獻中還能查到很多關系式,這里就不再舉例了,總之牽扯到的和分子表面有關的量都包含在Multiwfn的輸出信息里了,代入公式就能算了。