使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據
使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據
文/Sobereva@北京科音
First release: 2020-May-19 Last update: 2023-Jul-13
1 前言
在日常量子化學研究中,計算焓、熵、自由能等熱力學數據是最常涉及的問題。主流量子化學程序如Gaussian、ORCA等都自帶了振動分析功能,在任務結束后會自動給出熱力學數據。但是用這些程序來獲得熱力學數據往往并不方便,也有很多局限性。為了能令廣大量子化學研究者在熱力學數據計算方面極盡便利,筆者開發了Shermo程序,在此文將簡要介紹并給出使用例子。
Shermo程序的原文已經發表,使用Shermo程序計算熱力學數據發表文章時請務必記得引用,也十分建議大家閱讀:
Tian Lu, Qinxue Chen, Shermo: A general code for calculating molecular thermochemistry properties, Comput. Theor. Chem., 1200, 113249 (2021) DOI: 10.1016/j.comptc.2021.113249
上面的論文正式發表前也發在了論文預印本網站ChemRxiv上,見https://doi.org/10.26434/chemrxiv.12278801,沒有權限訪問上面的正式版文章的話也可以看這個預印版,內容基本一樣,引用時請務必引用上面的正式版。
筆者之前還寫過《Shermo:計算氣相分子配分函數和熱力學數據的簡單程序》(http://www.shanxitv.org/315)一文,那篇文章里介紹的Shermo是1.0版,是本文介紹的Shermo的前身。那個1.0版沒有多大實際應用價值,功能很少,使用也很不方便。
2 Shermo的功能和特點
Shermo是一個免費的可以獨立運行的計算分子熱力學數據的程序,需要從量子化學程序振動分析的輸出文件里讀取信息來進行計算,計算時基于理想氣體假設(各種量子化學程序給出的熱力學數據也都是如此)。
Shermo有以下特點:
? 可以讀入四種最流行的量子化學程序的輸出文件(可以是振動分析,也可以是優化+振動分析),包括Gaussian、ORCA、GAMESS-US、NWChem。還可以讀入CP2K第一性原理程序的振動分析的輸出文件
? 可以計算所有常見的熱力學量,包括內能、焓、熵、自由能、等壓和等容熱容、配分函數
? 頻率校正因子可以對ZPE、熵、升溫對焓/內能的增加量、熱容同時分別設置(不像Gaussian等程序里只能設一個全局校正因子)
? 可以非常方便地對溫度和壓力進行掃描來考察熱力學量隨溫度和壓力的變化
? 默認使用諧振近似模型考慮振動對熱力學量的貢獻(Gaussian等程序給出的熱力學數據就是用的這個方法),同時還支持Truhlar和Grimme各自提出的準RRHO方法考慮低頻振動的貢獻,對柔性體系可以得到明顯更合理的結果
? 平動、轉動、振動、電子激發對各種熱力學量的貢獻可以分別輸出,而且各個振動模式的貢獻也可以單獨輸出,這對于分析影響熱力學量的內在因素、解釋不同體系熱力學量的差異非常有益
? 可以給出一批構型/構象的Boltzmann分布比例和構象權重的熱力學數據
? 可以考慮濃度變化(如氣相標準態到液相標準態)導致的自由能改變
? 可以通過雙擊圖標執行,也可以通過純命令行方式運行,因此可以非常容易地嵌入到批處理腳本中,從而一次性計算一大批體系
? Shermo不用安裝也不用配置運行環境就能直接執行,不像Python腳本那樣還得先裝個Python,因此腦盲也能順利使用
? Shermo的輸出信息極其簡單易懂,而且手冊寫得特別詳細,所有熱力學量計算的基本原理和公式都在附錄里介紹了
由上可見,Shermo在熱力學數據計算方面既強大又靈活方便,可謂分子熱力學數據計算離不開的工具。不僅把一些很繁瑣的事情變得極其簡單,還彌補了不少空白。此外,Shermo算的結果的可靠性在很多情況下也高于量子化學程序直接輸出的結果。比如Gaussian不支持準RRHO方法,因此對于柔性大體系計算的自由能可能有多達幾甚至十幾kcal/mol的誤差;ORCA判斷點群時容易判斷錯,導致轉動對稱數識別錯誤,進而令轉動對熱力學量的貢獻錯誤;GAMESS-US的轉動常數計算得有問題,也因此導致轉動對熱力學量的貢獻計算得有問題。
稍有一定經驗的Gaussian用戶都知道其自帶的計算熱力學數據的freqchk工具,如今有了Shermo之后freqchk就可以徹底扔了。不僅freqchk沒有上述的Shermo的大多數優點,而且使用時還必須提供chk文件,如果沒保留的話就瞎了,而且為了用freqchk還得裝個Gaussian。而對于ORCA、GAMESS-US等其它程序用戶,連類似freqchk的工具都沒有,就更離不開Shermo了。另外,獨立的KiSThelP和GoodVibes程序雖然也能計算熱力學量,但和Shermo相比就差多了。
3 Shermo程序的使用簡介
Shermo程序的細節看Shermo手冊里的說明,這里我只是把Shermo程序最最基本的一些信息簡單提一下。
Shermo程序的可執行文件和手冊可以在程序主頁http://www.shanxitv.org/soft/shermo上下載。文件包里的Shermo.exe是Windows下的可執行文件,沒有后綴的是Linux下的可執行文件。settings.ini是用來設置運行參數的文件。
Shermo程序既可以通過交互式方式運行,也可以通過命令行方式運行,后者便于將Shermo嵌入批處理腳本來進行批量計算。
在Windows下運行Shermo通常是雙擊Shermo.exe圖標來啟動,程序會先從當前目錄下的settings.ini中讀取運行參數并顯示在屏幕上。輸入文件路徑后,程序就會從輸入文件中讀取電子能量、振動頻率、原子質量等信息,然后開始計算熱力學數據并輸出。即便對于巨大體系,也是一瞬間就能算完。
在Linux下運行時,可以進入Shermo目錄后輸入./Shermo命令來啟動。如果你想在任意目錄下都能通過Shermo命令啟動之并讓其從Shermo目錄下的settings.ini中載入運行參數,則在~/.bashrc文件里加入以下兩行,之后重新進入終端即可。
export PATH=$PATH:/sob/Shermo_2.0
export Shermopath=/sob/Shermo_2.0
(這里假設/sob/Shermo_2.0是Shermo可執行文件和settings.ini所在的目錄)
如果在Linux下運行時你嫌編輯settings.ini文件麻煩,也可以直接指定運行參數,比如
Shermo example/G16_H2CO_freq.out -T 350 -sclZPE 0.9806
就代表用Shermo處理example/G16_H2CO_freq.out,溫度設為350 K,ZPE校正因子設為0.9806。而其它沒有明確指定的參數則使用當前settings.ini里設置的。
settings.ini文件里的選項在手冊2.3節有詳細介紹,在此文件自帶的注釋里也有簡要介紹。諸如在settings.ini里看到有ilowfreq參數,就說明以命令行方式使用時可以用-ilowfreq [參數值] 的形式直接指定數值。
在線使用:除了下載使用外,Shermo也可以通過https://atomistica-online-shermo.anvil.app網站在線使用,用戶直接將計算化學程序的輸出文件上傳,根據情況對計算方式進行設置,就可以馬上返回Shermo計算輸出的結果。此在線平臺是Stevan Armakovi?開發的,有使用相關問題請與之聯系。通過此在線平臺使用Shermo時,除了要引用Shermo原文外,還應同時引用平臺作者的文章https://doi.org/10.1080/08927022.2022.2126865。
4 Shermo使用實例
下面通過一些實例介紹如何使用Shermo結合主流量子化學程序做各種熱化學分析,在Shermo手冊里還有更多更具體的例子。如果你對熱力學量計算原理的知識極為匱乏,強烈建議先看看Shermo手冊的附錄了解基本常識,否則不可能正確理解結果的含義、在研究文章中正確地分析討論。
如上所述,Gaussian、ORCA、GAMESS-US、NWChem的振動分析或優化+振動分析的輸出文件都可以給Shermo當輸入文件用,下面的例子我們就用一般量子化學研究者最常用的Gaussian來做優化+振動分析。
如果你急于體驗Shermo,或者在看下面的文字時在某些操作上有困惑,可以看看這個簡單的Shermo操作演示視頻,一些常用的功能和用法都體現了:《使用Shermo程序計算各種熱力學數據的基本操作演示》(https://www.bilibili.com/video/BV1EN411X7b3/)。
4.1 計算氣相下甲醛的熱力學數據
這里我們以一個簡單分子甲醛為例計算350 K下的各種熱力學數據。本例涉及到的輸入輸出文件可以在這里下載:http://www.shanxitv.org/attach/552/H2CO.zip。
此例我們用B3LYP/6-31G*進行優化和振動分析,而用更好的CCSD(T)/cc-pVTZ級別計算電子能量。如果不理解這么做的原因,看《淺談為什么優化和振動分析不需要用大基組》(http://www.shanxitv.org/387)。簡單來說,電子能量的誤差主導了內能、焓、自由能的誤差,而電子能量對計算級別的要求又顯著高于優化和振動分析,所以電子能量的計算應當用更好的級別。
B3LYP/6-31G*下做優化和振動分析的輸出文件是本文文件包里的H2CO_optfreq.out。基于優化后的結構再在CCSD(T)/cc-pVTZ下算單點能,輸出文件是本文文件包里的H2CO_SP.out,從中可見電子能量是-114.3338033 a.u.。如果你不知道在哪里讀電子能量,看《談談該從Gaussian輸出文件中的什么地方讀電子能量》(http://www.shanxitv.org/488)。
這里我們先以交互式的方式執行Shermo。用文本編輯器編輯Shermo目錄下的settings.ini文件,將里面的E=后面的值改為-114.3338033(如果用默認值0的話,電子能量會用從輸入文件中讀取的,因此對于本例來說將對應B3LYP/6-31G*級別的電子能量,這顯然太糙了),注意等號和數值之間必須有個空格。再將T=后面的值設為350,代表在350 K下分析。為了得到更準確的結果,最好通過頻率校正因子來消除由于諧振近似和計算級別自身原因帶來的系統性誤差,這點在《談談諧振頻率校正因子》(http://www.shanxitv.org/221)中有詳細介紹,沒看過者之后一定要看。B3LYP/6-31G*級別下的ZPE校正因子為0.9806,因此我們將sclZPE=后面的值設為這個值。當前級別下其它的頻率校正因子(比如計算熵用的校正因子)都很接近與1,所以我們保持默認值1.0不變。
保存settings.ini后啟動Shermo,首先我們會看到以下運行參數信息,和我們在settings.ini中設的一致。為了確保計算結果無誤,每次都應當注意檢查這里。
Running parameters:
Printing individual contribution of vibration modes: No
Temperature: 350.000 K
Pressure: 1.000 atm
Scale factor of vibrational frequencies for ZPE: 0.9806
Scale factor of vibrational frequencies for U(T)-U(0): 1.0000
Scale factor of vibrational frequencies for S(T): 1.0000
Scale factor of vibrational frequencies for CV: 1.0000
Low frequencies treatment: Harmonic approximation
然后將H2CO_optfreq.out的圖標拖到Shermo窗口里,此時路徑就自動產生了。按回車后首先看到分子的信息
======= Molecular information =======
Electronic energy: -114.33380330 a.u.
Spin multiplicity: 1
Atom 1 (C ) Mass: 12.000000 amu
Atom 2 (O ) Mass: 15.994910 amu
Atom 3 (H ) Mass: 1.007830 amu
Atom 4 (H ) Mass: 1.007830 amu
Total mass: 30.010570 amu
Point group: C2v
Rotational symmetry number: 2
Principal moments of inertia (amu*Bohr^2):
6.335702 46.693826 53.029529
Rotational constants relative to principal axes (GHz):
284.852589 38.650532 34.032760
Rotational temperatures (K): 13.670753 1.854931 1.633313
This is not a linear molecule
There are 6 frequencies (cm^-1):
1197.2 1279.7 1562.4 1848.9 2920.0 2972.3
以上信息中的電子能量是settings.ini中我們自己設的,而自旋多重度、原子質量、頻率都是從輸入文件中讀取的。轉動慣量以及與其相關的轉動常數和轉動溫度都是Shermo基于原子坐標和原子質量計算出來的。點群和轉動對稱數是Shermo基于當前幾何結構直接判斷的。如果此處顯示的信息有任何和實際不符,則接下來的計算結果將沒意義,因此每次最好看一眼。
接下來程序分別輸出了體系整體平動、整體轉動、分子內振動和電子激發各自對內能(U)、焓(H)、熵(S)、自由能(G)、等容熱容(CV)、等壓熱容(CP)和配分函數(q)的貢獻。輸出的格式緊湊、內容非常清晰易讀,還用了多種單位輸出以方便用戶。只要你仔細看過Shermo手冊的附錄,或者參加過北京科音的初級/基礎量子化學培訓班(見http://www.shanxitv.org/355)并仔細復習過,就肯定能輕易看懂這些信息,所以我就不再多說了。CV和CP的差異,以及H與U的差異僅來自于平動的貢獻,因此只有平動部分是將它們分別輸出的。
======= Translation =======
Translational q: 5.810322E+030 q/NA: 9.648265E+006
Translational U: 4.365 kJ/mol 1.043 kcal/mol
Translational H: 7.275 kJ/mol 1.739 kcal/mol
Translational S: 154.502 J/mol/K 36.927 cal/mol/K -TS: 12.92 kcal/mol
Translational CV: 12.472 J/mol/K 2.981 cal/mol/K
Translational CP: 20.786 J/mol/K 4.968 cal/mol/K
========= Rotation ========
Rotational q: 9.016795E+002
Rotational U: 4.365 kJ/mol 1.043 kcal/mol =H
Rotational S: 69.045 J/mol/K 16.502 cal/mol/K -TS: 5.776 kcal/mol
Rotational CV: 12.472 J/mol/K 2.981 cal/mol/K =CP
======== Vibration ========
Vibrational q(V=0): 1.014765E+000
Vibrational q(bot): 3.094088E-011
Vibrational U(T)-U(0): 0.227 kJ/mol 0.054 kcal/mol =H(T)-H(0)
Vibrational U: 69.323 kJ/mol 16.569 kcal/mol =H
Vibrational S: 0.770 J/mol/K 0.184 cal/mol/K -TS: 0.064 kcal/mol
Vibrational CV: 3.509 J/mol/K 0.839 cal/mol/K =CP
Zero-point energy (ZPE): 69.10 kJ/mol, 16.51 kcal/mol 0.026317 a.u.
======== Electron excitation ========
Electronic q: 1.000000E+000
Electronic U: 0.000 kJ/mol 0.000 kcal/mol =H
Electronic S: 0.000 J/mol/K 0.000 cal/mol/K -TS: 0.000 kcal/mol
Electronic CV: 0.000 J/mol/K 0.000 cal/mol/K =CP
振動對內能的貢獻(Vibrational U)一方面來自于零點能,即ZPE,另一方面來自于從0 K升至當前溫度過程中導致內能的增加量,即U(T)-U(0),它們都單獨輸出了。
最后,程序輸出了總結果。配分函數是所有上面四部分貢獻的乘積,各種熱力學校正量(Thermal correction)和熵都是上面四部分貢獻的加和:
===========================
========== Total ==========
===========================
Total q(V=0): 5.316403E+033
Total q(bot): 1.621008E+023
Total q(V=0)/NA: 8.828094E+009
Total q(bot)/NA: 2.691746E-001
Total CV: 28.453 J/mol/K 6.800 cal/mol/K
Total CP: 36.767 J/mol/K 8.788 cal/mol/K
Total S: 224.317 J/mol/K 53.613 cal/mol/K -TS: 18.765 kcal/mol
Thermal correction to U: 78.053 kJ/mol 18.655 kcal/mol 0.029729 a.u.
Thermal correction to H: 80.963 kJ/mol 19.351 kcal/mol 0.030837 a.u.
Thermal correction to G: 2.452 kJ/mol 0.586 kcal/mol 0.000934 a.u.
Electronic energy: -114.3338033 a.u.
Sum of electronic energy and ZPE, namely U/H/G at 0 K: -114.3074860 a.u.
Sum of electronic energy and thermal correction to U: -114.3040744 a.u.
Sum of electronic energy and thermal correction to H: -114.3029660 a.u.
Sum of electronic energy and thermal correction to G: -114.3328693 a.u.
上面也給出了電子能量與熱力學校正量的加和,這就是我們平時經常考察的熱力學量了,包括內能、焓、自由能。比如此處的Thermal correction to G代表當前我們設的350 K時的自由能的熱校正量,它與電子能量的加和就是350 K下的自由能,即Sum of electronic energy and thermal correction to G后面的值。而電子能量與ZPE相加,得到的是0 K下的內能/焓/自由能,即Sum of electronic energy and ZPE后面的值。
如果你想考察各個振動模式對各種熱力學量的貢獻,從而更深層地了解熱力學量的本質、探討各振動模式對其的影響,就把settings.ini里的prtvib后面的值改為1(輸出到屏幕上)或-1(輸出到當前目錄下的vibcontri.txt里)。這里我們將之設為-1,然后重新運行Shermo來處理H2CO_optfreq.out,得到的vibcontri.txt內容如下:
Note: The wavenumbers shown below are unscaled ones
Mode Wavenumber Freq Vib. Temp. q(V=0) q(bot)
cm^-1 GHz K
1 1197.25 0.35893E+05 1722.57 1.00734069 0.08599170
2 1279.68 0.38364E+05 1841.18 1.00521977 0.07243629
3 1562.40 0.46840E+05 2247.95 1.00162690 0.04036762
4 1848.86 0.55428E+05 2660.10 1.00050056 0.02237882
5 2920.03 0.87540E+05 4201.26 1.00000612 0.00247431
6 2972.29 0.89107E+05 4276.46 1.00000494 0.00222226
Mode Wavenumber ZPE U(T)-U(0) U(T) CV(T) S(T)
cm^-1 kcal/mol kcal/mol kcal/mol cal/mol/K cal/mol/K
1 1197.25 1.67835 0.02513 1.70348 0.35594 0.08633
2 1279.68 1.79391 0.01910 1.81301 0.28854 0.06491
3 1562.40 2.19024 0.00727 2.19750 0.13358 0.02399
4 1848.86 2.59181 0.00265 2.59445 0.05749 0.00855
5 2920.03 4.09340 0.00005 4.09345 0.00175 0.00016
6 2972.29 4.16668 0.00004 4.16672 0.00147 0.00013
以上信息輸出了全部6個振動模式的波數、頻率、振動溫度,以及它們對配分函數、ZPE、從0 K升溫至當前溫度令內能的增加量(也等價于令焓的增加量)、內能、等壓熱容和熵的貢獻。由數據可見頻率越低的振動模式對U(T)-U(0)、CV(T)、S(T)的貢獻越大,而頻率越高的振動模式對ZPE和U(T)的貢獻越大(注:ZPE占U(T)的大頭)。
如果大家想考察其它溫度或壓力下的熱力學數據,相應地修改一下settings.ini里的T和P,重新運行即可。使用Shermo還可以非常容易地對溫度和壓力進行掃描。比如當前我們想考察各種熱力學量從50 K到1000 K之間的變化,就把settings.ini里的T=后面的值改為50,1000,10,這里10代表掃描步長。啟動Shermo后還是載入H2CO_optfreq.out,算完后當前目錄下就有了scan_UHG.txt和scan_SCq.txt,前者包含了U、H、G以及它們與電子能量的加和,后者包含了S、熱容、配分函數。例如scan_SCq.txt的前幾行內容如下:
Unit of S, CV and CP is cal/mol/K, q(V=0)/NA and q(bot)/NA are dimensionless
T(K) P(atm) S CV CP q(V=0)/NA q(bot)/NA
50.000 1.000 37.961 5.962 7.949 3.623341E+006 8.877273E-068
60.000 1.000 39.411 5.962 7.949 7.513361E+006 3.415672E-055
70.000 1.000 40.636 5.962 7.949 1.391943E+007 3.668237E-046
80.000 1.000 41.697 5.962 7.949 2.374593E+007 2.337871E-039
...略
這兩個文件可以非常容易地作圖。比如把scan_UHG.txt的前幾行刪掉后,就可以直接拖入Origin程序導入其中。將溫度作為X軸,內能、焓、自由能的熱校正量作為Y軸,繪制成的Line+Symbol圖如下所示
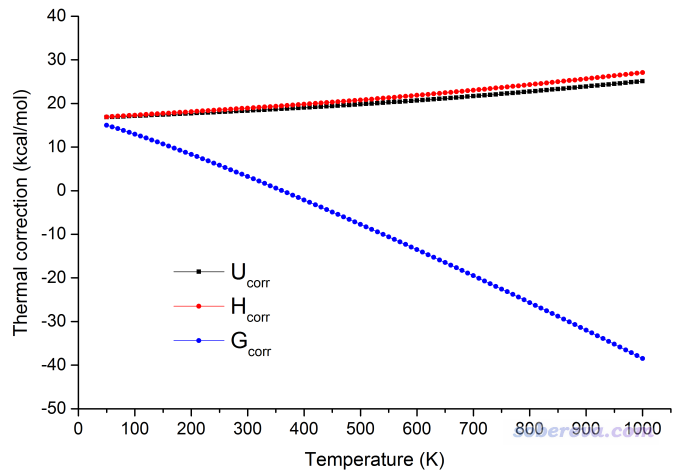
之所以溫度越高焓的熱校正量(Hcorr)比內能的熱校正量(Ucorr)高得越多,是因為前者比后者多個RT,顯然T越大差異就越大。之所以體系溫度越高自由能的熱校正量(Gcorr)越低,并且一開始為正,溫度較高后甚至變成了負值,這是因為G里面有-TS項,而熵必定是正值。
類似地,對壓力也可以進行掃描,只要將settings.ini里的P也指定下限、上限、步長即可。如果對溫度和壓力都設成設了上下限和步長,則Shermo會進行二維掃描。
如果你想在Linux下純粹靠命令行執行而不改settings.ini文件,對于跑當前的溫度掃描例子來說,在按照本文第3節說的修改過~/.bashrc后,運行以下命令即可,非常方便:
Shermo H2CO_optfreq.out -T 50,1000,10 -sclZPE 0.9806 -E -114.3338033
4.2 計算水環境中柔性分子瑞德西韋的熱力學數據
4.2.1 前言
瑞德西韋這個體系我之前在《使用Molclus結合xtb做的動力學模擬對瑞德西韋(Remdesivir)做構象搜索》(http://bbs.keinsci.com/thread-16255-1-1.html)中有過介紹和研究,此物對于治療COVID-19有較好作用,這里我們計算一下它的熱力學數據。這個體系的柔性非常大,因為它有很多可旋轉的鍵。對于這樣的體系,在計算時需要做特殊考慮:
(1)必須使用準RRHO(quasi-RRHO)模型代替RRHO模型。RRHO(rigid-rotor harmonic oscillator)是指用諧振近似模型考慮體系內部運動對熱力學量的貢獻,這也是Gaussian、GAMESS-US等絕大多數量子化學程序計算熱力學數據時候用的模型。RRHO對于甲醛那種剛性體系沒問題,只要考慮了頻率校正因子后結果通常就是比較準確的。但是對于柔性較大的體系,RRHO就可能造成明顯誤差了。因為柔性體系往往有很多低頻模式(一般是指諧振頻率在100 cm-1以下的那些振動模式),RRHO模型計算的它們對熱力學量的貢獻不可靠,而且頻率越低越不適用,尤其是計算出來的熵的誤差很大。為了解決這個問題,Truhlar課題組的文章(比如J. Phys. Chem. B, 115, 14556 (2011))通常是將低于100波數的頻率人為改為100波數后再計算各種熱力學數據。雖然這么做看起來任意性太強,物理意義不太清楚,但從實效來說比起不做這種處理通常明顯更為合理。另一種是Grimme在Chem. Eur. J., 18, 9955 (2012)中提出的做法,他將RRHO模型與自由轉子模型算的振動對熵的貢獻進行了線性插值,此時約200波數以上的振動模式的結果和RRHO模型算的基本一樣,而約50波數以下的振動模式的結果和自由轉子模型算的基本一樣,而在約50~200波數范圍內在RRHO和自由轉子模型的結果間平滑過渡。Minenkov在J Comput Chem., 44, 1807 (2023)中還建議將這種插值方式也同時應用到振動對內能的貢獻上,這樣對低頻的熱力學考慮更一致,而且實測發現對內能的計算精度有所改進。Truhlar、Grimme、Minenkov這三種方法都可以比RRHO顯著更好地描述低頻模式對熱力學量的貢獻,都可以稱為準RRHO或modified RRHO (mRRHO),在Shermo中都支持,分別對應ilowfreq=1、2、3。Grimme的做法明顯比Truhlar更好,改為Minenkov的做法還可能有更進一步提升。算柔性體系的時候應當用Grimme或Minenkov的準RRHO(我更推薦后者),而算剛性體系的情況,由于沒有低頻,用準RRHO還是RRHO都可以,結果幾乎沒區別。關于這個問題更多的介紹和討論看Shermo的手冊和前述的Shermo的論文。如今準RRHO已被越來越多的做理論計算的人所了解,算含有低頻的柔性體系、弱相互作用體系如今還用RRHO的話很可能被內行審稿人批評。
(2)應當考慮熱力學量的構象平均。柔性體系往往有很多熱可及構象,也就是在當前溫度下,有不止一個構象出現比例明顯大于零。出現比例可以按照Boltzmann分布公式根據構象之間的相對自由能計算,見《根據Boltzmann分布計算分子不同構象所占比例》(http://www.shanxitv.org/165),而這些構象的結構可以通過構象搜索程序獲得,其中我最推薦Molclus,免費靈活方便準確,詳見其主頁http://www.keinsci.com/research/molclus.html。實際體系的電子能量、內能、焓應當根據分布比例對各個構象計算結果進行權重平均,而熵在權重平均的基礎上還要額外考慮構象熵(表達式見手冊。這是由于構象間可以相互變換所帶來的額外的熵)。自由能就用權重平均的焓和熵根據G=H-TS關系照常來算即可。構象平均問題在Shermo中可以很方便地考慮,只需要提供個構象列表文件即可。
對于分子團簇來說,比如水的四聚體,會有多種熱可及構型,計算熱力學量的時候也需要對各個構型按上述方式考慮。Molclus也可以方便地對分子團簇做構型搜索,見《genmer:生成團簇初始構型結合molclus做團簇結構搜索的超便捷工具》(http://bbs.keinsci.com/thread-2369-1-1.html)里面的說明和例子。
4.2.2 計算單個構象的熱力學數據
下面,我們首先對已知的瑞德西韋在水中最穩定的構象計算標況下各種熱力學數據,此結構如下:
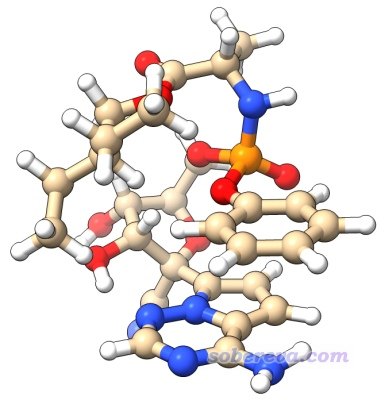
此體系的優化和振動分析是用Gaussian在B3LYP-D3(BJ)/6-31G*在氣相下做的,輸出文件是Shermo文件包里的example目錄下的G16_remdesivir_optfreq.out。之后通過ORCA在此結構上用更高級別的PWPB95-D3(BJ)/def2-QZVPP結合SMD溶劑模型表現的水環境計算了電子能量,輸出文件對應example\ensemble\orcaSP00001.out,從中可看到電子能量為-2321.3677188 a.u.。我們將settings.ini里的內容做如下設置:
E=后面的值改為-2321.3677188
確認T=后面的值為298.15
sclZPE=后面的值改為0.9806(DFT-D色散校正對頻率校正因子的影響可忽略不計,所以還是用B3LYP/6-31G*的校正因子)
ilowfreq=后面的值改為2,代表使用Grimme的準RRHO模型
啟動Shermo并以G16_remdesivir_optfreq.out為輸入文件,結果如下,這個就是瑞德西韋當前構象在水環境中的各種熱力學量了
Sum of electronic energy and ZPE, namely U/H/G at 0 K: -2320.7549750 a.u.
Sum of electronic energy and thermal correction to U: -2320.7137635 a.u.
Sum of electronic energy and thermal correction to H: -2320.7128193 a.u.
Sum of electronic energy and thermal correction to G: -2320.8212651 a.u.
大家也可以算一下ilowfreq=后面的值為0,也就是用RRHO模型算的結果,你會發現自由能為-2320.8303608 a.u.,與上面的值相差多達5.7 kcal/mol。如果你具體分析的話會發現這主要來自于熵的差異,這充分說明對于較大柔性體系用RRHO模型會造成顯著誤差,因此就算不是為了圖方便而是為了圖精確,對于柔性大體系也不建議直接用Gaussian等程序直接輸出的自由能。
需要注意的是,若想得到嚴格的溶液標準態(298.15K,1 M)情況下體系的自由能,還需要將上面給出的自由能-2320.8212651再加上1.89 kcal/mol(0.003012 a.u.),這對應氣相標準態(298.15K,1 atm)→溶液標準態轉化的自由能變,這點在《談談隱式溶劑模型下溶解自由能和體系自由能的計算》(http://www.shanxitv.org/327)有專門說明,沒看過者強烈建議仔細看看。
實際上Shermo直接就提供了計算濃度改變導致的自由能變的功能,都省得自己手動算了,Shermo手冊里有詳述和計算公式。簡單來說,你只要把settings.ini里的conc設為目標濃度即可。比如當前settings.ini里T=350、P=2,若你設conc= 1.5M,則Shermo運行后不僅會輸出(350K,2atm)狀態的自由能,還會輸出delta-G of conc. change,這就是從當前(350K,2atm)狀態轉變為(350K,1.5M)狀態的自由能變,之后輸出的Gibbs free energy at specified concentration就是(350K,1.5M)狀態的自由能。顯然,若設T= 298.15且conc= 1M,最后Gibbs free energy at specified concentration給你的就是液相標準態自由能。
注:上面計算溶液中的自由能的做法雖然簡單,但在原理上來說其實不是最完美的,因為如《談談隱式溶劑模型下溶解自由能和體系自由能的計算》所述,SMD模型結合M05-2X/6-31G*級別算出來的溶解自由能才是最準的,而上面這種做法在本質上等于在其它級別(PWPB95-D3(BJ)/def2-QZVPP)下算了溶解自由能。不過這沒有明顯問題,從實際精度角度來講結果完全可以接受。你若不怕麻煩,就是想用最理想的做法來算,就按照《談談隱式溶劑模型下溶解自由能和體系自由能的計算》里的過程,用Shermo先計算氣相下自由能,再手動在M05-2X/6-31G*級別下計算溶解自由能,二者相加后再加上標準態改變的自由能變就行了。
4.2.3 計算構象分布比例和構象權重的熱力學數據
在前述的《使用Molclus結合xtb做的動力學模擬對瑞德西韋(Remdesivir)做構象搜索》一文中得到了好多能量較低的瑞德西韋的構象,下面我們就取其中最低的三個構象,通過Shermo來計算它們的構象分布比例和構象權重的熱力學數據。自由能更高的構象由于貢獻很小,所以這里就不納入考慮了。
我們創建一個后綴為.txt的文本文件,比如叫做list.txt,里面每一行指定一個振動分析或優化+振動分析的輸出文件的路徑。如果想用更好的電子能量,在路徑后面加上分號作為分隔,后面寫上電子能量數值即可。此例的文件是下面這樣
example\ensemble\gau00001.out;-2321.367718855799
example\ensemble\gau00002.out;-2321.363532347723
example\ensemble\gau00003.out;-2321.369898466825
這里的電子能量可以從example\ensemble\中的以orca為開頭的相應構象的PWPB95-D3(BJ)/def2-QZVPP級別下的單點能任務里讀到。這里假定你通過雙擊Shermo圖標啟動,所以路徑寫的是相對于Shermo.exe的相對路徑。
settings.ini還是用上面的例子的。啟動Shermo后,將list.txt載入,馬上就得到下面的輸出
Processing example\ensemble\gau00001.out... ( 1 of 3 )
Processing example\ensemble\gau00002.out... ( 2 of 3 )
Processing example\ensemble\gau00003.out... ( 3 of 3 )
#System U H G S CV
a.u. a.u. a.u. J/mol/K J/mol/K
1 -2320.713764 -2320.712819 -2320.821265 954.971 657.837
2 -2320.709745 -2320.708801 -2320.817499 957.191 657.295
3 -2320.715999 -2320.715054 -2320.822180 943.341 654.902
System 1 Relative G= 2.401 kJ/mol Boltzmann weight= 27.380 %
System 2 Relative G= 12.289 kJ/mol Boltzmann weight= 0.507 %
System 3 Relative G= 0.000 kJ/mol Boltzmann weight= 72.113 %
Conformation weighted data:
Electronic energy: -2321.369269 a.u.
U: -2320.715355 a.u.
H: -2320.714411 a.u.
G: -2320.822488 a.u.
S: 951.727 J/mol/K Conformation entropy: 5.132 J/mol/K
CV: 655.718 J/mol/K
CP: 664.032 J/mol/K
可見每個體系的熱力學數據都分別給出了,然后給出了相對于自由能最低的那個體系的相對自由能,并由此計算出了玻爾茲曼權重(即分布比例)。最后給出了考慮構象平均的各種熱力學數據,其中為了便于分析考察,構象熵也單獨給出了(構象熵已經納入到S:后面的數值了,不要再手動加進去)。由以上輸出可見,第3個構象占了主導,而第1個構象也不可忽略,其中自由能最高的構象2的貢獻可忽略不計。
如上一節所述,如果要得到溶液中1 M標準態的各個構象的以及構象平均的自由能,應當給這里輸出的各個構象的自由能以及構象權重平均的自由能都手動加上1.89 kcal/mol。是否加上1.89 kcal/mol不影響構象間的相對自由能,也因此不影響玻爾茲曼分布比率。
值得一提的是構象分布比例對自由能很敏感,這就要求電子能量計算精度必須足夠好,而且必須恰當考慮溶劑效應。如果在list.txt里只寫路徑而不寫分號和電子能量,則電子能量會自動用那三個.out里讀取的氣相的B3LYP-D3(BJ)/6-31G*的結果,你會發現構象3的分布比例達到99.9%,嚴重不合理。
5 通過shell腳本調用Shermo做批處理
通過寫shell腳本,可以調用Shermo非常容易地進行批處理。舉個例子,當前目錄下有一批.log文件,我們想計算它們標況下的熱力學量,并且用0.975的ZPE校正因子,用Grimme的準RRHO方式考慮低頻。假設你用的是Bash環境(比如用的Linux,或者在Windows下通過cmder等方式模擬Bash環境),那么可以創建一個文本文件比如叫getGall.sh,把以下內容寫入到此文件中
#!/bin/bash
rm -f getGall.txt
for inf in *.log
do
echo Processing ${inf} ...
echo ${inf} >> getGall.txt
./Shermo ${inf} -sclZPE 0.975 -ilowfreq 2 | grep "Sum of electronic energy and thermal correction to G:" | cut -d: -f 2 >> getGall.txt
done
假設getGall.sh和Shermo可執行文件就在當前目錄下,給它們加上可執行權限后,輸入./getGall.sh運行此腳本,運行后就在當前目錄下得到了getGall.txt文件,里面記錄了各個文件名以及Shermo計算出來的自由能值,如下所示
Cs-atom-in.log
-705.4867512 a.u.
Cs-ion-in.log
-705.2690829 a.u.
Cs-ion-out.log
-705.2490426 a.u.
K-atom-in.log
-1285.2091502 a.u.
K-ion-in.log
-1284.9920128 a.u.
K-ion-out.log
-1284.9852452 a.u.
...略
上面這個腳本稍微有一點shell腳本編寫常識和Linux下的命令的知識就能理解是如何工作的。大家稍微舉一反三就能利用Shermo非常方便地實現各種批處理。如果你對shell腳本編寫一無所知又想學習的話,強烈建議看看《詳談Multiwfn的命令行方式運行和批量運行的方法》(http://www.shanxitv.org/612),里面由淺入深對腳本編寫做了淺顯易懂的介紹并給了很多實用例子。
6 總結&其它
本文介紹了Shermo程序的基本特點、基本用法,并且通過實例介紹了如何將Shermo用于實際問題。由例子可見通過Shermo來計算各種熱力學數據前所未有地方便、靈活,以往需要很多操作步驟的麻煩過程都被簡化到極致,而且還支持準RRHO模型以合理地考慮低頻模式的貢獻,因此Shermo是日常應用性量子化學研究中離不開的工具。
為了避免很多人嫌本文太長就不看了,本文寫得比較簡單,還有很多細節、更多用法說明、更多例子都沒有給出,詳見Shermo的手冊。如果對Shermo有任何問題,看了手冊還是不明白,歡迎在計算化學公社論壇(http://bbs.keinsci.com)的量子化學版求助。
順帶一提,Gaussian等程序還支持更復雜的計算模型,即非諧振計算、受阻轉子,在某些情況下用這些處理結果能更準確一些,但耗時高得多得多,不適合用于中、大體系。這種情況的輸出文件也不被Shermo所支持,Shermo只支持諧振近似的振動分析的輸出文件(也即是各種量子化學程序做振動分析時默認的情況)。
如果你的體系是單個原子,不要做優化,不僅沒意義,而且Gaussian等程序立馬就會報錯。對于單個原子就直接做個振動分析,把輸出文件給Shermo用就完了。
Shermo,以及各種量子化學程序在計算熱力學數據的時候都是將體系當成理想氣體對待的,如果你想計算凝聚相的熱力學數據,應當用能夠描述周期性的分子動力學程序、第一性原理程序來做,這不屬于Shermo涉及的范疇。值得一提的是,Shermo的settings.ini里有個imode設置,如果設為1,則平動和轉動對熱力學量的貢獻會被忽略,這適合用于計算固體、表面、被吸附分子的熱力學量,因為它們沒有整體的平動和轉動。
如果你用的量子化學程序不是Shermo直接支持的,也照樣可以用Shermo來分析。如手冊所示,Shermo定義了私有格式shm,其中包含了計算熱力學數據所需要的所有信息,格式非常簡單。因此,如果你想讓Shermo也能基于其它量子化學程序振動分析的數據來計算熱力學量,自己寫個小程序將輸出文件轉化成shm格式,再給Shermo當輸入文件即可。
經常有Shermo的用戶問為什么Shermo算的熱力學校正量和Gaussian輸出的不一致,在此專門說一下。要想Shermo輸出的熱力學校正量和Gaussian直接輸出的嚴格一致,Shermo的settings.ini里的設定必須滿足:
? T=和P=分別與Gaussian計算時設的溫度和壓力一致(Gaussian默認的情況相當于T= 298.15、P= 1.0)
? 頻率校正因子和Gaussian設的一致(如果Gaussian計算時沒用scale關鍵詞指定,則sclZPE、sclheat、sclS都應當為1.0)
? 熱力學量計算模型和Gaussian一致。Gaussian用的是RRHO模型,對應于ilowfreq= 0
如果以上都滿足,結果還不一致,且體系結構有對稱性,大概率是Gaussian的振動分析部分的代碼對體系的點群判斷有誤,導致轉動對稱數判斷不對,進而導致算出的轉動對熱力學校正量的貢獻錯誤。而Shermo判斷點群的功能明顯更穩健,不一致的情況一律以Shermo為準(有多次用戶問我此問題的時候我最后都發現倆程序對點群判斷不一致,每次都是Shermo是正確的而Gaussian是錯誤的。可能是Gaussian判斷點群的閾值過于嚴格)。
偶爾有人問我Shermo的sclfreq參數設的是計算U(T)-U(0)的頻率校正因子,為什么他查文獻查到的都是H(T)-H(0)的頻率校正因子,這倆頻率校正因子是一回事么?顯然是一回事,有最基本的熱力學數據計算常識就能理解。H(0)和U(0)是相同的,H(T)和U(T)在理想氣體近似下就相差個RT,這是平動部分貢獻的,和振動沒有任何關系,顯然給H(T)-H(0)和給U(T)-U(0)用的頻率校正因子完全是一碼事。再次提醒,如果你缺乏熱力學數據計算的常識知識,一定仔細看看Shermo程序手冊的附錄。