淺談為什么優化和振動分析不需要用大基組
文/Sobereva @北京科音
First release: 2017-Aug-26 Last update: 2023-Jul-31
量化計算中有兩個常識,大部分人想必都知道
(1)優化和振動分析必須在相同級別下進行
(2)在高耗時的優化+振動分析時用中小基組,而只在隨后的單點能計算時才用大基組,這樣做比起所有過程都用大基組耗時大為降低而精度降低很少
其中(1)的原因很好解釋,因為如果振動分析用的級別(包括各種影響勢能面的因素,如積分格點精度、溶劑模型等)與幾何優化時不同,相當于振動分析時并不是在勢能面的極小點的位置進行的(即便用的結構是之前優化得到的),此時振動分析結果顯然沒有意義。而(2)的原因,是因為優化和振動分析結果對基組的敏感性遠低于能量計算。正好最近在QQ群里有人又提到此事,筆者遂通過一個簡單的HF分子的計算數據來展現這一點。雖然不能光用一個分子就以偏概全,但很大程度上是能夠以小見大的。計算使用Gaussian16完成,理論方法為B3LYP。如果缺乏基組選用的基本知識,看此文前強烈建議仔細閱讀《談談量子化學中基組的選擇》(http://www.shanxitv.org/336)。
來看不同基組下計算的H-F鍵能(即E(H)+E(F)-E(HF)),優化的鍵長,以及諧振頻率。計算分子能量時鍵長用的是相應基組下優化的。
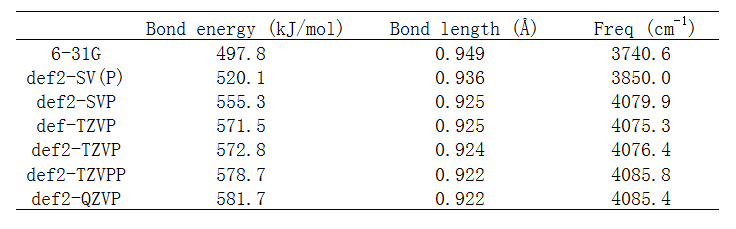
首先看def2-SVP/TZVPP/QZVP這個序列的數據。按照這個順序,基組質量是系統性地提升的,其基組尺寸類似于cc-pVDZ/TZ/QZ序列。我們通常說,優化用2-zeta帶極化這個檔通常就夠了,從上表確實可見相對于很大基組def2-QZVP的結果,def2-SVP的鍵長誤差才0.3%,振動頻率誤差才0.13%,如果要求不高的話這點誤差完全可以接受,然而其鍵能的誤差則達到26.4kJ/mol,相當于4.5%,完全不能忽略。再對比def2-TZVPP和def2-QZVP的結果,前者相對于后者的鍵長、振動頻率的誤差根本察覺不到(僅0.0003埃和0.4cm-1),但能量上還是有3kJ/mol的誤差,對于高精度熱力學數據計算,這種程度誤差是仍是不可忽略的,而且高精度計算通常是用后HF,此時def2-TZVPP與def2-QZVPP在算能量相關問題上的差距會更大。上面的數據充分說明優化+振動分析結果對基組的敏感性遠低于能量,因此前者用的基組建議比后者低一個檔來節約時間。另外值得一提的是,由于做振動分析時通常還會考慮頻率校正因子(詳見http://www.shanxitv.org/221),因此用大基組在精度上實際上并不會帶來任何好處。雖然原理上來說在大基組優化的結構下用大基組算能量,比起在中小基組優化的結構下用大基組算能量,對于能量相關問題的計算準確度要更高,但由于中小基組下優化的誤差已經不大,再加上在極小點附近勢能面非常平緩(即結構的稍微變化基本不會帶來什么能量變化),因此不用擔心優化+振動分析用中小基組來節約時間的做法會帶來能量計算精度上的損失。如果你真是想要很高精度結構和能量數據,那么優化用到def2-TZVPP就已經絕對足夠了,再提升完全是白費時間,而算能量時基組則完全有必要用到def2-QZVP,特別是對于后HF計算而言。
我們再關注一下上面表中其它基組的結果。如《談談量子化學中基組的選擇》提到的,對于一般問題沒有必要給氫加極化,但是和氫有密切相關的問題則應當給氫加極化,當前就是此種情況。對于HF分子,def2-SV(P)等價于砍掉了def2-SVP上氫的p極化函數的版本,def2-TZVP等價于砍掉了def2-TZVPP上氫的d極化函數的版本。由數據可見,砍掉氫的極化對結果影響確實不小,特別是連p極化都砍掉時,哪怕是鍵長、振動頻率的誤差的增加都已經到令人惱火的程度。由于給氫加p極化對耗時增加其實不算太多(相對于給重原子增加高角動量極化函數而言),因此有必要給氫加p極化時不要吝嗇,即起碼用def2-SVP或6-31G**這個檔。再看超惡心的連重原子的極化都沒有的6-31G,誤差比def2-SV(P)又明顯進一步增大,鍵能誤差已經快100kJ/mol了。對比def-TZVP和def2-TZVP的結果,雖然后者比前者昂貴很多(很大程度上是因為對F加了f極化所致),但是各方面精度都差不太多,因此def2-TZVP無福消受時用def-TZVP是很好選擇。
為了直觀地展現為什么幾何優化和振動分析對基組敏感度低(當然前提是起碼已用到def2-SVP這個檔),下面在不同基組下對HF的勢能面進行了掃描,如下所示。圖中的能量零點是相應基組下H與F原子無限分離的情況。
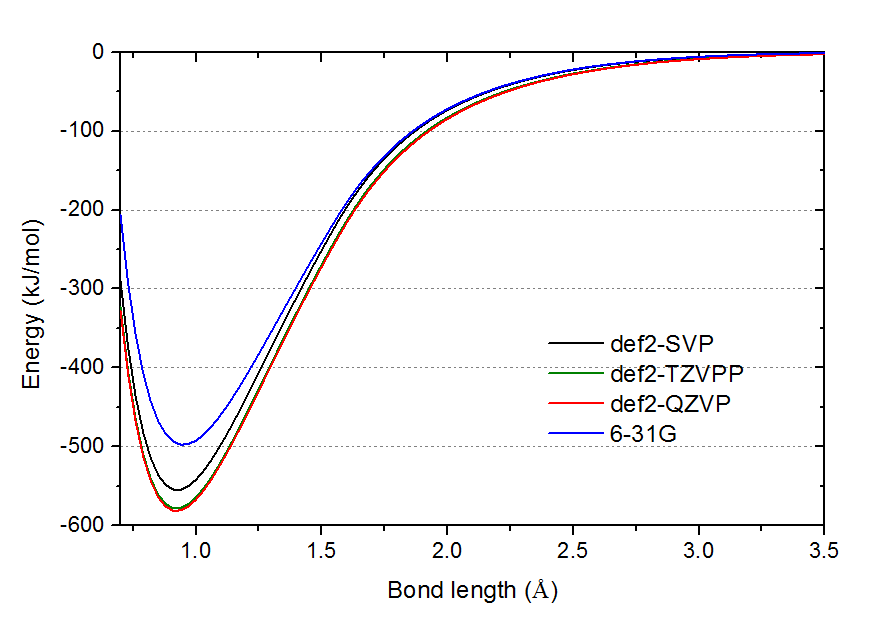
由圖可見def2-TZVPP與def2-QZVP的曲線已經幾乎精確重合,直接反映在優化結果和振動分析結果幾乎相同上。def2-SVP的曲線谷底明顯與def2-TZVPP的有一段距離,所以能量誤差明顯,但谷底橫坐標位置卻幾乎和def2-TZVPP的沒區別,肉眼難以分辨,所以幾何優化結果誤差幾乎可以忽略。而6-31G,不僅勢阱深度離譜,肉眼都可以看出谷底位置與def2-TZVPP的有一定偏離。
勢能曲線谷底位置的曲率正比于振動頻率。雖然def2-SVP的振動頻率誤差已很小,但由上圖,肉眼看過去還是容易憑直覺覺得其極小點的曲率和def2-TZVPP的有明顯差異。為了更容易地對比曲率,下圖把def2-SVP和6-31G的曲線進行平移,使其極小點與def2-TZVPP的相重合。
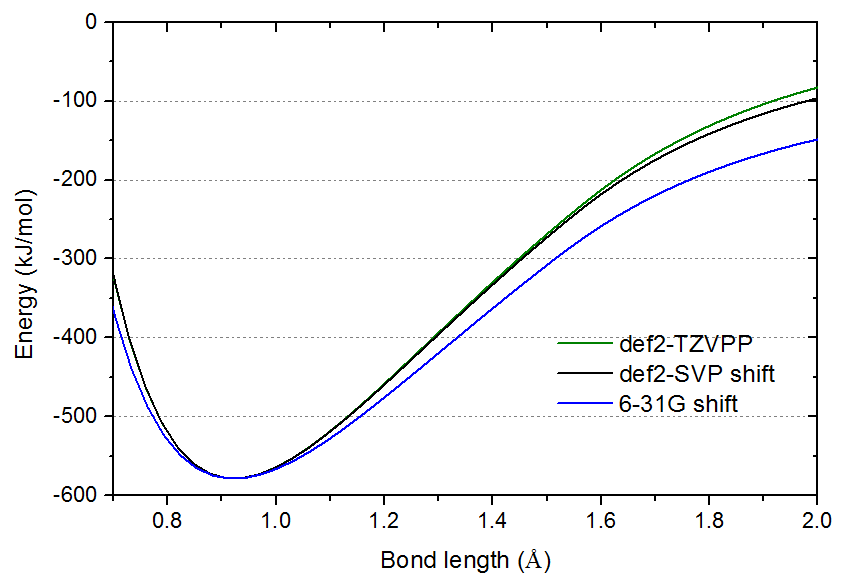
由上圖可見,極小點附近def2-SVP和def2-TZVPP的曲線極為吻合,因此曲率也幾乎完全相同,只有到了距離平衡位置較遠的區域二者才有可察覺的差異。因此也只有計算比如倍頻時,由于涉及到勢能面更廣的范圍,兩種基組下的結果才可能有不可忽略的差異。而6-31G真是糟糕透頂,不僅能量計算超爛,連極小點曲率都和def2-TZVPP的大相徑庭,明顯低估了曲率,因此頻率也嚴重低估。
本文的數據清楚地表明,對幾何優化和振動分析不需要大基組,比如def2-SVP一般就夠滿足需要了,除非精度要求頗高,但是這絕對不意味著可以偷工減料到使用連重原子的極化都沒有的6-31G之流。還要注意的是,不同體系對基組的敏感性是有差異的,比如優化過渡金屬的配位鍵鍵長,def2-SVP和def2-TZVP的結果差異往往挺明顯,而文本的情況主要適合普通有機體系。
不光是能量,諸如偶極矩、(超)極化率、NMR等諸多與電子結構直接相關的屬性對基組的敏感度也是遠高于幾何優化和振動分析的,因此計算它們之前的優化過程也建議用中小基組。值得一提的是計算Raman和ROA計算實際上分為兩個過程(1)優化和振動分析得到正則坐標 (2)計算極化率對正則坐標的導數。由于如前所述(1)對基組要求低,彌散函數更起不到什么作用,而彌散函數對(2)的結果改進明顯(原因容易理解,沒彌散函數時極化率算得超爛),因此Raman或ROA在Gaussian中允許兩步分開做,用戶可以在(1)的時候用不帶彌散的基組節約時間,而只在(2)的時候用帶彌散的基組。
為節約時間,幾何優化+振動分析不僅可以用比能量計算更小的基組,還可以用更便宜的理論方法,這種做法的合理性與上文討論的類似。比如CCSD(T)算能量而DFT做幾何優化和振動分析,或者前者用雙雜化泛函后者用普通泛函,這都是非常流行、劃算的搭配。雖然小基組優化+大基組算能量對內行人屬于常識,但為了讓外行讀者也能明白此做法的合理性,論文里可以引用相關文章,可以引用比如《使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據》(http://www.shanxitv.org/552)里介紹的筆者的Shermo程序的原文Comput. Theor. Chem., 1200, 113249 (2021) DOI: 10.1016/j.comptc.2021.113249,里面在計算高精度熱力學量的時候就用了這種做法。
在J. Chem. Theory Comput. (2023) DOI: 10.1021/acs.jctc.3c00388還專門系統性測試了幾何優化+振動分析用從小到大不同基組時對最終計算出的熱力學量的影響,發現大多數情況對最終結果影響都小于1 kcal/mol,同樣證明本文的觀點。同時此文還指出存在低頻模式時,反應自由能對優化+振動分析用的基組會更敏感,但如果使用了準RRHO模型計算熱力學校正量代替Gaussian等程序默認用的RRHO,則敏感度會大幅降低。這充分體現出含有低頻模式時,使用Shermo程序基于準RRHO模型計算自由能變的重要性。
另外,liyuanhe寫了一篇《自由能計算對優化與單點級別的敏感性測試》(http://bbs.keinsci.com/forum.php?mod=viewthread&tid=6609),與本文的內容有一定相關性,建議閱讀。