靜電效應主導了氫氣、氮氣二聚體的構型
靜電效應主導了氫氣、氮氣二聚體的構型
文/Sobereva @北京科音 2013-Nov-6
氫氣和氮氣分子是最基本、最簡單的無極性分子。由于沒有極性,所以人們普遍認為由它們構成的二聚體(H2)2、(N2)2和(H2)(N2)都是范德華二聚體,也就是分子間相互作用純粹靠范德華作用。然而J. Mol. Model., 19, 5387-5395的名為Revealing the nature of intermolecular interaction and configurational preference of the nonpolar molecular dimers (H2)2, (N2)2, and (H2)(N2)的文章則打破了這個傳統觀念,明確指出了靜電效應對氫氣、氮氣二聚體產生的關鍵性的影響,證明了二聚體的構型傾向性完全由靜電效應所控制。在此帖就介紹一下這個觀點新穎、內容有趣的工作。文章的?網址為http://link.springer.com/article/10.1007%2Fs00894-013-2034-2,文章可在這里下載/usr/uploads/file/20150610/20150610051705_37495.pdf。
文章是針對二聚體的構型傾向性問題來進行討論的。氫氣、氮氣在形成二聚體時,有以下典型構型
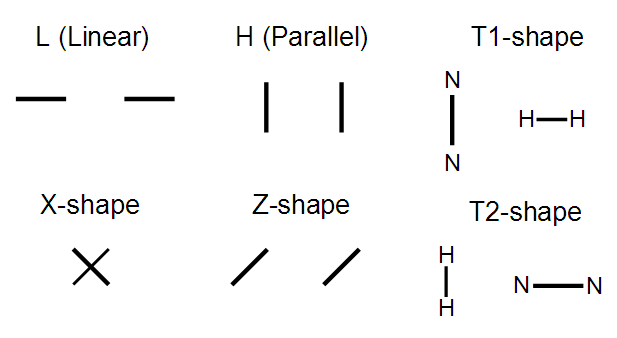
(H2)2、(N2)2和(H2)(N2)的構型傾向性以前有不少文章都研究過。此文在MP2/jun-cc-pVTZ對二聚體進行優化,并且通過aug-cc-pVnZ (n=T, Q)來外推得到CCSD(T)/CBS相互作用能,并考慮了BSSE,這比以往研究所用級別都高,但結論相仿佛。根據能量高低,確定出二聚體的構型穩定性順序是:
(H2)2:T>Z>X>H>L
(N2)2:Z>T>X>H>L
(H2)(N2):L>H>X>T1>T2
可見(N2)2和(N2)2這樣的由同種分子構成的二聚體都喜歡T和Z構型,但是L構型最不穩定;而H2和N2構成的混合二聚體(H2)(N2)的構型傾向性則最傾向于L構型,而討厭T構型。為什么二聚體會存在構型傾向性?為什么同種分子和異種分子構成的二聚體的構型傾向性截然相反?這篇文章提出了一種新的基于靜電勢的分析方法,以十分簡單直觀的方式完美地說明了這個問題,顯示出靜電作用的重要性。
在討論分子間作用前,先研究下H2和N2的靜電勢的特征。以下是它們的靜電勢平面圖。紅色和藍色等值線分別代表靜電勢為正和為負的區域。黑色等值線對應分子范德華表面(電子密度=0.001 a.u.)。由于分子間弱相互作用與范德華表面內部關系不大,所以不用管黑色等值線內部的區域。
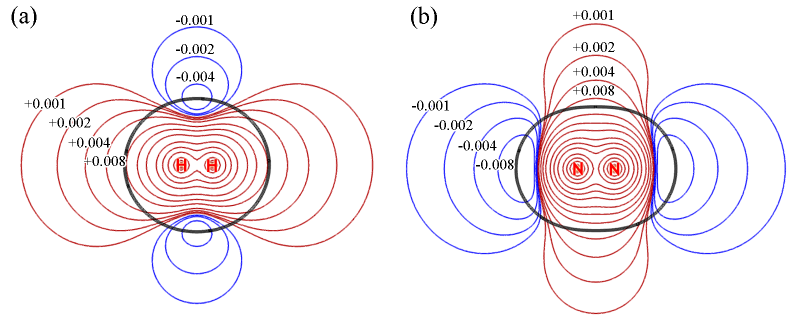
由上圖可見,H2和N2的靜電勢分布不僅顯示出十分顯著的各向異性特征,而且,它們的靜電勢特征幾乎完全相反!H2在分子軸上靜電勢為正,然而N2卻明顯為負。H2在環繞分子軸的區域靜電勢為負,而N2卻為正。這樣奇怪的靜電勢分布是怎么來的?通過考察它們的電子變形密度圖我們可以得到答案,如下所示
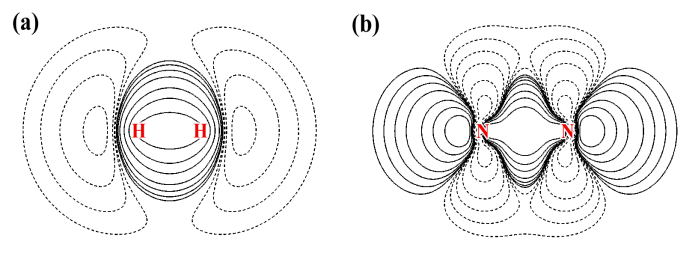
圖中實線代表原子形成分子后電子密度增加的區域,虛線代表減少的區域。分子的靜電勢由兩部分構成,電子密度貢獻負值,原子核電荷貢獻正值。對于H2,形成分子后電子密度往兩個氫中間移動構成共價鍵,相應地在分子軸向上電子密度就降低了。于是,分子兩端由于電子密度抵消不掉核的貢獻,靜電勢就成了正值。而由于共價鍵區域電子密度增加,對靜電勢的貢獻超越了核電荷,因此在環繞分子軸的區域靜電勢為負(但是離原子核很近的區域還是遠遠抗衡不了核的貢獻,靜電勢依然為正)。
對于N2,形成分子后分子兩端出現了孤對電子,對靜電勢有很大的負貢獻,這是為什么分子兩端靜電勢明顯為負。然而,雖然形成了三重鍵,電子密度已經往分子中間凝聚了很多,為何繞分子軸的區域的靜電勢卻還是正的?結合著靜電勢變形圖去觀察,原因就一目了然了
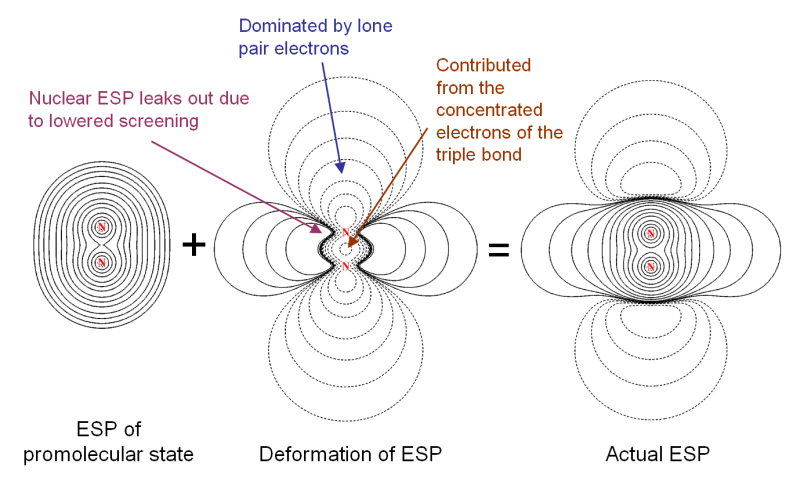
圖中ESP of promolecular state代表兩個孤立狀態的氮原子的靜電勢相疊加的靜電勢圖,這對應于形成分子前狀態(promolecular狀態)的靜電勢。有人證明過,孤立原子的靜電勢肯定處處為正,所以promolecular狀態的靜電勢圖處處為正是理所應當的。圖中Deformation of ESP顯示了從promolecular狀態到實際分子狀態過程中靜電勢是如何變化的。可以看到的確由于形成了三重鍵使得電子密度向分子中央轉移,從而導致了分子中間靜電勢變得明顯更負了。但是,這卻使得圖中紫色箭頭附近的電子密度明顯降低(對照變形密度圖上能明顯看到),于是原子核產生的靜電勢就仿佛從紫色箭頭所示區域“漏”了出來,最終導致繞著分子軸的區域的靜電勢明顯為正。實際的分子靜電勢,正是ESP of promolecular state和Deformation of ESP這兩幅圖的疊加。可見通過考察靜電勢變形圖,對于搞明白當前體系的靜電勢是如何形成的是極有幫助的。
考察完了單體的靜電勢圖,現在將圖根據體系二聚體構型進行疊加,各種構型的穩定性的差異就變得一目了然了!對于(N2)2如下所示。(H2)2和這極為類似,就不給出了
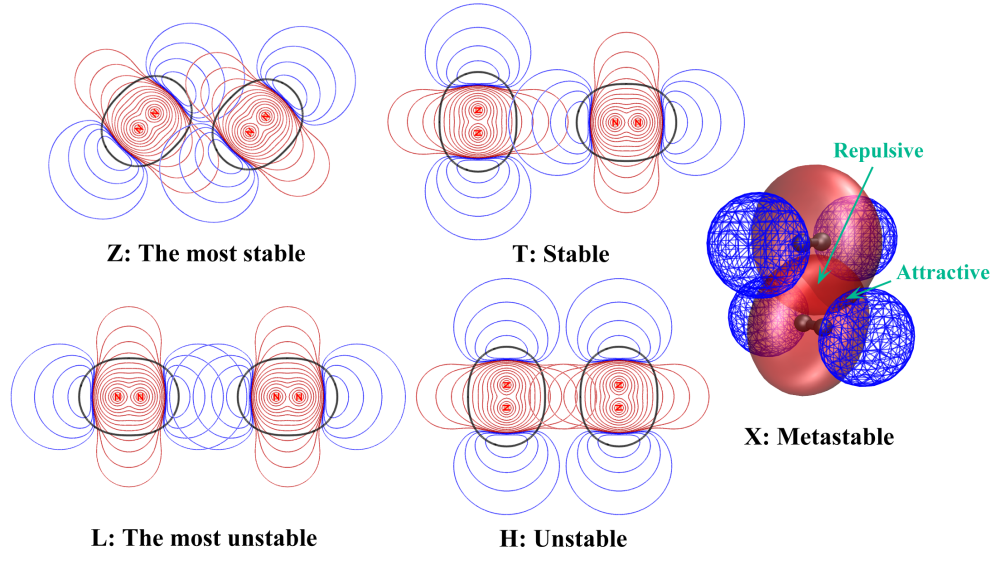
基于靜電勢互補思想,文章假設兩個分子間靜電勢以符號相反的方式重疊程度越大,則靜電吸引作用越強,體系越穩定;反之,以符號相同的方式重疊程度越大,則靜電互斥作用越大,體系越不穩定。從圖中來看,這個假設完全合理,可以完美解釋為何(N2)2的構型穩定性順序是Z>T>X>H>L。對于Z構型,紅藍等值線重疊程度比其它構型都大,解釋了為什么Z構型是(N2)2最穩定的構型。T構型的紅藍重疊程度比Z略小,因此比Z構型穩定性稍弱。X構型當中既有符號相同方式重疊的區域,也有符號相反方式重疊的區域,所以是亞穩的狀態(為了表現清楚重疊區域文章將之作成了等值面圖)。H和L構型的靜電勢都是以符號相同方式重疊的,而且L構型重疊程度更大,因此H不穩定,L更不穩定。注意這里說的穩定與否是相對而言的,不穩定并非代表不能形成相應構型的二聚體,畢竟分子間還有色散作用來穩定它們,但是色散作用的取向性很弱,對這些小分子的構型取向的影響遠遠抵不過靜電作用。
再來通過靜電勢疊加圖看看為什么(H2)(N2)的構型穩定性順序與(H2)2和(N2)2截然相反,即L>H>X>T1>T2
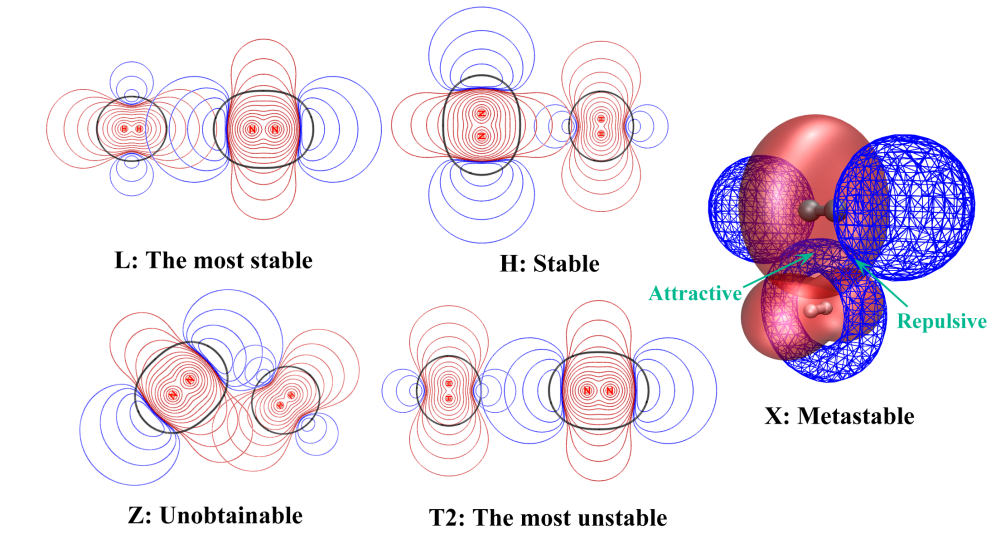
由于H2和N2在軸向上靜電勢正好相反,并且以L構型可以讓它們的重疊程度最大,所以L最穩定。H、X、T2的相對穩定性順序也可以按照前述方法通過考察靜電勢重疊方式和重疊程度來圓滿解釋。Z構型根本得不到,因為這種情況下,如圖所示,靜電勢在兩個區域同時以符號相同方式重疊,由于靜電互斥很強,即便一開始把體系擺成Z構型,在優化過程也會立刻跑到L構型去。
可見這種靜電勢分析方法非常簡單直觀而且可靠。不僅可以解釋已知的穩定性順序,對于新穎的體系,包括多聚體體系,還可以以這種方式通過擺弄靜電勢圖來預測構型穩定性,“設計”出穩定的構型,就像樂高玩具一樣。這和前線分子軌道理論某種程度也有點相仿佛,前線軌道理論要求反應過程中HOMO與LUMO盡可能好地以符號相同方式重疊,而靜電勢疊加分析則表示,若想形成穩定二聚體,應當以靜電勢符號相反方式盡可能多地重疊。不過這種靜電勢分析也并非沒有局限性,對于范德華作用強的情況,比如pi-pi堆積,或者體系電子云容易發生極化并且又遇上帶凈電荷或高極性體系而使得靜電勢分布會發生較大改變的情況,就得考慮更多因素。
值得一提的是,通常人們分析靜電勢一般都是討論分子表面上的靜電勢,雖然對于此文的體系也可以嘗試這么討論,但是顯然沒有單體的靜電勢圖疊加這樣能把靜電勢的互補程度這么直觀、顯著地展現出來。靜電勢疊加圖分析是個很有用的靜電勢的新的分析方法,建議大家在研究中嘗試。用Multiwfn程序(http://www.shanxitv.org/multiwfn)可以非常容易地作出這種靜電勢平面圖,也包括promolecular狀態的靜電勢圖、靜電勢變形圖,以及電子變形密度圖。
通過四極矩-四極矩相互作用模型進行分析,也能對這些二聚體的構型傾向性問題進行一定程度的解釋,詳見文中3.3節的討論。實際上以前也有人通過這種模型去討論(H2)2和(N2)2的構型傾向性問題,但是遠沒有用靜電勢圖疊加分析這么直觀,而且四極矩也只是對非極性分子電荷分布的最低階近似描述,沒靜電勢分析更準確。
文中還做了DFT-SAPT能量分解分析,這種分析相對于傳統的SAPT(對稱匹配微擾理論)更精確,關鍵是令分子內相關作用通過交換相關泛函來表現,以DFT計算取代了SAPT所用的HF。在文章的補充材料里對原理和細節進行了很詳細的講解,很值得一看。DFT-SAPT分析表明導致這些二聚體不同構型穩定性差異的原因確實是靜電作用,和靜電勢圖疊加分析的結論完全一致。而色散作用的大小則與構型穩定性順序缺乏相關性,因此不是影響構型的主導因素。甚至于,對于穩定的構型,靜電作用能和色散作用能已經在同一水平上,若缺失了靜電作用的話二聚體的結合能都要大打折扣。
文章在計算這幾個二聚體時用了很多方法,以CCSD(T)作為金標準來比較其它方法的可靠性。結果表明DFT-SAPT算的結合能與CCSD(T)極其接近,計算量卻小了不少,還免得考慮BSSE問題。MP2不好。各種DFT方法中B3LYP-D3表現差強人意,起碼是所有泛函中最好的,因此若想研究N2、H2團簇的話,若高級別后HF算不動,則B3LYP-D3是首選。而M11很坑爹,雖然比M06-2X新,而且在擬合參數時也考慮了弱相互作用,但結果甚爛。明尼蘇達系列泛函真是后繼無人,江郎才盡了,新版本凈是胡搞瞎搞,亂擬合。PM7是專門考慮了弱相互作用的半經驗方法,對于弱相互作用起關鍵作用的大體系(如蛋白、長鏈烷烴)的計算是很好的選擇,不過通過對這些二聚體的計算來看,PM7對于精細活兒還是不行。而B3LYP這老東西,眾所周知對色散作用沒轍,實測結果可見,就連束縛態都得不到(相互作用能全都為正!),讓它算的話二聚體就崩了。