DFT-D色散校正的使用
注:本文主要講DFT-D3。筆者后來又寫了文章專門介紹DFT-D4,見《DFT-D4色散校正的簡介與使用》(http://www.shanxitv.org/464)。
DFT-D色散校正的使用
文/Sobereva @北京科音
First release: 2013-Nov-7 Last update: 2023-Jun-16
1 前言
很多傳統的交換-相關泛函,諸如B3LYP,由于相關勢的長程行為不對,完全不能描述色散作用,而諸如常見的PBE、PW91對色散作用描述也極差。因此它們用于研究色散作用主導的問題結果差得一塌糊涂,比如物理吸附、長鏈烷烴之類的大分子構象、弱極性分子團簇等等。解決這些泛函對色散作用描述能力很差的最有效的方法就是引入經驗的色散校正項。不同的人提出過不同的色散校正方法,如TS、XDM、VV10等,其中最成功、也是目前最為流行的是Grimme提出的DFT-D,有以下版本
(1) JCC,25,1463(2004):DFT-D1。已過時
(2) JCC,27,1787(2006):DFT-D2。已過時
(3) JCP,132,154104(2010):DFT-D3。比DFT-D2更嚴謹,整體精度更好,支持元素更多(支持從H到Pu),對幾乎所有主流泛函都提供了參數,而且幾乎不令計算耗時有任何增加,實現也很容易,如今幾乎所有主流量化程序都支持DFT-D3
(4) JCP,147,034112(2017):DFT-D4。比DFT-D3的改進在于可以考慮實際電子結構對色散校正能的影響,但計算方式復雜得多,目前只有較少程序支持
DFT-D對原本描述色散作用很差的泛函在色散作用描述上的改進立竿見影,例如筆者在J. Mol. Model., 19, 5387 (2013) http://link.springer.com/article/10.1007%2Fs00894-013-2034-2一文中比較了B3LYP加和不加DFT-D3校正時對氫氣、氮氣二聚體的計算結果,數據表明B3LYP根本沒法得到二聚體穩定構型,或者說實際存在的構型下算得的二聚體相互作用能都是正的。而加上DFT-D3校正后,即B3LYP-D3,對這些二聚體的相互作用能計算結果則與金標準CCSD(T)起碼定性一致。讀者可以在自己的文章中引用這篇文章來說明色散校正的重要性。即便是靜電主導的弱相互作用,諸如氫鍵、鹵鍵,盡管傳統泛函也能勉強湊合用,經過DFT-D校正后也能令計算精度顯著提高。由于DFT-D同時也改進了中程的相關作用的描述,因此順便對DFT泛函的熱力學性質(尤其是牽扯過渡金屬的)的計算精度也帶來少許改進。可以說加上DFT-D校正有益無害。自從DFT-D流行起來后,曾經密度泛函對弱相互作用描述不好的老黃歷徹底被顛覆,密度泛函搖身一變成了最為有效的計算弱相互作用的方法,特別針對是較大體系。同時大量相關的測試文章的涌現也讓很多人清楚認識到了傳統泛函對弱相互作用有多差。也應當了解的是,色散校正是一大類方法,除DFT-D之外還有很多其它的色散校正方法,諸如TS、XDM、VV10、vdW-DF、MBD等等,只不過DFT-D是最最流行、被支持最廣泛而且也是最便宜的。其它的各種色散校正方法筆者在北京科音基礎量子化學培訓班(http://www.keinsci.com/workshop/KBQC_content.html)里會專門講。
原則上說,DFT-D3可以與任何交換相關泛函相結合。甚至對于弱相互作用描述已經很不錯的雙雜化泛函、M06-2X,加上DFT-D3后性能也能得到稍微的改進。但是也有一些出名的泛函本身就標配了特定形式的色散修正項,比如B97D、ωB97XD和B2PLYPD,在泛函定義的時候就專門給它們標配了DFT-D2形式的校正,顯然就不能再給它們加上DFT-D3修正了。泛函結合DFT-D3校正后通常用“泛函名”+“-D3”來稱呼,例如BLYP結合DFT-D3就叫BLYP-D3。
關于DFT-D在筆者另外的帖子里有更多討論,見《亂談DFT-D》(http://www.shanxitv.org/83)和《談談“計算時是否需要加DFT-D3色散校正?”》(http://www.shanxitv.org/413)。本文的重點是介紹一下DFT-D校正能如何通過Grimme的DFT-D3程序來計算,以及DFT-D如何在Gaussian、ORCA和GAMESS-US中啟用。但在此之前先把目前用得最多的DFT-D3的形式介紹一下。
2 DFT-D3的兩種形式
DFT-D3實際上有兩個版本,差異在于阻尼函數形式。阻尼函數用來調節色散校正在近程、中程距離時的行為,以避免double-counting問題(傳統DFT泛函能夠較好描述近距離的相關作用,如果近距離時校正能還較大的話就導致重復了)。DFT-D3原文當中用的是零阻尼(zero-damping)形式,這也是通常說的DFT-D3。而后來在JCC,32,1456(2011)中通過比較,發現使用物理意義更明確的Becke-Johnson阻尼(BJ-damping)可以讓結果稍微更好點,對分子內色散作用的描述優勢更顯著些,這種校正形式通常被稱為DFT-D3(BJ)。不過多數文章中在使用DFT-D3校正時并不做顯著區分,表面寫的是DFT-D3但實際上可能用的是DFT-D3(BJ)。2.1 零阻尼
DFT-D校正能加到原先泛函計算的體系能量上就是校正后的能量。基于零阻尼的DFT-D3校正能寫為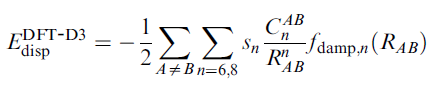
其中R_AB代表AB原子間的距離,上標n就代表了距離的n次方。C是原子間色散校正系數,依據一定規則進行計算。s_n是刻度因子。零阻尼函數f的表達式為
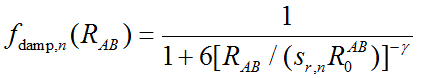
零阻尼形式對于每個泛函有4個可調參數,即s6、s8、sr,6、sr,8。實際上所有泛函的sr,8都是1。對于普通泛函,s6也為1。所以DFT-D3用于普通泛函時只需要擬合兩個參數s8和sr,6即可。對于雙雜化泛函,s6是一個小于1的值,也需要進行擬合來確定。
2.2 BJ阻尼
基于BJ阻尼的DFT-D校正能的形式為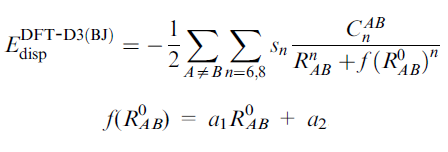
BJ阻尼使得中、近程距離的色散校正能雖很小,卻并不接近于0。對于HF也可以用DFT-D3校正(HF對色散作用能完全無力),但只能用BJ而不能用零阻尼形式。對于M05/06/08系列明尼蘇達系列泛函,如M06-2X,只能用零阻尼而不能用BJ阻尼,因為這類泛函已經表現出了中程相關,所以要用零阻尼形式來避免因引入中程校正而導致的double-counting。之后發展的某些明尼蘇達系列泛函如MN15倒是也能結合BJ阻尼。
上面的式子表明DFT-D3校正是基于原子對的,每一對原子對校正能有各自的貢獻,但實際上的色散作用不是精確的對可加和的,還有多體項。于是DFT-D3還包含了三體項對校正能貢獻。但由于對結果影響很小,所以考慮DFT-D3校正時一般不計算三體項,不過一些研究表明對于很大體系,考慮三體項還是會有不可忽略的改進的。
由于DFT-D的形式簡單,一階和二階解析導數很容易得到,所以原先DFT能做到幾階解析導數在校正后依然能做到幾階。而三體項,目前只有一階解析導數。
3 DFT-D3程序的使用
Grimme的DFT-D3程序是用來計算DFT-D色散校正能的,程序一直在更新,下載地址見https://www.chemie.uni-bonn.de/grimme/de/software/dft-d3/get_dft-d3。用戶只需要提供原子坐標,程序就能立刻算出校正能以及校正能的導數。對于常用的泛函,DFT-D3的參數基本上都已經齊全。不過由于目前主流量子化學程序都已經直接支持了DFT-D3,所以Grimme這個程序一般沒必要單獨去用。
編譯過程很簡單。對于Linux系統,下載后解壓,進入目錄輸入make命令即得到了dftd3可執行程序,默認調用的是ifort來編譯。對于Windows系統,假設使用的是Intel visual fortran,編譯方式是新建項目,然后把壓縮包內的.f文件以及param文件都加入項目然后編譯即可。筆者編譯好的Linux 64bit版和Windows版的DFT-D3程序都可以在這里下載:/usr/uploads/file/20150609/20150609203011_54761.rar。壓縮包內帶有.exe后綴的是windows版,不帶后綴的是Linux版。
程序壓縮包里包含手冊,對運行參數介紹得很清楚。在Linux下,下面命令計算的是DFT-D3(BJ)對test.xyz里的體系的針對BLYP泛函的色散校正能
./dftd3 test.xyz -func b-lyp -bj
如果你用的是Windows,需要進入命令行模式(cmd或powershell)然后同樣以如上方式通過命令行指令來使用DFT-D3。因為DFT-D3程序沒有交互式的界面,因此無法靠雙擊dftd3.exe圖標來運行,必須通過命令行方式來運行!
程序會輸出一堆參數,最后給出校正能
Edisp /kcal,au: -3.3486 -0.00533628
以a.u.為單位的色散校正能會同時寫入到當前目錄下的.EDISP文件中。
例子中的test.xyz是體系的xyz格式的坐標:
6
ltwd
C 0.00000000 0.42021400 0.00000000
H -0.45599500 1.43114200 0.00000000
O 1.20173900 0.23372100 0.00000000
N -0.94137600 -0.56316900 0.00000000
H -0.64194700 -1.52713700 0.00000000
H -1.92633700 -0.35287300 0.00000000
第一行是原子數,第二行是標題,之后就是原子名和以埃為單位的坐標。
-func后面接的是所用的泛函,必須按照turbomole的泛函寫法來寫,諸如b3-lyp、pbe0、pbe、b2-plyp、cam-b3lyp、b2gp-plyp、m062x。如果不知道怎么寫,可以到dftd3.f源文件里去搜b3-lyp,然后就能看到各種泛函的寫法以及相應的參數,比如會看到
...
case ("tpss0")
rs6 =0.3768
s18 =1.2576
rs18=4.5865
case ("pbe0")
rs6 =0.4145
s18 =1.2177
rs18=4.8593
...略
-bj代表用BJ阻尼,-zero代表用零阻尼。若寫-old代表用DFT-D2形式。
DFT-D3程序默認不計算三體項,如果要計算的話就加上-abc。
加上-grad的話程序還會計算各個原子的色散校正能的梯度并寫入到當前目錄下的dftd3_gradient文件中。
加上-anal的話程序還會輸出每個原子對對色散校正能的貢獻。例如
analysis of pair-wise terms (in kcal/mol)
pair atoms C6 C8 E6 E8 Edisp
1 2 6 1 0.889542D+01 0.166327D+03 -0.1088 -0.1480 -0.25679
1 3 6 8 0.177185D+02 0.428060D+03 -0.1695 -0.2748 -0.44422
1 4 6 7 0.198682D+02 0.501857D+03 -0.1813 -0.3033 -0.48467
...略
就說明比如1號和3號原子之間的作用對色散校正能的貢獻是-0.44422 kcal/mol。
用-anal的時候可以定義片段。方法是在當前目錄下寫一個名為fragment的文件,每行代表每個片段包含的原子,例如內容為
2-4
1,6
這代表第一個片段包含2、3、4號原子,第二個片段包含1、6號原子。剩下的第5號原子就自動作為第三個片段。程序會輸出
group # atoms
1 2- 4
2 1 6
3 5
group i j Edisp
1 -- 1 -0.74
2 -- 1 -1.58
2 -- 2 -0.25
3 -- 1 -0.43
3 -- 2 -0.35
3 -- 3 0.00
由此可見片段1內的3個原子彼此間色散校正能是-0.74 kcal/mol,1、2號片段之間色散校正能是-1.58 kcal/mol。片段3就一個原子,所以片段內的沒有色散校正能。以上數值加和就是總的校正能。
對于諸如B3LYP這樣的泛函,由于完全表現不了色散作用,因此對于諸如B3LYP這樣的泛函的DFT-D3校正能,特別是零阻尼下的,就可以近似視為是色散作用能。因此,利用DFT-D3程序我們可以直接計算出分子間色散作用能的大小。例如我們計算水二聚體,將兩個水分別定義成兩個片段,那么DFT-D3程序在-func b3-lyp -zero時給出的這兩個片段間的校正能就可以當成是這兩個水之間的色散作用能。盡管這種做法不怎么嚴格,Grimme也并不鼓勵這么做,但從實際結果上看這么做基本還算合理。可以算是個計算分子間,或者兩個分子當中的任意指定的片段之間色散作用能的便利的方法,但精度只能算得上是定性級別的。想準確計算分子間色散作用能,最可靠的方法是做SAPT(對稱匹配微擾理論)得到相互作用能的色散成份,但這一方面比較耗時、麻煩,另一方面也沒法簡單分離出指定局部片段間的色散作用能。還一種做法是使用Multiwfn (http://www.shanxitv.org/multiwfn)做基于力場的能量分解,既可以給出色散作用能,還可以分解成原子對的貢獻,物理意義比利用DFT-D3校正能得到相對來說更強一些,見《使用Multiwfn做基于分子力場的能量分解分析》(http://www.shanxitv.org/442)。
下面介紹下怎么在幾個常見的量子化學程序中直接用DFT-D校正。
4 在Gaussian中使用DFT-D校正
4.1 Gaussian03
在G03中完全不支持DFT-D。G03里計算弱相互作用體系比較令人為難,支持的泛函對弱相互作用都不好。相對而言最好的就是M05-2X,但只有G03后期版本才支持。4.2 Gaussian09 A、B、C版
在G09 D.01版之前不支持DFT-D3,但是支持了一些標配DFT-D2校正的泛函,即B97D、ωB97XD、B2PLYPD,另外還支持了2008年提出的對弱相互作用很好的M06-2X。靠ωB97XD和M06-2X,基本上就足矣對付各種弱相互作用體系了,二者的性能在伯仲之間,后者略微占優。這兩個泛函在G09里分別寫為wB97XD和M062X。不過這兩個泛函計算速度比起B3LYP這樣傳統的泛函要慢很多。若想精度更高可以用雙雜化結合色散校正的泛函B2PLYPD。在使用B97D、ωB97XD和B2PLYPD計算很重的原子時可能會出現諸如這樣的提示R6DR0: No vdW radius available for IA= xx,這就代表由于DFT-D2不含序號為xx的元素的參數而無法計算。解決辦法只有升級到D.01及以后的版本改用參數更全的DFT-D3校正,或者用其它合適的泛函或后HF方法。
雖然前面介紹了免費的DFT-D3程序,但是DFT-D3程序只能在給定結構上計算色散校正能和梯度,沒法直接讓DFT-D3校正在Gaussian進行優化的時候就體現出來,然而色散作用對弱相互作用體系構型影響卻往往很大,所以不在優化時就表現色散校正的話沒有意義。但實際上,如果不怕麻煩倒也是有辦法讓G09與DFT-D3程序直接相結合來進行優化的。在G09當中有個external關鍵詞,可以在Route section中添加諸如external='./dftdopt.sh',這樣在優化過程中Gaussian就會試圖通過調用外部腳本./dftdopt.sh來得到它傳回來的當前坐標下的能量、受力(甚至Hessian矩陣)。而外部腳本自身也可以調用g09。因此,如果我們自行編寫這個腳本,讓這個腳本讀取優化過程中傳遞出來的當前步的坐標,并調用另一個g09計算出此坐標下的能量和受力(用force關鍵詞),然后再讓腳本調用DFT-D3程序算出色散校正的梯度并加到剛才的受力上,就得到了包含DFT-D3色散校正的當前坐標下的受力,再將受力傳回給G09的優化進程。這樣就等于G09在優化時就帶著DFT-D3校正的效果了。但是據我所知沒有這樣的現成的腳本,自己寫的話需要一定水平(難者不會,會者不難),大家有興趣的話可以參考post-G程序(http://faculty1.ucmerced.edu/ejohnson29/2.cfm?pm=432&lvl=2&menuid=618)里提供的一個腳本,此腳本的目的是讓優化時能帶著XDM校正的效果(XDM算是另一種色散校正形式,依賴于波函數,目前遠不如DFT-D3普及)。還可以參考《將Gaussian與Grimme的xtb程序聯用搜索過渡態、產生IRC、做振動分析》(http://www.shanxitv.org/421)和《將Gaussian與ORCA聯用搜索過渡態、產生IRC、做振動分析》(http://www.shanxitv.org/422)文章當中的腳本對external關鍵詞的利用。
4.3 Gaussian09 D.01版及之后
從G09 D.01開始直接支持DFT-D3。使用方法很簡單,原先的泛函名字不用動,只要額外寫上EmpiricalDispersion=GD2就做DFT-D2校正;寫上EmpiricalDispersion=GD3就做零阻尼的DFT-D3校正;寫上EmpiricalDispersion=GD3BJ就做DFT-D3(BJ)校正。例如# B3LYP/aug-cc-pVDZ EmpiricalDispersion=GD3BJ opt就代表讓B3LYP結合DFT-D3(BJ)校正來進行幾何優化,也即使用B3LYP-D3(BJ)方法進行優化。如果嫌寫EmpiricalDispersion=GD3或GD3BJ太羅嗦,也可以簡寫為em=GD3或GD3BJ。啟用了DFT-D校正后,若用了#P,在Gaussian計算時會看到這樣的信息
R6Disp: Grimme-D3(BJ) Dispersion energy= -0.0018363766 Hartrees.
Nuclear repulsion after empirical dispersion term = 41.9082499513 Hartrees.
顯然,Gaussian在計算時實際上是將DFT-D校正能先加到核互斥能里面了。最后輸出的總能量就是DFT-D校正后的能量。
對于G09 D.01及之后,以下含有DFT-D校正的泛函直接用寫關鍵詞就行了,可以不必用“原始泛函名”+“EmpiricalDispersion”的方式來調用
B2PLYPD3、B97D3、mPW2PLYPD、B97D、wB97XD、B2PLYPD
其中末尾是D3的結合的都是DFT-D3(BJ),其余的結合的都是DFT-D2。
從G09 D.01開始還支持了在JCTC,8,4989中提出的一種包含色散校正的泛函APF-D(Austin-Petersson-Frisch),并且這種泛函里的色散校正形式也可以像DFT-D一樣通過EmpiricalDispersion=PFD加在其它泛函上。不過可靠性很難講,不建議用。
B3LYP-D3(BJ)是當前筆者很推薦的計算弱相互作用的泛函,精度好,可靠性高,速度也比M06-2X和wB97XD都快很多。不過論相互作用能計算的絕對精度,比M06-2X-D3(0)稍差一點。總的來說,在雜化泛函里,B3LYP-D3(BJ)的精度是名列前茅的,這點從Phys. Chem. Chem. Phys., 19, 32184 (2017)文章補充材料的表20可以體現。
注意G09 D.01版D3(BJ)計算頻率時色散校正的貢獻是不完全準確的,因為忽略掉了依賴于r^-8的那項。對于力常數較大(較硬)的振動模式這個問題的影響可忽略,但對于力常數較小(較軟)的振動模式就會造成一定誤差,往往會導致虛頻的出現(即便優化后已經準確處在極小點位置了)。但是零阻尼沒有這個問題,所以G09 D.01的用戶如果要算頻率的話,還是在零阻尼下優化為宜。不過D3(BJ)的這個問題在G09 E.01版已經得到了修正。
從D.01版開始還支持了對PM6半經驗方法加DFT-D3校正,直接寫PM6D3即可。
4.4 關于在Gaussian09/16中自定義DFT-D3參數
-----
2020-Jul-1補充:下文說的通過環境變量自定義DFT-D3參數的做法只適合Gaussian 16 B.01及之前,從G16 C.01開始需要通過IOp直接定義,具體來說,把以下IOp設為NNNNNNNN代表把相應參數設為NNNNNNNN/1000000
IOp(3/174):S6
IOp(3/175):S8
IOp(3/176):SR6
IOp(3/177):A1
IOp(3/178):A2
例如
用TPSSh-D3(BJ):TPSSh em=GD3BJ IOp(3/174=1000000,3/175=2238200,3/177=452900,3/178=4655000)
用MN15L-D3(0):MN15L em=GD3 IOp(3/174=1000000,3/175=0,3/176=3338800)
用MN15-D3(BJ):MN15 em=GD3BJ IOp(3/174=1000000,3/175=786200,3/177=2097100,3/178=7592300)
用BHandHLYP-D3(BJ):BHandHLYP em=GD3BJ IOp(3/174=1000000,3/175=1035400,3/177=279300,3/178=4961500)
用BHandHLYP-D3(0):BHandHLYP em=GD3 IOp(3/174=1000000,3/175=1442000,3/176=1370000)
注意Gaussian做多步任務時,IOp設置僅對第一個任務生效。因此以這種方式定義D3參數做opt freq任務時,freq任務是接收不到IOp的,會導致freq和opt用的不是同一個方法而造成嚴重問題。因此此時opt和freq必須分別做。
-----
在G09/16中開著DFT-D3做計算前,如果已經通過環境變量定義了DFT-D3參數,那么計算時就會直接用自定義的DFT-D3參數。利用這點,一方面可以替換內置D3參數,另一方面,對于沒有內置D3參數的泛函,我們可以通過這種方式使其也能支持D3校正。Gaussian里內置了哪些泛函的D3參數,數值是多少,在手冊的DFT部分都可以看到。
對于DFT-D3(0),如前所述有s6、s8、sr,6、sr,8四個參數,在Gaussian里只允許你自定義前三個,可通過GAUSS_DFTD3_S6、GAUSS_DFTD3_S8、GAUSS_DFTD3_SR6環境變量設置,而sr,8固定為1.0(要改只能改源碼)。對于DFT-D3(BJ),如前所述有s6、s8、a1、a2四個參數,可通過GAUSS_DFTD3_S6、GAUSS_DFTD3_S8、GAUSS_DFTD3_ABJ1、GAUSS_DFTD3_ABJ2環境變量設置。環境變量定義的數值除以1000000就是對應的D3參數數值。
例如,G16里支持MN15,但是至少對于G16(起碼對于B.01來說),還沒有內置DFT-D3參數,因此沒法直接用MN15-D3。不過,好在在Grimme的GMTKN55數據庫文章Phys. Chem. Chem. Phys., 19, 32184 (2017)的補充材料的Table S3里可以看到MN15-D3(BJ)的參數,為
S6=1.0
S8=0.7862
a1=2.0971
a2=7.5923
因此,在計算之前,Linux系統的終端里輸入以下內容(假設是Bash shell)
export GAUSS_DFTD3_S6=1000000
export GAUSS_DFTD3_S8=786200
export GAUSS_DFTD3_ABJ1=2097100
export GAUSS_DFTD3_ABJ2=7592300
之后再用比如MN15/6-311+G(d,p) em=GD3BJ關鍵詞,計算的結果就將對應于MN15-D3(BJ)/6-311+G(d,p)級別。在《Gaussian中非內置的理論方法和泛函的用法》(http://www.shanxitv.org/344)一文中也提到過使用這種方式實現G09不支持的DSD-PBEP86-D3(BJ)的計算。
再比如,MN15L的D3參數在G16里(起碼對于B.01而言)是沒有內置的,好在GMTKN55文章的Table S4當中給了MN15L-D3(0)參數:
S6=1.0
sr,6=3.3388
S8=0.0
因此在使用諸如MN15L/def2TZVP em=GD3關鍵詞計算之前應當用以下命令設置環境變量
export GAUSS_DFTD3_S6=1000000
export GAUSS_DFTD3_SR6=3338800
export GAUSS_DFTD3_S8=0
常有人問怎么常用的TPSSh在Gaussian里加不了D3。實際上這個泛函的D3參數早就有了,只不過Gaussian一直沒納入進去而已(起碼直到G16 C.01還不直接支持)。也是從GMTKN55文章Table S3里可以直接得到參數,使用諸如TPSSh/def2TZVP em=GD3BJ計算之前先運行以下命令即可
export GAUSS_DFTD3_S6=1000000
export GAUSS_DFTD3_S8=2238200
export GAUSS_DFTD3_ABJ1=452900
export GAUSS_DFTD3_ABJ2=4655000
wB97XD的作者后來提出個wB97X-D3,把原先用的DFT-D2校正改成了DFT-D3,算弱相互作用精度得到了一定提升,這在ORCA中支持。但可惜沒法通過自定義D3參數的方式在Gaussian里面用,因為這個泛函很特殊,sr,8參數是1.094,而Gaussian中沒法通過環境變量設這個參數(只允許為1.0)。
5 在ORCA中使用DFT-D校正
寫上D3ZERO代表啟用零阻尼DFT-D3校正,寫上D3或者D3BJ啟用DFT-D3(BJ)校正,例如!B3LYP TZVP d3代表B3LYP-D3(BJ)/TZVP水平。如果要計算三體校正項,同時再寫上ABC即可。對于B2PLYP和mPW2PLYP,ORCA也提供了相應關鍵詞用來直接調用其包含色散校正版本,即B2PLYP-D、B2PLYP-D3、mPW2PLYP-D、mPW2PLYP-D3。-D的對應結合DFT-D2,-D3的對應結合DFT-D3(BJ)。
值得一提的是ORCA中的DFT-D模塊實際上就是直接內嵌的Grimme的DFT-D3程序,所以輸出信息和DFT-D3程序一模一樣。而Gaussian在計算DFT-D校正的時候則是用的Gaussian自己的人寫的代碼。
對于純泛函,ORCA可以用RI-J密度擬合技術使得計算速度有巨大提升,見《大體系弱相互作用計算的解決之道》(http://www.shanxitv.org/214)。因此在ORCA里,通過GGA泛函結合DFT-D3是計算柔性大體系構象、大體系之間弱相互作用的極為理想的選擇,本人推薦BLYP-D3(BJ),盡管精度比B3LYP-D3(BJ)稍遜色一點,但開RI后速度有顯著優勢。Phys. Chem. Chem. Phys., 19, 32184 (2017)文章的表6體現出,在計算弱相互作用方面,BLYP-D3(BJ)在純泛函里幾乎是最優秀的。
ORCA從4.1版開始支持了DFT-D4,寫上D4關鍵詞即可使用,實際上在內部也是調用的Grimme提供的DFT-D4子程序。
另外,ORCA也支持vdw-DF(van der Waals Density Functional)方式來考慮色散作用,通過VV10非局域形式的泛函得到色散校正能,可以結合一些GGA、雜化泛函。由于計算要涉及到雙空間坐標積分所以計算速度慢,而且不支持解析梯度。一般來說比DFT-D3沒什么好處,不必使用,但對于金屬或其它電子密度變化較大的體系(氧化態、離子化態)可能比DFT-D3更合用,因為DFT-D3不能體現實際電子結構,而只依賴于坐標。不過由于已經有了能夠體現實際電子結構的DFT-D4,vdW-DF的意存在義就大為降低了。
6 在GAMESS-US中使用DFT-D校正
在$DFT部分寫上DC=.T.就可以對DFTTYP所定義的泛函加上DFT-D3校正。IDCVER=1/2/3/4分別對應使用DFT-D1、DFT-D2、DFT-D3(0)和DFT-D3(BJ),默認是3。實際上,只要定義了IDCVER,就會自動打開DC=.T.,所以只寫IDCVER=4就夠了,沒必要再寫DC=.T.。
默認不計算三體校正項,想計算的話就寫DCABC=.T.。
對于B97D和ωB97XD,直接寫DFTTYP=B97-D和DFTTYP=wB97X-D即可,不要設定DC、IDCVER。
和ORCA一樣,GAMESS-US的DFT-D模塊也是直接把Grimme的DFT-D3程序內嵌進去,輸出信息和獨立運行DFT-D3時一致。目前GAMESS-US在調用DFT-D的時候有一些明顯bug,比如用了Bq原子,就會說找不到DFT-D參數而報錯。