使用Multiwfn做基于分子力場的能量分解分析
使用Multiwfn做基于分子力場的能量分解分析
文/Sobereva @北京科音
First release: 2018-Sep-19 Last update: 2023-Jul-1
0 前言
本文將介紹筆者提出的基于分子力場的能量分解方法的原理以及它在流行的波函數分析程序Multiwfn (http://www.shanxitv.org/multiwfn)中和使用。我將這個方法命名為energy decomposition analysis based on forcefield,可以簡稱為EDA-FF。此方法耗時極低,結果物理意義明確,不僅在一些場合可以替代較昂貴的基于波函數的能量分解方法,而且還具有一些獨特優勢,諸如結果可以可視化、可方便地考察分子內弱相互作用等。目前,已有諸多文章使用了EDA-FF方法研究問題,并且得到了很有意義的結果,例如Phys. Chem. Chem. Phys., 25, 16707 (2023)、ACS Omega, 4, 13408 (2019)、J. Lumin., 223, 117198 (2020)、Nano Today, 33, 100868 (2020)、ACS Materials Lett., 2, 691 (2020)、Chem. Paper, 74, 3847 (2020)、J. Sep. Sci., 44, 2957 (2021)、Optik, 241, 167063 (2021)、Phys. Chem. Chem. Phys., 23, 4681 (2021)、Ind. Eng. Chem. Res., 59, 22605 (2020)等。
如果你將本文介紹的方法應用于你的研究中,在引用Multiwfn原文的同時也請引用筆者的這篇文章,可以視為EDA-FF的原文:Mat. Sci. Eng. B, 273, 115425 (2021) DOI: 10.1016/j.mseb.2021.115425。其中筆者對EDA-FF方法做了簡要的介紹,并將之用于研究18碳環與石墨烯的相互作用,這篇文章在《18碳環(cyclo[18]carbon)與石墨烯的相互作用:基于簇模型的研究一例》(http://www.shanxitv.org/615)里有專門的介紹。
如果你對Multiwfn不了解,建議參看《Multiwfn入門tips》(http://www.shanxitv.org/167)、《Multiwfn FAQ》(http://www.shanxitv.org/452)、《Multiwfn波函數分析程序的意義、功能與用途》(http://www.shanxitv.org/184)。
1 基于力場的能量分解的原理
能量分解是量子化學分析方法中的一個重要組成,它可以把片段間總相互作用能分解為有物理意義的能量項以便于考察相互作用的本質,這在《Multiwfn支持的弱相互作用的分析方法概覽》http://www.shanxitv.org/252)一文中有簡要介紹。實際上,基于形式非常簡單的分子力場(forcefield),也可以對弱相互作用的成份進行拆解。雖然分子力場已被廣泛用于分子動力學等領域,但是基于分子力場做能量分解研究的文章極少。考慮到通過力場做能量分解的潛在應用價值,筆者將之寫入了Multiwfn程序中作為主功能21的子功能1,經實測發現效果不錯。
分子力場里所謂的非鍵相互作用包括靜電作用(electrostatic)和范德華作用(van der Waals),后者可劃分為起排斥作用的“交換互斥項”(repulsion)和起吸引作用的“色散項”(dispersion)。如果你對原子間相互作用本質缺乏了解,很建議讀一下《談談“計算時是否需要加DFT-D3色散校正?”》(http://www.shanxitv.org/413)中的相關介紹。大多數分子力場采用對勢形式來計算原子間非鍵相互作用的靜電(ele)、交換互斥(rep)和色散吸引(disp)部分,公式如下所示
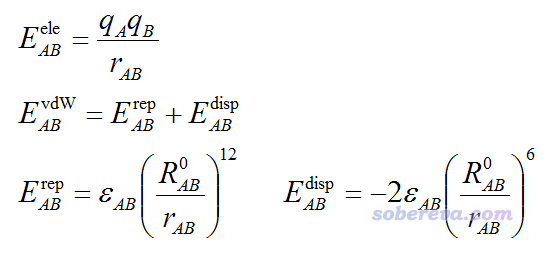
其中A,B是原子標號,q是原子電荷,r是原子間距離,ε是范德華作用勢阱深度,R0是原子間非鍵距離,當r=R0時原子間范德華作用能恰等于勢阱深度。
ε和R0是在分子力場里定義的。不同力場里根據原子所處化學環境的不同定義了不同原子類型,多數力場是根據原子類型來定義的范德華參數,不同原子類型的范德華參數有的相同有的不同。實際計算原子間范德華作用時用的參數一般是基于原子的范德華參數通過混合規則來產生的,比如UFF力場用的是下圖第一行的規則,不同原子類型間的ε和R0取兩個原子類型的ε和R0的幾何平均。而對于AMBER和GAFF力場,規則如下圖第二行所示,ε混合規則與UFF相同,但是力場對每個原子定義的是非鍵半徑參數R*,原子間的非鍵距離參數通過相應原子的非鍵半徑加和得到。
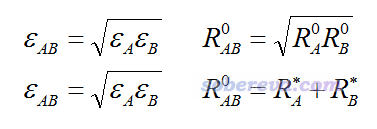
如上可見,計算原子間非鍵相互作用能非常簡單。要想計算特定片段間的非鍵相互作用,就把片段間每一對原子的非鍵作用加和即可。這就是基于力場做能量分解的原理,很容易理解。Multiwfn目前支持流行的AMBER99、GAFF和UFF力場做能量分解,這三種力場的函數形式都是相同的,都是最簡單形式的分子力場,靜電作用僅通過原子電荷來體現,并沒有像一些更復雜力場那樣考慮原子多極矩或者可極化效應。(以后Multiwfn也可能會支持這些更復雜的力場形式)
Multiwfn中基于力場的能量分解功能相對于Morokuma、SAPT等主流的基于波函數的能量分解方法有以下優勢
·速度非常快,對很大的體系也只要一瞬間就能給出結果。而基于波函數的能量分解方法很難用到一百多個原子的體系(有的只能用到幾十原子體系)
·片段可以非常自由地劃分,想考察哪兩個區域的相互作用就相應地輸入原子編號來定義即可
·分子內弱相互作用可以方便地考察。而對于基于波函數的能量分解方法,考察分子內弱相互作用需要把分子拆成片段,其中牽扯很多麻煩的事情,具體細節上也很具有任意性。
然而基于力場的能量分解也有很多局限性:
·受制于分子力場簡單的函數形式,能量分解精度和基于波函數的方法還有差距,不能在定量精度上有太高要求
·不同力場支持的元素不同,要考察的片段里面有力場不支持的元素就沒法用
·計算原子電荷的方法存在一定任意性,而且有的弱相互作用注定沒法基于原子電荷來定性正確表現,比如鹵鍵是由于鹵原子有sigma-hole特征所產生的,這需要考慮原子四極矩或者非原子中心的點電荷才能描述
·給出的結果沒法體現片段間相互作用所產生的電子云的極化、電荷轉移等因素的影響。
·只能考察弱相互作用,而沒法考察化學鍵這樣的強相互作用(這方面即便是SAPT等很多基于波函數的能量分解方法也沒法考察)
做這種能量分解所用的原子電荷必須對分子范德華表面附近的靜電勢有很好的重現性,否則不可能靠原子電荷較可靠地計算片段間靜電相互作用。因此使用的原子電荷首選是擬合靜電勢電荷,其中最常見的是MK和CHELPG電荷。如果對擬合靜電勢電荷不了解,參看《RESP擬合靜電勢電荷的原理以及在Multiwfn中的計算》(http://www.shanxitv.org/441)和《原子電荷計算方法的對比》(http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml)。所用原子電荷對靜電勢重現性哪怕達到“不錯”的檔次都太不夠,比如用ADCH、CM5、AM1-BCC等電荷,雖然對靜電勢重現性也不錯,僅次于擬合靜電勢電荷,但是算出來的靜電相互作用能和擬合靜電勢電荷還是有一定差距的。
關于能量分解時力場的選擇,如果是有機體系,就用AMBER或者GAFF就挺好。這兩個力場的原子類型的名字雖然不同(一個很大差別是AMBER的是大寫,GAFF的是小寫),但實際上GAFF的范德華參數是從AMBER力場繼承過來的,主要差別在成鍵參數上,因此基于哪個力場做能量分解都可以。雖然Multiwfn的能量分解也支持UFF力場,但一般不建議用UFF做能量分解,如后文的例子所示,對于哪怕合理的結構,UFF也往往嚴重高估互斥作用,甚至令本身穩定結合的分子間相互作用為正。不過將結構用UFF力場優化后可以消除這個問題,但由于UFF力場優化出的弱相互作用體系的結構往往也不太理想,所以能量分解結果還是不如AMBER和GAFF好。UFF力場最大好處是支持元素非常廣泛,幾乎覆蓋了整個周期表。
用于做能量分解的幾何結構應當是通過靠譜的級別進行優化過的,如果是來自于X光衍射晶體結構,應當凍結重原子的位置而對氫原子進行優化,因為氫原子的位置準確度很差,往往只是經驗性地確定的。
2 基于力場的能量分解在Multiwfn中的使用
其實基于力場做能量分解,利用諸如GROMACS等分子動力學就能做,但是真要用起來,過程很麻煩。Multiwfn專門設計了一個模塊來做這種能量分解,在設計上已經盡可能把分析流程簡化了(但注定不可能做到完全傻瓜化)。基本使用流程如下:
(1)對體系中每類分子都創建一個文本文件(分子類型文件),里面包含分子中各個原子的原子類型和原子電荷。然后再寫一個文本文件(分子列表文件),里面是分子類型文件的路徑,還有相應類型分子的數目,詳見后文。
(2)啟動Multiwfn,讀取一個含有當前體系結構信息的Multiwfn可以支持的輸入文件。哪些文件被Multiwfn支持且帶有結構信息,在《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》。(http://www.shanxitv.org/379)里有明示,比如你用.fch、.mol、.pdb、.xyz、.wfn、.molden等等格式都可以
(3)進入主功能21(能量分解主功能)中的子功能1(基于力場的能量分解模塊)。
(4)用選項3定義讀取分子列表文件,從而給體系中各個原子分配原子類型和電荷。如果你要用的力場不是默認的AMBER & GAFF,則讀取前先選選項-1切換成要用的力場。
(5)用選項2來定義片段,先設置要定義的片段數,然后輸入各個片段包含的原子序號,輸入格式很靈活,比如3,5-9,12-20,69。第(4)步和第(5)的順序無所謂,可以互換。
(6)最后,選擇選項1開始進行分析。各個片段間的相互作用能及物理成分,以及片段里各個原子對片段間相互作用能的貢獻都會輸出到屏幕上。
在寫分子列表文件和分子類型文件的時候一定要*萬分注意*,把分子列表文件和其中分子類型文件按順序完全展開之后,原子的順序必須和Multiwfn啟動時載入的文件里的原子順序完全一致,否則會由于原子電荷和原子類型指認順序錯誤導致結果完全不合理。比如說,體系是三個水和兩個乙醇構成的五聚體,結構信息里分子出現順序是water,ethanol,ethanol,water,water,如果水分子的分子類型文件是C:\water.txt,乙醇的分子類型文件是C:\ethanol.txt,則分子列表文件內容就應當為
C:\water.txt 1
C:\ethanol.txt 2
C:\water.txt 2
對于AMBER和GAFF力場,每個分子類型文件里的第一列為原子在力場中的原子類型,第二列是原子電荷,比如對于用AMBER力場描述的乙醇,可以為:
CT -0.236494
HC 0.080697
HC 0.042845
HC 0.080697
CT 0.348325
H1 -0.039425
H1 -0.039425
OH -0.609585
HO 0.372365
對于UFF力場,雖然一種元素有的也對應多種原子類型,但由于范德華參數只取決于元素,因此用UFF力場時分子類型文件應當只包含一列,即原子電荷,而原子類型不用定義。
原子類型怎么指定?一種做法是根據原子類型的定義和實際體系中原子所處于的化學環境來人為判斷。力場原文里以及一些涉及到分子力學的程序的一些文件中都有說明。比如AMBER的原子類型可以去看AMBER94力場原文,見J. Am. Chem. Soc., 117, 5179 (1995)的表1。GAFF的原子類型在其原文J. Comput. Chem., 25, 1157 (2004)表1里有介紹。為了方便,筆者在本文的文件包(見下一節開頭)里也提供了parm99.dat和gaff.dat,這是AmberTools程序包里的參數文件,開頭部分有AMBER99和GAFF力場的各種原子類型的說明。顯然,自己這么去指認比較累,特別是體系原子數較多的情況,這時候可以利用第三方程序幫助我們指認。比如用AMBER力場做能量分解的話,我們可以用比如GaussView指認原子類型,見后文的例子。如果用GAFF力場的話,可以用比如免費的AmberTools中的Antechamber程序指認原子類型。其實個別原子類型指認不太準確也沒太大問題,比如AMBER力場中H1、H2、H3原子類型對應的范德華參數相差不大。有時候可能體系中有的原子沒有完全合適的原子類型,這個時候可以用這種元素的其它原子類型湊合一下。另外,如果你用的是AMBER或GAFF力場,但是當前體系里有個別元素(如許多過渡金屬元素)在此力場中不支持,那么也可以借用UFF力場的參數來湊合一下,做法是在分子類型文件中把相應原子類型寫為UF,程序看到有原子類型叫UF,自動就會用UFF力場對應的參數。值得一提的是,用GaussView指認原子類型的有時候可能顯示的是問號,說明沒能成功指認,這個情況就必須按上述方式自己手動指定這個原子的原子類型。
建議在選擇選項1進行分析之前,用選項4把所有片段中的原子的類型和電荷輸出到屏幕上,大致檢查一下設定是否正確。如果有嚴重錯誤,對照元素名、原子類型和原子電荷,應該很容易就能發現。
Multiwfn的基于力場的能量分解功能中可以定義無數個片段,片段包含的原子范圍是任意的,但是不能有某個原子同時處于多個片段里。可以把一個分子劃分為不同片段考察分子內弱相互作用,但要注意,這些片段間至少要隔三個化學鍵(相對于鍵連關系而言,而不是原子間距而言),因為更近的話原子間的作用就不完全屬于弱相互作用范疇了,此時通過力場的非鍵作用項來計算它們之間的相互作用是嚴重不合理的(這也是為什么一般分子力場里忽略相隔一個和兩個化學鍵的原子間的非鍵作用,而對于相隔三個化學鍵的非鍵作用要么忽略要么刻意被大幅度削弱)。
如果計算前選一次選項-3,則計算過程中會把片段間每一對原子間的相互作用能都輸出到當前目錄下的interatm.txt文件中,便于你深入了解細節。如果計算前選了一次選項-4,那么計算過程中就會把各個原子對片段間總的/靜電/互斥/色散相互作用能分別寫入到當前目錄下的atmint_tot.pqr、atmint_ele.pqr、atmint_rep.pqr和atmint_disp.pqr文件中,便于你通過著色方式一目了然地考察原子的貢獻,后文有例子。
選項-2可以把計算靜電相互作用用的1/r算符改為1/r^2算符,顯然這樣算出來的靜電相互作用能會減小許多。加入這個設計是因為曾經有一些人利用這種做法近似地等效表現極性溶劑(諸如水)對靜電作用產生的屏蔽效果。當然,真要嚴格把溶劑效應考慮到能量分解中,應當使用隱式溶劑模型,但是在Multiwfn中尚不支持。還有種等效考慮溶劑效應的做法是用Multiwfn的能量分解功能先照常計算片段間靜電相互作用能,然后加上溶劑效應的極性部分對相互作用能的影響。有各種各樣的隱式溶劑模型可以實現這個目的,參看《談談隱式溶劑模型下溶解自由能和體系自由能的計算》(http://www.shanxitv.org/327)、《談談分子模擬中的隱式溶劑模型與GB模型》(http://www.shanxitv.org/42)。比如你是用Gaussian,你可以帶著scrf=solvent=[溶劑名]關鍵詞通過"E(復合物)-∑E(單體)"公式計算溶劑下的結合能,然后去掉這個關鍵詞再這么計算真空下的結合能,將兩次結合能求差,作為溶劑效應對靜電作用的影響。(溶劑效應的非極性部分對結合產生的影響也可以類似地計算,仔細看過http://www.shanxitv.org/327這篇博文就知道怎么弄。但這部分既沒法完全歸屬到色散作用也沒法完全歸屬到交換互斥部分,只能作為一個額外的項)
3 實例
下面通過一些例子演示如何用Multiwfn做基于力場的能量分解。只要大家把這些例子中的操作完全領會了,親自操作一遍,那么只要舉一反三,就可以容易地把這種分析用于其它任何體系。下面的例子用到的文件都可以在此下載:http://www.shanxitv.org/attach/442/file.rar。
本文使用的Multiwfn為2018-Sep-19更新的3.6(dev)版,絕對不要用更老版本。本文用到的Gaussian是G16 A.03版,GaussView是6.0.16版。
3.1 水二聚體
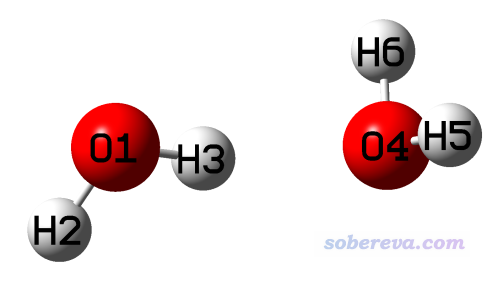
首先我們看一個最簡單的例子,兩個水分子通過氫鍵形成的二聚體,如下所示。
結構優化過程中我們使用優化弱相互作用體系又便宜又靠譜的B3LYP-D3(BJ)/6-311G**來實現。相關的文件都提供在了本文文件包的waterdimer目錄下,這些文件包括:
dimer_opt.gjf和dimer_opt.out:對水二聚體優化的輸入和輸出文件,原子順序是O1 H2 H3 O4 H5 H6
dimer.mol:用gview打開dimer_opt.out,然后保存的.mol文件,記錄了優化后水二聚體的結構信息
water_opt.gjf和water_opt.out:對單分子水優化的輸入和輸出文件。注意此文件里的原子順序與二聚體中是完全對應的,即O H H,這點非常重要
water.fch:在water_opt任務中產生的水分子的fch文件,包含了其B3LYP/6-311G**級別的波函數信息
mollist.txt:分子列表文件。其內容只有一行,即water.txt 2
water.txt:水分子的分子類型文件,包含它的原子類型和原子電荷信息
我們看到文件包里給出的water.txt內容如下:
OW -0.737121
HW 0.368560
HW 0.368560
這說明第一個原子類型是OW,電荷為-0.737121,其余兩個原子類型是HW,電荷為0.368560。下面說一下這個文件是怎么得來的。
如果大家比較熟悉AMBER分子力場,自然而然就知道水中的氧原子類型是OW,氫是HW。但如果你不知道該怎么設原子類型的話,又懶得自己去看力場原文,就把含有水分子結構信息的文件(比如文件包里提供的water.fch或water_opt.out)拖到gview里,點擊界面上圖標是粗體的A的按鈕進入原子列表編輯器(Atom list editor),點擊桔紅色的M按鈕把原子類型顯示出來,然后點擊兩次AMBER Type那一列的標題,此時窗口應當處于以下狀態:
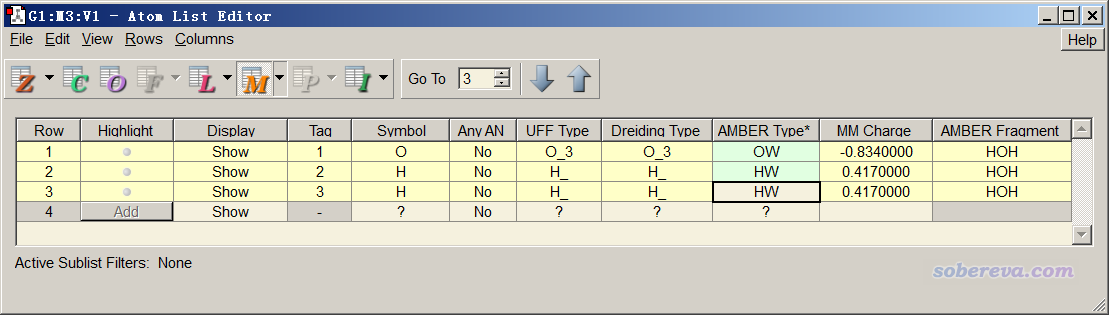
然后點擊File - Export Data,保存的文件名輸入water,就得到了water.txt。然后,通過Ultraedit等文本編輯器的列模式把除了AMBER Type那一列以外內容的列刪掉,再把此文件里的第一行刪掉,此時water.txt里就只有各個原子的原子類型了。然后我們計算水分子的MK原子電荷,啟動Multiwfn,載入water.fch,然后輸入
7 // 布居分析
13 // MK電荷
1 //開始計算
結果為
Center Charge
1(O ) -0.737121
2(H ) 0.368560
3(H ) 0.368560
然后按照Multiwfn手冊5.4節說的方法把所得原子電荷從命令行窗口復制到剪切板上,再用Ultraedit的列模式粘到water.txt里,就得到了文件包給出的water.txt了。
下面,我們開始做能量分解分析。將water.txt拷到當前目錄下(如果你通過雙擊方式啟動Multiwfn程序就拷到Multiwfn目錄下),然后依次輸入
dimer.mol //含有二聚體結構信息的文件(如果你優化二聚體時保留了fch文件,載入fch文件當然也可以)
21 //能量分解
1 //基于力場的能量分解
3 //載入原子類型和原子電荷
mollist.txt //分子列表文件的實際路徑。此時程序就會從mollist.txt所記錄的當前目錄下的water.txt中讀取原子類型和電荷,賦到當前體系中的兩個水分子上
2 //定義片段
2 //將定義兩個片段
1-3 //片段1包含的原子序號
4-6 //片段2包含的原子序號
如果想確認一下已定義的片段中的原子電荷和原子類型是否已經確實設好了,可以選選項4看一眼,輸出為
*** Fragment 1:
Atom: 1(O ) Charge: -0.737121 Type: OW
Atom: 2(H ) Charge: 0.368560 Type: HW
Atom: 3(H ) Charge: 0.368560 Type: HW
*** Fragment 2:
Atom: 4(O ) Charge: -0.737121 Type: OW
Atom: 5(H ) Charge: 0.368560 Type: HW
Atom: 6(H ) Charge: 0.368560 Type: HW
可見原子類型和電荷都是正確的。
然后我們選選項1就可以分析了,一瞬間就輸出了結果,如下所示:
Contribution of each atom in defined fragments to overall interfragment interac
tion energies:
Atom 1(O ) Elec: 12.53 Rep: 3.85 Disp: -2.21 Total: 14.17
Atom 2(H ) Elec: -6.24 Rep: 0.00 Disp: 0.00 Total: -6.24
Atom 3(H ) Elec: -16.87 Rep: 0.00 Disp: 0.00 Total: -16.87
Atom 4(O ) Elec: -23.52 Rep: 3.85 Disp: -2.21 Total: -21.88
Atom 5(H ) Elec: 6.47 Rep: 0.00 Disp: 0.00 Total: 6.47
Atom 6(H ) Elec: 6.47 Rep: 0.00 Disp: 0.00 Total: 6.47
Interaction energy components between all fragments:
Electrostatic Repulsive Dispersion Total
Frag 1 -- Frag 2: -21.15 7.71 -4.43 -17.87
輸出的單位都是kJ/mol。以上信息顯示,兩個水分子間總相互作用能為-17.87 kJ/mol,這個值和CCSD(T)/CBS算的高精度結果(見S66測試集原文J. Chem. Theory Comput., 7, 2427 (2011))給出的-20.58 kJ/mol雖然有一定誤差,但是已經比較接近了,至少用于定性討論是絕對夠的,對于非常廉價的分子力場來說能算到這樣的精度也算不錯了。以上數據也指出靜電作用對水分子的結合產生了決定性的貢獻,貢獻高達-21.15 kJ/mol,因此毫無疑問這種一般強度的氫鍵的主要本質就是靜電作用(有些文章做一大堆軌道分析基本都是鬼扯,完全沒弄清楚主次)。色散作用也產生了貢獻,但相對次要。而交換互斥作用則在一定程度上抵消了靜電和色散產生的吸引作用。
在S66測試集的原文中,作者通過DFT-SAPT方法給出的水二聚體的色散作用能與靜電作用能的比值為0.29,我們基于力場算出來的是4.43/21.15=0.21,也算與DFT-SAPT的結果定性相符。因此從水二聚體這個簡單體系可見,只要用的力場和原子電荷合適,基于經典力場的能量分解一般還是靠譜的。力場計算結果和量化計算結果相符這么好的情況其實也比較有限,有時候差得不少,但即便如此,基于力場的能量分解給你的靜電/交換互斥/色散的比值還是有非常有意義的。甚至于比如你用基于力場給出的靜電相互作用能與總相互作用能的比值乘上量子化學算出來的結合能作為真實的靜電作用能的近似估計,在我看來也未嘗不可。
以上輸出的信息也告訴了你各個原子對片段間相互作用的貢獻,便于你認清哪些原子對片段間結合起到關鍵影響。如果你定義了N個片段,則給出的就是各個原子對這N個片段間相互作用能的貢獻。所有原子貢獻值加和等于總相互作用能(假設體系就有兩個原子A和B,且各自定義為一個片段,那么這里給的A原子的貢獻就相當于A-B之間相互作用能的一半)。由上面給出的數據可見每個原子的影響都不容忽視,畢竟體系里各個原子間距離都不遠。對吸引作用產生最大貢獻的是O4原子對應的靜電作用(-23.52),而O4正是氫鍵受體原子,所以這個結果很容易理解。作為與O4直接發生氫鍵作用的H3也通過靜電作用對結合產生了很大貢獻(-16.87)。數據里看到只有氧原子的Rep和Disp不為0,這是因為HW這種氫的原子類型對應的范德華勢阱參數為0,力場刻意忽略它對范德華作用的貢獻(這是有原因的),而只表現它的靜電作用。
如果你在能量分解界面里選擇一次選項-3將其狀態從默認的No切換成Yes,之后再選1進行分析時,程序會把片段間每一對原子的距離(埃)、相互作用能(kJ/mol)及其成份都輸出到當前目錄下的interatm.txt中,本例的此文件內容為
******* Between fragment 1 and fragment 2:
Atom_i Atom_j Dist(Ang) Electrostatic Repulsive Dispersion Total
1 4: 2.873 262.78 7.71 -4.43 266.05
1 5: 3.176 -118.86 0.00 0.00 -118.86
1 6: 3.176 -118.86 0.00 0.00 -118.86
2 4: 3.346 -112.79 0.00 0.00 -112.79
2 5: 3.762 50.16 0.00 0.00 50.16
2 6: 3.762 50.16 0.00 0.00 50.16
3 4: 1.916 -197.02 0.00 0.00 -197.02
3 5: 2.312 81.64 0.00 0.00 81.64
3 6: 2.312 81.64 0.00 0.00 81.64
從以上數據會發現,其實每一對原子間相互作用能都很大,關鍵來自于靜電相互作用。比如兩個氧原子O1和O4,由于電荷相同,而且數值不小,離得又近,因此靜電互斥能高達262.78 kJ/mol。由于計算片段相互作用能時,原子間靜電相互作用項很大程度正負抵消,因此片段間靜電相互作用能,以及原子對片段間結合能的貢獻量看起來數量級都遠沒有上面那么大。
3.2 circumcoronene與鳥嘌呤-胞嘧啶的三聚體
在J. Chem. Theory Comput., 9, 3364 (2013)一文給出的L7弱相互作用測試集中,有一個體系是circumcoronene(以下簡寫為C3)與鳥嘌呤(G)和胞嘧啶(C)的三聚體,以下簡稱為C3GC,其補充材料里給的結構已經在TPSS-D/TZVP級別下優化過了,如下所示。本節我們就對這個體系基于AMBER力場做一下能量分解分析,相關的文件都在本文文件包里的C3GC目錄下。
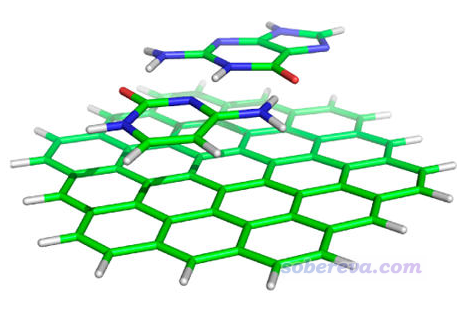
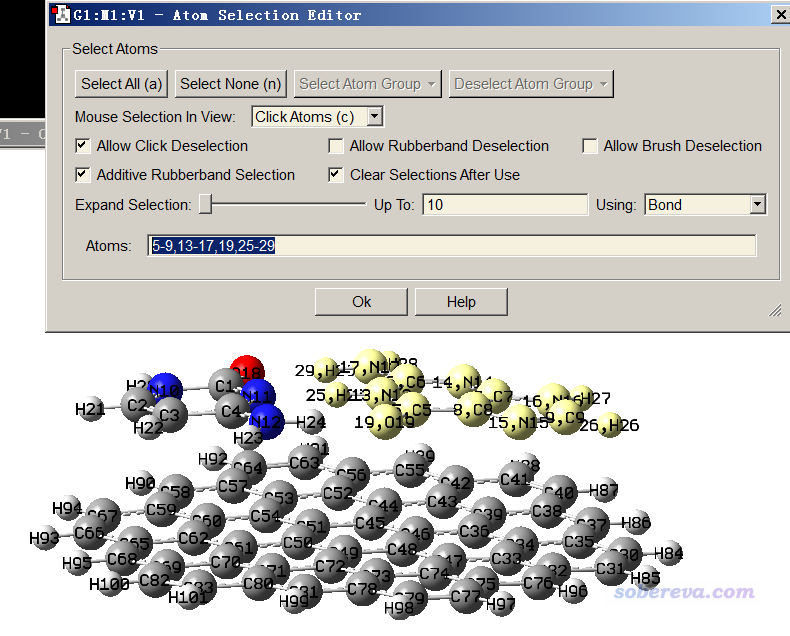
只有當所有類型分子里原子序號都是連著的時候,才能用Multiwfn做基于力場的能量分解計算,否則沒法通過分子列表和分子類型文件對體系中各個原子設定電荷和原子類型。L7弱相互作用測試集的原文里補充材料里給的結構文件是C3GC.xyz,這個文件沒法直接用,因為這里面單體里原子的序號不是連著的。怎么判斷是不是連著,可以在可視化程序里把原子序號顯示出來考察,但肉眼挨個看編號有時候比較累,最簡單的判斷方法如下:先把C3GC.xyz載入到Multiwfn,用主功能100的子功能2的選項1將之轉換為C3GC.pdb(做轉換是因為gview不支持.xyz格式),再將此pdb文件載入到gview里,在任意一個分子的任意一個原子比如C5上點右鍵,選Select Fragments of Atom C5(從gview 6開始才有這個選項),此時這個分子的原子就都被選中了,然后點Tools - Atom Selection,此時文本框里顯示的序號是5-9,13-17,19,25-29,一看就知道序號不連著,如下所示。
那么怎么讓序號連著?方法很多,最簡單的做法是進入gview的原子列表編輯器,點擊下圖示意的按鈕
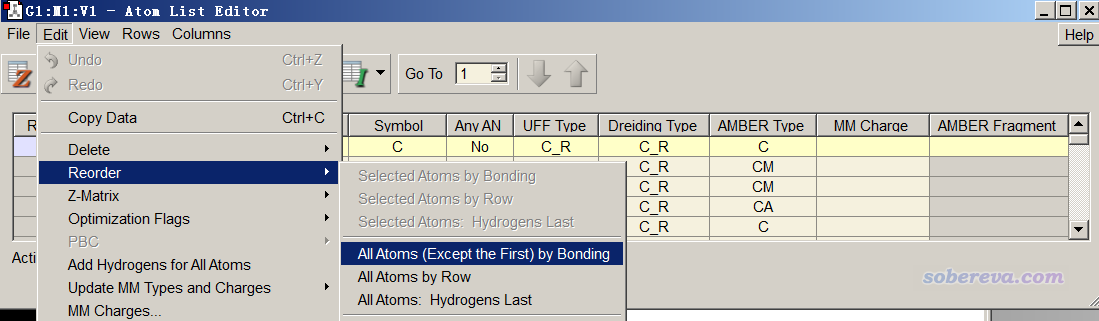
之后,圖形窗口中所有原子序號都按照成鍵關系排序了,因此這三個片段里所有原子序號就都連著了,不信的話可以按上述方法檢驗一下。當前序號如下所示,可以看到胞嘧啶的原子序號是1-13,鳥嘌呤的序號是14-29,C3的序號是30-101。
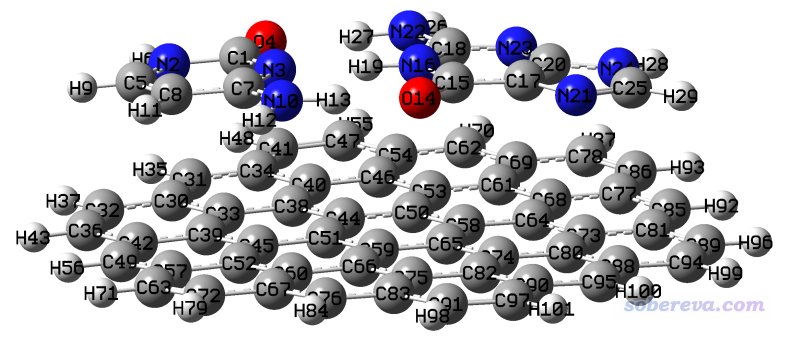
然后我們把這個序號重排好的結構保存為C3GC.pdb,覆蓋原先的同名文件,并且在gview里把各個片段分別拷到不同的新窗口里,按照上一節所說的做法把gview判斷出的AMBER力場的原子類型導出來,三個片段對應的文件分別命名為C3.txt、G.txt、C.txt。然后把每個片段都保存成.gjf文件,修改關鍵詞為B3LYP/6-311G**,用Gaussian計算它們,得到對應的.fch文件。然后按照上一節的做法把各個.fch文件放到Multiwfn里計算MK原子電荷,再把各個單體的原子電荷分別拷到C3.txt、G.txt、C.txt里面作為第二列。最終處理好的這三個文件已經提供在本文的文件包里了。
注:由于C3這個片段較大,有72個原子,計算擬合靜電勢電荷計算量也較大,因此用Multiwfn計算的時候強烈建議讓程序借用Gaussian里的cubegen工具,詳見http://www.shanxitv.org/435,此時在普通Intel 4核CPU下耗時不到3分鐘。直接在Gaussian算單點的時候順便算MK電荷也可以,加上pop=MK關鍵詞即可,同時最好寫IOp(6/42=6),否則由于擬合靜電勢過程默認用的擬合點數偏少,結果不太可靠。
最后,寫一個分子列表文件mollist.txt,內容為C3.txt、G.txt、C.txt的實際路徑和對應的分子數目(顯然都為1),并且順序必須和C3GC.pdb里記錄的分子順序完全一致,因此內容為(假設文件都放到了C:\下)
C:\C.txt 1
C:\G.txt 1
C:\C3.txt 1
現在開始做能量分解分析。啟動Multiwfn,輸入
C3GC.pdb
21 //能量分解
1 //基于力場的能量分解
3 //載入原子類型和原子電荷
mollist.txt //輸入mollist.txt的實際路徑
2 //定義片段
3 //設3個片段
1-13 //片段1包含的原子序號(C部分)
14-29 //片段2包含的原子序號(G部分)
30-101 //片段3包含的原子序號(C3部分)
PS:如提示所示,如果你要對此體系進行多次分析,嫌每次定義片段敲一遍鍵盤麻煩,設定片段數那一步可以輸入0,然后輸入含有片段定義的文件路徑。文件里每一行對應一個片段里的原子序號。
選擇選項1,分析結果如下(原子對結合能貢獻部分的輸出略)
Electrostatic Repulsion Dispersion Total
Frag 1 -- Frag 2: -120.98 60.26 -45.54 -106.27
Frag 1 -- Frag 3: 1.88 44.86 -94.69 -47.95
Frag 2 -- Frag 3: 0.71 62.08 -132.62 -69.84
數據體現出,G-C之間結合非常強,高達-106.27 kJ,主要原因在于靜電相互作用非常大,這直接源于GC之間形成了三對氫鍵。而C3和G、C之間的相互作用能也不小,這主要是由于它們之間有顯著的pi-pi堆積作用,而pi-pi堆積作用本質又是色散作用,所以可見C3-G和C3-C之間的色散作用強度很大,比起G-C之間的大多了。由于C3就是個石墨烯片,與G、C直接作用區域是明顯無極性的(即原子電荷非常小),因此C3與G、C之間的靜電作用微乎其微。
筆者也使用了計算弱相互作用比較靠譜的B3LYP-D3(BJ)/6-311+G**結合counterpoise校正對G-C、C3-G和C3-C間的結合能做了計算,結果為
G-C(Frag 1 - Frag 2):-143.97 kJ/mol
C3-C(Frag 1 - Frag 3):-56.69 kJ/mol
C3-G(Frag 2 - Frag 3):-76.27 kJ/mol
可見C3和G、C之間計算結果和基于力場算的很接近,但是G-C之間的結果差得比較多。這體現基于分子力場計算這種強度很大的弱相互作用的時候定量精度是比較有限的,此時別太拿定量數據說事,但用于討論物理成分的比例還是沒問題的,不至于有明顯誤導。
值得一提的是,由于包括AMBER在內的一般分子力場沒有考慮多體項和可極化效應,因此算出來的三個片段總結合能和1-2、1-3、2-3結合能的加和是相同的。但是實際上,如果用量子化學來計算,E(123)-E(1)-E(2)-E(3)這樣嚴格算出來的三聚化能和用三種二聚體模型算的1-2、1-3、2-3的結合能加和是不同的,因為還存在耦合項,這是通過一般分子力場所無法體現的。
pqr格式被不少可視化程序所支持,它和pdb格式很類似,但是pqr的每一行在原子坐標后面記錄的是原子電荷和原子范范德華半徑,在《使用Multiwfn+VMD以原子著色方式表現原子電荷、自旋布居、電荷轉移、簡縮福井函數》(http://www.shanxitv.org/425)一文中有詳述。將Multiwfn和VMD結合使用,可以通過對原子著色,一目了然地考察各個原子對片段間結合能的貢獻(實際上在《通過獨立梯度模型(IGM)考察分子間弱相互作用》http://www.shanxitv.org/407一文中就是用了類似策略,但IGM展現出的原子對片段間結合產生的貢獻是簡單估計出來的,明顯沒有當前的能量分解這么有物理意義)。我們在能量分解界面里選擇一次-4 Toggle if outputting atom contributions to .pqr files將之狀態切換為Yes,然后再次選擇選項1進行能量分解分析,算完之后當前目錄下就出現了atmint_tot.pqr、atmint_ele.pqr、atmint_rep.pqr和atmint_disp.pqr(這些文件已提供在了本文文件包C3GC目錄下的pqr目錄下),這四個文件中的原子電荷那一列的數據分別對應于各個原子對片段間的總/靜電/交換互斥/色散相互作用能的貢獻,和屏幕上輸出的值實際上是相同的。比如atmint_disp.pqr中片段1中的C1原子的原子電荷那一列的值就對應這個原子與片段2和片段3的所有原子的色散相互作用能的一半。將atmint_tot.pqr載入到VMD中繪制出來,設成根據Charge屬性進行著色,把色彩刻度下限和上限從默認值分別改為-50和50,把G、C部分用CPK方式顯示(selected atoms框里通過fragment 0 1來選取),把C3部分用Licorice風格顯示(selected atoms框里通過fragment 2來選取),同時把氫鍵顯示出來,把色彩變化方式設為BWR,此時圖像如下(操作細節如果不懂就參考http://www.shanxitv.org/425里面詳細描述的步驟):
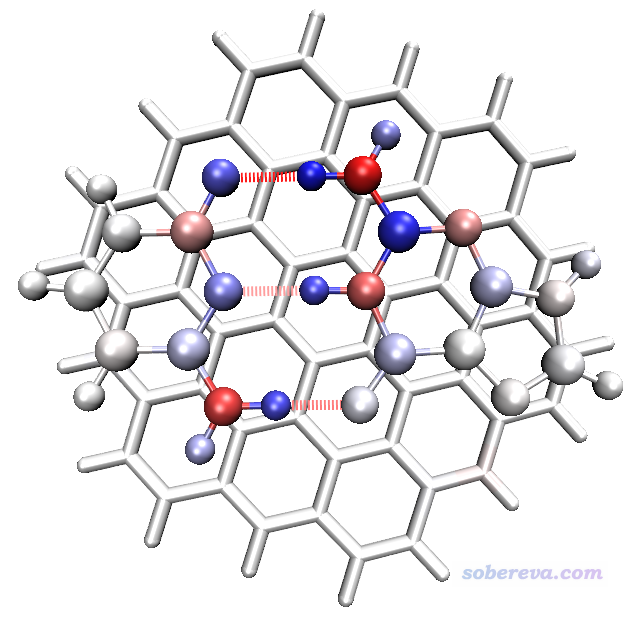
由于當前色彩刻度用的是藍-白-紅,因此圖中顏色越藍的原子,對應對總結合能的貢獻值越負(起到越顯著的吸引作用),越紅的原子則起到越顯著的互斥作用。而偏白色的原子,起到的作用就比較小了。從這個圖上一眼就可以看出,形成每條氫鍵的氫鍵受體原子和與之作用的氫原子基本上都明顯是藍色,因此對結合的穩定性貢獻極大;而氫鍵給體重原子顏色都是紅色,說明它不利于結合,這是因為氫鍵給體重原子和氫鍵受體原子都帶有較大而且符號相同的電荷,它們之間存在顯著靜電互斥作用。如果你想把細節搞得更清楚,可自行嘗試把某個氫鍵給體原子設為一個片段,然后把其它片段的所有原子設成另一個片段,再來繪制這張圖。與氫鍵作用區域比較遠的G、C的原子以及C3的所有原子顏色都比較淡,并不是它們對片段間結合基本沒起到作用,而是起到的作用相對來說太弱,因此在當前默認的色彩刻度下展現不充分。
假設我們想通過原子著色直觀地考察一下C3與GC堿基對之間的色散作用,則接著在能量分解界面里這樣輸入
2 //重新定義片段
2 //定義兩個片段
1-29 //片段1,定義為GC堿基對
30-101 //片段2,C3部分
1 //做能量分解分析
屏幕上輸出以下內容,和之前C3-G和C3-C片段數值加和相同
Electrostatic Repulsion Dispersion Total
Frag 1 -- Frag 2: 2.59 106.94 -227.31 -117.79
當前目錄下產生了四個pqr文件,這些文件已提供在了本文文件包C3GC目錄下的pqr2目錄下。把其中atmint_disp.pqr拖到VMD里,按照之前的做法顯示成原子著色效果,但是把色彩刻度設為-10到10,并且選Display - Orthographic把視角設成正交,此時看到的圖像如下
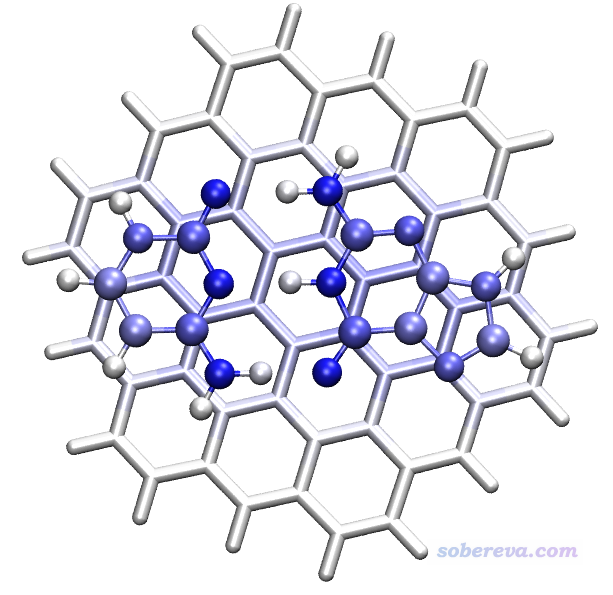
上圖中,顏色越藍的原子對C3與GC之間的色散吸引作用越大。由圖可見,GC上各個重原子對色散作用貢獻相仿佛,主要也是因為它們距離C3平面的距離都差不多,而且原子上帶的電子數也相差不太大。GC上的氫原子都貢獻微乎其微,這體現出氫原子由于帶的電子數很少,而且由于其電負性小,在實際分子中其電子往往又被吸走不少,所以產生的色散作用很小。在C3上,直接與GC接觸的那些碳的顏色呈現淺藍,說明對色散作用有明顯貢獻,而離GC比較遠的原子產生的貢獻就很小了,這也體現出色散作用隨距離衰減很快這個特點,它是隨距離r增加呈1/r^6衰減的。
注:上圖中GC上的重原子之所以很藍而C3上的對等位置的原子卻沒那么藍,是因為C3原子很多,GC上每個重原子與C3上一大片原子有色散作用,所以數值總和較大。而由于GC上本身原子數少,所以C3上每個原子只能與數目并不多的GC上的原子作用,故數值總和不是太大。如果你想讓C3部分原子顏色更凸顯一些,可以單獨把C3那個Representation的色彩刻度范圍設小一點,比如設-6到6。
肯定有讀者想到,要是能把GC之間的三個氫鍵的鍵能獨立求出來該多好。怎么實現這個目的,沒有唯一做法,這相當于對體系進行劃分。一個容易想到的做法是直接把氫鍵給體和受體部分定義為兩個片段,比如我們考察N10-H13...O14這條氫鍵,輸入
2 //重新定義片段
2 //定義兩個片段
10,13 //片段1為N10-H13...O14中的給體部分
14 //片段2為N10-H13...O14中的受體部分
1 //做能量分解分析
結果是
Electrostatic Repulsion Dispersion Total
Frag 1 -- Frag 2: 71.27 21.78 -9.40 83.65
明明氫鍵作用的作用能應該是個負值,結果卻成了正值,成了互斥作用,因此以這種劃分方式試圖求得氫鍵鍵能是明顯不靠譜的,究其原因在于靜電作用是長程作用,不能光把N10-H13...O14這一小塊區域作用考慮了而完全忽略了其余原子間的作用。筆者也嘗試了不少其它做法,雖然有的做法可以把氫鍵鍵能的數量級算對(例如把N10、H12、H13、O14原子對GC間的總結合能的貢獻量加和),但是沒法正確體現三條氫鍵的相對強度關系,主要一方面也是這因為這三條氫鍵挨得太近,互相耦合太厲害,而且極化作用明顯,還牽扯到共振輔助等電子層面的效應。如果是出現多條氫鍵且出現位點離得比較遠的情況,通過考察相應一塊區域片段間的相互作用能,還是可以說明氫鍵鍵能的。
在《DFT-D色散校正的使用》(http://www.shanxitv.org/210)一文中提到過,如果通過DFT-D3方法,用對應于完全沒法描述色散作用的泛函的零阻尼的參數來計算片段間色散校正能,那么可以近似地估計片段間色散作用。筆者通過這種做法計算了色散作用能,如下所示,括號外的是基于B3LYP參數的,括號里的是基于BLYP參數的,單位都從程序給出的kcal/mol轉化為了kJ/mol。
Frag 1 -- Frag 2: -21.67 (-26.65)
Frag 1 -- Frag 3: -71.84 (-87.78)
Frag 2 -- Frag 3: -94.60 (-115.10)
用BLYP和B3LYP的參數估算色散作用能誰更準確,沒有SAPT能量分解數據作為參照的話很難說,但無論如何,我們看到以這種方式估計的色散作用能雖然在定量上和前面通過AMBER力場給出的有不小差異,但是趨勢是完全相符的,尤其是BLYP的結果和AMBER力場算的在定量上也差得不遠。PS:實際上有人在J. Chem. Theory Comput., 13, 1638 (2017)中建議在專門擬合的特殊參數下做DFT-D3校正能計算來作為可靠的DFT-SAPT方法給出的色散作用能的近似,不過沒受到什么關注。
使用UFF做基于力場的能量分解通常不太靠譜,比如對當前體系結果為
Electrostatic Repulsion Dispersion Total
Frag 1 -- Frag 2: -120.98 848.28 -80.36 646.94
Frag 1 -- Frag 3: 1.88 52.65 -107.41 -52.87
Frag 2 -- Frag 3: 0.71 68.89 -143.58 -73.99
可見C3與G、C的相互作用比較正常,相對大小與AMBER算出來的相同,但是G-C的相互作用能居然是正值,一看成份就知道是因為交換互斥作用被嚴重高估。這不是個別現象,而是常見現象,這正是為什么我不建議通過UFF做能量分解的原因。
如果你要研究的體系特別大,比如幾百原子,從頭算方法算單點都極為困難,也因此難以得到擬合靜電勢電荷,那么可以用一些雖然非常便宜的、只依賴于幾何結構甚至只依賴于連接關系,又對靜電勢重現性依然不錯的原子電荷,比如MMFF94電荷、對擬合靜電勢電荷擬合參數的EEM電荷(Multiwfn可以計算,見手冊4.7.5節的例子和 3.9.15節的原理介紹),但是結果對靜電作用描述的準確度相比用擬合靜電勢電荷對有的體系可能會大打折扣。比如筆者嘗試過,如果用基于向B3LYP/6-31G*級別的擬合靜電勢電荷擬合參數的EEM電荷,則G-C之間的靜電相互作用能就只有-74.26 kJ/mol了,明顯偏小了。如果你研究的體系是比如蛋白質、核酸與小分子的作用,那應該通過力場直接定義的殘基的電荷拼接得到這些生物大分子的電荷,用GROMACS、AMBER等適合生物體系的動力學程序都可以給你。
3.3 18碳環與石墨烯之間的相互作用
參見《18碳環(cyclo[18]carbon)與石墨烯的相互作用:基于簇模型的研究一例》(http://www.shanxitv.org/615),里面有計算細節的描述且直接給了輸入文件。
3.4 8字雙環分子OPP與18碳環之間的相互作用
下圖出自《8字形雙環分子對18碳環的獨特吸附行為的量子化學、波函數分析與分子動力學研究》(http://www.shanxitv.org/674)介紹的筆者的Phys. Chem. Chem. Phys., 25, 16707 (2023)文章,各個原子對18碳環與主體分子OPP之間的相互作用能的貢獻通過對原子著色進行了直觀展現,對此例做EDA-FF用到的結構文件和輸入、輸出文件在本文文件包里C18_OPP目錄中提供了。另外,下圖中綠色等值面是IGMH圖,介紹見《使用Multiwfn做IGMH分析非常清晰直觀地展現化學體系中的相互作用》(http://www.shanxitv.org/621)。
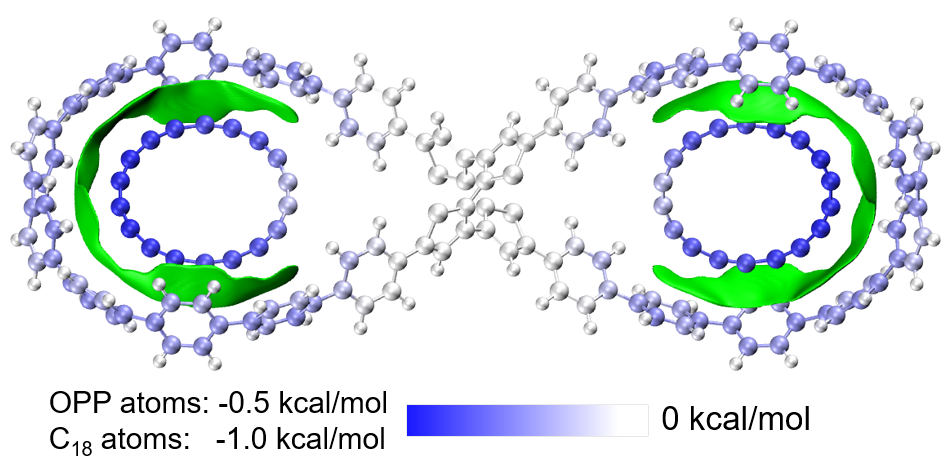
4 總結&其它
本文介紹了基于分子力場的能量分解的思想、在Multiwfn中的使用,并通過兩個典型體系展現了這種能量分解的實用價值。讀者只要舉一反三,就可以很容易地把這種能量分解用于各種體系上。希望讀者在搞清楚原理、認清基于力場的能量分解的局限性和獨特優點的基礎上,靈活、恰當地運用此方法討論實際問題。
關于做基于力場的能量分解所用的原子電荷,最后再多說幾句。對于復合物體系,在計算原子電荷時,應當使用單體在孤立狀態下的模型進行計算,因為基于這樣的原子電荷算的片段間的相互作用能的物理意義才明確,即對應的是忽略極化和電子轉移效果時候的靜電相互作用。而如果直接用復合物體系算原子電荷來做這種能量分解分析,那么算出來的靜電作用能就說不清楚到底是什么了,雖然或許從結果的數值角度來說還挺不錯。而且,用復合物結構計算擬合靜電勢電荷時,由于很多原子可能被包埋比較厲害,此時算出來的這些原子的電荷是明顯不準確的,用于計算單體間靜電作用能時會有嚴重誤導性。
擬合靜電勢電荷是明顯受構象影響的,將這種電荷用于能量分解目的時,原理上最理想的做法是直接取復合物中每個單體的結構直接計算。但是這樣做可能會比較麻煩和耗時(當然如果你以精度為重則應當不怕麻煩),比如一個體系有8個同種分子,你就得算8次,而且每個分子還得作為不同類型的分子來考慮,得分別寫分子類型文件并設定原子電荷。所以為了省事,如果體系當中這類分子的每個副本的構象差異不大,可以對同種類型分子只給一套原子電荷,因此就優化這個分子并且計算原子電荷即可,正如3.1節水分子二聚體那種。如果某些副本之間構象差異比較大,最好還是把構象顯著不同的副本當成不同的分子類型、單獨計算原子電荷為宜。(使用在《RESP擬合靜電勢電荷的原理以及在Multiwfn中的計算》http://www.shanxitv.org/441中提到的構象平均的擬合靜電勢電荷或者構象依賴性小的RESP電荷雖然看似也可以,但由于這種做法對于特定構象的分子表面靜電勢重現性會打折扣,所以不太建議在當前情況下使用)。
有用戶問為什么他用本文的方法Multiwfn給出來的單體間總作用能為正,有以下幾個可能原因,請讀者根據原理檢查
(1)體系沒在合理級別下優化,導致位阻作用太強
(2)選擇的力場不合適(比如本來能用AMBER/GAFF的情況,卻為了圖省事用了不那么理想的UFF)
(3)指認的原子類型有問題,導致有的原子的范德華參數不合理
(4)原子電荷用的不合理,導致靜電吸引強度被低估
另外也有可能靠普通力場描述當前單體間相互作用過于粗糙,比如可能有些片段間的極化作用很強、軌道相互作用不可忽視(比如強度往往挺大的帶電荷氫鍵就是這種情況,見《透徹認識氫鍵本質、簡單可靠地估計氫鍵強度:一篇2019年JCC上的重要研究文章介紹》http://www.shanxitv.org/513),此時就不適合用本文介紹的方法分析了,而應當做量子化學層面的能量分解,見此文的能量分解部分的簡述:《Multiwfn支持的弱相互作用的分析方法概覽》(http://www.shanxitv.org/252)。