18碳環（cyclo[18]carbon）與石墨烯的相互作用：基于簇模型的研究一例

18碳環（cyclo[18]carbon）與石墨烯的相互作用：基于簇模型的研究一例

文/Sobereva@北京科音  2021-Sep-18

1 前言

自從2019年Science, 365, 1299 (2019)報道在凝聚相觀測到18個碳組成的環狀體系18碳環（cyclo[18]carbon）之后，碳環類體系一直是研究的熱點，筆者做了大量研究并發表過一系列工作，匯總見http://www.shanxitv.org/carbon_ring.html，目前還有相關研究正在進行中。2020年底筆者讀到一篇Iyakutti等人發表的研究18碳環和12碳環與石墨烯相互作用的理論計算文章：Materials Science and Engineering: B, 263, 114895 (2021)。這個研究題材不錯，我卻驚訝地發現此文里的問題比《我對一篇存在大量錯誤的J.Mol.Model.期刊上的18碳環研究文章的comment》（http://www.shanxitv.org/584）里我評論的那篇文章存在的問題還嚴重得多。于是筆者很快寫了一篇文章，其中一半內容是對Iyakutti等人文章里嚴重問題的斧正，避免誤人子弟，另一半內容是我在真正合理的模型下用準確可靠的方法對18碳環與石墨烯相互作用進行探究并提出我的觀點。此文于投出去后經過長達約9個月的漫長審稿，近期已經被接收并發表：Materials Science and Engineering: B, 273, 115425 (2021) https://doi.org/10.1016/j.mseb.2021.115425。在2021年10月19日之前可以使用此鏈接免費閱覽：https://authors.elsevier.com/a/1dfyA3HXllBg4w，歡迎大家閱讀。

下面將首先對我這篇文章里的18碳環與石墨烯相互作用的研究進行介紹，包含大量使用簇模型考察吸附問題的細節和要點的說明，相關文件也給了，一定程度上也算是一篇教程，對于讀者研究類似問題會有幫助。讀者以類似此文的方法和模型做相關問題計算的時歡迎引用筆者的這篇Materials Science and Engineering: B文章的研究作為范例。之后，本文會對Iyakutti等人文章里存在的嚴重問題進行討論，以避免一些理論計算初學者以及碳環類體系的研究同行犯同樣的錯誤。

2 18碳環與石墨烯的相互作用特征

為了研究18碳環與石墨烯的相互作用，必須構建個恰當的碳環吸附在石墨烯上面的模型。這類吸附問題用CP2K、Quantum ESPRESSO等第一性原理程序通過周期性模型計算無疑是可以的，特別是用《使用Multiwfn非常便利地創建CP2K程序的輸入文件》（http://www.shanxitv.org/587）里的做法創建CP2K輸入文件非常方便。但當前體系并不太適合用第一性原理程序來做，原因有二：(1)如筆者在Carbon, 165, 468 (2020)文中所指出的，正確描述18碳環這個特殊體系必須用雜化泛函，然而雜化泛函在周期性計算時耗時頗高，而當前體系又需要用原子數很多的基底，所以算起來特別費勁 (2)第一性原理程序支持的理論方法普遍明顯少于Gaussian、ORCA等主流量化程序，選擇余地太小。所以本研究中使用量子化學程序基于簇模型，即用有限尺寸的孤立結構代替無窮延展的體系，考察18碳環在石墨烯上的吸附。下面把各種相關細節和研究結果說一下。用簇模型研究吸附問題筆者還另有一篇博文《使用量子化學程序基于簇模型計算金屬表面吸附問題》（http://www.shanxitv.org/540），感興趣的讀者可以看看，其中包含一些本文省略的信息。

為了算18碳環與石墨烯的復合結構，要把石墨烯晶胞復制延展得足夠大，保留其中一層，再恰當刪原子，最終令剩下的石墨烯片段比18碳環尺寸明顯大一圈，大一圈是為了避免邊界效應太強而導致有限尺寸的石墨烯片段不能等效表現無限延展的石墨烯。并且要考慮到18碳環在優化后可能出現的滑移，因此不要過于吝嗇石墨烯的尺寸（有些人在構建模型時太摳門，不留足夠余量。若到時候被審稿人質疑邊界效應太強，還得改模型重算，付出更多代價，得不償失）。之后將石墨烯的邊緣用氫飽和避免出現懸鍵，并對這些氫的位置進行優化使之位置合理。然后再把復合物放在石墨烯上方三點幾埃的位置（通常的pi-pi堆積距離），并且讓18碳環的中心基本對準石墨烯片段的中央，如下圖左側所示

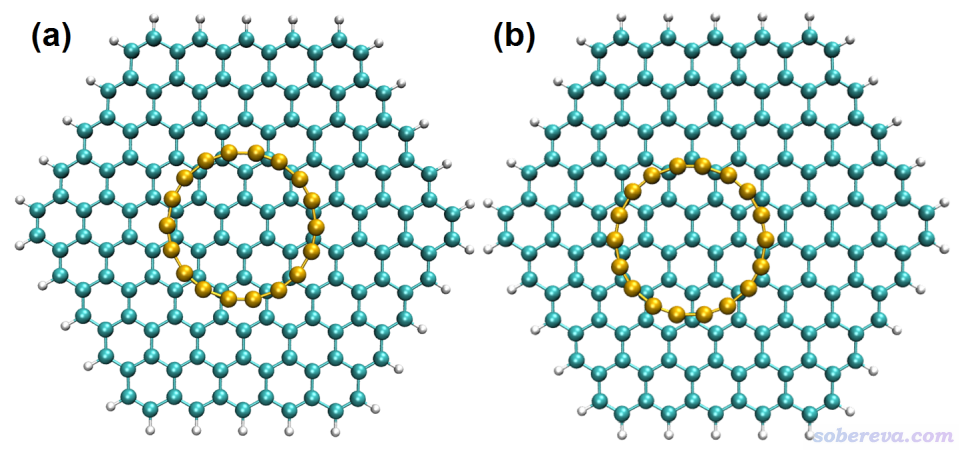
之后對復合物進行幾何優化，優化時凍結石墨烯片段邊界一圈的碳原子以及與之相連的氫原子的坐標，操作見《在Gaussian中做限制性優化的方法》（http://www.shanxitv.org/404）。之所以凍結了邊緣，是為了避免18碳環與石墨烯相互作用導致石墨烯出現變形（雖然變形程度肯定會非常低），在現實當中由于當前石墨烯片段外圍還有其它碳束縛它的結構，故這種結構變化是理應不該出現、需要人為避免的。優化出來的無虛頻的結構就是上圖右側的結構，可見碳環中心正好對著石墨烯的一個碳原子。最終的結構中的碳環相對于初始結構有了平移，但到最后它與石墨烯的邊界原子仍有足夠的距離，因此可以放心用于之后的計算。實際優化后發現18碳環與石墨烯幾乎保持嚴格平行，距離為3.334埃。優化后18碳環和石墨烯的結構幾乎都沒有發生改變，碳環里面化學鍵變化都沒有超過0.001埃，體現這種pi-pi堆積作用對幾何結構的影響非常微弱。也因此，算它們的相互作用的時候不需要刻意考慮單體的變形能。優化后的結構的xyz文件可以在http://www.shanxitv.org/attach/615/C18-graphene.xyz下載。

之后筆者計算了石墨烯片段與18碳環的高精度結合能，結果是-27.4 kcal/mol（-114.6 kJ/mol），這已經是很大的數值了，說明18碳環與石墨烯之間的pi-pi堆積作用相當強，能達到這種強度的pi-pi堆積是不多見的。在《全面探究18碳環獨特的分子間相互作用與pi-pi堆積特征》（http://www.shanxitv.org/572）里提到過，之前筆者算的兩個18碳環之間的pi-pi堆積結合能是-9.2 kcal/mol，遠不如18碳環與石墨烯之間的作用強。

要注意對碳環-石墨烯復合物的理論研究中對計算級別的選取上是非常講究的。對于體系特征、理論方法、基組、程序如果沒有充分的理解就一通瞎算，完全不可能得到有意義、令人信服的數據，所以下面將在計算級別和程序選擇方面做充分的說明，令讀者了解怎么算得又快又好。

優化和振動分析筆者使用的是Gaussian程序，因為其優化算法是幾乎所有量子化學程序里最好、最穩健的，而且在普通泛函下做振動分析的速度相對其它程序來說幾乎是最快的。優化和振動分析是在ωB97XD泛函下做的，這個泛函優化弱相互作用體系結構不錯，比較穩健，而且根據筆者之前的測試，它對18碳環的幾何和電子結構描述得都很合理，所以筆者之前發表的一系列碳環類體系的研究文章基本用的都是這個泛函。由于整個復合物原子數多達198個，而且其中碳的數目非常多，大約折合250~300原子的普通有機體系的計算量，所以即便在筆者的不算差的36核機子上也不能用的基組太大。由于石墨烯的原子占復合物的絕大部分，而且相對于18碳環來說其重要性稍低，因此就用保底的6-31G*基組（用6-311G*無疑更好，但算不動，而且對此體系的幾何優化結果的影響應當是肉眼難以察覺的程度）。18碳環是最為關鍵的部分，自然應當用比石墨烯更大的基組，即需要用混合基組算這個復合物，見《詳解Gaussian中混合基組、自定義基組和贗勢基組的輸入》（http://www.shanxitv.org/60）。根據筆者在J. Mol. Model., 27, 42 (2021)中專門做過的基組對18碳環描述能力的全面測試，至少6-311G*才能定性正確描述18碳環的結構，因此本研究對復合物中的18碳環使用質量不錯但也不過于浪費的def-TZVP基組，它介于便宜的def2-SVP和較昂貴的def2-TZVP之間，且比6-311G*略大，相關信息見《談談量子化學中基組的選擇》（http://www.shanxitv.org/336）。由于當前復合物里18碳環相對于石墨烯滑移方向的勢能面特別平緩，因此優化又難收斂、又容易出虛頻，這種情況必須非常耐心，嚴格按照《量子化學計算中幫助幾何優化收斂的常用方法》（http://www.shanxitv.org/164）和《Gaussian中幾何優化收斂后Freq時出現NO或虛頻的原因和解決方法》（http://www.shanxitv.org/278）里的做法反復折騰最終總能收斂到無虛頻的結構。另外，筆者在振動分析期間遭遇了CPHF方程難收斂問題，最終加上CPHF=grid=fine后解決。此復合物的振動分析在36核機子上花了20小時完畢，供讀者參考。振動分析的輸入文件可以在http://www.shanxitv.org/attach/615/complex_freq.gjf下載。

研究弱相互作用復合物顯然免不了要算結合能，算這么大的體系的結合能也是很講究的。算單點能首選是ORCA，里面利用RIJCOSX數值技術可以讓雜化泛函耗時巨幅降低，簡介見《大體系弱相互作用計算的解決之道》（http://www.shanxitv.org/214）。當前研究文章中筆者用的是當時最新的ORCA 4.2.1。ωB97X-V比ωB97XD算弱相互作用能明顯更準，僅次于普通泛函里算弱相互作用最好的ωB97M-V一丁點，筆者發現它做碳環類體系的SCF時往往比ωB97M-V更容易收斂。另外，ωB97X-V和ωB97XD一樣都是遠程100% HF成份泛函（見《不同DFT泛函的HF成份一覽》http://www.shanxitv.org/282），這樣的泛函對18碳環及類似物都可以正確描述。綜合這些因素，筆者算18碳環和石墨烯的結合能時用了ωB97X-V，它也是筆者在《全面探究18碳環獨特的分子間相互作用與pi-pi堆積特征》（http://www.shanxitv.org/572）當中介紹的筆者研究18碳環分子間相互作用的Carbon, 171, 514 (2021)文章里算弱相互作用能的泛函。之所以筆者沒用ωB97X-V做幾何優化，一方面是Gaussian不支持它，而支持它的ORCA做優化的算法遜于Gaussian而且振動分析速度慢，另一方面是ORCA 4.2.1不支持它的解析梯度，對當前體系優化不可能算得動。雖然從ORCA 5.0開始由于VV10色散校正有了解析導數（見《談談ORCA 5.0的新特性和改變》http://www.shanxitv.org/604），使得它做當前體系優化也能實現了，但還是沒有解析Hessian，因此振動分析根本沒法做，所以碳環類體系的優化+振動分析還是在Gaussian里用ωB97XD是首選（必須用ORCA的話，可以用比其更好一丁點的后繼者ωB97X-D3）。

在ORCA開了RIJCOSX時，普通泛函即便結合高質量基組算挺大的體系，耗時也不很高，因此算18碳環與石墨烯的結合能時筆者用了較高質量的def2-TZVP。不過，單憑這樣的基組算弱相互作用能還是差點意思的，有三種改進方式，都考慮了當然最好，至少也得考慮其一：
(1)加彌散函數。在《談談彌散函數和“月份”基組》（http://www.shanxitv.org/119）中專門說過彌散函數對于改進弱相互作用能很重要，尤其是基組沒到4-zeta檔次時。但是對當前體系加彌散函數的話沒有標配的輔助基組，而用ORCA里的autoaux自動生成輔助基組又很容易出現線性相關問題導致沒法算，遂不考慮。
(2)提升到4-zeta，如def2-QZVPP。但對于當前這么大體系，def2-QZVPP在一般條件下根本算不動
(3)考慮BSSE校正，見《談談BSSE校正與Gaussian對它的處理》（http://www.shanxitv.org/46），這對于def2-TZVP這樣沒彌散函數的3-zeta檔次基組算弱相互作用的改進是很明顯的。ORCA里可以用免費的gCP方法實現，簡介見《大體系弱相互作用計算的解決之道》（http://www.shanxitv.org/214），也可以用更嚴格但需要多花幾倍耗時的Counterpoise方式，實現方式見《在ORCA中做counterpoise校正并計算分子間結合能的例子》（http://www.shanxitv.org/542）。筆者在當前研究中采用了后者。
前面我給出的18碳環與石墨烯的結合能最終是在ωB97X-V/def2-TZVP + counterpoise組合下算的，ORCA輸入文件可以在http://www.shanxitv.org/attach/615/counterpoise.inp下載，里面用了grid6 gridx6關鍵詞提升積分格點精度使得結果更準確、SCF也更容易收斂（如果是ORCA 5.0及以后版本就沒必要寫了，默認的格點就已經夠好了）。在筆者的36核機子上此任務花了7個半小時算完。當前的結果已經基本算是時下主流雙路服務器能承受的計算耗時下最好的結果了。

光是用量子化學程序做做結構優化、算算結合能，顯然研究顯得太過于空洞。接下來就是研究弱相互作用的百寶箱Multiwfn要做的事了，其中支持大量重要的分析方法，見《Multiwfn支持的弱相互作用的分析方法概覽》（http://www.shanxitv.org/252）。筆者的文章里使用了獨立梯度模型（IGM）圖形化展現了18碳環與石墨烯的相互作用，所得圖像如下所示。此方法的介紹見《通過獨立梯度模型(IGM)考察分子間弱相互作用》（http://www.shanxitv.org/407）和《使用Multiwfn結合CP2K通過NCI和IGM方法圖形化考察固體和表面的弱相互作用》（http://www.shanxitv.org/588）。

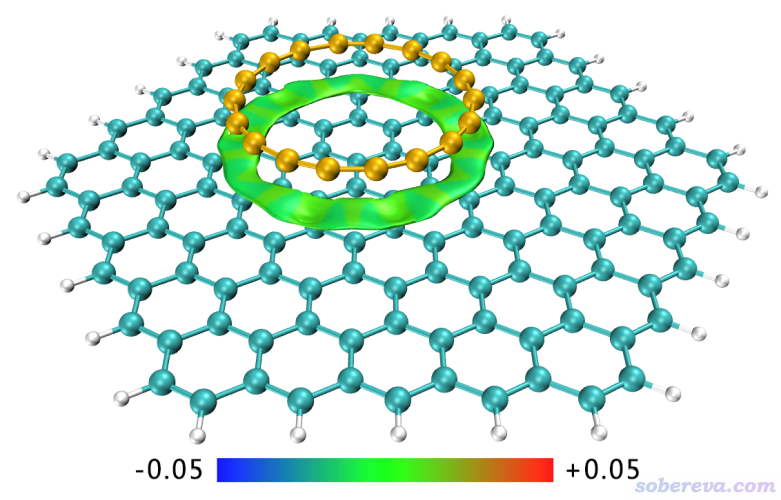
上圖中環狀綠色的IGM方法定義的δg_inter的等值面非常清晰地展現出了18碳環與石墨烯之間的pi-pi堆積的主要作用區域。等值面是根據sign(λ2)ρ函數進行著色的，等值面全是綠色代表這部分作用區域的電子密度很低，是pi-pi堆積作用的典型特征，前述的筆者研究文章Carbon, 171, 514 (2021)里的18碳環pi-pi堆積二聚體的IGM圖也是如此。

筆者之前提出了一種基于力場的能量分解分析方法EDA-FF并實現在了Multiwfn程序里，已經被不少文章所使用，詳見《使用Multiwfn做基于分子力場的能量分解分析》（http://www.shanxitv.org/442）。這個方法是基于分子力場考察片段間相互作用項，非常便宜且靈活，而且可以把每個原子對結合能的貢獻以著色方式展現，明顯便于研究者直觀考察各個原子對結合起到什么作用。EDA-FF方法也被筆者用于研究18碳環與石墨烯之間的相互作用上。這里用的力場是AMBER力場，石墨烯里的原子都用CA原子類型（對應芳香環上的碳），18碳環的原子都用CZ原子類型（對應sp雜化的碳）。原子電荷都簡單地當成零，因為18碳環里以及石墨片層中的每個碳都是等價的，顯然原子電荷都理應為0。使用EDA-FF算出來的18碳環與石墨烯間的結合能為-25.4 kcal/mol，這和我們前面用量子化學方法算的可靠的結合能-27.4 kcal/mol吻合很好，這暗示哪怕用非常簡單的分子力場，也是可以合理描述18碳環與純碳物質（除了石墨烯外，還有富勒烯、碳納米管等）之間的相互作用的，因此此文證明了以普通力場描述18碳環參與的弱相互作用的可行性，是個有意義的發現。

文中將Multiwfn做EDA-FF分析輸出的文件結合VMD可視化程序繪圖，清晰直觀地展現了石墨烯的各個原子對18碳環與石墨烯之間結合能的貢獻，如下圖所示，色彩刻度條單位是kJ/mol（注：原文有筆誤，EDA-FF部分的kcal/mol應為kJ/mol）。

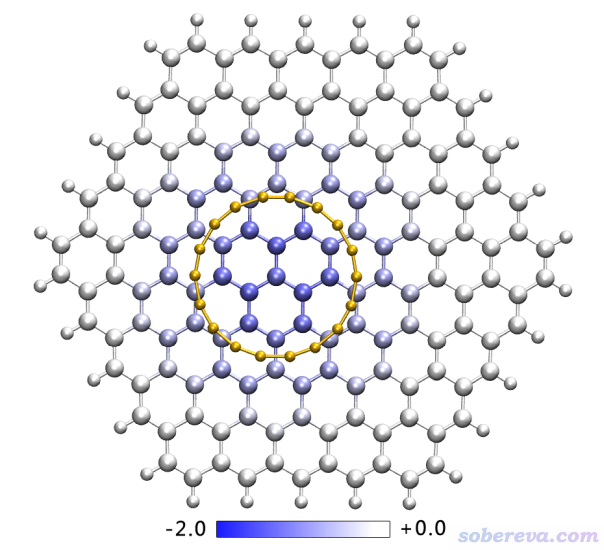
上圖中顏色越藍的原子對結合的貢獻越大，即對結合能數值貢獻越負。由圖可見越接近18碳環中心的碳原子對結合起到的貢獻越大，越往外的碳貢獻越小，石墨烯邊界的原子的貢獻都可以忽略不計。之所以越接近碳環中心的碳對結合能貢獻越大，這可以通過筆者提出的范德華勢角度予以清晰直觀的解釋，見《談談范德華勢以及在Multiwfn中的計算、分析和繪制》（http://www.shanxitv.org/551）。從此文給出的范德華勢的圖上可以看到18碳環的范德華勢在環的上、下方是最負的，自然使得處在那些區域的石墨烯原子對結合貢獻最大。還值得一提的是，從石墨烯原子對結合的貢獻這個角度上也可以證明當前用的石墨烯片段已經夠大了，倘若邊界原子也有不小貢獻的話則說明應當把石墨烯再往外擴一圈。前面是從圖形上考察，從具體數值上看，石墨烯上碳原子對結合能貢獻最大的是-1.3 kJ/mol，即上圖最藍的那個。文中也考察了碳環上的原子對石墨烯與碳環結合能的貢獻，發現數值都在-2.9~-3.0 kJ/mol這個很窄的范圍，說明每個碳的貢獻都較大且很均衡，這是因為每個碳都與石墨烯里一大片碳原子有色散吸引作用。

Multiwfn做上述的18碳環-石墨烯的EDA-FF分析用到的輸入文件和輸出結果都可以在http://www.shanxitv.org/attach/615/EDA-FF.zip下載。

3 Iyakutti等人研究文章存在的問題

前述的Iyakutti等人研究文章里面的問題實在太多，基本上看不到什么正確的內容，結論完全是誤導性的。下面說一下其中存在的一些關鍵問題。

他們用的是VASP在PW92泛函下對18碳環和石墨烯做的研究，得到的結構如下所示

一看就知道計算模型完全不合理，取的晶胞尺寸太小，明顯會導致18碳環和其相鄰鏡像存在嚴重的自相互作用。而且碳環看起來是彎曲的，有可能是優化得有問題，亦很可能是由于和相鄰鏡像距離太近導致出現了顯著互斥作用而擠彎了。

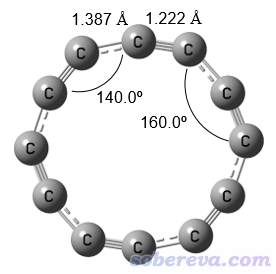
文中說18碳環是“the bond lengths are equal and the bonds are made entirely of double bonds”，這是完全錯誤的說法。在Science, 365, 1299 (2019)中都已經實驗證實了18碳環是長-短鍵交替的，估計作者連這篇文章都沒認真看過。另外，我以及其他研究者的一系列理論計算也都證明了18碳環鍵長的不均等性，在本文專門列了個表：

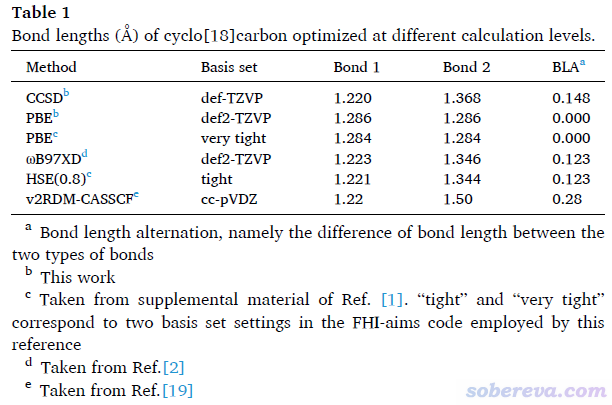
可見筆者在高精度的CCSD/def-TZVP級別優化出的18碳環是明顯長-短鍵交替的，ωB97XD/def2-TZVP的結果與之相符也較好。最近有篇文獻用高精度方法v2RDM-CASSCF算了18碳環，雖然其用的基組cc-pVDZ太爛，故定量準確度不行，但結果至少也是鍵長不相等。Iyakutti他們之所以算出來C-C鍵長都是相同的，在于他們用的是純泛函，而根據我在Carbon, 165, 468 (2020)中以及未發表的全面測試，目前沒有任何一個純泛函能正確描述18碳環鍵長交替的結構，例如上面表里的PBE下優化的結果也正是如此。值得一提的是，VASP、Quantum ESPRESSO等第一性原理程序里沒法用ωB97XD這種范圍分離泛函，用全局雜化泛函又太貴，非要用這些程序來研究18碳環及類似體系可以用修改后的近程雜化泛函HSE06，雖然它比純泛函貴得多但已經是相對最便宜的選擇了。原本這個泛函近程HF成分為25%而長程為0%，沒法正確描述18碳環，但在Science, 365, 1299 (2019)的補充材料里作者將其近程HF成份改為80%后就可以不錯地描述18碳環的結構，對應上面表格里的HSE(0.8)，可見它和ωB97XD的結果頗為一致。有的程序里可以直接自定義泛函實現HSE(0.8)，如果沒法自定義的話，若原本支持HSE06，也可以很簡單地修改源代碼來使用。

Iyakutti等人的文章里還優化了12碳環的結構，并聲稱鍵長是相同的，這也是錯誤的結論。筆者在可靠的CCSD/def-TZVP級別下也優化了12碳環，所得結構如下，可見鍵長并不是均等的，是C6h點群

Iyakutti等人的文章用的泛函不僅沒法正確描述12和18碳環本身，還完全不能正確描述碳環與石墨烯的pi-pi堆積作用。pi-pi堆積本質是色散作用，在《全面探究18碳環獨特的分子間相互作用與pi-pi堆積特征》（http://www.shanxitv.org/572）和《談談“計算時是否需要加DFT-D3色散校正？”》（http://www.shanxitv.org/413）里面我都提到過，因此計算所用的泛函必須能合理地描述色散作用才行。然而他們的文章用的泛函描述色散作用極差，還沒帶色散校正，所以優化出的結構中18碳環與石墨烯之間的距離明顯不合理，達到了3.92埃，比前文筆者在合理的級別下優化出的3.334埃大得多，而且這個距離也已經明顯超過常規pi-pi堆積距離范圍了。

最令我吃驚的是Iyakutti等人文章里關于18碳環電子組態的這段文字：
The carbon atom’s electronic configuration will be either 1s4 2s2 or 1s2 2s4. In that scenario, the acquired electronic configuration of carbon may be 1s2 2s4, resonating with 1s2 2s2 2p2.
...
This 2s4 electrons of the carbon atoms in the rings may be forming double
bonds with the two nearby carbon atoms.
...
we believe that the acquired electronic configuration of carbon might be
1s2 2s4.

他們居然以為1s、2s軌道都能占4個電子，這甚至缺乏本科程度的基本化學知識，不知Pauli不相容原理為何物。看到原文的這段時我對此文的審稿人構成更加好奇了（PS：此期刊IF目前4.0，檔次并不算低）。為了說明18碳環里碳原子的電子組態是什么樣，筆者在ωB97XD/def2-TZVP級別下做了自然布居分析（NPA），結果是1s2 2s0.9 2p3.1，更具體來說，每個2p軌道上的電子數都差不多是1，這和化學直覺相符。

另外，Iyakutti等人的文章里還把18碳環視為是由單、三鍵組成的，這是許多研究者都抱有的錯誤認識，完全忽視了電子離域性，之前我在《我對一篇存在大量錯誤的J.Mol.Model.期刊上的18碳環研究文章的comment》（http://www.shanxitv.org/584）介紹的文章里已經專門針對這個問題做了討論，這里不再累述，建議讀者一看。