在Gaussian中做限制性優化的方法
0 前言
量化計算時一般做的幾何優化叫做全優化(full optimization),與之相對的叫做限制性優化,即優化時凍結某些變量來實現特殊目的。經常有人在網上問Gaussian里怎么做限制性優化,每次都回復很麻煩,在本文就統一說一下。本文內容至少適用于Gaussian 09/16。對于有解析導數的方法,限制性優化并不會減低計算量,因為不管是否將某些變量凍結,所有原子的導數依然會照常計算,只不過其中被凍結的不會在優化過程中利用且不會納入收斂判據而已。順帶提醒一下,初學者千萬不要亂凍結,否則可能中途出錯,或者難收斂,或者結果缺乏物理意義。凍結時一定要先搞清楚目的。另外,只要是做了凍結,那么優化肯定不會收斂到全局空間極小點,而只能夠收斂到扣除被凍結變量的子空間當中的極小點去,因此用這樣的結構再做振動分析,往往會出現虛頻,這是非常正常的。
下面按照凍結的類型分別介紹做法。文中會涉及笛卡爾坐標、內坐標、冗余內坐標優化的概念,不清楚的話建議看此文中相關介紹:《量子化學計算中幫助幾何優化收斂的常用方法》(http://www.shanxitv.org/164)。
1 凍結某些原子坐標
凍結原子坐標常見有以下目的:(1)已經有了分子的X光衍射的結構,但由于只有重原子位置能準確測定(前提還是解析度足夠高的情況),氫原子位置一般只是近似/粗略加上去的,故需要凍結重原子位置而對氫原子位置進行優化
(2)研究固體表面吸附。往往利用3~4層原子表現固體表面,最底層原子一般要被凍結來表現體相結構,而其余原子允許在優化自由弛豫
(3)用簇模型研究酶催化問題。建模時把體系的活性中心摳出來后,一般要將邊界的氨基酸的骨架原子凍結,以免優化時候體系嚴重變形、坍塌
在Gaussian中可以以不同方式凍結某些原子的笛卡爾坐標,但是并沒有辦法只凍結某個笛卡爾分量。
1.1 用0、-1設置凍結
最簡單的凍結某些原子坐標的方法就是在原子名后面把要凍結的寫-1,不凍結的寫0,opt后面最好寫上cartesian。例如# B3LYP/6-31G** opt=cartesian
Title Card Required
0 1
O 0 0.00000000 0.00000000 -0.11081188
H -1 0.00000000 0.58397589 0.44324751
H -1 0.00000000 -0.58397589 0.44324751
觀看輸出文件里的軌跡,表面上看會發現兩個氫還是動了,這是因為Gaussian總是把體系調整到標準朝向下,如果對這個任務寫上nosymm關鍵詞避免此行為,則看到的軌跡中這兩個氫的位置就始終不動了。關于nosymm關鍵詞更多信息看《談談Gaussian中的對稱性與nosymm關鍵詞的使用》(http://www.shanxitv.org/297)。
上面的例子中=cartesian可以不寫,但不寫的話,程序會在默認的冗余內坐標下做限制性優化,對當前任務會使得優化所需步數多得多,而且會發現H-H的距離在最終結構和初始結構間有非常輕微的變化(屬于算法層面的很細節問題,涉及到內坐標與笛卡爾坐標相互轉換之類),因此建議還是寫上=cartesian。
當原子較多時,而且要凍的原子又不連著,手動去寫-1就比較麻煩了,此時可以用gview。比如考察一個有限長度的碳納米管里面塞入三個水的情況,假設我們想把碳納米管坐標完全凍住,只允許水被優化,那么可以在gview里把碳納米管部分選中成為黃色,如下所示
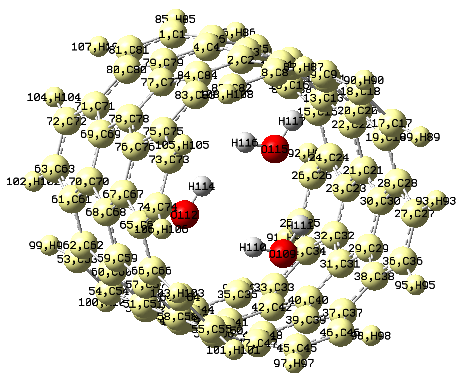
然后進入Tools - Atom Groups,把類別切換到Freeze,然后點擊Freeze(Yes)那一行中的+號把選中的區域添加到這個凍結組里。此時體系就被分為凍結和不凍結的兩個組了,如下所示
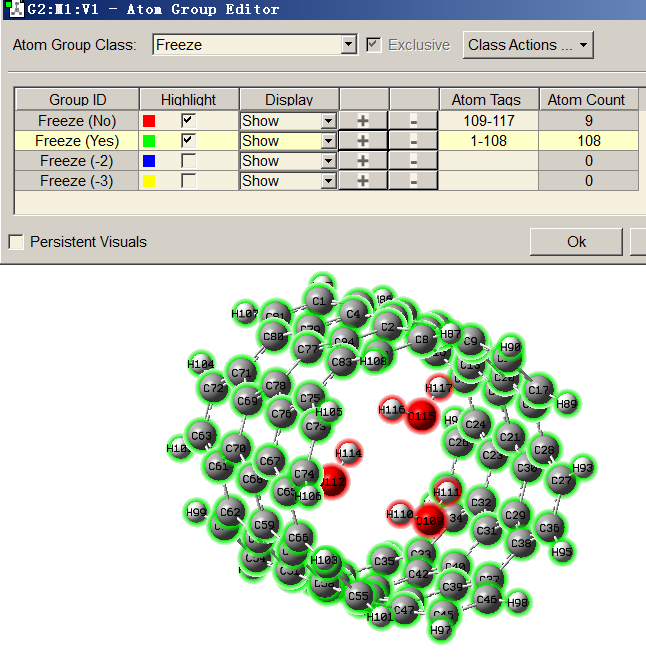
然后保存輸入文件,就會看到碳納米管部分的原子后頭都有-1,水的后頭都是0了,之后恰當設置關鍵詞計算即可。
1.2 用opt=readopt設置凍結
用opt=readopt來設置凍結往往比上一節的做法方便得多。用opt=readopt時Gaussian會建立一個被優化的原子的列表,默認情況下所有原子都在這個列表里,因此所有原子都會被優化。我們可以用notatoms把某些元素或者某些原子從被優化列表中去除,例如以下例子不會優化碳、氧,而只優化氫# PM6 opt=readopt
test
0 1
C 0.00000000 0.00000000 -0.56221066
H 0.00000000 -0.92444767 -1.10110537
H -0.00000000 0.92444767 -1.10110537
O 0.00000000 0.00000000 0.69618930
notatoms=C,O
在notatoms后面也可以直接指定不被優化的原子的序號,也可以和元素名混寫。例如上例也可以寫為notatoms=1,4或notatoms=C,4。對于大體系,如果想立刻得到某個區域的原子序號從而能夠直接寫在notatoms后面,可以在gview里將那個區域選成黃色,然后進入Tools - Atom Selection, 直接把窗口中顯示的序號信息復制到notatoms后面。
readopt里還可以用noatom把優化列表清空、用atom把某些原子加入優化列表。比如如果寫noatoms atoms=1,5-70 notatoms=N,O就代表先把被優化列表清空,然后把1,5-70原子加入,再把其中N和O元素的原子去掉。因此,最終被優化的原子就是1,5-70當中的非N,O元素的原子了。可見opt=readopt是非常靈活方便的。
用opt=readopt時實際上也是在冗余內坐標下進行的優化,而且筆者發現沒法在opt里寫cartesian改成Cartesian坐標下優化,此時一開始就會報錯。
1.3 在冗余內坐標下設置凍結
Gaussian優化默認就是在冗余內坐標下做的,用opt=modredundant時可以在末尾空一行寫上對冗余內坐標下優化額外做的修改和設定,modredundant意味著modify redundant internal coordinate。在末尾空一行處寫原子序號,后面寫個F(代表freeze),就表明這個原子被凍結,效果和原子后頭寫-1是一樣的,可以寫任意多個。下面的例子將兩個氫凍住# B3LYP/6-31G** opt=modredundant
Title Card Required
0 1
O 0.00000000 0.00000000 -0.11081188
H 0.00000000 0.58397589 0.44324751
H 0.00000000 -0.58397589 0.44324751
2 F
3 F
2 凍結某些內部變量
2.1 在內坐標下凍結
在內坐標下優化時,可以把內坐標表示的輸入文件里的一些變量進行凍結。坐標后面空一行寫的是允許被優化的變量,再空一行寫的是凍結的變量。因此下例會在優化時會保持鍵角為80度。注意opt后面必須寫z-matrix,否則優化會在冗余內坐標下進行,以內坐標方式定義的凍結就不生效了。#p B3LYP/6-31G** opt=z-matrix
constraint optimization
0 1
O
H 1 B1
H 1 B2 2 A1
B1=0.76533395
B2=0.76533395
A1=80.0
如果內坐標中有的直接寫成了數值形式,有的以變量表示,則只有變量表示的內坐標會被優化。因此下例只會優化鍵角,而鍵長始終固定在0.9埃。
O
H 1 0.9
H 1 0.9 2 A1
A1=80.0
2.2 在冗余內坐標下凍結
在冗余內坐標下設置內坐標的凍結很方便,被凍結的內坐標可以隨意定義,并不僅限于輸入文件里出現的內坐標。比如優化水分子時候讓H-H距離保持固定,可以寫成# B3LYP/6-31G** opt=modredundant
Title Card Required
0 1
O 0.00000000 0.00000000 -0.11081188
H 0.00000000 0.58397589 0.44324751
H 0.00000000 -0.58397589 0.44324751
2 3 F
如果F前面寫三個原子序號,就代表凍結這個鍵角;寫四個原子序號,就代表凍結這個二面角,而且可以寫無數多個。比如某個體系,寫了opt=modredundant,然后末尾空一行寫了
3 6 F
1 2 12 14 F
55 F
58 F
6 1 7 F
就代表優化時凍結了3-6距離、1-2-12-14二面角、55和58號原子坐標、6-1-7角度。
3 廣義化的內坐標(GIC)下設置凍結簡例
Gaussian16開始增加了GIC,可以在優化過程中比冗余內坐標做更靈活的設定。詳細說明見http://gaussian.com/opt/的GIC Info頁,本文不打算細談,只是給兩個只有利用GIC才能實現的限制性優化的例子。第一個例子是在優化中令兩個變量的差值保持恒定。addGIC代表從末尾讀取額外的GIC設定,然后定義了兩個GIC鍵長項,又定義了二者的差值項rcons,(freeze)代表令這個項在優化過程中被凍結。因此優化過程中兩個O-H鍵長的差值始終不變(此例一開始相差0.1埃,最后還是相差0.1埃)
# B3LYP/6-31g(d) opt=addGIC
test
0 1
O 0.00000000 0.04716583 0.07081661
H 0.00000000 0.69230018 -0.40226021
H 0.00000000 -0.69230018 -0.44220387
b12=R(1,2)
b13=R(1,3)
rcons(freeze)=b12-b13
第二個例子是在優化二聚體時始終保持兩個單體幾何中心距離恒定,這是氨氣與水二聚體的例子
#p PM7 opt(gdiis,maxcyc=100,addgic)
Title Card Required
0 1
N -1.51786076 -1.12768292 2.39707540
H -1.11590788 -2.26462122 2.39707540
H -1.18452166 -0.65628274 3.21357213
H -1.18452166 -0.65628274 1.58057866
O -1.16213343 -0.15012738 6.00166916
H -0.20213343 -0.15012738 6.00166916
H -1.48258801 0.75480845 6.00166916
XC1=XCntr(1-4)
YC1=YCntr(1-4)
ZC1=ZCntr(1-4)
XC2=XCntr(5-7)
YC2=YCntr(5-7)
ZC2=ZCntr(5-7)
F1F2(freeze)=sqrt[(XC1-XC2)^2+(YC1-YC2)^2+(ZC1-ZC2)^2]*0.529177
可見用XCntr、YCntr、ZCntr可以把某個片段的幾何中心的X、Y、Z坐標定義為GIC變量從而在之后被引用。在定義GIC變量時可以使用數學運算符和簡單數學函數,此例我們把將兩個單體幾何中心間的距離定義為了F1F2變量,并且將狀態設成了freeze,故優化過程中只有單體內部結構發生變化,而單體幾何中心間距離始終不變。優化過程中GIC變量的數值會在輸出文件中體現,由于GIC默認輸出的是原子單位,因此例子中乘了0.529177把Bohr轉化成常用的埃來輸出。
GIC看起來很好很強大,但是也不要太有過高的期待,因為用限制項設多了或設復雜了很容易運行中途報錯。
4 沒有解析梯度時的優化
沒有解析梯度的理論方法做幾何優化時,用的是EF算法優化(而且沒法改成別的)。由于此時是通過有限差分方式計算受力,耗時很高,而且每一步的耗時正比于被優化的變量數,因此程序要求用戶必須明確指定哪些變量要被優化,被優化的變量要寫成變量形式。下例在沒有解析梯度的CCSD(T)級別下優化水分子,只優化兩個氫的Z坐標#p CCSD(T)/def2TZVP opt nosymm
niconiconi
0 1
O 0.00000000 0.00000000 0.11930801
H 0.00000000 0.75895306 Z2
H 0.00000000 -0.75895306 Z3
Z2=-0.43723204
Z3=-0.40723204
上面例子寫成內坐標形式當然也可以。如果坐標部分寫成下面這樣沒有變量表示的情況
O 0.00000000 0.00000000 0.11930801
H 0.00000000 0.75895306 -0.43723204
H 0.00000000 -0.75895306 -0.40723204
則程序會認為要被優化的變量數為0,由于沒事可干,會直接報下面的錯誤:
************************************************
** ERROR IN INITNF. NUMBER OF VARIABLES ( 0) **
** INCORRECT (SHOULD BE BETWEEN 1 AND 50) **
************************************************
這個提示也顯示了,EF算法優化的時候,被優化的變量最多只能有50個。