談談Gaussian中的對稱性與nosymm關鍵詞的使用

談談Gaussian中的對稱性與nosymm關鍵詞的使用

文/Sobereva @北京科音

First release: 2015-Jun-27   Last update: 2021-Nov-21

經常有人問Gaussian中的nosymm關鍵詞怎么用、什么時候用，網上也有很多帖子、資料都涉及nosymm，但是很多都明顯錯誤，誤人子弟。還有很多人亂用nosymm，不僅沒什么意義還白浪費了大量時間。故寫此文澄清一下nosymm的用法，以正視聽。

1 關于利用對稱性

為了更好地理解nosymm，首先說說對稱性問題。

沒對稱性的分子所屬點群就是C1，有對稱性的分子則屬于比C1更高階的點群。量化計算中電子積分的計算是很耗時的部分，對于有對稱性的分子，要算的電子積分中會有很多是等價的，利用對稱性的話就可以避免計算大量重復的積分，從而大大節約時間。一些計算在其它部分也能利用對稱性顯著節約時間，如積分變換、導數計算等，而且不光能節約時間，很多時候還能顯著降低對內存/硬盤的占用。對稱性越高的體系，利用對稱性可以帶來越多的加速，例如用XEON E5-2650v2 16核+G09 D.01在CCSD(T)/def2-TZVP級別下計算面對面構型的苯二聚體單點能，在實際的D6h點群下（這屬于很高階的點群）計算只用一個半小時，而不啟用對稱性的話則需要多達兩天半才能算完。

啟動對稱性還有個好處是Gaussian可以顯示出軌道、電子態、振動模式的不可約表示。如果不啟用對稱性，即總是當成C1對稱性來算，即便體系本身有對稱性，不可約表示也會都顯示為A，此時軌道的不可約表示就只能基于等值面圖判斷、電子態的不可約表示需要自己再對占據軌道的不可約表示做直積得到、振動模式的不可約表示也只能基于正則振動坐標的箭頭圖來判斷了，這就麻煩多了。另外，允許程序利用對稱性，且正確判斷出了實際點群的時候，還可以確保不同不可約表示表示的分子軌道在SCF過程中不發生混合，這對于考察一些問題以及SCF收斂有時會有幫助。

由于利用對稱性時有上述優點，所以Gaussian默認是啟動對稱性的。計算一開始時會自動根據一定算法和閾值判斷輸入文件里分子的點群。比如苯分子，如果輸入文件里的結構完全或幾乎滿足D6h對稱性，那么Gaussian就會把它判斷為D6h對稱性，并按照D6h的情況來做后續計算。如果輸入文件里的結構偏離D6h略明顯，但接近其它更低階的點群，就會被判斷為更低階的點群，比如C2v，也可能完全判斷不出對稱性，即判斷為C1。

輸入文件里的坐標稱為輸入朝向（Input orientation）。Gaussian為了判斷和利用對稱性，會先把輸入文件里的坐標調整到標準朝向（Standard orientation）下，然后再進行點群的判斷及后續的各種計算。這個調整過程會把體系進行平移，使原子核電荷中心處于笛卡爾坐標原點，并且根據一定規則對體系進行旋轉，具體規則這里不細談，感興趣的讀者可以看手冊里Standard Orientation Conventions這一節的介紹。例如，在計算苯分子的時候，如果你在gview里把分子擺成歪斜著并且中心偏離原點，若在計算過后用gview打開輸出文件，就會看到分子已經處在了XY平面，并且苯分子中心被挪到了笛卡爾坐標原點，這就是苯分子在標準朝向下的坐標。值得一提的是，哪怕體系沒有對稱性，即C1點群，Gaussian也會照樣把體系弄到標準朝向下導致體系被平移和旋轉。下面是一個示意圖

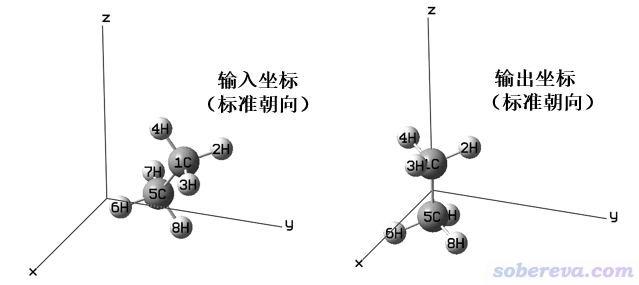
將體系弄到標準朝向會帶來一些麻煩的問題。有些時候，我們必須要求體系的位置和朝向是和輸入文件里一致的。比如，我們要沿著某個鍵的鍵軸加用field關鍵詞外電場，我們設好了外場矢量，但是如果體系朝向被Gaussian旋轉到標準朝向了，那么外電場的方向就不合我們的意愿了（除非輸入文件里的坐標已經是標準朝向的坐標），顯然結果無意義。再比如，我們按照《使用Multiwfn作電子密度差圖》（http://www.shanxitv.org/113）用Multiwfn作二聚體和兩個單體之間的密度差圖來考察單體形成復合物后電子是怎么轉移的，這就要求復合物里面的坐標和單體中的坐標完全一致。如果在計算中允許Gaussian自動把體系平移旋轉，那么最后得到的單體及復合物的.wfn/wfx或.fch文件中，單體的原子坐標和它在復合物里的坐標就不對應了，顯然密度差圖也就毫無意義了。Multiwfn里作CDA分析（《使用Multiwfn做電荷分解分析(CDA)、繪制軌道相互作用圖》http://www.shanxitv.org/166）和ETS-NOCV分析（《使用Multiwfn通過ETS-NOCV方法深入分析片段間的軌道相互作用》http://www.shanxitv.org/609）也同樣要求整體和片段中的原子坐標必須對應。

2 nosymm的用處

理解了上面關于對稱性的討論，就很容易理解nosymm的帶來的好處和壞處了。nosymm的含義是：讓Gaussian在計算中完全不利用對稱性。

nosymm的用處1：用了nosymm后Gaussian就不會再試圖去判斷和利用對稱性，因此也就不會把體系搞到標準朝向下，這就確保了實際計算過程中的坐標和輸入文件里的坐標一致，從而可以避免前面說的諸如外加電場、作密度差圖、CDA、ETS-NOCV分析時遇到的問題，所以做這些任務的時候總要加上nosymm。

nosymm的用處2：做幾何優化、柔性掃描的時候，Gaussian會把每一步的坐標都調整到標準朝向，這往往導致笛卡爾坐標變化不連續（但內坐標變化是連續的），導致在GaussView里觀看優化、掃描軌跡過程中體系朝向會發生劇烈跳變，從而難以考察結構變化過程。解決方法有二，其一就是用nosymm，這樣優化的每一步的結構都不會被弄到標準朝向下，而只會輸出Input orientation坐標，gview也只會讀這些坐標，優化/掃描過程的軌跡看起來就連續了。其二就是不讓gview去讀取每一步的standard orientation坐標（默認情況）而改為讀取input orientation坐標，方法見此文《觀看Gaussian優化軌跡時避免結構跳變的方法》（http://www.shanxitv.org/289）。

nosymm的用處3：nosymm還有個情況也應該加，也就是做對稱破缺計算的時候（詳見《談談片段組合波函數與自旋極化單重態》http://www.shanxitv.org/82），如果體系本身是有對稱性的，那么加上nosymm往往才能得到對稱破缺態。比如將乙烯扭轉到90度讓pi鍵被破壞，此時是雙自由基狀態，如果直接用UB3LYP/6-31G* guess=mix可能因為波函數對稱性的約束還是得到閉殼層波函數，而加了nosymm就可以得到雙自由基狀態了。

nosymm只有以上三個用處，如果你的情況不屬于這三個，就別用nosymm！！！對于有對稱性的體系，用nosymm帶來的壞處是很明顯的，首先是不能利用對稱性來加速計算，其次是沒法顯示不可約表示。有些人不懂nosymm有什么用就總是盲目地寫上nosymm，往往沒帶來任何益處，當體系有對稱性時還因此白浪費了大量計算時間。我總是向初學者強調：如果不清楚某些關鍵詞是干什么的，就一律不要寫！！！ 沒看過此文的話建議看看：《常見的多余的和被濫用的Gaussian關鍵詞》（http://www.shanxitv.org/331）。

3 關于幾何優化中維持/破壞對稱性

經常有人問在Gaussian的幾何優化中怎么維持對稱性、怎么破壞對稱性，這里明確說一下。首先弄清楚兩個事實：

（1）在默認的允許利用對稱性時，即便優化一開始把體系判斷成了高對稱性，優化過程中也可能對稱性發生降低甚至變為完全沒有對稱性。原因要么是因為當前計算級別下低對稱性的能量更低，有可能由于一些數值層面的問題破壞了對稱性（用彌散函數時容易出現此問題，DFT格點積分精度不夠高時也可能會出現此問題，尤其是對M06-2X這種對積分格點精度要求高的泛函來說。參考《密度泛函計算中的格點積分方法》http://www.shanxitv.org/69）。

（2）在使用nosymm禁止使用對稱性時，一開始的高對稱性結構也依然可能繼續保持下去。例如，計算D3h對稱性的NH3（原子都處在同一平面，呈正三角形），即便寫了nosymm，最后優化出來還是D3h結構，這是因為體系中原子都處在一個平面上，優化過程中受到向平面外的力的分量為0，因此會平面結構會一直保持。

所以，對稱性是否會在優化中改變，或者說對稱性是否會被限制在初始對稱性下，和是否使用nosymm沒必然的關系。

如果你想在優化過程中100%保證對稱性肯定不發生改變，唯一做法是用內坐標描述結構，而且根據對稱性來寫內坐標，使得對稱等價的坐標共享相同的變量（比如苯，讓六個C-C鍵都共享一個鍵長變量），且優化的時候用opt=z-matrix讓Gaussian在內坐標下優化。當然，這么按照對稱性寫內坐標對于原子數較多的體系是很麻煩的事情，往往還要借助虛原子。PS：雖然Gaussian里有IOp(2/16=2)可以讓優化過程中對稱性發生改變時沿用舊對稱性，但實際發現不怎么奏效。

對于有對稱性的體系的計算，一般的考慮方式是：先讓初始結構在gview里做對稱化成為你期望的點群，然后用Gaussian優化，查看輸出文件確保任務最開始時判斷對了實際點群（如果沒判斷對，用symm=loose）。如果優化過程中點群發生了不希望的降低，且你用了彌散函數，把彌散函數去掉重新優化看看；對于DFT，可以進一步提升積分格點精度再試（如G09的用戶可以加int=ultrafine試試，G16的用戶可以加int=superfine試試）。如果重新優化后對稱性還是出現了下降，換成其它你覺得對此體系也靠譜的泛函，也可以嘗試不依賴于積分格點的MP2（前提是適合當前體系）或CCSD（量力而行）。如果對稱性還是下降了，那么有極大的可能性高對稱性結構確實是不穩定的，最后收斂到的低對稱性的結構才是真正的極小點，因此此時若非要保持高對稱性則結果沒有物理意義。如果最后雖然判斷出的對稱性下降了，但肉眼觀看結構時發現和高對稱性的結構幾乎看不出什么區別，那么你就當這個結構是高對稱性的結構即可，寫文章時也可以說它是有高對稱性的，對稱性的下降可能只是一些很trivial的數值因素引起結構的十分細微的變化，無需在意（之后你甚至可以再做個對稱化變成高對稱性后直接算后續的單點之類任務）。

如果你刻意允許優化過程中對稱性發生變化從而避免被限制在初始的對稱性（因為初始的對稱性可能不一定是實際極小點結構所具有的），一般做法是人為破壞初始結構中的對稱性。比如一個平面體系，你懷疑實際結構不是平面的，那你就隨便稍微扭曲其中的一個二面角，或者利用《Multiwfn中非常實用的幾何操作和坐標變換功能介紹》（http://www.shanxitv.org/610）里介紹的功能產生對所有原子隨機位移后的結構，這樣初始結構就沒有對稱性了，優化時也不可能被強行維持在有對稱性的結構上。如果優化后肉眼上看結構又自發變得有對稱性了，那就是說明此體系在當前級別下極小點結構就是有對稱性（如果你是講究的人，建議對稱化后再重新做優化，結構精度會稍微更高，還能同時給出不可約表示）。另外，你也可以先對有對稱性的結構直接做幾何優化+振動分析，如果發現優化后的結構仍有對稱性但是有虛頻，且虛頻的振動模式是會導致對稱性方式破壞的，就按照虛頻模式稍微調節一下結構然后繼續優化，通常得到的就是無虛頻且對稱性比之前更低的實際極小點結構了。

4 其它問題

有人問symm=loose、veryloose是干嘛的。前面提到了，Gaussian會通過一定算法和閾值來根據輸入文件里的坐標判斷體系的點群。默認的判斷標準比較嚴，即坐標稍微有些偏離點群對稱性，就認不出來相應的點群。這有時候會帶來些麻煩。比如說，在gview里，選擇自帶的庫里的C60，將它對稱化后會看到被gview識別成了Ih點群，但是保存成Gaussian輸入文件，然后在Gaussian計算時就會發現被Gaussian判斷成了C1點群（也可能判斷成別的，和版本有關）。這是因為輸入文件里的笛卡爾坐標數值精度有限，我們需要用稍微寬松一點的判斷標準，即symm=loose關鍵詞，才能讓Gaussian判斷出它的實際點群Ih，此時計算速度和C1時完全不在一個數量級。symm=veryloose代表使用更寬松的判斷標準。

另一個流行的量子化學程序ORCA不會利用對稱性加速計算，因此也不會像Gaussian那樣把體系弄到標準朝向下，因此沒有類似nosymm這種用途的關鍵詞。也有其它一些程序有類似于Gaussian的做法，比如PSI4程序也會自動把體系搞到標準朝向下，如果想實現nosymm的效果，需要寫nocom要求不允許平移，以及noreorient不允許旋轉朝向，例如：
molecule MOL {
nocom
noreorient
C      0.00000000   -0.74034185    0.01363083
H      0.87837906   -1.12996571   -0.50403292
...
}