密度泛函計算中的格點積分方法

密度泛函計算中的格點積分方法

文/Sobereva @北京科音
First release: 2010-SEP-3  Last Update: 2011-Aug-23

本文主要介紹密度泛函計算方法中的一個重要部分--格點積分方法，并給出具體的Fortran代碼，同時討論與之相關的問題。

1. 簡介

在密度泛函(DFT)計算中，在計算交換相關能時，需要做這樣一個積分Exc[ρ]=∫ε(ρ(r))dr，積分是對全空間進行的。在Hartree-Fock計算中涉及的單、雙電子積分都是通過復雜推導，使積分充分簡化，再進行精確數值積分。而Exc[ρ]這個積分不得不直接求解，以容忍一定的積分誤差和效率的降低為代價。這一方面是由于ε(r)的函數形式往往十分復雜，難于通過推導簡化；另一方面是交換相關泛函種類太多，目前就有百余種，如果使用一個通用的積分方法，以后新的交換相關泛函就能容易地加入程序中。另外，這個積分在其它計算中也常用到，比如電子的熵也可視為ρ(r)的泛函，獲得它要計算S[ρ]=∫(ρ(r)/N)Ln(ρ(r)/N)dr，其中N是體系總電子數。這類積分不僅理論意義重要，在實際中也明顯影響DFT計算的速度，有不少文章對其計算方法進行了研究，試圖尋找又快又準的方法，目前用得最多的方法就是本文要介紹的格點積分方法。

后文內容涉及數值積分的知識，若不了解，建議先看看數值方法書的插值求積方法部分，高斯積分在本文末的附錄進行了介紹和討論。

2. 積分的轉化

對這個積分，Becke在1988年提出了一種很好的解決辦法[JCP 88,2547]，也是本文主要介紹的。后來又有人做過諸多改進以提高效率，但是基本原理沒有改變。在更早之前雖然也有人對求解這類積分做過研究，比如AIM分析中的一些積分原子盆內函數值的算法，但用在DFT計算中效率都太低。

如何更有效率地積分一個函數，要分析函數本身的特點。交換相關泛函的行為主要決定于ρ(r)的行為，例如形式最簡單的交換泛函就是Slater提出的，被積函數為ρ(r)^(4/3)。為了簡便，下面直接將ρ(r)作為被積函數來討論。孤立原子電子密度在原子核處存在cusp，在核附近也很大，隨著與原子核距離的增加近似呈指數衰減。在形成分子后，雖然電子密度發生了變形，但仍然可以用孤立原子電子密度的疊加來近似表達。即是說，雖然積分是全空間的，三個維度積分范圍從負無窮到正無窮，但原子附近的區域需要更高的積分精度，所以直接使用笛卡爾坐標積分是很不明智的，最佳方法是以原子核為中心通過球極坐標積分，使原子附近有較高的積分格點密度，使更重要區域被更準確地積分。

當然，直接對每個中心進行球極坐標積分會使積分區間重復。最容易想到的解決辦法是將分子空間劃分為一個個原子空間，逐個積分再加和，于是可以將∫F(ρ(r))dr寫為∑[i]∫W_i(r)*F(ρ(r))dr，W_i(r)決定了哪些區域屬于第i個原子。劃分的標準并不唯一，最簡單的是通過Voronoi多面體方式劃分，二維情況如下圖所示：

在每兩個原子間做中垂面，圍出來的一個個多面體就是原子的空間。當然，垂面的位置也可以根據原子半徑進行一定調整。對于這種離散的劃分方法，在積分第i個中心時：
W_i(r)=1  當r處于i原子空間內
W_i(r)=0  當r處于i原子空間外

但是這種離散的劃分在實際計算中有所不妥，因為下一節介紹的單中心積分最適合光滑、連續的函數，而這種劃分得出的被積函數W_i(r)*F(ρ(r))在被截處呈階梯狀，不滿足這個條件，所以積分并不準確。Becke提出的是模糊的劃分方法。首先考慮雙原子情況，編號一個為a一個為b，以a為參考原子，定義μ(a,b)=(r_a-r_b)/R(a,b)，其中r_a、r_b分別為空間某點到a、b原子核的距離，R(a,b)是a,b原子核間距離。所有μ(a,b)=0的點，即所有r_a=r_b的點，構成了a,b原子間中垂面，在a原子這半邊-1<=μ<0，在b原子這半邊0<μ<=1。如果以r處的μ(a,b)是否大于0作為W_a(r)等于0或1的判據，則又回歸到離散的劃分。

若使離散的劃分變為模糊的劃分，也就是允許原子空間之間可以有交疊，但保證∑[i]W_i(r)=1，就有可能讓被積函數平滑，使積分精度增加。現在定義一個函數p(μ)=1.5*μ-0.5*μ^3，然后定義s(μ)=0.5*(1-p(μ))，s(μ)的圖形如下圖k=1的曲線所示。如果對p(μ)先進行迭代再代入s(μ)，比如說迭代兩次，就得到s(μ)=0.5*(1-p(p(p(μ))))，其函數圖形就是下圖的k=3，每迭代一次k就增加1。從圖可見，迭代次數越多圖形在μ=0處變化越陡，或者說越不光滑。當k=∞時就還原為了前面提到的離散劃分。所以，選取一個不很大的k值（Becke建議用k=3），將相應的s(μ)作為W(μ)就使得空間被模糊地劃分了，在參考中心處格點權重為1，延伸到相鄰原子處格點權重為0，在二者之間權重函數平滑過渡。由于F(ρ(r))和W_i(r)都是光滑的，所以在單中心積分時的被積函數W_i(r)*F(ρ(r))也是光滑的，能夠容易地被較精確地積分。

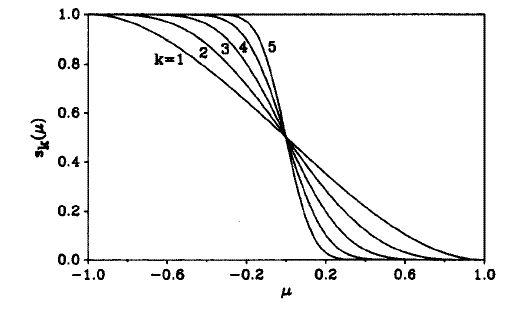
對多原子情況，某個位置上第i個原子的實際權重等于在此處原子i與所有其它原子j之間權重的乘積，即W_i(r)=∏[i/=j]s(μ(i,j))，注意μ(i,j)是r的函數。所以當某原子被其它原子包圍時，只有它附近一定區域內其權重數值比較大，離它越遠處屬于它的成分就越小。如果s(μ(i,j))使用的是前面離散劃分的話，即μ(i,j)小于0和大于0時s分別為1和0，則W_i(r)=1的區域就是第i個原子的Voronoi胞腔。空間的模糊劃分方法并不僅有Becke提出的這一種，例如Hirshfeld劃分也是比較著名的[TCA 44,129]，并且有明確的物理意義，原本用在計算Hirshfeld電荷上，筆者認為也完全可以用于密度泛函積分當中，但目前未見報道。

最后，為了滿足∑[i]W_i(r)=1條件，還需要做歸一化：W_i(r)=W_i(r)/∑[j]W_j(r)，這樣就獲得了最終的W_i。

3. 單中心球極坐標的積分

3.1 簡介

此節討論怎么求單中心球極坐標積分∫W_i(r)*F(ρ(r))dr，為了省事，簡寫為∫f(r)dr。為避免混淆，本文中大寫的W_i是指的空間劃分時的權重系數，小寫的w_i是指的單中心積分時的權重系數。

在球極坐標下，此積分寫為：
∫[0,2π]∫[0,π]∫[0,∞) f(r)*r^2*sinθdθdφdr  其中R是徑向坐標
選取適當的正交多項式，對被積函數進行變換，做三重高斯積分就能得到結果。將f(r)*R^2*sinθ簡寫為q(r)，則實際計算時的形式為：∑A_k∑A_j∑A_i*q(r_i,j,k)，其中A_i、A_j、A_k代表積分徑向、θ部分、φ部分時的積分節點的權重系數，r_i,j,k代表相應的求積節點的位置。在實際計算中，事先把三個積分分量的權重系數乘在一起成為A_i,j,k并保存在一個數組里，比如叫weight；然后將相應的求積節點位置由球極坐標轉換為笛卡爾坐標：
x=R*sinθ*cosφ
y=R*sinθ*sinφ
z=R*cosθ
并保存在數組里，比如叫coord。積分就成了∑[n]weight(n)*coord(n)，計算十分簡單。這兩個數組的大小就是三個積分方向的積分節點數的乘積，比如φ用32個點，θ用16個點（因為積分范圍比φ小一倍，所以一半的點數），R用75個點，則總共要算16*32*75=38400個點。

然而這樣將θ和φ部分獨立積分的效率并不高。實際上對于單位球面積分有不少人專門做了研究，若不將θ和φ分離，而是一起考慮，可以用更少的點達到相同的積分精度。所以只需要把原積分變量r分離為徑向和角度兩部分即可，即∫f(r)dr=∫dR∫dΩ f(r)*R^2。下面具體來看如何積分角度部分，積分通式為∫q(Ω)dΩ。

3.2 角度部分積分

積分單位球面（半徑R=1）目前用得最普遍的是Lebedev提出的方法，也是將∫q(Ω)dΩ轉化成積分節點和權重的乘積，即∑[i]A_i*q(r_i)。Lebedev在一系列文章中陸續給出了能精確積分越來越高階球諧函數的積分節點和權重，隨著積分精度增加積分節點數也隨之增加，從最小的可精確積分l=3的球諧函數的6個節點，到最多的可精確積分l=131的球諧函數的5810個節點，可根據對精度的要求從中選擇合適的節點數。Lebedev系列的節點位置和權重都具有反演和八面體旋轉不變性的特點。

有位活雷鋒寫了個Lebedev-Laikov.F發布到了CCL上供大家使用，其中的子程序用于生成Lebedev積分節點坐標和權重系數，見：http://www.ccl.net/cca/software/SOURCES/FORTRAN/Lebedev-Laikov-Grids/
在Lebedev-Laikov.F中，生成節點的子程序名字都以LD開頭，后面接著生成的點數，比如LD0170生成170個點，LD5294生成5294個點。對稱唯一部分的節點的信息是以列表方式儲存的，然后會通過GEN_OH子程序生成對稱部分的點。下面是生成110個Lebedev節點信息的示例程序：
program ltwd
integer,parameter :: num=110
real*8,dimension(num) :: x,y,z,w
call LD0110(X,Y,Z,W,N)  //傳入容量與節點數相同的一維數組接收結果。最后一個參數沒什么用，隨便傳進一個整數即可，返回值就是生成的節點數。
do i=1,num
 write(1,"(4f15.10)") x(i),y(i),z(i),w(i)
end do
end
運行之后節點信息會保存在當前路徑下fort.1中。作散點圖，如下所示

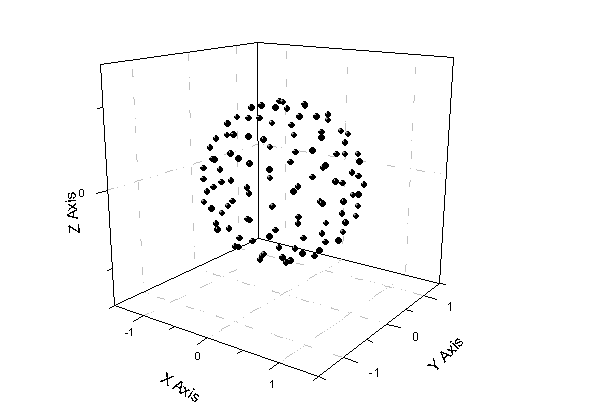
所有點的距離與原點都為1。權重系數已歸一化，即sum(w)=1，也因此最后的結果要乘以4π。因為若被積函數是常數1，即每個積分節點函數值為1，乘上權重加和值為1，但實際值是4π（半徑為1的球面表面積為4π）。

用Lebedev格點積分球面雖然比分別積分φ和θ部分效率更高，但也有一點點缺點，即可選的積分節點數目是離散的，比如要么取350個點，要么取434個點，沒法取350至434之間的值；而且節點數有上限，Lebedev-Laikov.F里最多只有5810個點的情況，再多就沒辦法了。而φ和θ獨立積分時節點數設定是很隨意的，且積分節點和權重可以很容易地自行算出。在一些量子化學程序里角度部分積分同時支持這兩種情況，比如Gaussian里自定義格點通過int=grid=mmmnnn指定，mmm指的是徑向節點數，nnn是角度積分的Lebedev節點數（最多974個），如75434代表共75*434=32550個點。如果寫的是-mmmnnn，則nnn指的是θ的點數，φ的點數為2*nnn，如-96032代表共96*32*64=196608個點。

3.3 徑向部分積分

接下來具體介紹下徑向部分的積分，也就是求∫q(R)*R^2 dR，區間為[0,∞)。徑向部分的積分的方法很多，也被不同程序所采納（據悉Gaussian用的是Euler-Maclaurin積分），多數是基于高斯積分，可參看JCC 24,732。在使用不同正交多項式做高斯積分時需要對被積函數做不同變換，但用哪種高斯積分更準確難有定論，在不同情況下精度相對高低并不一定。Becke最初用的是第二類Chebyshev多項式做高斯積分，這種徑向積分方法用在實際計算中即便不是最好，但至少也不錯，下面將具體介紹。

從本文附錄中看到，用第二類Gauss-Chebyshev積分時權重函數應當為(1-x^2)^0.5，被積區間應該為[-1,1]，然而這與當前要積分的函數形式和區間都不符。所以需要變換，x∈[-1,1]與R∈[0,∞)之間可以用這個式子轉化：R=(1+x)/(1-x)*P，其中P是某個常數，也可以先把它當成1，在后文才會涉及。

將R=(1+x)/(1-x)*P代入∫q(R)*R^2 dR, [0,∞)，因dR=2*P/(1-x)^2*dx，故
原式=∫2*P^3*(1+x)^2/(1-x)^4*q(R)dx, [-1,1]。現在還沒有積分時需要的權重函數(1-x^2)^0.5，但可以變換出來，式中的(1+x)^2/(1-x)^4=(1+x)^1.5/(1-x)^4.5*(1+x)^0.5*(1-x)^0.5=(1+x)^1.5/(1-x)^4.5*(1-x^2)^0.5，故
原式=∫2*P^3*(1+x)^1.5/(1-x)^4.5*q(R) *(1-x^2)^0.5 dx, [-1,1]
由于(1-x^2)^0.5是權重函數，所以實際被積函數就是2*P^3*(1+x)^1.5/(1-x)^4.5*q(R)。將積分節點x_i代入式子并乘上相應根的權重系數w_i加和即可，即
原式=∑[i]2*P^3*(1+x_i)^1.5/(1-x_i)^4.5*q(R_i)*w_i，其中R_i=(1+x_i)/(1-x_i)*P
n階（即n個根）第二類Chebyshev多項式的每個根（即積分節點）x_i=cos(i*π/(n+1))，權重系數w_i=π/(n+1)*sin(i*π/(n+1))^2。

為了計算時方便，上式可再轉化一下。由于1-x_i^2=1-cos(i*π/(n+1))^2=sin(i*π/(n+1))^2，所以w_i=π/(n+1)*(1-x_i^2)=π/(n+1)*(1+x_i)*(1-x_i)，代入原式，成為：
∑[i]2*π/(n+1)*P^3*(1+x_i)^2.5/(1-x_i)^3.5*q(R_i)
可以將q(R_i)前面的這一串一起作為權重系數，所以最終
∫q(R)*R^2 dR=∑[i]w_i*q(R_i)，其中
w_i=2*π/(n+1)*P^3*(1+x_i)^2.5/(1-x_i)^3.5
R_i=(1+x_i)/(1-x_i)*P
x_i=cos(i*π/(n+1))
推導完畢。

4. 積分格點的調整

通過對積分格點進行調整，能使積分更有效率。

由于不同元素的原子半徑不同，格點分布應當做相應調整。在R_i=(1+x_i)/(1-x_i)*P式子中，可見P為第二類Gauss-Chebyshev積分在積分區間中點(x=0)處R的值，Becke認為P應當設為原子共價半徑的一半（對于氫，只設為原子共價半徑），這樣原子共價半徑越大，徑向格點分布將越往外延展，可以更好涵蓋電子密度較大的區域。

s(μ)函數在自變量等于0，即兩原子中垂面處為0.5，這個中垂面位置也應當根據原子共價半徑做適當調整。為此，Becke將s(μ(i,j))的自變量替換為ν(i,j)，它與μ(i,j)的關系為：ν(i,j)=μ(i,j)+a(i,j)*(1-μ(i,j)^2)。目的就是找一個a(i,j)，當r_i/r_j=R_i:R_j=χ(i,j)時ν(i,j)恰為0，其中R_i和R_j為i,j原子共價半徑。為此，先令ν(i,j)=0，則a(i,j)=μ(i,j)/(μ(i,j)^2-1)，在r_i/r_j=R_i:R_j時，μ(i,j)=(r_i-r_j)/R(i,j)=(r_i-r_j)/(r_i+r_j)=(χ(i,j)-1)/(χ(i,j)+1)，因此a(i,j)就確定了。推導中假設格點在i,j軸線上，所以R(i,j)=r_i+r_j。當a(i,j)小于-1/2和大于1/2時直接分別設為-1/2和1/2。筆者發現，若將所有原子設成具有相同數目的徑向和角度格點，則做上述調整只會令積分精度下降，只有如下對不同原子用不同格點數目時上述調整才會提高積分精度。Becke用的是Bragg-Slater共價半徑，但其中氫的半徑為0.25埃，用于調整格點時顯得有些過小，為得到更好結果，Becke將之改為0.35埃。

對于主量子數小的原子，可以用更少的徑向格點以提高計算速度。經筆者實踐，對n=1的原子用35個徑向格點，每增加一個殼層增加15個格點比較合適。由于在內側的原子周圍電子密度變化比處于邊緣的原子更為復雜，所以應當用更多的格點積分角度部分，邊緣原子使用230個Lebedev節點、內側原子使用434個Lebedev節點比較合適，同時內側原子也最好增加15個徑向格點。這樣設定已經有很高的積分精度了，如果要求更高，可以再提高格點數目。

經過上述步驟生成的格點還可以進行裁剪(grid pruning)，在確保積分精度不明顯下降的情況下合理地去掉一部分格點可以節省計算時間。裁剪方法很多，例如徑向節點會有一部分點距離中心非常遠，雖然這些點權重很大，但是函數數值極小，對結果的貢獻微乎其微，若將距離積分中心超過10 bohr的格點一律忽略（也可以根據原子半徑來調整此標準），一般能節省1/5的計算量，至少對于第三周期及以下的原子的結果幾乎沒有影響。再比如，離原子核較近的內層電子受分子環境影響小，所以離原子近的ρ(r)比中等距離處的ρ(r)更接近球對稱分布、變化得更平滑，所以可以對內側區域用更少的格點做角度部分積分。在Gaussian程序中的fine格點是每個原子徑向部分用75個點，角度部分最多302個點做積分，原本共22650個點，經過自動裁剪后只剩約7000多個點，僅是之前的1/3。

如何調整、裁剪格點任意性比較強，因此有人提出了標準化的格點設定方法，例如SG-1、SG-0格點。使用這些格點時，角度、徑向積分方法是指定的，每種元素的所用格點設定也是事先優化好的，在相同數目格點下用這樣的標準格點一般能得到比隨意地調整、裁剪更好的積分效果。例如使用SG-1格點設定時，徑向應使用Euler-Maclaurin積分，角度應使用Lebedev積分，所有原子徑向都是50個點，角度部分格點數取決于格點的徑向坐標，離被積中心從近到遠角度格點數分為6、38、86、194、86五個部分，分界位置取決于原子所在周期（在原文中有列表，通過考察對能量的影響獲得）。無論原子的元素類型、在內側或者在邊緣，每個原子都是大約3700個點，不做任何額外的格點調整與裁剪。SG-1格點結果十分接近更昂貴的徑向50、角度194格點的結果，對中等體系誤差一般低于0.0003 a.u.，當然現在來看SG-1格點積分精度不高，但由于計算量小，計算大體系是合適的。后來提出的SG-0格點中徑向積分改成了更好的MultiExp方法，角度格點數分界設定被更加細化，每個原子僅有約1500個點，雖然精度只是SG-1的一半，但是計算速度也快了一倍，對于諸如生物大分子體系的預計算是很合適的。

如果被積函數的行為比較有特點，最好根據其特點調整格點設定，上文已隱含地體現了這一點，比如拉普拉斯值函數由于在原子核附近劇烈波動，相對于徑向變化相對平滑的ρ(r)，用更多的徑向格點往往能使結果改進得更多。

5. 積分代碼

這個子程序是筆者的Multiwfn程序中的一部分，出于本文的目的做了一定簡化，是上述算法的具體實現，用來積分一個體系的ρ(r)，由此可以更清楚地了解計算流程。此程序用到了一些外部變量和子程序，在注釋中已說明。

subroutine intfunc
use function !引用外部變量與函數
use util
implicit real*8 (a-h,o-z)
real*8,allocatable :: potx(:),poty(:),potz(:),potw(:) !接收Lebedev格點位置和權重的數組
type(content),allocatable :: gridatm(:)  !content類型在別處定義的，包含x,y,z,value四個元素，都是real*8。gridatm儲存格點位置和權重
real*8 smat(ncenter,ncenter),Pvec(ncenter) !ncenter是總原子數。smat儲存s(ν(i,j))，Pvec儲存歸一化前的w_i(r)
integer :: bondmat(ncenter,ncenter) !成鍵矩陣記錄兩個原子間是否成鍵，成鍵為1，不成鍵為0

maxsph=434 !假設角度部分最多有434個格點
maxrad=80 !假設徑向最多有80個格點
allocate(potx(maxsph),poty(maxsph),potz(maxsph),potw(maxsph),gridatm(maxrad*maxsph))

!生成成鍵矩陣，原子成鍵數超過1就說明是內部原子，要用更多格點。
bondmat=0
do i=1,ncenter
 do j=i+1,ncenter
  ! distmat是已算好的距離矩陣。covr第n個元素是周期表中原子序數為n的共價半徑。這里用的共價半徑來自Dalton Trans. 2008,2832。a(i)%index是第i個原子的原子序數。
  if ( distmat(i,j) < 1.15D0*(covr(a(i)%index)+covr(a(j)%index)) ) bondmat(i,j)=1
 end do
end do
bondmat=bondmat+transpose(bondmat) !成鍵矩陣是對稱的

rintval=0 !這是將被累加的變量，由于儲存最終的積分值
covr(1)=0.35D0/b2a !對氫原子用0.35埃的共價半徑。由于covr記錄的是以波爾為單位，用b2a=0.529177249轉換單位。
call cpu_time(time_begin) !用于計算總耗時，便于研究積分格點設置與計算精度的關系。

do iatm=1,ncenter !循環每個原子
 write(*,"(' Processing center',i6,'(',a2')')") iatm,a(iatm)%name !a(iatm)%name是被積分的原子的元素名
 if (a(iatm)%index<=2) then
  radpot=35 !設定徑向格點數。radpot是外部定義的整數變量。
 else if (a(iatm)%index<=10) then
  radpot=50
 else
  radpot=65
 end if
 if (sum(bondmat(iatm,:))==1) then !判斷此原子是在內側還是邊緣
  sphpot=230 !設定角度部分格點數。sphpot是外部定義的整數變量。
 else
  sphpot=434 !內側的原子更多的徑向和角度格點
  radpot=radpot+15
 end if
 if (sphpot==230) call LD0230(potx,poty,potz,potw,isphnum) !生成以0,0,0為原點，在半徑為1的球面上分布的Lebedev格點坐標。
 if (sphpot==434) call LD0434(potx,poty,potz,potw,isphnum)

 iradcut=0 !徑向格點與參考中心的距離隨徑向格點序號增加而遞減，徑向格點中序號在iradcut及之前的點將被扔掉以節省時間。
 parm=covr(a(iatm)%index)/2 !parm指的是前文(1+x_i)/(1-x_i)*P中的P
 if (a(iatm)%index==1) parm=covr(a(iatm)%index) !對氫原子半徑不除以2
 do i=1,radpot !循環每一徑向殼層。將第二類Gauss-Chebyshev積分的權重和Lebedev角度積分的權重組合。并生成每個點的笛卡爾坐標。
  radx=cos(i*pi/(radpot+1)) !生成radpot階第二類Chebyshev多項式的每個根，即前文的x_i。pi是外部定義的π的數值
  radr=(1+radx)/(1-radx)*parm !由x_i生成R_i，也就是徑向積分的節點
  radw=2*pi/(radpot+1)*parm**3 *(1+radx)**2.5D0/(1-radx)**3.5D0 *4*pi !徑向積分的權重系數，順便把球面積分時要乘的4*π也乘了進去。
  gridatm( (i-1)*sphpot+1:i*sphpot )%x=radr*potx !一次設定一層節點的坐標和權重。徑向坐標radr乘上以0,0,0為原點的單位球面上的Lebedev點的笛卡爾坐標，得到的就是在半徑為radr的球面上的Lebedev點的笛卡爾坐標。
  gridatm( (i-1)*sphpot+1:i*sphpot )%y=radr*poty
  gridatm( (i-1)*sphpot+1:i*sphpot )%z=radr*potz
  gridatm( (i-1)*sphpot+1:i*sphpot )%value=radw*potw !將徑向和角度部分的權重函數組合。
  if (iradcut==0.and.radr<10) iradcut=i-1 !大于radr的R_i將被截掉，記錄在編號為何值時截斷
 end do

 !當前積分節點是以0,0,0為中心，下面將中心轉移到被積原子上
 gridatm%x=gridatm%x+a(iatm)%x
 gridatm%y=gridatm%y+a(iatm)%y
 gridatm%z=gridatm%z+a(iatm)%z
 do i=1+iradcut*sphpot,radpot*sphpot !從不被截掉的節點開始循環每個節點
  rnowx=gridatm(i)%x !為了寫的時候方便，改用rnowx,rnowy,rnowz表示
  rnowy=gridatm(i)%y
  rnowz=gridatm(i)%z
  rfuncval=fdens(rnowx,rnowy,rnowz) !fdens是外部函數，計算此點的被積函數值，這里就是指ρ(r)。

  !計算這個格點的空間劃分權重W_i
  smat=1.0D0
  do ii=1,ncenter !為計算所有的s(ν(i,j))，循環每一對兒原子
   ri=dsqrt( (rnowx-a(ii)%x)**2+(rnowy-a(ii)%y)**2+(rnowz-a(ii)%z)**2 ) !計算r_i
   do jj=1,ncenter
    if (ii==jj) cycle !s矩陣對角元沒用，不重新賦值，值仍為1。
    rj=dsqrt( (rnowx-a(jj)%x)**2+(rnowy-a(jj)%y)**2+(rnowz-a(jj)%z)**2 ) !計算r_j
    rmiu=(ri-rj)/distmat(ii,jj) !計算μ(i,j)

    !根據原子半徑調整原子空間劃分，也就是將μ(i,j)轉化為ν(i,j)
    chi=covr(a(ii)%index)/covr(a(jj)%index) !計算χ(i,j)
    uij=(chi-1)/(chi+1)
    aij=uij/(uij**2-1)
    if (aij>0.5D0) aij=0.5D0
    if (aij<-0.5D0) aij=-0.5D0
    rmiu=rmiu+aij*(1-rmiu**2) !此時的rmiu就是ν(i,j)

    tmps=1.5D0*(rmiu)-0.5D0*(rmiu)**3 !做三次迭代
    tmps=1.5D0*(tmps)-0.5D0*(tmps)**3
    tmps=1.5D0*(tmps)-0.5D0*(tmps)**3
    smat(ii,jj)=0.5D0*(1-tmps) !得到s(ν(i,j))=0.5(1-p(p(p(ν(i,j)))))
   end do
  end do
  Pvec=1.0D0
  do ii=1,ncenter !計算W_i(r)=∏[i/=j]s(μ_i,j)。注意因為現在smat對角元為1，乘它等于沒乘
   Pvec=Pvec*smat(:,ii)
  end do
  weight=Pvec(iatm)/sum(Pvec) !做歸一化，得到最終的W_i(r)
  rintval=rintval+rfuncval*weight*gridatm(i)%value !原子空間劃分權重weight和單中心積分權重gridatm(i)%value之積就是此點的總權重。總權重乘上此點被積函數值，對所有中心的所有節點累加，最終得到的就是積分結果。
 end do
end do

!顯示用時和最終結果
call cpu_time(time_end)
write(*,"(' Totally evaluated',i10,' points',' took',f8.2,' seconds')")  icount,time_end-time_begin
write(*,*)
write(*,"(' Final result:',f20.10)") rintval
end subroutine

以3-21G下計算的一氟乙烷為例，積分電子密度期望值為26，實際積分值為26.0000073079，還是很準確的。在Multiwfn里也可以積分拉普拉斯函數，期望值為0，此體系中積分值為-0.0006034985，也還是不錯的。若將所有原子都用徑向75、角度770個點，積分電子密度結果為25.9999996466，積分拉普拉斯值函數結果為-0.0000250146，精度都提高了一位，但速度也慢了，要計算的點數從92130增加到了211792。注意由于Multiwfn讀入的.wfn文件有效數字只有7、8位，與期望值的偏差很大程度是由于輸入精度不夠高造成。為了代碼簡潔易懂，上面代碼的格點設定沒有做充分的優化，大家可嘗試對不同徑向殼層使用不同數目的角度格點以增加積分效率。

在KS-DFT計算中為了獲得KS算符矩陣元，需要算這樣一個積分：V_i,j=∫η_i(r)*V(r)*η_j(r)dr，其中V(r)是交換相關勢，η_i是i個基函數。積分方法與前述完全一樣，只不過是將被積函數由ε(ρ(r))改成η_i(r)*V(r)*η_j(r)而已。由于矩陣元很多，這個積分也要算很多次，會很慢。但可以事先把V(r)和各個η_i(r)在積分格點上的值存起來，算不同的矩陣元的時候調用相應的已算好的值即可，速度就很快了。

6. 格點積分方法的一些問題

由于交換相關泛函的形式復雜，有限格點數目的格點積分不是完全精確的積分，隨之帶來一些問題需要注意。

因為分子的朝向是任意的（沒有固定方向外場等外部因素時），所以在任何朝向下量子化學方法都應當給出完全相同的結果，稱為旋轉不變性。然而積分格點方法并不能完全滿足這一點，尤其是在較糙的格點下，旋轉不變性明顯被破壞。旋轉依賴性大本質上也體現了積分精度差。在徑向20個、角度50個格點下，有人計算HOOF分子，某種方式旋轉前后結果相差達0.001 a.u.，而一般單點計算要求收斂到0.00005 a.u.，雖然SCF收斂了，但能量的計算精度實際上根本沒達到要求。

造成旋轉依賴性的原因可以從下圖考察，這是一個水分子體系，假設空間是二維，黑點代表積分氫原子時的一個殼層上的角度積分格點，格點十分粗糙。圖中下半部分的情況相對于上半部分雖然分子轉動了，但是積分格點分布并沒變，沒有隨著分子轉動而轉動（不過格點的中心總在原子核上），因而相當于被積函數改變了，由于積分不是完全精確的，這層球面積分在旋轉前后結果是不一樣的，也因此總能量是不同的。在大體系下，由于積分次數增加，誤差可能會累積，使能量的旋轉依賴性從絕對值上看更顯著。

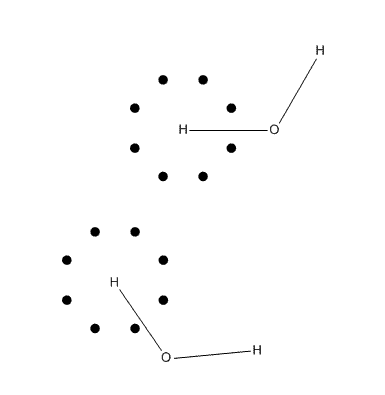
雖然在量子化學程序中一般都會自動令分子處于標準朝向，也即一個分子只有一個朝向，看似沒有了旋轉不變性問題，但實際上只是掩耳盜鈴罷了，標準朝向本質上也是任意的，積分精度太低的問題仍存在著。由于積分節點越多，積分越準，所以可以通過用更精細的格點來減輕旋轉依賴性的問題。在一般量子化學程序默認的格點設置下，旋轉依賴性很小，可以忽略，積分精度也能滿足一般要求。但是如果要求計算精度較高，不僅要把SCF收斂限設得更嚴，也要用更多的積分格點，否則根本達不到目的。

在頻率計算時也要注意積分格點的影響。如果對應于整體轉動模式的頻率不很接近于0（比如超過20/cm），則表明算出來的分子內振動的頻率與真實的能量極小點處的相應振動頻率偏差不小。對于非DFT計算，可以通過設嚴結構優化的收斂限來解決，在Gaussian中使用opt=tight一般就可以了。然而在DFT下優化并計算頻率，除了設嚴優化收斂限外還需要使用更精細的積分格點，一方面能使優化出的結構更為正確，另一方面也使能量的二階導數更為準確，得到的整體轉動模式的頻率將明顯下降，一些微小的虛頻也能夠消除。若使用更緊的優化收斂標準時不搭配更精細的積分格點，結果可能更糟，在Gaussian中，opt=tight建議結合int=ultrafine，opt=verytight建議結合int=grid=199974。

積分精度和實際體系、被積函數是有很大關系的。用一套積分格點設定積分一個體系的某種函數能精確到比如小數點后6位，絕不意味積分另一個體系另一套函數就能達到這個精度。在積分一個新函數時，期望值一般無法事先知曉，也不知道積分能精確到什么程度，此時可以逐漸提高格點數，分析結果收斂情況，看至少用多少格點時結果與使用十分精細格點時結果之差已經小到可以接受的程度。有人擔心在用一個新的交換相關泛函時是否應當提高積分格點數目，這樣的擔心不無道理，但不同交換相關泛函之間行為的差異絕不至于積分到相同精度時需要的積分格點數目會相差幾倍的程度，一般都用相同的格點設置即可，當然謹慎一些的話也可以去分析隨格點數目增加的收斂性。也有人指出Meta-GGA類型的泛函（比如M05-2X）由于其中引入了動能密度，導致對積分格點比GGA泛函更為敏感，用這類泛函時可以使用大一些的格點精度。

某種積分格點+積分方法的結果的誤差有一定的系統成分，比如離核較近區域的積分誤差。雖然粗糙積分的誤差會比較大，但是在求差的時候可以抵消掉一部分，使化學上感興趣的相對值并不那么差。所以，在格點不夠精細時，在比較不同體系能量差的時候應當使用相同積分格點下的結果；另外在這種情況下即便是對相同體系，在不同程序中由于積分格點的設定和積分方法的不同，算出來的結果也可能有一定差異，故應當用相同程序算出的結果相對比。另：因此比較不同程序計算相同問題的結果差異時不要用DFT的結果相比較（一般HF計算結果都是一致的），除所用非格點精度很高，免得把格點設定的差異對結果的影響摻進去。

 

附錄：高斯積分

一個普通的積分I=∫[a,b]w(x)f(x)dx可近似成∑[i=1,n]A(i)f(x(i))，高斯積分的目的是僅使用n個節點，就能完全精確積分能夠展開為最高階為2n-1的x的多項式的被積函數f(x)。w(x)是權重函數。

設P(x)為某n階多項式，可以將f(x)以某種方式寫成這種形式：f(x)=q(x)P(x)+r(x)。由于f(x)是2n-1階多項式，所以q(x)和r(x)的階數顯然小于等于n-1。此積分等價于I=∫[a,b]w(x)q(x)P(x)dx+∫[a,b]w(x)r(x)dx。若P(x)選用的是在[a,b]范圍內帶權w(x)的正交多項式（即此條件下對任何小于其階數的多項式正交），則∫[a,b]w(x)q(x)P(x)dx=0。這樣消了I的第一項就成了I=∫[a,b]w(x)r(x)dx。

由于r是小于等于n-1階的多項式，故這個積分一定能用n個點精確計算，即I=∫[a,b]w(x)r(x)dx=∑[i=1,n]A(i)r(x(i))，其中節點{x(i)}在[a,b]內選取是任意的，計算相應處的r(x)值，然后再根據現成公式算相應的A(i)即可。但是r(x)卻是未知的，如果將節點選為P(x)在[a,b]內的n個根（根據正交多項式的性質可證明此區間內恰有n個根），則f(x(i))=q(x(i))P(x(i))+r(x(i))=q(x(i))*0+r(x(i))=r(x(i))，因此積分公式最終轉化為I=∑[i=1,n]A(i)f(x(i))，可以直接算出結果，其中權重系數A(i)可以通過解線性方程組獲得，也可以由此公式計算：A(i)=∫[a,b]w(x)R(x)^2dx/R(x(i))/P'(x(i))，其中P'(x)是P(x)的導數，R(x)是相應于P(x)的n-1階多項式。

根據不同的權重函數和積分范圍需要選用不同的正交多項式，例如積分∫(-∞,+∞)x^2*exp(-x^2)dr，若將exp(-x^2)當做權重函數，從數學手冊上就能找到在(-∞,∞)范圍內帶權exp(-x^2)的正交多項式，即厄米多項式，此時積分就被稱為高斯-厄米積分。x^2是二階多項式，根據2n-1的規則，可知至少2個點才能準確積分（點數可以增多，但結果和兩點結果一樣）。厄米多項式的根x(i)和積分系數A(i)在數值方法的書里一般都會給出解析形式，并給出n=5以內的具體數值。如n=2時x(1)=-2^0.5/2，x(2)=2^0.5/2，A(1)、A(2)皆為pi^0.5/2，故此積分結果為A(1)f(x(1))+A(2)f(x(2))=pi^0.5/2*(-2^0.5/2)^2+pi^0.5/2*(2^0.5/2)^2=0.8862。僅用兩個點就準確計算了積分，可見效率很高。常見的用于高斯積分的多項式還有第一類、第二類切比雪夫多項式、拉蓋爾多項式、勒讓德多項式、雅可比多項式，可參閱Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables高斯積分章節（第九版887頁）。

如果被積函數表面上看找不到現成的正交多項式，可以考慮進行變換。比如積分范圍在[0,+∞)內沒有能用的正交多項式，但積分變量變換到[0,+1]下有合適的正交多項式，則可改變積分變量來調整積分范圍。被積函數也可以變換形式，例如[-1,1]范圍內積分k(x)*x可以變化為k(x)*x/(1-x^2)^0.5*(1-x^2)^0.5，其中k(x)為某一函數。這樣(1-x^2)^0.5可以當做權重函數用第二類切比雪夫多項式來積分k(x)*x/(1-x^2)^0.5。同一個被積函數f(x)可以以不同方式變換為w(x)g(x)形式，然后根據w(x)選用相應正交多項式來積分，其變換方法不是唯一的，且注意變換被積變量來映射積分范圍也會改變f(x)。如何變換更合理，要看哪種變換后g(x)能更接近于多項式展開形式，越接近則積分越準確。

還有一種辦法是根據權重函數和積分區間自行構造對應的正交多項式，需要通過迭代關系由1階開始一階一階升高地遞推，直到得到要求的階的多項式，然后算它的根和每個根的權重，這個過程比較麻煩，見Numerical Recipes 3ed P181。

如果用n個點計算積分，但函數不能用小于等于2n-1階多項式完全精確地展開，則高斯積分并不是準確的，但一般也比n個點的梯形公式積分準確很多。高斯積分如果想靠增加節點來明顯增加精度，函數應當盡量是光滑的，這樣才容易近似展開成多項式的形式。隨著節點數的增多，可以精確地積分由更高階多項式組合的函數，被積函數形狀就允許更復雜，即便仍不能精確展開，至少也能被更加精確地描述而使結果更好。如果函數不光滑、存在奇點則很不利，不易用多項式的組合展開，高斯積分的優點難以發揮，往往復化梯形公式的效果更好。如果被積函數整體有奇點，但是若將函數整體的一部分作為權重函數考慮時被積函數無奇點，則使用對應于權重函數的正交多項式就可以比較準確地積分。

幾種常用正交多項式的權重函數和積分區間：
Legendre: 1  [-1,1]
Jacobi: (1-x)^a*(1+x)^b  (-1,1) 其中a,b>-1
Chebyshev first kind: 1/(1-x^2)^0.5  (-1,1)
Chebyshev second kind: (1-x^2)^0.5  [-1,1]
Laguerre: exp(-x)  [0,∞)
Hermite: exp(-x^2)  (-∞,∞)