大體系弱相互作用計算的解決之道
大體系弱相互作用計算的解決之道
文/Sobereva @北京科音
First release: 2013-Dec-18 Last update: 2018-Jun-3
1 前言
以DFT-D為代表的一大類色散校正方法使得大體系弱相互作用的計算成為了可能,介紹和使用見《DFT-D色散校正的使用》(http://www.shanxitv.org/210)。筆者曾在《亂談DFT-D》(http://www.shanxitv.org/83)一文的最后指出了不同計算能力下最推薦的計算方法,但這些推薦只是理論上的。而實際計算中,影響耗時的因素極多,除了理論上的計算量之外,還直接決定于計算程序的選擇,以及數值上的加速方法。在本文中,筆者將從完全實用性的角度出發,討論在普通計算條件下,如何選擇最佳的計算級別準確研究大體系的弱相互作用問題。
想準確計算大體系弱相互作用,又不想盲目地傻拼計算量,必須需要“法寶”。下面一節將會簡要介紹這樣7個法寶,分別是:PM7、MOZYME、MOPAC程序、DFT-D、gCP、密度擬合近似&COSX,以及ORCA程序。然后在第3節通過綜合運用這些法寶,給出對于不同數目原子的體系最適合使用的計算方法。在第4節,將會通過各種實例展示實際計算耗時并進行討論。最后一節總結本文。
首先特別值得一提的是,靠最主流最常用的Gaussian這樣的程序,即便用上了DFT-D,想準確處理大體系,那也只能一味地花費很高的代價傻算,就算降低到6-31+G**這樣對于弱相互作用計算低得不能再低的基組,若無對稱性(大的弱相互作用體系基本都沒有對稱性)在普通計算條件下處理上百個原子的體系都挺困難,此時弱相互作用計算準確度也比較差。然而,如果改用ORCA的話,將會感覺ORCA簡直開了掛,發現曾經建立在腦中的“計算精度-計算耗時”方面的經驗被完全顛覆,仿佛打開了一扇通往新世界的大門!
2 七個法寶
2.1 PM7半經驗方法
對于巨大的體系,DFT無論結合什么法子,是無論如何也處理不動的(當然,SCC-DFTB這樣的半經驗層面上的DFT是另外一回事)。如果用力場,準確度往往很有限,普適性差,而且經常缺乏合適的參數。半經驗方法往往是唯一的選擇,盡管其重要性已經很大程度上被人們忽視和遺忘。
傳統的半經驗方法,諸如主流的AM1、PM3,以及后來重新參數化而成的RM1和PM6,對于弱相互作用都比較差勁,就連氫鍵這樣帶有主要靜電成份的弱相互作用尚不好,就更別提范德華作用了。自從色散校正在從頭算、DFT領域流行開來后,人們紛紛把半經驗方法也結合上色散以及其它分子間作用的校正項,使得半經驗方法對弱相互作用的表現能力有了質的飛躍。包括AM1-D、PM3-D、OM1/2/3-D、PM6-DH1、PM6-DH2、PM6-DH2X、PM6-DH+、PM6-D3H4和PM7。其中2007年由McNamara和Hillier提出的AM1-D和PM3-D用的人比較少。2008年提出的OMx-D系列只有其作者Walter Thiel的MNDO2005程序才能算,這東西不公開給大家用(筆者鄙夷這種行為),所以自然也流行不起來,據說OM2-D的弱相互作用計算準確度能達到DFT-D的水準。2009年提出的PM6-DH1是在PM6基礎上加上了色散、氫鍵校正項,后來很快被2010年提出的改進版PM6-DH2所取代。2011年的PM6-DH2X則是在PM6-DH2基礎上又增加了對鹵-氧和鹵-氮型的鹵鍵校正。2012年又提出了PM6-D3H4,除了氫鍵、色散校正項外還引入了Pauli互斥校正項,可能這是目前最好的基于PM6對弱相互作用進行校正的方法。前述幾種修正PM6的方法都是Hobza等人提出的,2010年另一個人Korth也提出了一種PM6加上氫鍵和色散校正的形式,名為PM6-DH+,比PM6-DH2好,但未必比PM6-D3H4好,另外此方法還存在勢能面在一些過程中表現得不平滑的問題。PM7是PM3、PM6和MOPAC的作者J.J.P. Stewart于2013年提出的最新的半經驗方法,改進了其上一代PM6存在的一些缺陷,從統計數據上看熱力學性質計算并沒什么顯著提高,但是這次在訓練參數的過程中著重地考慮了弱相互作用體系,并且引入了弱相互作用的校正項,使得弱相互作用計算比起PM6有了長足進步。PM7由于比較新,目前來說和PM6-D3H4、PM6-DH+相比較誰對于弱相互作用更準確還不好說,但應該在伯仲之間。目前來說,PM7是整體上最好的半經驗方法,巨大體系弱相互作用計算個人最推薦PM7。不過即便從統計數據上看,PM7以及各種修正PM6的方法在弱相互作用計算誤差上都很小,和DFT-D系列相比還是有差距,可靠性差距更大,所以對于DFT-D能算得動的體系最好先用DFT-D,但是半經驗方法可以作為初算,比如估計一下大致的作用能、初步優化一下結構,或者做動力學、構象搜索之類的很耗時的任務。
2015-Jul-18補充:根據DOI: 10.1021/acs.jctc.5b00296對大體系相互作用能的測試,PM7雖然計算復合物結構還不錯,但計算相互作用能比PM6-D3H4和PM6-D3(PM6簡單地加D3校正)差不少。另外,在《PM7、PM6-DH+半經驗方法在優化堿基對兒時的失敗》(http://www.shanxitv.org/217)一文中筆者發現PM7在優化堿基對兒時會誤把兩個堿基優化成不在同一平面,而PM6-D3H4和PM6-D3都沒有這個問題。由于PM6-D3H4和PM6-D3也已經在MOPAC中支持了,因此現在筆者建議用PM6-D3H4或PM6-D3而非PM7。
2018-Jun-3補充:相比于使用上述半經驗方法,Grimme提出的GFN-xTB方法往往更為理想,穩健性更強,普適性更好,十分推薦使用。GFN-xTB類似于半經驗版本的DFT,可以通過Grimme開發的免費的xtb程序實現。xtb程序使用容易,而且效率比MOPAC更高,而且并行效率好得多。申請地址見https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/xtb/xtb。GFN-xTB和xtb程序在《盤點Grimme迄今對理論化學的貢獻》(http://www.shanxitv.org/388)中有更多提及。xtb的基本用法在此文里有介紹:《將Gaussian與Grimme的xtb程序聯用搜索過渡態、產生IRC、做振動分析》(http://www.shanxitv.org/421)。
2.2 MOZYME技術
MOZYME是J.J.P.Stewart提出的一種基于定域化軌道加快半經驗計算的技術,具體細節在這里不談,可以參閱其原文IJQC,58,133(1996)。不像許多基于定域化軌道的方法,也就是僅限于作者自己發paper曬曬數據而無法真正投入廣泛應用,MOZYME是有巨大實用意義的,加速效果是極其顯著的,這將在后面的測試中看到。而且MOZYME是個黑箱方法,并不需要用戶額外去考慮什么。MOZYME的存在使得半經驗能方法處理的體系尺度大了兩個數量級以上,能達到幾萬個原子的體系。而且MOZYME不光能用于單點計算,還能用于幾何優化、搜索過渡態、動力學等需要導數的場合,不過只能用于閉殼層基態。對于大體系弱相互作用問題,MOZYME技術引入的誤差通常是很小的(起碼對于體系的尺度而言)。但對于極少數電子結構無法通過Lewis式表現的體系,有可能SCF過程會收斂到激發態上而不正確,不過這個問題對于生物分子這類成鍵方式典型的體系肯定不會出現。MOPAC的后期的商業版本以及免費版本中從2009版開始都支持MOZYME。MOZYME也僅在MOPAC中實現,是MOPAC的一個重要亮點。
2.3 MOPAC
MOPAC是最著名的專門做半經驗計算的程序。到7.0版本一直是開源免費的,在90年代MOPAC成為Fujitsu公司的商業軟件。后來MOPAC的作者Stewart離開了Fujitsu自己成立了公司并發布了MOPAC2007,然后又出了MOPAC2009,最新的是MOPAC2012,它對學術用戶是免費的但不開源。MOPAC2012只是一個大的版本號,具體版本號在不斷頻繁升級。最新版本下載地址見http://openmopac.net,windows版只有5兆多,license可以免費索取。MOPAC2012已經是個非常成熟穩定而且功能相當全面的程序,手冊撰寫也很詳細,見http://openmopac.net/manual/index.html。最新版的MOPAC2012支持的能較好處理弱相互作用的方法包括PM6-DH2、PM6-DH2X、PM6-DH+、PM6-D3(PM6結合DFT-D3校正)、PM6-D3H4、PM6-D3H4X、PM7。雖然有很多量子化學程序都能做半經驗計算,包括Gaussian在內,但是能用半經驗方法做的任務類型遠不及MOPAC(諸如周期性計算),而且對新的半經驗方法的支持程度遠不如MOPAC,諸如Gaussian中能用的最好的半經驗方法只有PM6,尚不支持任何考慮弱相互作用校正的半經驗方法。MOPAC的MOZYME技術更是其它程序所沒有的。MOPAC2012中把PM7和MOZYME組合使用可謂是對付巨大弱相互作用體系的一個利器。
MOPAC2012的安裝方法見《MOPAC2012安裝方法》(http://www.shanxitv.org/262)。
MOPAC2012的使用比較簡單,典型的輸入文件例子如下:
PM7 CHARGE=-10 MOZYME
molecule
All coordinates are Cartesian
O 4.71271832 0 9.26971072 0 -7.55066164 0
C 4.13662696 0 9.48826045 0 -8.82968461 0
C 2.75025629 0 8.84701245 0 -8.99475234 0
...(剩余的坐標)
第一行輸入的是關鍵詞。這里用PM7,電荷為-10,并且啟用MOZYME技術(默認不啟用)。第二、三行是用戶隨意定義的文字。坐標部分單位默認為埃。XYZ坐標后面的0代表這個原子坐標不做優化,如果所有坐標后面都是0就代表這是個單點任務,如果有的坐標后面是1,就代表當前任務是優化,并且優化這些寫1的坐標。如果寫1SCF關鍵詞則無論是否有的坐標后面是1,都只做單點計算。
在Windows下,將輸入文件保存為.mop為后綴,然后雙擊之就開始運算,并在當前目錄下得到.out輸出文件和.arc檔案文件(只記錄關鍵性信息)。現有的MOPAC結果的可視化工具都不很好用,對于大體系的優化,往往想看優化任務的軌跡來考察優化任務是否合理,這可以用筆者開發的mopac2xyz工具(http://www.shanxitv.org/212)結合VMD實現。
注意半經驗方法給出的能量不是絕對能量,而是生成焓,所以數量級上和從頭算程序給出的體系能量相差甚遠。但是求相對能量時和平常一樣。比如求分子間相互作用能,直接把復合物的生成焓與每個片段的生成焓相減即可。
2.4 DFT-D
DFT-D已經在上文提到的《DFT-D色散校正的使用》和《亂談DFT-D》中反復介紹了,這里就不再提了。
2.5 gCP
gCP是提出DFT-D的Grimme在JCP,136,154101(2012)提出的一種很簡易的獲得BSSE校正能的方法。筆者當初覺得這個方法沒什么意思,有點胡搞,但后來發現,gCP對于幫助幾百個原子的大體系弱相互作用計算實在是有重要意義。這里先談一下BSSE問題。
BSSE(基組重疊誤差)問題在《談談BSSE校正與Gaussian對它的處理》(http://www.shanxitv.org/46)當中有詳細討論。BSSE本質上由于基組不完備所引起,會導致弱相互作用計算結果顯著不準(半經驗、SAPT方式計算無BSSE問題)。很大程度上解決BSSE問題的方法一種是使用含有較多彌散函數的基組,或者至少是分裂價數較多的基組,例如4-zeta基組的BSSE就很小了,因為最外層基函數已經體現出了半彌散特征;另一種是使用Counterpoise (CP)方法進行校正。但這兩種做法都使計算量劇增。另外彌散函數較多時還會導致SCF收斂困難,而使用CP時則沒法獲得解析梯度,使得幾何優化耗時極高,而且CP通常只能解決分子間BSSE問題,分子內BSSE問題很難靠CP解決。
之所以不含彌散函數的小基組在計算弱相互作用上結果差,其實關鍵因素就在于BSSE。普遍提倡在計算弱相互作用時加上彌散函數,其實從實效上講就是在于減輕BSSE。換句話說,對于分子間相互作用的計算,彌散函數起到的作用和CP實際上是相仿佛的。這點從JCP,134,084107(2011)的圖4上體現得非常清楚,cc-pVDZ+CP和aug-cc-pVTZ的平均誤差很相近。所以說,如果用CP來解決掉BSSE問題,那么對于分子間相互作用計算就不太需要彌散函數了(雖然再加上彌散的話結果還能再改善一點點)。
gCP的全稱是geometrical counterpoise,這是基于原子坐標和預先擬合的參數進行簡單經驗校正來獲得BSSE校正能的方法,校正函數十分簡單,就像DFT-D校正一樣不需要額外耗時。而且gCP可以直接解決分子內BSSE問題,因此比起CP還更有優勢。不過gCP畢竟只是近似方法,它得到的BSSE校正能的準確度和直接做CP相比還是會有一定偏差的。gCP的參數一方面決定于基組,一方面決定于理論方法。gCP已經向6-31G*、def2-SVP、def2-TZVP這樣主流的雙、三zeta基組和極小基MINIS(scaled MINI極小基)等基組擬合了參數。理論方法只分為兩種,HF和DFT,不同的泛函對應的gCP參數相差很小,所以gCP對各種泛函使用了統一的參數。
gCP的實際效果很明顯。比如用def2-SVP這種不含彌散函數的雙分裂價基組計算弱相互作用原本是不可能的,精度不可接受,然而加上gCP后弱相互作用計算結果就和參考標準def2-QZVP較為接近了。而def2-TZVP,已經比def2-SVP強不少,加上gCP后結果還能進一步改善,而且比起def2-SVP結合gCP時更接近def2-QZVP。
gCP可以結合DFT-D3校正一起使用,完全沒有矛盾,例如都加到BLYP上可以構成BLYP-gCP-D3。注意有些人誤以為DFT-D參數當中就已經把BSSE問題給等效解決了,實際上根本不是這么回事!DFT-D3在擬合參數的時候是在def2-QZVP下進行的,此基組雖然還留有一點點BSSE問題,但問題已經很小了,所以DFT-D3的參數幾乎沒有等效解決BSSE問題,而且DFT-D3的函數形式本身也沒法像gCP這樣解決BSSE問題。因此,DFT-D3用來解決傳統泛函弱相互作用描述差,gCP解決基組層面上的問題,gCP和DFT-D3一起用就把理論和基組的問題都解決了,使得便宜方法+便宜基組下的弱相互作用計算精度依然很不錯,很適合對付大體系。
HF以及不同DFT方法結合gCP和DFT-D3后弱相互作用計算精度各不相同。BLYP-gCP-D3不是最好但也挺不錯,強烈推薦使用。B3LYP-gCP-D3比它沒明顯優勢,而且計算量更大,不建議用。雖然M06-2X本身計算弱相互作用很不錯,但是gCP和它結合效果并不好。令人意外的是,HF-gCP-D3結合MINIS極小基居然計算結果相當不錯,估計是恰好誤差比較好地抵消了。大抵是由于這個發現,Grimme在JCC,34,1672(2013)提出一個所謂的HF-3c方法,相當于HF-gCP-D3-SRB/MINIX,SRB是額外引入的解決短程基組不完備性的校正項,MINIX是一種較輕原子用極小基而較重原子用雙分裂價基的專為HF-3c特制的基組。HF-3c結果不錯,已經被ORCA支持。但是筆者比較鄙夷HF-3c方法,物理意義差,結果好主要是誤差抵消得好,對于特殊情況沒準很爛,不算很靠譜,而且HF比起純泛函計算量大得多(特別是使用密度擬合近似時,見后文)。
gCP的計算程序可以從這里下載:https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/gcp/gcp。
編譯方式:假設用的是ifort,就把Makefile里的# FC = ifort去掉注釋,并把-static去掉,然后make即可。
典型的運行方式比如:./gcp water.xyz -level dft/svp,瞬間即得到gCP校正能。water.xyz是體系結構的xyz文件,-level后面接理論方法和基組,這里即假設計算級別為DFT方法結合def2-SVP,詳見手冊。加上-grad參數可以輸出校正能的梯度,加上-hess可以輸出它的Hessian。
2.6 密度擬合近似和COSX
密度擬合近似(Density-fitting approximation)是一種數值上的近似技術,可以大大降低處理雙電子積分上的計算消耗,同時引入的誤差可以基本忽略不計。密度擬合近似下的雙電子積分的表達式從形式上類似于(但不相同)插入了RI(Resolution-of-the-identity,即1=∑|m><m|),所以密度擬合近似在一些文獻和程序中被稱為RI近似。
密度擬合近似的關鍵是把原先的基函數φ(也叫軌道基函數)的乘積通過輔助基函數χ的線性組合來近似表達,即
φ_p*φ_q≈∑[k]c_pq,k*χ_k
組合系數c是通過擬合得到的,這是密度擬合近似名字的由來。注意這并非是對于電子密度來擬合,而是對于廣義的密度,即基函數的乘積來擬合。擬合方式的方法很多,一般用的是通過最小化庫侖積分誤差來實現,即最小化這個雙電子積分
(ρ_pq-ρ'_pq|1/r12|ρ_pq-ρ'_pq),其中ρ_pq=φ_p*φ_q是精確的乘積,ρ'_pq=∑[k]c_pq,k*χ_k代表擬合的乘積。
采用上面這種擬合方式時,(pq|1/r12|rs)這樣的雙電子-四指標積分就被直接轉化為了通過(pq|1/r12|k)這種雙電子-三指標的積分的組合來表達,積分本身的計算因此更簡單了。對于HF、DFT中的庫侖部分的計算,這種技術也避免了儲存和處理四指標積分,而只需要儲存和處理雙、三指標的數據,故在構建HF/KS算符的過程上也省了大量時間,細節可以參看ORCA3.0手冊6.2.2.3節。盡管三指標積分->四指標積分變換過程本身需要一點時間,但這和密度擬合技術帶來的利益相比是微不足道的。由于純泛函(即非雜化泛函)不含HF交換部分,只含庫侖部分(J),因此密度擬合近似令純泛函的計算速度有了質飛躍,快了一個數量級以上,而且儲存空間消耗也大為降低,這被稱為RI-J技術。RI-J技術已經廣泛普及,諸如Gaussian、Turbmole、ORCA、Molpro、PSI、Q-Chem等主流程序都已經支持它。
密度擬合技術也可以用在加速HF交換部分(K)的計算,稱為RI-K,但由于基于三指標積分構建K的過程比構建J麻煩、耗時得多(可參見PCCP,4,4285(2002)),所以帶來的加速效果明顯不如用在庫侖部分那么大,RI-K也沒有RI-J那么流行,像Gaussian就不支持。如果密度擬合既用在J也用在K上面,就叫做RI-JK。對于雜化泛函或HF,雖然RI-JK會帶來顯著的速度提升,但是計算速度遠不及純泛函結合RI-J。由于RI-K方式計算K的速度和占據軌道數目存在正比關系,所以所用基組越大,RI-K帶來的加速就越顯著。而對于大體系(占據軌道數很多)使用小基組的時候RI-K就起不到多少加速作用。
密度擬合技術的另一個重要的應用是加速MP2,這稱為RI-MP2。MP2任務在微擾計算部分主要的時間都花在了雙電子積分變換過程,其中最耗時的一步變換的復雜度是O(N_occ*N_AO^4),其中N_occ是占據軌道數目,N_AO是基函數數目。而使用密度擬合近似后,最耗時的變換成為了O(N_occ^2*N_vir^2*N_aux),其中N_aux是輔助基函數的數目,這比起原先O(N_occ*N_AO^4)計算量大大降低了,因為N_AO=N_occ+N_vir,N_aux雖然大于N_AO但還是在一個數量級上的。整個MP2的計算過程中,對于大基組來說,實際上往往多數時間不是花在了微擾計算上,而是花在了HF迭代過程上。為了整體計算更快,RI-MP2任務中可以再結合RI-JK來加速HF部分的計算。現在很流行的雙雜化泛函是雜化泛函的SCF能量與基于相應DFT軌道的MP2能量的線性組合,也可以同樣地同時用密度擬合技術加速DFT和微擾這兩部分的計算。密度擬合技術在量子化學上還有很多重要應用,由于和本文主題無關這里就不再多提了。
在ORCA中有個RIJONX,也叫RIJDX,實際上這就是指對于雜化泛函/HF只用RI-J加速庫侖部分,而交換部分照常計算。ONX的全稱是HFX calculated with O(N),其含義是HF交換部分由于隨距離衰減得比較快,因而涉及較遠距離時可以對積分進行屏蔽,對于大體系K的計算量是O(N),即隨著基函數增加計算量是線性增加的,這實際上是比較理想化的情況。對于基組較大的時候,光是中、小體系就已經算不動了,即便對于很大體系有線性標度意義也不大。
與RI-K不同的加快交換部分計算的近似方法是COSX,這是ORCA的頭目Frank Neese在Chem. Phys.,356,98(2009)中提出的,也是ORCA的一個重要亮點。COSX屬于半數值積分方法,它在計算K的時候又做解析積分又做基于數值格點的積分。相比RI-K,COSX擅長處理大體系,體系越大比RI-K的優勢就愈明顯。通常來說,COSX在小體系(約30個原子以下)沒RI-K快,40左右個原子時二者速度相仿佛,100個原子時COSX的耗時就完全和RI-K不在一個境界了,幾百個原子時那就只能用COSX才算得動了。COSX比RI-K的好處還在于COSX的內存消耗要小很多,另外對于開殼層體系RI-K的速度比閉殼層時耗時加倍,而COSX則沒這個問題。一般大小的格點下COSX引入的誤差和RI-K相仿佛,都很小而基本可以忽略。對于雜化泛函的計算本來HF雜化部分就引入得比較有限,因此RI-K和COSX帶來的誤差就更小了。若想進一步減小COSX的誤差,只要增加積分格點的數目就可以(在ORCA里用Gridx設,比如用Gridx4甚至Gridx5),當然耗時也會相應增加。RI-K比COSX有一個好處是誤差總為正,而COSX的誤差時正時負,因此求相對能量時RI-K的誤差抵消得可能會稍微比COSX好一點。COSX和RI-J結合使用分別加速交換和庫侖部分就叫做RIJCOSX。對于小體系大基組計算一般建議用RIJK來加速,對于大體系則建議用RIJCOSX。對幾十個原子的體系通常RIJK和RIJCOSX對絕對能量引入的誤差明顯小于1kcal/mol,如果是求相對能量,誤差還能抵消掉不少。
密度擬合計算必須得有輔助基組(Auxiliary basis sets,也稱密度擬合基組)才行。輔助基組如同一般意義上的基組,它定義了每種元素原子所攜帶的輔助基函數的數目和特征。一般用的輔助基組用的都是普通的原子中心的高斯函數,既包含非收縮的也包含收縮的,所以和一般的基組在形式上無異。顯然如果輔助基組是完備集,那么密度擬合近似就不再是近似,而是完全精確的了,當然這不可能做到。實際所用的輔助基組的尺寸必然是有限的。既不能太小,太小了沒法較準確還原出軌道基函數的乘積,結果不準確;而太大的話計算量又太高。所以實際所用的密度擬合基組必須大小合適,并且最好是專門為特定基組優化過的。Ahlrichs系列基組和Dunning相關一致性基組以及其它個別基組都專門有人優化出了匹配的輔助基組。這些輔助基組根據用處主要分為三類,一種是帶有/J后綴的(Coulomb fitting),專門用于RI-J或者RIJCOSX;一種是/JK后綴的(Coulomb+Exchange fitting),專門用于RI-JK;一種是/C后綴的(Correlation fitting),專門用于RI-MP2。例如,def2-TZVPP就有def2-TZVPP/J、def2-TZVPP/JK和def2-TZVPP/C。/J、/JK和/C型輔助基組在優化GTF指數和確定收縮方式時的目標分別是令密度擬合近似在體系的庫侖能、交換能和MP2相關能上引入的誤差盡量小。無論是哪類密度擬合基組,其尺寸都要比標配的軌道基組要大,并且含有更高角動量函數。對于同一種軌道基組,這三類密度擬合基組的大小關系總是/C > /JK > /J,這是因為較少數量的輔助基函數就能讓庫侖能的計算誤差在較低水平,而若想不給相關能帶來明顯誤差,就不得不用更多以及含有更高角動量的輔助基函數。高級別密度擬合基組可以用在低級別軌道基組上,而且比使用標配的密度擬合基組結果更好,例如cc-pVTZ/JK和cc-pVTZ/C都可以用于在cc-pVTZ上做RI-J,而且比結合cc-pVTZ/J時稍微好一點點。再比如6-31G**可以用cc-pVTZ/J做RI-J或RIJCOSX,雖然cc-pVTZ/J不是給6-31G**優化的,但因為cc-pVTZ比6-31G**大得多,所以它的標配的輔助基組用于6-31G**毫無問題,盡管有些浪費。有的時候我們會砍掉一些意義不大的高角動量函數來降低計算時間,比如def2-QZVPP(-g,-f)代表從重原子和氫原子上分別去掉最高角動量函數g和f,這時沒有標配的輔助基組,但是我們可以放心地直接用def2-QZVPP/J、/JK、/C。反之,高級別軌道基組結合低級別的輔助基組,比如def2-TZVP用def2-SVP/J結果就會較差,或者用/J代替/JK輔助基組做RI-JK計算也會帶來較明顯的誤差。對于沒有標配輔助基組的情況(特別是對于Pople系列基組,目前都沒有標配的),也有自動的方法可以生成輔助基組,而且結果也可靠,但這樣得到的輔助基組比起專門優化的輔助基組要大不少,故計算明顯更耗時,所以建議在使用密度擬合計算時還是應盡量用那些有合適的輔助基組的軌道基組,def2-系列基組的輔助基組很全,因此往往是首選。最后值得一提的是在ORCA程序中,對于后HF任務,可以同時用兩類密度擬合基組,即在SCF過程中使用/J或/JK,而在相關部分計算中使用更大的/C來保證精度損失較小。
2.7 ORCA
要問哪個量子化學程序最有前景,答案一定是ORCA。ORCA從90年代后期開始開發,是個非常優秀,功能全面,代碼效率很高,不斷迅速發展完善的程序,而且還是免費的(不過不開源)。從基態到激發態,從單點到幾何優化,從大體系DFT計算到小體系高精度耦合簇計算,以及NEVPT2、MRCI等多參考態計算全都做得挺好。溶劑模型、標量相對論計算、NMR計算等ORCA也都支持。而且ORCA還逐漸支持其它多數程序沒有的功能,諸如密度矩陣重整化群(DMRG)、F12顯式相關計算、DLPNO-CCSD(號稱能把耦合簇計算用到上百個原子)。特別是ORCA充分利用了密度擬合技術,并且結合獨家的COSX方法,計算速度比起普通量化程序有了驚人的飛躍,更是極大程度地顛覆了基于DFT的弱相互作用計算的格局。在RI-J的時候ORCA還默認使用RI-split-J方法進一步加快計算,這不影響精度,對大基組時加速效果明顯。另外ORCA上手也比較容易,手冊寫得比較詳細,有原理介紹和實例。想必如果ORCA有個gview水準的圖形界面,并且再有個Exploring Chemistry With Electronic Structure這樣的教程書的話,將會打開初學者市場,從而對量子化學研究領域產生將難以估量的影響,Gaussian的市場肯定會嚴重縮水,而像Q-Chem、Turbomole等其它收費程序的生存空間就更小了。ORCA遭人詬病的是不支持利用對稱性來加速計算(但可以判斷對稱性),實際上這不算大問題,密度擬合技術已經使ORCA比很多程序開對稱性時快得多了。而且特別是對于大體系弱相互作用的計算,體系一般都是沒有對稱性的,所以不支持對稱性并不是問題。
ORCA和Grimme有緊密的合作,所以DFT-D3、gCP以及HF-3c等Grimme提出的與弱相互作用相關的方法全都直接被ORCA所支持。
ORCA的主頁是https://orcaforum.cec.mpg.de。雖然在上面免費注冊一下后就可以直接下載,但下載速度可能比較慢,因此我也傳了一份到百度網盤上:http://pan.baidu.com/s/1eQh9nai,這是Windows和Linux版的Orca 3.0.2版可執行程序,包括手冊,以及并行計算需要的OpenMPI。
ORCA解壓后就能直接用,運行方式如orca Mio.txt > akiyama.out,這里假設orca目錄已經納入了系統的PATH環境變量。ORCA是以MPI方式并行的,如果要并行運行,先到http://www.open-mpi.org下載最新的OpenMPI并安裝到系統上,然后輸入文件里寫上pal2、pal3...pal8就代表2核、3核...8核并行,然后帶著絕對路徑去調用orca即可(不需要mpirun之類),例如d:\study\orca301\orca Love_live.txt > niconiconi.out。如果要用更多核就得在輸入文件里寫成%pal nprocs x end,x是調用的核數,無上限。
ORCA的輸入文件寫起來比較容易,例如
!BLYP D3 GCP(DFT/SVP) def2-SVP def2-SVP/J pal4 nopop
%maxcore 1000
* xyz 0 1
O 4.71271832 9.26971072 -7.55066164
C 4.13662696 9.48826045 -8.82968461
...略
C 2.75025629 8.84701245 -8.99475234
C 7.66851269 1.97163671 1.43096468
*
!后面的關鍵詞代表用BLYP計算,帶DFT-D3校正以及DFT/SVP級別的gCP校正,軌道基組為def2-SVP,def2-SVP/J作為RI-J的輔助基組。對于純泛函ORCA是默認開啟RI-J的,所以不用寫額外關鍵詞開啟它。nopop是避免計算完之后輸出一大堆特別冗長一般又沒用的布居分析數據(這類分析最好用Multiwfn程序)。maxcore設定每個核最大的內存使用量(MB),實際使用量可能超過之,比如此例可能總共會用到5G多,所以maxcore別設得太大,否則一旦物理內存不夠而調用虛擬內存的話速度將巨慢。xyz代表輸入的是笛卡爾坐標,默認為埃。0 1代表凈電荷為0,單重態。
再比如關鍵詞一行寫成這樣
!RI-PWPB95 D3 def2-QZVPP def2-QZVPP/JK def2-QZVPP/C RIJK grid4 tightscf nopop pal4
就代表使用PWPB95雙雜化泛函,SCF步驟用def2-QZVPP/JK輔助基組做RI-JK來加速,方法名字前寫上了RI-說明在微擾計算時也使用密度擬合近似來加速,并且基于def2-QZVPP/C輔助基組。由于此例計算精度要求高,用了tightscf來設嚴收斂限。
2018-Apr-30補充:注意,從ORCA4.0開始,輔助基組定義方式相較于ORCA3.0有了極大的變化。上文的def2-SVP/J應改為def2/J,而def2-QZVPP/JK應改為def2/JK。下文提到的def2-QZVPP(-g,-f)基組在ORCA4.0中也沒法直接用相應關鍵詞使用了。
ORCA中交換相關泛函的積分格點包含七個級別,從grid1到grid7精度依次增加。ORCA默認在DFT的SCF過程中使用較低質量的積分格點(Grid2),而在最后計算最終能量時才切換到較高質量格點(Grid4)計算交換相關能,這稱為multigrid方法,使得計算量又小精度又有保證。然而SCF過程中使用較低格點質量還是會給結果帶來可以察覺到的誤差的。為了不因為積分格點帶來的誤差污染了雙雜化泛函+def2-QZVPP這么高級別的計算水準帶來的優秀結果,上例使用了grid4關鍵詞來讓SCF過程也使用較好質量的積分格點,此時在計算最終能量時程序會自動切換到更高的Grid5。對于一般泛函下的計算一般不需要特意指定格點精度和調整收斂限,用默認的就行了,但對于頻率計算等任務建議總是加上grid4 tightscf。如果還想進一步提高格點精度(雖然已完全沒有必要),可以寫grid5,并且還可以通過寫上%method FinalGrid 6 end來讓最后一次計算時自動切換到更高grid6。
順帶一提,ORCA計算后會產生.gbw文件,包含基組、軌道等信息。通過自帶的工具orca_2mkl xx -molden可以將xx.gbw轉換為molden輸入文件。最強大的波函數分析工具Multiwfn(http://www.shanxitv.org/multiwfn)可以載入它來做波函數分析,包括各種各樣的弱相互作用的分析,如RDG分析、AIM分析、定量分子表面靜電勢分析等等,參見《Multiwfn波函數分析程序的意義、功能與用途》(http://www.shanxitv.org/184)、《Multiwfn支持的弱相互作用的分析方法概覽》(http://www.shanxitv.org/252)。使用Multiwfn的主功能0還可以很方便地查看分子軌道圖形,見《使用Multiwfn觀看分子軌道》(http://www.shanxitv.org/269)。
2.8 雜談其它的加速方法
直接用從頭算算不動的體系人們有時考慮用雜化方法,比如通過ONIOM技術將半經驗、分子力學和從頭算結合三者相互組合。ONIOM,或者更一般的QM/MM技術對于研究大體系確實很有用,但是對于大體系的弱相互作用計算,筆者認為這些方法沒有太大用武之地,原因很多。原因之一是PM7、PM6-DH+等方法結合MOZYME技術已經能處理很大體系了,用于生物大分子都沒問題,結果也不錯,所以遇上從頭算算不動的情況直接用半經驗就行了,用不著把方法進行雜化。用了雜化方法,可能由此帶來的誤差都比半經驗方法本身的誤差要大很多。怎么去劃分不同理論級別處理的區域也是件麻煩事。而且若是靠比如ONIOM結合從頭算與半經驗,Gaussian現在支持的半經驗又沒有對弱相互作用算得好的,低級別區域弱相互作用考慮得太差也不行。如果是從頭算或半經驗與MM混合到一起用,又要涉及指定力場參數的問題,往往在操作上搞得很麻煩。總而言之,ONIOM、QM/MM對于大體系弱相互作用的研究很難派上用場。
還有一種技巧是使用混合基組減小計算量,比如一個大分子和一個小分子結合要算結合能,只把結合的區域附近的原子用帶彌散的大基組,這樣做沒有問題,實現也容易。不過一般倒也沒必要用,因為如果使用下一節推薦的方法,哪怕是大體系,也能算得挺快挺準。
另一種處理大體系常用的做法就是把體系簡化成模型,只把關鍵區域摳出來(比如蛋白質活性位點),把邊緣原子用比如甲基給飽和上,其余原子要么忽略要么用背景電荷方式來表現出靜電作用。這么做完全可以,雖然表面上沒QM/MM嚴格,但是省事不少。不過如何簡化還是需要一定計算化學經驗和化學直覺的,簡化得過度結果不準,簡化不夠則計算量還是太大。
還有很多線性標度的方法都能幫助處理大體系,MOZYME前面已經提過了,這里主要說的是從頭算/DFT層面上的線性標度方法。這種方法非常多,原理也不同,大致思想要么是基于定域化軌道,要么是把體系分成片段依次計算再組合上。無數人在這方面做了幾十年的研究,相關paper無數,沒完沒了地曬加速比,但始終沒產生多少實際應用價值。關鍵的原因就是方法不夠黑箱化,能應用或者適用的體系非常狹窄,比如只對直鏈體系加速效果好而碰上復雜點的結構就啞火,有的方法處理不了含有大共軛的體系,有的方法則只限于比如很理想化的蛋白體系,等等。總之從原文數據上來看結果甚好,但是實際應用中到處碰壁,操作起來甚是麻煩。沒有流行起來的另一個重要原因是被主流程序支持不夠,主流的量化程序大多都沒支持那些作者自吹是線性標度的方法,很大程度上也是因為這些方法實用性、實際效果差,相對而言較好的也就是FMO (Fragment MO)方法,已在GAMESS-US里被充分支持。總之現階段來看那些線性標度方法表面上顯得對于研究大體系弱相互作用很有用處,但絕大多數都停留在理論層面上,實際上應用價值不大,除非自己已經把這方面理論和操作研究得爐火純青了,能玩得得心應手。
ORCA從3.0加入的DLPNO-CCSD(T)技術值得一提。CCSD(T)眾所周知耗時極高,且隨著體系尺度的增加計算量飆升,二十多個以上原子的體系都幾乎算不動。DLPNO-CCSD(T)基于局域相關思想,是前身LPNO-CCSD(T)的改進版,令無論多大體系的CCSD(T)計算都有線性標度的效果,號稱目前已經能把CCSD(T)做到650個原子的蛋白,而且此方法基本是黑箱,不需要用戶調什么參數,很有前景。理論上說DLPNO-CCSD(T)對于精確研究大體系弱相互作用很有用。不過本文并不涉及DLPNO-CCSD(T),因為它比起ORCA做雙雜化泛函耗時遠遠要高得多,而且為了讓CCSD(T)充分發揮效果必須得用頗大的基組,更是給計算雪上加霜,而且DLPNO技術本來也會帶來一些誤差,所以從實效上講遠不如雙雜化泛函合算。
3 不同尺度弱相互作用體系的最佳計算方法
基于上面介紹的7個法寶,對于不同尺度的體系的弱相互作用研究(能量計算而非幾何優化)筆者推薦的計算方法如下,從大體系到小體系排序,共分為8個檔。這些體系假定是以C、H、N、O為主的有機分子。第1項是用MOPAC2012來做計算,2~6項用ORCA來做計算,列出的就是在ORCA中實際要寫的關鍵詞。對于7、8,用什么程序來做都可以,由于這屬于小體系范疇所以在本文中不做討論,值得一提的是ORCA的CCSD(T)計算效率是很高的。
1 >500個原子:PM6-D3H4結合MOZYME
2 >300個原子:BLYP D3 GCP(DFT/SVP) def2-SVP def2-SVP/J
3 >150個原子:BLYP D3 GCP(DFT/TZ) def2-TZVP def2-TZVP/J
4 >60個原子:BLYP D3 def2-QZVPP(-g,-f) def2-QZVPP/J
5 >40個原子:RI-PWPB95 D3 RIJCOSX def2-QZVPP(-g,-f) def2-QZVPP/J def2-QZVPP/C grid4 tightSCF(/J可改用/JK以減小密度擬合的誤差)
6 二、三十個原子:RI-PWPB95 D3 RIJK def2-QZVPP def2-QZVPP/JK def2-QZVPP/C grid4 tightSCF
7 十幾個原子:CCSD(T)/jul-cc-pVTZ或may-cc-pVQZ
8 <10個原子:CCSD(T)/CBS (aug-cc-pVTZ->QZ外推。想更精確再加上counterpoise校正,耗時將增加近2倍)
用上面這些計算方法計算相應尺度的體系,在目前主流的Intel 4核CPU的機子上,一般都是可以在幾個小時內計算完畢的。這些計算方法的弱相互作用計算誤差和對應的體系的尺寸是正相關的。體系越大,可以忍受的絕對誤差當然也就越大。無論是上面所列的哪個計算級別,對相應尺度的體系來說弱相互作用精度都是足以令人滿意的。
如果計算能力比較好,比如有16核機子,或者不怕花時間,比如一個體系算幾天也無妨,那么所用的計算級別就可以提高一兩個檔。反之,如果打算計算大批量體系(比如用于分子篩選的目的),或者用于初步估算結果,或者用于幾何優化等,那么就可以把計算水準降低兩、三個檔。另外筆者特別推薦使用PM7或PM6-DH+對幾十個或更多原子數目的體系進行優化,雖然幾十個原子的體系用DFT也照樣能優化得動,但由于在半經驗下優化速度極快,幾乎不費時間就能得到較好的初始構型,再接著用DFT來優化可以讓收斂快得多。
這些推薦的計算方法里有一些值得說明和討論的地方,前文中尚未提及,將在下面說說。
第8個檔當中用了基組外推技術以達到完備集,完全消除因有限基組而導致的計算誤差,這在《談談能量的基組外推》(http://www.shanxitv.org/172)當中有詳細討論。在第7個檔當中用了月份基組,這種基組把aug-cc-pVnZ系列基組的對結果影響不大的高角動量彌散函數適當地除去,大大節約了計算量,這在《談談彌散函數和“月份”基組》(http://www.shanxitv.org/119)當中有詳細討論。在第5、6個檔當中用了PWPB95-D3,這幾乎是對于弱相互作用計算最好的雙雜化泛函,好于雙雜化泛函中最流行的B2PLYP-D3。
結合DFT-D3校正后密度泛函方法對弱相互作用計算精度整體來說是:雙雜化泛函>雜化泛函>GGA泛函,計算耗時也是這個順序。之所以上面推薦的方法中直接從雙雜化泛函(PWPB95)直接切換到GGA泛函(BLYP),而沒有經過普通雜化泛函的過渡,是因為雙雜化泛函的計算量不比雜化泛函多多少,額外多出的微擾部分的計算耗時往往還少于雜化泛函在SCF迭代過程上的耗時。所以如果用得起雜化泛函的話還不如干脆就用雙雜化泛函來得到更好的精度。而GGA泛函不需要計算HF交換部分,靠RI-J技術可以讓GGA泛函的計算速度比雜化泛函(哪怕已經用了RI-JK或RIJCOSX來加速)高好幾倍甚至甚至一個數量級,所以雜化/雙雜化泛函難以對付的大體系可以靠GGA泛函輕松地對付。雖然雜化泛函眾所周知對于一般問題諸如熱力學量的計算比起GGA泛函強得多,但是對于弱相互作用的計算,結合DFT-D3后它們的性能差異其實很小,例如B3LYP-D3只是比BLYP-D3在定量上略有點兒優勢而已,更不會有什么定性差異。所以從實際角度來看雜化泛函+D3的性價比不高,故沒有納入推薦。
def2系列基組是Ahlrichs等人在2005年提出的,是Turbomole程序的御用基組,def2-QZVPP是其中最大的,和cc-pVQZ在一個級別。def2-QZVPP相對于def2-QZVP只是對于某些元素把高角動量基函數數目稍微增加了一點而已,對于C、H、N、O沒有區別。def2-QZVPP(-g,-f)是def2-QZVPP的高角動量閹割版,這在前面已經提到了,閹割導致的精度損失幾乎可以忽略。之所以推薦的計算級別中使用的是def2-QZVPP(-g,-f)或def2-QZVPP卻沒有使用對于弱相互作用計算很常用的aug-cc-pVTZ,這是有幾個重要原因的:
(1)def2-QZVPP(-g,-f)本身只比aug-cc-pVTZ大一點點而已,但aug-cc-pVTZ目前沒有/J而只有/JK和/C輔助基組,aug-cc-pVTZ/JK比起def2-QZVPP/J大很多。用aug-cc-pVTZ/JK當輔助基組做RI-J和RIJCOSX計算比起用def2-QZVPP/J更耗時,所以從實際耗時上aug-cc-pVTZ吃虧。
(2)aug-cc-pVTZ的彌散函數容易引基函數線性依賴問題導致收斂困難。而def2-QZVPP/(-g,-f)的最外層基函數是半彌散的,既適合弱相互作用計算,也不至于帶來收斂上的問題。
(3)DFT-D3參數本身是在def2-QZVP下擬合的,用在def2-QZVPP/(-g,-f)上也可以說是完美的,而aug-cc-pVTZ雖然本身很適合弱相互作用的計算,但對于使用DFT-D3校正的情況比起def2-QZVPP/(-g,-f)是沒有優勢的。盡管aug-cc-pVTZ的彌散函數使得BSSE問題比def2-QZVPP更小,但后者的BSSE問題其實已經很小了,而且這一丁點問題已經被等效地吸進DFT-D3的參數里了。
第(3)點討論也表明沒必要,也不應該在DFT-D3校正結合def2-QZVPP/(-g,-f)使用時使用Counterpoise校正處理BSSE問題,不光是此基組BSSE問題已經很小,沒多少校正余地,還因為DFT-D3參數已經等效地考慮了此基組殘余的這點BSSE問題,再去做Counterpoise校正反倒會引入誤差。而且做這個校正還會多花幾倍的時間。
雖然本文討論的是弱相互作用計算,但是上面推薦的8種計算級別就算是對于一般類型問題的研究也是十分理想的。但是此時def2-QZVPP就沒必要用了,建議降到def2-TZVPP來節省時間。
MP2和雙雜化泛函的積分變換過程是很耗儲存資源的,對于大體系,光是儲存在內存往往不夠,還需要在硬盤上大量讀寫數據。在ORCA里可以指定積分儲存方式來降低儲存消耗,以盡量減少甚至避免因硬盤的讀寫而拖慢速度。儲存方式包括UCDOUBLE、CDOUBLE、UCFLOAT和CFLOAT四種。UC代表不壓縮數據,C代表壓縮。壓不壓縮不影響結果,壓縮后可一定程度減少儲存資源的使用量(減少得比較有限)。DOUBLE代表雙精度方式儲存積分,FLOAT代表單精度方式儲存積分,比雙精度所需儲存資源減小了一倍。對于單點計算,單精度儲存積分完全沒有問題,對結果的帶來的誤差筆者發現在1E-8a.u.級別,比密度擬合近似帶來的誤差小得多得多。不過據說個別情況下用單精度儲存時MP2梯度和弛豫的密度對個別體系有誤。顯然CFLOAT是最省內存的模式,而默認的UCDOUBLE是最耗內存的。對于小體系用默認的UCDOUBLE就行,對于大體系,如果儲存資源緊張或者長時間狂讀寫硬盤,建議用CFLOAT(直接寫上這個關鍵詞就行),盡管壓縮/解壓過程會耗費計算量,但是由于降低了硬盤讀寫量,而硬盤I/O速度又是計算機的瓶頸,所以對于整個計算是有加速效果的。
通常認為6-31+G*是計算弱相互作用的底限基組,再低就沒可信度了,像是M062X/6-31+G*這種組合通常來說是窮得不能再窮的弱相互作用計算級別。而使用ORCA的話,在下面將會看到原本這種級別算起來都吃力的情況都可以享受def2-QZVPP(-g,-f)。而更大的體系,也不必窘迫地糾結于如何在有限的計算能力下以最好的方式設定彌散函數,gCP優雅地擺脫了弱相互作用計算對彌散函數的依賴性。
2018-Apr-30補充:對于一百多個原子的情況,目前筆者最推薦的是Grimme在2018年提出的B97-3c方法,而不再推薦上文提到的BLYP-gCP-D3。B97-3c在ORCA中已經支持,它是修改版B97純泛函與mTZVP基組、D3校正、SRB校正的組合。SRB (short-range basis)用于校正純泛函高估鍵長的問題。mTZVP是def-TZVP的修改版,減少了氫的極化而增加了氧的極化,對Ar之后用的是def2-TZVP。B97-3c沒有gCP校正項,因為此項的效果在參數化過程中已直接等效體現進去了。B97-3c的耗時高于前面提到的HF-3c,而精度好得多。不過由于純泛函在ORCA中可以充分利用RIJ加速,因此對于大體系其實比HF-3c耗時高得很有限。
4 實例
這一節將通過多個實例展現不同計算級別下的耗時,體系由大到小。計算條件就是普通的家用機的條件,CPU為Intel i7-2630QM(4核,最高頻率2.5G),雙通DDR3-1333 16GB內存。系統為Win7-64bit。ORCA為3.0.1版,Gaussian為09W A.02版,MOPAC2012為13.331W版。Gaussian計算時都用了SCF=conver=6關鍵詞,因為G09默認的Tight收斂限過嚴,所以適當降低點以節省時間(依然足夠精確)。計算時間統計的是實際總耗時而非CPU時間,若未注明都是開啟了四核并行。計算任務都是算體系的單點能。
下面實例中如果測試了多個計算方法,則方法前面打星號的是筆者推薦的用于這個體系的計算級別。
4.1 水盒子
兩個水盒子的結構如下

水盒子1:12426atoms
PM7 MOZYME 4threads 14.4min,-282616.10434 KCAL/MOL,內存用了1.2GB
水盒子2:25095atoms
PM7 MOZYME 4threads 98.6min,-576587.48001 KCAL/MOL,內存用了4.5GB
可見即便是一兩萬個原子的體系,在普通計算條件下,利用MOPAC2012結合它特有的MOZYME技術也照樣能應付得了。如果內存足夠大,做到幾萬個原子的體系也是有可能的,完全能計算納米級別體系的弱相互作用。
4.2 ETK蛋白,3944個原子
PM7 MOZYME 1/4threads 323.8/325.5s -16765.64836 KCAL/MOL,用了300MB內存
可見對于幾千個原子的普通大小的蛋白,用MOPAC2012來計算易如反掌。同時也看到在目前的MOPAC2012 13.331W版里,對于MOZYME計算,用單線程和4線程實際上速度基本沒有差異。由于并行化目前還沒帶來什么效果,為了最大程度利用計算資源,如果你有n個核,可以同時算n個任務。MOPAC原本是不支持并行的,在撰寫本文時MOPAC2012才剛剛支持并行不久,估計是程序現階段還沒把MOZYME的并行化搞好。
其它半經驗方法的耗時
PM6-DH+ MOZYME 4threads 349.6s -16405.40799 KCAL/MOL
PM6 MOZYME 4threads 342s -14168.08555 KCAL/MOL
PM3 MOZYME 4threads 330s -10619.64239 KCAL/MOL
RM1 MOZYME 4threads 295s -13358.60313 KCAL/MOL
AM1 MOZYME 4threads 271s -10033.36276 KCAL/MOL
可見,不同半經驗方法耗時大致都在一個水平上。從生成焓來看,PM6-DH+和PM7的結果很接近,然而AM1和PM3則大大低估了生成焓,在很大程度上和它們表現弱相互作用很差有關。而RM1和PM6的結果則介于AM1/PM3和PM7之間,在側面上說明RM1、PM6對弱相互作用的表現能力可能在AM1/PM3和PM7之間。
4.3 DNA
這是個DNA片段,左圖共380個原子,含6個堿基對兒;右圖共754個原子,含12個堿基對兒
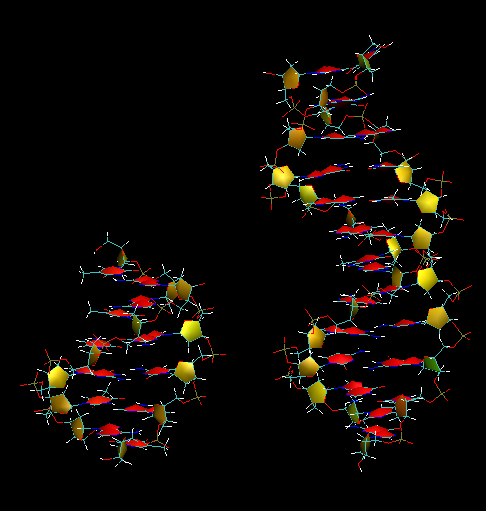
754個原子
PM7 4threads 超過7小時計算尚未完成
PM7 MOZYME 1/4threads 58.88/57.8s -1161.85336 KCAL/MOL
可見MOZYME極其重要,不用MOZYME根本沒法算。
389個原子
PM7 1/4threads 56.2s/34.6s -2463.90001 KCAL/MOL
PM7 MOZYME 4threads 10.9s -2463.88277 KCAL/MOL
*BLYP D3 GCP(DFT/SVP) def2-SVP def2-SVP/J 124min
這樣幾百個原子的體系在MOPAC中不用MOZYME終于也能算了,并且并行化終于對計算速度有提升,但是并行效率還是很低。開了MOZYME后計算時間能省好幾倍。MOZYME帶來的誤差可見非常之小,僅有0.117kcal/mol,對于幾百個原子的體系完全可以忽略不計。
得益于RI-J技術,在ORCA中,BLYP在def-SVP基組(大小與6-31G**相仿佛)下也能容易地處理這樣好幾百個原子的大體系!并且結合DFT-D3和gCP校正,弱相互作用計算準確度很不錯。
4.4 DNA小片段-小分子復合物,196個原子
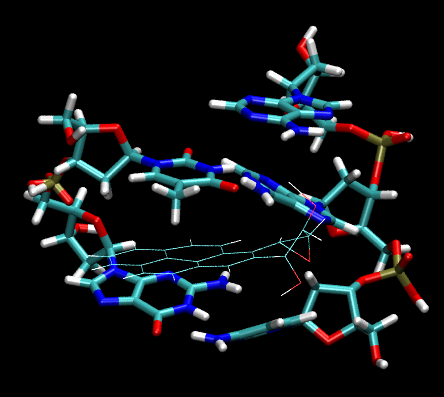
PM7 MOZYME 4threads 2.5s
*BLYP D3 GCP(DFT/TZ) def2-TZVP def2-TZVP/J 91.4min
BLYP D3 GCP(DFT/SVP) def2-SVP def2-SVP/J 21.7min
對這樣的約200個原子的體系,半經驗計算只需要一眨眼的功夫,做幾何優化也非常容易。BLYP在def2-TZVP級別也能很容易地計算,僅花了一個半小時,雖然比起用def2-SVP長了幾倍,但還是值得的。
4.5 包夾復合物,92個原子
這實際上是Grimme的S12L弱相互測試集(Chem.Eur.J.,18,9955(2012))中的體系2a。
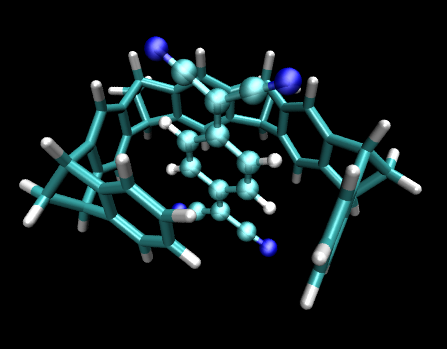
*BLYP D3 def2-QZVPP(-g,-f) def2-QZVPP/J 58.3min
BLYP D3 def2-QZVPP def2-QZVPP/J 116min
BLYP D3 GCP(DFT/TZ) def2-TZVP def2-TZVP/J 20.3min
B3LYP D3 GCP(DFT/TZ) def2-TZVP def2-TZVP/J RIJCOSX 126min
在BLYP下,可見def2-QZVPP(-g,-f)比def2-QZVPP節省了一半時間,閹割掉的高角動量函數對于DFT計算準確度的影響很小,所以建議用def2-QZVPP(-g,-f)結合BLYP。如果降低一個計算檔次用TZVP,那就更容易了,看完一話新番(而且還跳OP、ED),正好就算完了。這么大的體系,靠ORCA在QZ級別下做計算僅用1個小時,而要讓Gaussian算還不知道得算到猴年馬月去。
雜化泛函B3LYP,即便靠RIJCOSX加速,計算耗時還是比相同基組下的開了RI-J的純泛函多了好幾倍,TZ下都比BLYP在QZ下慢,所以劃不來,何況在D3+gCP校正下B3LYP幾乎并不比BLYP強。
4.6 C60
B3LYP def2-TZVP(-f) def2-TZVP/JK RIJK 159.8min 11cyc -2285.47162975a.u.
*B3LYP def2-TZVP(-f) def2-TZVP/J RIJCOSX 47.6min 10cyc -2285.47245742a.u.
此例主要展示一下RIJCOSX和RI-JK的差異。可見對于這種大小的體系,RIJCOSX的計算速度已經完勝RI-JK。二者間能量差有0.00083(0.52kcal/mol),誰更接近準確值不好說,不過肯定都差得不大。
4.7 GCGC四堿基堆疊,57個原子
RI-PWPB95 D3 RIJCOSX def2-QZVPP(-g,-f) def2-QZVPP/J def2-QZVPP/C grid4 tightSCF 134.1/405.8min
斜杠前是SCF步驟的耗時,斜杠后是總耗時。將近60個原子的體系,睡一覺的功夫,在QZ級別下雙雜化泛函計算就完成了,這個級別下的弱相互作用計算精度已經很完美了。
4.8 多環芳烴,37個原子
BLYP D3 def2-QZVPP(-g,-f) def2-QZVPP/J grid5 (同時寫上%method FinalGrid 6 end) 10.0min -996.4176595a.u.
BLYP D3 def2-QZVPP(-g,-f) def2-QZVPP/J grid4 8min -996.4176418a.u. Error=0.01kcal/mol
BLYP D3 def2-QZVPP(-g,-f) def2-QZVPP/J 5.8min -996.4173819a.u. Error=0.17kcal/mol
B3LYP D3 def2-QZVPP(-g,-f) def2-QZVPP/J RIJCOSX grid4 gridx4 56.4min -996.1652457a.u.
B3LYP D3 def2-QZVPP(-g,-f) def2-QZVPP/J RIJCOSX grid4 44min -996.1651966a.u. Error=0.03kcal/mol
B3LYP D3 def2-QZVPP(-g,-f) def2-QZVPP/J RIJCOSX 42.3min -996.1650320a.u. Error=0.13kcal/mol
B3LYP D3 def2-QZVPP(-g,-f) def2-QZVPP/JK RIJK grid4 35.2min -996.1646612a.u.
RI-PWPB95 D3 def2-QZVPP(-g,-f) def2-QZVPP/JK def2-QZVPP/C RIJK grid4 tightscf 39.5/67.3min -996.1346210a.u.
RI-PWPB95 D3 def2-QZVPP(-g,-f) def2-QZVPP/J def2-QZVPP/C RIJCOSX grid4 tightscf 57.2/87.6min -996.1351977a.u.
*RI-PWPB95 D3 def2-QZVPP def2-QZVPP/JK def2-QZVPP/C RIJK grid4 tightscf 57.5/99.3min -996.1694133a.u.
可見BLYP在QZ級別下算這種大小的體系非常輕松,也就是B站看兩個MAD的功夫。
測試中比較了積分格點對結果和耗時的影響。BLYP的計算以Grid5 + FinalGrid 6作為參考值,檢驗了其它格點設定下的誤差。可見在grid4的時候結果已經非常精確了,沒必要再提高到grid5。用默認的積分格點比grid4時快30%,但會因此帶來誤差(0.16kcal),倒是完全屬于可以接受的范圍。
可以看到B3LYP的耗時比BLYP高了一個數量級。RI-JK對大體系的速度遠不如RIJCOSX,但是對于原子較少的此例,RI-JK反倒還占了點優勢。建議在幾十個原子的范圍內使用RI-JK。由于此例比C60要小,所以RIJCOSX和RI-JK間的結果差異更小,僅為0.23kcal/mol。標注的Error是相對于grid4 gridx4時的誤差。可見RIJCOSX的格子設定對于結果影響甚微,用gridx4比用默認的格子耗時增加了不少,但是結果并沒什么差異。對于雜化泛函的計算,由于用grid4額外增加的耗時相對于總耗時甚微,所以建議總是寫上grid4,特別是打算做雙雜化泛函計算時。
對于雙雜化泛函,用RI-JK照樣比RIJCOSX快。RI-JK時,使用def2-QZVPP(-g,-f)基組,SCF和微擾部分分別占了總耗時的58.7%和41.0%,微擾部分耗時比SCF部分還低。整個PWPB95計算時間比B3LYP僅多了不到一倍,而精度提升不少,所以用ORCA做雙雜化泛函真是超劃算!像這樣幾十個原子的體系強烈建議在PWPB95/def2-QZVPP(-g,-f)級別下做。把def2-QZVPP(-g,-f)提升到def2-QZVPP給總耗時帶來了近一半的增加,雖然看似對絕對能量影響明顯,實際上對相對能量影響甚微。如果你是完美主義者不喜歡閹割,不妨用def2-QZVPP。
用這個體系,我們也比較一下G09和ORCA的速度差異。斜杠前是平均每輪迭代的耗時。下面討論的一律是平均每輪迭代的時間,因為影響迭代次數的因素復雜,總時間不易公平比較。
Gaussian09 A.02:
BLYP/def2-SVP 0.29/3.8min 13cyc -995.123921070
B3LYP/def2-SVP 0.48/5.3min 11cyc -995.505684
M062X/def2-SVP 0.59/6.5min 11cyc -995.110736706
BLYP/def2-TZVP 3.0/42.4min 14cyc -996.230052831
B3LYP/def2-TZVP 9.3/102min 11cyc -996.593814788
-----(括號內代表密度擬合帶來的加速比)
BLYP/TZVP 0.68/13.7min 20cyc -996.1872818
BLYP/TZVP/Auto 0.34/4.8min(2.0x) 14cyc -996.1887121 Error=0.90kcal/mol
BLYP/TZVP/TZVPfit 0.25/3.5min(2.7x) 14cyc -996.1908830 Error=2.26kcal/mol
ORCA(noRI代表避免默認使用密度擬合):
BLYP def2-SVP noRI 0.47/5.6min 12cyc -995.12384177
B3LYP def2-SVP noRI 0.5/5min 10cyc -994.92024998
M062X def2-SVP noRI 0.6/4.2min 7cyc -995.10510837
M062X def2-SVP noRI grid4 0.67/4.7min 7cyc -995.11062471
BLYP def2-TZVP noRI 6.5/84.7min 13cyc -996.22983135
B3LYP def2-TZVP noRI 7.7/77.3min 10cyc -996.00838771
-----(括號內代表密度擬合帶來的加速比)
BLYP def2-SVP def2-SVP/J 0.06/0.72min 12cyc(7.8x) -995.12468812 Error=0.53kcal/mol
BLYP def2-TZVP def2-TZVP/J 0.18/2.2min(36.1x) 12cyc -996.23055140 Error=0.31kcal/mol
BLYP def2-SVP def2-SVP/JK 0.06/0.73min 12cyc(7.8x) -995.12417598 Error=0.21kcal/mol
BLYP def2-TZVP def2-TZVP/JK 0.2/2.4min(32.5x) 12cyc -996.23023270 Error=0.25kcal/mol
B3LYP def2-SVP def2-SVP/J RIJCOSX 0.25/2.5min(2.0x) 10cyc -994.9211858 Error=0.59kcal/mol
B3LYP def2-SVP def2-SVP/JK RIJK 0.34/4.1min(1.5x) 12cyc -994.9203942 Error=0.09kcal/mol
B3LYP def2-TZVP def2-TZVP/JK RIJK 0.98/11.8min(7.8x) 12cyc -996.0085860 Error=0.12kcal/mol
我們先考察不使用密度擬合時BLYP、B3LYP、M06-2X在def2-SVP和def2-TZVP下的平均每輪迭代時間,ORCA對于純泛函速度慢于Gaussian不少,而雜化泛函和meta雜化泛函下兩個程序速度在伯仲之間。計算耗時顯然都是M062X>B3LYP>BLYP。ORCA下使用meta雜化泛函計算時務必加上grid4,否則由數據可見誤差能達到3kcal/mol的程度,這是因為眾所周知meta雜化泛函對格點敏感性較高(而G09所用的積分格點精度比ORCA高不少,所以不用做特殊考慮)。ORCA和Gaussian的BLYP及M062X結果相符程度較好,但B3LYP相去甚遠,這是因為ORCA的B3LYP用的是25%的HF成份而非原文定義以及Gaussian中所用的20%成份。ORCA里寫B3LYP/G才是用B3LYP的原始定義,此時def2-SVP下的結果為-995.5056201,和Gaussian的結果很相符。
比較可見,在Gaussian中用B3LYP/def2-TZVP算這個體系,每輪迭代的時間都足夠ORCA啟用RI-J時做一次BLYP/def2-QZVPP(-g,-f)任務!整個B3LYP/def2-TZVP的耗時在ORCA中做一次PWPB95/def2-QZVPP都綽綽有余!同時可見,隨著基組從def2-SVP增大到def2-TZVP,Gaussian的總耗時增加一個多數量級,若讓Gaussian做B3LYP/def2-QZVPP,耗時可能都夠ORCA跑幾十次PWPB95/def2-QZVPP了!
下面再來考察密度擬合給計算速度和結果帶來的影響。通常大家不怎么提Gaussian的密度擬合,主要原因是Gaussian在這方面比較殘疾,支持的密度擬合基組太少,而且加速不明顯,另外也只支持RI-J,而不支持加速交換部分和MP2部分。Gaussian中自帶的TZVP密度擬合基組是給老版本TZVP用的,寫成BLYP/TZVP/TZVPfit形式來使用,比起BLYP/TZVP加速比僅僅是2.7x,雖然有效果,但是比較有限,而且引入的誤差達到2.26kcal/mol,是不可忽略的。Gaussian也支持自動生成密度擬合基組,寫上Auto即可,前文提到過這樣自動生成的密度擬合基組較大,所以加速比降到2.0x,但是精度比標配的TZVPfit好,引入的誤差為0.9kcal/mol。
再來看ORCA的密度擬合。RI-J使得使用/J輔助基組下BLYP/def2-SVP的計算速度達到noRI時的7.8倍,對于def2-TZVP,加速比則達到了36倍!和原先已經完全不在一個境界了。對于B3LYP,在使用def2-SVP基組時,RI-JK和RIJCOSX都沒給計算速度帶來質的提升,然而在def2-TZVP基組時,提升顯著,速度是原先的7.8倍,但比起RI-J的提升幅度還是差得很遠。原因在之前討論過,密度擬合技術加速交換部分比起加速庫侖部分難得多。另外測試結果也清楚體現出基組越大密度擬合帶來的收益越顯著,這在前面也已經討論過。
密度擬合引入的誤差和體系大小有一定關系,對這個體系ORCA的RI引入的誤差<0.6kcal/mol,是完全可以接受的(別忘了實際關心的是相對能量,能抵消很多),這比起Gaussian的密度擬合的誤差小得多。此例RI-JK的誤差看起來甚小,既有巧合成份,一定程度上也得益于計算庫侖部分用了比/J更大的/JK輔助基組,至少證明了RI-JK是很可靠的,在高精度弱相互作用計算中使用RI-JK是可以放心的。注意對于BLYP的計算,如數據所示,如果把/J輔助基組改成更大的/JK,RI-J雖然多耗時一點點,但是誤差減小了。也即是說,RI-J和RIJCOSX計算中若想減少誤差,使用比/J更大的/JK是個聰明的辦法,盡管/JK原本是為了做RI-JK才提出的。
5 總結
大抵從2005年起,弱相互作用計算技術的發展就在飛速發展中,而且還在不斷加速,benchmark文章已經滿天飛,特別是DFT-D受關注度極高。但是,除了DFT-D,正如本文所介紹討論的,還有很多其它理論方法、數值技術和程序上的進展都給弱相互作用計算的領域帶來深刻變革,重要程度絲毫不亞于DFT-D。本文在第3節給出的推薦是筆者認為在撰文時最佳的用于各種尺度體系的弱相互作用計算方法。想必在幾年之后,又有更多更好的方法、技術被提出并在主流程序中實現,本文推薦的方法屆時肯定還需要根據實際形勢進行一定調整。
值得一提的是,在《18碳環(cyclo[18]carbon)與石墨烯的相互作用:基于簇模型的研究一例》(http://www.shanxitv.org/615)介紹的筆者的論文中對約200原子的非常大的復合物體系做了幾何優化、振動分析和高精度弱相互作用計算,在里面有很多對計算級別選擇的討論,很建議讀者一讀,是對本文的補充。