談談能量的基組外推
1 前言
量子化學計算中一個主要的誤差來源是基組不夠大,或者說距離完備基組極限差距較大。用越大的基組計算耗時越多。對于一些性質,如能量、優化出的結構、偶極矩等,隨著基組的增大計算結果會逐漸收斂。只要知道收斂趨勢的數學形式,就可以通過較小的基組的計算結果外推出較大基組下的結果,乃至完備基組(Complete basis set, CBS)下的結果。對于很高精度計算,例如小體系高精度弱相互作用計算,外推到CBS已經成了司空見慣的做法。本文將介紹單點能外推至CBS的方法,并給出實例。2 HF/DFT能量的外推
基組外推的前提條件是所用的基組序列必須是以系統方式構建的。對于這樣的基組序列,隨著基組的增大,可以確保結果的誤差逐步、平穩地降低,有明確的收斂趨勢。對于Dunning相關一致性基組(cc-pVnZ系列、aug-cc-pVnZ系列等)、ANO系列基組、Jensen的極化一致性基組(pc-n系列)、Ahlrich的def2系列基組等,都符合這個要求。比如可以用cc-pVDZ、cc-pVTZ、cc-pVQZ計算的三個能量外推到CBS的能量。而諸如Pople系列基組則不符合要求,例如不適合使用諸如3-21G*、6-31G*、6-311+G(2d,p)的計算結果外推至CBS,雖說他們的誤差肯定越來越小,但誤差降低的趨勢并不平滑,沒有可循的收斂趨勢以用于外推。基組外推的公式并不唯一,有的簡單有的復雜。對于不同基組序列,最佳的外推公式也可能有微小的不同。
對于Dunning相關一致性基組(或ANO系列),SCF能量(指HF、DFT能量)收斂趨勢符合以下指數關系,可以通過它們來外推至CBS:
E_SCF(L)=E_SCF(∞)+A*exp(-α*L)
或
E_SCF(L)=E_SCF(∞)+A*exp(-α*√L)
這兩種用誰都可以,結果差異甚小。其中A、α是需要確定的參數,E_SCF(∞)就是我們最終想要得到的CBS下的SCF能量。L是基組所含基函數所具有的最高角量子數。例如對于Dunning相關一致性基組,L=2對應cc-pVDZ,因為它對于主族重原子最高角動量為d,角量子數是2。類似地,L=3對應cc-pVTZ、L=4對應cc-pVQZ...由于式中包含E_SCF(∞)、A、α這三個常數,所以原則上需要按基組由低到高依次計算三次能量才能獲得它們。顯然最便宜的選擇就是用DZ/TZ/QZ來外推,此時結果已經很準了,一般沒必要用更高貴的諸如TZ/QZ/5Z來外推。
為了避免外推時的麻煩,對于不同的基組序列有人事先擬合了α參數,因此實際外推時只需要計算兩次能量就行了。以下數值取自ORCA手冊2.9版6.1.3.4節
對于cc-pVnZ系列,L=2/3的外推α=4.42,L=3/4的外推α=5.46
對于def2系列,L=2/3的外推α=10.39,L=3/4的外推α=7.88
假定α是已知量,我們就可以直接寫出E_SCF(∞)的表達式。設
E_SCF(N)=E_SCF(∞)+A*exp(-α*√N)
E_SCF(M)=E_SCF(∞)+A*exp(-α*√M)
2式可寫為A=[E_SCF(M)-E_SCF(∞)]/exp(-α*√M),代入1式,經過整理得:
E_SCF(∞) = [ E_SCF(M)*exp(-α*√N) - E_SCF(N)*exp(-α*√M) ] / [exp(-α*√N) - exp(-α*√M)]
由于HF、DFT形式上是基于單電子近似的,所以基組只要能夠合理表現出單電子性質就夠了,這對基組質量要求并不很高,因此能量隨基組增大收斂得也比較快。SCF計算通常在3-zeta級別結果已經很好了,4-zeta級別就挺接近CBS極限了。因此對于SCF計算做CBS外推的意義不是非常大。另外順帶一提的是,單電子性質實際上并不需要很高角動量來描述,比如對于主族元素,角動量函數達到f就已經足夠了,引入g及更高角動量函數對結果幾乎不會有什么改進,遠不如把計算量投入在增加低角動量的基函數上來得有用。
3 相關能的外推
后HF計算在HF基礎上考慮了電子相關作用(主要是庫侖相關)以改進結果。合理描述電子相關作用就要能夠較好地描述出電子間的相關穴。由于這是雙電子性質,明顯比描述單電子性質對基組質量有更高的要求。尤其是相關穴的cusp(歧點)特征,對于非R12/F12方式的后HF計算,需要很大基組才能充分準確描述(高角動量函數起著關鍵性作用),這是由于通過單電子基函數乘積的方式來描述cusp效率很低所致。由于內在本質的不同,相關能的收斂趨勢和HF能量的收斂趨勢也有顯著不同,因此在外推時需要分別進行,最后將CBS下HF能量和CBS下相關能加和得到總的CBS能量。(注:雖然HF波函數能夠在當前級別下精確表現Fermi相關,這是雙粒子性質無誤,但實際上它是Slater行列式的反對稱化的要求而自然而然產生的,并非是靠大基組來表現的)
Klopper-Helgaker的形式是最常用的外推相關能的方法,理論依據也最明確,即:E_corr(L)=E_corr(∞)+A*L^(-3)
實際上,自旋相同電子間(singlet pair)的相關能和自旋相反電子間(triplet pair)的相關能收斂趨勢也是不同的,前者隨L^(-3)而收斂,后者隨L^(-5)而收斂,嚴格的做法是分別擬合這兩種相關能。但由于后者隨L增加明顯收斂得更快,因此通常在外推時不考慮后者,而直接用上面給出的外推公式。
Klopper-Helgaker公式只含兩個未知量E_corr(∞)和A,因此只需要用基組序列中L相鄰的兩個基組各算一次能量即可。假設一個是L=M,一個是L=N,則
E_corr(M)=E_corr(∞)+A*M^(-3)
E_corr(N)=E_corr(∞)+A*N^(-3)
第二個式子可寫為A=[E_corr(N)-E_corr(∞)]/N^(-3),代入到第一個式子,得
[E_corr(M)-E_corr(∞)]*M^3=[E_corr(N)-E_corr(∞)]*N^3
整理一下,得到了明確的CBS相關能計算公式:
E_corr(∞) = [E_corr(N)*N^3 - E_corr(M)*M^3] / (N^3 - M^3)
由于相關能隨基組收斂得較慢,所以外推是很有必要的。選用基組序列中哪兩個基組外推相關能是很關鍵的問題,直接影響外推結果準確度。對于實在算不動的情況,就用DZ/TZ來外推,但由于DZ級別質量太低,不能指望外推出的結果真的能接近CBS極限,實際上也就是比TZ強一點罷了,甚至更糟也有可能。通常都用TZ/QZ來外推,這樣的結果比較可靠,但也仍不能指望達到CBS極限。可以期望外推出的結果精度會比外推時所用的最大基組高出一級,如TZ/QZ推出來的約是5Z的精度(視具體情況而定,可能比5Z更好或更差),這樣的精度已經相當高了。
Truhlar等人的相關能外推公式更為廣義:
E_corr(M)=E_corr(∞)+A*M^(-β)
當β=3,就回到了Klopper-Helgaker公式。為了使外推更準確,對不同基組序列應擬合不同的β值,下面列舉一些(更多的見ORCA手冊里基組外推部分)
對于cc-pVnZ系列,L=2/3的外推β=2.46,L=3/4的外推β=3.05
對于def2系列,L=2/3的外推β=2.4,L=3/4的外推β=2.97
由于對于L=3/4的外推β很接近3,所以此時或更高級別的外推建議都用3,理論依據更強。而L=2/3的外推時β建議用擬合值。
另外也有別的小眾一些的外推方法,比如Varandas提出的,見JCP, 126, 244105 (2007),結果和上面介紹的沒什么區別,形式還更為復雜,這里就不再多提了。需要外推至CBS都是高精度計算的場合,因此必須計算方法精度也必須比較高才能讓總能量誤差較小。然而高級別方法結合大基組的計算往往無福消受,這時候可以運用一些技巧。例如,一種常見的近似獲得CCSD(T)/CBS下相關能的方法是:
E_corr(∞)_CCSD(T) ≈ E_corr(∞)_MP2 + [ E_corr(Small)_CCSD(T) - E_corr(Small)_MP2 ]
也就是說在MP2級別下將相關能外推到CBS,然后加上小基組下CCSD(T)和MP2相關能的差值,就近似獲得了CCSD(T)下外推到CBS的相關能,這比起直接在CCSD(T)下外推省時多了。當然,這個近似成立的條件是CCSD(T)和MP2的相關能差異受基組影響不大,實際上這個條件通常是合理的。
4 實例:N2的能量外推
這里以N2作為具體例子來外推HF能量和MP2相關能。以下是cc-pVDZ/TZ/QZ/5Z/6Z計算的能量(hartree),鍵長為1.100314埃,Δ代表相關能部分。E_HF(DZ)=-108.953748406
E_HF(TZ)=-108.982940693(-0.029192287)
E_HF(QZ)=-108.990532392(-0.007591699)
E_HF(5Z)=-108.992208035(-0.001675643)
E_HF(6Z)=-108.992531280(-0.000323245)
ΔE_MP2(DZ)=-0.3070859654
ΔE_MP2(TZ)=-0.3743967513(-0.067310786)
ΔE_MP2(QZ)=-0.3994430246(-0.025046273)
ΔE_MP2(5Z)=-0.4098026746(-0.010359650)
ΔE_MP2(6Z)=-0.4145085175(-0.004705843)
括號里是相對于上一個數值的變化,將它作圖,如下所示
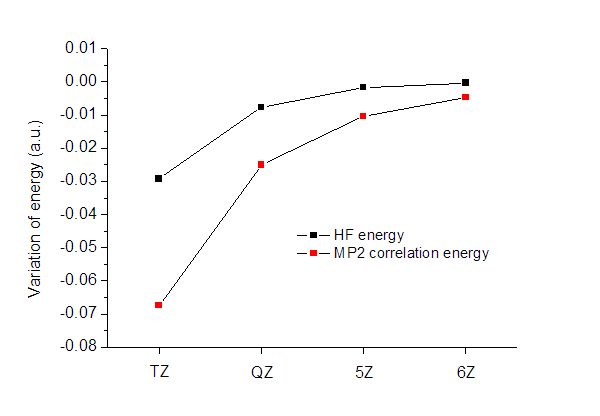
可見,HF能量收斂得明顯要比相關能快得多,QZ級別的HF能量精度已經很高了,而相關能收斂得卻仍不十分充分。雖然相關能占總能量比重很小,但是相關能計算的不準確卻是總能量誤差的主要來源。
利用第二節的HF能量外推公式,以及L=2/3時α=4.42、L=3/4時α=5.46的參數,可以得到以下結果,這可以方便地用Excel來做。括號里是相對于外推時用的最大基組下結果的差值。
E_HF(DZ/TZ->CBS)=-108.9924345(-0.014689896)
E_HF(TZ/QZ->CBS)=-108.9928198(-0.002287408)
通過比較可見,用DZ/TZ外推的結果頗接近直接用6Z計算的結果。而TZ/QZ外推的結果明顯比起6Z更為精確,可以認為就是CBS極限的結果了。
利用第三節的Klopper-Helgaker相關能外推公式,可以得到以下結果
ΔE_MP2(DZ/TZ->CBS)=-0.402738135(-0.0283413837)
ΔE_MP2(TZ/QZ->CBS)=-0.417720035(-0.0182770104)
通過比較可見,用DZ/TZ外推的結果介于QZ和5Z之間(更接近于QZ)。TZ/QZ外推的結果比6Z稍好點。和外推HF能量相比,外推相關能對總能量的影響明顯更大,這凸顯了相關能外推的重要性。另外也看出,相關能外推的效果比起HF能量外推要弱,沒法在較低級別基組下就一下子外推出很高級別基組下的結果。又由于相關能隨基組收斂慢,所以如果對結果精度要求很高,外推相關能盡量要在TZ/QZ甚至更高級別下做,DZ/TZ外推的結果離CBS極限的差距還較大。
如果L=2/3外推時用Truhlar的公式,β用推薦的2.46,則
ΔE_MP2(DZ/TZ->CBS)=-0.413728888(-0.0393321367)
明顯比Klopper-Helgaker公式外推的結果更接近于高級別基組外推的結果。所以L=2/3外推時推薦用Truhlar公式結合最佳的β參數。
想得到由TZ/QZ外推出的MP2/CBS能量,只要將-108.9928198和-0.417720035加和即可。
要注意的是,化學上感興趣的并非總能量,而是相對能量,外推對結果的影響還是會在求差值過程中所大幅抵消的。求差值時,要么所有體系都做外推(而且要用相同基組外推),要么都不外推;如果有的外推有的不外推,結果誤差會巨大。
5 考慮BSSE時的外推
分子間相互作用能一般這樣計算,也就是所謂超分子方式計算:E_AB=E_A-E_B
E_A和E_B是兩個單體的能量。單體的幾何結構用自由狀態的還是復合物狀態的依情況而定,這和本文內容無關。
想要得到CBS下的相互作用能,就是對E_AB、E_A和E_B都按照上述過程外推至CBS能量。但實際上問題沒有這么簡單。因為計算E_AB時需要考慮基組重疊誤差(BSSE),詳見http://www.shanxitv.org/46。對于以色散作用主導的高精度計算考慮BSSE尤為重要,此時哪怕是aug-cc-pVQZ級別的計算,BSSE的影響仍不可忽視。通常就是用Counterpoise來解決BSSE,這使得復合物能量的外推過程變得略麻煩些,所以專門在這一節說說。
經過Counterpoise方式對BSSE校正后的AB能量E_AB'這樣計算(下文中的符號帶一撇皆代表做了BSSE校正):
E_AB'=E_AB+E_BSSE
E_BSSE = (E_A - E_A,bAB) + (E_B - E_B,bAB)
其中
E_AB:A、B基組下AB復合物的能量
E_A,bAB:A、B基組下A的能量
E_B,bAB:A、B基組下B的能量
E_A:A基組下A的能量
E_B:B基組下B的能量
對于后HF計算,BSSE校正能分為對HF能量的校正E_BSSE_HF和對相關能的校正E_BSSE_corr:
E_BSSE_HF = (E_A_HF - E_A,bAB_HF) + (E_B_HF - E_B,bAB_HF)
E_BSSE_corr = (E_A_corr - E_A,bAB_corr) + (E_B_corr - E_B,bAB_corr)
BSSE校正后的HF能量和相關能即為
E_AB'_HF=E_AB_HF+E_BSSE_HF
E_AB'_corr=E_AB_corr+E_BSSE_corr
以這種方式得到不同基組下的E_AB'_HF和E_AB'_corr,就可以按照前述方法直接外推出CBS下的復合物的HF能量和相關能。這樣比起在不考慮BSSE條件下,即使用E_AB_HF和E_AB_corr來外推更為合理。如果在aug-cc-pVTZ/QZ級別外推,由于BSSE的影響不是很大,所以外推時不考慮BSSE問題也不大,但如果要求精度很高,仍建議將BSSE考慮進去。
雖然諸如Gaussian程序直接提供了counterpoise關鍵詞,從而可以一步就得出E_BSSE,這對于HF/DFT很方便,但是對于后HF外推,必須得分別得到E_BSSE_HF和E_BSSE_corr,這就只能自行手算。我建議此時使用Ghost原子的方法手動依次計算A、B、A,bAB、B,bAB體系并提取各自的HF能量和相關能,然后計算E_BSSE_HF和E_BSSE_corr,而不要靠counterpoise關鍵詞,否則從輸出文件中找數據時容易弄混。如果整體有對稱性,這樣比起直接用counterpoise關鍵詞在效率上也有好處,因為counterpoise關鍵詞會對涉及的所有計算都關閉對稱性,而手動算的話,計算E_AB、E_A、E_B時還能開著對稱性以節約時間。
6 實例:考慮BSSE時外推氫氣-氮氣二聚體能量
下面就以氫氣-氮氣二聚體平行構型為例來說明怎么得到二聚體的考慮了BSSE的外推至CBS下的能量,外推通過aug-cc-pVDZ/TZ來實現,理論方法用CCSD(T),程序用G09 B.01。這是筆者在J. Mol. Model.19,5387的研究中涉及到的計算。先在CCSD(T)/aug-cc-pVTZ下計算,以下是route section和坐標部分
計算E_AB:
#p ccsd(T)/aug-cc-pvtz
N 0.00000000 0.55705000 -0.42673900
N 0.00000000 -0.55705000 -0.42673900
H 0.00000000 -0.36881700 2.98717200
H 0.00000000 0.36881700 2.98717200
計算E_A:
#p ccsd(T)/aug-cc-pvtz
N 0.00000000 0.55705000 -0.42673900
N 0.00000000 -0.55705000 -0.42673900
計算E_A,bAB:
#p ccsd(T)/aug-cc-pvtz nosymm
N 0.00000000 0.55705000 -0.42673900
N 0.00000000 -0.55705000 -0.42673900
H-Bq 0.00000000 -0.36881700 2.98717200
H-Bq 0.00000000 0.36881700 2.98717200
計算E_B:
#p ccsd(T)/aug-cc-pvtz
H 0.00000000 -0.36881700 2.98717200
H 0.00000000 0.36881700 2.98717200
計算E_B,bAB:
#p ccsd(T)/aug-cc-pvtz nosymm
N-Bq 0.00000000 0.55705000 -0.42673900
N-Bq 0.00000000 -0.55705000 -0.42673900
H 0.00000000 -0.36881700 2.98717200
H 0.00000000 0.36881700 2.98717200
HF能量就是輸出文件中SCF Done:后面的,CCSD(T)能量搜索CCSD(T)=就能找到,它減去HF能量就是CCSD(T)的相關能。計算結果如下:
E_AB_HF=-110.11354966
E_A_HF=-108.98075536
E_A,bAB_HF=-108.98078589
E_B_HF=-1.13304859
E_B,bAB_HF=-1.13305499
E_AB_corr=-0.43998843
E_A_corr=-0.39983017
E_A,bAB_corr=-0.39989990
E_B_corr=-0.03956792
E_B,bAB_corr=-0.03957422
故aug-cc-pVTZ級別下:
E_BSSE_HF=0.00003692
E_BSSE_corr=0.00007603
E_AB'_HF=-110.11351274
E_AB'_corr=-0.43991240
把上述計算在aug-cc-pVQZ下再算一遍,可得:
E_BSSE_HF=0.00001463
E_BSSE_corr=0.00003224
E_AB'_HF=-110.12069678
E_AB'_corr=-0.46017610
可見在aug-cc-pVQZ下BSSE的影響明顯比aug-cc-pVTZ要小。
由于沒有aug-cc-pVnZ的α參數,三點外推又麻煩,所以這里就不外推HF能量了,直接用aug-cc-pVQZ下的HF能量作為CBS下的。如果要外推也可以湊合用相應L=3/4的cc-pVnZ的α參數,和理想的aug-cc-pVnZ的α參數差異不會很大。
利用aug-cc-pVTZ/QZ下的E_AB'_corr,按Klopper-Helgaker公式外推得到CBS下的CCSD(T)相關能-0.47496313。將它與aug-cc-pVQZ下的E_AB'_HF=-110.12069678加和,最終得到二聚體的考慮了BSSE的CBS下的能量-110.59565991。令它減去外推到CBS的單體的CCSD(T)能量即是單體間相互作用能。