透徹認識氫鍵本質、簡單可靠地估計氫鍵強度:一篇2019年JCC上的重要研究文章介紹
透徹認識氫鍵本質、簡單可靠地估計氫鍵強度:一篇2019年JCC上的重要研究文章介紹
文/Sobereva@北京科音 2019-Sep-15
0 前言
氫鍵是最重要的分子內和分子間相互作用類型之一,盡管已經有巨量文章對其從各個角度進行探討,但即便到現在依然是一個研究的熱點,尚有很多未探究充分、透徹的問題。2019年9月,北京科音自然科學研究中心(http://www.keinsci.com)連同伊朗Islamic Azad大學以及捷克科學院的研究者,發表了一篇名為Exploring Nature and Predicting Strength of Hydrogen Bonds: A Correlation Analysis Between Atoms-in-Molecules Descriptors, Binding Energy and SAPT theory的文章,見J. Comput. Chem., 40, 2868-2881 (2019) DOI: 10.1002/jcc.26068。此文章利用量子化學計算和波函數分析,充分討論了氫鍵的本質,并提出了新的氫鍵分類和估計氫鍵強度的方法,文章內容非常具有普遍意義,內容豐富,值得關注。下面就依次對此文章的亮點和重點做簡明直白的介紹,更詳細內容請閱讀原文。此文中的波函數分析部分全部使用Multiwfn(http://www.shanxitv.org/multiwfn)程序完成。
1 亮點1:構造了具有代表性的氫鍵作用體系
為了揭示氫鍵本質、討論如何估計氫鍵強度,此文首先構造了一批氫鍵二聚體,如下所示
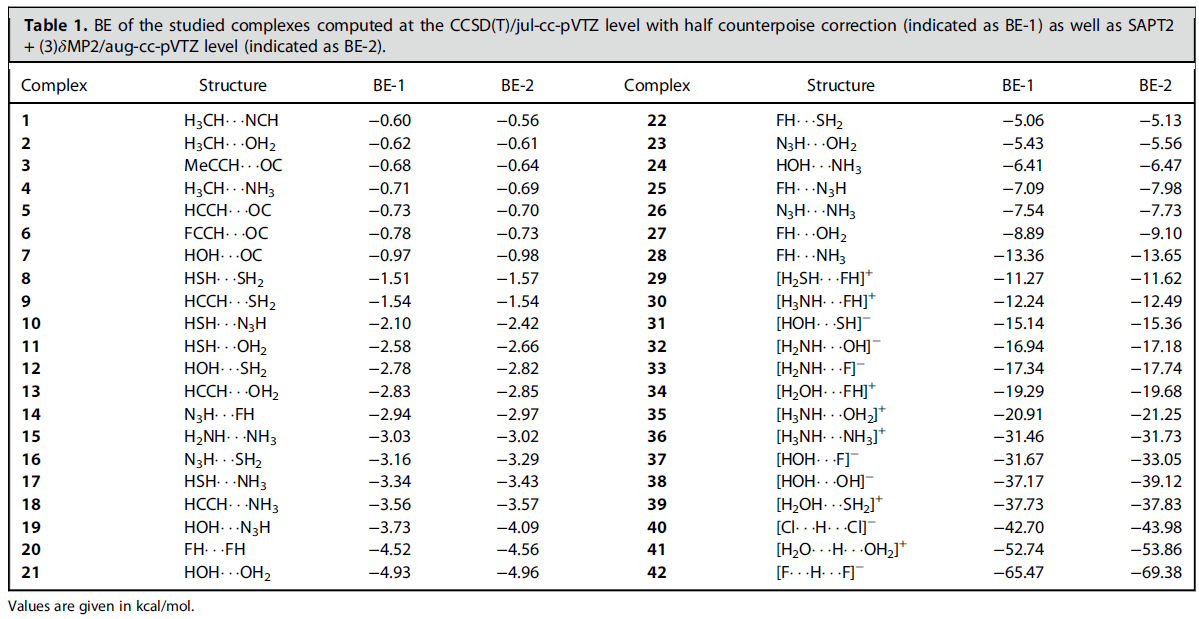
這套氫鍵二聚體有幾個特點:(1)樣本數很大,使得后續分析討論依據充分 (2)體系非常有代表性,常見的氫鍵類型X-H...Y (X,Y=O,N,F)都被納入其中 (3)中性和帶電荷氫鍵體系同時包含,結合能涵蓋了從極弱到極強所有范圍,因此可以提供關于氫鍵全面的視角 (4)樣本都是由恰當選取的小分子構成,可以充分避免氫鍵以外的作用區域對討論氫鍵時的干擾。以上體系都通過B3LYP-D3(BJ)/ma-TZVP級別做了幾何優化,所得結構可以從文章的補充材料里獲得。
如上表所示,此文通過高精度的CCSD(T)/jul-cc-pVTZ級別計算了結合能(Binding energy, BE),還通過PSI4程序通過高階SAPT方法SAPT2+(3)δMP2結合aug-cc-pVTZ基組做了能量分解并同時得到結合能。文中數據體現這樣的高階SAPT方法不僅對中性體系結果和金標準CCSD(T)非常接近,即便對于帶電荷體系也能得到合理結果,表明SAPT分析完全可以放心地用于帶電荷氫鍵。在此文的補充材料里還證明,通過代入簡單的線性回歸公式,可以令CCSD(T)/jul-cc-pVTZ級別算的結合能很好地重現更準確但也昂貴得多的CCSD(T)/CBS(TZ->QZ外推)級別算的結合能。
考慮到本文構造的氫鍵數據集非常全面、有代表性,且提供了高精度結合能數據,因此可以在未來作為檢驗更廉價計算級別計算精度的測試集。
2 亮點2:通過能量分解充分展現了氫鍵的作用本質
SAPT是目前被使用最多、最被廣為接受的能量分解方法,它能將結合能分解成不同的物理成分,從而更好地理解相互作用的本質。雖然SAPT早已被大量用于氫鍵體系的研究中,但是像此文這樣使用SAPT非常系統、全面地考察大批量典型氫鍵的文章還非常少。文中對上述42個氫鍵二聚體分別給出了結合能當中的靜電作用(Elst)、色散作用(Dis)、誘導(Ind)、交換互斥(Rep)部分各自的貢獻,其中前三項對于氫鍵的形成起到正貢獻,它們所占貢獻的比例在下圖給出
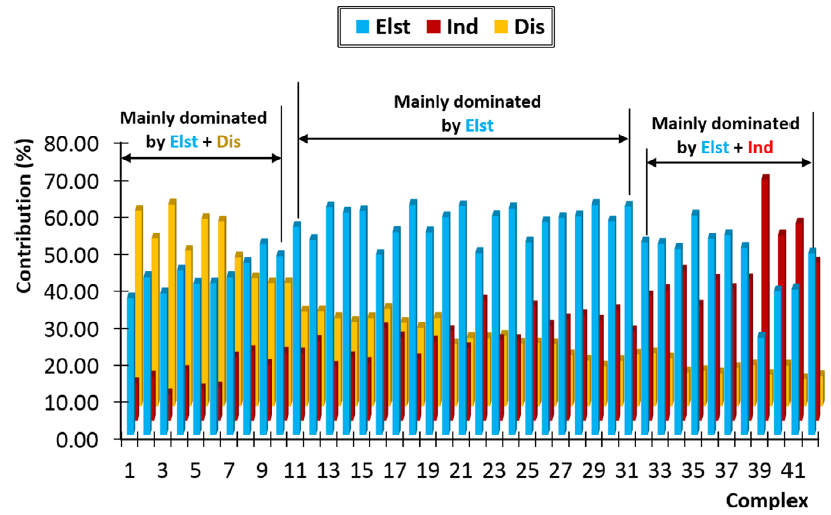
圖中前28個體系是中性氫鍵二聚體,后14個是帶電荷氫鍵作用。圖中從左到右總的排列順序是氫鍵作用逐漸增強。由圖可以一目了然發現,不同強度的氫鍵有著十分不同的本質。強度很低的氫鍵主要是通過靜電吸引和色散吸引效果一起維持的。而中等強度氫鍵,比如水二聚體,靜電吸引作用占絕對主導,而色散吸引和誘導作用一起起到輔助效果。非常強的氫鍵大多數是帶電荷氫鍵,由圖可見這種情況下靜電和誘導作用共同起到關鍵性角色,而色散作用相對而言可以忽略不計。注意SAPT方法給出的“誘導項”本質上體現的是電荷轉移、極化、軌道相互作用。
3 亮點3:一種新的氫鍵分類
根據SAPT分析數據和計算的氫鍵結合能,文中提出一種全新的氫鍵分類:

這種分類方法相對于以往其他研究者提出的分類方法的關鍵好處在于,這種分類將氫鍵強度(由結合能BE體現)和氫鍵本質直接關聯了起來。研究者們根據理論計算或實驗觀測到的氫鍵結合能,通過對照上表就能馬上認識到這種氫鍵的主要本質大概是什么。由于此文考慮的樣本較大,而且不是拘泥于特定類型體系,因此這個分類不僅可靠而且普適。再加上這個分類簡單直白,所以很適合納入教科書,對于學生正確理解氫鍵的本質很有好處。
4 亮點4:構建了氫鍵結合能與其能量成分之間的關系
按照常規邏輯,要想得到SAPT中的能量成分,肯定是要做SAPT能量分解的,但是研究者為此需要學習專門的程序的使用(PSI4或Molpro等),還需要付出計算代價。此文發現對于中性氫鍵作用體系,氫鍵結合能與各個能量成分間可以擬合出很好的線性關系,如下所示
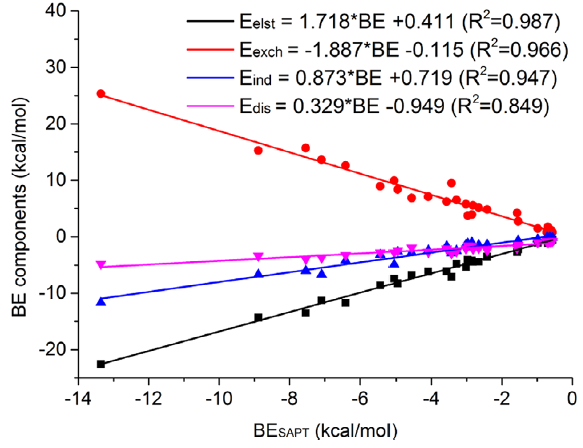
圖中的式子中自變量BE是結合能。因此研究者只要通過一般方法計算出氫鍵結合能,直接代入上面的公式,就可以立馬估計出各個SAPT能量成分了,省事極了!雖然不同的氫鍵體系都有一定個性,嚴格討論時仍免不了需要直接做SAPT計算,但至少這套關系式足夠給出定性正確的能量成分,用于粗略討論足夠了。注意用這套式子有個前提,就是你算的結合能必須確實只由某個氫鍵作用所主導,體系其它部分的作用相對而言可以忽略。
上面的圖也體現出,氫鍵的所有能量項的絕對值都是隨著氫鍵強度增加而增加的,對氫鍵形成產生正貢獻的靜電、色散、誘導作用增強時,起到負貢獻的交換互斥作用也隨之增加,很大程度上抵消掉結合作用。此外還可以看到,隨著氫鍵增強,誘導作用增加的速度明顯比色散作用增加的速度要快,即色散作用對氫鍵強度不是很敏感。對于強度只有<10 kJ/mol的弱氫鍵,色散作用不僅比誘導作用強,甚至和靜電作用起到的地位不分伯仲,而當氫鍵強度進一步增加后,色散作用起到的地位就墊底了。
5 亮點5:證明了通過氫鍵的鍵臨界點處的電子密度可以可靠地估計氫鍵強度
弱相互作用是波函數分析(wavefunction analysis)方法的常見研究對象。有很多研究者通過Atoms-in-molecules理論定義的鍵臨界點(BCP)的屬性(電子密度、電子密度的拉普拉斯函數、能量密度、勢能密度等等)分析氫鍵的本質和估計氫鍵的強度。也有些人提出了一些指標,比如CVB指數、ΔΔVn指數來考察氫鍵強度。此前有一個知名的關系是Espinoa在Chem. Phys. Lett., 285, 170 (1998)提出來的BE=V(BCP)/2,即氫鍵的結合能約等于氫鍵的鍵臨界點處勢能密度的一半。然而,Espinoa的關系局限性非常大。首先,他當年考察氫鍵體系用的結合能的計算精度在如今來看非常差,而且他的文章只考慮了X-H...O (X=C,N,O)型氫鍵。
到底被使用廣泛的Espinoa的估計氫鍵強度的公式準不準確?能不能找到更好的估計氫鍵強度的關系?這是一個極其重要的問題。因為,如果能確定一個簡單且可靠的估計氫鍵強度的方法,那么就可以比較廉價地近似得到高精度量子化學方法計算的結果。更重要的是,利用這種關系可以估計一些不容易直接計算的氫鍵鍵能。比如說分子內氫鍵鍵能就不好算,因為這通常需要把體系進行截斷、對截斷處進行飽和,還得恰當對結構進行調節以避免嚴重位阻等問題,相當麻煩。再比如,有時候兩個分子間形成多對氫鍵,一般的算分子間作用的方法只能給出總的作用能,想得到每個氫鍵各自的作用能很不容易實現。
此文將CCSD(T)算的42個氫鍵二聚體結合能與BCP處的電子密度ρ進行了線性擬合,如下所示
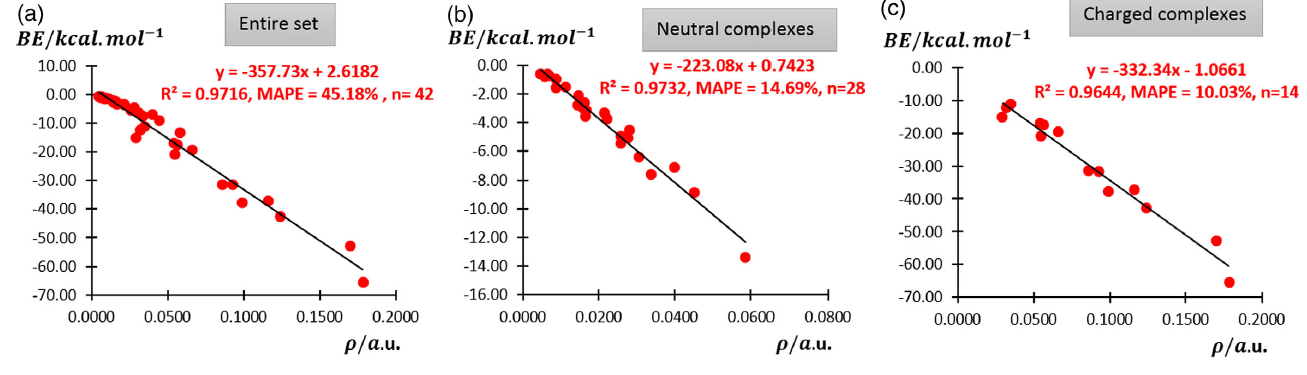
由圖可見,如果把帶電荷和不帶電荷的總共42個氫鍵體系直接擬合,雖然R^2看起來不差,但是MAPE(平均絕對百分誤差)很大,因此這樣擬合的關系在預測氫鍵作用能上沒實際意義。然而,如上圖(b)和(c)所示,若對中性和帶電荷的氫鍵二聚體分別進行擬合,那么對二者都可以得到理想的線性關系,不僅R^2很高,同時MAPE很低,擬合出的公式很有實際意義。也就是說,我們只需要對氫鍵復合物先用量子化學程序進行幾何結構優化,同時產生含有波函數的文件(如.wfn、.fch、.molden),然后用Multiwfn程序做電子密度的拓撲分析得到要考察的氫鍵的BCP處的電子密度(這個過程耗時幾乎可忽略不計),再代入圖中的公式,就可以直接得到較準確的氫鍵結合能。這樣算出的結果準不準?假設有個中性體系的氫鍵的結合能是-5.0 kcal/mol(接近水二聚體的氫鍵強度),乘上MAPE=14.69%后可知,誤差才0.7 kcal/mol而已,這樣的誤差實際上比起很多廉價方法(比如PM6-D3H4、PM7半經驗方法)得到的氫鍵結合能準得多,很多時下算弱相互作用流行的DFT泛函也未必達得到這個精度。
為了考察是否能用BCP處的其它屬性,或者一些與氫鍵有關的指標來準確預測氫鍵強度,文中也對它們與氫鍵結合能的關系做了回歸分析,MAPE如下所示

由表可見,用BCP處的能量密度(H)、bond degree(H/ρ)、勢能密度的絕對值除以拉格朗日動能密度(|V|/G),都不能通過擬合關系很好預測氫鍵強度,至少比用電子密度來預測要差不少。Espinoa提出的用V/2來預測氫鍵結合能的做法也并不理想(對中性氫鍵MAPE達到23.35%),因此從此以后不應當再用這個關系估計氫鍵結合能。至于基于電子定域化函數定義的CVB指數,以及基于原子核位置靜電勢定義的ΔΔVn指數,雖然與氫鍵結合能確實有相關性,但從上面表格里的MAPE值來看也不算理想。因此此文有個發現值得強調:雖然BCP處的電子密度是最容易算的、形式最簡單的量,但是基于它來預測氫鍵強度比用形式更復雜、看似更高級方式定義的量效果還好!
6 其它
在一些文章指出,SAPT的誘導項(E_ind)與共價作用程度有密切聯系,甚至被一些文章直接拿來衡量共價作用程度。而在一些AIM研究文章里指出BCP處的|V|/G和H/ρ與共價作用也關系密切。考慮到這點,此文將|V|/G和H/ρ向E_ind進行了擬合。結果發現對于中性體系,|V|/G與E_ind之間可以通過二次函數很好地關聯起來,暗示出BCP處|V|/G越大,氫鍵的共價成分越強,證明了將BCP處的|V|/G用于討論不同中性體系的氫鍵的共價性是合理的。
想全面研究氫鍵本質,不僅要考慮平衡位置(優化后的復合物結構)下氫鍵的特征,還應當考察不同作用距離下氫鍵的特征。因此文章的補充材料里的S3一節里取了弱氫鍵、中等強度氫鍵以及帶電荷的強氫鍵各一例,對SAPT總能量和各個分量隨作用距離的變化情況進行了掃描和分析,如下所示
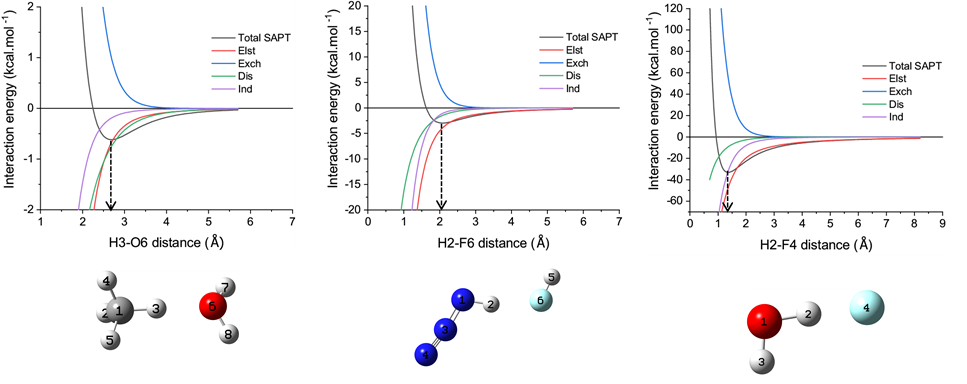
由圖明顯可見不同的作用成份隨氫鍵距離增加時衰減行為明顯不同,詳細分析討論請看原文補充材料,在這里不再細談。
7 總結
這篇JCC文章選取了非常有代表性的大批氫鍵體系,基于高精度的數據,從各個角度對氫鍵本質進行了深入的分析探討,對于正確了解氫鍵本質非常有益,并且文中給出的氫鍵分類方法和估計氫鍵結合能的方法極具實用性,值得推廣。這幾點通過此文的Table of content圖非常直觀地體現了出來(其中電子密度ρ和結合能ΔE的單位分別用的是a.u.和kcal/mol):

8 相關閱讀
本文提出的根據BCP處電子密度估計氫鍵鍵能的方法在Multiwfn手冊4.2.1節以及《計算分子內氫鍵鍵能的幾種方法》(http://www.shanxitv.org/522)中給了實際例子,你會發現用起來非常簡單,而且計算耗時極低。關于Multiwfn做AIM拓撲分析的更多信息,見《使用Multiwfn做拓撲分析以及計算孤對電子角度》(http://www.shanxitv.org/108)和Multiwfn手冊4.2節的各種例子。關于怎么用Gaussian等程序產生給Multiwfn用的輸入文件,見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。
上面提到的CVB指數的介紹和計算方法見:《使用Multiwfn計算CVB指數考察氫鍵強度》(http://www.shanxitv.org/461)。
前述的ΔΔVn指數是怎么定義的,以及如何用Multiwfn計算,見Multiwfn手冊4.1.2節。
用Multiwfn可以實現的各種研究弱相互作用的方法匯總見《Multiwfn支持的弱相互作用的分析方法概覽》(http://www.shanxitv.org/252),其中還對能量分解做了簡介。
使用PSI4做SAPT計算,以及掃描各個SAPT能量項隨作用距離的變化可參考《考察SAPT能量分解的能量項隨分子二聚體間距變化的簡單方法》(http://www.shanxitv.org/469)。
分子間弱相互作用的本質簡介,以及上文中提到的B3LYP-D3(BJ),見《談談“計算時是否需要加DFT-D3色散校正?”》(http://www.shanxitv.org/413)。
文中用到的ma-TZVP基組用法見《給def2以ma-方式加彌散函數的Gaussian格式的基組定義文件(含所有def2支持的元素)》(http://www.shanxitv.org/509)。
文中提到的counterpoise校正的原理,以及為什么文中用一半Counterpoise校正,在此文有提及《談談BSSE校正與Gaussian對它的處理》(http://www.shanxitv.org/46)。