使用Multiwfn計算CVB指數考察氫鍵強度
使用Multiwfn計算CVB指數考察氫鍵強度
文/Sobereva@北京科音
First release: 2019-Feb-5 Last update: 2019-Feb-6
摘要:本文介紹基于電子定域化函數(ELF)定義的用于衡量氫鍵強度的CVB指數,并且演示怎么在Multiwfn程序(http://www.shanxitv.org/multiwfn)中計算。掌握這個方法,在討論氫鍵問題的時候相當于多了一個很有用的工具。
1 CVB指數的思想以及計算方法
core-valence bifurcation (CVB)指數是最初在Theor. Chem. Acc., 104,13 (2000)中由Silvi等人提出的一種考察氫鍵強度的方法,它利用了電子定域化函數(ELF)的拓撲分析的思想。如果對ELF不熟悉的話,請參閱《ELF綜述和重要文獻小合集》(http://bbs.keinsci.com/thread-2100-1-1.html)。后來有不少文章都使用了這個指數討論氫鍵,比如Struct. Chem., 16, 203 (2005)、J. Phys. Chem. A, 115, 10078 (2011),在一篇從理論角度分析氫鍵的綜述Chem. Rev., 111, 2597 (2011)中也對CVB指數進行了介紹。
一般的氫鍵可以寫為D-H...A的形式,其中D是氫鍵給體原子(donor),A是氫鍵受體原子(acceptor)。用ELF盆分析的語言來描述的話,這塊區域由以下的ELF盆構成:
V(D,H):D和與之成鍵的H共同構成的價層(valence)盆
C(D)和C(A):D原子和A原子的內核(core)盆
V(A):A原子的價層盆
相鄰的盆之間都有所謂的二分點(bifurcation point),對應于拓撲分析語言里的(3,-1)型ELF臨界點。如果你不懂什么叫二分點、不懂怎么計算的話,可以看看《在Multiwfn中單獨考察pi電子結構特征》(http://www.shanxitv.org/432)一文中對ELF-pi函數考察其二分點的例子,本文第四節的例子也通過ELF拓撲分析考察了二分點。
CVB指數在Theor. Chem. Acc.那篇文章中的定義為:CVB index = ELF(C-V) - ELF(DH-A)
其中ELF(C-V)代表內核盆與價層盆之間的二分點數值,ELF(DH-A)代表V(D,H)與V(A)之間的二分點數值,也即H與A原子間(3,-1)型ELF臨界點的ELF數值。CVB指數越負,通常氫鍵越強,這點在原文以后后續一些文章里都通過實例進行了驗證。比較強的氫鍵的CVB指數一般明顯為負;極強、帶有明顯共價特征的氫鍵可以達到很負的數值;中等強度氫鍵的CVB指數一般在0附近;較弱的氫鍵的CVB指數一般明顯為正。其實為什么會這樣也不難理解,因為氫鍵越強,H和A之間的距離通常越近,H...A作用的共價性也會越顯著,勢必ELF(DH-A)會越大、導致CVB index越負。其實說白了,CVB指數的名字雖然重在core-valence二分點數值,但真正關鍵的其實是ELF(DH-A)的數值,不同氫鍵的ELF(DH-A)的差異遠比ELF(C-V)大得多得多。
在CVB指數的原文里,對CVB指數的計算細節沒有說清楚,這導致之后不同文章在計算CVB指數的時候用的具體做法不同,而且CVB指數原文里的數據還存在錯誤,尤為明顯的錯誤是把符號搞反了,而且在后來的某些相關文章中和CVB有關的敘述還往往是錯的,總之被搞得一團糟,那些文章里的CVB數值也很難或根本無法重現出來。
筆者在Multiwfn里專門加入了CVB指數的自動計算功能,是主功能200的子功能1,只要輸入D、H、A原子的序號即可計算。在Multiwfn中計算CVB指數的做法是筆者提出來的,筆者認為這種方式計算不僅耗時很低(基本上秒算)、操作極簡單、實現極容易,而且意義明確。
在Multiwfn的這個功能中,CVB指數定義為:CVB index = ELF(C-V,D) - ELF(DH-A)
其中,ELF(DH-A)不是通過拓撲分析搜索出來的精確的V(D,H)與V(A)之間的二分點的數值,而是在H-A連線上計算ELF曲線,從中取H和A之間ELF極小點的數值,因為這樣計算容易得多。而且由于精確的二分點位置幾乎就在H-A的連線上,因此Multiwfn中這種近似方式得到的ELF(DH-A)與按照CVB指數原始定義計算的ELF(DH-A)幾乎沒有差異。
上式中ELF(C-V,D)的物理意義是D原子上的core-valence二分點數值。Multiwfn中雖然也可以通過其強大的拓撲分析功能(主功能2)得到準確的這種二分點位置和數值,但這種二分點在實際中往往不好考察,同一個原子可能有多個這樣的二分點,在選取上有任意性。而且如果是第二周期之后的原子,二分點會更多,考察時更麻煩。而且筆者也認為,用精確的二分點也并沒有太強的物理意義,因為它們往往都不在D-H連線方向上,因此和氫鍵特征也聯系不緊密。考慮到這些,在Multiwfn自動計算CVB指數的功能中,ELF(C-V,D)是直接取D-H連線上相應的ELF極小點數值。
Multiwfn自動計算CVB指數的功能中會計算三個量,思想很簡單,如下所示:
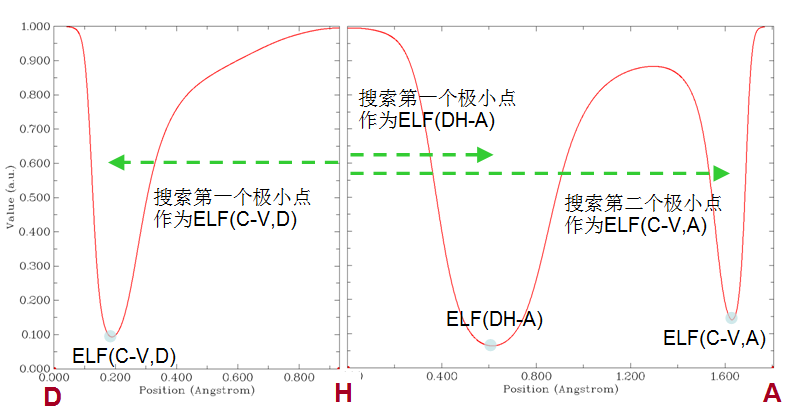
實際上你也完全可以通過主功能3來繪制ELF曲線(例子看Multiwfn手冊4.3節),并讓程序給出極小點位置和數值,由此手動得到CVB指數,只不過使用Multiwfn自動計算CVB指數的功能在操作上方便得多。上圖中順帶搜索到的ELF(C-V,A)并沒什么實際用處,但是可能有的用戶對此感興趣,所以程序也會順帶輸出。
由于Theor. Chem. Acc.那篇文章里的數據有一定問題,而且對測試體系計算氫鍵結合能用的級別在現在來看非常爛(B3LYP/6-31G**),因此文中的數據不足為信。筆者用這篇文章里的一部分氫鍵二聚體,在可靠的B3LYP-D3(BJ)/def2-TZVP下優化并得到波函數文件,使用Multiwfn自動計算CVB指數的功能做了計算,并且用計算氫鍵結合能精度很高的MP2/jul-cc-pVQZ結合counterpoise校正計算了氫鍵結合能,結果如下
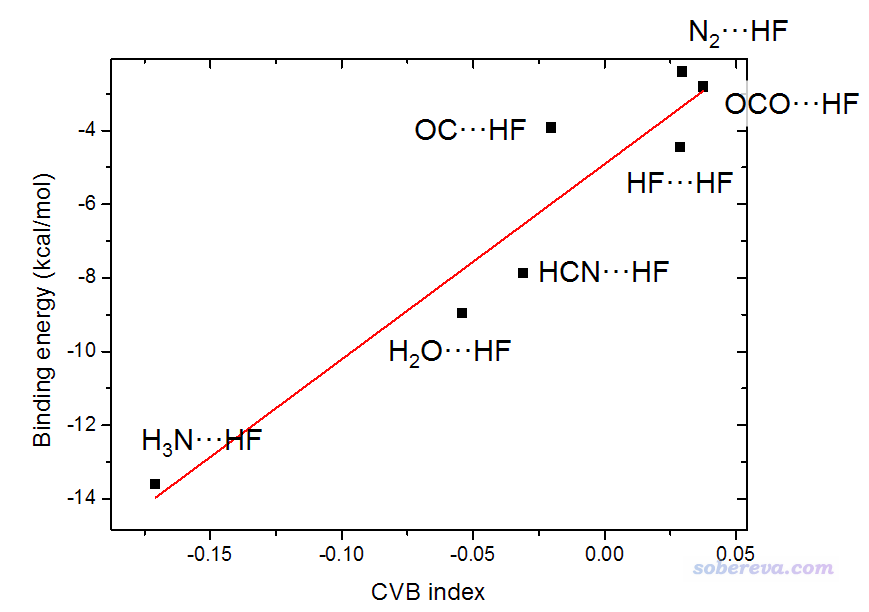
可見,CVB指數和氫鍵結合能之間的線性關系雖然不算完美,但線性關系還是很顯著的。如果把OC...HF這個例外不計的話,那么線性關系就很理想了。
其實,CVB指數的兩個組成部分自身也與氫鍵強度存在明顯相關性(起碼對這批體系而言),如下所示
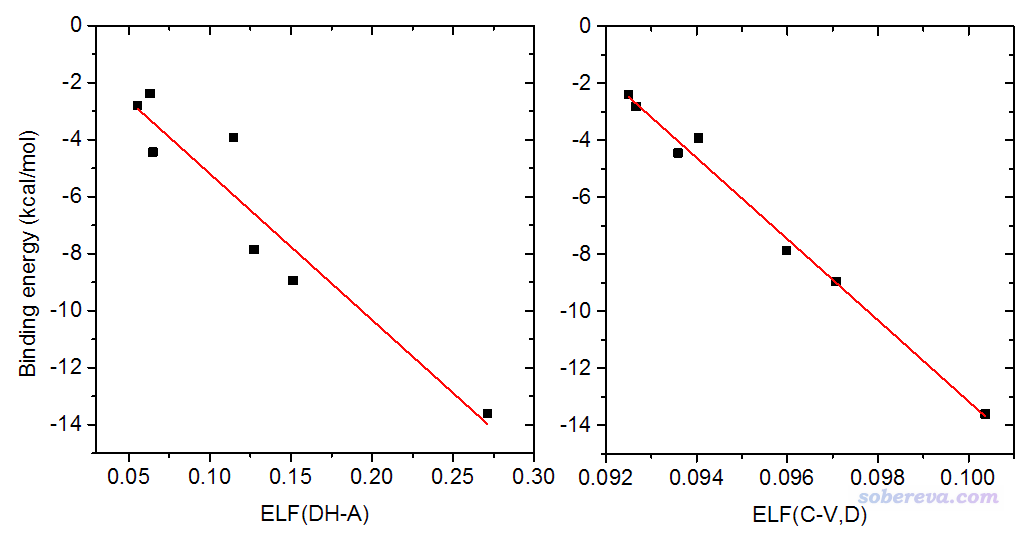
由于“CVB指數 vs 結合能”的圖和“ELF(DH-A) vs 結合能”很相似,所以CVB指數的重點是ELF(DH-A),哪怕忽略ELF(C-V,D)其實也無大礙。ELF(C-V,D)與結合能的線性關系很好,但并不好從物理意義上解釋原因,同時也可以看到對不同氫鍵其數值差異很小。總之,當你用CVB指數討論氫鍵的時候,也可以順帶檢驗一下其兩個組成部分和氫鍵強度的相關性。
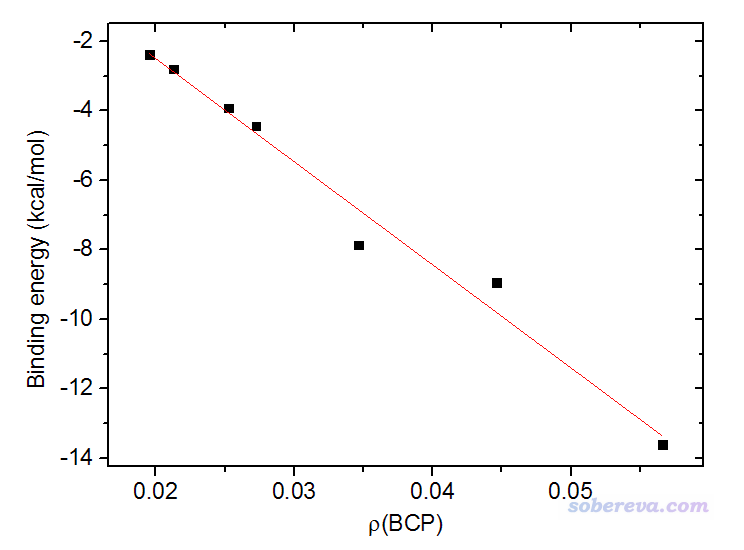
值得一提的是,對這些氫鍵二聚體,筆者發現AIM理論里的鍵臨界點(BCP)的電子密度ρ(BCP)和結合能的關系頗好,如下所示(筆者也考察了BCP處勢能密度,發現與結合能的線性關系遠沒有這么好)。ρ(BCP)用Multiwfn可以非常容易地計算,見《使用Multiwfn做拓撲分析以及計算孤對電子角度》(http://www.shanxitv.org/108)。AIM的相關知識看《AIM學習資料和重要文獻合集》(http://bbs.keinsci.com/thread-362-1-1.html)。關于此項研究,筆者專門發表了論文,主要內容介紹見《透徹認識氫鍵本質、簡單可靠地估計氫鍵強度:一篇2019年JCC上的重要研究文章介紹》(http://www.shanxitv.org/513),此文對于氫鍵的研究意義很大,請讀者務必一讀。
2 CVB指數在Multiwfn中的計算一例:HF...HF
只有在2019-Feb-5及之后更新的Multiwfn中才有CVB指數自動計算功能。不了解Multiwfn的話看《Multiwfn入門tips》(http://www.shanxitv.org/167),不知道怎么產生Multiwfn需要的輸入文件的話看《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。常見的.fch、.molden、.wfn等格式都可以作為CVB指數計算功能的輸入文件。
下面以HF...HF作為例子演示在Multiwfn中計算CVB指數,由Gaussian 16 A.03在B3LYP-D3(BJ)/def2-TZVP下優化并產生的wfn文件是examples目錄下的HF_HF.wfn,體系結構如下
啟動Multiwfn,輸入
examples\HF_HF.wfn
200 // 其它功能(part2)
1 // 計算CVB指數和相關的量
2,1,3 //氫鍵給體原子、氫原子和氫鍵受體原子的序號
輸出信息如下
Core-valence bifurcation value at donor, ELF(C-V,D): 0.0936
Distance between corresponding minimum and the hydrogen: 0.743 Angstrom
Core-valence bifurcation value at acceptor, ELF(C-V,A): 0.1408
Distance between corresponding minimum and the hydrogen: 1.628 Angstrom
Bifurcation value at H-bond, ELF(DH-A): 0.0648
Distance between corresponding minimum and the hydrogen: 0.614 Angstrom
The CVB index, namely ELF(C-V,D) - ELF(DH-A): 0.028768
各項是什么含義,只要仔細看了上一節就肯定明白。輸出中還順便把相應的ELF曲線極小點與氫原子之間的距離顯示了出來。
3 某些極強氫鍵的特殊考慮
對于某些極強的氫鍵,由于H和A之間的作用也非常強,存在顯著共價特征,此時V(D,H)二分為V(D)和V(H),例如下圖所示的體系(由于O-H-F基本在一條直線上,所以就不把O-H和H-F的ELF曲線圖單獨繪制了,而是為了省事直接繪制O-F連線上的圖)。
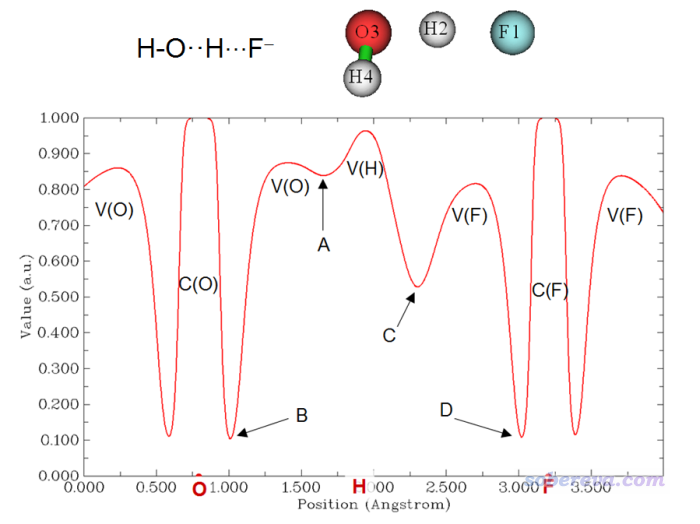
此體系中,由于F形式上是以F-陰離子形態存在,與帶正電的氫的作用極強,這使H和F之間已經存在不可忽視的共價性(而一般氫鍵的主要本質是靜電作用),因此在對應的二分點C位置,ELF數值遠大于一般強度氫鍵的情況。H與F強烈吸引,導致水分子中的O3-H2鍵遭到很大破壞,拉長了O3-H2的距離,也同時導致V(H2)獨立的ELF盆的出現,因此曲線上出現了極小點A。
像上面這種明顯不具備典型D-H...A氫鍵特征的體系,前述的Multiwfn的CVB指數自動計算方法是明顯不適用的,強行用的話結果是沒意義的,必須通過主功能3作圖并手動計算。這個體系可以認為存在兩種氫鍵O-H...F和O...H-F,二者的結合能存在明顯差異,其CVB指數在計算的時候也應當分別考慮:
考察O-H...F時,CVB index = ELF(B) - ELF(C)
考察O...H-F時,CVB index = ELF(D) - ELF(A)
由于ELF(B)和ELF(D)差不太多,而ELF(A)顯著大于ELF(C),因此O...H-F的CVB指數明顯更負,體現O...H-F的結合強度比O-H...F肯定大得多。
在Multiwfn手冊的3.200.1節當中還有關于CVB指數更多的信息,有興趣的讀者建議看看。
4 氫鍵受體不是單一原子情況時CVB指數的計算
有很多氫鍵的受體并不是特定的某個原子,比如pi-氫鍵,是以富集的pi電子云作為氫鍵受體。這種情況下,也沒法用前述的Multiwfn中自動計算CVB指數的功能來計算,而需要根據實際情況手動進行計算。這里以HF...乙烯二聚體作為例子。B3LYP-D3(BJ)/def2-TZVP下優化并產生的波函數文件是examples目錄下的C2H4_HF.wfn。其結構如下
先計算ELF(C-V,D)。按照之前用到的做法,在F7-H8連線方向上繪制ELF,查看對應的極小點即可。啟動Multiwfn并輸入
examples\C2H4_HF.wfn
3 //繪制曲線圖
9 //繪制ELF
0 //設定延展距離
0 //延展距離設為0(使得圖的兩端正好是兩個原子核位置)
1 //輸入兩個原子序號定義直線
7,8
把彈出來的圖關閉,后處理菜單選擇6,在屏幕上看到
Minimum X (Bohr): 0.356648 Value: 0.94377038E-01
這個極小點的數值0.0944即是ELF(C-V,D)。
對于當前體系的ELF(DH-A),我們應當通過做ELF拓撲分析找到對應H8與乙烯pi區域之間的ELF二分點位置來得到其數值。接著在Multiwfn里輸入
0 //返回主菜單
2 //拓撲分析
-11 //選擇要做拓撲分析的函數
9 //ELF
6 //在特定圓球內隨機撒初猜點的方式找臨界點
4 //將圓球中心定義為三個原子的中點
1,4,8 //將C1,C4,H8的中心作為圓球的中點,這時圓球的區域內理應會包含當前要找的氫鍵處的ELF二分點
0 //開始在圓球內隨機撒初猜點來找臨界點(撒的點數可以事先通過選項11設定,圓球半徑也可以自設)
-9 //返回拓撲分析主界面
0 //觀看臨界點分布
看到的圖如下所示,為了清楚,這里只顯示出(3,-1)和(3,-3)型ELF臨界點,分別是桔球和紫球。
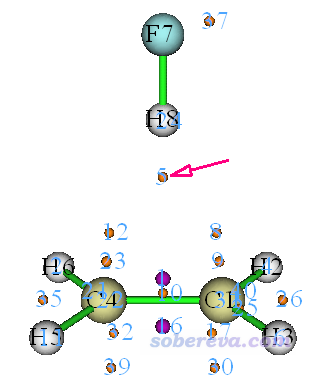
我們看到在H8與pi電子區域之間找到了ELF二分點,即5號臨界點。點右上角的RETURN退出圖形窗口,選擇選項7考察臨界點屬性,再輸入5,在屏幕上看到
Electron localization function (ELF): 0.1240943921E+00
即此體系氫鍵的ELF(DH-A)=0.1241。因此,此氫鍵的CVB指數為0.0944-0.1241=-0.0297。
由于這個體系對稱性較高,其實不做拓撲分析也可以得到ELF(DH-A),也就是用主功能3繪制H8與C1-C4的中點連線上的ELF曲線,然后從中取對應的極小點,數值和上面做拓撲分析得到的完全一致。但如果體系對稱性不那么高,顯然就沒法這么通過ELF曲線圖比較準確地得到實際二分點位置的ELF值了。