使用Multiwfn對第一超極化率做雙能級和三能級模型分析
使用Multiwfn對第一超極化率做雙能級和三能級模型分析
文/Sobereva@北京科音 2019-Sep-6
1 前言
研究第一超極化率(beta)的文章里經常做一種叫雙能級模型的分析用于闡明影響beta的關鍵因素、便于討論不同體系beta大小差異的原因,比如在筆者的J. Comput. Chem., 38, 1574 (2017)中就用了這種方式討論。之前筆者在《談談計算第一超極化率的雙能級公式》(http://www.shanxitv.org/361)里專們對此方法進行了介紹。本質上,雙能級公式就是從《使用Multiwfn基于完全態求和(SOS)方法計算極化率和超極化率》(http://www.shanxitv.org/232)文中介紹的計算beta的完整的SOS公式中簡化來的。
使用雙能級公式的前提之一是必須有一個激發態是關鍵態(crucial state),也就是它對beta的貢獻遠大于其它激發態,因此可以只用基態和這個激發態來討論beta。然而很多情況下關鍵態難以確定、模棱兩可,甚至有時候明顯能看出就是需要同時考慮兩個激發態才能定性正確描述實際的beta,比如第一激發態和第二激發態振子強度都較大而它們的能量差很小,此時就明顯不能強行用雙能級分析了,得同時把這兩個激發態一起考慮,筆者管這叫三能級模型,推導過程見下一節。
為了便于大家實現雙能級和三能級分析,從2019-Sep-6更新的Multiwfn開始,在完全態求和(SOS)模塊里新增了子功能20,專門進行雙/三能及分析,使用相當容易,下面就進行介紹。首先筆者把方法的原理介紹一下,然后給出一個具體分析例子。Multiwfn可以在其主頁http://www.shanxitv.org/multiwfn免費下載。不了解Multiwfn的話看《Multiwfn FAQ》(http://www.shanxitv.org/452)。
2 原理
在2019-Sep-6及之后更新的Multiwfn手冊的3.200.8.2節里對雙能級、三能級公式的推導做了非常詳細的說明,十分建議一看。這里只是簡單提一下關鍵點。
SOS方法計算beta張量的ABC分量公式如下
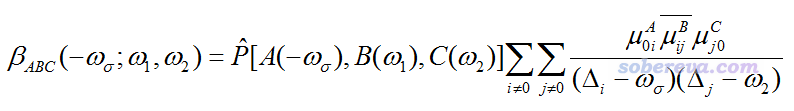
對于靜態極限(ω=0)的情況,ZZZ分量的公式可以寫為以下形式
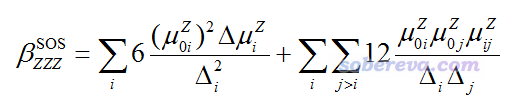
其中Δi是第i激發態的激發能,μ0i_Z是基態到第i激發態的躍遷偶極矩的Z分量,μij_Z是第i激發態到第j激發態的躍遷偶極矩的Z分量,Δμi_Z是第i激發態的(非弛豫密度對應的)偶極矩矢量與基態偶極矩矢量之差的Z分量。
由上式可見,靜態beta的ZZZ分量可以寫為每個激發態獨自的貢獻以及不同激發態之間耦合所產生的貢獻之和。如果只有一個激發態起到主導地位,那就可以用下面的雙能級模型討論
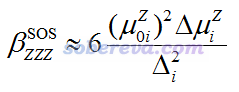
如果有兩個激發態同時起到關鍵地位,哪個都不能簡單地忽略,那就得用下面的三能級模型討論,包括兩個激發態自身的貢獻和二者的耦合項
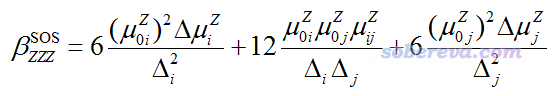
再強調一下,用雙/三能級模型討論影響beta大小的因素的時候必須滿足以下兩條:
(1)beta的總值必須能被beta_XXX、beta_YYY、beta_ZZZ其一所主導,這樣我們才能針對起到主導作用的分量來進行雙/三能級模型的分析來解釋影響beta總大小的主要因素(注:為此,有的時候可能需要在計算前對體系做恰當的旋轉來使得以上三個分量之一最大化,從而便于雙/三能級分析)
(2)打算用雙能級分析時,必須有一個激發態對被考察的beta分量的貢獻遠大于其它激發態;打算用三能級分析時,必須有兩個激發態的貢獻遠大于其它激發態。
通常,Donor-pi-acceptor型體系可以滿足以上要求。分析前應當令Donor-acceptor連線的方向(或者更廣義地說,電子激發時電荷轉移的方向)平行于某個笛卡爾軸,以滿足上面第(1)條。
3 實例
下面就用一個典型的Donor-pi-acceptor型體系“氨基-聯苯-硝基”作為例子說一下怎么用Multiwfn做雙能級和三能級分析。用到的輸入文件滿足Multiwfn手冊3.21節開頭里說的對輸入文件的要求即可。簡單來說,對于Gaussian用戶,一般需要做TDDFT計算,并且寫上IOp(9/40=4)關鍵詞,計算后產生的fch和輸出文件都需要保留。本例用到的文件D-pi-A.fchk和D-pi-A.out已經提供在了程序包的examples\excit目錄下(注:這個計算任務是在CAM-B3LYP/6-31g(d)級別下完成的,對于考察超極化率來說,用這種不帶彌散函數的基組不可能得到準確的結果,但本文僅作為演示,所以暫且忽略這點)。
首先我們產生Multiwfn的SOS模塊的輸入文件,這需要依賴D-pi-A.fchk和D-pi-A.out里的信息計算出各個態的偶極矩和態之間的躍遷偶極矩。啟動Multiwfn后依次輸入
examples\excit\D-pi-A.fchk
18 //電子激發分析
5 //計算各個態的偶極矩和態之間的躍遷偶極矩
examples\excit\D-pi-A.out
3 //將結果導出為當前目錄下的SOS.txt文件
然后就可以做雙/三能級分析了。在此之前,返回主菜單,進入主功能0看一眼體系的朝向,如下所示。可見體系是順著X方向的,因此我們之后要考察的是beta_XXX。而且如果你有計算beta的常識的話,也會知道這種體系beta_XXX主宰了總beta,即考察beta_XXX就等于近似考察了總beta。
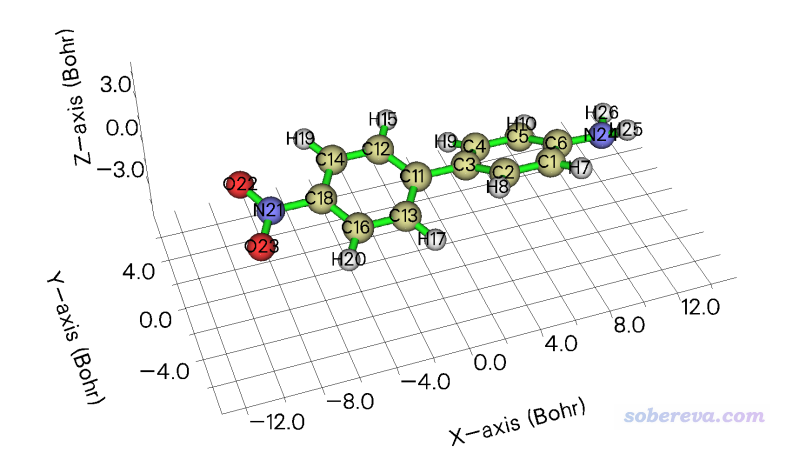
啟動Multiwfn,輸入
SOS.txt //載入當前目錄下的SOS.txt
200 //其它功能 (Part 2)
8 //通過完全態求和(SOS)方式研究(超)極化率
20 //雙/三能級分析?
此時程序將激發態的基本信息輸出了出來,便于用戶選擇被考察的態
Excitation energy (E,eV) and transition dipole moment (X,Y,Z,total) between gro
und state to excited states (a.u.)
State 1 E= 3.9069 X= 0.44441 Y= -0.00044 Z= -0.00182 Tot= 0.44442
State 2 E= 4.0624 X= 2.52778 Y= -0.00309 Z= -0.00733 Tot= 2.52779
State 3 E= 4.4166 X= -0.00263 Y= -0.00167 Z= -0.02343 Tot= 0.02364
State 4 E= 4.7912 X= 0.00069 Y= 0.34055 Z= -0.01274 Tot= 0.34079
State 5 E= 4.8872 X= -0.00391 Y= 0.19205 Z= -0.17054 Tot= 0.25687
由上可見,第2激發態的躍遷偶極矩的模(Tot值)明顯大于其它的態(相應地振子強度也大),而且它的激發能又比較低,因此這就是典型的關鍵態(crucial state)。接著輸入
1 //考察X方向,即被分析的是beta_XXX
2 //將第2激發態用于雙能級分析
馬上輸出了以下信息
Excited state 2
Excitation energy 4.0624 eV
Transition dipole moment component: 2.5278 a.u.
Oscillator strength component: 0.635943 a.u.
Variation of dipole moment component: 6.5629 a.u.
beta evaluated by the two-level model: 11289.099582 a.u.
前面介紹雙能級公式中涉及的激發能、躍遷偶極矩、偶極矩相對于基態的變化在上面都給出了,對于后兩者指的是我們選擇的X分量。另外,由這些數據折算的振子強度的X分量也給出了(具體公式看手冊3.200.8.2節)。利用這些信息,我們就可以討論這個體系與與它類似的體系的beta的差異主要來自于哪些因素。
PS:大家也可以嘗試把被分析的方向設為Y或Z,會發現算出的數值都非常接近于零,這也主要在于第2激發態的躍遷偶極矩的Y和Z分量都近乎為0。
接下來我們用三能級模型進行考察。在Multiwfn窗口里輸入
20 //再次做雙/三能級分析?
1 //再次考察beta_XXX
1,2 //將激發態1、2用于三能級模型分析
結果如下
Excited state 1
Excitation energy 3.9069 eV
Transition dipole moment component: 0.4444 a.u.
Oscillator strength component: 0.018904 a.u.
Variation of dipole moment component: -1.0098 a.u.
Excited state 2
Excitation energy 4.0624 eV
Transition dipole moment component: 2.5278 a.u.
Oscillator strength component: 0.635943 a.u.
Variation of dipole moment component: 6.5629 a.u.
Transition dipole moment between states 1 to 2: 1.475397 a.u.
Contribution of excited state 1: -58.048845 a.u.
Contribution of excited state 2: 11289.099582 a.u.
Contribution of cross term: 927.898744 a.u.
beta evaluated by the three-level model: 11251.731412 a.u.
上面給出的第2激發態的信息和之前我們做雙能級分析的時候得到的相同。上面的信息包含了三能級公式里面涉及到的所有量。當必須用三能級模型才能說明問題的情況,大家就可以對不同體系考察上述這些量對beta_XXX的影響。
從上面的輸出也可以看到第1激發態自身的貢獻(-58.0),以及第1激發態與第2激發態之間耦合產生的貢獻(927.9)相對于總值11251.7來說都很小,體現出用雙能級模型其實就足夠了,把第1激發態納入作為三能級模型考察也不會得到更多信息。也很容易理解為什么第1激發態的獨自貢獻(-58.0)那么小,因為雙能級模型指出某個激發態對beta的貢獻正比于其偶極矩相對于基態的變化量以及躍遷偶極矩的平方。
原理上來說,還可以做四能級、五能級...分析,但是由于基本不可能用得到,所以Multiwfn也就沒留出相應功能。由于三能級分析的時候已經給出兩個激發態自身以及激發態之間的耦合項了,因此若想同時考慮更多能級,靠多次使用三能級公式就可以等效實現(比如想用2、3、4激發態做四能級分析,通過做2-3、2-4、3-4三次三能級分析就可以等效實現)。
順帶一提,有時候我們的電子激發計算的輸出文件里可能有很多態,比如50個乃至上百個,但使用雙/三能級公式考察的時候一般只會牽扯到最低的幾個,顯然此時對輸出文件里所有激發態都做偶極矩、躍遷偶極矩的計算完全沒必要,會造成大量無意義的耗時。為此,可以恰當設定Multiwfn的settings.ini里的maxloadexc,比如設為5,那么主功能18的子功能5就只會讀入前5個激發態,計算偶極矩和躍遷偶極矩也只對它們計算,比起算所有激發態會省時甚巨,此時產生的SOS.txt就足矣用于做雙/三能級分析了。