計算分子內氫鍵鍵能的幾種方法
計算分子內氫鍵鍵能的幾種方法
文/Sobereva@北京科音
First release: 2019-Nov-23 Last update: 2022-May-26
0 前言
計算分子間弱相互作用,包括計算最常被研究的氫鍵的鍵能,已經有非常成熟、準確的方法,比如最常用的就是用CCSD(T)等高精度方法,拿復合物的能量減各個單體的能量。有時我們需要研究分子內氫鍵的鍵能,但計算方法并不唯一,哪種方法最合理也爭議頗多,沒有普遍的共識,而且本身這也不是實驗上可以測定的。盡管如此,由于研究分子內氫鍵鍵能在很多方面(如考察和對比構象穩定性)非常重要,我們還是需要了解有哪些方法可以計算。本文就以下面這個分子作為例子,介紹幾個計算內氫鍵的方法。
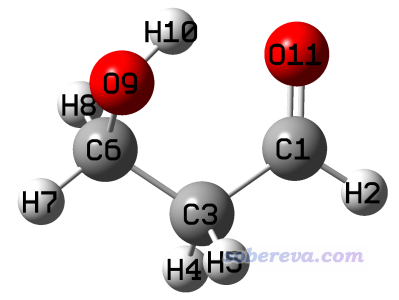
本文例子用到的所有Gaussian輸入、輸出文件以及fch文件都可以在這里下載:http://www.shanxitv.org/attach/522/intraHB.rar。其中用到ma-TZVPP基組的時候利用了《給def2以ma-方式加彌散函數的Gaussian格式的基組定義文件(含所有def2支持的元素)》(http://www.shanxitv.org/509)里提供的基組定義文件。
優化都使用B3LYP-D3(BJ)/def-TZVP級別進行,對各個結構的能量計算使用M06-2X/ma-TZVPP(對這個不算大的體系用更高精度的CCSD(T)/CBS也算得動,用當前級別是圖省事,而精度也已經不錯,足夠說明問題)。本文計算的都是電子能量,不牽扯熱力學數據。本文下面計算的是氫鍵相互作用能,負值代表內氫鍵的形成令體系能量降低,但為了表述省事,下文簡稱為氫鍵鍵能。
本文使用的Multiwfn可以在官網http://www.shanxitv.org/multiwfn免費下載。相關常識看《Multiwfn FAQ》(http://www.shanxitv.org/452)。Gaussian用的是Gaussian 16 A.03。
1 基于鍵臨界點的電子密度估計內氫鍵鍵能
Atoms-in-molecules (AIM)理論利用氫鍵的鍵臨界點(BCP)位置的屬性考察氫鍵特征。筆者在《透徹認識氫鍵本質、簡單可靠地估計氫鍵強度:一篇2019年JCC上的重要研究文章介紹》(http://www.shanxitv.org/513)中介紹了筆者在J. Comput. Chem., 40, 2868 (2019)中提出的基于BCP位置的電子密度預測氫鍵鍵能的公式,其中參數是向高精度的CCSD(T)/jul-cc-pVTZ + counterpoise級別算的氫鍵結合能擬合的。對于中性氫鍵體系,預測公式為
E_HB = -223.08*ρ(BCP)+0.7423
此處氫鍵鍵能E_HB單位為kcal/mol,ρ(BCP)的單位為a.u.。經過文中的對比,發現此方法比起其它文獻里提出的基于氫鍵描述符的預測公式精度都更好。文章中擬合公式是對分子間氫鍵進行的擬合,這里我們也將之用于內氫鍵的預測。
本文文件包里sp_B3LYP.gjf是對優化后的結構在B3LYP-D3(BJ)/ma-TZVPP級別下進行單點任務,得到的fch文件是sp_B3LYP.fch。JCC文章中在擬合預測公式時用的波函數正是B3LYP-D3(BJ)/ma-TZVPP級別得到的,這是為什么此例也用這個級別做AIM分析。
啟動Multiwfn程序,載入sp_B3LYP.fch,然后依次輸入
2 //拓撲分析
2 //搜索核臨界點
3 //用每一對原子的中點搜索臨界點
0 //觀看臨界點
在圖形界面右邊把CP labels開啟,看到下圖
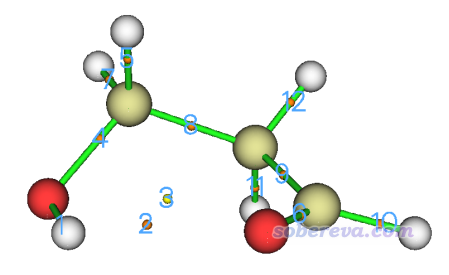
很明顯,對應內氫鍵的BCP的序號是2。然后輸入7進入考察臨界點屬性的選項,然后輸入2,查看這個臨界點的各種性質,從屏幕上可看到
Density of all electrons: 0.1535708348E-01
即曰ρ(BCP)=0.015357 a.u.。代入到上面的公式里,氫鍵鍵能為-223.08*0.015357+0.7423=-2.68 kcal/mol。按照前述JCC文章里的分類標準,這屬于較弱氫鍵范疇,靜電吸引作用占主要因素,而色散作用也不可忽略。
本文的文件包里sp_M062X.fch是對優化后的結構用M06-2X/ma-TZVPP做單點產生的,同樣做AIM拓撲分析,得到的ρ(BCP)是0.015222 a.u.,氫鍵鍵能計算結果是-2.65 kcal/mol,和基于B3LYP-D3(BJ)/ma-TZVPP波函數分析的很相近,可見上述JCC文章里的預測公式對計算波函數用的DFT泛函并不敏感。
需要注意的是,有一些內氫鍵并沒有對應的BCP,原因在《使用IRI方法圖形化考察化學體系中的化學鍵和弱相互作用》(http://www.shanxitv.org/598)里介紹的我發表的IRI方法的原文里做了深入討論,強烈建議一讀。對這種情況,只能通過IRI、IGMH(http://www.shanxitv.org/621)等方法圖形化展現,但沒法用本節介紹的方法定量計算內氫鍵鍵能。
2 使用Molecular Tailoring Approach方法估計內氫鍵鍵能
在J. Phys. Chem. A, 110, 12519 (2006)等文章中,作者提出一種叫Molecular Tailoring Approach (MTA)的方法計算內氫鍵鍵能。文中對此方法的敘述比較抽象,這里筆者用比較易于理解的方式說明。看下面的示意圖
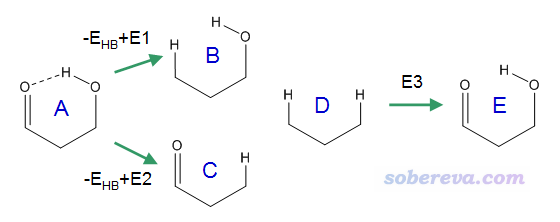
其中A是原先的體系,B、C、D是人為把基團替換成氫的情況,E是虛構的不存在內氫鍵的情況。
圖中示意了三個轉化過程
-E_HB + E1 = B - A,因此E1 = B - A + E_HB。其中E1是把=O變成H的能量變化
-E_HB + E2 = C - A,因此E2 = C - A + E_HB。其中E2是把OH變成H的能量變化
E3 ≈ - E1 - E2
由于E_HB = A - E,而E = D + E3,經過簡單推導可知E_HB ≈ A + D - B - C。
用MTA方法計算本文體系涉及的文件都在本文文件包的MTA目錄下,對A、B、C、D四種狀態都做了單點計算(不要分別做優化)。其中A的結構就是對本文體系優化后的結構,B、C、D是把A的結構的基團在GaussView里替換為氫的情況,鍵軸方向和原先一致,替換后C-H鍵長度是GaussView默認的1.07埃。
將能量從四個.out文件提取出來按照上式運算,結果為627.51*(-268.358311297-118.441683680+193.666146710+193.130292306) = -2.23 kcal/mol,此數值和基于ρ(BCP)估計的差不太多。
MTA方法看起來不錯,原理比較清楚,手動實現也不難,但在Int. J. Quantum Chem., 119, e26001 (2019)中作者發現MTA方法的噪音比較大。比如對一系列內氫鍵進行測試,對有的體系明明ρ(BCP)比別的更大,但MTA方法算出來的內氫鍵強度反倒更低,如下圖所示
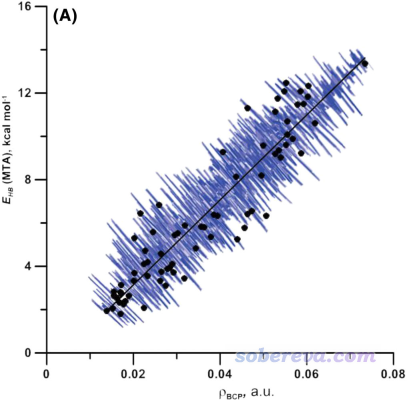
為了減小數據噪音,作者建議將MTA方法與基于BCP屬性、振動頻率變化、氫的NMR化學位移變化等描述符的經驗預測方法組合到一起用于預測氫鍵鍵能。但這么做太繁瑣,還不如就直接用本文第1節的基于ρ(BCP)的預測公式,又省事又靠譜。不過,基于ρ(BCP)的方法目前只擬合了用于氫鍵的參數,而MTA方法在原理上也可以用于分子內鹵鍵等其它情況。
3 通過比較不同構象能量估計內氫鍵鍵能
將原本有氫鍵的構象通過扭轉某些單鍵對應的二面角,成為氫鍵被破壞的構象,對比前后的能量變化,是常用而且原理非常易于理解的計算內氫鍵鍵能的手段。但這種調整構象算氫鍵鍵能的做法在原理上算不上嚴格,因為讓氫鍵破壞的同時,免不了會帶來位阻效應的變化、其它位置弱相互作用的變化等因素,如果這些因素十分明顯的話,顯然得到的能量差就不能很好地衡量內氫鍵鍵能了。為了讓這些伴生效應出現得盡量小,我們在具體實現上應當注意這三點:(1)扭轉哪個鍵?(2)扭轉多少度?(3)扭轉后是否做優化或者限制性優化?
我們下面對本文的例子考慮兩種修改構象的方式。
3.1 扭轉C-C鍵
我們將C3-C6扭轉,使得羥基遠離羰基氧,之后進行優化,可以得到一個無虛頻的局部極小點構象,如下所示。優化和單點計算的文件在本文文件包里conf2目錄下。
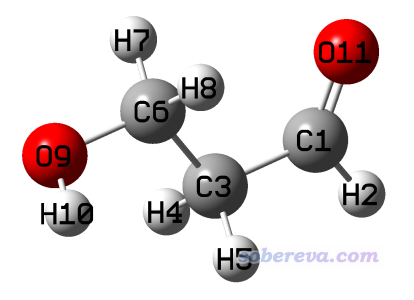
將原本有內氫鍵的結構能量與這個求差,由此估計出內氫鍵鍵能是627.51*(-268.358311297+268.353235417) = -3.18 kcal/mol。
3.2 扭轉O-H鍵
我們這回旋轉C-O鍵,讓形成氫鍵的氫避開氫鍵受體,之后如下所示。為了減小位阻效應,注意讓羥基的氫與對面的C-H呈交錯式。
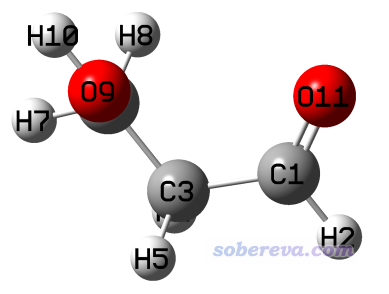
由于這個結構附近沒有局部極小點,因此不能去直接優化。但如果完全不做優化,物理意義又不太好,比如沒法通過自發弛豫來一定程度消除人工修改結構引入的額外位阻效應,因此筆者做了限制性優化,保持C-C-O-H鍵角是180度。限制性優化相關介紹見《在Gaussian中做限制性優化的方法》(http://www.shanxitv.org/404)。優化和單點任務的文件在本文的文件包里rotH目錄下提供了。
將原本有內氫鍵的結構能量與這個求差,由此估計出內氫鍵鍵能是627.51*(-268.358311297+268.353289743) = -3.15 kcal/mol。
可見上述兩個修改構象的做法算出的氫鍵鍵能非常接近。有文章指出扭轉O-H鍵這種做法會高估鍵強度,因為當O-H轉開之后,由于氧和氧之間會有一定靜電互斥使得體系能量升高。在筆者來看,本節做法算出來的內氫鍵鍵能適合作為一個鍵能的上限看待。本文第1節的基于ρ(BCP)進行估計的結果-2.65 kcal/mol與這一節的-3.1 kcal/mol接近,而大小稍微小一點,這種對照檢驗體現出靠ρ(BCP)進行估計是靠譜的,而MTA那個方法算出來的-2.23 kcal/mol則有可能低估了實際氫鍵強度。
4 其它方法
除本文介紹的外,還有其它一些方法。比如如果氫鍵給體和受體基團之間隔的化學鍵比較多,可以在適當的位置把中間鏈接區域去掉一截,然后邊緣補氫,例如下面這樣
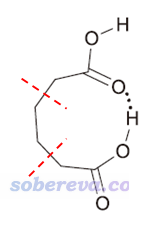
如果補氫后,兩個片段在截斷處的原子挨得較近,可以通過扭轉一些化學鍵讓這個區域的片段間的重疊彼此避開。然后以常規計算二聚體結合能的方式得到整體與兩個片段的能量差,就是內氫鍵鍵能了(不需要對二聚體模型和各個片段進行優化,要不然二聚體會嚴重變形)。
對于不是特別小的內氫鍵作用體系,如果有地方把氫鍵給體或受體挪到別處去從而使氫鍵破壞(換句話說,跟那個地方的氫彼此交換),則通過挪動前后的能量差也可以估計氫鍵鍵能。
對于二取代苯類型體系,在J. Phys. Chem. A, 108, 10834 (2004)利用了以下三種方法考察了氫鍵鍵能,即右側物質的總能量減去左側物質的總能量
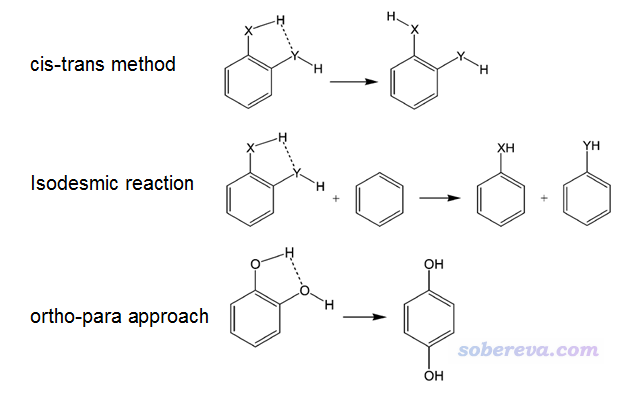
其中cis-trans方法和前面3.2節是一回事,被文章認為有高估氫鍵強度的傾向。Isodesmic reaction(等鍵反應)這種方法反應物和產物中各種類型鍵的數目保持不變,JPCA這篇文章認為此方法也不可靠,而認為最可靠的是ortho-para方法,相當于前面說的挪動基團位置的做法對二取代苯的一個特例。但其實ortho-para方法也并非嚴格,畢竟哪怕這兩個基團之間沒有氫鍵作用,把二取代苯的一個基團從另一個基團的鄰位挪到對位也會對體系的能量所有影響。