RESP擬合靜電勢電荷的原理以及在Multiwfn中的計算
補充1:后來又寫了《計算RESP原子電荷的超級懶人腳本》(http://www.shanxitv.org/476),腳本會自動調用Gaussian和Multiwfn完成所有需要的計算,使得RESP電荷計算過程驚人的簡單,從初始結構文件到給出最終RESP電荷,僅僅一行命令就能實現!
補充2:筆者后來寫了《RESP2原子電荷的思想以及在Multiwfn中的計算》(http://www.shanxitv.org/531),其中介紹的RESP2電荷是RESP的擴展,更恰當地考慮了溶劑對溶質電荷分布的極化效應,比起RESP電荷更適合用于凝聚相的分子動力學目的,強烈建議看完本文后一看。
RESP擬合靜電勢電荷的原理以及在Multiwfn中的計算
文/Sobereva@北京科音
First release: 2018-Sep-13 Last update: 2022-Aug-27
摘要:本文介紹在分子動力學領域非常常用的擬合靜電勢電荷和Kollmann提出的RESP型擬合靜電勢電荷的原理和思想,并介紹Multiwfn程序中十分強大、靈活的RESP電荷計算模塊,演示如何通過此模塊計算標準的RESP電荷以及考慮了各種自定義約束時的擬合靜電勢電荷。仔細閱讀本文后,讀者會充分感受到Multiwfn是計算RESP電荷最方便、最快捷、最靈活、最普適的工具,再也沒有必要用其它程序去算了。本文對原理、實現細節、用法介紹得非常詳細,如果你僅僅是想立刻計算RESP電荷,那么直接看一下2.1節的RESP模塊的簡要介紹,再看3.1節的例子并效仿去做即可,理解能力正常的人2分鐘內就能學會!
本文內容對應Multiwfn最新版本的情況,不要用老版本,否則情況可能與本文明顯不符。最新版本可在其主頁http://www.shanxitv.org/multiwfn下載。如果對Multiwfn不了解,可閱讀《Multiwfn入門tips》(http://www.shanxitv.org/167)和《Multiwfn波函數分析程序的意義、功能與用途》(http://www.shanxitv.org/184)。
PS:由于Multiwfn計算RESP電荷方面的各種優越性,目前已經有大量已發表的文章都是用Multiwfn算的RESP電荷,比如J. Membrane Sci., 605, 118105 (2020)、J. Mol. Liq., 305, 112845 (2020)、Molecules, 25, 895 (2020)、Phys. Chem. Chem. Phys., 22, 5577 (2020)、ACS Appl. Polym. Mater., 2, 685 (2020)、J. Phys. Chem. B, 124, 1148 (2020)、J. Am. Chem. Soc., 142, 18174 (2020)、Nature Sustainability (2023) DOI: 10.1038/s41893-023-01172-y等等,以往的靠Antechamber算RESP電荷的做法可以完全棄了。
如果你的研究中使用Multiwfn計算了RESP電荷,請在發表的文章中提及并務必引用Multiwfn啟動時提示的程序原文。也建議同時按照《Multiwfn使用的高效的靜電勢算法的介紹文章已于PCCP期刊發表!》(http://www.shanxitv.org/614)末尾的說明引用介紹Multiwfn中靜電勢計算算法的文章。
1 原理
1.1 擬合靜電勢電荷簡介
原子電荷是描述化學體系電荷分布最常用的一種模型,每個原子帶的凈電荷用一個位于原子核的點電荷來描述,計算方法并不唯一,筆者在《原子電荷計算方法的對比》(http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml)一文中對此有充分的介紹和對比討論。原子電荷計算方法可分為很多類,其中擬合靜電勢電荷是其中極為重要的一大類,筆者在《擬合靜電勢電荷的計算方法》(http://bbs.keinsci.com/thread-221-1-1.html)對各種擬合靜電勢電荷有較全面介紹,如果你連靜電勢都不懂是什么的話,推薦閱讀《靜電勢與平均局部離子化能綜述合集》(http://bbs.keinsci.com/thread-219-1-1.html)中的相關資料。
簡單來說,擬合靜電勢電荷通過使原子電荷能盡可能好地重現基于波函數計算的分子范德華表面附近和外側的靜電勢來得到(換句話說,是通過最小二乘法最小化基于原子電荷計算的與基于波函數計算的靜電勢在這些擬合點上的偏差得到,并同時通過拉格朗日乘子法約束原子電荷加和等于體系凈電荷)。由于對這些區域的靜電勢重現性越好的原子電荷才能越好地通過經典的庫侖公式描述分子間靜電相互作用,而擬合靜電勢電荷在原理上又是對靜電勢重現性最好的原子電荷,因此擬合靜電勢電荷在基于經典力場的分子動力學領域特別受寵,被使用極其廣泛。平時我們做分子動力學研究中,遇到一個新的小分子要模擬,通常就用擬合靜電勢電荷作為其原子電荷(但由于往往需要考慮與力場兼容性,可能有其它更恰當的選擇)。
擬合靜電勢最常見、最知名的就是Merz-Kollman (MK)和CHELPG這兩種,求解過程都是先根據幾何結構和原子范德華半徑確定分子范德華表面附近和外側的擬合點位置,再基于波函數計算這些位置上的靜電勢,然后構造A矩陣和B矢量,做個q=A^(-1)B的矩陣運算,所得的q矢量就包含了求出來了擬合靜電勢電荷,具體公式和細節在Multiwfn手冊3.9.10節有介紹。MK和CHELPG結果通常差異不太大,算法上的差別僅在于擬合點位置的設置上不同,CHELPG的結果在旋轉不變性角度上比MK稍微好一點(旋轉不變性是指體系整體朝向發生改變時對結果的影響,理應不該受到影響。但由于擬合點分布的原因,結果或多或少會有一點旋轉依賴性)。
原子范德華半徑在《簡談原子半徑》(http://www.shanxitv.org/255)中有介紹,有不同定義。計算擬合靜電勢電荷時用的原子半徑一般是和范德華半徑差不多的半徑,半徑選取的不同,擬合點的位置和數目就會不同,因此會影響結果。MK和CHELPG原文里都直接給出了一些原子的半徑定義,但只對前三周期做了定義。而涉及更后面的元素時該用什么半徑,沒有確切答案,有人建議用UFF力場的非鍵半徑除以1.2作為缺半徑時候用的半徑,這種做法是基本合理的。
MK和CHELPG電荷計算過程中都有格點密度的概念。對于MK電荷指的是在原子范德華表面附近及外側的各個殼層上單位面積中的擬合點數,對于CHELPG電荷則體現在原子范德華表面附近及外側一定距離內的三維空間中均勻分布的擬合點的密度。原理上,格點密度越高,格點數就越多,擬合結果就越準確,旋轉依賴性同時也越低,但在計算靜電勢上花的耗時也越多。
1.2 擬合靜電勢電荷用于柔性分子模擬時的特殊考慮
對于模擬剛性分子的情況,MK和CHELPG電荷都非常適合,不需要考慮其它原子電荷計算方法。然而,對于有多重構象的柔性分子,基于MK和CHELPG為代表的一般的擬合靜電勢電荷做模擬主要存在以下問題:
(1)結果對構象依賴性較大。柔性分子有很多不同構象,動力學模擬過程中構象經常發生變化,而擬合靜電勢電荷計算結果又對構象很敏感。如果只用一個構象去計算擬合靜電勢電荷并基于這種電荷做模擬研究,顯然會對動力學行為以及不同構象間相對能量的計算結果帶來誤導性,因為只靠一套電荷注定沒法較均衡、公平地描述不同構象。
(2)單一構象下擬合的原子電荷不能體現原子的等價性。例如甲醇的甲基上的三個氫是化學等價的,在一般溫度的動力學模擬過程中甲基也會頻繁發生旋轉,因此理應三個氫具有相同的電荷,然而任何構象下擬合出來的這三個氫的擬合靜電勢電荷都不是全同的(因為體系沒有順著甲基鍵軸的三重旋轉對稱性),因此這個問題也會給模擬帶來一定不合理性。
(3)被包埋的原子電荷擬合不準確。靜電勢擬合點都分布在分子范德華表面附近及外側一定距離內,對于與多個原子相連的原子(如sp3雜化的碳),尤其是大分子內部的原子,由于它們距離擬合點較遠,這些原子電荷的擬合質量較低、數值不確定性大。而且,隨著構象變化,這些原子的電荷波往往很顯著,故這些原子的存在也等同于加劇了擬合靜電勢電荷的構象依賴性問題。
只有把上述問題解決,才可以較好地把擬合靜電勢電荷用在柔性分子的動力學模擬問題中。
對于上述問題(1),一種比較好的解決辦法是在擬合過程中考慮多構象。先確定各個構象權重,然后在構建A矩陣和B矢量的元素的時候利用各個構象下的擬合點并同時考慮權重值,這樣得到的原子電荷就至少可以對權重比較大的那些構象的分子表面的靜電勢都有較好的描述。這種做法在J. Am. Chem. Soc., 114, 9075 (1992)一文中專門做了討論。當然,這種考慮多構象的做法對于可旋轉的鍵比較多的柔性分子會非常昂貴,因為體系的構象數是隨可旋轉的鍵增加呈指數型增加的。PS:還有一種做法是把各個構象下分別計算的擬合靜電勢電荷做權重平均,但結果在原理上不如在擬合過程中就考慮多構象那么好。
對于上述問題(2),可以在擬合過程中對化學等價的原子施加等價性約束以使得它們的原子電荷相同,具體實現是把A矩陣的這些原子對應的行進行合并(即加和到一起),再把列也進行合并,對B矢量的相應的行也進行合并,最后求解此時維度已變小的矩陣方程來得到原子電荷,這樣化學等價的原子就對應同一個電荷值了。PS:還有一種做法是先照常算出擬合靜電勢電荷,然后把化學等價的原子電荷取平均,但這樣做得到的電荷對靜電勢的重現性不如前面說的做法好,人為因素更大。
對于上述問題(3),在Kollman的RESP電荷原文中提出的解決思想是在衡量基于原子電荷與基于波函數算的靜電勢偏差的函數中引入懲罰函數,使得非氫原子的電荷有被拉低的傾向。他們選擇的是雙曲形式(hyperbolic)的懲罰函數,其中涉及一個緊密度參數b和一個限制強度參數a,前者一般都設0.1,而后者可以在實際計算時調節,數值越大懲罰函數效果越強,原子電荷被拉低的傾向越明顯,也會同時導致靜電勢重現性變得越差。顯然a參數要恰當選擇,一般取小于等于0.001的值,也有文獻用比較大的0.01。實測發現,引入這種形式的懲罰函數使得那些處于體系較外側,因此與擬合點距離比較近故數值確定性較高的原子的電荷計算結果受影響相對較小,而令那些被包埋因而擬合質量較差的原子的電荷較明顯地被拉低,由此很大程度上削弱了它們的數值不確定性。Kollman認為這種做法也明顯降低了擬合靜電勢電荷的構象依賴性,而且又不會像考慮多構象那樣顯著增加計算耗時。引入雙曲形式的懲罰函數后,擬合靜電勢電荷不再能一步求解出來,而需要做迭代直到所有原子電荷變化都很小。由于迭代時每一步計算量很小,所以是否引入雙曲函數并不會對耗時帶來太大影響。
一般使用基于原子電荷和基于波函數在擬合點上計算的靜電勢的偏差的RMSE和Relative RMSE(RRMSE)來衡量所得原子電荷對靜電勢的重現性。對于單個結構來說,使用上述任何特殊做法后,都會令RMSE/RRMSE相對于標準的MK或CHELPG的情況產生一定程度的增大,但是考慮到可以解決普通擬合靜電勢方法對于柔性分子在模擬中存在的明顯問題,犧牲一些靜電勢重現精度、容忍RMSE/RRMSE稍微變大是明顯值得的。
順帶一提,擬合靜電勢方法有個很大局限性就是對深度包埋的原子注定沒法得到能真實反映其帶電狀態的原子電荷,比如對碳納米管包夾小分子的體系計算其中小分子的原子電荷,以及計算周圍被配體圍滿的過渡金屬的電荷,擬合靜電勢電荷方法是不可能準確體現其實際電荷分布特征的,因為這些原子離大部分或者所有擬合點都太遠,它們的原子電荷對擬合點處靜電勢重現性影響甚微,因此擬合靜電勢方法也不可能算準它們的實際電荷。這個問題無論利用上述提及的任何手段都無法解決,因此只能用其它原子電荷計算方法,比如筆者提出的原子偶極矩校正的Hirshfeld電荷(ADCH),或者知名的NPA等。不過,如果你計算原子電荷的最終目的僅是通過原子電荷表現體系與體系外部其它原子的靜電相互作用而不在于了解實際電荷分布狀況,那么對上述存在原子深度包埋的體系用擬合靜電勢電荷完全沒問題。
1.3 RESP電荷
Kollman等人在J. Phys. Chem., 97, 10269 (1993)中提出的Restrained ElectroStatic Potential (RESP)電荷可以說是到目前為止最適合用于柔性小分子做分子模擬(包括動力學、構象分析、分子對接等)用的原子電荷,很大程度解決了MK/CHELPG電荷存在的前述問題。RESP電荷的擬合分為以下兩步,利用到了上一節提到的許多思想。
? 第一步:擬合電荷時使用雙曲懲罰函數對非氫原子施加弱限制(a=0.0005),不約束原子的等價性,所有原子的電荷都被擬合。這一步允許原子電荷變化有最大的自由度,以充分讓極性原子盡可能好地擬合靜電勢。
? 第二步:擬合電荷時使用雙曲懲罰函數對非氫原子施加強限制(a=0.001),只允許sp3雜化的碳、亞甲基的碳,以及它們上面的氫的電荷被擬合,而其它原子的電荷保持上一步最后的狀態。擬合中還約束每個-CH3, =CH2, -CH2-基團上的氫的電荷保持等價性。
之所以RESP電荷分成兩步,是因為作者經過謹慎測試發現,只有這么做,才能既解決普通擬合靜電勢電荷用于柔性分子的模擬時存在的問題,又不令外加限制和約束對靜電勢的重現性和原子電荷的質量帶來太大損害。
RESP原文里用的擬合點分布和MK電荷相同,但也完全可以改用CHELPG電荷的擬合點分布。雖然Kollman等人認為RESP電荷已經很大程度減小了普通擬合靜電勢電荷的構象依賴性,但是,如果比較講究的話,在擬合RESP電荷的時候還是應當同時按照上一節所述,在擬合過程中考慮多構象。
正由于RESP電荷很適合分子動力學模擬目的,因此在RESP電荷提出后,著名的蛋白質與核酸力場AMBER從其94版開始將RESP電荷作為了其獲得原子電荷的標準方法。后來發展的普適性有機小分子力場GAFF也將RESP電荷作為御用電荷,和AMBER相兼容的以描述糖類為主的GLYCAM力場也基于RESP電荷。不過,GLYCAM為了充分考慮構象依賴性問題,是先對每種單糖在TIP3P水模型下模擬50~100ns,取100~200個結構,對每個結構計算RESP電荷后再取平均。
能算RESP電荷的程序不多,以往最知名、最常用的是免費的AmberTools程序包里的用于產生Amber程序用的有機小分子拓撲和力場信息的Antechamber程序,通過這個程序產生RESP電荷時它會自動調用RESP電荷提出者開發的代碼。用Antechamber產生RESP電荷比較麻煩,得先用它產生帶有特定關鍵詞的Gaussian輸入文件,Gaussian算完了之后得讓它再讀入Gaussian輸出文件,因此使用者非得有Gaussian不可,而且Antechamber的運行參數也不怎么好記,此外,此程序對于無機或者金屬有機體系都沒法處理。還有個有點名氣的計算RESP電荷的在線程序叫R.E.D.(http://upjv.q4md-forcefieldtools.org/RED/),這網站做得什么時候看都鬧心、看著眼暈,反正我是完全用不明白,感覺把簡單問題嚴重復雜化了。鑒于目前沒有真正方便、好用的計算RESP電荷的程序,筆者在Multiwfn的布居分析(主功能7)中加入了RESP電荷計算功能,使用簡單至極,而且這個模塊的設計極為靈活和普適,能做的事絕不僅限于計算RESP電荷,這在后文將做介紹。有了Multiwfn就再也沒必要用Antechamber和R.E.D.了。
PS 1:NWChem、CP2K、Gaussian16 >=C.01版也號稱能計算RESP電荷,但實際上那僅僅是支持在擬合靜電勢電荷計算過程中加入懲罰函數而已,根本不算是一般意義的RESP電荷。
PS 2:只要擬合點位置完全相同,那么對一般體系,Multiwfn算的RESP電荷就和Antechamber給出的精確相同。但由于Antechamber利用的是Gaussian的MK電荷計算功能產生的擬合點,而Multiwfn和Gaussian產生MK擬合點位置的代碼有一定差異,因此Multiwfn和Antechamber算的RESP電荷也略有出入,但二者都是完全合理的。相關說明詳見《關于為什么Multiwfn算的出RESP電荷與Antechamber的有所差異》(http://www.shanxitv.org/516)。
一個與RESP電荷關系比較密切的是AM1-BCC電荷,它在動力學模擬領域用得也很多。此電荷于J. Comput. Chem., 21, 132 (2000)提出,目的是以很便宜的方式就可以得到接近HF/6-31G*下計算的RESP電荷。AM1-BCC計算速度極快,它首先在AM1級別優化結構并基于AM1算的靜電勢得到擬合靜電勢電荷,這步耗時不高,之后會再做個查表方式的鍵電荷校正(BCC),這步更是幾乎完全不花計算時間。AM1-BCC算起來比RESP省事不少,只需要用Antechamber通過一個命令就可以計算。不過,AM1-BCC電荷在原理上終究只是RESP電荷的近似,對應的也只是不咋地的HF/6-31G*級別的RESP電荷,鑒于在如今的計算條件下,基于DFT優化一百多原子的結構并計算靜電勢都不是難事,而且做模擬的專業人士相對于圖省事、省時更看重結果的好壞,特別是再加上誕生了Multiwfn這極為便利的計算RESP電荷的工具,我覺得就完全沒有必要用AM1-BCC了,除非你要快速處理大批量分子。
1.4 在擬合靜電勢計算過程中施加電荷約束
計算擬合靜電勢電荷時,可以通過拉格朗日乘子法添加各種約束條件。其中最有意義的是添加電荷約束條件,就是讓某個原子的電荷或者指定的一批原子的電荷總和等于特定值。前面提到,標準的RESP電荷的第二步計算時,除了sp3雜化的碳、亞甲基的碳以及它們上面的氫以外的各個原子的電荷都保持第一步計算的結果,這就是通過這種約束來實現的。電荷約束還可以實現很多特殊目的:
(1)生物大分子、聚合物等體系都是一個個單元聚合而成的,這樣的大分子中每個組成單元部分被稱為殘基,描述這類體系的力場都是對每種殘基來給出原子電荷,因此整體電荷就由各個單體拼接而成。顯然每個單體的凈電荷得是整數。我們若想自己計算殘基的原子電荷,就可以將殘基兩端用恰當的基團或片段進行封閉,然后通過電荷約束另殘基部分電荷為期望的整數。(也有做法是不做電荷約束,而是之后自己手動調節殘基里的原子電荷使殘基的凈電荷為整數,但這樣顯然任意性太強,原理上也遠不如用電荷約束好)
(2)有的力場比如GROMOS,利用了電荷組(charge-group)概念來降低cut-off方式計算靜電作用的誤差。每個電荷組包含數個原子,里面所有原子電荷加和為整數,比如每個羧基的總電荷要求為0,而它解離掉質子后電荷要求為-1。為了獲得與電荷組概念相兼容的擬合靜電勢電荷,就可以利用電荷約束來保持各個片段的電荷為指定的整數。
(3)有的時候可能基于二聚體或多聚體波函數來計算擬合靜電勢電荷,我們希望每個分子的電荷都為0,那么就可以利用電荷約束來實現。
顯然,用電荷約束的時候所得擬合靜電勢電荷的RMSE或RRMSE肯定是大于不用約束時候的。電荷不能瞎約束,既得滿足自己的特殊目的,又必須能大致符合實際電荷分布特征,亂約束會令所得電荷對靜電勢的重現性大打折扣,使模擬結果變差。
上述提到的內容的一些具體公式本文就不給出了,感興趣者可參閱Multiwfn手冊3.9.16節。
1.5 關于計算擬合靜電勢電荷的量子化學計算級別的選用
包括RESP在內的擬合靜電勢電荷計算結果直接受到量子化學中幾何優化和計算靜電勢用的計算級別的影響。這里對計算級別的選用做一下建議。
(1)結構優化:對于計算擬合靜電勢電荷的目的,結構必須經過優化,但結構優化精度只要達到不錯就可以了,不用要求超級精確,當然也不能太次。一般情況,理論方法就用常用的B3LYP即可,如果你不是量子化學內行的話,那么建議你在優化時總是帶上DFT-D3色散校正。對前三周期元素,基組就用6-311G**即可。如果體系里有第四周期及之后的原子,對它們就用SDD贗勢和它標配的贗勢基組即可。
(2)計算靜電勢:泛函還是用B3LYP就可以。帶不帶DFT-D3校正對靜電勢計算結果無任何直接影響,因此可帶可不帶。如前述的《原子電荷計算方法的對比》一文的圖5所示,只要基組達到中等質量,繼續增大基組對結果也沒有什么顯著影響。對前三周期元素基組用6-311G**就夠了,過渡金屬還用SDD即可,而諸如Br、I等第四周期及之后的主族元素,我建議用lanl08(d),這是帶d極化函數的贗勢基組(SDD贗勢原始標配的贗勢基組對主族是不帶d極化函數的,因此對靜電勢的描述注定不會很理想)。
如果對上述提及的名詞和相關知識不了解,請仔細閱讀《DFT-D色散校正的使用》(http://www.shanxitv.org/210)、《簡談量子化學計算中DFT泛函的選擇》(http://www.shanxitv.org/272)、《談談量子化學中基組的選擇》(http://www.shanxitv.org/336)、《談談贗勢基組的選用》(http://www.shanxitv.org/373)。
如果打算把擬合靜電勢電荷用在溶劑環境下進行模擬,那么在幾何優化和計算靜電勢的時候都應當通過隱式溶劑模型表現溶劑環境。溶劑環境對幾何結構影響往往不太大,但對于靜電勢影響總是很顯著,尤其是對于極性較大的溶劑來說。這是因為溶質的電荷分布會被溶劑所顯著極化,對于隱式溶劑模型而言,溶劑的介電常數越大,表現出的溶劑對溶質電荷的極化效應就越強。對于像水這樣極性很大的溶劑,顯然計算擬合靜電勢電荷的情況若不考慮隱式溶劑模型來反映出溶質的電荷分布被溶劑極化的現象,這樣的原子電荷無論用在顯式還是隱式水模型下的動力學模擬中,結果都會顯著不合理。對于Gaussian用戶,就用默認的IEFPCM隱式溶劑模型即可。如果對這些內容不了解,參見《談談隱式溶劑模型下溶解自由能和體系自由能的計算》(http://www.shanxitv.org/327)。
比如你要模擬一個不含第四周期及之后元素的普通有機分子在乙醇中的動力學行為,若你是Gaussian用戶,那么你只需要用# B3LYP/6-311G** em=GD3BJ opt scrf=solvent=ethanol關鍵詞做計算,同時通過%chk指定chk文件產生的位置,等任務結束后,將chk轉換為fch文件,然后交給Multiwfn計算MK或CHELPG或RESP電荷即可,這樣算出來的電荷也正對應于B3LYP/6-311G**級別的靜電勢。如果不知道怎么把chk轉換成fch,參見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)中關于fch文件部分的說明。
若你計算擬合靜電勢電荷最終是打算結合可極化力場去用,那么擬合靜電勢的時候就別再用隱式溶劑模型了,因為外環境對溶質的可極化效果此時不需要由原子電荷等效地體現,而是有專門的項(如可極化偶極、Drude振子)來體現。
注:如果你的原子電荷是用于溶劑環境下的非可極化力場的分子動力學模擬目的,其實最理想的做法并不是像上述那樣直接在隱式溶劑模型下算RESP電荷,而是將隱式溶劑模型下和氣相下算的RESP電荷取平均,這稱為RESP2(0.5)電荷。關于這點,筆者在另一篇文章做了非常詳細的闡述,做分子動力學的人務必在讀過本文后閱讀:《RESP2原子電荷的思想以及在Multiwfn中的計算》(http://www.shanxitv.org/531)。
2 Multiwfn中的擬合靜電勢電荷計算功能
本節介紹一下Multiwfn中的擬合靜電勢電荷計算功能的設計和使用。
2.1 Multiwfn中的兩個與擬合靜電勢電荷有關的模塊
Multiwfn里目前有兩套計算擬合靜電勢電荷的模塊:
(1)主功能7中的子功能12和13,分別用于計算標準的CHELPG和MK電荷。此功能在很老的Multiwfn版本中就有。
(2)主功能7中的子功能18,這叫RESP計算模塊,一方面可以用于計算標準形式的RESP電荷,另一方面可以計算帶有自定義的電荷約束、原子等價性約束、懲罰函數參數的MK和CHELPG擬合靜電勢電荷。而且擬合過程中支持多構象。
相比之下,(1)的功能比較簡單,沒太多好說的。(2)遠比(1)更強大、更普適,選項較多,因此在下文就專門介紹一下。
使用這兩個模塊要求Multiwfn的輸入文件里包含波函數信息,更確切來說,是至少包含GTF信息。哪些輸入文件包含GTF信息,看過《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)就自然明白了。量子化學程序產生的諸如.wfn、.wfx、.fch、.gms、.molden等格式的文件都可以作為輸入文件。由于Multiwfn支持格式豐富,Gaussian、ORCA、GAMESS-US、NWChem、Molpro等幾乎所有主流量化程序都可以結合Multiwfn計算RESP電荷。至于Dmol3和ADF之流,由于用的基函數形式嚴重非主流,因此永遠不可能被Multiwfn支持。
如果你的CPU核數多于四核,別忘了啟動Multiwfn之前把settings.ini里的nthreads設為實際CPU核數,以使用所有CPU核心并行計算來降低耗時。
Multiwfn在計算包括RESP在內的擬合靜電勢電荷過程中需要基于波函數計算所有擬合點的靜電勢。如果你的CPU核數少于10核,而且你使用.fch/fchk作為Multiwfn的輸入文件,并且你機子里裝了Gaussian,那么建議讓Multiwfn自動調用Gaussian目錄下的cubegen工具來代替Multiwfn自身的代碼計算靜電勢,這樣可以降低耗時百分之幾十。做法是在Multiwfn目錄下的settings.ini文件里把cubegenpath參數設為機子里Gaussian目錄下cubegen程序的實際路徑。
2.2 Multiwfn中的RESP計算模塊的選項
進入Multiwfn主功能7的子功能18(RESP計算模塊)后會看到一堆選項,其含義光看選項上的文字就應該能理解。下面依次說說。
如果你想按照Kollman在RESP原文里定義的做法來計算標準的RESP電荷,直接選選項1即可。由于這個過程包含兩個步驟,所以被稱為two-stage RESP fitting。
如果你想只想計算普通的擬合靜電勢電荷,選擇選項2即可。這個過程只需要一步,因此也叫one-stage ESP fitting。在計算前,你可以用選項4來設定計算時對非氫原子施加的雙曲懲罰函數的a、b參數大小,用選項5設定原子等價性約束,用選項6設定電荷約束。默認情況下,懲罰函數的b=0.1、a=0.0005,要求每個CH3和CH2基團中的氫的電荷等價,不施加電荷約束。
用選項4也可以人為修改標準RESP電荷計算過程中每一步的懲罰函數參數。在選項4和5里分別由用戶自定義的等價性約束和電荷約束不僅對于one-stage ESP fitting有效,對于two-stage RESP fitting也有效,但僅對其第一步生效(根據標準的RESP擬合過程可知,在其第二步自定義約束是基本沒意義的,或者說這樣會和方法本身定義的約束方式造成沖突)。
設計算RESP電荷和計算普通擬合靜電勢電荷時都可以在擬合時考慮多構象,只要計算前先選-1,從外部文件中讀取各個構象路徑以及構象權重即可。
默認情況下是基于MK擬合點來計算的,如果想改用CHELPG的,選選項3可以修改。而且用選項3選擇分布擬合點的方法后,還可以設定擬合點分布的具體參數,比如對于MK來說可以設每平方埃的點數、擬合點有幾層等。Multiwfn默認的格點密度已經足夠大了,一般不需要再調得更大。
計算標準RESP電荷,以及計算普通擬合靜電勢電荷但要求CH3和CH2基團中的氫的電荷等價時,程序需要利用原子間連接關系來進行判斷哪些原子的電荷要被擬合、哪些是要求等價的氫原子等等。默認情況下,兩個原子間距離小于二者CSD共價半徑和的1.15倍就被當成成鍵。如果覺得連接關系和期望的不符,一個做法是選擇選項7,從指定的.mol文件中讀取連接關系。.mol也叫MDL file,是一種常用的記錄分子結構的格式,其中有連接關系字段。.mol用常用的gview就可以生成,gview里把哪些原子之間用鍵連上,保存出來的.mol文件里的連接關系就會有相應的體現。另外,也可以在Multiwfn主功能0里面修改連鍵的閾值,哪些鍵此時是連著的直接從圖形窗口就能看到,把閾值調到所有原子間鍵連關系都合適后,再進入RESP模塊進行計算,則計算時用的鍵連關系和主功能0的圖形窗口中看到的將是一樣的。
先選擇一次選項8把狀態切換為Yes后,在計算RESP或普通擬合靜電勢過程中,Multiwfn會從用戶輸入的Gaussian的pop=MK或pop=CHELPG并帶有IOp(6/33=2)關鍵詞的任務的輸出文件中直接讀取擬合點的位置和擬合點上的靜電勢數值,此時Multiwfn就不會自己去設定擬合點位置并計算靜電勢了。另外,Gaussian還有個選項IOp(6/42=x),x是設定用pop=MK做擬合靜電勢電荷計算時候每平方埃上的擬合點數,建議用6,這也正對應于Multiwfn默認的情況。一般來說,從Gaussian輸出文件里讀取擬合點的這個功能一般用不著,但如果你習慣在服務器上做計算,而在配置不怎么樣的PC上用Multiwfn做分析和寫文章,那么就這個功能就能派上用場了,在PC上計算擬合靜電勢電荷時直接讀服務器上產生的帶有擬合點信息的Gaussian輸出文件即可。還有,如果你可能對一個體系多次計算擬合靜電勢電荷,每次計算用不同的設置,那么產生帶有擬合點信息的Gaussian輸出文件后,就不用每次做擬合靜電勢計算的時候重算靜電勢了,省了很多時間。
注意:pop=MK或CHELPG IOp(6/33=2) IOp(6/42=x)關鍵詞必須對單點任務加,絕對別用在opt任務上,否則優化任務中Gaussian會對初始結構輸出一次靜電勢擬合點信息,對最后結構也會輸出一次靜電勢擬合點信息,兩次顯然是不同的。如果讓Multiwfn讀取這樣任務的輸出文件,Multiwfn就會被搞糊涂,讀取的可能是初始結構的擬合點信息,顯然此時的結果可能是嚴重不合理的。
Multiwfn擬合靜電勢時可以考慮額外的擬合點,也就是對于非原子中心位置的點也可以對其擬合電荷,這對于某些情況很有意義,見3.6節。
Multiwfn一般以交互式方式運行,但也完全可以以命令行方式運行,一條命令就可以直接計算出擬合靜電勢電荷了,見《計算RESP原子電荷的超級懶人腳本(一行命令就算出結果)》(http://www.shanxitv.org/476)。還可以寫腳本批量計算一大堆分子的RESP電荷,方法見手冊5.2和5.3節的說明。
有一些更細節上的東西這里就不提了,大家可參閱Multiwfn手冊3.9.16節,對應RESP計算模塊的介紹。下面就通過各種實例來演示Multiwfn的RESP計算模塊的使用,同時也幫助大家更好地理解RESP電荷的思想還有前述的諸多討論。
3 計算實例
下文用到的所有文件都可以在此下載:http://www.shanxitv.org/attach/441/file.rar。本文用的Gaussian是G16 A.03,Multiwfn用的是2018-Sep-11更新3.6(dev)版。
3.1 標準的RESP電荷計算實例:乙醇環境中的多巴胺
下面我們對簡單有機小分子多巴胺計算標準的RESP電荷。此體系有多個構象,這里我們用的是在《gentor:掃描方式做分子構象搜索的便捷工具》(http://bbs.keinsci.com/thread-2388-1-1.html)中搜索出來的能量最低的構象,如下所示。
Gaussian的優化任務輸入文件如下所示,坐標部分略,完整文件是本文文件包里的dopamine-single下的dopamine.gjf。
%chk=dopamine.chk
# B3LYP/6-311G** em=GD3BJ opt scrf=solvent=ethanol
Title Card Required
0 1
算完后把dopamine.chk用formchk轉成fch。啟動Multiwfn,依次輸入
dopamine.fch
7 //布居分析與原子電荷計算
18 //RESP模塊
1 //計算標準RESP電荷
在普通4核Intel CPU下,只需要10秒左右就算完了。如果你讓Multiwfn調用cubegen來計算靜電勢的話,耗時還能節約一半。輸出信息最后顯示的就是標準的RESP電荷,如下所示
Center Charge
1(O ) -0.5406591096
2(O ) -0.5360249634
3(N ) -1.0237492930
4(C ) -0.3004859752
5(C ) 0.1711380986
6(C ) 0.5622482232
7(C ) -0.3931634336
8(C ) -0.2705581837
9(C ) 0.2620223130
10(C ) -0.3419200343
11(C ) 0.2508650859
12(H ) 0.0727236261
13(H ) 0.0727236261
14(H ) -0.0640806350
15(H ) -0.0640806350
16(H ) 0.1956777773
17(H ) 0.1606950156
18(H ) 0.2044556422
19(H ) 0.3674982935
20(H ) 0.3689299792
21(H ) 0.4257617766
22(H ) 0.4199828057
Sum of charges: 0.0000000000
RMSE: 0.002097 RRMSE: 0.110460
結果非常正常。注意看的話,會發現12和13號氫,以及14和15號氫的原子電荷精確相同,因為它們都是-CH2-基團上的氫,在RESP計算的第二步被強制約束相等。輸出的RMSE和RRMSE值都不大,一般達到當前程度的數值,就算擬合質量比較不錯了,而如果RMSE和RRMSE都很大,則說明靠原子電荷模型已經無法準確描述體系范德華表面附近及外側的靜電勢了,而需要用更復雜的電荷分布模型(比如在原子核或化學鍵上引入點偶極矩、點四極矩之類)。
最后程序問你是否把算出來的原子電荷導出到當前目錄下的dopamine.chg文件中,如果輸入y就會導出。chg文件的格式很簡單,就是記錄元素名、原子坐標和電荷值。Multiwfn里的某些功能是需要靠chg文件作為輸入文件提供原子電荷信息的,比如若你將chg文件作為輸入文件就可以用Multiwfn的主功能3、4、5計算和繪制基于原子電荷產生的靜電勢,以及通過主功能7的子功能-2基于原子電荷計算指定片段間的靜電相互作用能。
在計算過程中輸出了不少信息,為了便于大家更好地理解計算細節,下面解讀一下。
計算一開始程序先確定擬合點的位置,在屏幕上輸出當前計算用的原子半徑,以及總擬合點數,如下所示。如果碰到第四周期及之后的元素,此處程序會讓你輸入那些元素的半徑,一般就直接按回車讓程序用UFF半徑除以1.12的值即可。
Atomic radii used:
Element:H vdW radius (Angstrom): 1.200
Element:C vdW radius (Angstrom): 1.500
Element:N vdW radius (Angstrom): 1.500
Element:O vdW radius (Angstrom): 1.400
Number of MK fitting points used: 13394
然后程序就對擬合點計算靜電勢。算完靜電勢之后程序就開始RESP電荷的第一步的計算,即對非氫原子施加弱限制(a=0.0005)計算常規的擬合靜電勢電荷。前面提到,施加雙曲形式的懲罰函數時需要迭代求解,因此從下面的輸出看到程序作了迭代。到了第7輪的時候,原子電荷最大變化值已經小于閾值0.000001了,于是宣告收斂。
No charge constraint is imposed in this stage
No atom equivalence constraint is imposed in this fitting stage
**** Stage 1: RESP fitting under weak hyperbolic penalty
Convergence criterion: 0.00000100
Hyperbolic restraint strength (a): 0.000500 Tightness (b): 0.100000
Iter: 1 Maximum charge variation: 1.0067306224
Iter: 2 Maximum charge variation: 0.0503406929
Iter: 3 Maximum charge variation: 0.0040155661
Iter: 4 Maximum charge variation: 0.0003425806
Iter: 5 Maximum charge variation: 0.0000329903
Iter: 6 Maximum charge variation: 0.0000032384
Iter: 7 Maximum charge variation: 0.0000003207
Successfully converged!
然后程序開始RESP電荷第二步的計算,輸出信息如下所示
**** Stage 2: RESP fitting under strong hyperbolic penalty
Atoms equivalence constraint imposed in this fitting stage:
Constraint 1: 12(H ) 13(H )
Constraint 2: 14(H ) 15(H )
Fitting objects: sp3 carbons, methyl carbons and hydrogens attached to them
Indices of these atoms:
4C 12H 13H 6C 14H 15H
Convergence criterion: 0.00000100
Hyperbolic restraint strength (a): 0.001000 Tightness (b): 0.100000
Iter: 1 Maximum charge variation: 1.0237531514
Iter: 2 Maximum charge variation: 0.0068739119
Iter: 3 Maximum charge variation: 0.0000294328
Iter: 4 Maximum charge variation: 0.0000001351
Successfully converged!
由輸出可見,程序根據RESP電荷的計算規則以及原子連接關系,自動判斷出12H和13H是需要被視為等價的,14H和15H也是需要被視為等價的。然后程序告訴你4C、12H、13H、6C、14H、15H要么是sp3或甲基碳,要么是這些碳上的氫,因此按照RESP電荷的標準計算規則,這些原子的電荷需要在第二步進一步進行擬合,而且施加強限制(a=0.001)。最后經過四步就收斂了。對于某些體系,第二步沒有原子需要進一步擬合電荷,此時第二步就會直接跳過。
如前所述,計算包括RESP在內的擬合靜電勢電荷時也可以直接從Gaussian輸出文件里讀取擬合點位置和靜電勢值。先用文件包里dopamine-single目錄下的dopamine_pop_MK.gjf(里面的坐標是已優化好的坐標)做計算得到同名的out文件,然后在Multiwfn的RESP計算界面里選擇一次選項8,再選1開始標準的RESP電荷計算,并按照提示輸入.out文件的路徑,之后一瞬間RESP電荷就算完了,和前面貼的計算結果差異最多就零點零幾的數量級,差異來自擬合點數目和位置的不同。
3.2 考慮多構象的RESP電荷計算實例:氣相的多巴胺
在《gentor:掃描方式做分子構象搜索的便捷工具》(http://bbs.keinsci.com/thread-2388-1-1.html)中通過DFT計算發現,多巴胺在氣相下有四種構象能量明顯低于其它構象,在常溫下出現比率占明顯的主導。此例我們就演示一下在計算RESP電荷過程中考慮這四種構象的權重平均。
為了能根據Boltzmann公式獲得各個構象的出現比率,首先我們來計算這四種構象的自由能。怎么計算自由能在《談談隱式溶劑模型下溶解自由能和體系自由能的計算》(http://www.shanxitv.org/327)中說得很明確。我們這里就用比較一般的做法來計算,先用檔次一般的B3LYP-D3(BJ)/6-311G**做優化和振動分析獲得自由能的熱校正量,然后基于此結構再用更好但也更貴的M06-2X/def2-TZVP級別計算單點能,相加就是精度比較好的常溫下的自由能,而且總耗時也不算太高。而計算靜電勢的fch文件我們還是用B3LYP-D3(BJ)/6-311G**下產生的就夠了,當然你用M06-2X/def2-TZVP計算產生的也行,結果原理上更好,但由于基組更大,計算靜電勢過程中耗時也會更高。相應的輸入輸出文件都在本文文件包里的dopamine_4conf目錄下。
計算出四個構象的相對自由能后(以自由能最低的為零點),代入《根據Boltzmann分布計算分子不同構象所占比例》(http://www.shanxitv.org/165)文中的表格里,即可得到Boltzmann權重,如下所示:

PS:如果你想得到溶劑下的Boltzmann權重,應當利用SMD溶劑模型計算溶解自由能,加到上面的氣相自由能上,然后再計算Boltzmann權重。這點在《談談隱式溶劑模型下溶解自由能和體系自由能的計算》中有詳述。
把前面opt freq任務產生的四個構象的chk文件都轉化成.fch并拷到當前目錄下。然后創建一個文本文件,比如叫conf.txt,內容是每個構象的輸入文件相對于當前目錄的路徑或者絕對路徑,后面是權重值。權重加和顯然必須為1。如果不懂什么叫“當前路徑”的話看《將文件快速載入Multiwfn程序的幾個技巧》(http://www.shanxitv.org/237)。本例conf.txt內容如下所示
dopamine1.fch 0.0848
dopamine2.fch 0.0265
dopamine3.fch 0.4844
dopamine4.fch 0.4041
啟動Multiwfn,載入上面任意一個.fch(此處目的僅僅是讓程序獲得能夠用于判斷原子連接關系的分子結構信息,因此載入的哪怕只是當前體系任意一個構象的.pdb、.mol、.xyz這樣只包含結構信息的文件也行),然后依次輸入
7 //布居分析與原子電荷計算
18 //RESP模塊
-1 //載入構象列表
conf.txt //構象列表的實際路徑
1 //計算標準RESP電荷
擬合靜電勢電荷的耗時幾乎完全在計算靜電勢上,考慮N個構象的時候,要計算的靜電勢的次數就會變成只考慮一個的時候的大約N倍,因此當前例子耗時明顯高于上一節的例子。考慮4個構象時計算結果如下
Center Charge
1(O ) -0.512712
2(O ) -0.494615
3(N ) -0.759750
4(C ) -0.234393
5(C ) 0.060417
6(C ) 0.314094
7(C ) -0.343044
8(C ) -0.116067
9(C ) 0.271250
10(C ) -0.390258
11(C ) 0.268994
12(H ) 0.085643
13(H ) 0.085643
14(H ) -0.025277
15(H ) -0.025277
16(H ) 0.143222
17(H ) 0.122552
18(H ) 0.184873
19(H ) 0.285920
20(H ) 0.286160
21(H ) 0.404082
22(H ) 0.388544
Sum of charges: 0.000000
Conformer: 1 RMSE: 0.002885 RRMSE: 0.176042
Conformer: 2 RMSE: 0.002727 RRMSE: 0.163666
Conformer: 3 RMSE: 0.002234 RRMSE: 0.146771
Conformer: 4 RMSE: 0.002102 RRMSE: 0.134091
Weighted RMSE: 0.002249 Weighted RRMSE 0.144547
考慮多構象時,Multiwfn會對每個構象分別給出RMSE和RRMSE,以及給出權重平均的RMSE和RRMSE。從數據可見,當前的原子電荷對構象3和4的靜電勢重現性比起對構象1和2好不少,原因不難理解,因為conf.txt中構象3和4的權重明顯比1和2大得多,因此所得原子電荷更側重對構象3和4周圍靜電勢的描述。
如果你只考慮一個構象,即在conf.txt里把dopamine1.fch權重設為1而把其它權重設為0,則輸出的誤差為(此時原子電荷值與只用dopmaine1.fch按照上一節的過程來計算的相同)
Conformer: 1 RMSE: 0.002047 RRMSE: 0.124925
Conformer: 2 RMSE: 0.002862 RRMSE: 0.171810
Conformer: 3 RMSE: 0.003391 RRMSE: 0.222734
Conformer: 4 RMSE: 0.004172 RRMSE: 0.266133
可見此時的原子電荷對構象1的靜電勢表現得很不錯,RMSE和RRMSE數值很小,而對實際中出現幾率最大的構象3和4則描述質量不佳,顯然模擬結果肯定也不算很理想。這體現出對柔性分子考慮構象權重的重要性。哪怕你就是為了省事,擬合靜電勢的時候只打算考慮單個構象,那么也應當盡可能用自由能最低的結構。
考慮多構象的時候也是可以直接從Gaussian輸出文件里直接讀擬合點坐標和靜電勢值的。就是對各個構象先用IOp(6/33=2,6/42=6) pop=MK進行計算,相應的輸出文件已經提供在文件包里dopamine_4conf目錄下的ESP子目錄中了。比如把這四個.out文件都拷到C:\下,然后把confESP.txt寫成如下內容
C:\dopamine1_ESP.out 0.0848
C:\dopamine2_ESP.out 0.0265
C:\dopamine3_ESP.out 0.4844
C:\dopamine4_ESP.out 0.4041
載入fch或任意含有當前體系結構信息的文件后,進入RESP計算功能,選-1,把confESP.txt的路徑輸進去,然后選一次選項8,再選擇1計算RESP電荷,Multiwfn就會從這些Gaussian輸出文件中讀取各個構象的擬合點信息和靜電勢值并進行電荷計算了,結果馬上就會輸出出來。
3.3 施加等價性約束時的擬合靜電勢電荷計算實例:磷酸二甲酯
磷酸二甲酯在B3LYP-D3(BJ)/6-311G**下優化的結構如下所示。
此體系的兩個甲氧基其實是化學等價的,實際模擬過程中容易繞O-P鍵旋轉,因此O5、O6的電荷應當相同,C7、C11的電荷應當相同,同時兩個甲基上總共六個氫(H8,H9,H10,H12,H13,H14)的電荷也理應相同。但是只考慮一個構型的話,是顯然得不到這樣的結果的。比如對上圖結構直接用標準的RESP方式計算電荷,結果是O5=-0.378、O6=-0.435,明顯缺乏等價性。本例就以此體系為例演示如何計算出滿足上述等價性要求的擬合靜電勢電荷,我們將用RESP模塊做帶有自定義的原子等價性或電荷約束條件的一步方式(one-stage)的擬合靜電勢電荷計算。
首先建立一個文本文件,比如叫eqvcons.txt,里面每一行的原子會被要求在擬合時保持電荷相同。因此當前情況應當寫成下面這樣(先后順序隨意):
5,6
7,11
8-10,12-14
然后啟動Multiwfn,載入本文文件包里C2H7O4P目錄下的C2H7O4P.fch,然后依次輸入
7 //布居分析與原子電荷計算
18 //RESP模塊
5 //設置擬合靜電勢計算時用的原子等價性約束(不改的話,對于一步方式的擬合,默認是約束每個CH2和CH3基團上的氫電荷相同)
1 //從外部文件中讀取等價性約束
eqvcons.txt //等價性設置文件的實際路徑
2 //做一步方式的擬合靜電勢計算
計算結果如下。如屏幕提示所示,默認用的是弱限制參數(a=0.0005),這可以自己改。
Center Charge
1(P ) 1.120525
2(O ) -0.622980
3(O ) -0.588773
4(H ) 0.410987
5(O ) -0.403464
6(O ) -0.403464
7(C ) 0.035298
8(H ) 0.069429
9(H ) 0.069429
10(H ) 0.069429
11(C ) 0.035298
12(H ) 0.069429
13(H ) 0.069429
14(H ) 0.069429
Sum of charges: 0.000000
RMSE: 0.002541 RRMSE: 0.136047
可見結果完全滿足我們做的等價性約束設置,原子電荷數值也都很合理,很有化學意義。如果我們不做自定義約束,而用默認的設置,則RRMSE結果為0.113024。雖然我們做自定義等價性約束令RRMSE有所增高,體現所得電荷對當前構型的靜電勢重現性略有下降,但是RRMSE并未增加太多,所以我們我們當前做的約束絲毫不算胡來。
注意設定等價性約束的時候不同批次原子之間不能有重疊,比如要求2-5等價而且4,8-10也等價是明顯不行的。
在標準兩步式RESP電荷計算時也照樣可以設置電荷約束、等價性約束,但只是對第一步起效(默認情況下,第一步的時候既沒有用任何等價性約束也沒有使用電荷約束)。對于此例,載入上述eqvcons.txt后選擇選項0做兩步式RESP擬合,會發現最終結果里O5和O6的電荷相同了,但是C7、C11的電荷不同,不同甲基上的氫的電荷也不同。這是因為自定義約束對于第二步不生效,而且按照定義,第二步RESP擬合時甲基氫、甲基碳會被重新擬合。
3.4 施加電荷約束時的擬合靜電勢電荷計算實例:擬合水環境下天冬氨酸殘基的原子電荷
一般的蛋白質力場都會直接定義常見的各種氨基酸殘基的原子電荷,在力場原文、動力學程序自帶的庫文件等地方就能看到。但碰到一個力場原本沒有考慮的殘基的時候,顯然原子電荷得自己搞。雖然天冬氨酸(ASP)殘基在主流蛋白質力場里都已提供了原子電荷,但我們假定這是一個新的殘基,于是自己來擬合原子電荷。擬合的時候顯然不能直接拿一個孤立狀態的ASP氨基酸作為模型,因為它的羧基上的OH和氨基上的一個氫在它以殘基形式處于實際蛋白質中時是沒有的;當然更不能直接就把羧基的OH和氨基的氫給去掉,否則量子化學計算時電子結構將非常詭異,和殘基在實際蛋白質中的狀態大相徑庭。為了量子化學計算時能令殘基的電子結構比較接近于在蛋白質中的狀態,一般的做法是把殘基的氮端用乙酰封閉,把碳端用甲胺封閉,形成ACE-ASP-NME模型體系,對這個體系優化、計算擬合靜電勢得到的ASP殘基的原子電荷,就可以用于實際蛋白質的模擬中了。
蛋白質最典型的兩種二級結構就是alpha螺旋和beta折疊,從構成它們的殘基的角度看,在于殘基骨架的phi和psi角度不同(不懂這個的話看下文)。有人建議在擬合殘基靜電勢電荷的時候對骨架同時考慮這兩種構象,本例我們就這么干。還要注意,殘基的電荷必須為整數,我們當前考慮的是ASP在中性水環境中的狀況,ASP側鏈的羧基的質子會解離,因此計算的時候應當約束ASP殘基的凈電荷為-1,并且考慮到羧酸根的兩個氧是化學等價的,最好再對這兩個氧施加電荷等價性約束。而ASP側鏈的CH2基團上的兩個氫也應該要求等價。可見,當前這個例子綜合性比較強,多構象、電荷約束、等價性約束全都用上了,這個例子搞懂了再搞其它體系就都很簡單了。
首先我們用gview畫一個ACE-ASP-NME,把phi和psi角度設為對應典型右手alpha螺旋的情況,即分別為-90度和-60度,保存為Gaussian輸入文件alpha.gjf。再把兩個角度設為對應典型beta折疊的情況,分別為-100度和130度(注:只要看一下標準的Ramachandran圖就知道不同二級結構應該對應的典型的phi和psi角度)。然后把關鍵詞都改成對應B3LYP-D3/6-311G**級別的優化任務,加上scrf關鍵詞以通過默認的IEFPCM模型表現默認的溶劑(水)環境,并通過修改冗余內坐標設定把對應phi和psi的兩個二面角在優化過程中設成凍結(不這樣的話優化之后這兩個角度變化會非常厲害,畢竟當前缺乏實際二級結構環境的束縛),怎么做凍結在《在Gaussian中做限制性優化的方法》(http://www.shanxitv.org/404)里面明確說了。別忘了此體系凈電荷是-1。寫好的輸入文件都在本文文件包的ACE-ASP-NME目錄下。然后用Gaussian運行這兩個輸入文件,產生的.out文件在文件包里也提供了。優化后的兩個結構如下所示
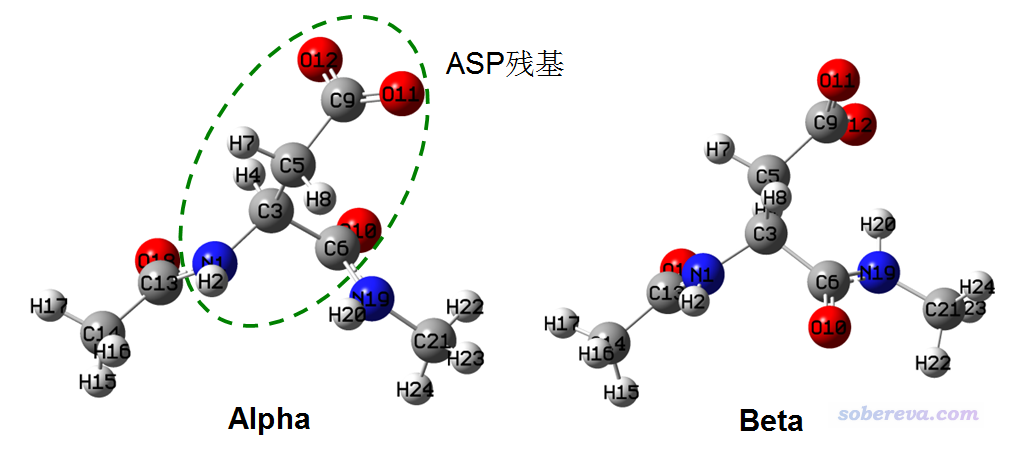
前面提到的phi角度指的就是圖中的6-3-1-13,psi角度就是指的1-3-6-19。
我們寫一個用來約束電荷的文件,比如叫chgcons.txt,里面每一行寫上一批原子序號以及期望的這些原子電荷的總和,設多少個約束都可以。當前,ASP殘基的原子序號是1-12(上圖綠色虛線所勾勒的范圍),我們希望它的總電荷為-1,因此在chgcons.txt里面寫
1-12 -1
(注:你考察的體系中原子序號不連續也沒關系,Multiwfn輸入序號的格式很靈活,比如寫1,5-7,13-15,20 1.5就代表要求1,5,6,7,13,14,15,20原子電荷的加和為1.5)
然后再寫一個原子等價性約束的文件eqvcons.txt,我們讓O11和O12等價,H7和H8等價,因此內容為
11,12
7,8
雖然體系兩端的每個甲基上的三個氫也應當保持等價,但是由于這部分不是我們當前關心的,所以就不用對它們設等價性約束了。
然后再寫一個構象列表文件比如叫conflist.txt,內容是計算后將chk轉化出的alpha.fch和beta.fch的實際路徑以及權重。這回我們就不以玻爾茲曼方式計算權重了,我們希望當前得到的原子電荷對此殘基在alpha螺旋和在beta折疊中都能較好地描述,所以權重就都簡單地設0.5。此文件內容應當如下所示,假設倆文件都放到了D:\下:
D:\alpha.fch 0.5
D:\beta.fch 0.5
之后啟動Multiwfn,載入alpha.fch和beta.fch任意其一,然后輸入
7 //布居分析與原子電荷計算
18 //RESP模塊
5 //設置做擬合靜電勢計算時用的原子等價性約束
1 //從外部文件中讀取等價性約束
eqvcons.txt //等價性設置文件的實際路徑
6 //設置做擬合靜電勢計算時用的原子電荷約束
1 //從外部文件中讀取電荷約束
chgcons.txt //電荷約束文件的實際路徑
-1 //讀取構象列表
conflist.txt //構象列表文件的實際路徑
2 //做一步方式的擬合靜電勢計算
結果如下所示
Center Charge
1(N ) -0.568030
2(H ) 0.298690
3(C ) 0.232066
4(H ) 0.003952
5(C ) -0.187247
6(C ) 0.580605
7(H ) 0.030942
8(H ) 0.030942
9(C ) 0.773254
10(O ) -0.602338
11(O ) -0.796419
12(O ) -0.796419
13(C ) 0.782297
14(C ) -0.680390
15(H ) 0.186825
16(H ) 0.185208
17(H ) 0.193426
18(O ) -0.651625
19(N ) -0.614772
20(H ) 0.370949
21(C ) 0.075908
22(H ) 0.053163
23(H ) 0.050423
24(H ) 0.048587
Sum of charges: -1.000000
Conformer: 1 RMSE: 0.002175 RRMSE: 0.017514
Conformer: 2 RMSE: 0.002087 RRMSE: 0.017379
Weighted RMSE: 0.002131 Weighted RRMSE 0.017446
以上計算結果非常合理,可見電荷約束、等價性約束全都生效了。而且由于對兩個構象的權重設為了相同,從RRMSE上看誤差都差不多,數值都不大,因此當前的擬合靜電勢電荷應該說可以比較好地描述ASP殘基在各種蛋白中的狀態。
如果計算時把alpha構象的權重設為1,而beta構象的權重設為0,則最終輸出的靜電勢重現性誤差為
Conformer: 1 RMSE: 0.002013 RRMSE: 0.016208
Conformer: 2 RMSE: 0.002786 RRMSE: 0.023200
可見如果只考慮一個構象做擬合靜電勢電荷計算,則所得電荷沒法很公平描述兩種構象。
我們再看如果計算過程不引入殘基的電荷為-1的約束條件會怎么樣。不設這個約束的話,殘基上的擬合靜電勢電荷加和為-1.033,靜電勢重現性誤差為
Conformer: 1 RMSE: 0.002158 RRMSE: 0.017375
Conformer: 2 RMSE: 0.002089 RRMSE: 0.017401
Weighted RMSE: 0.002124 Weighted RRMSE 0.017388
可見,即便不做約束,殘基的凈電荷和我們期望的-1.0差異也不大,也因此,做不做電荷約束對RRMSE基本沒什么影響。當然,做電荷約束的好處就是免得我們再去考慮怎么把殘基整體多出來的-0.033電荷盡量恰當地、人為地、偷偷摸摸地攤到殘基的原子電荷里。
注意,電荷約束和原子等價性約束雖然可以同時使用,但是電荷約束不能只施加于被約束為等價的一批原子中的一部分。比如約束2-4原子等價,又約束1-10原子的總電荷為特定值,這是可以的,但如果此時約束的是3-10原子的總電荷是某個值,或者通過約束把4號原子電荷固定為某個值,這就和等價性約束沖突了。
雖然不同批次的等價性約束牽扯的原子如前所述不能有交集,但是不同批次的電荷約束是可以有交集的。比如本例,我們既要求1-12的總電荷為-1,又要求ASP側鏈的COO部分電荷為-0.9,那就可以在chgcons.txt里寫
1-12 -1
9-11 -0.9
對于當前例子,如果你想輸入一個命令就能完成電荷計算,而不想敲多次鍵盤在界面里進行操作,那么先寫一個文本文件比如叫batch.txt,內容是在Multiwfn里每一步輸入的命令,如下所示:
7
18
5
1
eqvcons.txt
6
1
chgcons.txt
-1
conflist.txt
2
y
然后把batch.txt、alpha.fch和計算涉及的三個txt文件都放到Multiwfn目錄下,進入系統的命令行模式并進入Multiwfn目錄,輸入Multiwfn alpha.fch < batch.txt。算完后當前目錄下就會出現alpha.chg,里面最后一列就是算出來的擬合靜電勢電荷了。更多關于silent方式運行Multiwfn的信息參閱手冊5.2節。
3.5 利用局部或整體的點群對稱性設置等價性約束示例
3.5.1 例:某小分子
算下面這個體系的擬合靜電勢電荷,理應讓三個化學等價的氟的電荷相同,而且由于苯的局部空間等價性,理應讓其兩側的原子等價,即H5=H7、H10=H6、C2=C4、C3=C9。
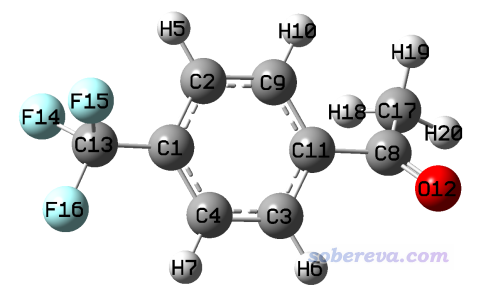
像這個體系小,手寫這些等價性關系還好,而有時候碰上較大體系,按照空間關系一個一個手寫等價性關系會很麻煩。此時可以讓Multiwfn根據各個區域的點群對稱性自動將對稱等價的原子寫入等價性約束設置文件,這里使用上面的分子示例一下。
啟動Multiwfn,然后輸入
CF3benCOCH3.fch
7 //布居分析與原子電荷計算
18 //RESP模塊
5 //設置做擬合靜電勢計算時用的原子等價性約束
11 //對整體或子結構的點群產生等價性約束并寫入到當前目錄下的eqvcons_PG.txt
接下來,我們要把體系中具有對稱性的片段里的原子序號依次輸進去。為了序號輸入方便,建議用GaussView打開上面的fch文件,用選擇工具將有對稱性的片段的原子選成黃色,然后在Tools - Atom Selection里把序號拷到Multiwfn窗口中。例如選成下面這樣
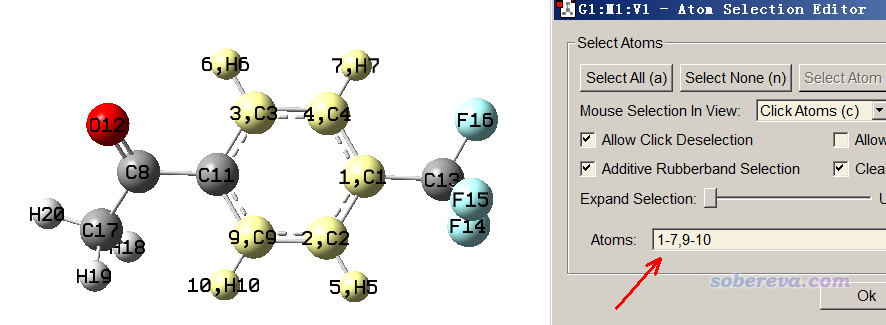
被選成黃色的片段是C2v點群,因此把對應的序號1-7,9-10提供給Multiwfn,Multiwfn就會將這塊區域的對稱等價的原子找出來并寫入到當前目錄下的eqvcons_PG.txt里。注:這里不能選中整個苯環,即1-7,9-11,因為這樣的話這個片段將是D2h,Multiwfn會將C1和C11也判斷為等價的。
按照上面的說明所述,我們現在在Multiwfn里輸入1-7,9-10,之后看到以下信息
Detected point group: C2v
Number of symmetry-equivalence classes: 4
Class 1 (C ): 2 atoms
2, 4
Class 2 (C ): 2 atoms
3, 9
Class 3 (H ): 2 atoms
5, 7
Class 4 (H ): 2 atoms
6, 10
Accept and append to eqvcons_PG.txt in current folder? (y/n)
可見對稱等價的原子判斷正確,因此我們選擇y。此時你若打開當前目錄下的eqvcons_PG.txt,會看到這4批等價性關系已經被寫入了。
我們再利用這個功能把三個F也加入等價性約束文件里。在Multiwfn窗口里接著輸入CF3的序號,即13-16,然后看到
Detected point group: C3v
Number of symmetry-equivalence classes: 1
Class 1 (C ): 3 atoms
14, 15, 16
判斷也正確,輸入y。之后輸入q來退出。最終當前目錄下的eqvcons_PG.txt內容為:
2, 4
3, 9
5, 7
6, 10
14, 15, 16
可見內容完全正確。之所以這里沒把甲基的三個氫也類似地設成等價,這是因為此例我們做兩步式標準RESP電荷擬合,在擬合的第二步自動就對這三個氫施加等價性約束了(顯然,如果你要做一步式擬合,就需要手動添加這三個氫的等價性約束)。
然后在Multiwfn窗口里輸入
1 //從外部文件中讀取等價性約束
eqvcons_PG.txt //等價性約束文件的路徑
1 //開始標準兩步式RESP電荷擬合
結果如下
Center Charge
1(C ) 0.009113
2(C ) -0.105600
3(C ) -0.140084
4(C ) -0.105600
5(H ) 0.128787
6(H ) 0.136148
7(H ) 0.128787
8(C ) 0.614008
9(C ) -0.140084
10(H ) 0.136148
11(C ) -0.047549
12(O ) -0.466965
13(C ) 0.434468
14(F ) -0.166721
15(F ) -0.166721
16(F ) -0.166721
17(C ) -0.451257
18(H ) 0.123281
19(H ) 0.123281
20(H ) 0.123281
Sum of charges: -0.000000
RMSE: 0.001518 RRMSE: 0.115139
電荷非常合理,且完全滿足我們期望的原子等價性。
3.5.2 例:暈苯(coronene)
再看一個具有較多原子且是高對稱性的例子,暈苯。
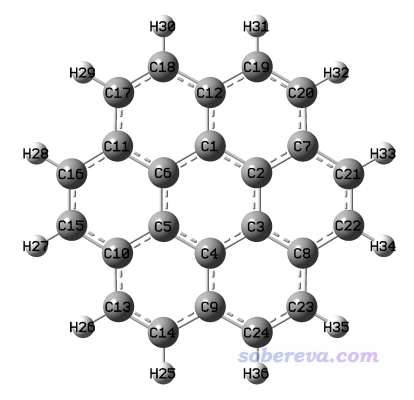
由于擬合靜電勢電荷的擬合點的分布并不滿足體系的對稱性(此例為D6h),因此結果也不滿足D6h對稱性。比如C17、C18的結果理應是相同的,但直接用標準兩步式RESP擬合算出來的結果分別是-0.2243和-0.2169。雖然差異不大,但終究令人不爽。雖然增加擬合點密度可以很大程度減小差異,但不能完全消除,而且還增加擬合過程耗時。最佳的解決辦法是根據對稱性施加等價性約束,但這么大體系,手寫等價性約束非常費力,還容易搞錯。這種情況我們也可以效仿上例讓Multiwfn識別點群來解決。
啟動Multiwfn然后輸入
coronene.fch
7 //布居分析與原子電荷計算
18 //RESP模塊
5 //設置做擬合靜電勢計算時用的原子等價性約束
11 //對整體或子結構的點群產生等價性約束并寫入到當前目錄下的eqvcons_PG.txt
a //選所有原子
等價原子立刻就判斷出來了,完全正確
Detected point group: D6h
Number of symmetry-equivalence classes: 4
Class 1 (C ): 6 atoms
1, 2, 3, 4, 5, 6
Class 2 (C ): 6 atoms
7, 8, 9, 10, 11, 12
Class 3 (C ): 12 atoms
13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24
Class 4 (H ): 12 atoms
25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36
然后輸入以下內容,含義同上一個例子
y
q
1
eqvcons_PG.txt
1 //執行兩步式RESP擬合(由于對此體系,第二步沒有被擬合的對象,因此和一步式擬合結果相同)
最終結果中,如上提示的那四批原子的電荷都相同了,和期望的一致。前面提到的C17、C18的電荷都是-0.220866,非常合理。
值得一提的是,有時候你輸入片段里原子序號后,Multiwfn沒有提示點群,這說明點群判斷失敗。但點群判斷失敗時不代表對稱等價的原子沒有合理判斷出來,如果屏幕上提示的等價原子序號沒問題的話,仍然可以選y將之寫入eqvcons_PG.txt。如果發現連等價原子序號也有問題,那么可以按n取消,然后修改判斷閾值,比如輸入t 0.05代表把閾值設為0.05,之后再次輸入序號嘗試判斷。默認的閾值是0.1,改大、改小都可以試試。當點群正確顯示出來的時候等價原子肯定100%判斷對了。
另外,在RESP模塊的選項5里還可以選10來把對CH2、CH3上H的等價性約束的設置導出到當前目錄下的eqvcons_H.txt。若將此文件內容和前述的eqvcons_PG.txt內容合并,然后讀取,之后做一步式擬合,則可以令兩類約束同時生效(但注意兩種約束不能有沖突的項)。
3.6 例:對非原子中心的位置計算擬合靜電勢電荷
Multiwfn的RESP模塊既可以對原子核位置做電荷擬合,也可以同時對非原子中心的點電荷進行擬合,這些額外的點電荷可以用于增強對特殊區域如孤對電子、sigma穴附近的分子表面靜電勢的描述,這樣的思想已經應用于一些力場中,例如OPLS3力場、JCTC, 12, 3825 (2016)對G54A7力場的改進等。
對于18碳環體系,如果不考慮非原子中心的點電荷更是完全不能描述其分子表面靜電勢分布。此體系對靜電勢著色的范德華表面如下所示,出自筆者的研究18碳環體系的文章《一篇最全面、系統的研究新穎獨特的18碳環的理論文章》(http://www.shanxitv.org/524),此文強烈建議一看。
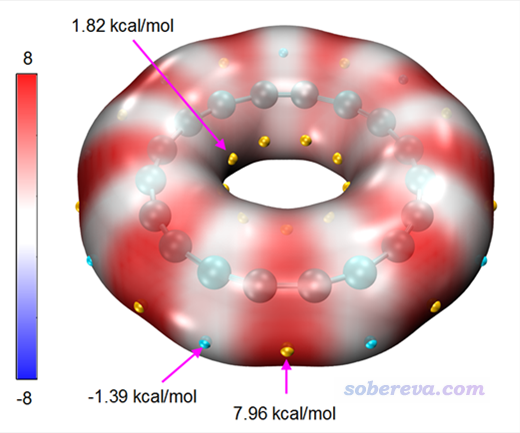
由于此結構具有D9h對稱性,如果照常計算RESP電荷,所有原子電荷將為0,顯然對分子表面靜電勢分布情況的描述能力為零,也不能描述此體系與其它體系之間的靜電相互作用。如果按照下圖,在Multiwfn計算RESP電荷時,同時將額外擬合中心放置于每個C-C鍵的中點,將可以得到下圖所示的擬合結果
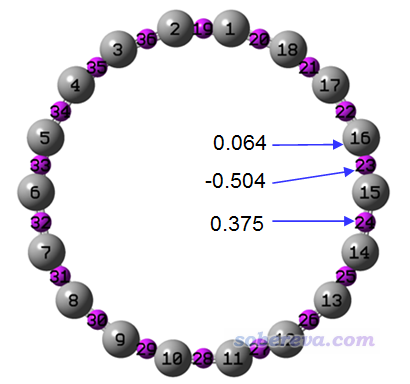
此時RESP模塊輸出的RMSE為0.00106。而如果不考慮這些額外擬合點,即直接照常計算RESP電荷(如前所述,結果會完全為0),則RMSE則高達0.00191。顯然考慮額外擬合點對于表現18碳環的分子范德華表面外靜電勢分布的改進有大約一倍之多。
具體怎么做上圖中的擬合,參見Multiwfn手冊4.7.7節的Example 6,過程相當簡單。
4 總結
本文介紹了擬合靜電勢電荷計算方法中的一些特殊的手段,包括等價性考慮、電荷約束考慮、多構象考慮、懲罰函數,這對于能獲得適合用于分子模擬的擬合靜電勢電荷非常重要,但很多人都沒有注意這些問題。Kollman等人提出的RESP電荷也正是綜合利用了其中許多手段并設計了兩步擬合過程,使得RESP成為最適合有機分子動力學模擬的原子電荷模型之一。非常流行的波函數分析程序Multiwfn加入RESP模塊之后,使得標準的RESP電荷的計算以及在普通擬合靜電勢計算過程中利用以上提及的特殊手段變得超級容易,也解決了很多以往計算擬合靜電勢過程中常碰見的難題。此模塊使用既簡單又相當靈活,遠勝于以往的RESP電荷計算程序。本文提供的多個例子將Multiwfn在這方面的強大做了充分的展現,同時也將計算擬合靜電勢電荷中需要考慮和留意的問題結合實例做了充分說明。希望讀者讀罷本文后多多把玩Multiwfn的RESP模塊,將之運用到自己的研究當中,并向國內外同行推廣。
附1:通過做兩次一步靜電勢擬合等效地實現標準RESP兩步擬合的示例
Multiwfn的RESP模塊里選項1所做的標準RESP電荷的兩步式的計算過程相當于是一個組合過程,由于選項2所做的一步式計算過程中可以自定義各種參數和設定,因此可以手動做兩次在不同設定下的一步式計算來等效實現標準RESP電荷的計算,這也使得用戶能夠對標準的RESP電荷計算過程根據特殊需要進行自定義和改造,甚至于如果有特殊情況,還可以自己搞一個三步法乃至N步法的靜電勢擬合過程。這里就拿一個甲醇作為示例,輸入文件為本文文件包里的methanol.fch。
直接對甲醇做標準RESP電荷計算結果如下
Center Charge
1(C ) 0.235333
2(H ) 0.004436
3(H ) 0.004436
4(H ) 0.004436
5(O ) -0.664522
6(H ) 0.415880
Sum of charges: 0.000000
RMSE: 0.003262 RRMSE: 0.196194
下面我們做一步法擬合靜電勢計算實現標準RESP電荷計算的第一步。在RESP模塊界面里依次輸入
5 //設置原子等價性約束
0 //不做等價性約束
2 //一步法擬合原子電荷
此時結果如下。默認用的雙曲懲罰函數參數和標準RESP電荷的第一步是一樣的
Center Charge
1(C ) 0.238915
2(H ) 0.045904
3(H ) -0.018089
4(H ) -0.018089
5(O ) -0.664522
6(H ) 0.415880
Sum of charges: -0.000000
RMSE: 0.002089 RRMSE: 0.125640
然后寫一個文本文件chgcons.txt,內容是把標準RESP電荷第二步不需要擬合的原子(對此例為羥基的原子)的電荷約束成上面算出的值,因此此文件內容為:
5 -0.664522
6 0.415880
然后在Multiwfn界面里依次輸入
n //不把剛才的電荷導出成chg文件
4 //設置雙曲懲罰函數參數
2 //設置限制強度參數a
0.001 //這是標準RESP電荷計算第二步用的a參數
0 //回到上一級菜單
5 //設置原子等價性約束
2 //將CH2和CH3基團中的氫的電荷保持等價性,這是標準RESP電荷第二步所要求的
6 //設置電荷約束
1 //讀取電荷約束設定文件
chgcons.txt
2 //一步法擬合原子電荷
會看到結果和前面給出的標準RESP電荷相同。
技巧:當體系比較大的時候,自己寫此例用到的chgcons.txt比較麻煩,還容易不慎弄錯序號之類。為避免這個麻煩,可以先在當前目錄下創建一個叫做chgcons_stage2.txt的空文件,然后做兩步RESP電荷擬合,程序在自動做第二步擬合前就會自動往這個文件里寫入在標準RESP擬合第二步時需要保持電荷不變的原子的序號和電荷,這樣就省得自己手寫chgcons.txt了。
附2:蛋白質配體的RESP電荷該用什么構象計算?
蛋白質-配體復合物是經常通過分子動力學研究的一類問題,這往往需要對小分子配體計算RESP電荷,經常有人問我應該取小分子的什么構象來計算、用不用先優化,我在這里統一說一下我的看法。
原理上,最理想的算這種情況的配體的RESP電荷的做法是:對真實的復合物動力學軌跡每隔一定幀數提取一次小分子結構算RESP電荷(直接算單點任務得到波函數文件就夠了),然后對所有幀取平均。這樣得到的RESP電荷可以對動力學過程中配體與外環境的作用有均衡的描述,而且哪個構象出現概率越大,哪個構象對計算的RESP電荷起到的權重越大、被照顧得越充分。但是這么做不僅麻煩、耗時高,而且由于原本并不知道配體的原子電荷,動力學也沒法跑。一個折中做法是先用比如ADCH、AM1-BCC這樣對分子表面靜電勢重現性還不錯的原子電荷作為配體的“初猜”電荷去跑復合物的動力學,然后計算各幀平均的配體的RESP電荷,再用新的配體的原子電荷跑復合物的動力學...反復如此,最后配體的原子電荷就能確定下來。但顯然這么做太折騰、太費時了,而且由于一些隨機性因素,還未必最后能收斂。
如果你的蛋白-配體復合物是X光衍射測的,而且解析度較高,那么可以直接把配體摳出來,只對氫的位置用量子化學優化(為什么要這么做看《實驗測定分子結構的方法以及將實驗結構用于量子化學計算需要注意的問題》http://www.shanxitv.org/569),然后算RESP電荷。這么做的合理性在于實驗測的復合物中配體的構象是比較理想的結合狀態,實際跑動力學的時候這種構象也應當是主導性的構象(假設模擬合理的話)。
如果你的蛋白-配體復合物結構是分子對接得到的,那么這個結構里配體的構象的合理性極其有限,甚至可能有明顯不合理之處,顯然不適合直接拿這樣的構象算RESP電荷(哪怕是對氫原子做優化后)。我的一般建議是:先以對接得到的結構為初猜結構做個常規的配體分子的幾何優化,然后計算RESP電荷,之后跑復合物的動力學。如果發現動力學過程中配體與蛋白質結合的主要構象與之前優化出來的配體構象相差不大,那么原子電荷就不用重新算;如果相差很顯著,說明之前算的RESP電荷可能對于描述蛋白-配體相互作用不夠理想,此時對動力學軌跡做個簇分析得到最有代表性的復合物構象,在動力學程序里對復合物做個力場級別的能量極小化,然后把配體摳出來直接算RESP電荷(不再經過量子化學優化),將之作為正式的復合物模擬用的配體的原子電荷即可。