簡談原子半徑

簡談原子半徑
文/Sobereva @北京科音
First release: 2014-Oct-24  Last update: 2018-Apr-25

經常有人問原子半徑的事，這里十分簡略地談談。

1 共價半徑

一般說原子半徑的時候多數情況就是指共價半徑。原子間形成化學鍵的時候，鍵的長度大體相當于這兩個原子的共價半徑之和。很多可視化程序判斷是否成鍵就是根據這個規則判斷的。例如在Multiwfn（http://www.shanxitv.org/multiwfn）中，默認設置下，只要兩個原子間距離小于它們的CSD共價半徑和的115%就在兩個原子間顯示化學鍵。當然，這種僅從幾何結構上判斷是否成鍵的規則是很粗糙的，沒有考慮電子結構。并且嚴格來講，成鍵只能說強弱，而沒有嚴格標準來判斷有或沒有。

原子在不同化學環境下的電子結構是不一樣的，例如C有sp、sp2、sp3雜化，也可以和不同原子形成不同種類的鍵，過渡金屬還有高自旋低自旋等等，每種情況都有不同的鍵長。然而，通常每一套半徑的定義對于每個原子只有一個值，所以原子的共價半徑應認為是考慮各種化學環境下的平均值。

下面介紹幾種常見的共價半徑。定義半徑的文章太多了，這絕不是完整的匯總。

雙原子分子鍵長的一半：這是最“純正”的共價半徑。雖然這種方式定義共價半徑意義很明確，但是并不適合作為普適的共價半徑定義。因為實際分子中，不同原子以不同形式的化學鍵相互連接，而雙原子分子的成鍵方式卻是固定的，比如氮氣分子是三重鍵，而氮原子在多數分子中形成的是單鍵，因此用N2鍵長的一半當N的共價半徑就有失偏頗。

CSD(Cambridge Structural Database)半徑：2008年提出，原文是Dalton Trans., 2008, 2832-2838。這是很可靠的，而且我個人也很推薦用的共價半徑。原子序號從1到96都有。其中的半徑通過統計CSD劍橋結構數據庫里面的數目龐大的分子晶體結構中的鍵長來得到。值得一提的是，對于碳，CSD半徑是對sp、sp2、sp3狀態分別給出的，對于Mn、Fe、Co，CSD半徑是對高自旋和低自旋分別給出的。

Slater-Bragg半徑：原文是J. Chem. Phys., 41, 3199 (1964)。這是對1920年的Bragg半徑的改進，思路都一樣，是根據晶體學測定的分子結構中的鍵長來統計得到的。

Pyykko半徑：原文是Chem. Eur. J., 15, 186-197 (2009)。包含1-118所有元素的半徑。取了一大堆分子，其中有的是實驗測定的結構，有的是高精度方法計算出來的結構，然后通過擬合讓原子半徑加和與測試集中的鍵長差異盡量小。

Suresh半徑：原文是J. Phys. Chem. A, 105, 5940-5944 (2001)。此方法對每種元素計算H3C-EH(n)這樣的體系，E是要考察的元素，然后將C-E的鍵長減去乙烷中C-C的鍵長的一半就得到了E的共價半徑。比如計算N的半徑的時候就計算H3C-NH2的C-N鍵長，把它再減去乙烷C-C鍵長的一半。這種方式計算共價半徑比較簡單，效果也不錯，但由于計算半徑時考慮的只是單重鍵情況，所以這種方式適合估計的是不同原子間形成單鍵的鍵長。

最后順帶說一下，對于某個體系中的一個化學鍵A-B，如果我們要基于此來求A的半徑和B的半徑，最合理的辦法就是計算原子核到AIM理論中的鍵臨界點(BCP)的距離。這樣得到的兩個原子半徑和就正好是這個化學鍵長。

2 離子半徑

形成離子化合物的時候，原子的狀態和形成共價鍵時候的差異實在太大，因此都用一套半徑來描述顯得不合理，故有人專門定義了離子半徑。陽離子半徑比起共價半徑明顯要小，而陰離子半徑則比共價半徑明顯要大。離子半徑加和值和離子間距離是比較吻合的。由于陽離子半徑相對于共價半徑的降低，以及陰離子半徑相對于共價半徑的增加，二者的數值大小比較相近，因此陰陽離子半徑的加和與兩個原子共價半徑的加和差異通常不太大，所以有人認為有一套共價半徑就足夠用于討論鍵長問題了，沒必要單獨考慮離子半徑。

下圖是Slater-Bragg半徑和不同的人定義的離子半徑的對比，括號里的值就是離子半徑與Slater-Bragg半徑的差值。

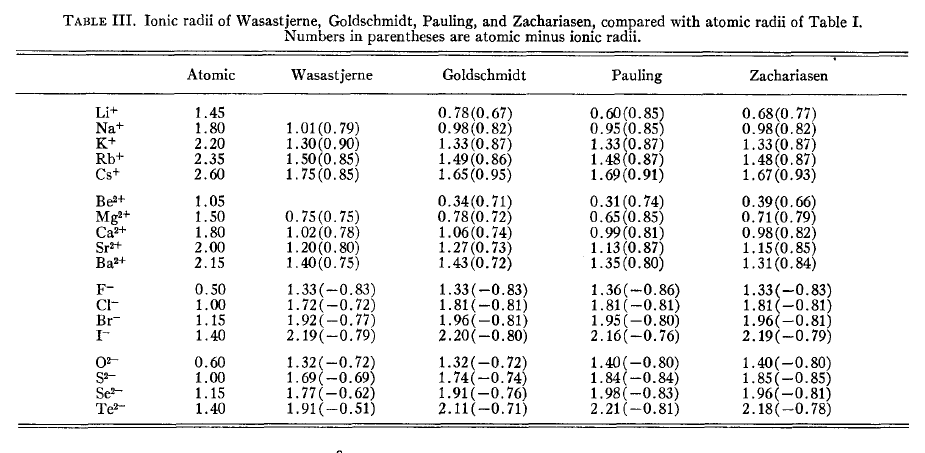
R.D.Shannon（不是搞信息熵的C.E.Shannon）離子半徑對元素的各種價態、配位數的情況都單獨列出了半徑，通過對大量晶體結構統計得到，表格很長，見Acta Cryst., A32, 751 (1976)。配位數越高，離子半徑也越大。

3 范德華半徑

如果原子間是以范德華作用吸引到一起的，那么平衡狀態下，原子間距離就大致是二者的范德華半徑和。如果原子間非共價相互作用很強，比如氫鍵、鹵鍵、pi-pi堆積等，那么會原子間的距離會明顯小于范德華半徑和，也就是彼此穿透了范德華表面。如果大于范德華半徑和，就表明原子間相互作用很弱了，可以不做考慮（但并非沒有，范德華作用隨距離呈1/r^6方式衰減）。

測定范德華半徑的方法很多。目前最常用、最廣為接受的范德華半徑就是bondi半徑，原文見J. Phys. Chem., 68, 441 (1964)，主要是靠低溫下晶體密度來推算出來的，同時考慮物質的其它方面的性質以加以驗證。Rowland和Taylor在J. Phys. Chem., 100, 7384-7391 (1996)通過更多晶體數據對bondi半徑進行了檢驗，發現bondi半徑確實比較合理，其半徑加和值和實際情況中原子接觸距離較吻合，但是推薦對氫用1.09埃（bondi半徑是1.2埃）。

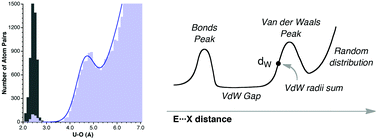
最近一篇文章Dalton Trans., 42, 8617-8636 (2013)中作者通過統計CSD數據庫里幾百萬個晶體中原子間距來得到范德華半徑，姑且叫做CSD范德華半徑，它把周期表基本覆蓋全了，比bondi的全面很多。這種方式獲得范德華半徑的原理通過下圖很容易理解，也就是統計數據庫里某一元素E和探針原子X（通常用氧）之間距離的出現頻數，會有兩個峰，第一個峰對應成鍵距離，第二個峰和非鍵接觸相關，利用后者的位置就能確定范德華半徑。

其它人提出的范德華半徑在此貼里有一覽表：
http://bbs.keinsci.com/forum.php?mod=viewthread&tid=69&extra=page%3D1
更多的和范德華半徑有關的討論可參見Inorganic Materials, 37, 871-885 (2001)。

UFF力場是十分著名的普適型力場。一些計算化學程序、理論文章提及的UFF半徑，對應于UFF原文J. Am. Chem. SOC., 114, 10024 (1992)的表1里的x_I那一列數值的一半。UFF半徑可以認為是一種范德華半徑。

從理論上也可以計算范德華半徑。Bader將電子密度為0.001和0.002 a.u.的等值面分別定義為氣相和凝聚相下分子的范德華表面。通過Multiwfn就可以很容易地計算，例子見本文文末的附錄。不過這種方式定義的范德華半徑比Bondi的要大出很多，會高估范德華作用導致堆積時原子的間距。

Boyd是專注于搞AIM分析的人，他在J. Phys. B: Atom. Molec. Phys., 10, 2283 (1997)提出了所謂的Boyd半徑，其實沒什么新意，就是效仿Bader的思路，不過是用電子密度=0.0001a.u.的位置來定義原子半徑，然后使用經驗公式對其進行scale來得到和一般范德華半徑相符的半徑大小。

4 其它

Pauling在他著名的《化學鍵的本質》里面也提供了共價、離子、范德華半徑，但是只有很少幾個元素，這被稱為Pauling半徑。

Hugo半徑：原文是Chemical Physics Letters, 480, 127-131 (2009)。這種半徑是推導出來的，計算公式是r=a0*√(I_H/I)，其中a0是氫的原子半徑，I_H是氫的電離能，I是當前元素的第一電離能。雖然推導過程比較嚴格，計算出來的半徑的變化趨勢也基本正確，但是有極不合理的情況，比如得出的H的半徑為1 Bohr，而Kr的半徑居然為0.99 Bohr，竟比H還小！Hugo半徑的大小比共價半徑小很多。

Modified CSD半徑：這是在Laplacian鍵級原文J. Phys. Chem. A, 117, 3100-3108 (2013)中順帶提出的一種特殊的半徑定義方式，通過對CSD半徑修改來得到，以更好地反映原子在實際分子中的特征。其思路容易理解。對同一周期元素（主族部分），越靠左的原子半徑越大，但是電負性越小，因此在實際分子中越容易失電子而使半徑變小；反之，越靠右的原子半徑越小，但是電負性越大，在實際環境中越容易得電子而增大其半徑。因此，Modified CSD半徑把每一行的主族元素的半徑都用第四主族元素的半徑代替，這樣的半徑就近似考慮了原子在實際化學環境中的膨脹和收縮，更符合實際情況。利用這種半徑來定義分子內原子的空間比起直接用CSD共價半徑合理得多。

附：用Multiwfn計算原子半徑一例

這里通過一個簡單例子，說明怎么用Multiwfn計算基于電子密度等值面定義的半徑。假設我們要計算用電子密度=0.002 a.u.等值面定義的Cl-的半徑。Multiwfn可以從主頁http://www.shanxitv.org/multiwfn免費下載。不了解者建議看《Multiwfn FAQ》（http://www.shanxitv.org/452）。使用的Multiwfn版本應當是2020-Feb-21及以后更新的。

首先我們要得到Cl-的波函數文件。比如這里我們用Gaussian來計算得到。輸入文件如下

# B3LYP/aug-cc-pVTZ out=wfn
[空行]
Title Card Required
[空行]
-1 1
Cl
[空行]
C:\Cl-.wfn

使用Gaussian運行之，之后就在C:\下得到了Cl-.wfn。然后啟動Multiwfn，輸入
C:\Cl-.wfn
12  // 定量分子表面分析
1  // 修改定義分子表面的方式（默認是電子密度=0.001 a.u.）
1  // 用電子密度等值面來定義
0.002  // 用0.002 a.u.等值面
6  // 開始分析
10  // 測量所有表面頂點距離原子核最遠和最近距離
1  // 原子序號是1
此時看到以下信息
The closest distance to the point:    3.920433 Bohr (    2.074604 Angstrom)
The farthest distance to the point:    3.921946 Bohr (    2.075405 Angstrom)

即表面頂點與原子核最遠的是2.075埃，這個就可以作為Cl-的原子半徑。當然，前面說了，電子密度=0.001 a.u.或0.002 a.u.都不是唯一的定義原子表面的方法。如果是要橫向對比凝聚相下的相對半徑差異，用上面方法計算的半徑是比較有意義的。

值得一提的是，類似這種做法也被用于確定分子動力學直徑，看《使用Multiwfn計算分子的動力學直徑》（http://www.shanxitv.org/503）。