AIM鍵臨界點處電子密度拉普拉斯值符號判斷相互作用類型失敗原因的圖形分析
AIM鍵臨界點處電子密度拉普拉斯值符號判斷相互作用類型失敗原因的圖形分析
文/Sobereva @北京科音
First release:2012-Sep-2 Last update: 2014-Mar-10
本文目的是通過圖形方法討論一下為什么通過AIM鍵臨界點處電子密度拉普拉斯值符號判斷相互作用類型很多時候是錯誤的,本質原因何在,以及如何判斷相互作用類型更為可靠。本文體系皆在B3LYP/cc-pVDZ下優化并產生波函數,由Multiwfn 2.5版繪圖,此程序可在http://www.shanxitv.org/multiwfn免費下載。
電子密度拉普拉斯值定義如下,它代表了電子密度在某處的總曲率。某處它為正,代表此處電子密度發散的;如果為負,代表電子密度是聚集的。

AIM理論中的鍵臨界點(BCP)出現在相鄰的相互作用的原子之間,這個點一般被認為是描述相應兩個原子相互作用的最關鍵的點,這個點的性質(密度、能量密度、動能密度、源函數等)常被用來討論成鍵特征。
有一個流行的通過AIM理論判斷兩個原子間相互作用類型的方法,也就是看這兩個原子間的鍵臨界點(BCP)的電子密度拉普拉斯值的符號。如果符號為負,就被認為是共價作用,其理由是共價相互作用的原子間由于共享電子對兒,會造成電子密度在成鍵區域聚集;如果符號為正,就被認為是閉殼層相互作用,比如離子鍵、氫鍵、鹵鍵、二氫鍵、pi-pi堆積之類,這些相互作用本質是靜電或范德華作用,不是靠共享電子對兒實現的,因此成鍵區域沒有電子密度的聚集,BCP處拉普拉斯值被順著鍵徑的方向上的電子密度的正曲率所主導而成為正值。
(注:閉殼層相互作用是相對于開殼層相互作用而言的。開殼層相互作用其實就是共價相互作用,一般是成鍵的兩個原子各提供一個自旋相反的單電子構成共享電子對兒,就像兩個自由基的結合。雖然配位鍵算是其中一方提供共享電子對兒,形式上看似是兩個閉殼層體系間發生的作用,但實際效果上屬于極性共價鍵,所以不歸在閉殼層相互作用范疇)
這種判斷相互作用的方式很多情況確實管用。乙炔的電子密度拉普拉斯值等值線圖如下所示,棕點代表核臨界點(NCP),藍點代表BCP。實線和虛線分別代表拉普拉斯值為正和為負的區域,很清晰地表現出電子密度在哪里聚集。C-C以及C-H之間BCP點落在虛線范圍內,故BCP處拉普拉斯值為負,正確地表現了這兩種鍵都是共價鍵。
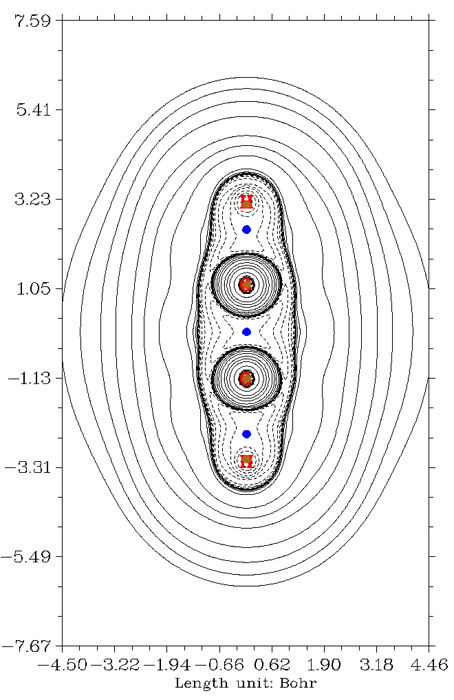
下圖是水的拉普拉斯值圖,由于氧和氫的電負性相差不少,所以是極性共價鍵。BCP依然是落在負值區域。相比于C-H鍵的情況,BCP的位置更偏向于H,這是因為氧吸電子能力比碳強,故分子環境中它在更大的區域內有更高的密度分布,因此O-H鍵徑上的密度極小點,即BCP點,就會進一步往H那邊移。
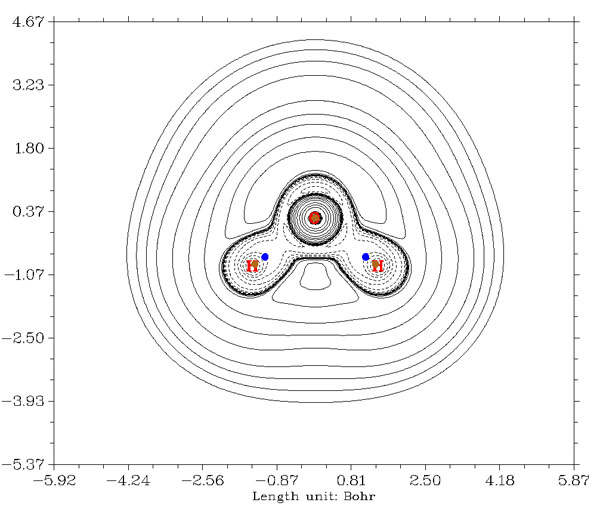
下圖是氟化鋰的拉普拉斯值圖,由于Li和F之間主要靠靜電作用維持,兩原子間找不到拉普拉斯值為負的區域。BCP處拉普拉斯值符號也顯然是為正,表現了這確實是閉殼層相互作用。
以上三個例子,顯示出BCP處拉普拉斯值符號確實能夠如實區分原子間相互作用是共價的還是閉殼層的。但是,絕對不代表BCP處拉普拉斯值符號就是區分共價和閉殼層相互作用的絕對標準,尤其對于成鍵形式難以估計的情況,只靠BCP處拉普拉斯值符號來證明是何種作用方式其可信度是很低的。
對于區分閉殼層相互作用與非極性(或弱極性)共價鍵,用BCP處拉普拉斯值符號來判斷基本是沒有問題的。而這種判斷方式主要失敗的地方通常在于極性較強的共價鍵。下圖是COCl2分子的拉普拉斯值圖,C-Cl間的BCP落在了負值區域,然而,C-O的BCP卻落在了碳附近的正值區域!因此,僅考察BCP拉普拉斯值符號就會誤將C-O鍵認為是閉殼層相互作用。(這一圈正值區域對應的是碳原子K和L殼層之間的密度發散的區域。)
直接從上圖考察拉普拉斯值分布,其實可以很清楚地看出C-O間是共價作用,因為在二者成鍵區域間有明顯的電子聚集區域。之所以靠BCP來判斷得到錯誤結論,顯然是因為對于當前體系,BCP點的位置并不具備什么化學意義。的確,BCP的定義在數學意義、物理意義上沒有什么值得質疑的,十分清楚明確,然而,BCP這個直接基于電子密度進行簡單拓撲分析的產物,能說出什么確切的化學上的意義?筆者認為不能。單獨從電子密度上,根本體現不出傳統化學觀念中的孤對電子、化學鍵等概念,我們看到的基本上只是由于原子核電荷造成的重原子核處有很高的峰,然后向四周整體呈指數型衰減,對任何分子的電子密度分布基本都是這種單調無趣的景象,化學上感興趣的分子電子結構特征根本展現不出來。BCP在兩個相鄰原子間的相對位置主要受到的是電子密度指數分布這一大趨勢的影響,它從定義上根本沒法與鍵的形成在理論上直接對應上,所以BCP所在位置也沒法告訴我們共價鍵形成的區域。尤其是對于強極性鍵,電子密度在原子間轉移強烈,嚴重影響了BCP的位置,這往往會使BCP和共價鍵區域偏離得很嚴重,以至于,像COCl2的情況,BCP沒出現在價層區域,卻落到原子里面去了。因此,我們不能總是單純僅僅靠BCP這一個點,何況還是缺乏化學意義的點的性質來討論一切相互作用問題。而電子密度拉普拉斯函數則體現出豐富的化學意義,它將原子間形成共價鍵時價層密度的凝聚很好地表現了出來,也體現了原子殼層等特征,這是因為拉普拉斯算符將電子密度函數中隱藏的難以發現的細微特征加以放大所致,對電子密度拉普拉斯函數做拓撲分析能得到的化學上有用的信息比起對電子密度做拓撲分析要多得多。實際上,不光是BCP缺乏化學意義,AIM理論對原子的劃分(劃分成原子盆)化學意義也不顯著,這直接造成了AIM電荷和化學觀念經常沖突。
由于BCP所在位置與共價鍵形成區域不對應造成通過其位置上拉普拉斯值符號判斷相互作用方式失敗的例子還有很多,例如硅烷和環硼氮六烷,如下所示,Si-H鍵和C-N鍵的BCP都稍稍越過拉普拉斯值正負區域邊界而跑到正值區域去了,用其符號而判斷成閉殼層相互作用就錯了。
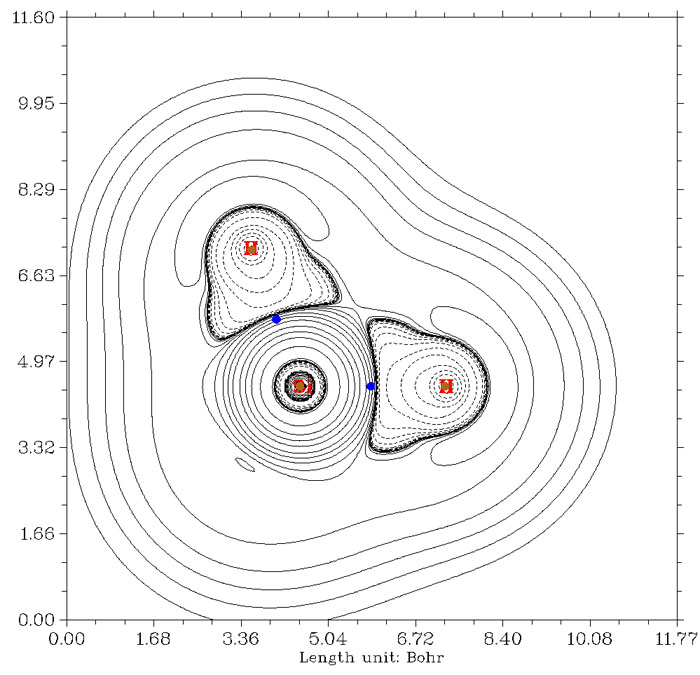
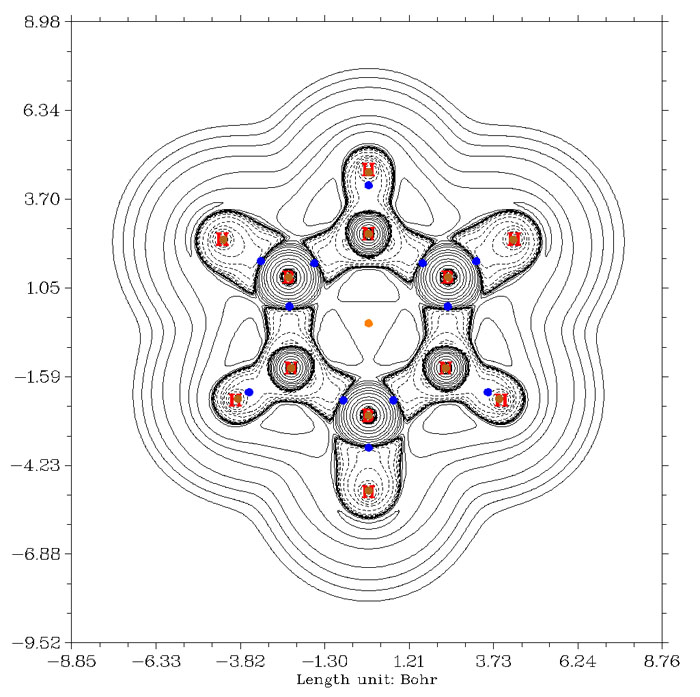
至于金屬配位鍵,用BCP處拉普拉斯值符號來判斷更不可靠,例如Ni(CO)4,下圖是全電子基組cc-pVDZ-DK結合DKH2相對論計算得到的拉普拉斯值圖。Ni-C間的BCP跨過正負值分界線不是一點點了,而是跨過了不少,因此用拉普拉斯值符號標準就會認為羰基和鎳是閉殼層相互作用。而實際上這是配位鍵,是屬于共價相互作用范疇的,可以清楚地從圖中看到這一點,碳附近有不少電子都沖著鎳凝聚起來,如果作ELF圖(可參見《電子定域性的圖形分析》http://www.shanxitv.org/63),配位鍵特征會看得更清楚。而羰基C-O鍵,按照BCP拉普拉斯值符號的標準也被誤認為是閉殼層相互作用了。
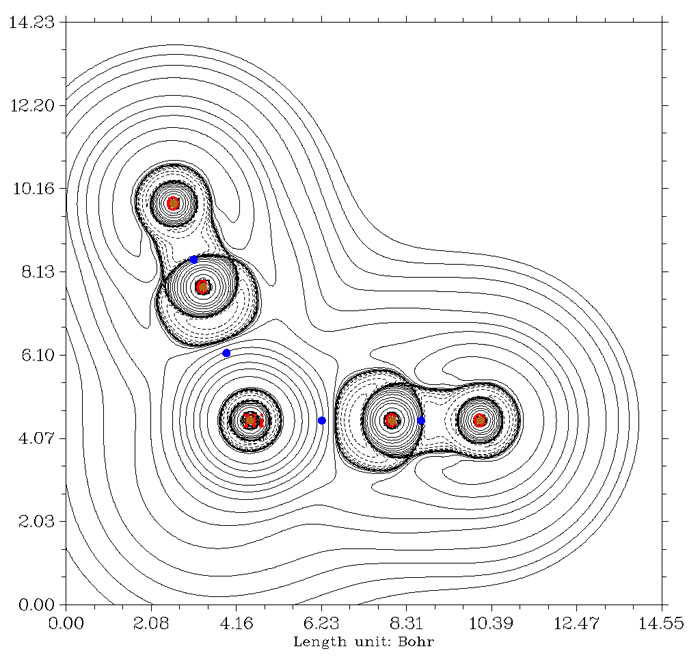
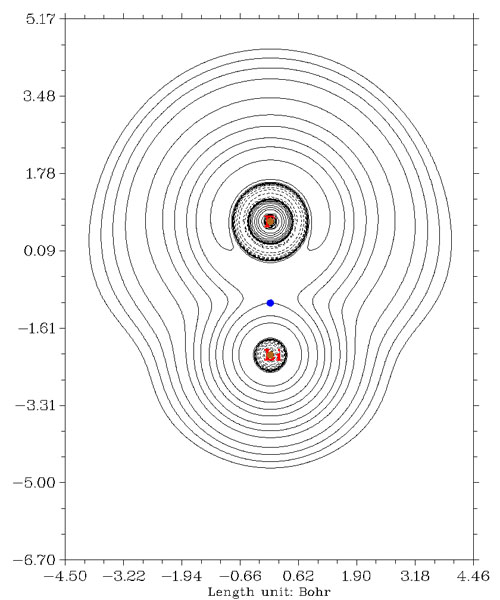
不光是BCP位置不合理造成無法用其上拉普拉斯值符號判斷相互作用類型,在個別情況下,由于所謂的非核吸引子的出現,會造成這種判斷方法完全沒法用。典型的例子就是Li2,拉普拉斯值圖如下所示
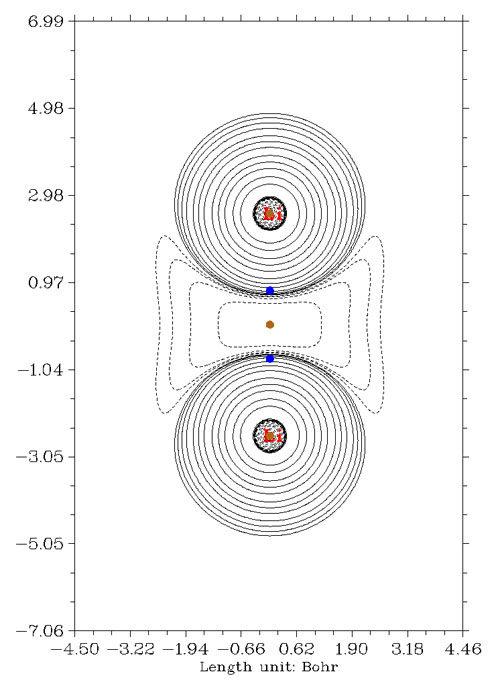
在兩個鋰正中間,平時本應該是BCP該出現的地方,卻有個電子密度極大點,因此形式上屬于核臨界點,然而這里卻又沒有原子核,故得名贗原子(pseudoatom),冠冕堂皇的稱呼叫做非核吸引子。由于本該是BCP的地方沒有BCP,所以此體系沒法靠BCP拉普拉斯值符號判斷成鍵類型。反倒是贗原子和鋰原子之間出現了BCP,落在拉普拉斯值正值區域,如果結論是“鋰原子和贗原子之間是閉殼層相互作用”,簡直莫名其妙,沒化學意義。而直接從拉普拉斯值圖上看,兩個鋰之間由于出現明顯電子凝聚,應當算共價作用,作ELF圖在相應區域也有很大的電子定域性區域,反映出共享電子對兒特征。
對于某些主要靠pi鍵構成而基本沒有sigma鍵參與的體系,由于其電子密度基本不在鍵軸上凝聚,位于兩原子正中間的BCP處拉普拉斯值會為正值(但不大),因此沒有正確表現出這實際上是共價作用。Si2就是這種情況,它由兩個pi鍵構成,其拉普拉斯值圖如下
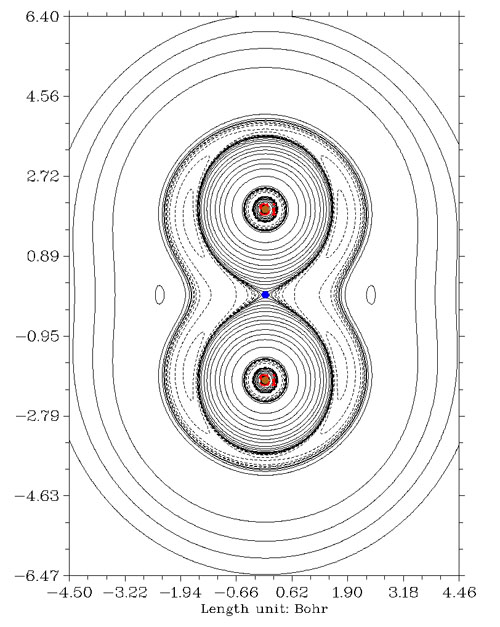
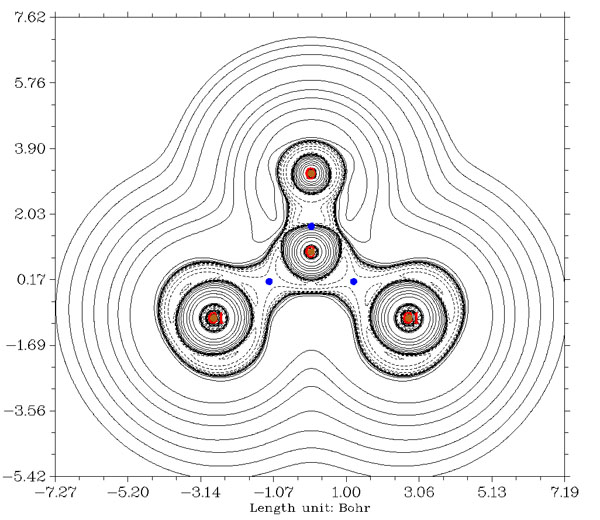
還有一些金屬間多重鍵情況,并不是因為BCP位置不合適造成相互作用方式判斷錯誤,而是電子密度拉普拉斯函數本身沒有能力展現這類特殊情況下的共價相互作用特征。搞化學的人比較熟悉的是[Re2Cl8]2-這個例子,1964年Cotton提出其中兩個錸之間具有四重鍵,包括一個sigma,兩個pi和一個delta鍵,它們都是由兩個錸的d軌道相互交疊組成的。通過高精度量子化學手段,根據EBO鍵級的定義,Roos等人得到錸錸之間鍵級是3.2的結論,見Angew. Chem. Int. Ed., 46, 1469 (2007)。[Re2Cl8]2-的電子密度拉普拉斯函數圖如下所示
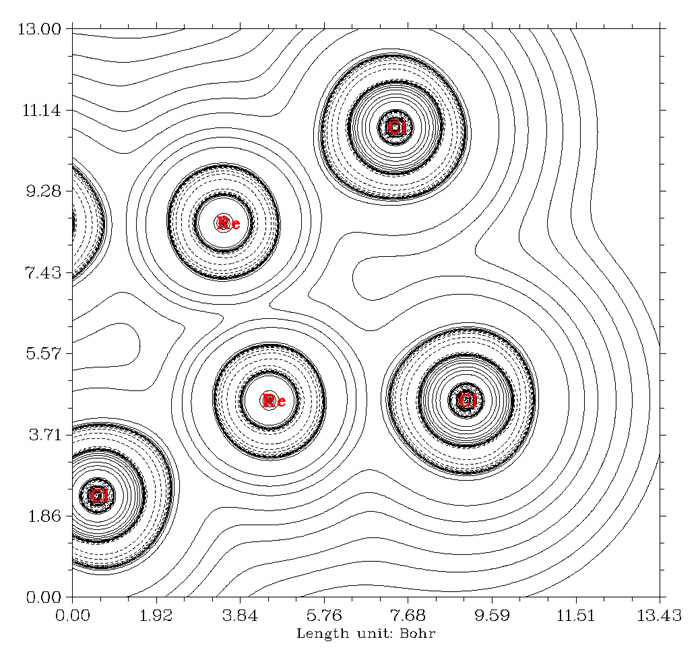
錸錸之間算作共價鍵是沒有問題的,然而圖中卻看不出它們之間的電子凝聚。筆者認為這是因為d軌道之間有效重疊程度較低,而涉及的空間區域又廣,導致共享的電子被平攤開而看不出來在局部凝聚了。其實不光是拉普拉斯函數,ELF函數也只能觀察到錸錸之間有一小圈定域性算不上太高的區域。如下所示(這是平面圖,能看到Re-Re間連線的兩側有數值稍微高一點的區域,若做成等值面圖看起來就是環形等值面)
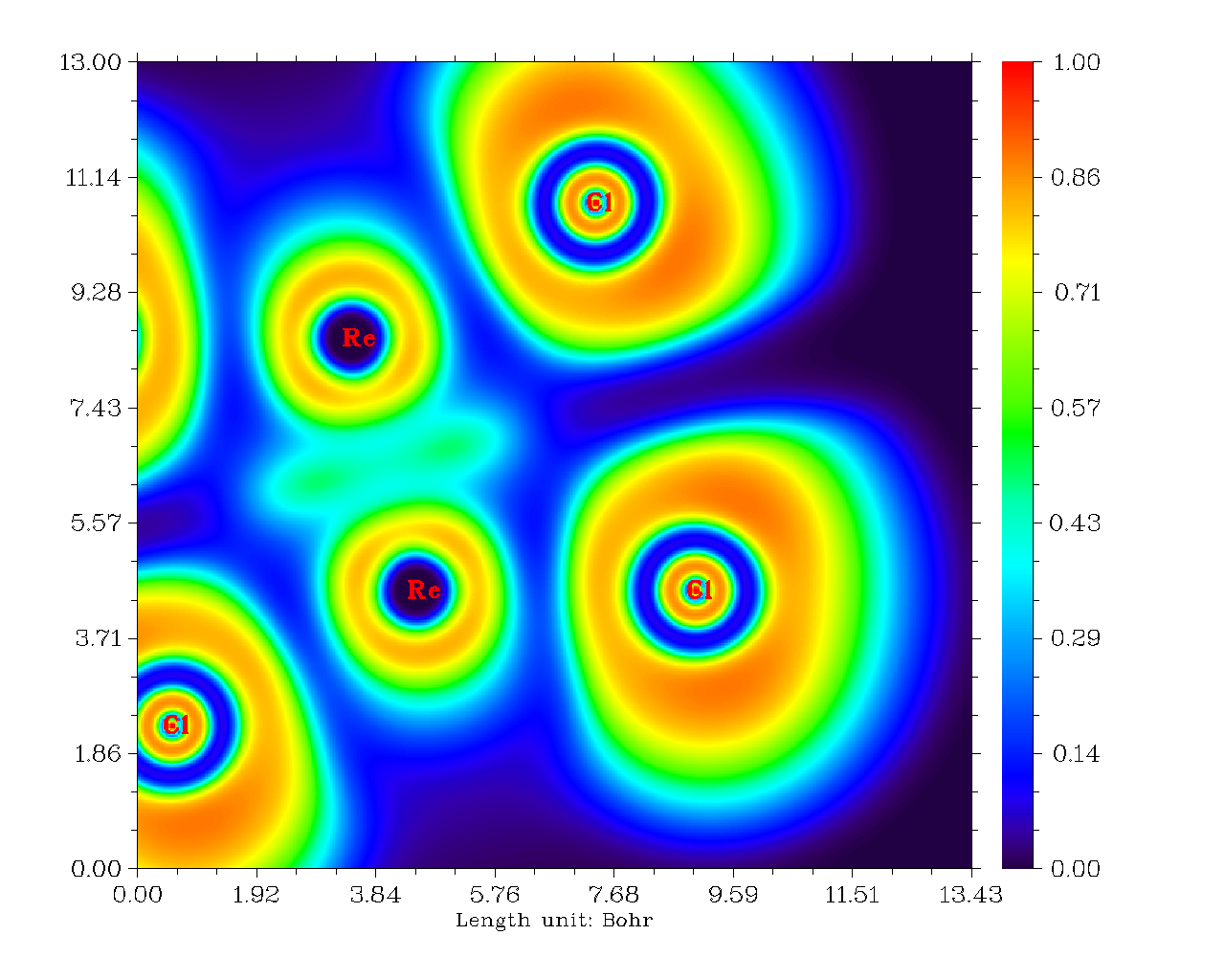
這樣無法用拉普拉斯函數反應共價性的金屬多重鍵的例子還有很多,比如Cr2、Mo2等等。
對于電子密度拉普拉斯函數用于電荷轉移鍵體系也特別需要注意。電荷轉移鍵我以后會專門另文介紹。簡而言之,電荷轉移鍵就是形式上看上去是共價鍵,但是本質又不是共價鍵的鍵。電負性越大、孤對電子越多的兩個原子間通常越容易形成電荷轉移鍵。最為極端的就是F2分子,教科書上幾乎都毫無疑問地把它當成典型的共價鍵,然而實際上,假設只用共價形式描述它來做價鍵理論計算,這個分子會直接解離掉。正因為電荷轉移鍵本質不是,或不完全是共價鍵,所以構成電荷轉移鍵的兩個原子間電子凝聚程度很低,甚至根本不凝聚。下圖左邊和右邊分別是F2的拉普拉斯函數和密度差圖(B3LYP/cc-pVDZ級別已能夠合理描述電荷轉移鍵)
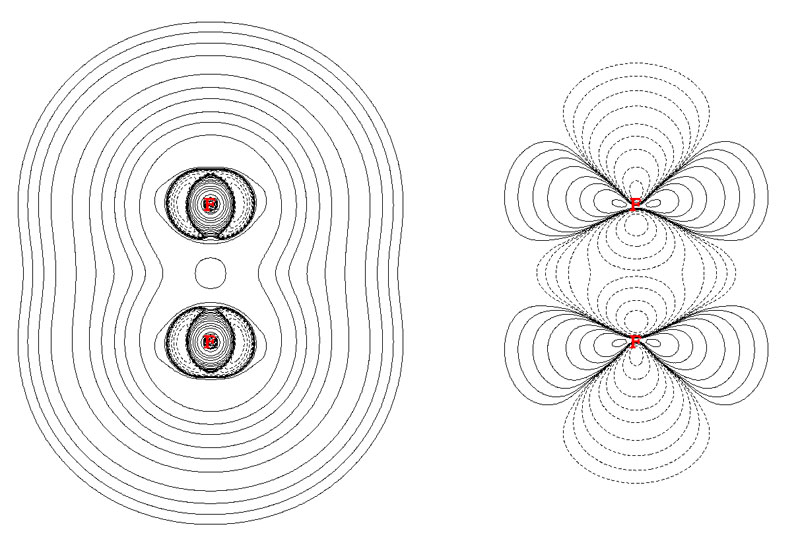
從拉普拉斯值圖上可見F2之間完全沒有電子凝聚區域。而從密度差圖上看,成鍵后兩個原子間不僅密度沒有增加,反倒還降低了。
有人誤以為F2是普通共價鍵,由于算出的BCP處拉普拉斯值為正,于是以此為證據說通過BCP的拉普拉斯值符號判斷成鍵類型的方式不可靠,其實是冤枉了這種判斷方法。的確,這種判斷方法不可靠,但原因不在這里,而是前文提及的那些。
有人提出了判斷電荷轉移鍵的判據(可參見http://www.ch.ic.ac.uk/rzepa/blog/?p=2251),認為BCP處電子密度顯著大于0,而拉普拉斯值也大于0,就算電荷轉移鍵。但這個條件只能算是判斷電荷轉移鍵的充分條件,而非必要條件。
其實,金屬多重鍵、電荷轉移鍵、存在贗原子的體系一般不常遇到,BCP處拉普拉斯值符號沒法普遍用于區分共價和閉殼層相互作用主要問題還是對于較強極性共價鍵時BCP的位置缺乏化學意義,代表不了成鍵區域的情況。其實解決方法也不難,就是研究拉普拉斯值的時候不要僅局限在這么一個點上。我們可以通過作圖直觀地通過電子凝聚方式判斷相互作用類型,當僅靠拉普拉斯值圖不容易判斷時還可以作ELF圖,通常可以得到更鮮明的圖景。利用Multiwfn程序,作這些圖十分簡單,熟練之后,從輸入文件名到彈出圖像整個過程最多也就用不了10秒鐘。筆者也提出了一個定量化的方法,稱為拉普拉斯鍵級,見JPCA,117,3100 (2013),在Multiwfn程序中對應于主功能9里面的8,它是通過原子間交疊空間內積分拉普拉斯值得到的鍵級,僅靠這一個鍵級值就可以反映鍵的強度和極性的程度,這也比起只考慮BCP一個點的拉普拉斯值要可靠得多。另外,也有人提出應當考慮整條鍵徑上各點的屬性。
除了用BCP處拉普拉斯值判斷相互作用類型以外,還有人用BCP處的其它屬性來判斷,例如正定動能密度除以電子密度、正定動能密度垂直于鍵徑的分量除以平行于鍵徑的分量、電子密度Hessian矩陣最大本征值的絕對值除以最小本征值的絕對值。還有人提出應當結合多種屬性值綜合判斷。然而這些判斷方法雖然用在不少體系上都沒問題,但是找到反例也不難,普適性難以保證。
還有一個很流行的判斷方法是看BCP處電子能量密度的符號,若為負,表明是共價作用;若為正,表明是閉殼層相互作用。電子能量密度就是電子正定動能密度和電子勢能密度的加和,全空間積分就是電子在當前體系中的能量,它也等價于哈密頓動能密度的負值。這個判據最初是在Angew. Chem. Int. Ed. Engl. 23, 627中提出的,這篇文章寫得十分草率,沒有道出明確的物理意義。不過這個判斷方法的普適性比起靠BCP處的拉普拉斯值符號判斷在實際中要好得多,比如Ni(CO)4和LiF的電子能量密度圖如下(從Multiwfn 2.5版開始,只要將settings.ini文件中的iuserfunc設為11,則選擇要繪制的實空間函數時選“100 User defined function”就等于選了能量密度。)
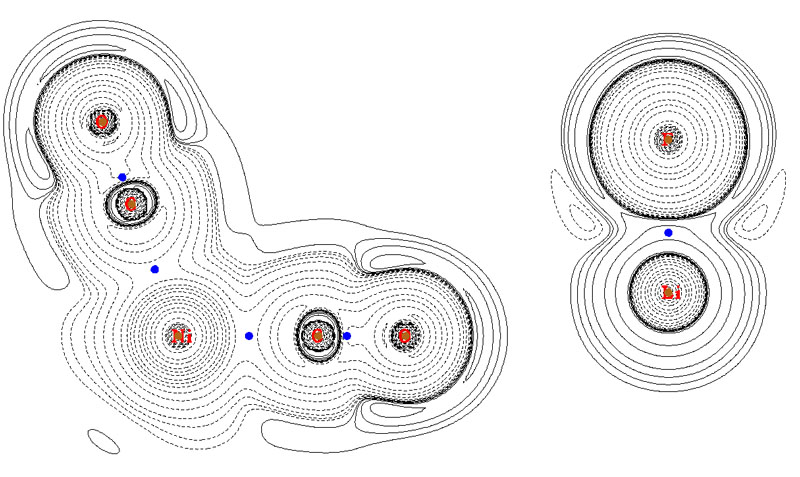
由圖可見,Ni-C和C-O的BCP處能量密度都為負,正確地表明是共價作用。而LiF的BCP落在正值區域,表現出閉殼層相互作用。然而,這個判斷方法也能輕而易舉地找到反例,比如氧化鈣的能量密度圖如下
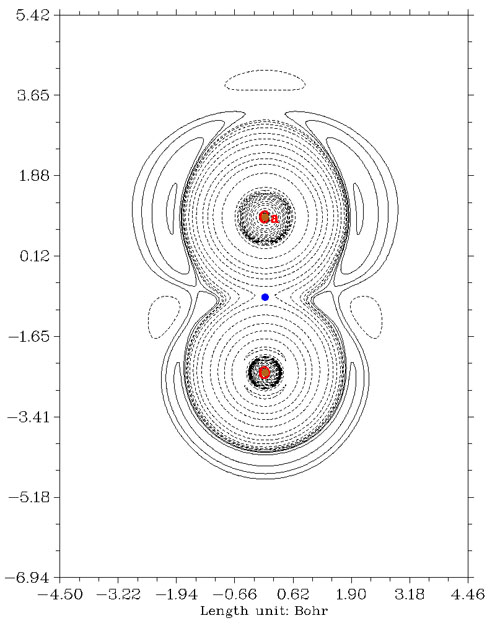
按一般常識,氧化鈣是離子相互作用,起碼共價性遠低于離子性,而且從ELF圖上也看不出原子間高定域性共價區域。然而,BCP的能量密度卻為負,誤認為是共價作用。所以,用這種判據也不要輕信,最讓人放心的還是作拉普拉斯值或ELF圖,物理意義明確,一目了然。