深入理解分子軌道對磁感生電流的貢獻
深入理解分子軌道對磁感生電流的貢獻
Deep understanding of contribution of molecular orbitals to magnetically induced currents
文/Sobereva@北京科音 2024-Mar-3
0 前言
施加外磁場會導致化學體系產生磁感生電流,考察磁感生電流是研究分子芳香性的重要方法。我之前寫過諸多博文介紹過,如《使用SYSMOIC程序繪制磁感生電流圖和計算鍵電流強度》(http://www.shanxitv.org/702)、《考察分子磁感生電流的程序GIMIC 2.0的使用》(http://www.shanxitv.org/491)、《使用AICD 2.0繪制磁感應電流圖》(http://www.shanxitv.org/294)、《衡量芳香性的方法以及在Multiwfn中的計算》(http://www.shanxitv.org/176)等。最常見的是考察整個分子的磁感生電流,而對于苯等平面體系,也經常區分成sigma和pi電子的感生電流分別考察,以更充分了解不同類型電子的離域性、對芳香性的貢獻。對于CTODZ和與之本質相同的CSGT計算感生電流方法,總的感生電流是可以精確寫為所有占據軌道貢獻之和的形式的,也因此原理上可以給出任意占據軌道對應的感生電流。軌道的感生電流會帶來感生磁場,對外磁場有屏蔽或去屏蔽效果,因此相應地可以得到各個軌道對NICS的貢獻,如《基于Gaussian的NMR=CSGT任務得到各個軌道對NICS貢獻的方法》(http://www.shanxitv.org/670)所展示的。
然而,單一軌道對感生電流和NICS的貢獻實際上是存在任意性的,過度解釋可能得到十分誤導性的結論。本文就專門詳細談一談這個問題,以令讀者正確理解軌道對感生電流的貢獻。并且還同時介紹一下如何根據占據軌道到空軌道之間的躍遷模型來預測和解釋一些體系的磁感生電流。本文許多內容和討論取材自J. Phys. Chem. A, 105, 9553 (2001)一文,這是一篇很經典的探討軌道與磁感生電流關系的文章。但這篇文章里很多部分寫得難懂,本文則盡可能說得清楚、明白、易懂。
1 分子軌道對感生電流貢獻的表達式
此文只討論閉殼層的情況,假設體系有N個電子,因此有N/2個占據軌道。如下式(1)所示,總的感生電流可以寫為所有占據軌道的加和形式,n是軌道序號。下式(2)給出了n軌道對r處感生電流矢量的表達式,B是外磁場矢量,d是測量原點(gauge origin),φ是無磁場下計算的分子軌道波函數,φ(1)是以二階微擾理論得到的外磁場作用下的φ的一階校正。
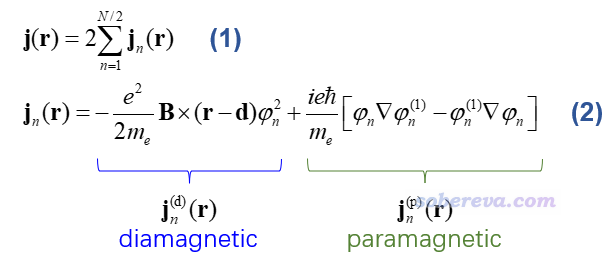
由上式可見,軌道的感生電流由paramagnetic(順磁)和diamagnetic(抗磁)兩部分構成,以下分別簡稱para和dia。dia電流是楞次定律說的給導體施加外磁場時產生的那種感生電流,正比于軌道上的電子的概率密度,它產生的感生磁場會在環形感生電流內部區域對外磁場產生削弱作用。而para部分完全來自于量子力學效應,直接牽扯到軌道波函數,方向與dia相反。
在完備基組下,體系總的感生電流計算結果是不依賴于d的選取的,但構成它的dia和para電流各自大小卻依賴于d,因此dia和para的劃分沒有嚴格的物理意義、也不存在唯一的劃分。而對分子軌道而言,不僅d的選取會影響此軌道的dia和para電流,對二者的總和也會產生影響。上式的dia部分里直接就有d,而para部分的φ(1)當中的φ(d)也依賴于d,具體表達式如下
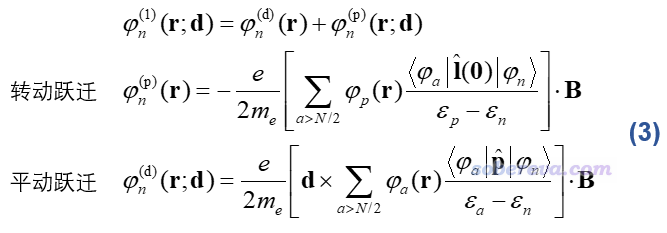
ε是分子軌道能量,p是單電子動量算符,l(0)=r×p是相對于笛卡爾坐標原點的單電子角動量算符。φ(p)和φ(d)分別涉及當前軌道向各個空軌道的轉動躍遷和平動躍遷。
如果計算所有位置的感生電流時使用統一的d,叫做common gauge-origin。這種做法平時基本不用,因為d的選取任意性太強而又會直接影響結果(也就某些情況有相對適合、意義較強的,比如算苯的時候可以把d設為環中央)。如果計算r處的感生電流用的d可表達為d(r)形式,即d也是像r一樣連續變化的且依賴于r,則被稱為CTOCD方法。SYSMOIC程序就是基于此方法計算感生電流。CTOCD有不同具體形式,其中CTOCD-DZ方法的名字中的DZ代表diamagnetic zero,它將d設為r,即算哪個位置的感生電流就把此時用的d設在哪里,使得上面(2)式中的dia項為0。雖然不能說把d設為r就有什么確切的物理意義,但起碼沒有common gauge-origin的d選取的表面上的任意性。
下面我把一般情況、d=r的情況、d=0的情況的感生電流表達式放在一起,便于大家弄清楚它們之間的異同、para和dia的定義。
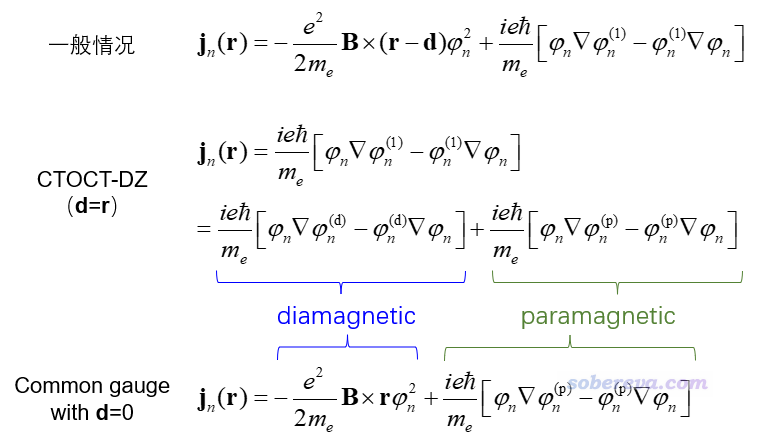
CTOCT-DZ方法由于d=r,所以上面“一般情況”中的B×(d-r)項就沒了,再把φ(1)=φ(p)+φ(d)代進去就得到了CTOCT-DZ的表達式。可見其中一部分由涉及平動躍遷的φ(d)所貢獻,這部分被習俗地視為CTOCT-DZ的dia項,另一部分由涉及轉動躍遷的φ(p)所貢獻,這部分被習俗地視為CTOCT-DZ的para項。而對應d=0的common gauge-origin的情況中φ(d)就不復存在了,φ(1)=φ(p),就有了上面的式子。由上式可見,CTOCT-DZ和d=0的情況的para項是相同的,但是dia項不同,因此兩種情況計算的軌道感生電流是不同的。
基組夠大的情況,總的感生電流近乎不依賴于d,因此可以用總的感生電流討論芳香性。而由于軌道的感生電流明顯依賴于d,所以絕對不能輕易拿一個軌道的感生電流的特征去判斷它對體系芳香性、電子離域有什么樣的貢獻,否則會造成誤導。但這不代表做感生電流的軌道層面的分解討論就沒實際意義,因為完備基組下某些軌道的感生電流的總和也是不依賴于d的。對純平面體系,sigma電子的感生電流和pi電子的感生電流可以精確分離,且二者都是不依賴于d的。具體為什么,是因為存在以下關系

由上面最后一個式子可見,某分子軌道的CTOCD-DZ和d=0的感生電流只相差一部分,它依賴于此軌道與其它占據軌道之間的平動躍遷。當所有占據軌道的感生電流加和時,n軌道的感生電流表達式中的n→m躍遷部分的貢獻和m軌道的感生電流表達式中的m→n躍遷部分的貢獻精確抵消了(因為軌道能量差是φ(d,occ)的分母項,ε_n-ε_m和ε_m-ε_n的符號相反),所以CTOCD-DZ和d=0得到的體系總感生電流是相同的。為什么對于純平面體系pi(或sigma)電子的總感生電流也不依賴于d?這是因為由于對稱禁阻原因sigma與pi軌道之間的<φ_m|p|φ_n>項精確為0(即在垂直于外磁場方向即便平移sigma軌道后也仍然與pi軌道正交),φ(d,occ)因此又可以分為只循環sigma軌道和只循環pi軌道部分的加和,即sigma和pi是兩個不同的block。所以所有pi軌道的感生電流加和時由于所有牽扯到的n→m和m→n(n和m皆為占據的pi軌道)的貢獻精確抵消原因,它不依賴于d。
2 苯分子的不同pi軌道的感生電流
這一節看一個實例,以更好地了解上一節的討論。下圖給出了苯的最低pi軌道(MO 17)以及兩個簡并的HOMO pi軌道(MO 20 21)各自的Multiwfn繪制的0.05 a.u.軌道等值面圖,以及SYSMOIC程序繪制的分子平面上方1 Bohr處的感生電流圖。所有三個軌道加和對應的總的pi感生電流圖也一起給出了。計算分別使用CTOCD-DZ形式(對應SYSMOIC里JBMAP結合-m DZ1選項),以及d=0的common-gauge情況(對應SYSMOIC里JBMAP結合-m CO選項,默認的d坐標(0,0,0)此時對應苯環中心)。幾何優化和產生波函數文件都是在B3LYP/6-31G*下進行的。
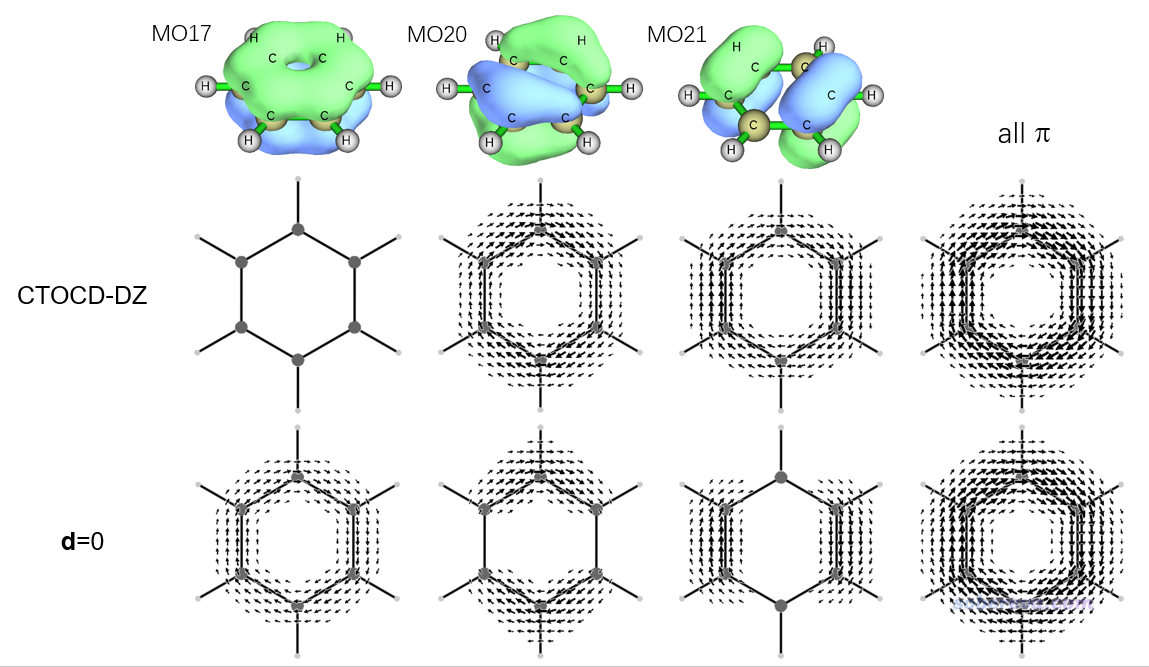
由上圖可見,CTOCD-DZ和d=0的總的pi感生電流基本沒有可查覺的差別,但是這兩種方法算出來的不同pi軌道的感生電流就相差顯著了。CTOCD-DZ的MO 17的感生電流極小,在當前作圖設置下甚至都看不到,而d=0時它的感生電流則很顯著,和其它pi軌道的差不多。其原因在于MO 17與低階的空軌道之間的平動和轉動躍遷都是禁阻的,只可能往能量很高的空軌道躍遷,又由于軌道能量差出現在φ(d)和φ(p)的分母項,自然CTOCD-DZ方法算出來的它的感生電流特別小。而反之,d=0方式計算軌道感生電流的公式里有B×rφ^2項,φ^2對應當前軌道概率密度,因此由于MO 17在整個六元環上分布得很均勻且密集,使得MO 17的d=0方法算的感生電流很顯著。也由于d=0的感生電流計算公式的這個特點,MO 20和21的感生電流顯著分布區域也和軌道波函數顯著分布的區域高度類似,而CTOCD-DZ的感生電流分布和軌道分布則沒有視覺上的顯著聯系。
對MO 17,CTOCD-DZ和d=0的圖像展現的信息有天壤之別。如果不懂以上原理的話,看CTOCD-DZ圖就會盲目以為MO 17的電子幾乎沒有在六元環上的離域性、跟pi芳香性沒聯系。而事實上,在碳環上完全均勻分布的MO 17顯然對苯的pi電子的全局離域有重要貢獻。所以,特定軌道的感生電流和軌道實質上體現的電子離域特征并沒有必然關聯,這點一定要注意!
那么是否軌道的感生電流一定不能用于討論軌道對芳香性的貢獻呢?在我來看,這種討論方式雖然由于上述原因而非常不推薦,但在特殊情況下還是可行的,比如上面d=0方法算的MO 17的感生電流確實體現出MO 17對芳香性有明顯貢獻。這里我闡述我的個人觀點:如果一個軌道對電子在某個環上的多中心離域完全沒有貢獻,那么無論怎么選擇d也算不出它有連貫環繞整個環的dia電流,例如內核電子軌道;而如果能有特定的d可以算出來它有連貫環繞整個環的dia電流,那么這個軌道對多中心離域就是有明顯貢獻的,如苯的MO 17。從前面的圖中還可以看到,d=0時的MO 20和21各自的感生電流都沒有在整個苯環上連成整體,但在CTOCD-DZ的情況下則連成了整體,根據以上我的觀點,這直接說明了這倆軌道確實對pi電子的六中心離域有直接貢獻。
CTOCD-DZ算的MO 17的感生電流極小,也很大程度反映在《基于Gaussian的NMR=CSGT任務得到各個軌道對NICS貢獻的方法》(http://www.shanxitv.org/670)文中以CSGT方式算的苯的各個分子軌道對NICS(1)zz的貢獻上,MO 17的貢獻(-1.58 ppm)遠低于MO 20和21的貢獻(-14.07 ppm)。CSGT方法是使用(2)式計算各處的感生電流密度,用Becke多中心積分方法通過Biot-Savart定律計算特定位置的磁屏蔽張量,每個積分格點用的d是此處的坐標往距離它最近的原子核一定程度移動得到的(基于各個原子的Becke權重確定)。SYSMOIC程序給出的CSGT方法算的MO 17的感生電流密度和CTOCD-DZ一樣也是微乎其微的。
3 基于軌道躍遷模型的解釋感生電流的例子
CTOCD-DZ算的軌道感生電流沒法展現出苯的最低pi軌道對六中心離域的貢獻,是否說明CTOCD-DZ沒啥實際優點?答案是否定的。一方面,CTOCD-DZ計算軌道感生電流時給定了明確的d的選取方式,因此消除了人為選擇的任意性;另一方面,CTOCD-DZ計算軌道感生電流的公式是可以嚴格分解為當前軌道向不同空軌道的躍遷貢獻的,這種形式被稱為完全態求和(sum-over-state, SOS)。SOS形式使得研究者可以從軌道間的平動和轉動躍遷角度來定性預測不同軌道的感生電流該是什么樣,以及深層次解釋和理解CTOCD-DZ實際算出來的軌道感生電流為什么是那樣,從而獲得重要的physical insight。其實還有不少其它的分子屬性也可以表達為SOS形式,例如我在《使用Multiwfn基于完全態求和(SOS)方法計算極化率和超極化率》(http://www.shanxitv.org/232)里介紹了(超)極化率就可以通過SOS形式來計算,并且經過簡化,還可以得到兩態和三態模型來分析討論影響第一超極化率的關鍵因素,見《使用Multiwfn對第一超極化率做雙能級和三能級模型分析》(http://www.shanxitv.org/512)和《談談計算第一超極化率的雙能級公式》(http://www.shanxitv.org/361)。
對于CTOCD-DZ方法計算的占據軌道n的感生電流,n向某個空軌道a的躍遷若能夠對它有顯著的貢獻,需要滿足三個條件
(1)對稱匹配。n→a必須要么平動躍遷允許(對dia電流有貢獻),要么轉動躍遷允許(對para電流有貢獻),要么都允許。對于有點群對稱性的體系來說,如式(3)所示,平動躍遷如果是允許的就意味著<φ(a)|p|φ(n)>不能精確為0,這要求n與a軌道不可約表示的直積對應的表示包含垂直于磁場的平移。轉動躍遷如果是允許的就意味著<φ(a)|l(0)|φ(n)>不能精確為0,這要求n與a軌道不可約表示的直積對應的表示包含繞著磁場方向的旋轉
(2)軌道重疊顯著。如果a和n的空間分布沒有明顯的重疊,自然平動和轉動躍遷肯定非常小、n→a躍遷不可能對n的感生電流有可查覺的貢獻
(3)能量相近。由于a和n軌道的能量差出現在式(3)的分母部分,因此只有較高的占據軌道與較低的空軌道之間的躍遷才可能對感生電流有明顯貢獻
下圖是JPCA文中在HF/6-31G*級別算的D6h點群的苯的前線軌道能級圖,小圓點是占據的電子,黑色箭頭是平動允許的軌道躍遷,苯處在XY平面上。例如e1g與e2u之間的直積是b1u+b2u+e1u,查特征標表可知e1u包含(x,y),與Z方向的外加磁場相垂直,因此平動躍遷允許。下圖所標注的a2u到e1g、e2u到b2g也類似地都是平動躍遷允許的。這些軌道之間沒有轉動躍遷是允許的,因為它們的不可約表示的直積都沒有包含繞Z軸旋轉的行為(Rz)。對于CTOCD-DZ方法,前面說過它只涉及占據軌道到空軌道的躍遷,因此此體系的感生電流僅來自于下圖中e1g(HOMO)到e2u(LUMO)的躍遷,而且完全是dia電流。D6h點群的不可約表示里只有e1u含有x和y行為,能量最低的占據pi軌道是a2u,僅和e1g直積可以得到e1u,而空軌道里最低的e1g軌道是能量很高的,因此這個占據pi軌道向e1g軌道躍遷導致的對dia電流的貢獻可忽略不計,這是為什么上一節看到CTOCD-DZ算的苯的MO 17的感生電流在圖上都看不到。
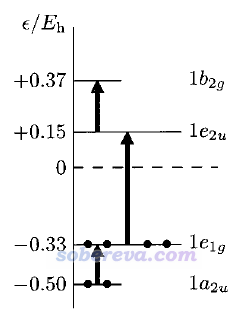
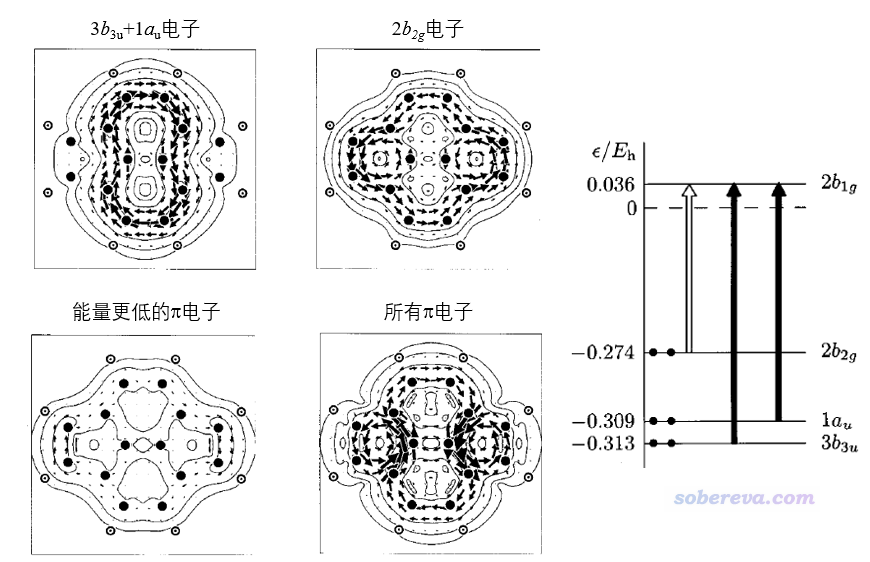
下圖是CTOCD-DZ計算的pyracylene的感生電流以及軌道躍遷示意圖,分子在YZ平面上,外磁場由屏幕內向著屏幕外順著X方向加(圖片取自前述JPCA文章,為了和我的習俗相同,我把文中的感生電流方向反轉了一下,順時針和逆時針分別對應dia和para電流)。下圖右側示意圖中實箭頭對應允許的平動躍遷(因為b3u與b1g的直積b2u包含y,au與b1g的直積b1u包含z),故b3u和au軌道貢獻順時針的dia電流;空心箭頭對應允許的轉動躍遷(因為b2g與b1g的直積b3g包含Rx),故b2g軌道貢獻逆時針的para電流。由于更低階pi軌道對感生電流貢獻甚微,所以總的pi感生電流的圖像特征基本等于b3u和au貢獻的dia電流以及b2g軌道貢獻的para電流的總和。由于同時有4個電子貢獻dia電流而只有2個電子貢獻para電流,故前者整體強度更大,這是為什么在這兩種電流方向相反的分子的上、下區域,總電流體現的是順時針特征。
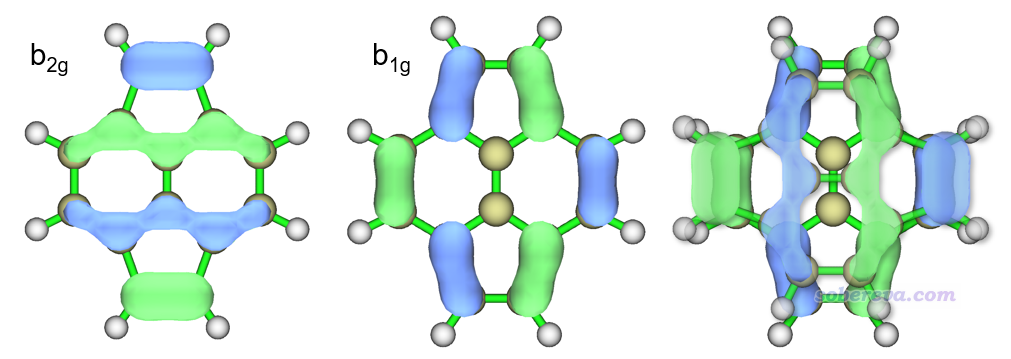
如果不通過群論知識,怎么判斷什么樣的軌道之間的轉動躍遷是比較顯著的呢?這可以結合圖形進行判斷和理解。若繞著磁場旋轉一個軌道后就可以令二者不再正交,那么它們之間的轉動躍遷就是允許的,這通常出現在兩個軌道的節面數目是相似的情況下。例如下圖所示的pyracylene的HOMO (b2g)→LUMO (b1g)的躍遷就是如此,最右邊的圖是把HOMO旋轉90度后和LUMO的重疊圖,可見相位完全匹配且高度重疊,因此這種躍遷能夠對para電流有顯著貢獻。
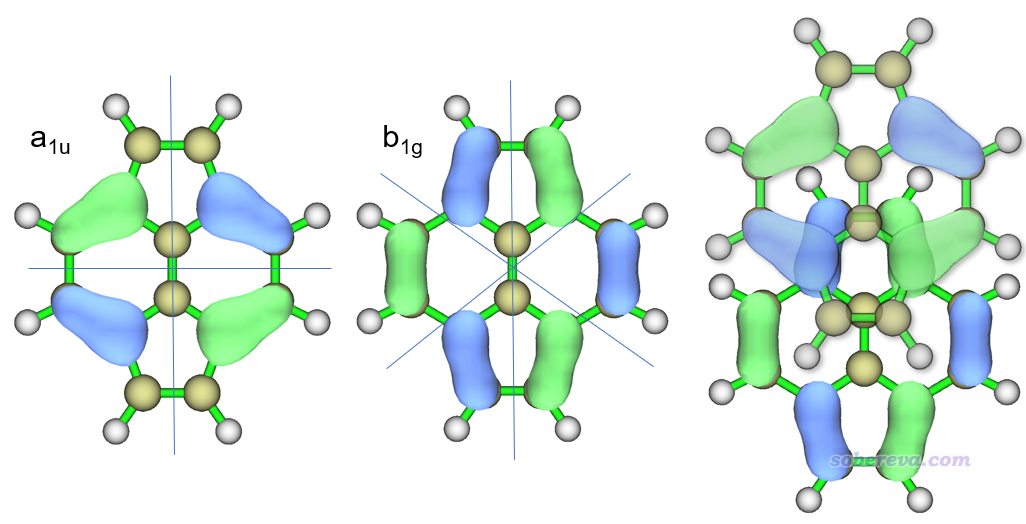
如果在垂直于磁場方向平移一個軌道后能夠與另一個軌道之間不再正交(一個軌道比另一個軌道多一個節面往往是這種情況),那么二者間的平動躍遷就是允許的。例如下圖所示的pyracylene的HOMO-1 (au)→LUMO (b1g)的躍遷就是如此,HOMO-1有兩個節面,LUMO有三個節面,最右邊的圖是把HOMO-1垂直于磁場平移后和LUMO的重疊圖,可見能是以相位匹配的方式重疊,重疊積分明顯不為0,因此這種躍遷能夠對dia電流有顯著的貢獻。
通過以上例子,可以看出利用占據-非占據軌道躍遷模型,確實可以對CTOCD-DZ方法計算的軌道感生電流予以預測,還能對總感生電流的特征從軌道角度進行深層次的解釋。前述JPCA文章里還有更多分析例子,包括苯的陰/陽離子、萘、并六苯、暈苯、碗烯,感興趣者可以看看。文章還總結出CTOCD-DZ計算的感生電流的規律,對滿足4n+2的普通碳單環體系,只有處于二重簡并的HOMO軌道上的4個pi電子對pi感生電流有明顯貢獻,而更低的軌道的貢獻可以忽略。而對于更復雜的多環分子,只有少量的前線pi占據軌道對感生電流有顯著貢獻,這是因為低階pi占據軌道往平動/轉動允許的pi空軌道上躍遷對應的能級差太大而必定貢獻很小,而低階pi占據軌道往前線pi占據軌道躍遷即便是平動/轉動允許的也沒用,因為占據-占據軌道的躍遷貢獻不在CTOCD-DZ方法中出現)。