用于非限制性開殼層波函數的雙正交化方法的原理與應用
用于非限制性開殼層波函數的雙正交化方法的原理與應用
文/Sobereva@北京科音
First release: 2018-Nov-11 Last update: 2021-Sep-10
摘要:本文非常簡要地介紹一下對非限制性開殼層波函數的alpha和beta軌道之間做雙正交化的方法,并且以三重態乙醇為例介紹如何在Multiwfn中實現,使得其alpha和beta軌道最大程度匹配,從而便于討論軌道。本文說的Multiwfn及其手冊是官網上最新版本的情況。
1 相關知識
眾所周知,非限制性開殼層計算(如UHF、UKS,以下簡稱為U)的時候alpha和beta是分別求解的,因此會產生alpha和beta這兩套自旋軌道。對于自旋多重度>1的體系,以及自旋多重度為1的對稱破缺態,由于自旋極化,會導致alpha和beta軌道不匹配,此時雖然alpha軌道自己是正交歸一的,beta軌道自己也是正交歸一的,但是alpha和beta之間不滿足正交歸一關系。更具體來說,第i號alpha軌道和第i號beta軌道之間重疊積分不為1,這倆軌道既可能軌道形狀稍有偏差,也可能完全不同。因此,對于非限制性開殼層波函數,討論軌道的時候必須分別去考察alpha和beta軌道,這是比較麻煩的事情。而且這種情況,體系的自旋密度是由所有占據軌道所決定的,因此沒法只拿某幾條軌道來討論自旋密度。(不知道什么是自旋密度的話看《談談自旋密度、自旋布居以及在Multiwfn中的繪制和計算》http://www.shanxitv.org/353)。
雖然限制性開殼層(RO)計算只會產生一套軌道,沒有上述U計算的麻煩,但是相對于U,RO計算耗時高、難收斂,自旋密度、體系總能量和軌道能量也都沒有U那么有意義,因此用RO回避上述問題也不是好的辦法。
實際上,在U計算之后,可以做雙正交化(biorthogonalization)變換來解決上述問題。雙正交化的具體細節和實現在Multiwfn手冊3.100.12節有詳述,本文就不細說了。簡單來說,雙正交化是對alpha和beta軌道進行酉變換,使得alpha和beta之間完美滿足或基本滿足正交歸一關系,同時又不破壞每種自旋軌道與其自己原有的正交歸一關系。雙正交化具體實現方式并不唯一,Multiwfn中的雙正交化方法分成三步,經過這三步變換后,每個alpha和與之序號相同的beta軌道一般可以達到近乎完美匹配,因此之后就只需要討論一套軌道即可(類似于RO軌道的情況)。
在雙正交化過程中每種自旋的占據軌道和占據軌道會發生混合、空軌道和空軌道會發生混合(具體來說是酉變換),而不同自旋軌道間不會發生混合。這種變換不會導致體系任何可觀測性質發生改變,因此如果使用雙正交化后的軌道去計算體系總能量、總電子密度、自旋密度等等,結果和U計算給出的是完全相同的,在這點上類似于軌道定域化。雙正交化后的軌道不再是Fock算符的本征函數,因此雙正交化軌道也沒有確切的軌道能量,而只能以Fock算符期望值的方式求軌道能量。
2 實例
2.1 三重態乙醇
下面我們對三重態乙醇做雙正交化,來看看雙正交化的實際效果和價值。首先我們先看一下UB3LYP/6-31G**下直接給出的這個體系三重態的幾個分子軌道等值面圖,如下所示。其中14號alpha軌道是alpha軌道中的HOMO,12號beta軌道是beta軌道中的HOMO。
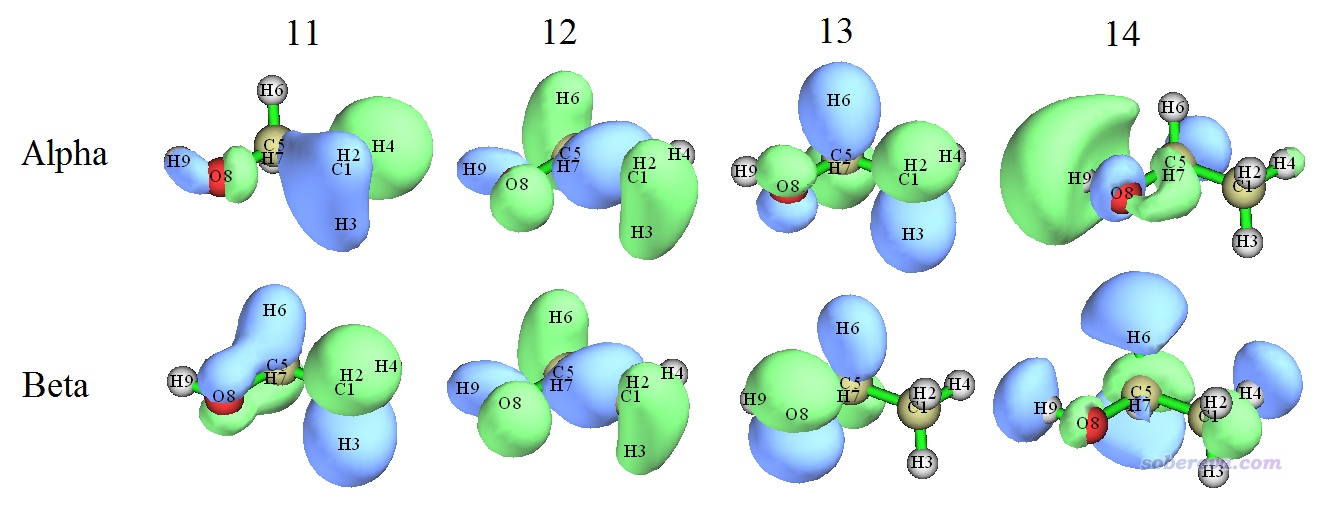
由圖可見,只有12號alpha與12號beta軌道匹配很好,形狀和相位都肉眼看不出顯著差別,而其它alpha和beta軌道之間完全匹配不上。alpha比beta占據軌道多兩個(13和14),但顯然當前情況我們不可能認為體系的自旋密度等于13和14號alpha軌道對應的密度之和,因為由于其它alpha和beta占據軌道形狀的不匹配,它們也對自旋密度有直接的影響。
在Multiwfn中做雙正交化需要的輸入文件必須包含基函數信息,具體看《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)、《Multiwfn入門tips》(http://www.shanxitv.org/167),對于Gaussian用戶就用fch文件即可。UB3LYP/6-31G**下三重態乙醇的fch文件已經在Multiwfn自帶的文件包里提供了,這里我們對它做雙正交化。
啟動Multiwfn,然后依次輸入
examples\ethanol_triplet.fch
100
12 //產生雙正交化軌道
2 //雙正交化過程中考慮所有軌道(對于大體系,為節約時間,可以此處選1略過空軌道之間的雙正交化,此時對于此例,在最終結果中編號在14以上的alpha和beta軌道將無意義)
0 //不計算雙正交化軌道能量
從屏幕上提示的信息可見雙正交化分為三步進行,比如第一步輸出的信息為
Doing biorthogonalization for alpha 1 to 14, Beta 1 to 12
Singular values of orbital overlap matrix:
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.9999
0.9999 0.9998 0.9995 0.9992
這說明這一步是對1~14號alpha軌道和1~12號beta軌道做雙正交化。下面的數值是經過雙正交化后的alpha和beta軌道間的重疊積分。當前顯示了12個等于或非常接近于1.0的數值,這代表這步雙正交化后1~12號alpha和1~12號beta軌道已經非常完美地一一對應了。其余的軌道的雙正交化會在接下來的步驟中進行。
之后Multiwfn把雙正交化后的軌道波函數自動導出為當前目錄下的biortho.fch文件,也把雙正交化后的軌道信息導出為當前目錄下的biortho.txt文件,此文件內容如下所示。
S = Singular value, E = Energy (in eV), O= Occupancy, A=Alpha, B=Beta
Orb: 1 S= 1.0000 O(A)= 1.0 O(B)= 1.0
Orb: 2 S= 1.0000 O(A)= 1.0 O(B)= 1.0
...[略]
Orb: 11 S= 0.9995 O(A)= 1.0 O(B)= 1.0
Orb: 12 S= 0.9992 O(A)= 1.0 O(B)= 1.0
-----------------------------------------------
Orb: 13 S= 1.0000 O(A)= 1.0 O(B)= 0.0
Orb: 14 S= 1.0000 O(A)= 1.0 O(B)= 0.0
-----------------------------------------------
Orb: 15 S= 1.0000 O(A)= 0.0 O(B)= 0.0
Orb: 16 S= 1.0000 O(A)= 0.0 O(B)= 0.0
Orb: 17 S= 1.0000 O(A)= 0.0 O(B)= 0.0
...[略]
通過這個文件可以非常方便地考察雙正交化后的alpha軌道與序號與之相同的beta軌道的匹配程度。由于上面列出來的軌道的S(Singular value,即相當于重疊積分)都很接近1,因此這些軌道的alpha-beta匹配程度都很好,只有alpha 12和beta 12的匹配程度稍差一點,但也很接近于1.0,因此這倆軌道的圖形從肉眼上應該很難分辨。上面信息里O代表Occupancy,就是占據數的意思,為了觀看方便,這個文件里把O(A)=O(B)=1.0、O(A)=1.0&O(B)=0.0和O(A)=O(B)=0.0三個部分用橫線做了分隔。
此時程序還問你是否現在就載入biortho.fch文件,如果選y將之載入的話,內存里的軌道就對應于雙正交化后的軌道了,之后你可以進入主功能0去查看軌道圖形,也可以用主功能0的圖形界面左上角的Orbital info.選項去查看這些軌道的基本信息,還可以用Multiwfn中的各種功能去分析軌道特征,比如計算軌道成分、軌道動能等。由于此例沒計算雙正交化軌道的能量,因此在導出的biortho.fch里“軌道能量”部分記錄的是上述輸出的singular value值。由于當前沒有雙正交化軌道的能量信息,因此當前biortho.fch里的這些軌道的序號順序并不對應于其軌道能量順序。
這里把11~14號雙正交化后的alpha和beta軌道列出:
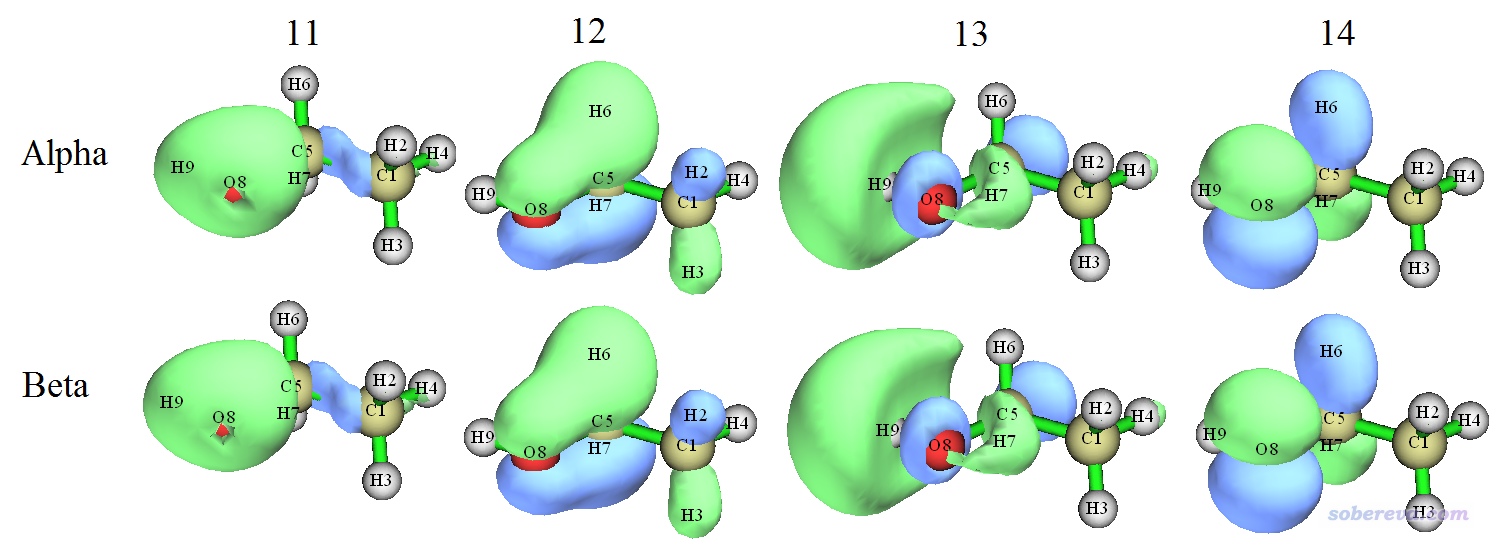
可見,雙正交化后alpha和與之序號相同的beta在軌道形狀上已經肉眼基本看不出任何區別了。此時,13和14號alpha軌道可以被冠以描述RO軌道時用的SOMO(單占據軌道)之名,這兩個軌道對應的密度的加和正好就是當前體系UB3LYP/6-31G**級別計算的三重態的自旋密度。對比本文上面的兩張圖,也可以看到在雙正交化前后,軌道特征往往差別不小。雙正交化后的第13號alpha軌道基本正好對應原先的第14號alpha軌道,而雙正交化后的第14號alpha軌道則不直接對應于之前任何一個alpha軌道,顯然必定是兩個或多個原先的alpha占據軌道發生了顯著混合才產生出來的。
值得一提的是,乙醇的單重態基態在B3LYP/6-31G**下計算產生的HOMO和LUMO軌道圖形如下
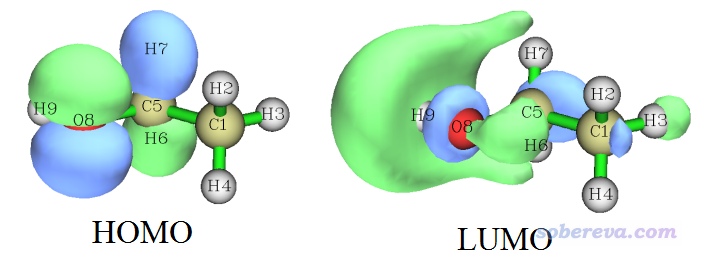
這個HOMO和LUMO分別非常像雙正交化后的14號和13號alpha軌道。因此我們可以立刻明白,乙醇從單重態基態激發到最低三重態的過程,如果以軌道躍遷方式描述的話,可以近似說成是HOMO→LUMO的躍遷,因為這樣躍遷后HOMO和LUMO就各有一個單電子了,這倆軌道又幾乎恰好和雙正交化后的兩個SOMO對應。像這樣重要的信息,如果我們不做雙正交化的話,是沒法這么容易了解到的。
2.2 三重態乙醇(計算雙正交化軌道能量)
這個例子還是考察三重態乙醇,和上例不同的是這次我們也讓Multiwfn產生雙正交化軌道的能量,這樣不僅可以討論更多信息,而且Multiwfn會根據能量對軌道排序,討論起來更方便。Multiwfn計算雙正交化軌道的能量需要利用Fock矩陣,Multiwfn可以通過兩種方式獲得這個矩陣:
(1)直接基于分子軌道能量和系數矩陣反解出來Fock矩陣。通常建議用這個方式,最為省事。但是如果使用了大量彌散函數,量子化學程序可能會自動去除一些線性相關基函數,這個時候就沒法用這個做法了,只能用下面的方法
(2)從特定文件里讀取。可以從記錄Fock矩陣的文本文件里讀取,也可以從.47文件里讀取(Gaussian可以直接產生),也可以從ORCA輸出文件里讀取,等等,詳情見Multiwfn手冊附錄7。
啟動Multiwfn,輸入
examples\ethanol_triplet.fch
100
12 //產生雙正交化軌道
2 //雙正交化過程中考慮所有軌道
1 //計算雙正交化軌道的能量,Fock矩陣通過分子軌道的能量和展開系數直接產生
y //根據能量對雙正交化軌道排序
此時產生了biortho.fch和biortho.txt,后者內容如下
...[略]
Orb: 10 S= 1.0000 E(A)= -13.621 O(A)= 1.0 E(B)= -13.450 O(B)= 1.0
Orb: 11 S= 0.9992 E(A)= -13.057 O(A)= 1.0 E(B)= -11.821 O(B)= 1.0
Orb: 12 S= 1.0000 E(A)= -11.918 O(A)= 1.0 E(B)= -11.866 O(B)= 1.0
-------------------------------------------------------------------------------
Orb: 13 S= 1.0000 E(A)= -11.439 O(A)= 1.0 E(B)= -5.806 O(B)= 0.0
Orb: 14 S= 1.0000 E(A)= -0.293 O(A)= 1.0 E(B)= 2.817 O(B)= 0.0
-------------------------------------------------------------------------------
Orb: 15 S= 0.9992 E(A)= 13.876 O(A)= 0.0 E(B)= 15.431 O(B)= 0.0
Orb: 16 S= 1.0000 E(A)= 15.057 O(A)= 0.0 E(B)= 15.305 O(B)= 0.0
Orb: 17 S= 1.0000 E(A)= 18.508 O(A)= 0.0 E(B)= 19.028 O(B)= 0.0
...[略]
由于這回我們要求Multiwfn計算雙正交化軌道的能量,因此這次的biortho.txt里顯示了算出來的軌道能量。由于我們也要求按照能量進行排序,因此可以看到軌道序號順序確實和軌道能量相同了。注意排序的時候是將序號相同的alpha和beta的軌道能量平均值作為依據來排序的。另外,排序是對每一個批次產生的雙正交化軌道分別進行排序的(上面信息中的兩條橫線把所有軌道分割成了三個批次),因此比如第2批次的軌道的能量不一定全都高于第1批次的軌道。
注:常有Multiwfn用戶問為什么他得到的序號相同的alpha和beta雙正交化軌道的形狀看起來非常相似,但能量卻差了非常多。這是因為開殼層體系的alpha和beta電子的分布通常不對稱,而且通常連alpha和beta電子數都往往不同,也因此alpha和beta對應的Fock算符不同。而由于軌道能量是相應自旋的Fock算符求期望得到的,因此哪怕形狀精確相同、序號相同的alpha和beta雙正交化軌道的能量也注定會不同。如果你就是死活非得要求相同序號的alpha和beta能量相同(就跟限制性開殼層RO計算的情況似的),那你姑且把相同序號的alpha和beta軌道能量取平均得了(雖說沒有明確的物理意義),這時的軌道能量相當于軌道波函數相對于alpha和beta電子的平均的Fock算符的期望值。
當前biortho.fch里的“軌道能量”信息是雙正交化軌道的真實能量了。如果我們選擇y載入biortho.fch,用主功能0的Orbital info.選項查看軌道基本信息,會看到下面這些,確實軌道能量和biortho.txt里顯示的相同。
1 E(au/eV): -19.26817 -524.3135 Occ: 1.000000 Typ: A
...[略]
11 E(au/eV): -0.47985 -13.0573 Occ: 1.000000 Typ: A
12 E(au/eV): -0.43799 -11.9184 Occ: 1.000000 Typ: A
13 E(au/eV): -0.42037 -11.4390 Occ: 1.000000 Typ: A
14 E(au/eV): -0.01078 -0.2933 Occ: 1.000000 Typ: A
76 ( 1) E(au/eV): -19.23884 -523.5155 Occ: 1.000000 Typ: B
...[略]
86 ( 11) E(au/eV): -0.43441 -11.8210 Occ: 1.000000 Typ: B
87 ( 12) E(au/eV): -0.43606 -11.8659 Occ: 1.000000 Typ: B
對于beta軌道,上面信息中括號里的序號是從第一條beta軌道開始計的,括號外的是從第一條alpha軌道開始計的。
看一下現在的第13號和第14號alpha軌道。如之前所述,這倆占據軌道幾乎完全描述了當前體系的單電子分布,因為其它的占據的alpha軌道都有與之匹配程度極高(重疊積分接近1)的beta占據軌道故而對自旋密度貢獻基本為0。這倆軌道的圖形和能量如下所示
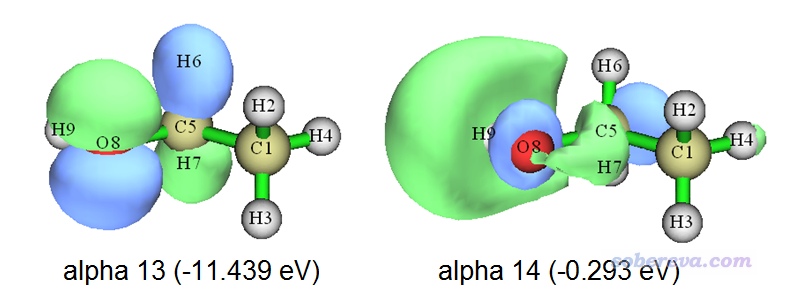
可見由于Multiwfn對軌道做了排序,當前軌道能量和軌道序號是一致的(而上例中沒排序,它倆序號是反著的)。另外,如果你將這倆雙正交化軌道和ethanol_triplet.fch里記錄的MO13(-10.083 eV)、MO14(-0.276 eV)對比的話,會發現軌道形狀相差不太大,能量也相差不算特別大,這也體現Multiwfn給出的雙正交化軌道的能量是合理的。
2.3 丁烷雙自由基
本節用到的fch文件可在此下載:http://www.shanxitv.org/attach/448/C4H8-singlet.rar。如果對雙自由基計算不了解,參看《CASSCF計算雙自由基以及雙自由基特征的計算》(http://www.shanxitv.org/264)和《談談片段組合波函數與自旋極化單重態》(http://www.shanxitv.org/82)。
通過非限制性開殼層以對稱破缺方式算的自旋極化單重態體系,比如雙自由基、反鐵磁性耦合體系,雙正交化也可以做,但是此時不可能使得每個alpha軌道都能與一個beta軌道完美相對應。比如對丁烷雙自由基體系,雙正交化時候的第一部分的輸出是這樣的
Doing biorthogonalization for alpha 1 to 16, Beta 1 to 16
Singular values of orbital overlap matrix:
1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
0.9998 0.9998 0.9998 0.9998 0.9992 0.9990 0.9989 0.3095
可見,此時雙正交化變換的效果是令alpha與beta凡是能匹配的都盡量匹配,這使得前15個軌道都有一一對應關系,重疊積分基本是1.0,但有一個alpha占據軌道就是沒法與beta占據軌道相配對,重疊積分才0.3095。這樣的輸出信息體現在雙正交化之后,我們可以就只依靠16號alpha和beta軌道來討論體系的單電子分布以及雙自由基本質特征。
順帶一提,如果想查看原本alpha和beta分子軌道之間的重疊積分,可以用Multiwfn主功能100的子功能5,具體說明詳見Multiwfn手冊3.100.5節。如果用這個功能里面的選項2輸出對上述雙自由基波函數的alpha MO和序號相同的beta MO之間的重疊積分,結果如下(以下只列出占據軌道部分)
Overlap between the 1th alpha and beta orbitals: 0.036957
Overlap between the 2th alpha and beta orbitals: -0.036727
Overlap between the 3th alpha and beta orbitals: -0.001295
Overlap between the 4th alpha and beta orbitals: 0.001066
Overlap between the 5th alpha and beta orbitals: 0.982456
Overlap between the 6th alpha and beta orbitals: -0.958735
Overlap between the 7th alpha and beta orbitals: 0.858202
Overlap between the 8th alpha and beta orbitals: -0.882210
Overlap between the 9th alpha and beta orbitals: 0.994529
Overlap between the 10th alpha and beta orbitals: -0.990360
Overlap between the 11th alpha and beta orbitals: 0.991034
Overlap between the 12th alpha and beta orbitals: -0.984323
Overlap between the 13th alpha and beta orbitals: 0.991434
Overlap between the 14th alpha and beta orbitals: -0.991413
Overlap between the 15th alpha and beta orbitals: -0.995594
Overlap between the 16th alpha and beta orbitals: 0.294899
可見,如果不做雙正交化,內核軌道部分(MO 1~4)alpha-beta匹配極差,看圖可知主要是因為碰巧定域在了不同原子上,這無所謂。而價層部分,7、8號軌道alpha-beta之間匹配得也不很完美,重疊積分還不到0.9,因此比如討論自旋密度、雙自由基特征時如果簡單忽略它們的影響原理上并不好,而在雙正交化后就僅僅需要關注第16號軌道了。請大家自行用Multiwfn基于本文提供的fch文件觀看以上提及的軌道的圖形。