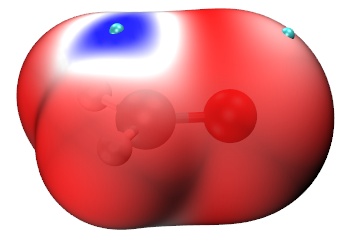
通過電子定域化函數(ELF)、價層電子密度分析討論親核進攻的方向

通過電子定域化函數(ELF)、價層電子密度分析討論親核進攻的方向

First release: 2021-Jul-6 Last update: 2023-Jul-5

1 前言

最近有人在思想家公社QQ群問我，怎么計算下圖的角度，其目的是解釋親核進攻方向問題

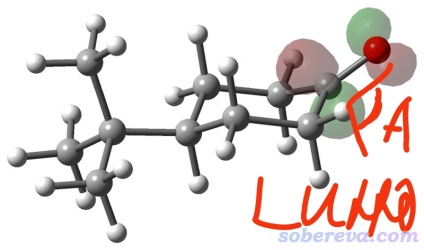
實際上，考察這個問題靠計算這個LUMO的角度不是什么好的做法。本身LUMO的物理意義就不嚴格，其分布特征受計算級別影響較大，而且跟親核反應的關系也不如概念密度泛函理論里面的福井函數f+和雙描述符緊密。

討論親核進攻方向這個問題真正比較好的做法使用Multiwfn做電子定域化函數（ELF）或價層電子密度分析。在筆者的量子波函數分析與Multiwfn程序培訓班（http://www.keinsci.com/workshop/WFN_content.html）里正好專門有一頁ppt和這個問題直接相關：

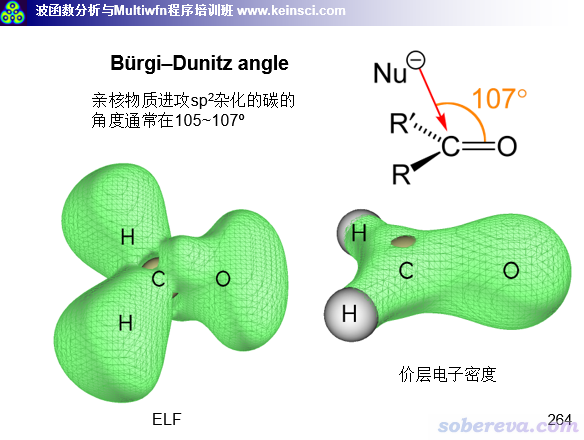
ppt中所示的伯基－丹尼茲角度（Bürgi–Dunitz angle）是親核加成立體電子效應的一個術語，它描述了親核加成反應中親核試劑進攻親電底物過程中的角度和方式。從上面的等值面圖可見，ELF展現出在親核進攻的方向上正好有一塊區域的ELF較小，體現出電子在這里定域性較弱。雖然ELF的大小和電子密度的大小在原理上并沒有直接的正相關性，但ELF在實際中可以表現出價層區域的電子由于形成孤對電子、共價鍵導致的自發凝聚的位置，因此上圖中ELF較小的地方體現了這個碳原子的價層電子相對發散的區域。由于這種地方原子核被價電子遮擋程度最低，明顯最容易被親核進攻。關于ELF更多的知識看《ELF綜述和重要文獻小合集》（http://bbs.keinsci.com/thread-2100-1-1.html）。

筆者在2018年發表的Revealing Molecular Electronic Structure via Analysis of Valence Electron Density（http://www.whxb.pku.edu.cn/EN/10.3866/PKU.WHXB201709252）一文中專門討論了價層電子密度的概念以及在化學問題的實際分析中的應用。價層電子密度是價層區域電子哪里多、哪里少的最簡單直接的衡量。從上圖可以看出，在易于發生親核進攻的方向，碳的價層電子密度明顯小于周圍的區域，因此原子核在這個方向被屏蔽得最少，直接解釋了伯基－丹尼茲角度的本質。

由上可見，在討論親核反應方向問題時，直接考察ELF、價層電子密度就可以，等值面圖用Multiwfn可以非常快捷方便地畫出來。但是，有時候我們需要做進攻夾角大小的討論、在不同類似體系間橫向對比。具體怎么將角度定量化沒有唯一方法，筆者建議用Multiwfn對這兩個函數做拓撲分析尋找恰當的臨界點，之后測量一下它與C=O鍵的夾角，就能進行定量說明了。

下面就給出使用Multiwfn做拓撲分析考察親核進攻角度的具體操作例子。作為例子的分子是甲醛，B3LYP/6-31G*下做幾何優化得到的wfn文件可以在http://www.shanxitv.org/attach/606/H2CO.wfn下載。Multiwfn程序可以在http://www.shanxitv.org/multiwfn免費下載，如果不熟悉此程序的話，務必看《Multiwfn入門tips》（http://www.shanxitv.org/167）和《Multiwfn FAQ》（http://www.shanxitv.org/452）。如果你都不會繪制上面的等值面圖的話，強烈建議看手冊4.5節，有豐富的例子。

筆者之前有一篇博文《使用Multiwfn做拓撲分析以及計算孤對電子角度》（http://www.shanxitv.org/108），其中第3節也介紹了Multiwfn對ELF做拓撲分析，并通過對應孤對電子的ELF極大點計算了孤對電子的角度。建議讀者也仔細看看，和本文有密切聯系。

2 電子定域化函數的拓撲分析

啟動Multiwfn，輸入H2CO.wfn的路徑并載入之，之后輸入
2 //拓撲分析
-11 //切換被分析的函數
9 //ELF
6 //在球形區域內設置一批初猜點
-1 //以每個原子核為中心的球形區域內隨機分布一批初猜點來搜索ELF的臨界點，默認每個原子附近3 Bohr內撒1000個點（注：能找到哪些臨界點和初猜位置有關。此選項每次撒的點的位置是隨機的。選一次-1可能只能找到一部分臨界點，之后再選一次或多次-1可能還能再找到其它的臨界點）
-9 //返回
0 //觀看結果

把窗口界面右側的設置改成下圖的情況，就看到下圖的圖像了

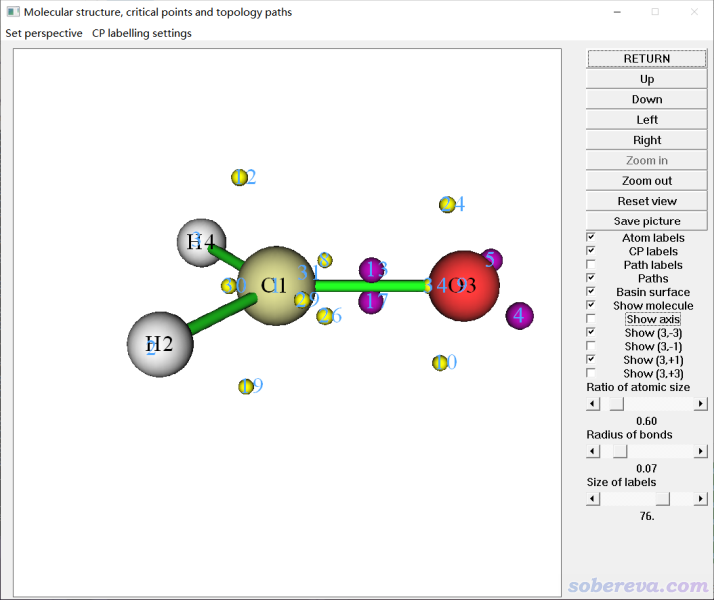
圖中的小球是當前被分析的函數的臨界點（critical point），即函數梯度為0的點，青色的文字是臨界點序號
。黃球是(3,+1)型臨界點，相當于在某個方向是極大點但在與之正交的方向是極小點。紫球是(3,-3)型臨界點，即ELF的極大點。從上圖可見，與親核進攻方向對應的ELF臨界點是12或19號(3,+1)臨界點。接下來我們只需測量一下這個臨界點與C1-O3的夾角即可。

點圖形界面右上角的RETURN按鈕關閉窗口，然后輸入
-9 //測量臨界點和原子間的幾何關系
c12 a1 a3 //c代表臨界點，a代表原子
測量的結果是106.67度。可見和常見的伯基－丹尼茲角度范圍很相符。

值得一提的是，在Multiwfn里可以把臨界點和等值面圖繪制在一起，這樣對臨界點的位置和意義可以理解得更清楚。這里就把ELF等值面圖也給畫出來。輸入以下命令
q //退出測量幾何關系的界面
-10 //返回主菜單
5 //計算格點數據
9 //ELF
2 //中等質量格點
-1 //觀看等值面圖

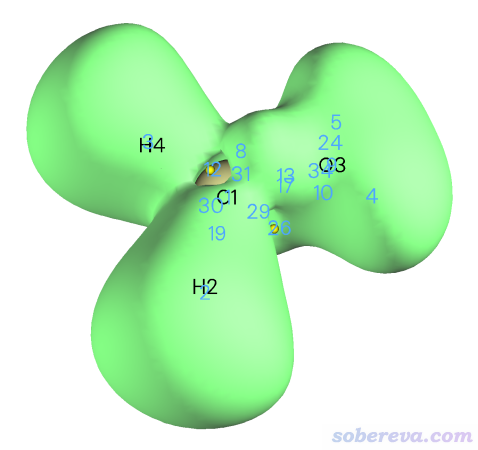
在圖形界面里把Isosurface value改成0.53，此時可以看到下圖。可見確實第12號臨界點就是對應價層ELF很小的那個區域。具體來說，這個位置在碳原子的徑向方向是ELF極大點，而在其它方向是ELF極小點，因此這個位置是ELF的(3,+1)型臨界點。

3 價層電子密度的拓撲分析

下面做H2CO.wfn的價層電子密度的拓撲分析。載入文件后輸入
6 //修改波函數
34 //將內層軌道占據數設為0。之后對電子密度進行分析就相當于對價層電子密度進行分析
-1 //返回
2 //拓撲分析（默認被分析的函數就是電子密度，所以不用改了）
6 //在球形區域內設置一批初猜點
-1 //以每個原子核為中心的球形區域內隨機分布一批初猜點來搜索價層電子密度的臨界點
-9 //返回
0 //觀看結果

恰當設置后，看到下圖。

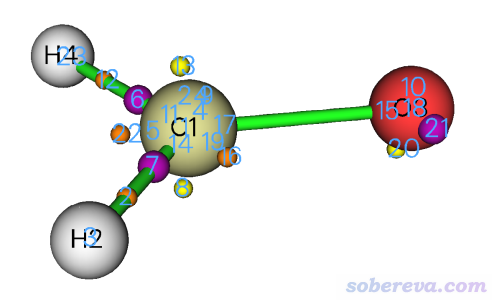
其中第8、13號臨界點對應的是價層區域電子密度最低的位置。點圖形界面右上角RETURN按鈕關閉窗口，然后輸入
-9 //測量臨界點和原子間的幾何關系
c13 a1 a3
測量的結果是95.47度。這個角度和基于ELF臨界點測量的有一定出入，畢竟這兩個函數的本質特征差異很大。由于夾角大于90度，因此還是能一定程度解釋進攻方向性問題的。

之后輸入
q //退出測量幾何關系的界面
-10 //返回主界面
5 //計算格點數據
1 //電子密度
2 //中等質量格點
-1 //觀看等值面圖
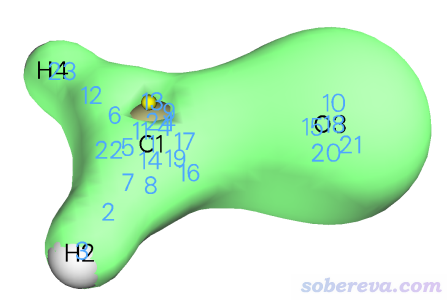
調節顯示方式后得到下圖，可見13號臨界點就是對應的價層電子密度最低的位置。

4 電子密度拉普拉斯函數

最后，再看另一個函數，電子密度拉普拉斯函數，它也能用來解釋親核進攻取向問題。筆者在Revealing Molecular Electronic Structure via Analysis of Valence Electron Density（http://www.whxb.pku.edu.cn/EN/10.3866/PKU.WHXB201709252）一文中對這個函數做了簡要介紹，并且將它、ELF以及價層電子密度三者的共性和差異做了對比討論，很建議大家看看。在很多問題上，這三個函數的分析結論是定性一致的。

電子密度拉普拉斯函數也可以用類似前面的例子通過Multiwfn做拓撲分析。不過比起ELF來說，對電子密度拉普拉斯函數做拓撲分析沒有額外優勢，而且更耗時，而且由于這個函數變化特別劇烈，收斂到臨界點也往往困難得多，因此這里只是繪圖考察一下。

我們先用Multiwfn繪制電子密度拉普拉斯函數的等值面圖。載入H2CO.wfn后依次輸入
5 //計算格點數據
3 //電子密度拉普拉斯函數
3 //高質量格點
-1 //觀看等值面圖

把Isosurface value設為-0.01，取消掉Show both sign復選框前的對鉤，現在看到下圖

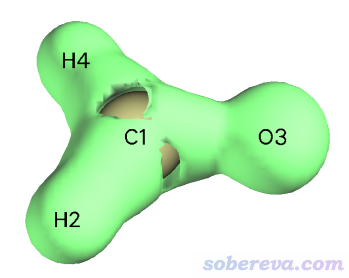
圖中的等值面把電子密度拉普拉斯函數明顯為負的區域展現出來了。這個函數為負的區域體現的是價層電子密度凝聚的區域。由圖可見在碳的上方有一塊空缺，實際上這個區域電子密度拉普拉斯函數為正，體現出電子在這個地方是發散的，顯然容易被親核進攻。

作一個平面圖可以看得更清楚。在主功能0里根據笛卡爾坐標軸可見，如果繪制X=0的YZ平面，就可以正好得到順著C=O鍵鍵軸并垂直于分子的截面圖，電子密度拉普拉斯函數在這個截面上的分布可以更清晰展現親核進攻的角度，下面就繪制一下。回到主菜單，然后輸入
4 //繪制平面圖
3 //電子密度拉普拉斯函數
2 //等值線圖
[按回車用默認格點數]
3 //YZ平面
0 //X=0
馬上圖就彈出來了。輸入以下命令調節一下作圖設置讓效果更好
3 //修改等值線設置
15 //用適合發表文章的設置
1 //保存并返回
-1 //重新繪圖

現在看到下圖

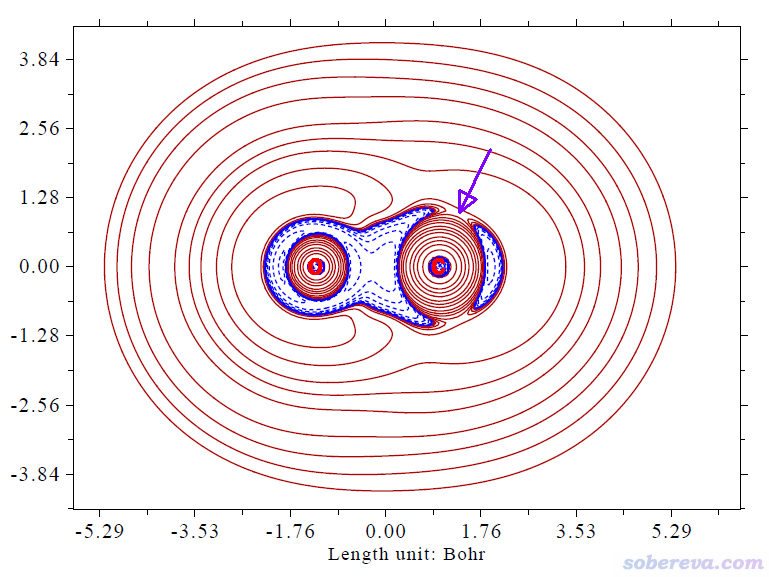
圖中我用紫色箭頭標注了親核進攻最容易發生的朝向。可見電子密度拉普拉斯函數能很好地體現親核進攻的方向性。

5 總結

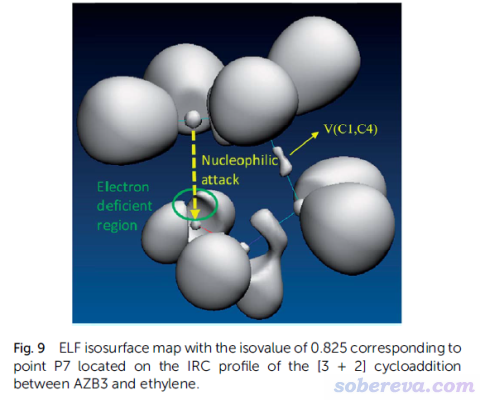
本文介紹了怎么通過對ELF和價層電子密度做拓撲分析來說明親核進攻的角度，還簡單示意了怎么繪制等值面圖對進攻的取向性予以直觀的展現。本文只考慮了一個最簡單的體系H2CO，大家可以將此文涉及的考察方式用于討論其它親核進攻取向的問題，比如SN2反應。下文是筆者參與的一篇3+2環加成反應的研究文章RSC Adv., 5, 62248 (2015) DOI: 10.1039/c5ra08614k里的圖，ELF等值面體現出下方的分子畫綠圈的部位有明顯被親核進攻的傾向性。

本文的方法所給出的親核進攻的角度只是適合用來定性討論、解釋已知事實，不要把角度的數值過度討論，除非是類似物之間的對比，比如考察取代基對進攻角度的影響。想獲得嚴格、準確的進攻角度，還是應當優化出過渡態，然后再進行測量。

補充：使用局部電子附著能討論親核進攻角度

在《使用Multiwfn通過局部電子附著能(LEAE)考察親核反應位點、難易及弱相互作用》（http://www.shanxitv.org/676）中介紹的局部電子附著能（LEAE）也可以用來討論親核進攻方向。按照文中的做法對B3LYP/6-31+G**級別計算的H2CO的波函數繪制的電子密度0.004 a.u.等值面的LEAE著色圖如下所示，色彩刻度從-0.15到0.0 a.u.按照藍-白-紅變化，青色小球是表面LEAE極小點。由此圖的藍色區域可以清楚看出親核進攻發生的方向，結論和前文的方法是一樣的。