談談分子間結合能的構成以及分解分析思想
談談分子間結合能的構成以及分解分析思想
On the components of intermolecular binding energy and idea of decomposition analysis
文/Sobereva@北京科音
First release: 2024-Dec-31 Last update: 2025-Mar-28
在我網上回答大量量子化學的問題的過程中,經常看到有些人搞不清楚對分子間相互作用有貢獻的量之間的關系、不知道怎么將結合能分解成不同部分考察影響結果的內在因素。這使我決定作一張圖,把分子間結合自由能的構成一次性梳理清楚,同時展現我的對分子間結合能的分解分析的思想,如下所示:
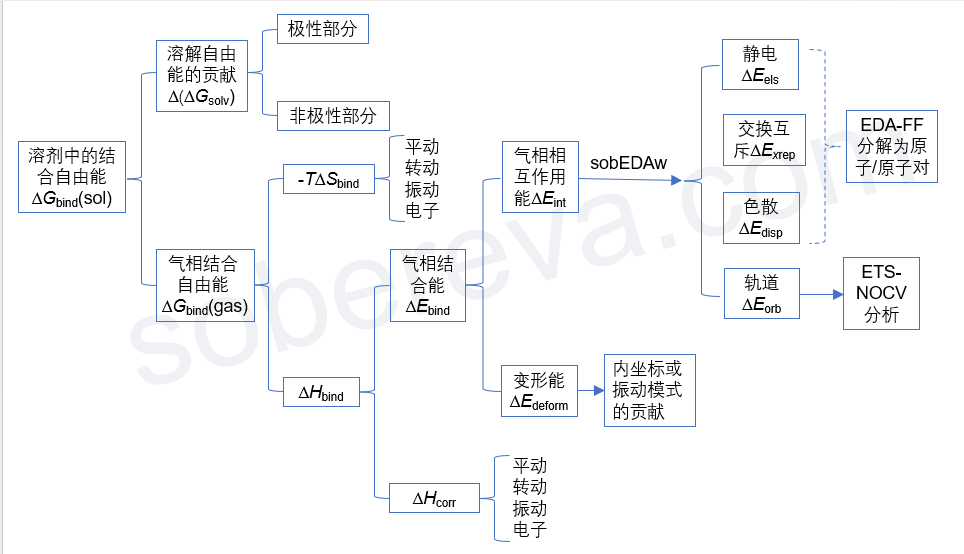
下面我會把圖中各項進行簡要的解釋,便于讀者理解每項是怎么回事、知道怎么計算,務必結合上圖看。上圖的源頭是“溶劑中的結合自由能”,因為這個是包含的成份最多,內涵最復雜的量。本文僅考慮兩個單體分子A、B間結合成為復合物AB的情況。
? 溶劑中的結合自由能ΔG_bind(sol):這是指在溶劑(sol)環境下,兩個分子從各自孤立狀態相互接近并形成二聚體過程中的自由能的總變化。即ΔG_bind(sol) = G_AB(sol) - G_A(sol) - G_B(sol)。如《談談隱式溶劑模型下溶解自由能和體系自由能的計算》(http://www.shanxitv.org/327)所述,溶劑下的體系的自由能G(sol)可以寫為氣相自由能G(gas)和溶解自由能ΔG_solv的加和,因此可以分解成兩個部分:
? 溶解自由能的貢獻Δ(ΔG_solv):這體現溶劑效應對分子間結合產生的影響,即復合物的溶解自由能減去每個分子的溶解自由能。這部分可正可負,為正代表溶劑效應不利于結合,通常出現在兩個單體間以靜電作用為主的情況,即溶劑效應對單體的總穩定化程度比對復合物的穩定化程度更顯著;為負代表溶劑效應有利于分子間結合,例如《全面揭示各種碳環與富勒烯之間獨特的pi-pi相互作用!》(http://www.shanxitv.org/727)所講的情況,溶劑的疏水效應能顯著促進富勒烯和碳環之間的結合。
溶解自由能可分為極性和非極性兩部分,因此討論溶劑效應對分子間結合產生的影響時可以具體討論這兩部分各自的影響是多大。隱式溶劑模型下溶解自由能的標準計算方式在前述的《談談隱式溶劑模型下溶解自由能和體系自由能的計算》里說了,是溶劑模型下的電子能量減去氣相下的電子能量。Gaussian做考慮SMD溶劑模型的單點計算時可以直接給出非極性部分對溶解自由能的貢獻,把溶解自由能減去這部分就是極性部分對溶解自由能的貢獻。復合物的溶解自由能的極性(非極性)貢獻減去每個單體的這部分,就是溶劑效應的極性(非極性)部分對結合自由能的貢獻。
? 氣相結合自由能ΔG_bind(gas):通過G_AB(gas) - G_A(gas) - G_B(gas)得到。氣相下G的計算方式見《使用Shermo結合量子化學程序方便地計算分子的各種熱力學數據》(http://www.shanxitv.org/552)。注意,如果你本身就是研究溶劑環境下的結合,而且溶劑效應對幾何結構的影響不可忽視,那么復合物和單體的opt和freq任務都應當在溶劑模型下做,即計算氣相自由能用的幾何結構是在溶劑模型下優化的,自由能熱校正量也是基于溶劑模型下振動分析信息得到的。
由于G=H-TS,故ΔG_bind = ΔH_bind - TΔS_bind,遂有了下面兩部分。
? ΔH_bind:ΔG_bind(gas)中的焓效應部分,即復合物的焓減去各個單體的焓
? -TΔS_bind:ΔG_bind(gas)中的熵效應部分,即復合物的熵減去各個單體的熵然后乘以-T。由于分子間結合會令熵大幅降低,ΔS_bind為負,因此這部分總是不利于分子間結合,稱為熵罰,而且溫度(T)越大明顯越不利結合。如果分子間無法形成足夠強烈的相互作用令ΔH_bind足夠負,那么它很可能被-TΔS_bind抵消掉導致分子間無法結合。我在北京科音初級量子化學培訓班(http://www.keinsci.com/KEQC)里給了相關計算例子,體現出在氣相標況下,水二聚體在熱力學上是無法自發形成的,但是能在分子間形成兩個顯著的氫鍵的甲酰胺二聚體是能形成的。
溫度對ΔH_bind的影響較小,而對-TΔS_bind影響巨大,因此分子間能否結合極大程度取決于溫度。在《8字形雙環分子對18碳環的獨特吸附行為的量子化學、波函數分析與分子動力學研究》(http://www.shanxitv.org/674)介紹的筆者的文章Phys. Chem. Chem. Phys., 25, 16707 (2023)里通過Shermo程序做了碳環、8字形分子OPP以及二者的復合物的熱力學量相對于溫度的掃描,并進而給出了ΔG_bind、ΔH_bind、-TΔS_bind隨溫度的變化,準確指出了分子間能結合的臨界溫度。前述的《全面揭示各種碳環與富勒烯之間獨特的pi-pi相互作用!》介紹的筆者的Chem. Eur. J., 30, e202402227 (2024)也做了這樣的分析。
如Shermo程序手冊附錄部分所講的熱力學數據計算常識所示,熵是由體系的平動、轉動、振動以及電子(躍遷或簡并)共同貢獻的,Shermo可以分別輸出,而且Shermo還能給出各個振動模式對熵的貢獻。通過這些信息可以深入了解熵的構成,并對各項在復合物和單體之間求差以進一步了解ΔS_bind的內在本質。
由于焓等于電子能量與焓的熱校正量之和,即H = E + H_corr,故ΔH_bind又可以分為以下兩部分:
? 氣相結合能ΔE_bind:即E(AB)-E(A)-E(B),其中E(AB)、E(A)、E(B)分別是AB、A、B的氣相的(即不帶溶劑模型的)電子能量,并且計算用的幾何結構是對它們各自分別優化后的。ΔE_bind體現出在氣相下,A、B從孤立狀態下結合為AB過程中的電子能量的變化。如果你不清楚什么叫電子能量,看《談談該從Gaussian輸出文件中的什么地方讀電子能量》(http://www.shanxitv.org/488)。注意,平時說結合能的時候可以指ΔG_bind也可以指ΔE_bind,只有前者才能體現熱力學上結合的可能性,后者只能用來討論分子間內在的作用強度、結合的驅動力。沒有前提的情況下說結合能的時候習俗上指的是更容易算的ΔE_bind,本文也是這個習俗。
? ΔH_corr:即復合物的H_corr減去各個單體的。這體現出分子間結合過程中熱力學效應對焓變的貢獻。理想氣體近似下H=U+RT,故雙分子結合的情況有ΔH_corr = ΔU_corr - RT,其中ΔU_corr是結合過程中內能的熱校正量的變化。類似于熵,U_corr也是能夠通過Shermo輸出平動、轉動、振動(包括ZPE在內)、電子躍遷的貢獻從而了解ΔU_corr的內在本質的。
ΔE_bind = ΔE_int + ΔE_deform,即氣相結合能可以分解為氣相相互作用能和變形能,下面專門說一下這兩項。
? 氣相相互作用能ΔE_int:即復合物的電子能量減去各個單體的電子能量,計算用的幾何結構都是優化后的復合物結構(單體的結構直接從優化后的復合物結構中摳出來,不再做優化)。
ΔE_int可以通過筆者提出的高效、普適、很流行的sobEDAw方法分解為分子間的靜電相互作用、交換互斥作用、軌道相互作用、色散作用,細節這里就不說了,在《使用sobEDA和sobEDAw方法做非常準確、快速、方便、普適的能量分解分析》(http://www.shanxitv.org/685)里有極其詳細的說明。
其中,軌道相互作用部分還可以通過《使用Multiwfn通過ETS-NOCV方法深入分析片段間的軌道相互作用》(http://www.shanxitv.org/609)介紹的ETS-NOCV方法進一步將其本質討論得很清楚。
《使用Multiwfn做基于分子力場的能量分解分析》(http://www.shanxitv.org/442)介紹的筆者提出的EDA-FF能量分解方法可以將靜電、交換互斥、色散作用都分解為原子對之間的貢獻和原子的貢獻,從而能對它們的本質和來源有確切的了解。但注意EDA-FF得到的這三項和sobEDAw給出的有所不同,畢竟計算原理相差很大,前者基于力場計算,而后者基于色散校正的DFT理論計算。另外,色散部分還可以按《使用Multiwfn圖形化展現原子對色散能的貢獻以及色散密度》(http://www.shanxitv.org/705)介紹的方式深入地分析。
? 變形能ΔE_deform:在分子形成復合物的整個過程中,單體分子會從孤立狀態的結構(單獨做優化得到的勢能面極小點結構)變成它在復合物中的結構,這會造成分子的能量增加,稱為分子的變形能,可以很容易地手動自行計算。結合能中的變形能ΔE_deform是各個分子的變形能的總和,顯然可以討論各個分子各自的貢獻。分子的柔性越強、分子間相互作用越強,其變形能傾向于越大。分子變形過程對應各個內坐標的變化,因此變形能可以分解為不同內坐標的貢獻來具體討論。還可以用類似《使用Dushin分解重組能和計算Huang-Rhys因子》(http://www.shanxitv.org/330)中提到的分解重組能的方式,把變形能分解為極小點結構下的不同振動模式的貢獻來討論。
以上算是把分子間結合自由能里的所有構成做了詳細的拆分介紹。把這些原理搞清楚了,在討論分子間結合強弱的時候就容易分析得比較深入透徹。如果你由于缺乏基本常識,看了上文之后還是不會計算里面的項,推薦通過北京科音初級量子化學培訓班(http://www.keinsci.com/KEQC)系統性學習一遍,自然就明白了。
順帶一提,有時有人問什么叫吸附能(adsorption energy)、和結合能的區別是什么,這里說一下。吸附能本質就是結合能,只不過前者是后者在特定語境下的稱呼,適用于描述一個相對較小的東西結合到一個相對較大的東西上的情況。比如《8字形雙環分子對18碳環的獨特吸附行為的量子化學、波函數分析與分子動力學研究》(http://www.shanxitv.org/674)一文的情況,18碳環比OPP雙環分子小得多,前者是客體,后者是主體,所以討論二者的結合時可以用吸附能這個詞,叫結合能也完全正確。而一個小分子吸附到一個固體表面上或者多孔材料中的能量變化,這時候就必須用吸附能這個詞描述了。雖然此時說結合能也沒本質錯誤,但由于固體表面/多孔材料比小分子大太多了,所以叫結合能太別扭、不符合習俗用詞。和結合能完全一樣,吸附能也可以用電子能量求差計算也可以用熱力學量求差計算,如果用自由能求差計算,建議明確叫吸附自由能以避免有誤解。
還有個詞叫復合能(complexation energy),和結合能完全是一碼事。注意如《談談BSSE校正與Gaussian對它的處理》(http://www.shanxitv.org/46)所說,Gaussian程序做counterpoise任務的時候會輸出complexation energy,但這是沒有考慮單體的變形能的,因此實質上是當前結構下的相互作用能。讀者應當根據語境恰當區分、變通這些詞。