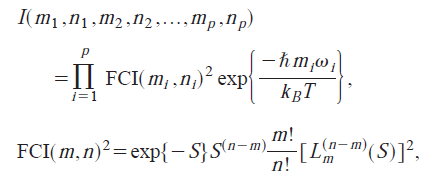使用Dushin分解重組能和計算Huang-Rhys因子
經常有做電荷轉移的人問怎么用Dushin程序、怎么算重組能、怎么把重組能分解為各個振動模式的貢獻、怎么計算Huang-Rhys因子,本文就結合實例專門說說這些問題。
1 重組能(reorganization energy)的計算
重組能是基于Marcus理論計算電子轉移速率的關鍵的量,具體分為內重組能和外重組能,前者衡量電子得/失后(或更廣義來說,電子態改變后)因幾何結構的弛豫導致的體系能量變化,外重組能則對應將周圍環境分子重新極化所花費的能量。外重組能不好算,溶液下往往經驗性地取0.2~0.6eV,晶體下則會小一個多數量級,也有些文章專門討論怎么算,如JPCL,1,941(2010)、JACS,130,12377(2008),本文我們只說內部重組能。看這張示意圖,有中性和帶電狀態兩個勢能面
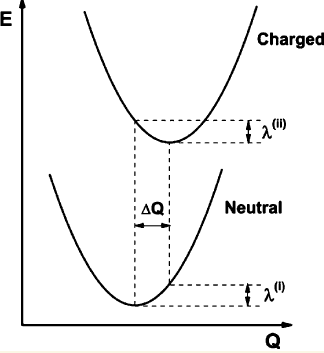
圖中重組能有兩部分,λ(I)和λ(II)。做Marcus理論計算時說的重組能是指二者絕對值之和。注:重組能的計算方式和定義可能令一些人混淆,可參考http://bbs.keinsci.com/thread-35003-1-1.html回帖里的討論。
具體來說,如果charged態是帶+1電荷的情況,算出來的重組能用λ+表示,也稱空穴重組能λh。如果charged態是帶-1電荷,算出來的重組能用λ-表示,也稱電子重組能λe。
根據上面的示意圖,很容易知道怎么計算λh和λe。例如計算λh,對應的示意圖:
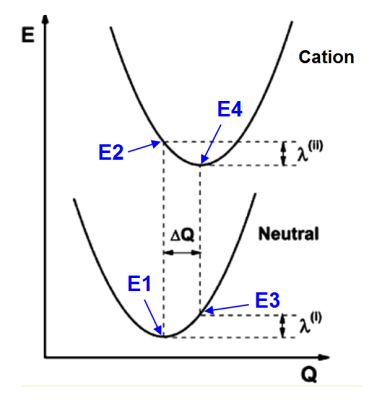
需要以下步驟
(a) 優化中性狀態結構
(b) 在(a)的結構下算中性狀態的能量E1
(c) 在(a)的結構下算陽離子狀態的能量E2
(d) 優化陽離子狀態結構
(e) 在(d)的結構下算中性狀態的能量E3
(f) 在(d)的結構下算陽離子狀態的能量E4
重組能為
λ(I)=|E3-E1|
λ(II)=|E2-E4|
λh= λ(I)+λ(II)
類似地,我們可以算電子態改變過程的重組能。本文我們實際算一個例子,考察吡啶的基態單重態S0和第一三重態激發態T1之間的兩種重組能λ(I)和λ(II),示意圖如下:
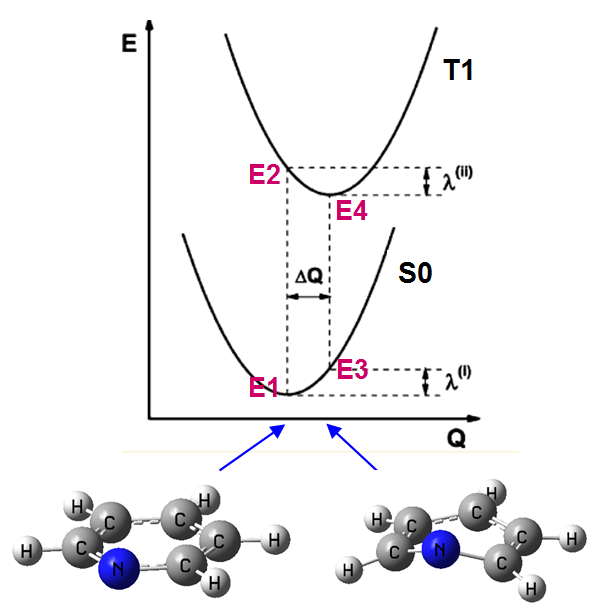
通常做單點計算比幾何優化用的級別要高,但為了省事,此例優化和單點計算都用B3LYP/def2SVP在G09 D.01下做。實際上,也只有幾何優化和單點都在同一級別時算出的重組能和后文提到的用dushin做重組能分解的結果才有可比性。算出來的圖上四個點的能量:
E1=-248.1053119 Hartree
E2=-247.9505667 Hartree
E3=-248.0570726 Hartree
E4=-247.9706883 Hartree
重組能為
λ(I)=E3-E1=30.27 kcal/mol
λ(II)=E2-E4=12.63 kcal/mol
可見,從S0平衡結構垂直躍遷到T1后,結構弛豫對應的重組能為12.63 kcal/mol,這個值比從T1垂直返回S0之后結構弛豫對應的重組能30.27 kcal/mol小很多。這也暗示了,在S0-T1極小點結構之間的方向上,S0極小點處的勢能面曲率大于T1極小點處的,因為以相同方式位移,S0態能量變化λ(I)比T1態能量變化λ(II)大得多。
2 重組能的分解
對于上面吡啶的例子,在S0極小點結構下做freq任務,可以得到S0下的3N-6個正則坐標。S0和T1兩個極小點之間的位移ΔQ可以分解為這些正則坐標的貢獻,第i個模式的貢獻記為ΔQ_i。諧振勢公式是E=(1/2)*k*x^2,基于這個公式,我們也可以將λ(I)分解為各個正則模式的貢獻,即λ_i=(1/2)*k_i*(ΔQ_i)^2,這里k_i代表相應振動模式的力常數。當然了,諧振模型終究只是對實際勢能面的近似,所以∑λ_i并不精確等于λ(I),但能定性相符。類似地,在T1極小點結構下做freq得到3N-6個正則坐標后,也可以得到它們對ΔQ和λ(II)的貢獻。S0和T1極小點下分別得到的3N-6個正則坐標是不同的,彼此間是線性變換關系,這個關系也叫Duschinsky旋轉或者稱Duschinsky混合效應,可表達為Q''=J*Q'+ΔQ,這里Q'和Q''分別代表兩個電子態極小點下的正則模式,J稱為Duschinsky矩陣,記錄了Q'與Q''間線性變換的組合系數。如果兩個態極小點下振動模式完全一致,則J是單位矩陣,說明沒有混合;J偏離單位矩陣越大說明混合越強烈。
提醒一下,對重組能分解時候都是基于末態極小點結構的正則模式來做分解,所以分解λ(I)要用S0極小點處的正則模式,分解λ(II)要用T1極小點處的正則模式。而不能用比如T1極小點處的正則模式分解λ(I),因為原理上說不通。
做重組能的分解和計算Duschinsky矩陣并不復雜,也有現成的程序可以做,下面介紹的Dushin就是其一。
3 Dushin程序的使用
Dushin程序由Reimers開發的,關于程序的一些原理細節可以看JCP,115,9103(2001),引用Dushin程序也應當引這篇文章。Dushin程序源代碼包可以在這里下載:http://bbs.keinsci.com/forum.php?mod=viewthread&tid=319。Dushin程序有自帶的說明文檔README,但寫得比較抽象,這里用人話說一下:3.1 編譯方法
Dushin是Fortran寫的,機子里得有Fortran編譯器才能編譯,Dushin默認的是ifort編譯器(gfortran應該也行,我沒試)。在Linux下編譯的過程是:下載后解壓,把compile里的ifort -g plot-modes.for subs.o recalc-freq.o proj0freq.o bmatred.o ddiag.o dmpower.o dmatinv.o -o ~/bin/plot-modes這一行前頭加上#給注釋掉,因為壓縮包里并沒有帶plot-modes.for文件,這個本身也用不上。然后執行./compile,就會調用ifort進行編譯,編譯好的可執行文件會產生在用戶主目錄的bin目錄下面,包括dushin、displace和compare-geom三個文件。然后可以在控制臺直接輸入dushin看是否能啟動,如果不能則需要把這個bin目錄添加到$PATH環境變量里。
為了便于那些不會編譯或不會Linux的人使用,筆者編譯了一份Windows版,下載鏈接:/usr/uploads/file/20160531/20160531072934_58293.rar。ifort編譯好的Linux版可以在這里下載:/usr/uploads/file/20160531/20160531072918_96449.zip。
3.2 使用方法
Linux版:進入含有輸入文件的目錄,直接輸入dushin即可運行。Windows版:把輸入文件拷入dushin程序目錄下,雙擊dushin.exe即可運行。運行完畢后會自動關閉窗口,如果不想讓窗口自動關閉就自己進DOS然后輸入dushin來執行(在dushin.exe所在目錄窗口下按住shift點右鍵選“在此處打開命令行窗口”)。
3.3 輸入文件
dushin的運行需要提供原子坐標、量化程序計算出的Hessian等信息,宣稱支持許多量化程序,本文只考慮Gaussian的情況。G94、G98、G03、G09的輸出文件dushin都支持。dushin.dat是dushin程序的主輸入文件,dushin啟動時就會載入當前目錄下的dushin.dat。下面是輸入文件的例子,詳細的參數介紹見README:
1 2
.
2 1 'S0 freq' 'S0_freq.out'
0 1 'T1 freq' 'T1_freq.out'
第一行第一項設定使用什么坐標進行分析,一般設1就行;第二項設定怎么匹配多個輸入文件里的原子順序,一般設2就行。
第二行是指定輸入文件所在目錄,如果就放在了當前目錄下就寫.就行。
第三行是空行。
第四行開始定義輸入文件。第一項是參考類型,對于第一個文件此項必須設2,之后的文件如果此項是1,代表Duschinsky矩陣是相對于第一個文件計算的,如果是0,代表是對后一個參考類型為1或2的分子計算的。第二項就設1就行了,第三項是這個文件的標簽可以隨意設,第四項是Gaussian freq任務輸出文件名。
一般來說,寫dushin.dat的時候就把上面這個例子里面的標簽名、文件名改一下就行,其它不用管。
上面dushin.dat中S0_freq.out、T1_freq.out是Gaussian的freq任務的輸出文件,都放在當前目錄下。計算時用的關鍵詞是#P freq b3lyp/def2svp,注意必須用#P,而且P必須大寫,否則dushin無法正確識別其中的信息。算完后把.chk用formchk轉換為同名的.fch文件,也放在當前目錄下。(對于Linux版,后綴用默認的.log和.fchk也可以被dushin識別)
注意如果用的是Windows版Gaussian,一定要手動在輸出文件最開頭插入這么一行: Entering Gaussian System, Link 0=g09,否則dushin無法識別文件。
3.4 輸出文件
dushin啟動后會在屏幕上會輸出大量信息,其中大部分都是用于調試的,用戶不用管。程序會在當前目錄產生一大堆輸出文件,主要有用的就這兩個:dushin.out:包含主要輸出信息的文件。其中Dushinsky matrix, ncs 2 in terms of ncs 1下面輸出的是第二個輸入文件的正則坐標(normal coordinates, ncs)是怎么由第一個輸入文件的正則坐標組合而成的,包括組合系數和貢獻百分比,只有貢獻較大的會被輸出。下面還會輸出Dushinsky matrix, ncs 1 in terms of ncs 2,是描述第一個輸入文件的正則坐標怎么由第二個輸入文件的正則坐標組合而成的。再往下是Displacement: in terms of nc of 1 THEN of nc of 2,前幾列是把位移和重組能按照第一個輸入文件中的正則模式分解的結果,后幾列是按照第二個輸入文件的正則模式分解的結果。Q是指位移在此正則坐標上的分量,lam是每個正則模式對重組能的貢獻量λ_i(cm^-1)。末尾total reorg energy (cm**-1, kcal/mol)就是∑λ_i,前兩個值單位是cm^-1,分別是第一個和第二個輸入文件的正則坐標對重組能貢獻的加和,后兩個值只不過是把單位換成了kcal/mol。
supplem.dat:包含了被計算的體系的正則坐標、頻率,Duschinsky矩陣,各正則模式對位移和重組能的貢獻(eV)。其實和dushin.out差不多,只不過輸出格式、單位變了變。
4 實例:對吡啶S0-T1的重組能進行分解
我們在B3LYP/def2SVP級別下將電荷和自旋多重度設為0 1和0 3來分別優化吡啶的S0和T1態結構,之后用得到的結構分別做freq計算,得到Gaussian輸出文件和fch文件。然后按3.3節的介紹恰當地寫個dushin.dat文件。之后把dushin.dat、兩個Gaussian輸出文件和兩個.fch文件都放在當前目錄下,啟動dushin,由于體系小計算量很低,馬上就運行完畢。本例用到的dushin輸入輸出文件在這里都提供了,請自行查看:/usr/uploads/file/20160531/20160531072953_56861.rar。輸出文件很容易理解。比如我們這里考察對λ(I)的分解,前面提到過λ(I)是T1垂直返回S0態后因結構弛豫造成的能量變化,末態是S0平衡結構,所以要看對S0正則模式的分解結果。從輸出文件中看到S0的3N-6個正則模式中對重組能貢獻量最大的兩個模式是427和721 cm^-1,貢獻值分別高達3607.6和2456.7 cm^-1,對位移貢獻分別達到4.112和2.610埃,對應的輸出信息為:
8 B1 freq= 427. Q= 4.112 lam= 3607.6 A" freq= 342. Q= 0.000 lam= 0.0
11 B1 freq= 721. Q= 2.610 lam= 2456.7 A' freq= 592. Q= 2.058 lam= 1252.4
為什么這兩個模式貢獻會這么大,用gview看一下振動矢量就知道了,如下所示
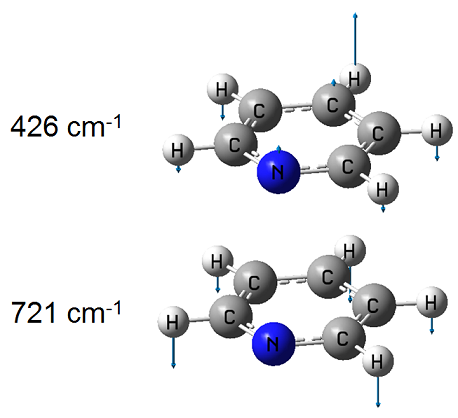
在本文前面的圖片我們看到過,吡啶T1極小點結構相對于S0極小點結構,氮原子往上翹了很多,而周圍的氫原子則下移了許多,導致分子就像是沿著中間稍微對折了一下,而從上面的振動矢量可見,按照這樣方式振動,正是會導致分子以這種方式發生扭曲,所以這兩個振動模式對重組能和位移的貢獻都很大。此分子的386 cm^-1的振動模式也是偏離平面的扭曲模式,但從振動模式上明顯會發現它并不會對S0-T1間結構變化產生任何貢獻,所以對重組能的貢獻也為0。
從輸出文件中的Duschinsky矩陣中我們可以了解S0極小點和T1極小點下正則模式之間的聯系。比如有這么一行輸出:
8 B1 427. 0.8697 75.6 100.0 7 A' 289.
意思是S0極小點下427 cm^-1這個模式有75.6%都是由T1極小點下289 cm^-1那個模式貢獻的,而100.0是代表T1的所有正則模式對S0這個模式的貢獻和是100%,程序為了避免信息量太大就沒輸出那些貢獻很小的T1正則模式。我們來看一下T1這個289 cm^-1模式的振動矢量
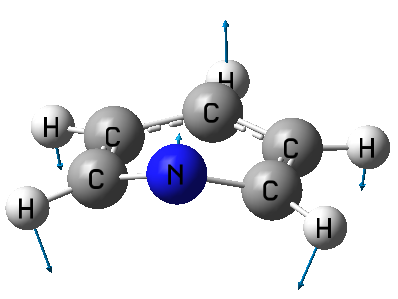
可見,這個模式的振動矢量和前面S0的427 cm^-1的振動矢量非常相似,這也解釋了為什么貢獻值能高達75.6%。
輸出文件末尾顯示S0極小點的各個正則模式對λ(I)以及T1極小點的各個正則模式對λ(II)的貢獻總和分別為32.87和18.23 kcal/mol,這和我們第一節直接按照定義算出來的值30.27和12.63 kcal/mol有一定偏差,但差異還算是可以接受范圍。
自行整理一下數據格式,就可以在Origin等程序里繪制不同頻率的振動模式對重組能的貢獻,使貢獻量一目了然,這種圖經常出現在文獻中。下圖是S0振動模式對λ(I)的貢獻圖
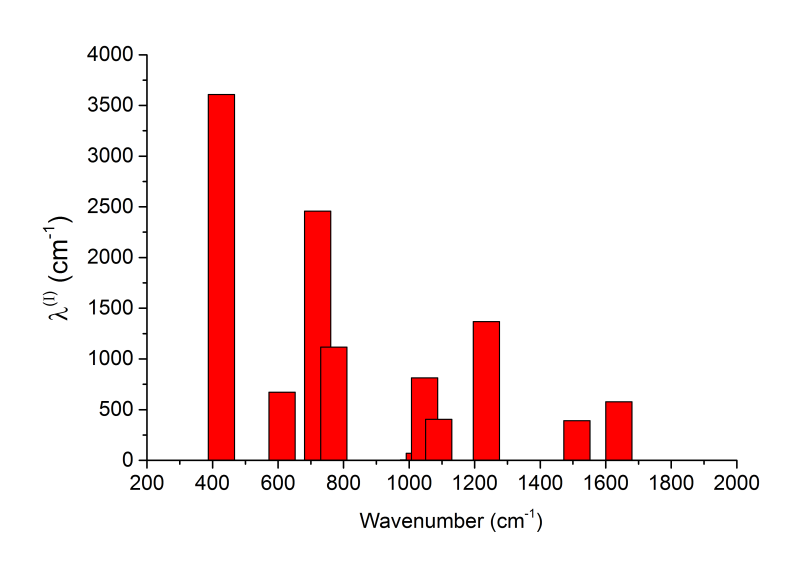
順帶一提,本例的dushin.dat里的輸入文件部分是這么寫的,
2 1 'S0 freq' 'S0_freq.out'
0 1 'T1 freq' 'T1_freq.out'
如果調換次序寫成
2 1 'T1 freq' 'T1_freq.out'
0 1 'S0 freq' 'S0_freq.out'
實際上結果還是一樣,只不過輸出的順序改了一下而已。所以寫的次序無所謂。
5 計算Huang-Rhys因子
Dushin程序并不直接輸出Huang-Rhys因子,自己簡單算一下即可。第i個振動模式對應的Huang-Rhys因子為S_i=λ_i/(h*ν_i),這個量是無量綱的。計算時應先把振動模式對重組能的貢獻λ_i轉換為以J為單位,振動頻率ν_i轉換為以s^-1為單位。比如S0的427 cm^-1模式的λ_i=3607.6 cm^-1,它對應的Huang-Rhys因子即為3607.6/219474.6363*2625500/6.02214179E23 / (427*2.99792458E10*6.6260696E-34)=8.45。這里分子部分先從cm^-1轉為Hartree再轉為J/mol再轉為J。順帶一提,利用Huang-Rhys因子,可以計算振動態躍遷對應的Franck Condon因子,結合振動能級的改變量,做Lorentzian展寬,就可以獲得振動分辨的電子光譜。在JCP,120,7490(2004)當中的式8給出了諧振模型下計算相對強度值的具體公式,是同時考慮p個正則模式的情況: