使用Multiwfn計算分子和晶體中孔洞的直徑
使用Multiwfn計算分子和晶體中孔洞的直徑
文/Sobereva@北京科音 2022-Jun-30
0 前言
化學研究中經常涉及到孔洞尺寸的問題,這和分子吸附、化學物質分離、分子識別等很多問題有關。Multiwfn有展現化學體系孔洞并計算其體積的功能,見《使用Multiwfn圖形化展示分子動力學模擬體系中的孔洞、自由區域》《http://www.shanxitv.org/539)和《使用Multiwfn可視化分子孔洞并計算孔洞體積》(http://www.shanxitv.org/408)。在很多研究中,都利用孔洞的直徑這個特別簡單的參數來說明孔洞的尺寸大小,這可以用于討論多孔物質的吸附分子能力等問題。如果結合《談談分子半徑的計算和分子形狀的描述》(http://www.shanxitv.org/190)和《使用Multiwfn計算分子的動力學直徑》(http://www.shanxitv.org/503)介紹的分子半徑/直徑,還可以討論某些分子是否能夠穿越孔洞、是否有可能結合到孔洞里。
有些情況計算孔洞的直徑比較簡單,比如富勒烯的內部直徑,可以直接測量穿過球心彼此在對面的兩個碳原子的距離,再減去兩個碳原子的范德華半徑即可。但有很多情況孔洞形狀是不規矩的,或者看似規矩,卻找不到合適的可借助的原子用于計算孔洞直徑。為了令孔洞直徑的計算盡可能準確且方便,筆者在Multiwfn程序中加入了計算孔洞直徑的功能,將在下文進行介紹,讀者會發現使用特別容易和靈活,而且借助VMD程序還能通過繪制圓球很清楚地可視化孔洞。
讀者務必使用2022-Jun-25及以后更新的Multiwfn程序,否則沒有本文介紹的功能。Multiwfn可以在主頁http://www.shanxitv.org/multiwfn免費下載,不了解著建議參看《Multiwfn FAQ》(http://www.shanxitv.org/452)和《Multiwfn入門tips》(http://www.shanxitv.org/167)。使用本文介紹的功能時請讀者按照程序要求恰當引用Multiwfn原文。
1 原理
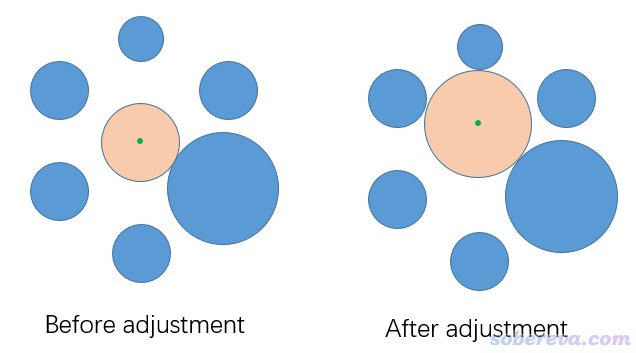
Multiwfn的計算孔洞半徑或直徑的思想很簡單。首先在整個體系中選擇圍繞孔洞出現的一批原子,然后再設一個球心(通常可以用那批原子的幾何中心),并計算它與那批原子的范德華球表面相接觸的半徑,如下圖左側橙色圓球所示,綠點是球的中心。多數情況不能直接用這個半徑當做孔洞的半徑,因為如果恰當調節球心位置,球的半徑還可以變得更大,從而更真實地描述孔洞實際半徑。Multiwfn會通過最陡上升法反復迭代調節球心位置使得球的半徑能夠盡可能變大。當球心位置收斂時(位移小于0.01埃),球的直徑就是孔洞的直徑了。此算法要求每一步的球心位置最大變化不超過0.3埃,即所謂的置信半徑。
用上述的方法確定孔洞直徑,最終結果和初始的球心位置有關。根據算法原理很容易理解,如果體系有多個孔洞,哪怕孔洞間甚至有一定交疊,只要令一開始的球心位置處在特定孔洞區域內,那么最終Multiwfn給出的就是那個孔洞的直徑。
計算的孔洞直徑和原子范德華半徑的選用顯然存在直接聯系,Multiwfn用的是最常用的Bondi范德華半徑,見J. Phys. Chem., 68, 441 (1964)。
這個功能雖然名義上是計算孔洞半徑/直徑,但也完全可以計算環狀體系的內徑,但應當結合實際情況決定是否有必要讓Multiwfn調節球心位置,以及如果調節的話,允許往哪個方向調節。Multiwfn中可以要求不做調節,或者只往X或Y或Z方向,或者只在XY或XZ或YZ平面上調節。例如有個環狀體系基本處在XY平面上,你想得到它的內徑,那就應當只允許在XY平面上調節球心位置,因為如果一旦允許在Z方向調節的話,由于每當球心Z坐標增加或減小時球的半徑就可能變大(視體系結構特征而定),因此球就會逐漸跑到Z無窮大或無窮小的地方去。如果你要計算的環不平行于某個笛卡爾平面,也可以先用Multiwfn的幾何變換功能讓這部分平行于某個笛卡爾平面,然后再計算孔洞,具體看《Multiwfn中非常實用的幾何操作和坐標變換功能介紹》(http://www.shanxitv.org/610)里面的相應功能的介紹。
2 使用
使用Multiwfn的這個功能可以用任意含有幾何信息的格式作為輸入文件,如pdb、xyz、fch、gjf、cif、mol2、mwfn等等,詳見《詳談Multiwfn支持的輸入文件類型、產生方法以及相互轉換》(http://www.shanxitv.org/379)。此功能明確支持周期性體系。
啟動Multiwfn,載入輸入文件,進入主功能100的子功能21后,再輸入cav即可進入此功能。也可以直接在Multiwfn的主界面直接輸入cav快捷進入。之后需要輸入一批用來檢測接觸從而確定圓球半徑的原子的序號,然后再設置球心的初始位置,以及選擇對球心調節的方式。通常結果迅速就會計算出來。
Multiwfn在給出孔洞半徑和直徑后,還會輸出在VMD程序里繪制圓球的命令。VMD是十分流行的可視化程序,可以在http://www.ks.uiuc.edu/Research/vmd/免費下載。將pdb、xyz等VMD支持的結構文件載入VMD后,再把Multiwfn在窗口里顯示的VMD作圖命令復制到VMD的文本窗口執行,就可以看到一個透明的圓球直觀地展現了孔洞。如果你不知道怎么從Multiwfn的文本窗口中復制出來文本信息,看Multiwfn手冊5.4節的說明。
讀者也可以參考《詳談Multiwfn的命令行方式運行和批量運行的方法》(http://www.shanxitv.org/612)里的做法,寫腳本批量調用Multiwfn進行計算。對于分子動力學軌跡,還可以通過腳本讓Multiwfn計算每一幀的孔洞大小,從而了解孔洞尺寸隨時間的變化情況。
3 實例
下面通過一些例子演示使用Multiwfn對各種體系計算孔洞直徑。用到的文件可以在http://www.shanxitv.org/attach/643/file.zip里得到。
3.1 例1:計算開口富勒烯衍生物的富勒烯部分的孔洞直徑
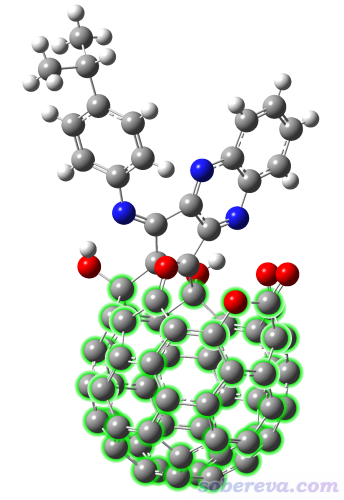
Org. Chem. Front., 9, 320 (2022)中報道了一些開口富勒烯衍生物,本例要考察的分子的晶體結構如下所示,將要對綠色所示的富勒烯部分計算其孔洞直徑。本例就不再對其結構做優化了,其結構文件是本文文件包里的open_fullerene.pdb。提示:在GaussView里,按住r鍵拖動劃框將這些原子選為黃色,然后在Tools - Atom selection里就能快速得到這部分的原子序號,為1,12-20,23-67,101。
啟動Multiwfn,然后輸入
open_fullerene.pdb //輸入實際路徑
cav //進入孔洞直徑計算功能
1,12-20,23-67,101 //將包圍孔洞的那些原子用于判斷接觸以確定球的半徑
1 //使用上面輸入的那些原子的幾何中心作為球心初始位置
1 //允許球心位置在各個方向自發調節
瞬間就算完了,從屏幕上看到以下信息
X/Y/Z of initial geometry center are 3.901518 3.594304 11.835946 Angstrom
Initial sphere radius is 1.677086 Angstrom
Step 1
Current coordinate: 3.901518 3.594304 11.835946 Angstrom
Gradient: 0.100734 -0.067365 0.157089 Norm 0.198399
Displacement: 0.026653 -0.017824 0.041564 Norm 0.052494 Angstrom
Goal: displacement norm < 0.01000000 Angstrom
Not converged, new coordinate: 3.928171 3.576480 11.877510 Angstrom
Sphere radius at new coordinate: 1.690599 Angstrom
...略
Step 5
Current coordinate: 3.939857 3.615266 11.899052 Angstrom
Gradient: 0.009072 0.022419 0.013652 Norm 0.027772
Displacement: 0.002400 0.005932 0.003612 Norm 0.007348 Angstrom
Goal: displacement norm < 0.01000000 Angstrom
Converged after 5 iterations
Final X/Y/Z of sphere center: 3.942257 3.621198 11.902664 Angstrom
Radius is 1.707257 Angstrom
Diameter is 3.414514 Angstrom
Volume is 20.844205 Angstrom^3
從以上信息可見,初始球心位置是3.901518 3.594304 11.835946 埃,對應于我們選中的那批原子的幾何中心,并且球的初始半徑是1.677埃。之后程序開始迭代,在第5步時位移小于了0.01埃,宣告收斂。最終球心位置是3.942257 3.621198 11.902664 埃,半徑是1.707埃,比自發調節之前更大了。最終的孔洞直徑是半徑的兩倍,即3.414埃,若將孔洞近似為理想圓球,體積是20.844埃^3。然后,屏幕上顯示了以下內容,這是在VMD里繪制圓球展示孔洞要用的命令。
color Display Background white
draw material Transparent
draw color yellow
draw sphere { 3.942 3.621 11.903 } radius 1.707 resolution 100
啟動VMD,將open_fullerene.pdb拖入VMD Main窗口載入,在Graphics - Representation里將Drawing Method設為CPK,再把Sphere Scale設小到0.7。然后將以上四行命令粘貼到VMD文本窗口里并按回車,就能看到下圖
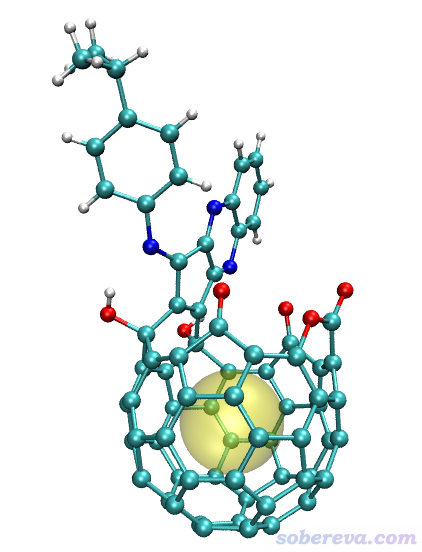
可見上圖中黃色圓球將孔洞很好地表現了出來。
3.2 例2:計算分叉碳納米籠的直徑
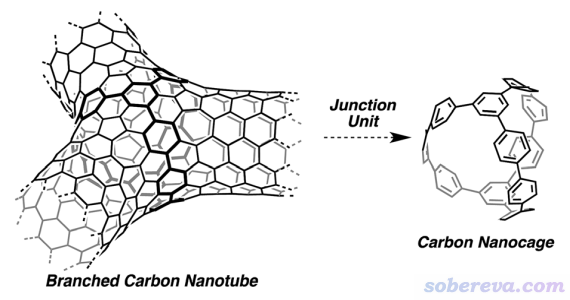
在Chem. Sci., 4, 84 (2013)中有人合成了下圖右側所示的三分叉碳納米籠,相當于三分叉碳納米管的連接部分。此例我們計算這個納米籠的直徑。此論文補充材料直接給的坐標對應的結構文件是本文文件包里的carbon_nanocage.xyz。
啟動Multiwfn,然后輸入
carbon_nanocage.xyz
cav
[按回車] //把所有碳原子用于判斷接觸以確定球的半徑
1 //使用上面輸入的那些原子的幾何中心作為球心初始位置,當前等同于整個分子的幾何中心
1 //允許球心位置在各個方向自發調節
得到直徑為14.255埃。按上一節的步驟,用Multiwfn給出的命令在VMD里作圖結果如下,非常清楚
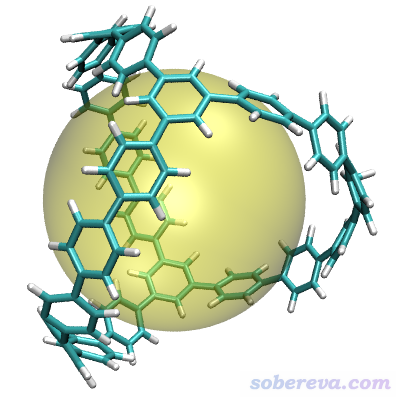
3.3 例3:計算18碳環衍生物的孔洞直徑
筆者對18碳環(cyclo[18]carbon)及其衍生物做過廣泛的研究,匯總見http://www.shanxitv.org/carbon_ring.html。其中,對于結合著羰基的18碳環C18-(CO)n的研究在《深入揭示18碳環的重要衍生物C18-(CO)n的電子結構和光學特性》(http://www.shanxitv.org/640)中還做了專門的介紹。此研究中涉及到一個C18-(CO)4同時脫兩個一氧化碳變成C18-(CO)2的過程,其過渡態如下所示。從坐標軸可見,整個體系基本是在XY平面上
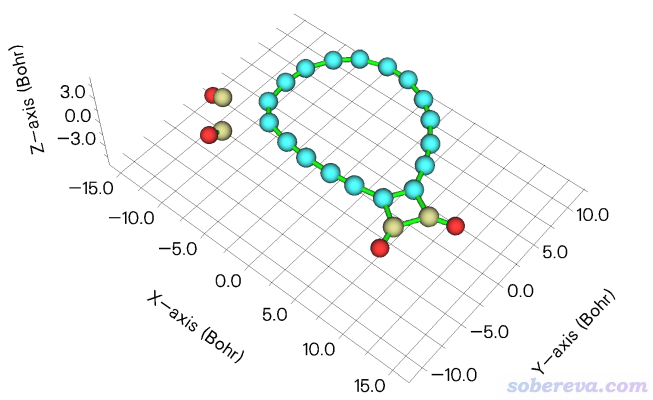
這一節我們對上圖中青色標注的碳環區域計算孔洞半徑,也相當于環的最大內徑。由于這個環的形狀非常不規矩,不用本文介紹的Multiwfn的功能的話是很難準確得到內徑的。上圖中青色的原子是1到18號原子。
啟動Multiwfn然后輸入
C18-(CO)4_TS.xyz
cav
1-18 //用碳環部分的原子判斷接觸以確定球的半徑
1 //使用上面輸入的那些原子的幾何中心作為球心初始位置
5 //只允許在XY方向調節球心位置(由于球心在Z方向不斷向上或向下移動過程中都會導致球的半徑越來越大,因此這里故意不讓球心自動在Z方向調節)
得到的孔洞直徑是2.974埃。還是按照前面的例子,在VMD里載入體系結構并用Multiwfn給出的命令畫出孔洞示意圖,如下所示,可見結果很合理。
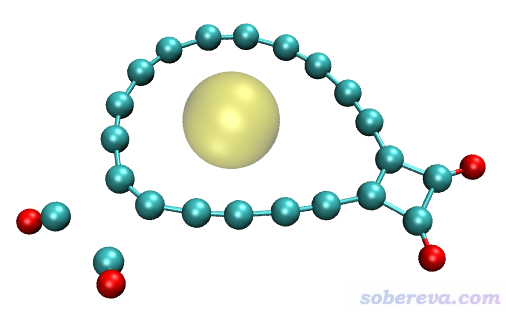
3.4 例4:計算MIL125晶體的孔洞直徑
本文文件包里MIL125.cif是MIL125的晶體結構文件。MIL125是一種基于Ti的MOF體系,有較大的孔洞,其結構如下所示
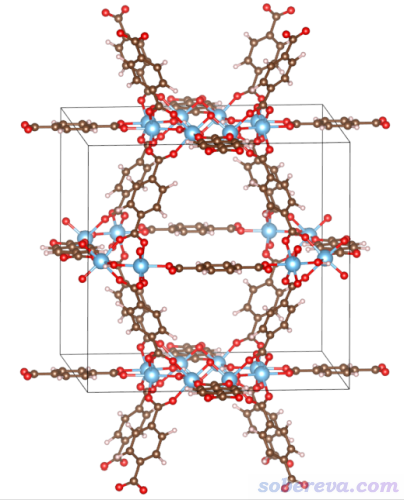
下面我們來計算它中心區域的孔洞。
啟動Multiwfn,然后輸入
MIL125.cif
cav
[按回車] //用體系里所有原子檢測接觸以確定球半徑
3 //使用晶胞中心作為球心初始位置
1 //允許球心位置做調整
從屏幕上的提示可見球心位置的調整僅1輪迭代就收斂了,相當于沒做調整。這是因為當前晶體里原子位置是相對于晶胞中心對稱的,而且恰好晶胞正中心正是最大孔洞的中心。屏幕上顯示的孔洞直徑為12.442埃。
之后在VMD里把描繪孔洞的圓球顯示出來,這里有一些細節需要注意。VMD,起碼是筆者目前用的1.9.3版,不支持載入cif文件,因此必須轉成VMD可以支持的格式。另外,即便轉換成能記錄晶胞信息的pdb格式,VMD自己也不支持顯示出位于邊界的原子的周期鏡像,因此邊緣如同缺了原子,顯得不太美觀。好在Multiwfn不僅可以用來把cif轉成pdb格式,同時還支持把邊界原子的鏡像原子添加到體系中,從而能讓VMD顯示出來,下面就演示一下。
返回Multiwfn的主菜單,然后進入主功能300的子功能7,選擇選項27,屏幕上顯示加入了64個邊界原子,之后進選項0在圖形界面里預覽一下,可以看到沒問題。關閉圖形窗口后,再選-2將當前結構導出為pdb文件。導出的MIL125.pdb文件在本文的文件包里已經提供了。
將MIL125.pdb載入VMD,然后在文本窗口輸入pbc box把晶胞邊框顯示出來,再輸入以下計算孔洞后Multiwfn在屏幕上提示的命令
color Display Background white
draw material Transparent
draw color yellow
draw sphere { 9.462 9.462 8.978 } radius 6.221 resolution 100
再把顯示方式設成Licorice,并把Bond Radius改為0.1,再在VMD Main窗口里選Display - Orthographic用正交視角后,看到的圖像如下,可見清楚地將MIL125中心的孔洞展現了出來
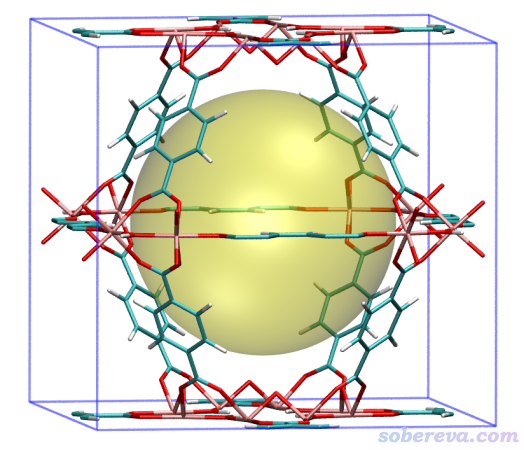
一個晶體里可能有不止一種類型的孔洞,直徑也有所不同。MIL125這個體系中雖然只有一種孔洞,但晶胞里各個角落實際上也都是孔洞的一部分。這里再演示一下怎么把MIL125邊角的孔洞進行計算和繪制。
啟動Multiwfn,然后輸入
MIL125.cif
cav
[按回車] //用體系里所有原子檢測接觸以確定球半徑
4 //手動輸入初始球心位置的分數坐標
0,0,0 //考察中心位于分數坐標(0,0,0)的孔洞
1 //允許球心位置做調整
這次得到的孔洞直徑還是12.442埃,而這回球心位于(0,0,0)。然后,重復上面的步驟進行繪制,看到下圖,可見清楚地把邊角位置的孔洞展現了出來。這里把坐標軸也顯示了出來,紅、綠、藍分別對應X、Y、Z方向
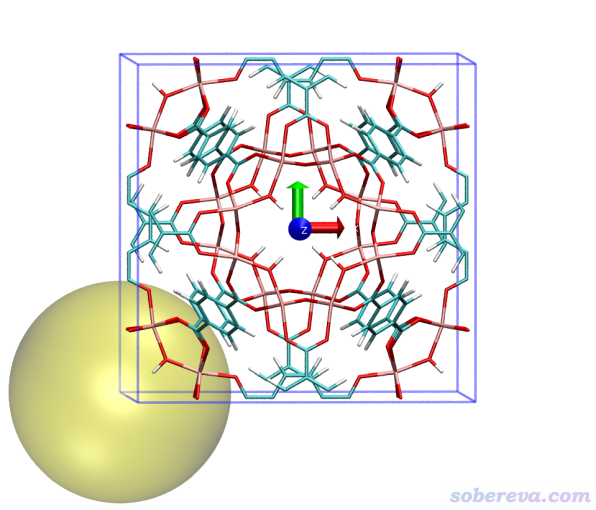
讀者若想同時繪制多個孔洞當然也可以。每次給Multiwfn提供不同的球心初始位置,得到繪制不同球心所用的VMD的繪圖命令,然后依次使用即可。繪制不同類型的孔洞前,還可以把draw color yellow里的顏色改成其它的,從而通過顏色區分不同類型的孔洞。
4 其它
有一些用戶問,為什么他算出來的孔洞半徑是負值,為什么用Multiwfn給的命令在VMD里畫不出圓球來。這明顯都是對本文介紹的方法的原理缺乏理解,而且頭腦里也沒有范德華半徑的基本概念所致。
比如對下圖左圖所示的環己烷,就明顯不能用本文的功能計算其中的孔洞直徑。進入Multiwfn主功能0后,把Ratio of atomic size設為4.0時,原子球半徑就等于范德華半徑,對應的圖就是下圖的右圖。可見,環己烷中間區域根本沒有空白,顯然沒法計算孔洞直徑。